Putting Chaos into Perspective: Evaluation of Statistical Test Suite

Implementations on Isolated Sequences of Arbitrary Length

Pol H

olzmer

, Manuel Koschuch

and Matthias Hudler

Competence Centre for IT Security, University of Applied Sciences FH Campus Wien, Vienna, Austria

Keywords:

Statistical Randomness Tests, NIST SP 800-22, Open Source, Binary Classiﬁer, Randomness-as-a-Feature.

Abstract:

Randomness is ambiguously deﬁned as the absence of structure, whereby reliable generation and evaluation

thereof imposes a complex problem. Efforts have been made to quantify randomness by developing random-

ness test suites as aggregation of selected statistical methods. This study aims to evaluate caveats developers

may encounter employing such methods, and compares the application of randomness test suites for arbi-

trary data to evaluate features of randomness. Therefore, an initial set of three open-source Python-based

implementations of the NIST SP 800-22 test suite have been analyzed and compared. The results indicate

no ”one-size-ﬁts-all” approach when assessing randomness; instead, it demonstrates how deviations between

speciﬁcation and implementation can lead to inaccurate results and erroneous conclusions about randomness.

1 INTRODUCTION

The concept of randomness is complex and counter-

intuitive, as it is by its very deﬁnition the absence of

structure or any predictability. Consider the follow-

ing sentence as an introductory example: ”A quick

brown fox jumps over the lazy dog!” and the question

of this 42 Byte isolated sequence being ”random” or

not. Given the human instinct, trained to look for pat-

terns, probably none would consider this sequence to

be ”random”. Nevertheless, common statistical meth-

ods and specialized test suites classify this sequence

as such (as we will also show in Section 5). This prob-

lem raises the question of how such methods perform

and for which application areas they are suitable be-

sides the evaluation of random number generators.

A variety of statistical methods exist to evaluate

randomness, which all have their own properties and

limitations. Statistical methods are often combined

into test suites to compensate for limitations by look-

ing at multiple results more broadly. In principle, a

sequence to be tested can represent any form of a data

stream. This includes more or less structured data,

such as TXT, DOC, PDF, over encrypted data, such as

XOR, RC4, AES, up to ”random” data generated by

Pseudo (PRNG) or True Random Number Generators

https://orcid.org/0000-0001-9046-7963

https://orcid.org/0000-0001-8090-3784

https://orcid.org/0000-0003-4879-018X

(TRNG). Knowledge of the data structure is required

to be able to process data. Ultimately, it all comes

down to a binary sequence as the only accurate rep-

resentation for any given data stream in information

systems, which may be considered chaos by humans

unable to (efﬁciently) process binary data.

The Python programming language was the pri-

mary tool used in this project. Compared to C, Python

is not the most efﬁcient language, yet it has become

a tool that has found great acceptance in many areas,

as in the ﬁeld of data science, where it is in no way

inferior to its colleagues R or Matlab. Even embed-

ded systems can beneﬁt from this popularity by us-

ing a subset of the Python standard library, called Mi-

croPython. Python has a large community that pro-

duces Free and Open Source Software (FOSS) on a

daily basis. However, FOSS is not automatically a

seal of quality. FOSS makes up a large share of the

tools used daily in many different domains. Major

projects have immense community support and are

usually well maintained, but minor personal projects

also exist. When browsing for tools, frameworks, or

packages, users usually install blindly, using package

managers, without looking at the code. Thus, one en-

joys the beneﬁt of a black-box that is easy to install,

always at hand, and implements all the desired func-

tions. Theory and practice are often far apart, and dif-

ferent implementations of the exact speciﬁcation op-

timally have identical results, even though a different

approach has been employed to reach a given state.

258

Hölzmer, P., Koschuch, M. and Hudler, M.

Putting Chaos into Perspective: Evaluation of Statistical Test Suite Implementations on Isolated Sequences of Arbitrary Length.

DOI: 10.5220/0011087400003194

In Proceedings of the 7th International Conference on Internet of Things, Big Data and Security (IoTBDS 2022), pages 258-266

ISBN: 978-989-758-564-7; ISSN: 2184-4976

 2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reser ved

1.1 Problem Statement

In a recent, yet unrelated, project using Tensorﬂow to

work with machine learning (or pattern recognition),

the assessment of randomness (or absence of any pat-

tern) was required as a feature of the employed model.

During this project, the question arose of how to col-

lect and use this property from arbitrary data to im-

prove the learning curve with measurement and to sort

by the amount of ”structure” supporting further devel-

opment. A cursory glance at Github looking for ran-

domness tests in Python revealed several projects im-

plementing well-established randomness test-suites.

However, the initially selected open-source imple-

mentation of a randomness test suite produced results

that could only be described as ”random” at the time,

mainly due to the rather short sequences tested. Fur-

ther comparisons and evaluations revealed noticeable

differences in the results of different implementations

of the same test suite. These ﬁndings raised funda-

mental questions about how developers should deal

with these problems, so these points were pursued,

deepened, and addressed in this work.

With this work, we want to provide the ﬁrst indi-

cators for developers on how to approach the prob-

lem of classifying an isolated sequences of arbitrary

length. In this context, an isolated sequence is deﬁned

as any stream of bits, which is evaluated without any

context besides the sequence length and ”amount of

structure” derived from statistical test results. While

this paper focuses on comparing speciﬁc implemen-

tations to identify problem areas, it does not aim to

evaluate the statistical methods but rather the difﬁcul-

ties developers face in implementing and using such.

1.2 Related Work

To the best of our knowledge, there are currently

no publications dealing with the practical problems

of evaluating the quality of open-source implementa-

tions of randomness test suites, focusing on the ap-

plications of diverse datasets and arbitrary length se-

quences to extract features of randomness.

Beside others, (Bastos et al., 2019; Parisot et al.,

2021; Popereshnyak and Raichev, 2021) et al. fo-

cus on the originally intended application of random-

ness test suites to evaluate and select random num-

ber generators. (Zia et al., 2022; Poojari et al., 2021;

Gao et al., 2022) et al. are trying to design new en-

tropy sources focusing on the constraint Internet of

Things (IoT). Others, are specialized in the evalua-

tion of short sequences based on block cipher (Sulak

et al., 2010), or specialized in the randomness of cryp-

tographic function mappings (Kaminsky, 2019).

However, none of them question the way on how

those evaluated randomness properties could be con-

sidered as a staggering feature. So with this work,

we want to make the ﬁrst steps towards addressing

this gap, not from a purely mathematical or statistical

but more of an ”expert in other areas” point of view.

This work focuses on applying (black box) statisti-

cal randomness test to extract features of randomness

by ”amount of structure”. This work evaluates struc-

ture as the opposite of randomness and addresses how

much data is required for an isolated sequence to de-

tect structure and dissolve chaos, which may be pro-

vided to data type classiﬁers as features.

2 BACKGROUND

2.1 Randomness

The analogy of the ”unbiased (fair) coin” is one at-

tempt to describe randomness that is easy to follow.

It assumes that elements can be generated in a se-

quence of evenly distributed values by tossing an un-

biased coin with sides labeled with values ”1” or ”0”.

Thereby, each coin ﬂip is independent of one another

and has a probability of 50% of producing a ”1” or

”0” (Bassham et al., 2010). Consequently, such a se-

quence has no structure that allows for prediction or

correlation. The concept of randomness may be re-

jected in philosophy and religion, where the concept

of fate is believed in. In cryptography, on the other

hand, there is no use for fate but in predictability

and probability instead. Random data can be gener-

ated using random number generators (RNG), which

come in two primary forms: Pseudo-RNG (PRNG)

and True-RNG (TRNG) (or simply RNG). A TRNG

gains randomness from non-deterministic physical

phenomena such as the LavaRand (Cloudﬂare, 2017)

or atmospheric noise (Haahr, 2018). PRNG uses a

deterministic algorithm that is fed some input values,

often deﬁned by a seed value. These types of RNG

are fast but can produce weak randomness if either

the algorithm is weak, the seed is known, or if enough

data has been collected so that the probability of pre-

dictability increases. Compared to TRNG, a PRNG

does not generate randomness, but chaos, which a

(non-linear) formula can model. Typically intersec-

tions of the two are used to create a usable Crypto-

graphically Secure PRNG (CSPRNG) that uses phys-

ical phenomena to create a source pool with high en-

tropy that serves as input to a robust algorithm that

generates an arbitrary amount of random data that is

unpredictable, no matter how much data was gener-

ated by the CSPRNG (Cloudﬂare, 2017).

Putting Chaos into Perspective: Evaluation of Statistical Test Suite Implementations on Isolated Sequences of Arbitrary Length

259

2.2 Statistics

Statistical tests are formulated to test the null hypoth-

esis (H0) that a given test sequence is random, in con-

junction with the alternative hypothesis (Ha) that the

sequence is not random. For each applied test, a deci-

sion is derived that accepts or rejects the null hypoth-

esis (Bassham et al., 2010). Since statistical methods

have their strengths and weaknesses, different meth-

ods are combined in test suites, which are all unique

in scope and application:

• Diehard: Published in 1996, this suite provides

a battery of 12 statistical tests for measuring the

quality of RNG. There is an improved variant

called Dieharder in native C, which, i.a., extends

the list of tests to 26. (Marsaglia, 1995; Robert

G. Brown, 2003)

• ENT: Statistical test for command-line applica-

tion released in 1998, which uses ﬁve tests to de-

tect the basic characteristics of random sequences

including Entropy, Chi-Square, and Arithmetic

Mean. (Walker, 1998)

• NIST SP 800-22: Originally released in 2001, the

NIST Special Publication 800-22 Rev. 1a pro-

vides 15 tests to evaluate the randomness of ar-

bitrary long binary sequences. The publication is

currently under review as of July 2021. (Bassham

et al., 2010)

• TestU01: Software library implemented in ANSI

C that offers a collection of 7 tests for the empir-

ical statistical testing of uniform RNG. (L’Ecuyer

and Simard, 2007)

3 RESEARCH DESIGN

This study evaluates the performance and quality of

a given set of randomness test suite implementations

through a quantitative and qualitative case study. Due

to the reputation, the number of tests, and availability

of implementations in Python, the National Institute

of Standards and Technology’s (NIST) Special Pub-

lication (SP) 800-22 (Bassham et al., 2010) was cho-

sen for the one randomness test suite to be used here.

This test suite provides the basis for all analyses, re-

sults, and conclusions drawn for arbitrary data and use

cases. We do not evaluate the NIST SP 800-22 it-self,

but open source implementations thereof. The NIST

SP 800-22 contains a set of 15 statistical tests. The

NIST recommends a minimum input sizes and addi-

tional prerequisites and conditions for each of these

tests to ensure the reliability, which will become an

important factor for our evaluation. Therefore, it has

to be noted that only at an input size of 1 Mbit all

15 randomness tests forming the test suite may be in-

cluded in the evaluation. The following list shows the

NIST SP 800-22 test battery and their recommended

minimum input size:

1. Frequency (aka. Monobit) Test 100 bit

2. Frequency within a Block Test 100 bit

3. Runs Test 100 bit

4. Longest-Run-of-Ones in a Block 128 bit

5. Binary Matrix Rank Test 38,912 bit

6. Discrete Fourier Transform Test 1,000 bit

7. Non-overlapping Template Matching

1 bit

8. Overlapping Template Matching 1,000,000 bit

9. Maurer’s ”Universal Stat.” Test 387,840 bit

10. Linear Complexity Test 1,000,000 bit

11. Serial Test 1 bit

12. Approximate Entropy Test 1 bit

13. Cumulative Sums Test 100 bit

14. Random Excursions Test 1,000,000 bit

15. Random Excursions Variant Test 1,000,000 bit

4 METHODS

The general methodology consists of three phases:

1. Determining a variety of NIST SP 800-22 test

suite implementations.

2. Generating appropriate datasets used for testing,

validation and results.

3. Preparing a common interface and validation

framework for automated tests.

4.1 Implementations

A set of three Python-based FOSS implementations

has been selected. A naming convention for the im-

plementations based on the authors’ initials is here-

after introduced to have a uniform way of identiﬁca-

tion; also, a color pattern is used to ease the interpre-

tation of the results and related graphs.

It is very important for us to emphasize that this

analysis is in no way intended to criticize or belit-

tle the listed implementations in any way. Providing

FOSS is hard work, and any comments in this work

should be considered constructive feedback and may

be used to improve the implementation. Any claim we

make has been validated to the best of our knowledge

and may not be covered by intentional use cases.

Additional eligibility checks apply

Features non-deterministic characteristics

IoTBDS 2022 - 7th International Conference on Internet of Things, Big Data and Security

260

• DJ aka. dj-on-github/sp800 22 tests (Johnston,

2017) (114 stars, 29 forks): The earliest im-

plementation in the list was created by David

Johnston, Engineer at Intel and author of ”Ran-

dom Number Generators, Principles and Prac-

tices” (Johnston, 2018). This implementation is

”simplistic” in terms of coding concepts.

• LP aka. InsaneMonster/NistRng (Pasqualini,

2019) (18 stars, 8 forks): This work by Luca

Pasqualini (SAILab) from the University of Siena

is inspired by the work of David Johnston. The

implementation is the ”most advanced” in terms

of coding concepts and is available as pip pack-

age thus, it is the most convenient to use and was

the starting point for this work.

• SA aka. stevenang/randomness testsuite (Ang,

2018) (50 stars, 12 forks): The Independent in

Comparison, implemented by Steven Kho Ang.

This implementation is characterised by the pro-

vision of an additional graphical user interface.

4.2 Datasets

This work is not focused on evaluating a single source

of data of a given length. Instead, results are acquired

by feeding data to each implementation and validating

the number of passed tests in relation to input length,

which results in a two-dimensional representation per

implementation with input length on the x-axis, and

the sum of S-values or P-values on the y-axis. But

there is also a z-axis, by means of different datasets,

which are staggered by the amount of expected ”struc-

ture”. Employed datasets are large blobs with more

than 100 MB of data of a common ”language” from

which at random a sample is extracted for a speciﬁc

test run. The datasets are chosen to cover all interest-

ing cases, not to focus on any speciﬁc scenario; there-

fore, the datasets are introduced without greater gen-

eration details. Depending on the generation process,

employed datasets are categorized into classes: ran-

dom, cipher, or encoding. Finally, the datasets are or-

dered as listed from expected ”randomness” to ”struc-

ture”. Many different types of data may be, and have

been, compared using our method. This list reﬂects

only a small selection of data sets with noteworthy at-

tributes spanning over the whole spectrum:

1. RND: ”True” randomness acquired via

RANDOM.ORG (Haahr, 2018) gained from

atmospheric noise, as the epitome of randomness.

2. DES: Weak block cipher in ECB mode using a

weak key to add structural distortion compared to

other cipher-modes, generated with OpenSSL.

3. ZIP: File archive of the aclImdb (Maas et al.,

2011) dataset to evaluate the amount of chaos in-

troduced by compression.

4. TXT: English text consisting of printable-ASCII,

based on a large movie review dataset (Maas et al.,

2011), which is further used as basis for genera-

tion of the DES, and ZIP datasets.

5. NUL: Straight binary sequence of all zeros (Null-

Bytes) which together with the all-ones sequence

can be argued as the epitome of structure.

4.3 Framework

A custom framework has been developed to overcome

considerable differences in how each implementation

handles inputs and provides output. These differences

make it cumbersome to operate and to compare the re-

sults manually. For this reason, a common interface

was designed for all implementations, and wrapper

functions were developed to enable large-scale auto-

matic tests to be carried out. This interface was then

embedded into custom applications based on Jupyter

notebooks, providing the easy-to-use ability to bench-

mark, plot, and analyze implementation characteris-

tics like quality and time. The open-source Python li-

braries pandas (McKinney et al., 2010; Pandas Devel-

opment Team, 2020) and matplotlib (Hunter, 2007)

were of priceless help here.

All randomness tests return one straightforward

metric, namely the probability, or P-value in short,

in the range of zero to one, which summarizes the

strength of the evidence against the null hypothesis.

Tests are then run against a decision rule based on a

signiﬁcance level of 10% for each test in the SP 800-

22 test suite, which means that any input for which

a test returns a P-value above the decision mark is

considered to be random by passing the test, with

a P-value of 1 stating perfect randomness. The re-

sult of this comparison is hereafter deﬁned as S-Value

(Success-Value). Some tests may have lower signif-

icance levels or additional checks for a positive S-

Value. This work mainly focuses on S-Values as

Key Performance Indicators (KPI) to ease compar-

isons over the whole spectrum, rather than gathering

enough P-Values for generic P-Graphs. P-Values are

suitable for evaluating data sources by generating vast

amounts of data while being too volatile to evaluate

isolated sequences, as can be seen in Figure 2.

The test spectrum covers different scenarios in

which the test suite may be applied, including the

number of tests, the quality of the results, and the cal-

culation speed in relation to different data lengths to

be tested. One would think the number of tests is al-

ways the same when using only the same test suite,

Putting Chaos into Perspective: Evaluation of Statistical Test Suite Implementations on Isolated Sequences of Arbitrary Length

261

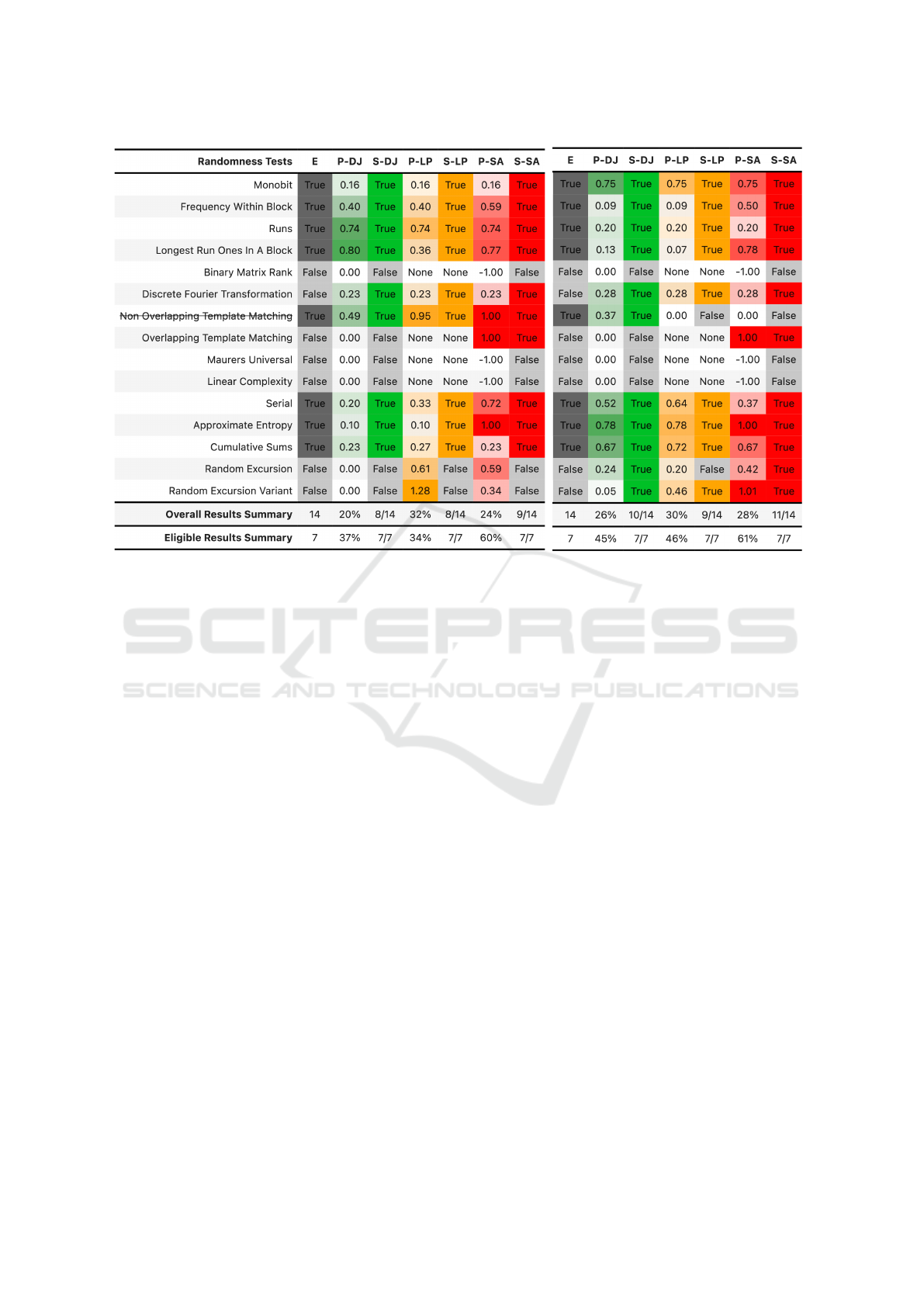
(a) 42B Pangram (TXT dataset) from the introductory Example.

(b) 42B Sample from the RND dataset.

Figure 1: [P]robability and [S]uccess Calculation for [E]ligible NIST SP 800-22 Tests.

yet not all tests are applicable for all input lengths or

may have other preconditions, as shown in the list of

the statistical tests involved. The input length is an

essential factor, as different use cases rely on shorter

or longer sequences of data, while the test suite it-

self is claimed to be applicable for an arbitrary length

of data; a given implementation may score differently

in some scenarios where the different length of se-

quences of the same data set are fed. Finally, the

speed of calculation, which naturally increases with

the number of tests and input length, is an important

factor that is not always tolerable. The growth is lin-

ear with occasional jumps, depending on how many

tests are effectively applied at a given length. For ex-

ample, testing a 128 bit value takes less than a sec-

ond but only runs reliably against 8 out of 15 tests.

On the other hand, to perform all 15 tests reliably, a

minimum length of about 1Mb is required, whereby

such a run takes between one and three minutes (on

high-performance hardware) depending on the imple-

mentation, as later discussed and shown in Table 1.

It should be noted that some implementations do not

respect the input size recommendations for all tests

or do not label the result appropriately to differentiate

between a failed and a non-eligible test. Non-eligible

tests should then be treated as unreliable or advisory,

if at all.

5 ANALYSIS

The selected implementations are analyzed using the

previously deﬁned framework and datasets. In order

to conclude on the deﬁned metrics and scenarios, the

framework has been used to develop multiple appli-

cations in form of Jupyter Notebooks, which focus on

details, average quality, and time for different datasets

and input lengths. With each run of an application, a

given dataset sample is fed to each implementation.

Each run is repeated for an increasing range of sample

length, starting at the same offset of the data source.

Note that a sample would randomly start at a different

offset for any following run, which allows evaluating

how the implementations react to the same input, as

it is fed with more data of the same sequence. The

results are returned as Pandas DataFrames and are

plotted for better visualization. The tools are not yet

publicly available; however, we plan on releasing the

Git repository as well as our entire datasets.

The manual analysis for isolated sequences is not

straightforward. Figure 1a shows the results for the

example pangram from the Introduction, a detailed

example of a single test run is discussed to show what

kind of values the randomness test suites return. Fig-

ure 1b on the other hand, shows the results for a se-

quence from the RND dataset of the same length. It is

IoTBDS 2022 - 7th International Conference on Internet of Things, Big Data and Security

262

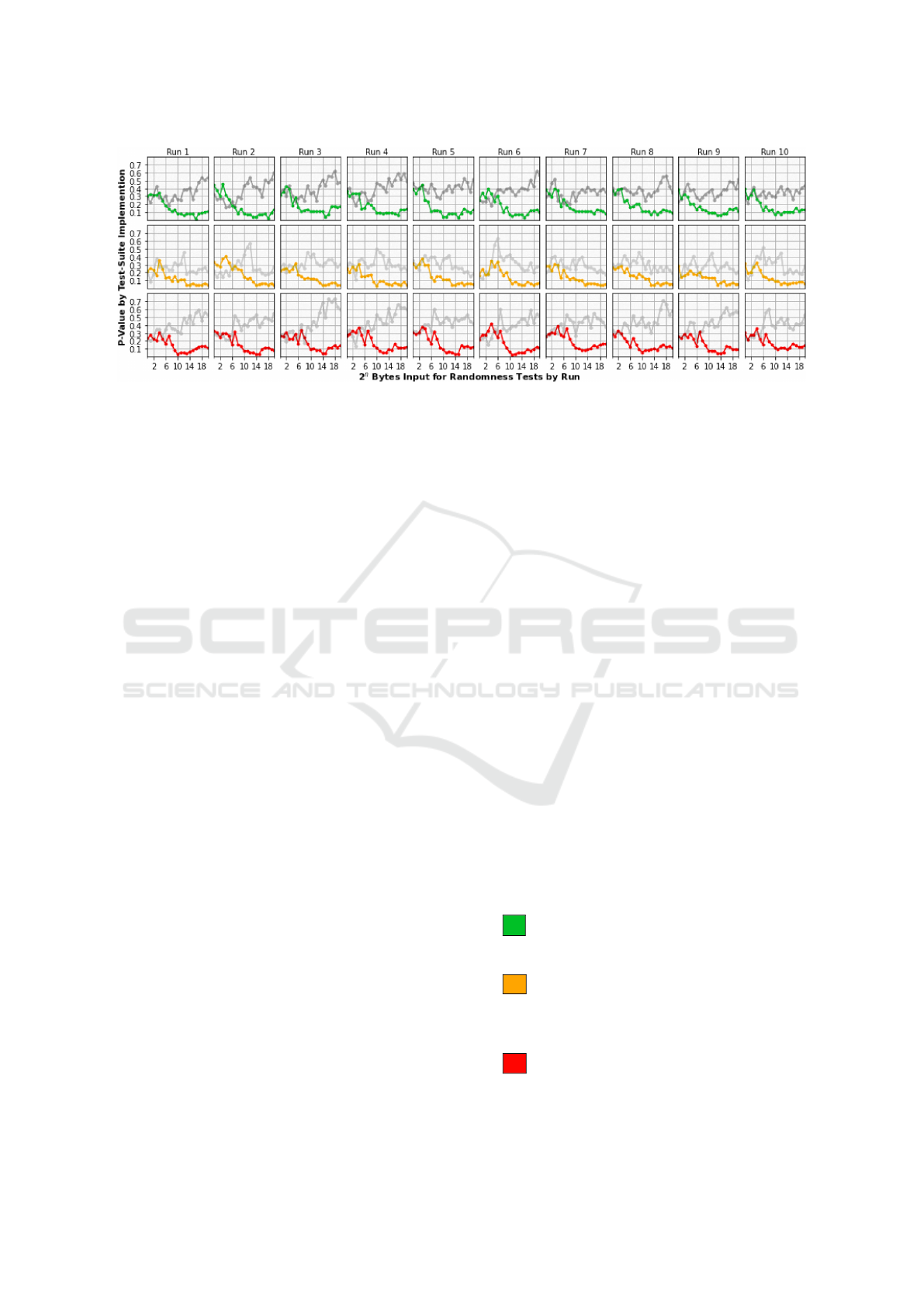
Figure 2: Example Results (P-Value) for the Datasets ”TXT” and ”RNG” (grey overlay) split by Run and Implementation.

intended to show that it is hard to conclude random-

ness, especially for short sequences. Note that these

results are presented as they are returned from the

actual implementations. Although the sum of the P-

values is higher on average for 1b, which is not always

true for other samples of the same dataset, all tests are

passed for 1a too, so that both examples pass all el-

igible randomness tests. P-Values may vary largely,

while S-Values are relatively constant. This fact is vi-

sualized in Figure 2, which shows the average results

of P-Values for applied randomness tests for ten runs

over the three different implementations. The result-

ing P-Values are used to average the test runs for Fig-

ures 4a and 4d in the Appendix. It is intended to show

that the results of both datasets are similar for short

sequences, then start to diverge with larger input se-

quences. Figure 2 reveals similar resulting curves for

the ”TXT” dataset, per run and implementation, while

the curve of the ”RND” dataset has no visible pat-

terns. Note that, with increasing structure, the runs re-

sulting curves feature correlate with a higher degree.

These detailed views are employed for manual

analysis of anomalies within the other tools, which

abstract or summarize these results per run instead

of every test. Some implementations do not dif-

ferentiate between zero and non-applicable (None)

tests. Also, some implementations have slightly dif-

ferent criteria for eligibility that differ from the SP

800-22. Note that the E column denotes all eligible

tests for the given sample data based on the NIST In-

put Size Recommendation (Bassham et al., 2010) and

that the Non-Overlapping Template Matching test is

not taken into consideration for the summary due to

its non-deterministic characteristics. Besides the de-

tailed view, the developed Notebook employs addi-

tional views for time and quality benchmarks, which

will be introduced in the following chapter.

6 RESULTS

For all datasets introduced, benchmarks were per-

formed on time, quality (S-Value), and accuracy (P-

Value). The test results for time can be seen in Ta-

ble 1. The results for accuracy and quality have been

added to the Appendix as Figure 3 and 4, respec-

tively. Each plot is the outcome of the average re-

sults for 100 runs with a maximum of 2

Bytes input

length, which required around 24 hours of calcula-

tion time on an 8-core (16-thread) Intel i9 CPU. The

graphs show the average P-Values and S-Values for

performed runs. Each benchmark run is performed

for n steps using the input size of 2

Bytes, where

n ∈ [0, 20]. The x-axis employs a logarithmic scale. 2

may be considered a minimum, but smaller sequences

are tested for completeness. Benchmark calculations

were threaded to optimize processor performance and

parallelize calculations. Note that the light-grey line

and area in the quality and accuracy plots, denotes the

maximum value that could be reliably achieved for a

given input length. Optimally, the results should not

exceed this line. The results show that the experiment

was successful, yet many points were not as expected.

The main observations, per implementation, are given

in the following list:

• DJ : Overall good results in time and quality. The

code leaves room for performance improvements.

Weaker in the detection of ”true” structure.

• LP : Decent quality but fails for input over 2

Bytes and worst in time. Best in eligibility checks.

Easiest to install and use. Scores have a small

peak at 2

Byte of input.

• SA : Decent quality, but the results are gener-

ally too high, yet the fastest in the set. Behaves

strangely at 2

Byte of input where scores peak.

Putting Chaos into Perspective: Evaluation of Statistical Test Suite Implementations on Isolated Sequences of Arbitrary Length

263

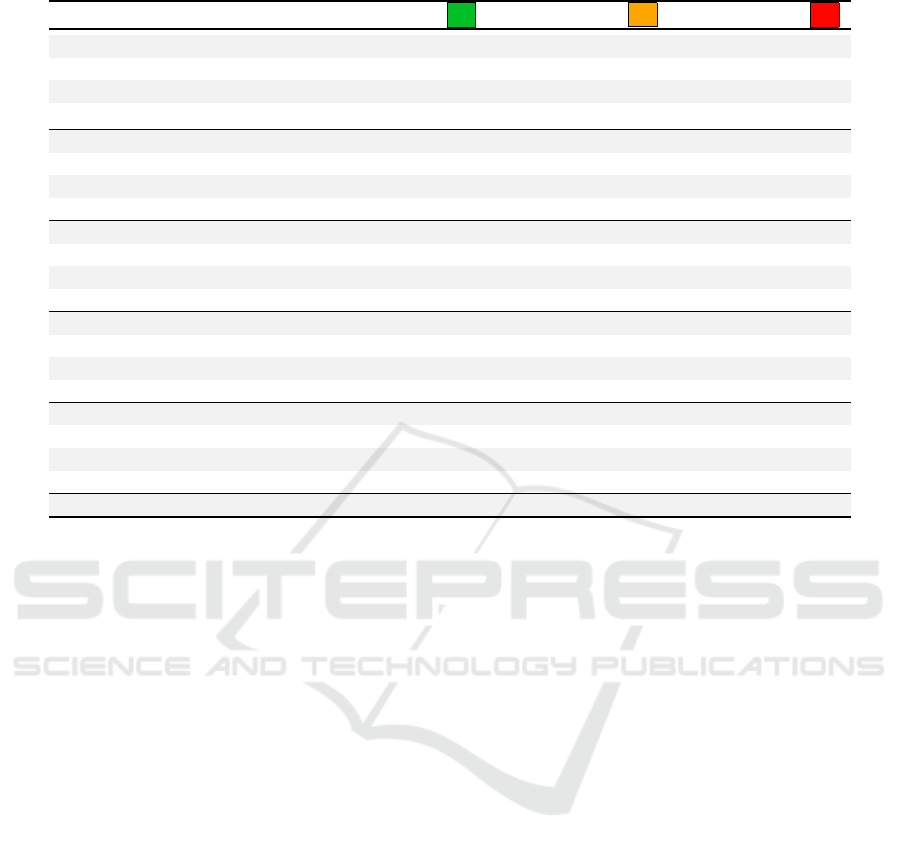
Table 1: Average Results of 10 Runs from 2

to 2

Byte Inputs for Time Calculation.

n 2

Byte 8·2

Bit

0 1 8 189ms 4ms 420ms

1 2 16 179ms 8ms 428ms

2 4 32 181ms 8ms 438ms

3 8 64 185ms 14ms 441ms

4 16 128 170ms 20ms 450ms

5 32 256 170ms 30ms 460ms

6 64 512 190ms 60ms 460ms

7 128 1 Ki 200ms 100ms 500ms

8 256 2 Ki 240ms 200ms 550ms

9 512 4 Ki 320ms 380ms 640ms

10 1 Ki 8 Ki 440ms 740ms 820ms

11 2 Ki 16 Ki 700ms 1s 429ms 1s 159ms

12 4 Ki 32 Ki 1s 189ms 2s 890ms 1s 850ms

13 8 Ki 64 Ki 2s 319ms 5s 950ms 3s 250ms

14 16 Ki 128 Ki 4s 320ms 11s 570ms 5s 960ms

15 32 Ki 256 Ki 8s 439ms 22s 850ms 11s 119ms

16 64 Ki 512 Ki 17s 350ms 48s 299ms 22s 730ms

17 128 Ki 1 Mi 1m 29s 900ms 2m 59s 240ms 43s 840ms

18 256 Ki 2 Mi 2m 57s 569ms 5m 47s 069ms 1m 26s 409ms

19 512 Ki 4 Mi 5m 55s 860ms 11m 31s 600ms 2m 53s 530ms

20 1Mi 8Mi 12m 9s 179ms 23m 21s 910ms 5m 52s 930ms

Our preliminary results are highly context-

dependent and require additional interpretation.

Some of the statistical tests evaluate at bit, byte, or

block level, which favor some structured or chaotic

datasets. Also, the results for inputs smaller than 2

have hardly any signiﬁcance. Finally, the number of

ineligible and, therefore, unreliable tests distort the

results. Full eligibility starts at 1Mbit. Note the dip

in the graphs as the length increases, which indicates

the input length at which the algorithm can recog-

nize structure within the chaos and starts to classify

sequences as being not so random. As expected, the

more structure attributed to the dataset, the further this

dip shifts to the left. In this way, DES in ECB mode

can be detected as no longer random, with a minimum

sample size of about 2

Byte.

Based on the results shown in Table 1, it can

be seen that the implementations strongly differ in

time consumed, where the fastest implementation for

smaller input became the slowest by a factor of four

for larger inputs. This fact is related to implemen-

tation differences, preliminary eligibility tests, and

thus the number of tests that are only ”unlocked” with

larger input. Python may not be committed to perfor-

mance, but the implementations would beneﬁt from it,

which could be achieved by multi-threading or by use

of the Python libraries NumPy in combination with

Numba just-in-time (jit) compilation to maximize par-

allel computing and efﬁciency. In addition, Numba

also provides CUDA support for the use of NVIDIA

Graphics Processing Units (GPU).

7 CONCLUSION

It can be concluded that the NIST SP 800-22 is only

partially suited to extract features of randomness from

isolated sequences and requires a lot of data to per-

form at full scale. For this, the calculations are too

computationally intensive to be applied to larger data

sets. Therefore, results for short sequences of 2

Bytes (1,024 bit) or less are hardly meaningful. We

also could show that the compared implementations

differ in results, although they implement the same

speciﬁcation, which should produce almost identical

results, highlighting the importance for developers to

be careful on selecting test suite implementations for

evaluation of RNGs or similar.

Future Work will show how to incorporate the re-

sults into applications to acquire better randomness

feature extraction by interpreting the relation between

input length, dataset, and the actual P-Values (or even

values of the tests internal state) to achieve better

accuracy using only KPIs while respecting a given

context. Until then, we mainly gain from these ﬁrst

results that developers looking for easy and reliable

ways to check for the randomness of a given solu-

tion should be careful when interpreting the results

IoTBDS 2022 - 7th International Conference on Internet of Things, Big Data and Security

264

of open-source implementations of randomness test

suites. Always take them with reservations, when in

doubt, use multiple different implementations or test

suites to get a holistic picture.

REFERENCES

Ang, S. K. (2018). stevenang/randomness testsuite. https:

//github.com/stevenang/randomness\ testsuite.

Bassham, L. E., Rukhin, A. L., Soto, J., Nechvatal, J. R.,

Smid, M. E., Barker, E. B., Leigh, S. D., Levenson,

M., Vangel, M., Banks, D. L., Heckert, N. A., Dray,

J. F., and Vo, S. (2010). Nist sp 800-22 rev. 1a. a statis-

tical test suite for random and pseudorandom number

generators for cryptographic applications.

Bastos, D. C., Kowada, L. A. B., and Machado, R. C. S.

(2019). Measuring randomness in iot products. In

2019 II Workshop on Metrology for Industry 4.0 and

IoT (MetroInd4.0 IoT), pages 466–470.

Cloudﬂare (2017). Lavarand in production: The nitty-

gritty technical details. https://blog.cloudﬂare.com/

lavarand-in-production-the-nitty-gritty-technical-details/.

Accessed: 2021-12-27.

Gao, B., Lin, B., Li, X., Tang, J., Qian, H., and Wu, H.

(2022). A uniﬁed puf and trng design based on 40-nm

rram with high entropy and robustness for iot security.

IEEE Transactions on Electron Devices.

Haahr, M. (1998–2018). RANDOM.ORG: true random

numbers. https://www.random.org. Accessed: 2021-

12-24.

Hunter, J. D. (2007). Matplotlib: A 2d graphics environ-

ment. Computing in Science & Engineering, (3):90–

95.

Johnston, D. (2017). dj-on-github/sp800 22 tests. https:

//github.com/dj-on-github/sp800\ 22\ tests.

Johnston, D. (2018). Random Number Genera-

tors—Principles and Practices: A Guide for Engi-

neers and Programmers. De—G Press.

Kaminsky, A. (2019). Testing the randomness of cryp-

tographic function mappings. IACR Cryptol. ePrint

Arch., 2019:78.

L’Ecuyer, P. and Simard, R. (2007). Testu01: A c library for

empirical testing of random number generators acm

transactions on mathematical software. http://simul.

iro.umontreal.ca/testu01/tu01.html. Accessed: 2021-

12-27.

Maas, A. L., Daly, R. E., Pham, P. T., Huang, D., Ng, A. Y.,

and Potts, C. (2011). Learning word vectors for sen-

timent analysis. In Proceedings of the 49th Annual

Meeting of the Association for Computational Lin-

guistics: Human Language Technologies, pages 142–

150, Portland, Oregon, USA. Association for Compu-

tational Linguistics.

Marsaglia, G. (1995). The marsaglia random number cdrom

including the diehard battery of tests of randomness.

https://www.stat.fsu.edu/pub/diehard.

McKinney, W. et al. (2010). Data structures for statistical

computing in python. pages 51–56.

Pandas Development Team (2020). pandas-dev/pandas:

Pandas.

Parisot, A., Bento, L. M. S., and Machado, R. C. S.

(2021). Testing and selecting lightweight pseudo-

random number generators for iot devices. In 2021

IEEE International Workshop on Metrology for Indus-

try 4.0 IoT (MetroInd4.0 IoT), pages 715–720.

Pasqualini, L. (2019). Insanemonster/nistrng. https://

github.com/InsaneMonster/NistRng.

Poojari, A., Nagesh, H., et al. (2021). Fpga implementation

of random number generator using lfsr and scrambling

algorithm for lightweight cryptography. International

Journal of Applied Science and Engineering, 18(6):1–

Popereshnyak, S. and Raichev, A. (2021). The development

and testing of lightweight pseudorandom number gen-

erators. In 2021 IEEE 16th International Conference

on Computer Sciences and Information Technologies

(CSIT), volume 2, pages 137–140.

Robert G. Brown, Dirk Eddelbuettel, D. B. (2003).

Dieharder: A random number test suite. http://

webhome.phy.duke.edu/

∼

rgb/General/dieharder.php.

Accessed: 2021-12-27.

Sulak, F., Do

ganaksoy, A., Ege, B., and Koc¸ak, O. (2010).

Evaluation of randomness test results for short se-

quences. pages 309–319.

Walker, J. (1998). Dieharder: A random number test suite.

https://www.fourmilab.ch/random/. Accessed: 2021-

12-27.

Zia, U., McCartney, M., Scotney, B., Martinez, J., and Saj-

jad, A. (2022). A novel pseudo-random number gen-

erator for iot based on a coupled map lattice system

using the generalised symmetric map. SN Applied Sci-

ences, 4(2):1–17.

APPENDIX

Benchmark Environment

• CPU: i9-9980HK

• macOS: 12.1.1

• Python: 3.8.12

• Jupyter-lab: 3.2.1

• Pandas: 1.3.1

• Matplotlib: 3.3.4

Benchmark Quality

See Figures 3 and 4.

Putting Chaos into Perspective: Evaluation of Statistical Test Suite Implementations on Isolated Sequences of Arbitrary Length

265

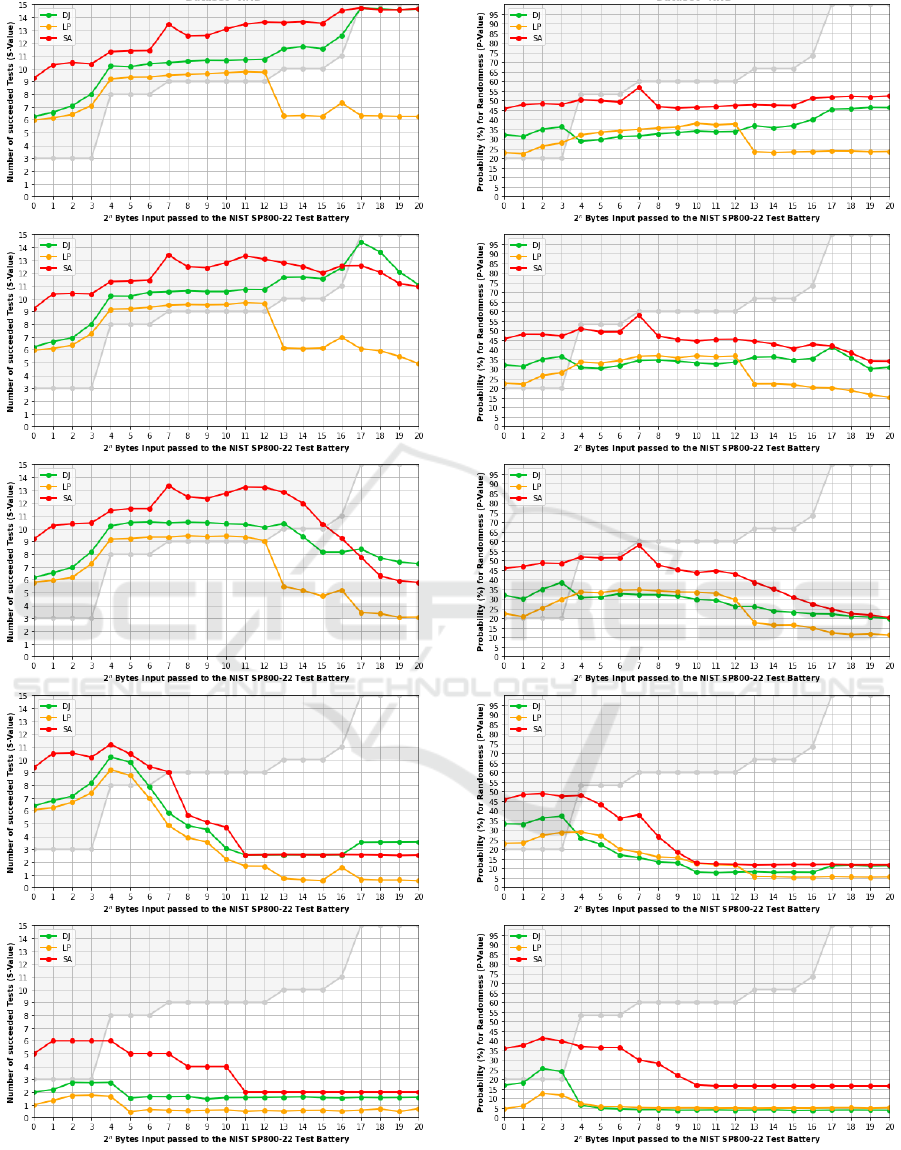
(a) Results (S-Value) for Dataset ”RND”.

(b) Results (S-Value) for Dataset ”DES”.

(d) Results (S-Value) for Dataset ”TXT”.

(e) Results (S-Value) for Dataset ”NUL”.

Figure 3: Average Succeeded Randomness tests of 100

Runs per Dataset with Inputs of Length from 2

to 2

Byte.

(a) Results (P-Value) for Dataset ”RND”.

(b) Results (P-Value) for Dataset ”DES”.

(d) Results (P-Value) for Dataset ”TXT”.

(e) Results (P-Value) for Dataset ”NUL”.

Figure 4: Average Probability for Randomness of 100

Runs per Dataset with Inputs of Length from 2

to 2

Byte.

IoTBDS 2022 - 7th International Conference on Internet of Things, Big Data and Security

266