
LMI Stability Condition for NCS with Packet
Delay and Event-triggered Control
M. Sami Fadali
EBME Department, University of Nevada, Reno, NV 89557, U.S.A.
Keywords: Networked Control, Stability, Packet Delay, Linear Matrix Inequality (LMI).
Abstract: This paper presents a controller design for networked control systems (NCS) with packet delay and event-
triggered control. The total network delay is assumed to be an integer multiple of a fixed sampling period so
that the overall system is time-varying with each model depending on the number of time delays. The design
methodology is applicable to an arbitrary number of packet delays, regardless of whether the delays are
random or deterministic. The methodology is applied to a simple example and Monte Carlo simulation results
show that the controller stabilizes the NCS and is robust with respect to random variations in the sampling
period and to changes in the probability of packet delays.
1 INTRODUCTION
Networked control systems (NCS) are control
systems where the controller receives information
from the plant and delivers control commands to the
actuator through a communication network (Antaklis,
et al., 2007; Li, et al., 2015). The shared network
connection between different components of the
control loop yields a flexible architecture and reduced
installation and maintenance costs (Hespanha, et al,
2007)0. With limited network resources, in many
applications it is beneficial to reduce the load on the
network by using event-triggered control (Yang,
2006), (Ge et al., 2021), (Lemmon, 2010). Control
actions are not updated unless this is warranted to
maintain satisfactory operation of the control system
and the need to relay information to the network from
a remote controller during periods where the current
control is satisfactory is eliminated.
With event-triggered control or with packet delay,
the interval between updates of the control signal
varies. This variation results in a system that switches
between different plant models with each model
corresponding to the interval between the last and
current control update. Switching requires careful
design to ensure that the switched system remains
stable and perform satisfactorily.
Although there are multiple results in the
literature for the stability analysis and design of linear
NCS (Garcia et al., 2014), there is still a need for a
simple design approach that yields a time-varying
controller that can handle arbitrary packet delays. We
exploit a well-known result for the stabilization of
linear parameter-varying systems (Pandey et al., 2017)
to design a time-varying controller for NCS with
arbitrary packet delays. Although the result was
intended for the design of gain scheduled control
systems, a special case of the result allows us to
exploit it for the design of NCS. The NCS model is
adopted from (Montestruque and Antaklis, 2004).
The resulting controller stabilizes the NCS regardless
of the switching regime between the models
corresponding to different packet delays. The
controller is obtained by solving a set of linear matrix
inequalities (LMIs). The number of inequalities
solved for the controller depends on the maximum
number of consecutive packet delays assumed for the
design.
An example is provided to demonstrate the
control system design. Simulation results show that
the design stabilizes the NCS regardless of the
switching regime associated with the packet delays.
In addition, if the system is designed for switching at
multiples of the sampling period, it is robust with
respect to random variations in the sampling period.
Thus, the sampling period need not be known exactly.
The next section reviews the NCS model of from
(Montestruque and Antaklis, 2004) and some
properties of switched systems. Section 3 presents our
controller design methodology, which is the main
Fadali, M.
LMI Stability Condition for NCS with Packet Delay and Event-triggered Control.
DOI: 10.5220/0011100500003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 99-104
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
99

result of this paper. Section 4 presents simulation
results and Section 5 is the Conclusion.
2 NETWORKED CONTROL
SYSTEM
Consider the linear plant
𝒙
𝑡
=
𝐴
𝒙
𝑡
+𝐵𝒖
𝑡
(1)
𝒚
𝑡
=𝐶𝒙
𝑡
+𝐷𝒖
𝑡
(2)
with networked control with constant matrices 𝐴∈
ℛ
×
,𝐵∈ℛ
×
,𝐶∈ℛ
×
,𝐷∈ℛ
×
. We adopt
the NCS model of (Montestruque and Antaklis, 2004)
and investigate the stability and controller design for
the system.
The plant model is not exactly known, and the
nominal model of the system with the matrices of the
same order as their true counterparts in (1) and (2) is
𝒙
𝑡
=
𝐴
𝒙
𝑡
+𝐵
𝒖
𝑡
(3)
𝒚
𝒕
=𝐶
𝒙
𝑡
+𝐷
𝒖
𝑡
(4)
The discrepancy between the actual and nominal
models results in the error
𝒆=𝒙−𝒙
,𝒙=𝒙
+𝒆 (5)
Subtracting the nominal from the actual dynamics
gives the error dynamics
𝒆
=
𝐴
𝒆+
𝐴
𝑥+𝐵
𝒖
𝑡
(6)
where we use the perturbation matrices
𝐴
=
𝐴
−
𝐴
,𝐵
=𝐵−𝐵
(7)
For an observable system, we use the control
𝒖
𝑡
=−𝐾𝒙
𝑘
,𝑡∈
[
𝑘ℎ,𝑘ℎ + ℎ
]
(8)
where 𝒙
𝑡
is the state estimate. Here, we first
assume that the state is measurable with a finite error
in the measurement. Substituting the control in the
system dynamics gives the closed-loop model
𝒙
𝑡
=
𝐴
𝒙
𝑡
−𝐵𝐾𝒙
𝑡
−𝒆
𝑡
(9)
𝒚
𝒕
=𝐶𝒙
𝑡
−𝐷𝐾𝒙
𝑡
(10)
Substituting in the error dynamics gives
𝒆
=
𝐴
+𝐵
𝐾𝒆
𝑡
+
𝐴
−𝐵
𝐾 𝒙
𝑡
(11
)
Combining error and nominal dynamics gives the
augmented stated vector
𝒛
𝑡
=
𝒙
𝑡
𝒆
𝑡
(12
)
Combining (9) and (11), we have the augmented
system dynamics
𝒙
𝑡
𝒆
𝑡
=
𝐴
𝒙
𝑡
𝒆
𝑡
−𝐵
𝐾
𝑘
𝒙
𝑡
𝒆
𝑡
(13
)
𝐴
=
𝐴
0
𝐴
𝐴
, 𝐵
=
𝐵−𝐵
𝐵
−𝐵
(14
)
The system is digitally controlled with a control
signal sent through a communication system to the
actuator and the controller receiving a signal from the
sensor. The following assumptions are used in the
sequel:
(i) The total delay, including plant to controller
𝑇
and controller to actuator 𝑇
, plus the
computational time is 𝑇
satisfies
𝑇
+𝑇
+𝑇
≤𝑙ℎ,𝑙 𝑖𝑛𝑡𝑒𝑔𝑒𝑟
(15
)
(ii) The delay 𝑇
can be predicted with
sufficient accuracy to design the system
using the sum
𝑇
+𝑇
+𝑇
=𝑙ℎ,𝑙 𝑖𝑛𝑡𝑒𝑔𝑒𝑟
(16
)
(iii) The sampling period 𝑁ℎ provides
sufficiently faster sampling than the Nyquist
rate dictated by the dynamics of the closed-
loop system.
(iv) The number of consecutive packet delays in
the NCS does not exceed 𝑙
.
(v) When event-driven control is used to reduce
the required network bandwidth, the effective
sampling period is in the range
[
ℎ,𝑙
ℎ
]
,
where 𝑙
is a variable but bounded integer,
𝑙
≤𝑙
.
(vi) The number of sampling periods between
two consecutive arriving packets does not
exceed an integer bound 𝑁, that is
𝑙
+𝑙
≤𝑁
(17
)
Under the above assumptions, ℎ is a suitable
sampling period for the NCS and the NCS can
function appropriately with the sampling period 𝑁ℎ
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
100

Discretizing the system with different sampling
periods that are a multiple of the fixed sampling
period ℎ, we have a system that switches arbitrarily
between the models
𝑒
, 𝑒
𝐵
𝑑𝜏
,𝑙=1,2,…,𝑁
(18)
The state-space model of the system is of the form
𝒙
𝑘+1
=
𝐴
𝒙
𝑘
+𝐵
𝒖
𝑘
,
𝑖∈
{
1,2,…,𝑁
}
(19)
𝒚
𝑘
=𝐶
𝒙
𝑡
+𝐷
𝒖
𝑡
(20)
The following result applies in this case.
Theorem 1. 0(Zhai et al., 2002) If all state matrices
𝐴
,𝑖=1,…,𝑁, are mutually commutative and Schur
stable, then the switched system (19) is globally
exponentially stable under arbitrary switching.
The result clearly applies in the case of Schur
stable state matrices in the form
𝐴
=
𝐴
,𝑖=1,…,𝑁
(21)
When applied to the NCS of (19), we have the
corollary.
Corollary: If the discrete-time NCS model of (19) is
Schur stable for a sampling period ℎ, then the
switched system (19) is globally exponentially stable
under arbitrary switching between sampling periods
𝑙ℎ,𝑙=1,2,…,𝑁, that are integer multiples of ℎ.
Remark 1
The stability condition is valid if the sampling period
varies randomly because the state matrices remain
mutually commutative based on the well-known
properties of the matrix exponential.
Remark 2
The stability condition is valid in the case of a matrix
perturbation Δ𝐴∈ℛ
×
such that the state matrix
𝐴+Δ𝐴 is Schur stable.
Remark 3
A necessary condition for the system to remain stable
under arbitrary switching is for all subsystem
matrices to be Schur stable. Otherwise, switching to
an unstable subsystem and subsequently remaining
there would result in an unstable switched system.
3 CONTROLLER DESIGN
This section presents a new approach for the design
for NCS with arbitrary switching between models
corresponding to different sampling rates. The
varying sampling rates correspond to periods where
no control signal is sent from the controller to the
actuator. This results in a sampling period in the range,
𝑙ℎ,𝑙=1,2,..…𝑁, where ℎ is the nominal sampling
period of the system and 𝑁 is an integer. The
switching can be deterministic or random because the
conditions are valid regardless of the switching mode.
The following theorem from (Pandey and Oliveira,
2017) provides stability conditions for a system that
switches between different linear models.
Theorem 2. (Pandey and Oliveira, 2017)
Consider a time-varying discrete-time linear system
of the form
𝐴
𝑘
=𝜉
𝑘
𝐴
𝐵
𝑘
=𝜉
𝑘
𝐵
(22)
𝜉
𝑘
=1,
𝜉
𝑘
>0,𝑖=1,…,𝑁
(23)
The system is stable with the control
𝐾
𝑘
=𝜉
𝑘
𝐾
𝐾
=𝐿
𝑋
(24)
if there exist positive definite matrices
𝑋
,,𝑌
,𝑍
,𝑄
,𝑖=1,…,𝑁 that the satisfy the LMI
𝑋
+𝑋
−𝑄
𝑋
𝐴
−𝐿
𝐴
𝑋
𝑄
−𝑅
𝐵
𝑍
−𝑌
−𝐿
𝑍
𝐵
−𝑌
𝑍
+𝑍
>0
(25)
𝑅
=𝐵
𝑌
+𝑌
𝐵
,𝑖,
𝑗
=1,…,𝑁
(26)
For an NCS, switching is between models that
depend on the number of packet delays, or the period
for event-triggered control. This effectively changes
the sampling period from 𝑇 to 𝑙𝑇,𝑙=1,2,…,𝑁,
where 𝑙−1 is the number of packet delays. Applying
Theorem 1 with 𝜉
𝑘
=1 for one 𝑖 value at a time
and 𝜉
𝑘
=0,𝑗≠𝑖 gives the following theorem.
LMI Stability Condition for NCS with Packet Delay and Event-triggered Control
101

Theorem 3
The NCS with packet delay and event-driven control
subject to assumptions (i-vi) such that the control
input is changed every 𝑙 sampling periods, 𝑙∈
{
1,2,…,𝑁
}
is stable with the control of (24) if the
LMIs of (25) have positive definite solution matrices
𝑋
,,𝑌
,𝑍
,𝑄
,𝑖=1,…,𝑁 for 𝑖,𝑗 = 1,…,𝑁
Proof
Theorem 2 provides a controller for arbitrary
switching subject to conditions (22-23). For NCS,
switching is between matrices with different
sampling periods corresponds to the case 𝜉
=1,𝜉
=
0,𝑗≠𝑖,𝑗∈{1,…,𝑁} . This clearly satisfies
condition (23). Hence, Theorem 3 follows directly
from Theorem 2.
Remark 4
Although Theorem 3 is stated for multiples of the
sampling period, the result is clearly valid for any set
of sampling periods. The results are even valid for
arbitrary random switching between a set of sampling
periods.
4 SIMULATION RESULTS
Consider the oscillatory behavior of the pair
𝐴=
0 1
−4 0
,𝐵=
0
1
The pair is modelled as
𝐴
=
0 1
−4.1 0.1
,𝐵
=
0
1
The perturbation matrices are
𝐴
=𝐴−𝐴
=
0 0
0.1 −0.1
𝐵
=𝐵−𝐵
=
0
0
;
We form the matrices of the augmented system
𝐴
=
𝐴0
𝐴
𝐴
, 𝐵
=
𝐵−𝐵
𝐵
−𝐵
For the purposes of controller design, assume that
package delay and event-triggered control result in
switching between two systems with sampling
periods ℎ and 2ℎ,ℎ=0.04s. The switching is
random with a probability 𝑝 of the nominal sampling
period ℎ and probability
1−𝑝
of period 2ℎ due to
event triggered control or packet delay. The model
corresponding to one sampling period ℎ=0.04 s
with no delay in the arrival of a package is
𝐴
=𝑒
=
0.9968 0.04 0 0
−0.1598 0.9968 0 0
0.0001 −0.0001 0.9967 0.04
0.0043 −0.0039 −0.1641 1.0007
𝐵
=𝑒
𝐵
𝑑𝜏
=
−4 −0.08 0 0
0.32 −4 0 0
0 0 −4 −0.08
0.01 0.01 0.33 −4
×10
The model corresponding to a sampling period
ℎ=0.08 s with delay in the arrival of a package due
to package delay or event triggered control is
𝐴
= 𝑒
=
0.9993 0.0191 0 0
−0.0764 0.9993 0 0
0 0 0.9993 0.0191
−0.002 −0.0019 −0.0784 1.0012
𝐵
= 𝑒
𝐵
𝑑𝜏
=
−7.97 −0.32 0 0
1.28 −7.97 0 0
0 0 −7.96 −0.32
−0.04 0.03 1.31 −8
×10
We solve the LMIs of Theorem 3 to obtain the
controller parameters using the MATLAB LMI
solver. The solutions can be improved by imposing
constraints on the norms of the matrices. Solving the
LMIs gives the gain matrices
𝐾
=
−1.3001 0.3355 0.0264 −0.0189
0.4269 −0.5425 −0.0092 0.012
0.0263 −0.008 −1.35 0.3613
−0.0226 0.0128 0.4567 −0.5667
𝐾
=
−1.3180 0.2617 0.0217 −0.0148
0.3617 −0.466 −0.0062 0.0092
−0.0213 −0.0059 −1.1788 0.2618
−0.0175 0.01084 0.3845 −04855
The design obtained by solving the LMIs results in a
slightly faster response for the pair
𝐴
,𝐵
corresponding to a longer delay but both subsystems
are asymptotically stable.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
102
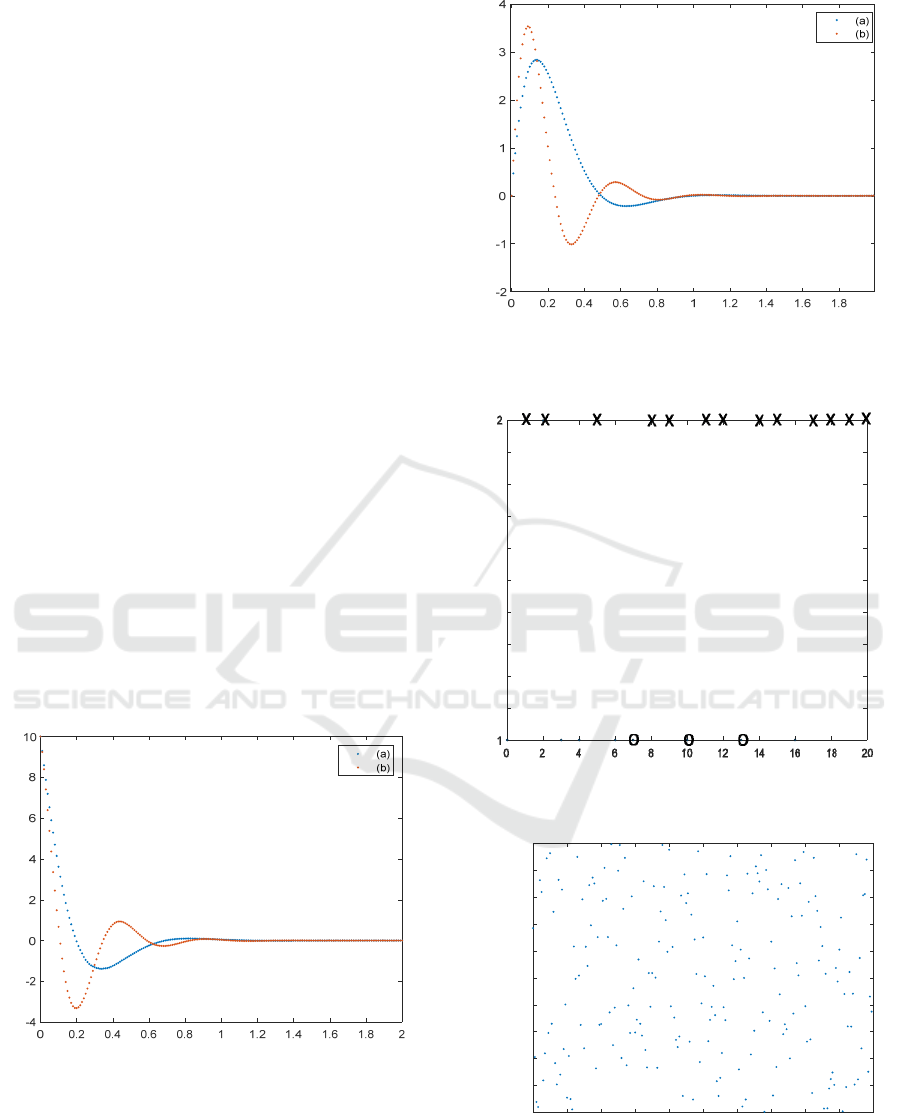
Using 100 Monte Carlo simulations for the system
under different conditions, we compare the
simulation results for the zero-input response. To
assess the robustness of the systems to random
changes in the sampling period, the system is
simulated (a) with switching between sampling
period ℎ and sampling period 2ℎ, the (b) with the
sampling period randomly switching between ℎ and
ℎ +Δℎ,Δℎ~𝑈[−0.1ℎ,0.1ℎ]. Plots of the average
evolution of the state variables are shown in Figures
1 and 2. Figure 3 shows the random switching
between sampling period ℎ and sampling period 2ℎ,
with an initial sampling period equal to ℎ. Figure 4
shows the random variation of the sampling period
Δℎ~𝑈[−0.1ℎ,0.1ℎ] . The simulation results show
that the state variables of the system converge to zero
with the controller resulting in a stable well-behaved
system. The random variation of the sampling period
results in a larger first peak and a more oscillatory
response but does not destabilize the system.
The system also performs well for different
probabilities 𝑝 of a sampling period ℎ=0.04 𝑠.
Figures 5 and 6 show the state evolution for 𝑝=0.6
and 𝑝=0.8, with probabilities of sampling period
2ℎ=0.08 𝑠 equal to 0.4 and 0.2, respectively.
Because the LMI for the delay that results in doubling
the sampling period gives a faster response, contrary
to intuition, the response is faster for the lower
probability 𝑝=0.6. However, the system performs
well for both probabilities, as do others not included
in the paper.
Figure 1: SEQ Figure \* ARABIC 1,. Plot of x
versus time
(a) switch between sampling period h and sampling period
2h (b) random variation Δh around h,
Δh~U[−0.1h,0.1h].
Figure 2: Plot of x
versus time (a) switch between
sampling period h and sampling period 2h (b) random
variation Δh around h,Δh~U[−0.1h,0.1h].
oo
o
p
p
Figure 3: Switching between the sampling periods h and 2h
for the NCS.
Figure 4: Plot of randomly varying sampling periods.
0 0.2 0.4 0.6 0.8 1 1.2 1.4 1.6 1.8 2
0.019
0.0192
0.0194
0.0196
0.0198
0.02
0.0202
0.0204
0.0206
0.0208
0.021
LMI Stability Condition for NCS with Packet Delay and Event-triggered Control
103
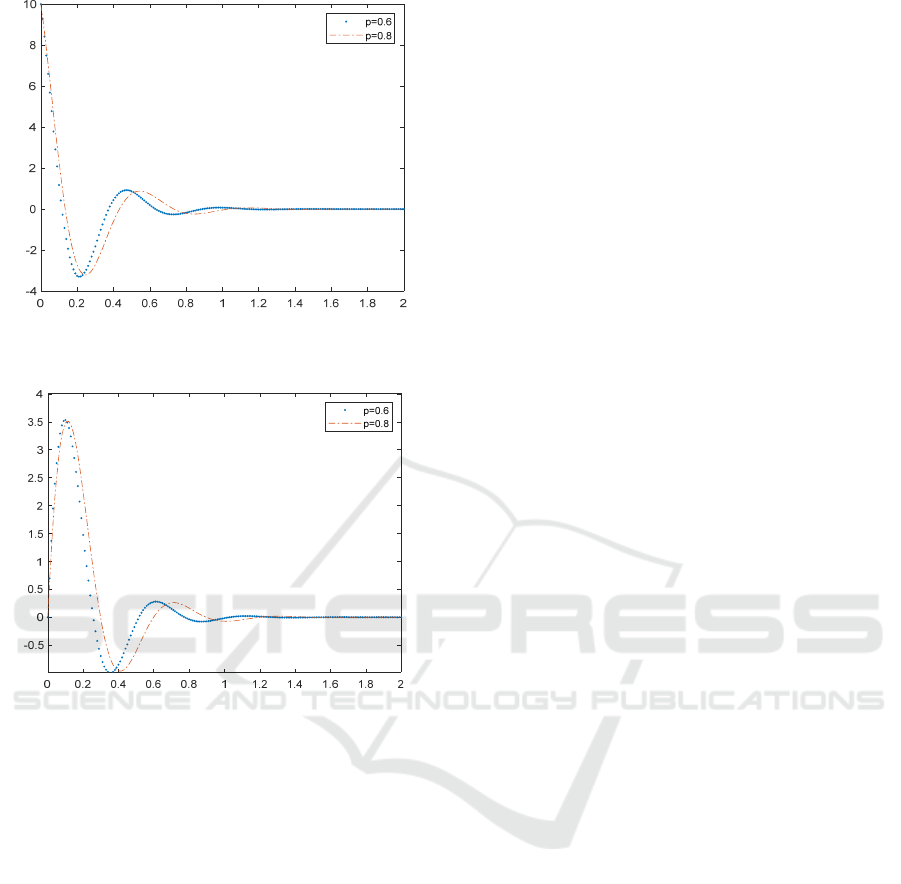
Figure 5: Plot of x
versus time for probability of sampling
period h (a) p=0.6 (b) p=0.8 s.
Figure 6: Plot of x
versus time for probability of sampling
period h (a) p=0.6 (b) p=0.8 s.
4 CONCLUSIONS
This paper presents a new controller design for linear
NCS with packet delays, event triggered control that
is robust with respect to random variations in the
sampling period. The approach is applicable to an
NCS with known upper bound on the number of
sampling periods between consecutive received
packages. The approach is valid for arbitrary random
switching between different models. Simulation
results show that the system is stabilized with random
switching between models and remains stable for
different probabilities of switching and random
variations in the sampling period. Future work will
provide an analysis of the robustness of the design
with respect to modelling errors and changes in the
sampling period and probability of switching.
REFERENCES
Antaklis, J., Baillieul, J. (2007). Special issue on
technology of networked control systems, Proc. IEEE,
vol. 95, no. 1.
Hespanha, J. P., Naghshtabrizi, P. and Xu, Y., (2007). “A
survey of recent results in networked control systems,”
Proc. IEEE, 2007, 95, pp. 138–162
Li, J., Yu, H., Liang, W., Zeng, P., Yuan, M. (2015). “A
survey of packet disordering existing in networked
control systems,” 2015 IEEE International Conference
on Cyber Technology in Automation, Control, and
Intelligent Systems (CYBER), Shenyang, pp. 1797-
1801
Yang, T. C., (2006). “Networked control system: a brief
survey,” IEEE Proc. Contr. Theory and Appl., 153, pp.
403–412.
Ge, X, Han, Zhang, Q.-L., Ding, D., (2021), “Dynamic
event triggered control and estimation: a survey,” Int. J.
Automation and Computing.
Lemmon, M., (2010). Event-triggered feedback in control,
estimation, and optimization. Lecture Notes in Control
and Information Science, vol. 406, pp. 293–358.
Garcia, E, Antaklis, P. J. and Monstrous, L. A., (2014).
Model-based Control of Networked Systems,
Birkhauser, Heidelberg.
L. A. Montestruque and P. Antaklis (2004). “Stability of
model-based network control systems with time-
varying transmission times,” IEEE Trans. Automat.
Contr., Vol. 49, No. 9, pp. 1562-1572.
Pandey, A. P. and Oliveira, M. C. (2017). “A new discrete-
time stabilizability condition for linear parameter-
varying systems,” Automatica, Vol. 79, pp. 214-217.
Zhai, G., Hut, B., Yasuda, K. and Michel, (2002). A. N.,
“Qualitative Analysis of Discrete-Time Switched
Systems,” Proc. 2002 American Control Conference,
Anchorage, AK May 8-10.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
104
