A Spatially Detailed Approach to the Assessment of Rooftop Solar

Energy Potential based on LiDAR Data

Mohammad Aslani

and Stefan Seipel

1,2

Department of Computer and Geo-spatial Sciences, University of G¨avle, G¨avle, Sweden

Division of Visual Information and Interaction, Department of Information Technology,

Uppsala University, Uppsala, Sweden

Keywords:

Deep Learning, Clustering, Segmentation, Solar Energy, LiDAR.

Abstract:

Rooftop solar energy has long been regarded as a promising solution to cities’ growing energy demand and en-

vironmental problems. A reliable estimate of rooftop solar energy facilitates the deployment of photovoltaics

and helps formulate renewable-related policies. This reliable estimate underpins the necessity of accurately

pinpointing the areas utilizable for mounting photovoltaics. The size, shape, and superstructures of rooftops

as well as shadow eﬀects are the important factors that have a considerable impact on utilizable areas. In

this study, the utilizable areas and solar energy potential of rooftops are estimated by considering the men-

tioned factors using a three-step methodology. The ﬁrst step involves training PointNet++, a deep network for

object detection in point clouds, to recognize rooftops in LiDAR data. Second, planar segments of rooftops

are extracted using clustering. Finally, areas that receive suﬃcient solar irradiation, have an appropriate size,

and fulﬁll photovoltaic installation requirements are identiﬁed using morphological operations and predeﬁned

thresholds. The obtained results show high accuracy for rooftop extraction (93%) and plane segmentation

(99%). Moreover, the spatially detailed analysis indicates that 17% of rooftop areas are usable for photo-

voltaics.

1 INTRODUCTION

Solar energy generated by rooftop photovoltaics is a

practical renewable energy resource that may provide

a portion of the energy demand of buildings in urban

areas (Joshi et al., 2021). Rooftop photovoltaics con-

vert each building from a passive power consumer to

an active power provider with low investment, thanks

to the steep decline in their deployment costs (B

odis

et al., 2019).

However, not all rooftop areas are utilizable for

photovoltaic deployment. Utilizable rooftop areas

are limited by various factors, the most important of

which are the shape, orientation, and superstructures

of roofs, as well as occlusion (Thebault et al., 2020).

A rooftop with proper orientation and no superstruc-

tures or surrounding objects oﬀers high solar energy

potential. In contrast, a north-facing rooftop with

many superstructures surrounded by tall buildings (in

the northern hemisphere) may not oﬀer high solar en-

ergy potential. In addition, the rooftop’s geographical

location and the local climate conditions may aﬀect

its solar energy potential.

Manually ﬁnding utilizable rooftop areas by con-

sidering the mentioned factors is laborious and im-

practical, particularly in large areas. Analyzing Li-

DAR datasets has been recognized as a potential way

to automate this laborious process (Gassar and Cha,

2021). LiDAR datasets provide the 3D spatial proﬁles

of the area and allow for automatic computation of

characteristics of rooftops and their surrounding ob-

jects, such as area, height, tilt, and azimuth. In this

context, one of the common methods of estimating

the total utilizable areas is by applying a set of coef-

ﬁcients that consider roof types (e.g., ﬂat or tilted),

obtained from LiDAR datasets (Byrne et al., 2015).

However, adjusting coeﬃcients in heterogeneous re-

gions is nontrivial, and thus the methods may lead to

inaccurate results. To address this issue, spatially-

based methods using geographical information sys-

tems (GIS) have been proposed, in which roof shapes

are ﬁrst modeled, and then their utilizable areas are

identiﬁed by considering the tilts and orientations of

roofs.

To model the shapes of roofs, it is necessary to ﬁrst

extract the footprints of rooftops. Numerous tech-

Aslani, M. and Seipel, S.

A Spatially Detailed Approach to the Assessment of Rooftop Solar Energy Potential based on LiDAR Data.

DOI: 10.5220/0011108300003185

In Proceedings of the 8th International Conference on Geographical Information Systems Theory, Applications and Management (GISTAM 2022), pages 56-63

ISBN: 978-989-758-571-5; ISSN: 2184-500X

niques have been suggested for rooftop extraction. In

this context, machine learning-based methods have

shown high potential. In (Aslani and Seipel, 2020),

support vector machines (SVMs) were employed to

identify rooftops. A new method named data reduc-

tion based on locality sensitive hashing (DRLSH) was

proposed to automatically select instances for training

SVMs. In (Aslani and Seipel, 2021), another instance

selection method for SVMs was developed, and it was

tested on a dataset for rooftop extraction. In (Shin

et al., 2022), PointNet++, a deep network, was used

to identify rooftops from LiDAR datasets.

Once rooftops have been extracted, their shape

(form) can be modeled. In (Lingfors et al., 2017),

roofs were modeled using a predeﬁned library of roof

shapes for the purpose of estimating solar energy po-

tential. More speciﬁcally, a model library that con-

tains common roof shapes (e.g., gable and shed) was

ﬁrst deﬁned, and the shape that best matches the cor-

responding point clouds was chosen. Following this

method, in (Mohajeri et al., 2018), SVMs were used

to choose the best-ﬁtting roof shape from a predeﬁned

library. However, this type of roof shape modeling

may overlook roof superstructures (e.g., chimneys),

which play an important role in identifying utilizable

areas. In (Sampath and Shan, 2010), another type of

approach was used in which roofs are modeled by ag-

gregating their constituent planar patches (roof faces)

extracted by plane segmentation. They used fuzzy k-

means clustering for plane segmentation. To enhance

clustering, a planarity test that distinguishes planar

from non-planar points was incorporated. In (Chen

et al., 2014), a RANSAC-like algorithm was used for

plane segmentation. In (Huang et al., 2015), region

growing was utilized for segmenting planar patches.

Unsuitable roof faces were then removed by applying

area, slope, aspect, and solar irradiation thresholds.

This approach does not require a predeﬁned library of

roof shapes and can model any polyhedral roof shape.

Most of the current spatially-based methods for

identifying utilizable areas are limited to manual dig-

itization or simpliﬁed roof shape modeling, and they

may not consider shadow eﬀects. This research iden-

tiﬁes utilizable areas with more spatial details by

considering roof shapes, roof superstructures, and

shadow eﬀects. Our methodology uses LiDAR data

to assess the solar energy potential of rooftops in any

area. It aims to automatically (a) extract rooftops us-

ing a deep learning-based method, (b) segment planar

rooftop patches using a clustering-based method, and

erations.

2 METHODOLOGY

This section describes our methodology for automati-

cally assessing rooftop solar energy potential. It lever-

ages LiDAR datasets and assumes that they have suf-

ﬁcient density to model the shape and desired super-

structures of roofs. LiDAR data contain 2.5D in-

formation about an area that can be used to model

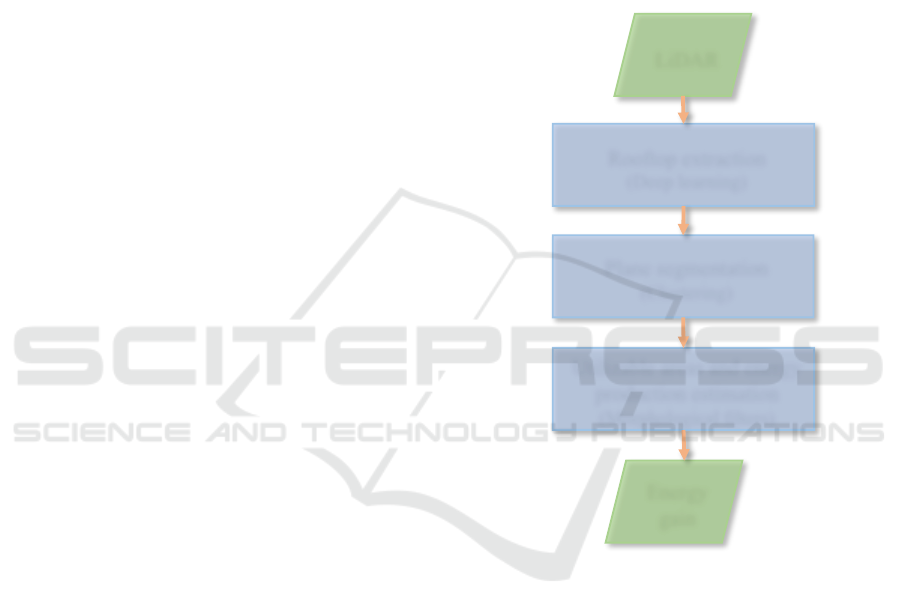
rooftops and solar irradiation. The methodology con-

sists of three main steps (Figure 1), explained in fur-

ther detail in the following subsections.

LiDAR

Rooftop extraction

(Deep learning)

Plane segmentation

(Clustering)

Utilizable areas and energy

production estimation

(Morphological filters)

Energy

gain

Figure 1: Overview of the methodology.

2.1 Rooftop Extraction

Extracting rooftops is required to determine the suit-

able areas where photovoltaics may be mounted.

Rooftop extraction is a semantic segmentation task in

which the points that comprise rooftops are identiﬁed.

Owing to the remarkable advancements of deep learn-

ing methods and their satisfactory performance in do-

ing semantic segmentation tasks, they are used in this

step. In particular, we use PointNet++ to segment

rooftops in LiDAR data (Qi et al., 2017). PointNet++

is a hierarchical neural network for semantic segmen-

tation of unorganized point data, and it enables multi-

scale point feature learning. It has the potential to be

trained without requiring parameters that are speciﬁc

to objects in LiDAR. A PointNet++ network con-

A Spatially Detailed Approach to the Assessment of Rooftop Solar Energy Potential based on LiDAR Data

sists of three layers: sampling, grouping, and mini-

PointNet layers. The sampling layer chooses a set of

points that forms the centroids of local regions. The

grouping layer constructs local regions sets around

the centroids. The mini-PointNet layer abstracts the

sets of local features into higher-level representations

using a series of convolution, normalization, relu, and

max-pooling layers. Please refer to (Qi et al., 2017)

for more details. To train PointNet++ for rooftop ex-

traction, we use labeled point clouds containing those

features (please see Section 3).

2.2 Plane Segmentation

In this step, the constituent planar patches of rooftops

are segmented. This step is required as photovoltaics

are installed by considering planar segments of roofs.

A digital surface model (DSM) is created from the

recognized rooftop points using interpolation. This

conversion makes the plane segmentation procedure

easier.

Plane segmentation is performed based on clus-

tering the normal vectors of pixels. A normal vector

of a pixel is perpendicular to the surface at the pixel,

and it is computed by ﬁtting a plane to the pixel and

its neighbors. Pixels on the same planar patch have

similar normal vectors, and thus, by grouping them

together, planar patches can be identiﬁed. Some pix-

els in each planar segment may, however, have nor-

mal vectors that are inconsistent with those of other

pixels in the same segment. These pixels are known

as non-planar pixels as they are placed in the vicin-

ity of more than one plane. Including these pixels in

clustering may disturb the creation of planar segments

since they shatter the boundaries of clusters of normal

vectors. As a result, non-planar pixels must be iden-

tiﬁed and excluded from clustering. The planarity of

each pixel is evaluated based on the Eigenvalues of a

3D covariance matrix of the pixel and its neighbors

(Awrangjeb and Fraser, 2014).

Initial planar segments are created by clustering

the normal vectors of planar pixels. To delineate clus-

ters, a minimum density divisive clustering (MDDC)

algorithm was used (Tasoulis et al., 2016). Its adapt-

ability (i.e., it requires no input parameters) and high

computational eﬃciency make it suitable for handling

large-scale plane segmentation. Since segmentation

using MDDC does not consider the spatial connectiv-

ity of pixels, each resulting patch may comprise mul-

tiple parallel planar segments that are spatially sep-

arated. To split multi-part patches, Euclidean clus-

tering based on pixel coordinates is applied (Rusu,

2009). Finally, the non-planar pixels, initially ex-

cluded, are assigned to the best segment using re-

gion growing. In this way, the problem of over-

segmentation that may arise in clustering is also re-

solved. This plane segmentation method can identify

all planar segments of a rooftop, even superstructures,

to the extent that the spatial resolution of the DSM al-

lows.

2.3 Utilizable Areas and Energy

Production Estimation

This step involves computing the solar energy poten-

tial of rooftops. As photovoltaics cannot be installed

over the entire area of a rooftop, it is necessary to

ascertain areas utilizable for photovoltaics to avoid

overestimation of energy production. Utilizable areas

are deﬁned as parts of rooftops where photovoltaics

can be reasonably installed. In this research, each pla-

nar segment is spatially scrutinized to identify its uti-

lizable areas.

Parts of planar segments should be kept free of

photovoltaics to ease accessibility as an installation

requirement of panels. Often, there should be a dis-

tance between the edge of photovoltaics and the seg-

ment that is known as service areas. To exclude these

areas, we utilize a morphological erosion operation

with a circular structuring element whose radius is

equal to the width of the service areas (Sundararajan,

2017). The erosion operation shrinks the roof face by

the width of the service area. In addition to service

areas, there might be some areas of planar segments

that are too small for a photovoltaic to ﬁt, and these

areas should be excluded. To do so, the algorithm

suggested in (Aslani and Seipel, 2022) is employed in

this paper. It iteratively applies a series of morpho-

logical opening operations and then aggregates their

results. The structuring elements of the opening op-

erations represent a photovoltaic with diﬀerent rota-

tions. The length and width of the structural elements

are the same length and width as the photovoltaics that

are being used.

After removing geometrically unsuitable areas,

the remaining planar segments are evaluated in terms

of solar irradiation. The segments whose average

solar irradiation is below a speciﬁc threshold SI are

removed. This is because photovoltaics are usually

not installed on rooftop areas with low solar irradi-

ation. In this way, planar segments that are mainly

in shadow or those with unsuitable tilts (e.g., too

steep) or azimuths (e.g., north-facing) are discarded.

It should be noted that the solar irradiation of each

segment is estimated using the solar model of Ar-

cGIS Desktop (Fu and Rich, 2000; Rich et al., 1994).

The solar model incorporates viewshed analysis to ac-

count for shadowing eﬀects. The viewshed analy-

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

sis generates a Boolean image indicating the extent

to which the sky is obscured by surrounding objects

as seen from a certain place in the DSM. In addition

to occlusion, the solar model takes into account site

orientation, atmospheric eﬀects, and variations in the

sun’s position, making it a reliable tool in estimating

global solar irradiation.

After the utilizable rooftop surfaces are extracted,

the energy potential of rooftops is determined. The

total solar electricity yield of a rooftop is calculated

according to Equation 1. S

and T

are the total solar

irradiance (in kWh/m

) and the tilt angle of the i-th

utilizable segment, e and p are the eﬃciency and per-

formance ratio of the photovoltaics, d is the area of

each pixel of the DSM (in m

), and N is the number

of utilizable segments of a rooftop. E is the total solar

electricity yield of a rooftop in kWh.

E = d · e · p ·

i=1

cosT

(1)

3 DATASETS

This study makes use of two diﬀerent datasets. Day-

ton Annotated LiDAR Earth Scan (DALES) is the ﬁrst

dataset (Varney et al., 2020) used to train and evalu-

ate PointNet++ for rooftop extraction. It is a publicly

available dataset, and it contains an extensive collec-

tion of LiDAR data from a wide range of environ-

ments, making it ideal for training deep networks. It

comprises 40 scenes that were manually labeled. The

second dataset is part of Uppsala city in Sweden, and

its LiDAR point cloud was produced by Uppsala mu-

nicipality

. It is used for plane segmentation and so-

lar energy estimation. We manually labeled planar

segments of rooftops to produce ground truth data for

plane segmentation evaluation. Figure 2 shows some

scenes from the datasets.

4 EXPERIMENTAL SETUP,

RESULTS, AND DISCUSSION

In this section, the methodology is applied to the

datasets, and the results are presented and discussed.

As mentioned in Section 2.1, the ﬁrst step of the

methodology is to extract rooftops, which is done by

utilizing PointNet++. 29 scenes out of 40 scenes from

the DALES dataset are used for training, and the re-

maining ones are used for testing. To eﬃciently take

advantage of the dataset, each scene is divided into

www.uppsala.se

small, non-overlapping tiles with a size of 50-by-50

meters. Each tile is then downsampled to contain only

9000 points, speeding up the training process. To train

the deep network, the Adam optimizer with a gradi-

ent decay rate of 0.9 is used (Kingma and Ba, 2015).

The maximum number of training epochs is set to 20,

with each epoch consisting of 485 iterations. At the

beginning of the training, the learning rate is set to

0.0005 and is reduced by a factor of 0.1 in epoch 10.

Regularization is used to minimize overﬁtting, and the

regularization factor is set to 0.1 (Murphy, 2012). The

output of PointNet++ is a per-point prediction, show-

ing which points are part of rooftops.

By applying the trained deep network to the test

scenes and comparing its results (predicted rooftops)

with the ground truth labels, the performance of the

trained deep network for rooftop extraction is eval-

uated. We use accuracy and intersection over union

(IOU) as two metrics to quantitatively measure the de-

gree to which the predicted and actual labels are sim-

ilar. These metrics are calculated according to Equa-

tions 2 and 3, where T P, FP, and FN are the numbers

of true positives, false positives, and false negatives,

respectively.

Accuracy =

T P

T P + FN

(2)

IOU =

T P

T P + FP + FN

(3)

Table 1 shows the evaluation results of rooftop ex-

traction in the test scenes of the DALES dataset. We

observe that the trained deep network has an accuracy

of 92.60% and an IOU of 87.38% on average, show-

ing its satisfactory performance in rooftop extraction.

Thus, the trained deep network can be applied to any

area. We employ it in the extraction of rooftops from

the second dataset. Figure 3 shows some examples

of rooftop extraction from the second dataset. The

boundaries of rooftops have been extracted and reg-

ularized using α-shape (Akkiraju et al., 1995) and

polyline compression (Gribov, 2019) algorithms, re-

spectively. The ﬁgure illustrates that rooftops have

been successfully separated from other objects. How-

ever, there are some cases where the trained deep net-

work fails to correctly identify rooftops. Figure 4

shows an example where the main part of a rooftop

has been missed.

Table 1: Rooftop extraction evaluation results.

Accuracy (%) IOU (%)

Average 92.98 87.75

In the next step, planar patches of rooftops are seg-

mented using clustering, followed by region growing.

A Spatially Detailed Approach to the Assessment of Rooftop Solar Energy Potential based on LiDAR Data

(a) (b)

Figure 2: Sample scenes from dataset 1 (a) and dataset 2 (b).

Figure 3: Some detected rooftops. The background orthophoto is only for visualization purposes.

Figure 4: Partially detected rooftop.

The MDDC algorithm used for clustering normal vec-

tors is adaptive, that is, it does not require any input

parameters. The height and angle thresholds used in

region growing were set to 10 cm and 7

◦

, obtained

using trial and error in a small part of the dataset.

Figure 5 shows plane segmentation results of some

rooftops. As seen in the ﬁgure, the plane segmenta-

tion method has been successful in the identiﬁcation

of roof faces. Minor superstructures, including vents

and small chimneys, that cannot be recognized as in-

dependent planar segments appear as holes in the seg-

ments. In this way, the impact of superstructures can

be considered in the identiﬁcation of utilizable areas.

We quantify the performance of plane segmentation

by comparing its results with the ground truth data.

Table 2 shows the performance of plane segmentation

in terms of accuracy and IOU. It suggests that most

planar segments have been accurately identiﬁed and

that the method is eﬀective.

Table 2: Plane segmentation evaluation results.

Accuracy (%) IOU (%)

Average 98.69 98.22

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

Figure 5: Plane segmentation results of some rooftops.

Figure 6: Annual global solar irradiation of some rooftops in the study area.

To pinpoint areas utilizable for photovoltaics, a

solar irradiation map of rooftops is necessary, in

addition to planar segments. This is due to cost-

eﬀectiveness considerations, which prevent photo-

voltaics from being installed over areas with low solar

irradiation. Figure 6 illustrates the annual global so-

lar irradiation distribution across some rooftops, com-

puted with ArcGIS Desktop. The eﬀects of shadows

cast by nearby objects can be seen in this illustration.

Utilizable areas of rooftops are identiﬁed by elim-

inating service areas as well as geometrically unsuit-

able and low-irradiated areas. To remove service ar-

eas, an erosion operation whose structuring element

has a radius of 30 cm is used. To eliminate areas that

cannot accommodate a photovoltaic panel, a series of

opening operations are used. The size of the struc-

turing elements of opening operations is set to 1.7 m

× 1.0 m, which is the common size of a commercial

rooftop photovoltaic panel. Moreover, the solar ir-

radiation threshold SI used to remove low-irradiated

areas is set to 1000 kWh/m

/year. Figure 7 shows

the resulting utilizable areas of some rooftops in the

dataset. As is evident from the ﬁgure, the impact of

minor superstructures, highlighted by white circles,

has been considered in the identiﬁcation of the uti-

lizable areas. Buﬀers with the width of service areas

A Spatially Detailed Approach to the Assessment of Rooftop Solar Energy Potential based on LiDAR Data

Figure 7: Utilizable areas of rooftops in the sample scene. White circles show the impact of superstructures.

Table 3: Comparing rooftop regions with utilizable regions over the entire study area.

Total area (m

) Total annual electricity yield (kWh)

Utilizable regions 699.83 90104.87

Entire rooftop regions 4224.43 403505.43

Ratio 16.57% 22.33%

have been excluded from planar segments. Moreover,

some large planar segments have been discarded due

to a lack of solar irradiation. It can be inferred that

the methodology is able to consider the shape, orien-

tation, and superstructures of rooftops as well as oc-

clusions in the identiﬁcation of the utilizable areas.

The total area (in m

) and annual electricity yield

(in kWh) for the rooftops and their utilizable parts

in the entire study area are shown in Table 3. The

electricity yield has been estimated using Equation 1,

where the eﬃciency and performance ratio of the pho-

tovoltaics were set to 0.16 and 0.75, respectively. Ac-

cording to this table, the utilizable regions based on

spatially detailed analysis comprise a small propor-

tion of the entire rooftops (16.6%), hence assessing

the solar energy potential of buildings based on the

entire rooftop areas may lead to an overestimation.

5 CONCLUSION

In this study, a three-step methodology was developed

to estimate the solar energy potential of rooftops.

Rooftops were recognized in LiDAR point clouds us-

ing deep learning. MDDC and Euclidean cluster-

ing were employed to delineate the initial planar seg-

ments of rooftops. Afterward, utilizable areas were

identiﬁed by excluding geometrically unsuitable and

low-irradiated regions as well as service areas from

the identiﬁed planar segments. Solar electricity yield

of utilizable areas was ﬁnally estimated.

Rooftop extraction and plane segmentation were

validated using ground truth data. The validation re-

sults showed that rooftops and their planar segments

were successfully extracted with 93% accuracy and

88% IOU and 99% accuracy and 98% IOU, respec-

tively. It was observed that the shape, orientation, and

superstructures of rooftops and shadow eﬀects were

satisfactorily considered in the identiﬁcation of utiliz-

able areas, and thus the methodology can provide a vi-

able means for practically valid rooftop solar energy

potential estimation. The methodology is beneﬁcial

for facilitating investment decisions on photovoltaics

deployment, particularly in areas where 3D city mod-

els are unavailable.

ACKNOWLEDGEMENTS

This work was partly funded by the European

Regional Development Fund (ERDF), contract ID

20201871. The authors would like to thank Uppsala

municipality for providing the data for this study.

GISTAM 2022 - 8th International Conference on Geographical Information Systems Theory, Applications and Management

REFERENCES

Akkiraju, N., Edelsbrunner, H., Facello, M., Fu, P., M

ucke,

P., E., and Varela, C. (1995). Alpha Shapes: Deﬁnition

and Software. In Proceedings on International Com-

putational Geometry Software Workshop, Minneapo-

lis.

Aslani, M. and Seipel, S. (2020). A fast instance selec-

tion method for support vector machines in building

extraction. Applied Soft Computing, 97:106716.

Aslani, M. and Seipel, S. (2021). Eﬃcient and decision

boundary aware instance selection for support vector

machines. Information Sciences, 577:579–598.

Aslani, M. and Seipel, S. (2022). Automatic identiﬁcation

of utilizable rooftop areas in digital surface models for

photovoltaics potential assessment. Applied Energy,

306, Part A:118033.

Awrangjeb, M. and Fraser, C. S. (2014). Automatic Seg-

mentation of Raw LIDAR Data for Extraction of

Building Roof. Remote Sensing, 6(5):3716–3751.

odis, K., Kougias, I., J

ager-Waldau, A., Taylor, N., and

Szab

o, S. (2019). A high-resolution geospatial assess-

ment of the rooftop solar photovoltaic potential in the

European Union. Renewable and Sustainable Energy

Reviews, 114:109309.

Byrne, J., Taminiau, J., Kurdgelashvili, L., and Kim, K. N.

(2015). A review of the solar city concept and meth-

ods to assess rooftop solar electric potential, with an

illustrative application to the city of Seoul. Renewable

and Sustainable Energy Reviews, 41:830–844.

Chen, D., Zhang, L., Mathiopoulos, P. T., and Huang, X.

(2014). A Methodology for Automated Segmenta-

tion and Reconstruction of Urban 3-D Buildings from

ALS Point Clouds. IEEE Journal of Selected Topics

in Applied Earth Observations and Remote Sensing,

7(10):4199–4217.

Fu, P. and Rich, P. M. (2000). The Solar Analyst 1.0 Man-

ual. Technical report, Helios Environmental Modeling

Institute (HEMI), USA.

Gassar, A. A. A. and Cha, S. H. (2021). Review of

geographic information systems-based rooftop solar

photovoltaic potential estimation approaches at urban

scales. Applied Energy, 291:116817.

Gribov, A. (2019). Optimal Compression of a Polyline

While Aligning to Preferred Directions. In 2019 In-

ternational Conference on Document Analysis and

Recognition Workshops (ICDARW), volume 1, pages

98–102.

Huang, Y., Chen, Z., Wu, B., Chen, L., Mao, W., Zhao, F.,

Wu, J., Wu, J., and Yu, B. (2015). Estimating Roof

Solar Energy Potential in the Downtown Area Using

a GPU-Accelerated Solar Radiation Model and Air-

borne LiDAR Data. Remote Sensing, 7(12):17212–

17233.

Joshi, S., Mittal, S., Holloway, P., Shukla, P. R.,

O Gal-

lach

oir, B., and Glynn, J. (2021). High resolu-

tion global spatiotemporal assessment of rooftop solar

photovoltaics potential for renewable electricity gen-

eration. Nature Communications, 12(1):5738.

Kingma, D. P. and Ba, J. (2015). Adam: A Method for

Stochastic Optimization. In International Confer-

ence on Learning Representations (ICLR), San Diego.

Ithaca.

Lingfors, D., Bright, J. M., Engerer, N. A., Ahlberg, J.,

Killinger, S., and Wid

en, J. (2017). Comparing the ca-

pability of low- and high-resolution LiDAR data with

application to solar resource assessment, roof type

classiﬁcation and shading analysis. Applied Energy,

205:1216–1230.

Mohajeri, N., Assouline, D., Guiboud, B., Bill, A., Gud-

mundsson, A., and Scartezzini, J.-L. (2018). A city-

scale roof shape classiﬁcation using machine learn-

ing for solar energy applications. Renewable Energy,

121:81–93.

Murphy, K. P. (2012). Machine Learning: A Probabilistic

Perspective. MIT Press, Cambridge, Massachusetts.

Qi, C. R., Yi, L., Su, H., and Guibas, L. J. (2017). Point-

Net++: Deep Hierarchical Feature Learning on Point

Sets in a Metric Space. In 31st Conference on Neural

Information Processing Systems (NIPS 2017), Califor-

nia.

Rich, P., Dubayah, R., Hetrick, W., and Saving, S. (1994).

Using Viewshed models to calculate intercepted so-

lar radiation: applications in ecology. American Soci-

ety for Photogrammetry and Remote Sensing Techni-

cal Papers, pages 524–529.

Rusu, R. B. (2009). Semantic 3D Object Maps for Everyday

Manipulation in Human Living Environments. PhD

thesis, Technical University of Munich, Munich, Ger-

many.

Sampath, A. and Shan, J. (2010). Segmentation and Recon-

struction of Polyhedral Building Roofs From Aerial

LiDAR Point Clouds. IEEE Transactions on Geo-

science and Remote Sensing, 48(3):1554–1567.

Shin, Y.-H., Son, K.-W., and Lee, D.-C. (2022). Semantic

Segmentation and Building Extraction from Airborne

LiDAR Data with Multiple Return Using PointNet++.

Applied Sciences, 12(4).

Sundararajan, D. (2017). Digital Image Processing A Sig-

nal Processing and Algorithmic Approach. Springer,

Singapore.

Tasoulis, N. G. P., Hofmeyr, D. P., and K., S. (2016).

Minimum Density Hyperplanes. Journal of Machine

Learning Research, 17(156):1–33.

Thebault, M., Clivill

e, V., Berrah, L., and Desthieux, G.

(2020). Multicriteria roof sorting for the integration

of photovoltaic systems in urban environments. Sus-

tainable Cities and Society, 60:102259.

Varney, N., Asari, V. K., and Graehling, Q. (2020). DALES:

A Large-scale Aerial LiDAR Data Set for Seman-

tic Segmentation. In 2020 IEEE/CVF Conference on

Computer Vision and Pattern Recognition Workshops

(CVPRW), pages 717–726.

A Spatially Detailed Approach to the Assessment of Rooftop Solar Energy Potential based on LiDAR Data