
Toward Cloud Manufacturing: A Decision Guidance Framework for
Markets of Virtual Things
Xu Han
a
and Alexander Brodsky
b
Department of Computer Science, George Mason University, 4400 University Drive, Fairfax, U.S.A.
Keywords:
Markets of Virtual Things, Decision Guidance, Formal Framework, Cloud Manufacturing.
Abstract:
In the value creation chain today, entrepreneurs have been faced with stiff hindrance in turning their innovative
ideas into marketable products due to the manufacturing-entrepreneurship disconnect in terms of accessibil-
ity, predictability and agility. Toward bridging this gap, in this paper we develop a formal mathematical
framework for markets of virtual things: parameterized products and services that can be searched, composed
and optimized. The proposed framework formalizes the notions of virtual product and service designs and
customer-facing specs as well as requirements’ specs. Based on these formal concepts, the framework also
formalizes the notions of search for and composition of virtual products and services that (1) are mutually
consistent with the requirement specs, (2) are Pareto-optimal in terms of customer-facing metrics such as cost,
product desirable characteristics and delivery terms; and (3) that are optimal in terms of customer utility func-
tion that is expressed in terms of customer facing metrics. We also propose the design of a repository of virtual
things and their artifacts, to be used in support of the virtual things’ markets. The proposed markets of vir-
tual things can lead to democratizing innovation by allowing entrepreneurs without design and manufacturing
expertise to bring their ideas to markets quickly.
1 INTRODUCTION
In the value creation chain today, entrepreneurs have
been faced with stiff hindrance in turning their in-
novative ideas into marketable products due to the
manufacturing-entrepreneurship disconnect in terms
of accessibility, predictability and agility ((Brodsky
et al., 2021)). In order for entrepreneurs to realize
their innovative ideas, they have to either (1) have
strong technical backgrounds and expansive knowl-
edge about product and process design, development,
manufacturing and testing, or (2) assemble a team of
experts who can help translate and convey the ideas
to the designers, developers, testers and manufactur-
ers. That is, entrepreneurs lack accessibility to man-
ufacturing capacity, predictability and agility to get
to market. Furthermore, the current approaches typ-
ically lead to sub-optimal outcomes due to informa-
tion loss during the ideation and communication pro-
cesses.
For manufacturers, due to a lack of market infor-
mation, significant amount of manufacturing capacity
a
https://orcid.org/0000-0002-3347-3627
b
https://orcid.org/0000-0002-0312-2105
is underdeveloped, idle or wasted, missing out oppor-
tunities to reach higher levels of economies of scale
to save cost and to create value. When entrepreneurs
find a rising market trend for a certain product, the
technical specs with all essential information that cap-
tures the complex features and properties of the prod-
uct can hardly be generated and passed in time to the
manufacturers that have the interest, availability and
resources to produce it. Furthermore, when the infor-
mation is passed from the entrepreneurs to the down-
stream channels, there is slow or no feedback. And
there is little or no opportunity for optimizing the de-
cision making and value creation processes. That is,
while manufacturers may have predictability for prod-
ucts they know how to produce, they lack access to in-
novative product ideas and related higher-margin rev-
enue opportunities, and the agility to respond to these
innovative ideas.
Clearly, entrepreneurs are in need of a simple
way of converting their product and service ideas to
manufacturing-ready technical specs so that they can
achieve easy accessibility, predictability and agility of
the ideation-to-production process. Trying to bridge
the gap, there has been significant research in para-
metric product and process design ((Gingold et al.,
406
Han, X. and Brodsky, A.
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things.
DOI: 10.5220/0011114100003179
In Proceedings of the 24th International Conference on Enterprise Information Systems (ICEIS 2022) - Volume 1, pages 406-417
ISBN: 978-989-758-569-2; ISSN: 2184-4992
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2009), (Yu et al., 2011), (LaToza et al., 2013), (Shin
et al., 2017)), analysis and optimization ((Egge et al.,
2013), (Shao et al., 2018)). Parametric design seems
to point out a promising direction as it offers the flex-
ibility to the entrepreneurs - setting and changing the
parameters enables high customizability, and a large
set of design alternatives can be generated for the en-
trepreneurs to choose from. Recently, a number of
start-ups, such as Xometry, Kerfed and Physna, have
taken important complimentary steps to simplify the
process from product specs to manufacturing orders.
However, none of the above-mentioned works has
specified how to present the artifacts of the design in a
way that the entrepreneurs would find straightforward
and intuitive to understand and practically work on,
while providing the manufacturers with all the prod-
uct and process designs necessary for manufacturing.
For different products, there is no consistent way to
reuse the models of the parts that can be shared. Fur-
thermore, when optimization is deployed to paramet-
ric designs, it is typically done in product and process
silos, as opposed to optimizing holistically across the
value chain, thus missing out the opportunity to reach
Pareto-optimal solutions in creating the products.
In order to enable the entrepreneurs to conceive
their ideas in a non-technical language but to ex-
press them in technically recognizable terms, we pro-
posed the concept of markets of virtual products and
services to support cloud manufacturing ((Brodsky
et al., 2021)). However, the proposed concept lacked
the mathematical formalization which is necessary to
provide the theoretical basis for developing market
systems. Bridging this gap is exactly the focus of this
paper.
More specifically, in this paper we develop a for-
mal mathematical framework for markets of virtual
things: parameterized products and services that can
be searched, composed and optimized. The proposed
framework formalizes the notions of virtual product
and service design and customer-facing specs as well
as requirements’ specs. Based on these formal con-
cepts, the framework also formalizes the notions of
search for and composition of virtual products and
services that (1) are mutually consistent with the re-
quirement specs, (2) are Pareto-optimal in terms of
customer-facing metrics such as cost, product desir-
able characteristics and delivery terms; and (3) that
are optimal in terms of customer utility function that
is expressed in terms of customer facing metrics. We
also propose the design of a repository of virtual
things and their artifacts, to be used in support of the
market.
The paper is organized as follows. In Section 2 we
give an overview of the idea and associated key con-
cepts. Then in Section 3 we present the mathematical
formalization framework of the V-things. We illus-
trate with an example to show how various artifacts in
the framework are organized for composition, analyt-
ical and optimization purposes in Section 4. And we
conclude with possible directions for future works in
Section 5.
2 OVERVIEW OF V-THING
FRAMEWORK
In the traditional ideation to production value creation
chain, the entrepreneurs conceive their ideas of cer-
tain products, work with designers to sketch out their
ideas, build the prototypes, and then pass the techni-
cal specs onto the manufacturers for production. The
process requires expertise in various capabilities, and
is often inaccurate, slow and rigid. We desire to over-
come these defects through the productivity frame-
work of V-things that employees a fundamentally new
approach of connecting entrepreneurs with manufac-
turers in a bootstrapped marketplace of virtual prod-
ucts and services (shown as the V-Things Markets on
the right in Figure 1).
Within the marketplace of V-things, the virtual
products can be presented by their parameterized
CAD design, and searched by their parameters. The
virtual services are the parameterized transformations
of virtual products (assembly, transportation, etc.).
All virtual products and services have their own an-
alytical model respectively that describes their impor-
tant characteristics ((Brodsky et al., 2017)). When the
entrepreneurs are searching and composing the virtual
products in the design environment, they can utilize
the AI-powered decision guidance system to reach
optimal decisions (shown as the V-Thing Decision
Guidance System on the left in Figure 1). The design-
ers and manufacturers can also proactively participate
in the discovery of new market demands within the
V-thing marketplace using the V-thing design tools.
And insights can be drawn by analyzing the data in
the system with the avail of Decision Guidance Ana-
lytics Language ((Brodsky and Luo, 2015)).
Take for example that an entrepreneur wants to
make a new product of a special type of bicycle that
is non-existent in the real world. She can start with
searching for any virtual products that are similar to
her idea in the V-things markets. If she finds none,
she will consider building her own bike. First, she
will initiate her virtual bike project, and start to de-
scribe her idea of the bike. She may use the design-
by-sketch and design-by-example features to gener-
ate a design spec from scratch, or she can specify a
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things
407
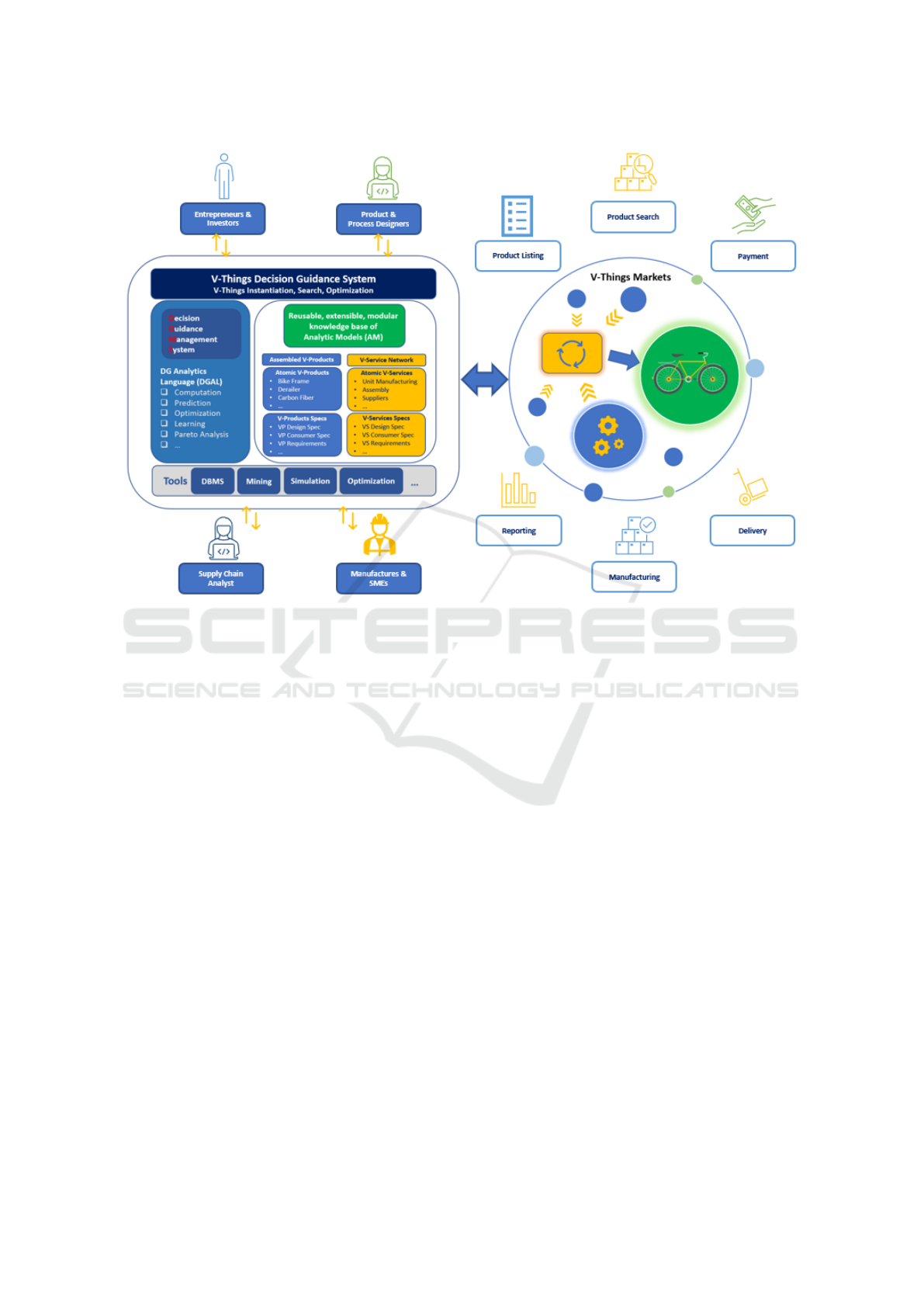
Figure 1: The V-Things Decision Guidance Ecosystem.
more definitive spec of the bike with its components
(bike frame, bike chain, tires, etc.). Second, she can
search again for the components of the bike as virtual
products in the marketplace, and if she cannot find
one, she can either design one or solicit for one with
a spec. The system will make recommendations and
guide her to make the best informed decisions along
the way. The entrepreneur can recursively find the
components or generate the specs of the components
for the bike that would closely approximate her orig-
inal idea. Third, she would solicit for the services
through which the components can be manufactured,
integrated and assembled into the final product. Af-
ter all constraints in the specs are verified to be fea-
sible by each virtual product component provider and
service provider, the entrepreneur can see the metrics
of manufacturing the bike that are generated and op-
timized by the analytical models (cost, time, carbon
emission, etc.). And she can see if the bike reflects
her original idea or not, then she can make a decision
whether to list the bike in the virtual marketplace.
If the entrepreneur thinks the product is satisfac-
tory and decides to take the go-to-market move, the
special bike virtual product will be made available for
the potential consumers in the marketplace. And the
entrepreneur can make further business decisions on
how to price, advertise, and deliver the product. The
potential consumers can see this special type of bike
in the V-things marketplace, what its physical proper-
ties and performance metrics are, how much it costs,
and how long it takes to deliver - everything about a
product that the consumers want to know except that
the product is in a virtual state in the sense that it is
“non-existent-yet” in the physical world.
If there is strong interest shown by the consumers
in the product, whether it comes through the number
of orders placed or the relevant discussions posted,
the entrepreneur will give the green light to put the
bike into actual production and start to ship it to the
consumers as a real product. She can take advantage
of the responsive market reaction as a pilot campaign.
After collecting enough user feedback data from the
marketing campaign and the product reviews, the en-
trepreneur can get informed of how well the con-
sumers have received this new product. From there
the entrepreneur can initiate a product launch with
calculated risk by listing the bike in the real-world
online or on-premise markets and sell the product to
the targeted user groups.
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
408

3 MATHEMATICAL
FORMALIZATION FOR
VIRTUAL THINGS
3.1 Virtual Products
Intuitively, a virtual product, which is defined for-
mally below, is a parameterized CAD design with
an associated analytic model that defines all feasible
parametric instantiations along with their consumer-
facing metrics. For example, a virtual product can
be a final product (a bike), a part of another prod-
uct (a bike fork or a wheel), or a raw material (steel).
The analytic models put the constraints on the virtual
products (the dimensions of the bike fork must fit that
of the wheels), and describe feasibility of the product
based on the parameters and metrics (a bike weighing
1 ton will be infeasible as it violates the tolerance of
the wheels).
Definition 3.1. A virtual product design spec (or VP
for short) is a tuple
V P =< domain, parametersSchema, metricSchema,
template, analyticModel, f easibilityMetric >
where
1. domain - is a set of all things under consideration.
E.g., all components that can be specified using
CAD design.
2. parametersSchema - is a set
PS = (p
1
, D
1
), . . . , (p
n
, D
n
)
of pairs, where for i = 1, . . . , n
(a) p
i
- a unique parameter name (e.g., geomet-
ric dimension, tolerance, density of material)
(fixed parameters vs decision variables)
(b) Di - the domain of p
i
3. metricSchema - is a set
MS = {(m
1
, M
1
), . . . , (m
k
, M
k
)}
of pairs, where for i = 1, . . . , k
(a) m
i
- a unique metric name (e.g., weight,
strength, volume, floatable (Boolean))
(b) M
i
- the domain of m
i
4. template - is a function
T : D
1
× · · · × D
n
→ Domain
which gives, for parameter instantiation
(p
1
, . . . , p
n
) in D
1
× ··· × D
n
, a specific thing in
the Domain of things.
5. analyticModel - is a function
AM : D
1
× · · · × D
n
→ M
1
× · · · × M
n
which gives, for parameter instantiation
(p
1
, . . . , p
n
) in D
1
× ··· × D
n
, a vector
(m
1
, . . . , m
k
), where (m
1
, . . . , m
k
) are metric
values in M
1
× · · · × M
k
. We will denote resulting
metric value m
i
, i = 1, . . . , n, using the (.) dot
notation as AM(p
1
, . . . , p
n
).m
i
or m
i
(p
1
, . . . , p
n
)
6. feasibilityMetric - is a Boolean metric name C in
{m
1
, . . . , m
n
} such that its corresponding domain
D = {T, F} in metricSchema MS (T to indicate
that parameter instantiation is feasible, and F oth-
erwise)
3.2 Specs of Virtual Products
In order to communicate the information between
multiple parties in the V-things marketplace, manu-
facturers may not want to disclose low-level design
parameters (in the parametric schema) but only dis-
close product metrics (in the metric schema) which
we assume contain all product information relevant
to consumers. For example, a consumer purchasing
a bike may only want to know the high-level com-
mercial and performance information about the bike
(such as price, weight, max speed and type) rather
than of the more granular supply chain metrics (such
as prices of the parts, dimensions of the bike pedals
and strength of the steel.) This notion is captured in
the concept of VP consumer-facing specs.
Definition 3.2. VP consumer-facing spec (or VP CFS
for short) is a tuple
δ =< domain, metricSchema, MFC >
where domain, metricSchema are as defined in VP,
and MFC : M
1
× ··· × M
k
→ {T, F} is a set of feasi-
bility constraints that tells, for every vector of metrics
in M
1
× · · · × M
k
, whether it is feasible or not.
Given a VP design spec, manufacturers may want
to extract a VP consumer-facing spec from it, defined
next.
Definition 3.3. VP consumer-facing spec derived
from VP design spec vp (denoted CFS(vp) for short).
Let
vp = (domain, parametersSchema, metricSchema,
template, analyticModel, f easibilityMetric)
be a VP design spec. The derived
consumer-facing spec CFS(vp) is a tuple
(domain, metricSchema, MFC), where MFC is
defined as follows: ∀(m
1
, . . . , m
k
) ∈ M
1
× ·· · × M
k
,
MFC(m
1
, . . . , m
k
) = ∃(p
1
, . . . , p
n
) ∈ D
1
×· ··×D
n
s.t.
(m
1
, . . . , m
k
) = AM(p
1
, . . . , p
n
) ∧C(p
1
, . . . , p
n
) = T
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things
409

Note: CFS(vp) defines the set of all feasible met-
ric vectors {(m
1
, . . . , m
k
)|(m
1
, . . . , m
k
) ∈ M
1
× ··· ×
M
k
∧ MFC(m
1
, . . . , m
k
)}
In order to enable the users to search for the VPs,
we introduce the VP Requirements spec. The purpose
of the Requirements spec is for the users to get con-
ditions for search as they put constraints on the VP
space.
Definition 3.4. VP (consumer) Requirements Spec
(or RS for short) is a tuple
RS =< domain, metricSchema,
ob jectiveSchema, ob jectives, MC, OC >
where
1. ob jectiveSchema is a set
OS = {(o
1
, O
1
), . . . , (o
l
, O
l
)}
of pairs, where for i = 1, . . . , l
(a) o
i
- a unique objective name (e.g., cost, risk,
time, etc.)
(b) O
i
- the domain of o
i
2. objectives: M
1
× ··· × M
k
→ O
1
× ··· × O
l
de-
fines objectives as a function of metrics i.e.,
ob jectives(m
1
, . . . , m
k
) is a vector of objective
values (O
1
, . . . , O
l
)
3. MC : M
1
× ·· · × M
k
→ {T, F} define feasibility
constraints in the metric space
4. OC : O
1
× ·· · × O
l
→ {T, F} define feasibility
constraints in the objective space
The user search should only render the results that
fall in the range of the constraints domains determined
by the product characteristics and specified by the
user. For example, a user searches for a bike with
weight not greater than 10 kg, and price not greater
than $200, then the result should only contain prod-
ucts that are feasible within the metrics ranges, and
also comply to the user specified objective domains.
Definition 3.5. VP Requirements Spec Constraints
Overall constraints of VP Requirements Spec
are the constraints C : M
1
× ··· × M
k
→ {T, F}
defined by: C(m
1
, . . . , m
n
) = MC(m
1
, . . . , m
n
) ∧
OC(ob jectives(m
1
, . . . , m
n
))
Note also that VP Requirements spec defines a set
of all feasible metric vectors R:
R = {(m
1
, . . . , m
n
)|(m
1
, . . . , m
n
) ∈
M
1
× · · · × M
n
∧C(m
1
, . . . , m
n
)}
To search for a VP in the marketplace, the user
specifies the VP Requirements Spec (RS), and the
system checks if any VP consumer-facing Spec (CFS)
matches the RS.
Definition 3.6. Search for VP
• Let
V P =< domain, parametersSchema,
metricSchema,template,
analyticModel, f easibilityMetric >
be a VP design spec. Out of parameter vec-
tor (p
1
, . . . , p
l
, . . . , p
n
) in parametersSchema, let
DV = (p
1
, . . . , p
l
) be designated as decision vari-
ables (without loss of generality). We use the term
fixed parameters for the vector of remaining pa-
rameters FP = (p
(l+1)
, . . . , p
n
).
• Let CFS =< domain, metricSchema, MFC > be a
VP (consumer-facing) Spec
• Let
RS =< domain, metricSchema,
ob jectiveSchema, ob jectives, MC, OC >
be a VP Requirements spec
• Let U : O
1
× · · · × O
l
→ R be a utility function
We say that:
• RS and CFS match (or CFS is feasible w.r.t. RS,
or CFS and RS are mutually consistent) if
1. they have identical domains and metric schema
(m
1
, M
1
), . . . , (m
k
, M
k
)
2. their joint constraint
C(m
1
, . . . , m
k
) = MC(m
1
, . . . , m
n
)
and OC(ob jectives(m
1
, . . . , m
n
)) and
MFC(m
1
, . . . , m
k
) are satisfiable
• A metrics vector (m
∗
1
, . . . , m
∗
k
) ∈ M
1
× ·· · × M
k
is
Pareto-optimal w.r.t. to RS and CFS if:
1. the joint constraint C(m
∗
1
, . . . , m
∗
k
) holds
2. there does not exist a metrics vector
(m
0
1
, . . . , m
0
k
) that
– satisfies the joint constraint C
– for objective vectors (o
∗
1
, . . . , o
∗
l
) =
ob jective(m
∗
1
, . . . , m
∗
k
) and (o
0
1
, . . . , o
0
l
) =
ob jective(m
0
1
, . . . , m
0
k
), (∀i = 1, . . . , l, o
0
i
>=
o
∗
i
) and (∃ j, 1 <= j <= l) such that o
0
j
> o
∗
j
• A metrics vector (m
∗
1
, . . . , m
∗
k
) ∈ M
1
× ·· · × M
k
is
optimal w.r.t. RS, CFS and U if:
(m
∗
1
, . . . , m
∗
k
) ∈ argmax(m
1
, . . . , m
k
)
∈ M
1
× · · · × M
k
(U(ob j ective(m
1
, . . . , m
k
)))
subject to C (m
1
, . . . , m
k
)
• Given a vector FP = (v
(l+1)
, . . . , v
n
) of fixed pa-
rameters, parameter vector (p
∗
1
, . . . , p
∗
n
) ∈ P
1
×
·· · × P
n
and the corresponding product p =
template(p
∗
1
, . . . , p
∗
n
) are Pareto-optimal w.r.t. RS,
VP and FP if:
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
410

1. the constraint C(p
∗
1
, . . . , p
∗
n
) =
MFC(AM(p
∗
1
, . . . , p
∗
n
)) and ∀ j = l + 1, . . . , n,
p
∗
j
= p
j
2. there does not exist a parameter vector
(p
0
1
, . . . , p
0
n
) that
– satisfies the constraint C, and
– for objective vectors (o
∗
1
, . . . , o
∗
l
) =
ob jective(AM(p
∗
1
, . . . , p
∗
n
)) and (o
0
1
, . . . , o
0
l
) =
ob jective(AM(p
0
1
, . . . , p
0
n
)), (∀i =
1, . . . , l)o
0
i
>= o
∗
i
) and (∃ j, 1 <= j <= l)
such that o
0
j
> o
∗
j
• Given a vector FP = (v
(l+1)
, . . . , v
n
) of fixed
parameters, a parameter vector (p
∗
1
, . . . , p
∗
n
) ∈
P
1
× · ·· × P
n
and the corresponding product p =
template(p
∗
1
, . . . , p
∗
n
) are optimal w.r.t. RS, VP, U
and FP if:
– (p
∗
1
, . . . , p
∗
n
) ∈ argmax(p
1
, . . . , p
n
) ∈ P
1
× ··· ×
P
n
(U(ob j ective(AM(p
1
, . . . , p
n
))) subject to
C(AM(p
1
, . . . , p
n
)) and ∀ j = l + 1, . . . , n, p
∗
j
=
p
j
Claim (follows directly from definitions): Given
CFS derived from VP, RS, U and let (m
∗
1
, . . . , m
∗
k
) =
AM(p
∗
1
, . . . , p
∗
n
). Then:
• (p
∗
1
, . . . , p
∗
n
) is Pareto-optimal w.r.t. RS and V P
⇐⇒ (m
∗
1
, . . . , m
∗
k
) are Pareto-optimal w.r.t. RS
and C FS
• (p
∗
1
, . . . , p
∗
n
) is optimal w.r.t. RS, V P and U ⇐⇒
(m
∗
1
, . . . , m
∗
k
) is optimal w.r.t. RS, CFS and U
3.3 Virtual Services
Intuitively, a virtual service is a parameterized trans-
formation function of zero or more virtual things into
zero or more virtual things. Virtual service is also as-
sociated with an analytic model, which gives metrics
of interest and the feasibility Boolean value, for every
instantiation of service parameters, which include pa-
rameters of input and output virtual things, as well as
additional internal parameters.
For example, a supply service transforms zero in-
put virtual things into output things that correspond to
a planned purchase (bike supply). Its metrics may in-
clude total cost and delivery time, as a function of pa-
rameters that capture catalog prices and ordered quan-
tities. Or, a manufacturing service transforms raw
materials and parts (virtual things) into products (vir-
tual things), like in the case of assembling bike parts
into a bike. Or, a CNC machining service transforms
an (virtual) input metal part into a processed (virtual)
part, after a series of drilling and milling operations
(turning steel material into a bike frame). Or, a trans-
portation service transforms (virtual) items at some
locations, into the same (virtual) items at some other
locations (shipping a bike from a factory to a cus-
tomer). Some services are associated with real-world
brick-and-mortar services; some may be defined by
a service network which involves sub-services. The
following definitions formalize these concepts.
Definition 3.7. A virtual service or VS is a tuple
V S = (input, out put, internalParametersSchema,
internalMetricSchema, analyticModel, f easMetric)
where
1. input - is a set {V T
i
|i ∈ I} of input virtual things,
where I is an input index set
2. out put - is a set {V T
i
|i ∈ O} of output virtual
things, where O is an output index set
3. internalParametersSchema - is a set
IPS = {(p
1
, D
1
), . . . , (p
n
, D
n
)}
of pairs, where for i = 1, . . . , n
(a) p
i
- a parameter name (e.g., quantities of input
or output things, prices, coefficients in physics-
based equations, control parameters of equip-
ment)
(b) Di - the domain of Pi
4. internalMetricSchema - is a set
IMS = {(m
1
, M
1
), . . . , (m
k
, M
k
)}
of pairs, where for i = 1, . . . , k
(a) m
i
- a metric name (e.g., cost, delivery time,
profit, carbon emissions)
(b) M
i
- the domain of m
i
Let the parametersSchema
PS = {(v
1
,V
1
), . . . , (v
s
,V
s
)}
be the union of parametersSchema of input
virtual products, output virtual products and
internalParametersSchemas.
Let the set
MS = {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
be the union of metricSchemas of input
virtual things, output virtual things, and
internalMetricSchema.
5. analyticModel - is a function
AM : V
1
× · · · ×V
s
→ MM
1
× · · · × MM
r
which gives, for parameter instantia-
tion (v
1
, . . . , v
s
) ∈ V
1
× ··· × V
s
, a vector
(mm
1
, . . . , mm
r
), where (mm
1
, . . . , mm
r
) are
metric values in MM
1
× ··· × MM
r
. We will
denote resulting metric value mm
i
, i = 1, . . . , r,
using the (.) dot notation as AM(v
1
, . . . , v
s
).m
i
or
m
i
(v
1
, . . . , v
s
)
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things
411

6. f easMetric - is a Boolean metric name C ∈
mm
1
, . . . , mm
r
such that its corresponding domain
D = {T, F} ∈ MS (T to indicate that parameter
instantiation is feasible, and F otherwise)
3.4 Specs of Virtual Services
Definition 3.8. VS Consumer Spec (projection on
metric space of VS) that only reveals partially to the
consumers is a tuple
< input, out put, internalMetricSchema, MC >
where
• input - is a set of VP (consumer-facing) specs
< domain, metricSchema, MFC >
• out put - is a set of VP (consumer-facing) specs
< domain, metricSchema, MFC >
• internalMetricSchema is a set
IMS = {(m
1
, M
1
), . . . , (m
k
, M
k
)}
of pairs, where for i = 1, . . . , k
1. m
i
- a metric name (e.g., cost, delivery time,
profit, carbon emissions)
2. M
i
- the domain of m
i
Let metric schema
MS = {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
be the union of metricSchemas of input
virtual things, output virtual things, and
internalMetricSchema.
• MC : MM
1
× · · · × MM
r
→ {T, F} which tells,
for every vector of metrics in MM
1
× ··· × MM
r
,
whether it is feasible or not.
Definition 3.9. VS Requirement Feasibility Spec is a
tuple
< input, out put, internalMetricSchema,
ob jectiveSchema, ob jectives, MC, OC >
where
• input is a set of (input) VP requirement specs
• out put is a set of (output) VP requirement specs
• internalMetricSchema is a set
IMS = {(m
1
, M
1
), . . . , (m
k
, M
k
)}
of pairs, where for i = 1, . . . , k
1. m
i
- a metric name (e.g., cost, delivery time,
profit, carbon emissions)
2. M
i
- the domain of m
Let metric schema
MS = {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
be the union of metricSchemas of input
virtual things, output virtual things, and
internalMetricSchema.
• ob jectiveSchema is a set
OS = (o
1
, O
1
), . . . , (o
l
, O
l
)
of pairs, where for i = 1, . . . , l
1. o
i
- a unique objective name (e.g., cost, profit,
time, carbon emissions )
2. O
i
- the domain of o
i
• ob jectives : MM
1
× ·· · × MM
r
→ O
1
× ·· · × O
l
defines objectives as a function of metrics, i.e.,
ob jectives(mm
1
, . . . , mm
r
) is a vector of objective
values (o
1
, . . . , o
l
) ∈ O
1
×·· · × O
l
associated with
metrics (mm
1
, . . . , mm
r
)
• MC : MM
1
× · · · × MM
r
→ {T, F}
• OC : O
1
× · · · × O
l
→ {T, F}
Definition 3.10. VS Requirements Spec Constraints
Overall constraints of VS Requirements Spec are
the constraints
C : MM
1
× · · · × MM
r
→ {T, F}
defined by:
(mm
1
, . . . , mm
r
) = MC(mm
1
, . . . , mm
r
)∧
OC(ob jectives(mm
1
, . . . , mm
r
))
Note also that VS Requirements Spec defines a set
of all feasible metric vectors R:
R = {(mm
1
, . . . , mm
r
)|(mm
1
, . . . , mm
r
) ∈
MM
1
× · · · × MM
r
∧C(mm
1
, . . . , mm
r
)}
Definition 3.11. Search for VS
• Let
V S = (input, out put, internalParametersSchema,
internalMetricSchema, analyticModel, f easMetric)
be a virtual service design spec.
• Let
PS = {(v
1
,V
1
), . . . , (v
s
,V
s
)}
be the parameter schema of VS.
• Let
MS = {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
be the metric schema of VS. Out of VS parameter
vector (v1, . . . , v
h
, . . . , v
s
) in internalParametersS-
chema, let DV = (v
1
, . . . , v
h
) be designated as de-
cision variables (without loss of generality). We
use the term fixed parameters for the vector of re-
maining parameters FP = (v
(l+1)
, . . . , v
s
).
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
412

• Let
CFS =< input, out put, internalMetricSchema, MC >
be a virtual service consumer-facing spec.
• Let
MS = {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
be the metric schema of CFS.
• Let
RS =< input, out put, internalMetricSchema,
ob jectiveSchema, ob jectives, MC, OC >
be a virtual service requirements spec.
• Let
MS = {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
be the metric schema of RS.
• Let U : O
1
× · ·· × O
l
→ R (the set of reals) be a
utility function, where O
1
, . . . , O
n
are the domains
from the objective schema
OC = {(o
1
, O
1
), . . . , (o
l
, O
l
)}
We say that:
• RS and CFS match (or CFS is feasible w.r.t. RS,
or CFS and RS are mutually consistent) if
1. they have the same input, output and metric
schemata {(mm
1
, MM
1
), . . . , (mm
r
, MM
r
)}
2. the joint constraint CC(mm
1
, . . . , mm
r
) defined
as the conjunction of C(mm
1
, . . . , mm
r
)
and MC(mm
1
, . . . , mm
r
) is satisfiable,
where C(mm
1
, . . . , mm
r
) is the overall con-
straint of the VS Requirements Spec, and
MC(mm
1
, . . . , mm
r
) is the metric constraint of
the VS consumer-facing spec
• A metrics vector (mm
∗
1
, . . . , mm
∗
r
) ∈ MM
1
× ·· · ×
MM
r
is Pareto-optimal w.r.t. to RS and CFS if:
1. the joint constraint CC(mm
∗
1
, . . . , mm
∗
r
) holds
2. there does not exist a metrics vector
(mm
0
1
, . . . , mm
0
r
) that
– satisfies the joint constraint CC
– for objective vectors (o
∗
1
, . . . , o
∗
l
) =
ob jective(m
∗
1
, . . . , m
∗
k
) and (o
0
1
, . . . , o
0
l
) =
ob jective(m
0
1
, . . . , m
0
k
) the following
holds: (∀i = 1, . . . , l, o
0
i
>= o
∗
i
) and
(∃ j, 1 <= j <= l) such that o
0
j
> o
∗
j
• A metrics vector (mm
∗
1
, . . . , mm
∗
r
) ∈ MM
1
×
·· · × MM
r
is optimal w.r.t. RS, CFS and U
if: (mm
∗
1
, . . . , mm
∗
r
) ∈ argmax(mm
1
, . . . , mm
r
) ∈
MM
1
× ··· × MM
r
(U(ob j ective(mm
1
, . . . , mm
r
)))
subject to CC(mm
1
, . . . , mm
r
)
• Given a vector FP = (v
(h+1)
, . . . , v
s
) of fixed pa-
rameters, parameter vector (v
∗
1
, . . . , v
∗
s
) ∈ V
1
×
·· · × V
s
(and the corresponding product p =
template(v
∗
1
, . . . , v
∗
s
) ) are Pareto-optimal w.r.t.
VS, RS and FP if:
– the following constraint is satisfied:
CC(v
∗
1
, . . . , v
∗
h
, . . . , v
∗
s
) = MC(AM(v
∗
1
, . . . , v
∗
s
))
∧(∀ j = h + 1, . . . , s, v
∗
j
= v
j
) ∧C(v
∗
1
, . . . , v
∗
s
),
where MC is the metric constraint from RS, and
C is the feasibility metric from VS.
– there does not exist a parameter vector
(v
0
1
, . . . , v
0
s
) that
*
satisfies the constraint CC, and
*
for objective vectors (o
∗
1
, . . . , o
∗
l
) =
ob jective(AM(p
∗
1
, . . . , p
∗
n
)) and
(o
0
1
, . . . , o
0
l
) = ob jective(AM(v
0
1
, . . . , v
0
s
)),
(∀i = 1, . . . , l, o
0
i
>= o
∗
i
) and (∃ j, 1 <= j <=
l) such that o
0
j
> o
∗
j
• Given a vector FP = (v
(h+1)
, . . . , v
s
) of fixed pa-
rameters, parameter vector (v
∗
1
, . . . , v
∗
s
) ∈ V
1
×
·· · × V
s
and the corresponding product p =
template(v
∗
1
, . . . , v
∗
s
) are optimal w.r.t. VS, RS, U
and FP if:
– (v
∗
1
, . . . , v
∗
h
, v
∗
(h+1)
. . . , v
∗
s
) ∈
argmax(v
∗
1
, . . . , v
∗
s
) ∈ V 1 × ··· × Vs
(U(ob j ective(AM(v
∗
1
, . . . , v
∗
s
)) subject to
CC(v
∗
1
, . . . , v
∗
h
, . . . , v
∗
s
) = MC(AM(v
∗
1
, . . . , v
∗
s
))
and (∀ j = h + 1, . . . , s, v
∗
j
= v
j
) and
C(v
∗
1
, . . . , v
∗
s
), where MC is the metric con-
straint from RS, and C is the feasibility metric
from VS.
Claim (follows directly from definitions):
Given CFS derived from VP, RS, U and let
(mm
∗
1
, . . . , mm
∗
r
) = AM(v
∗
1
, . . . , v
∗
s
), then:
• (v
∗
1
, . . . , v
∗
s
) is Pareto-optimal w.r.t. VS, RS, and
FP if and only if (mm
∗
1
, . . . , mm
∗
r
) are Pareto-
optimal wr.t. RS and CFS
• (v
∗
1
, . . . , v
∗
s
) is optimal w.r.t. VS, RS, FP and U if
and only if (mm
∗
1
, . . . , mm
∗
r
) is optimal wr.t. RS,
CFS and U
4 V-THING REPOSITORY
4.1 Architecture Overview
To enable rapid and convenient creation of V-things,
we put the definitions into a more recognizable form
of software implementation of the V-things market-
place. The challenge is how to organize the reposi-
tory so that the artifacts can be stored hierarchically
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things
413

and connected seamlessly to the conceptual schema.
In this section we show the organization of the fun-
damental artifacts (virtual products, virtual services,
specs, analytical models, utility functions, etc.) and
we demonstrate the composition of a V-thing with the
example of a virtual bike product.
Figure 2: The Repository Design.
We create a software project and separate the ab-
stractions of data objects and of model objects in the
repository (shown in Figure 2). On the high level,
the data folder contains the user-specified artifacts,
including the instances of V-things, and the spec in-
stances. These are all organized under the Bikes
project associated with the user. In the lib folder we
put the more functional elements including the tem-
plates, the analytical models and the V-thing operators
which can be readily reused.
Each artifact is stored in its own file in the sys-
tem, and has its unique file identifier in the entire sys-
tem. The identifier consists of the directory path from
the root to the folder containing the file plus the file
name. To achieve referential integrity in the file sys-
tem, it necessities that in the local environment, say,
within the same folder, each file and folder must have
a unique name, which is ensured by most of the mod-
ern operating systems.
4.2 Artifacts in the Repository
We view all the virtual things as the digital instances
in the form of parametric data. For broad compati-
bility, the data is stored as JSON objects in the form
of JSON files. And we differentiate the access rights
to the data based on the types of the instances or the
specific files which the user groups have interests in.
Figure 3: The Data Artifacts.
Under the userProjects directory, the users can ini-
tiate their virtual thing project ad hoc either by cre-
ating from scratch or by importing from a different
source. A user can have arbitrarily many projects of
interest created or imported. In our example, we have
created the Bikes project (Figure 3).
For the instance data associated with the virtual
bike product, there is a distinction between the V-
thing objects and their specs. While the specInstances
folder hosts all the specs (CFS, VP Spec, VS Spec,
RS, RS Constraints, etc.) for the V-thing, the vtIn-
stances folder hosts the actual instances of the V-
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
414

things in the vpInstances folder for virtual products
and the vsInstances folder for virtual services respec-
tively.
4.2.1 VP Instances
Specifically for a virtual product, vBike for example,
it can have zero, one or multiple instances depending
on how the user wants to instantiate the virtual prod-
uct. The vpInstances folder holds the instances for the
bike parts which are virtual products as well.
A virtual product instance is described by a JSON
file named by the virtual product plus an ID. Each
file contains one JSON object according to its schema
in the VP Design Spec. A example of the data in
vBike0.json file is shown in Figure 4.
For each virtual product instance file, it can have
an optional context header, marked by “@context”
annotation. Each entry within the context object spec-
ifies a shortcut for a directory path which we call a
context. Whenever the program processing data for
a virtual product, it would recognize and convert the
“@” annotated shortcut to the full path. The “model”
entry links the data to the analytical model. And the
“bike” sub-object contains the parametric data for the
virtual product. Important information as whether it is
an atomic product or a composite product is recorded.
And if it is a composite product, which means it has
composed of other virtual products, the components
are also recorded. And key metrics information for
the bike virtual product is attached.
Another example is shown below for an atomic
virtual product in Figure 5. The vBikeChain0.json file
contains the data of a virtual bike chain product. In-
stead of being composed by other products, it is an
atomic product, which can be used in a stand-alone
manner or as a component for other virtual products
and services.
4.2.2 VS Instances
For virtual services, the data is organized differently
than that of the virtual products. As the virtual ser-
vices describe the flow of materials and labor, they are
more process-based. While the users are interested in
the metrics of a service, the essential information for
the processes should also be captured by the virtual
services. An example of a bike assembly service is
shown in file bikeAssembly0.json (Figure 6).
The information about the flows is reflected in the
schematic sections of inflow, outflow, flows and prod-
ucts respectively. The inflows direct what products
and materials and how they are passed into the ser-
vice. The outflows are the virtual products that will
be rendered by the virtual service, and there can be
Figure 4: Composite VP Instance.
Figure 5: Atomic VP Instance.
none. The flows summarise how each product plays a
part role in comprising the final outflow product. And
the products section records the relevant parametric
data of the inflow products that will be used for pro-
cessing and analytical purposes in the service.
4.3 V-Thing Creation
While an atomic V-thing can be created from scratch
with the parameters schema, a composite V-thing may
have parts in it that are also V-things. A composite
V-thing may already contain all the data from its sub-
components, but if not, that means, some of the data
is stored in the V-thing files that may not have been
created, and thus instantiation is needed. References
are used as placeholders to point each missing part
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things
415

Figure 6: Bike Assembly VS Instance.
to a “yet-to-exist” V-thing which we call a partial V-
thing. In that case, the entrepreneur should solicit in
the V-thing Market for the missing parts with a spec.
Once a V-thing is provided in accordance to the spec,
an instantiation function will be applied that pulls in
the data from the component V-thing file, replaces the
reference, and renders a full data file for the compos-
ite V-thing.
For example, a virtual bike assembly service will
create a virtual bike product out of its parts (bike
chain, bike frame, brakes, derailers, front fork, gears,
Figure 7: Partial V-Thing.
Figure 8: Instantiated V-Thing.
handle bars, pedals, seats, tires, and wheels). Among
the parts, there is no suitable bike chain or bike frame
virtual product that is readily available in the market.
Then the entrepreneur lists her demand with the Re-
quirements Specs for the bike chain and bike frame
in the market, while she continues building the virtual
bike product through the assembly service. The parts
that await to be instantiated are marked with “@pro-
ductRef” annotation indicating the data is not yet
plugged in (under flows, bikeChain0 and bikeFrame0
have no correspondent entry under products as shown
in Figure 7). Once the data is ready for the compo-
nent V-things, the entrepreneur will go ahead and ap-
ply the instantiation function, and the full data file will
be generated for subsequent processing. (V-thing data
entries are attached under products for vBikeChain
and vBikeFrame as shown in Figure 8).
ICEIS 2022 - 24th International Conference on Enterprise Information Systems
416

4.4 Operators in the Repository
Operators are needed upon the repository in order to
adequately manipulate the V-things. A V-thing can be
created, updated, queried and deleted, and the oper-
ators should enable these operations. We implement
the operators as utility functions and group them un-
der the lib directory. When there is a need to conduct
certain operations on the V-things data, the user can
make use of the operators through the APIs or on the
user interface to interact with the V-things artifacts in
the repository.
In particular, we exemplify the instantiation oper-
ator which is of significance. The instantiation op-
erator, or instantiator, is a function that recursively
checks each component of a V-thing and instantiates
with the referenced data, turning the partial V-thing
into a full data file for further processing or analytical
use. Please note that the instantiator should not mod-
ify the original input. The contract for the instantiator
is as follows:
instantiator(input):
"""
Requires: non-null non-empty V-thing input
Effects: if input is an instantiated
V-thing, return a copy of this;
else recursively instantiate
each referenced component
"""
5 CONCLUSIONS
We developed a formal mathematical framework for
markets of virtual things or V-things: parameterized
products and services that can be searched, composed
and optimized. We also proposed a design of a repos-
itory of virtual things and their artifacts, to be used
in support of the market. The proposed markets of
virtual thing have the potential to make ideation-to-
manufacturing process considerably more accessible,
predictable and agile. This, in turn, can democratize
innovation by allowing entrepreneurs without design
and manufacturing expertise to bring their ideas to
markets quickly.
Many research questions remain open, including
how to develop a system for entrepreneurs to formu-
late their ideas in V-things, how to guide the users
to make optimized decisions, and how effective the
V-thing markets are in facilitating the ideation-to-
production process.
REFERENCES
Brodsky, A., Gingold, Y. I., LaToza, T. D., Yu, L., and Han,
X. (2021). Catalyzing the agility, accessibility, and
predictability of the manufacturing-entrepreneurship
ecosystem through design environments and markets
for virtual things. In Proceedings of the 10th Inter-
national Conference on Operations Research and En-
terprise Systems, ICORES 2021, Online Streaming,
February 4-6, 2021, pages 264–272. SCITEPRESS.
Brodsky, A., Krishnamoorthy, M., Nachawati, M. O., Bern-
stein, W. Z., and Menasc
´
e, D. A. (2017). Manu-
facturing and contract service networks: Composi-
tion, optimization and tradeoff analysis based on a
reusable repository of performance models. In 2017
IEEE International Conference on Big Data (IEEE
BigData 2017), Boston, MA, USA, December 11-14,
2017, pages 1716–1725. IEEE Computer Society.
Brodsky, A. and Luo, J. (2015). Decision guidance ana-
lytics language (DGAL) - toward reusable knowledge
base centric modeling. In ICEIS 2015 - Proceedings
of the 17th International Conference on Enterprise In-
formation Systems, Volume 1, Barcelona, Spain, 27-30
April, 2015, pages 67–78. SciTePress.
Egge, N. E., Brodsky, A., and Griva, I. (2013). An effi-
cient preprocessing algorithm to speed-up multistage
production decision optimization problems. In 46th
Hawaii International Conference on System Sciences,
HICSS 2013, Wailea, HI, USA, January 7-10, 2013,
pages 1124–1133. IEEE Computer Society.
Gingold, Y. I., Igarashi, T., and Zorin, D. (2009). Struc-
tured annotations for 2d-to-3d modeling. ACM Trans.
Graph., 28(5):148.
LaToza, T. D., Shabani, E., and van der Hoek, A. (2013).
A study of architectural decision practices. In 6th
International Workshop on Cooperative and Human
Aspects of Software Engineering, CHASE 2013, San
Francisco, CA, USA, May 25, 2013, pages 77–80.
IEEE Computer Society.
Shao, G., Brodsky, A., and Miller, R. (2018). Modeling and
optimization of manufacturing process performance
using modelica graphical representation and process
analytics formalism. J. Intell. Manuf., 29(6):1287–
1301.
Shin, S., Kim, D. B., Shao, G., Brodsky, A., and Lecheva-
lier, D. (2017). Developing a decision support system
for improving sustainability performance of manufac-
turing processes. J. Intell. Manuf., 28(6):1421–1440.
Yu, L.-F., Yeung, S. K., Tang, C., Terzopoulos, D., Chan,
T. F., and Osher, S. J. (2011). Make it home: automatic
optimization of furniture arrangement. ACM Trans.
Graph., 30(4):86.
Toward Cloud Manufacturing: A Decision Guidance Framework for Markets of Virtual Things
417
