Fostering Computational Thinking in Undergraduated Music

Conservatory Students

Marcella Mandanici

Music Conservatory ”L. Marenzio”, p.tta A.B. Michelangeli 1, 25121 Brescia, Italy

Keywords:

Computational Thinking, Music Technology, Programming Skills, The ”Four C’s”.

Abstract:

This paper presents and discusses the syllabus of a music technology course at undergraduate level in a Music

Conservatory. The aim of the course is to introduce the students to computational thinking through the use

of Pure Data, a free visual programming environment for music production. Starting from very basic notions

in music technology and in the use of the program, the students are guided towards the knowledge of the

fundamental steps of computational thinking in music production. Simple musical structures such as pattern

repetition, transposition, polyphony and chords are implemented with the use of loops, abstractions, cycles,

pattern storage systems and timing controls. While students become acquainted with these processes, also

creative group activities are proposed with the aim of exploring the potentialities of the numeric control of

sound events and musical form.

1 INTRODUCTION

Enhancing digital skills and competences for the dig-

ital transformation is one of the two priority areas of

the Digital Education Action Plan 2021-2027

. Pro-

moted by the European Union, the Digital Education

Action Plan supports the effort of the educational sys-

tems to adapt to the digital age. Digital competences

are considered an essential part of the curriculum of

the XXI century citizen mainly after the experience of

the Covid-19 pandemic, which led teachers and stu-

dents to adopt as soon as possible digital tools to pre-

serve school activities. For instance in the ﬁeld of mu-

sic education the importance of the use of web plat-

forms, music production software and in general of

digital music education tools emerged with unprece-

dented evidence, showing all their strong potentiali-

ties (Avanzini et al., 2021). This trend is conﬁrmed

by the ﬁgures collected in the open public consulta-

tion on the Digital Education Action Plan 2021-2027

which show that:

• almost 60% of respondents had not used distance

and online learning before the crisis

• 95% consider that the Covid-19 pandemic marks

a turning point for how technology is used in ed-

ucation and training

https://orcid.org/0000-0003-1863-4178

https://education.ec.europa.eu/focus-topics/digital/

education-action-plan

• over 60% felt that they had improved their digital

skills during the crisis

Computational thinking is the core of digital skills be-

cause it describes a set of attitudes and ways of think-

ing that allow humans to communicate with machines

(Cuny et al., 2010; Shute et al., 2017). According to

(Selby and Woollard, 2014), these can be represented

by three fundamental ideas:

• the thought process

• the concept of abstraction

• the concept of decomposition.

The though process includes ” ... formulating prob-

lems so their solutions can be represented as compu-

tational steps and algorithms.” (Aho, 2012) and im-

plies abilities in problem solving (Wing, 2011), anal-

ysis and pattern recognition. Abstraction is the pro-

cess of deciding what aspects of the problem to be

solved are essential and need to be included in the

algorithm and what can be neglected (Wing, 2008).

It implies the ability to generalize a problem among

many other similar cases and to write simpler and

more widely reusable code. Finally, decomposi-

tion is the ability of breaking down a big problem

into smaller parts and it is necessary when manag-

ing complex tasks (Selby and Woollard, 2014). Com-

https://ec.europa.eu/info/law/better-regulation/have-

your-say/initiatives/12453-Digital-Education-Action-Plan/

public-consultation

Mandanici, M.

Fostering Computational Thinking in Undergraduated Music Conservatory Students.

DOI: 10.5220/0011134600003182

In Proceedings of the 14th International Conference on Computer Supported Education (CSEDU 2022) - Volume 1, pages 449-457

ISBN: 978-989-758-562-3; ISSN: 2184-5026

449

putational thinking in education is also connected to

the ”Four C’s” that characterize the ”Learning and In-

novation Skills” for the XXI century learning. The

”Four C’s” stand for Critical thinking, Creativity, Col-

laboration and Communication and embrace a series

of social skills such as performance, simulation, ap-

propriation, multitasking, distributed cognition, col-

lective intelligence, judgement, transmedia naviga-

tion, networking and others (Jenkins, 2009). Critical

thinking refers to the ability of evaluating the relia-

bility of different information sources but also to the

ability of checking the effectiveness of different solu-

tions to solve a problem. Creativity is the ﬁnal stage

of the learning process in the revised Bloom’s taxon-

omy (Krathwohl, 2002), which considers the ability

of putting the elements together to produce a new co-

herent whole as the maximum level of cognitive de-

velopment. Creativity is also very important, mainly

when computational thinking is applied in the ﬁeld of

artistic expression.

Figure 1: The SAMR (Substitution, Augmentation, Modi-

ﬁcation and Redeﬁnition) model with its fundamental steps

(Enhancement and Transformation).

The SAMR model establishes four lev-

els of technology integration in education

(Hamilton et al., 2016). Starting from the lower

level (simple tool substitution), the model drives the

attention towards the higher one (content redeﬁni-

tion), stressing the cognitive value of discovering

tasks and performance possibilities impossible

without the use of technology (see Figure 1). Here is

where computational thinking in artistic production

hits its ﬁnal point, realizing artifacts and ways of

expression previously inconceivable. Giving a look

at the history of electronic and computer music

(Copeland and Long, 2017; Collins et al., 2013),

hundreds of examples of music ”redeﬁnition” and

”transformation” can be found in the evolution and in

the artistic use of sound synthesis techniques and al-

gorithmic composition, providing thus the best proof

of the intimate connection between computational

thinking and creativity. Collaboration is the ability

of working together to reach a common goal. It is

particularly important in the process of technology

integration because it helps in overcoming difﬁculties

and knowledge gaps (consider for instance the role

of blogs and online communities of practitioners

where to share information and solutions to speciﬁc

problems). Finally, communication is a fundamental

ability when working with others. It is also the

core of the artistic work and of its propagation

through customized platforms, social media and

video production.

In spite of the long and important tradition

of electronic and computer music - which is in-

timately connected to computational thinking - re-

ally very few examples of application of this kind

of knowledge can be found in music education

(Israel-Fishelson and Hershkovitz, 2022). In Section

2 current approaches, software and tools are presented

with the aim of providing a short overview of compu-

tational thinking in music education. Particularly the

work of V.J. Manzo (Manzo, 2016) has inspired the

design of the course presented in this paper, which

will be examined in detail in Section 3. The character-

istics of computational thinking and the peculiarities

of the ”Four C’s” above discussed will be referenced

in the presentation of the course contents, with a par-

ticular focus on creativity that should be regarded as

one of the most important goals of the course. Assess-

ment methods and tools will be discussed in Section

4, and conclusions drawn in Section 5.

2 COMPUTATIONAL THINKING

IN MUSIC EDUCATION

The few experiences of computational thinking in

music education found in literature refer to a limited

set of approaches and software tools. Some of them

address the problem of introducing computational

thinking from the very early stages of school curricu-

lum through various strategies. (Bell and Bell, 2018)

suggest an interesting embodied experience of a phys-

ical parallel sorting network, a game which results

in obtaining elements in ascending order. Extension

of this game beyond simple numerical values can in-

volve various domains such as music (putting sounds

or notes in ascending order) or language (putting

names in alphabetical order, or story elements in

temporal order), and so on. Beyond demonstrating

the power of abstraction in a very simple and effec-

tive way, this game also recalls the concept of al-

CSME 2022 - 3rd International Special Session on Computer Supported Music Education

450

gomotricity, which is an approach based on kines-

thetic learning activities aimed at highlighting spe-

ciﬁc computer science topics (Bellettini et al., 2014).

Another activity proposed by (Bell and Bell, 2018) is

the use of little robots programmed to reach spe-

ciﬁc positions on a physical stave as to produce

sound events (melodies or chords). This idea de-

rives directly from the famous Logo turtle by Sey-

mour Papert, the father of computer-based environ-

ments aimed at teaching computation to children

(Resnick et al., 1988). The same authors also em-

ploy Scratch, a very popular visual programming

language, used both at elementary and university

level (Maloney et al., 2010). As Greher and Heines

afﬁrm in their book (Greher and Heines, 2014), al-

though Scratch is designed for children it offers

important tools for teaching computational thinking

such as code blocks, global and local variables, lists,

loops, conditionals, etc. Another popular similar re-

source is Blockly, a visual block language develop-

ment kit that allows the building of programs aimed

at various educational goals (Trower and Gray, 2015).

Blockly has been used by (Barat`e et al., 2017) to

build a platform for melody composition and ma-

nipulation, or by (Gorson et al., 2017) to produce a

sound composition tablet application. Another trend

in the development of computational thinking is the

use of command-line languages for music produc-

tion. These are Sonic Pi (Aaron et al., 2016) and

Ear Sketch (Engelman et al., 2017). While Sonic Pi

is more oriented towards live performance impro-

visations, Ear Sketch aims at engaging students to

learn programming through sound. Both programs

address high school and university students. Vi-

sual programming is very popular among musicians,

as the main software in use belong to this family

of programs (MAX

and Pure Data

). The Pure

Data free programming environment has been used

by (Hancock, 2014) to develop a play-based learn-

ing course to introduce Conservatory students to mu-

sic programming. A step by step approach is fol-

lowed by (Manzo, 2016) who - reﬂecting the tradi-

tional environment division of Max, MSP (audio) and

Jitter (video) - presents basic programming activities

in three main domains: algorithmic composition and

music training (MIDI); audio playback, processing

and effects (audio); live and recorded video. Partic-

ularly in the ﬁrst section of the book the author pro-

vides the very basic notions of programming in the

MAX environment to lead the students to the produc-

tion of simple musical structures (scales, intervals and

chords). This is an interesting approach for Conserva-

https://cycling74.com/products/max

https://puredata.info/

tory students for at least two reasons: ﬁrstly very ba-

sic music features may unveil their algorithmic side,

showing how computational thinking is deeply rooted

in music analysis; secondly the step-by-step method

followed by the author very well shows the process of

abstraction from particular cases towards more tidy,

less redundant and general ways of formulating the

same algorithm. These ideas inspired the methodol-

ogy and contents of the music technology course that

is the focus of this paper.

3 COURSE DESIGN

In the current programs for undergraduate instrumen-

tal studies in Italian Conservatories the technological

courses (Acoustics and Music Technology) weight re-

spectively 2 and 3 ECTS (less than the 3% of the over-

all 180 ECTS). Thus very often they are underesti-

mated by teachers and students as they result com-

pletely disconnected from the other subjects of the

curriculum. Yet, what little technological integration

is entrusted only to these subjects. This is why the

design of the course of Music Technology is so im-

portant and should be regarded as the only occasion

to meet computational thinking in the whole under-

graduate Conservatory curriculum.

3.1 Course Objectives

The course activities aim at the following goals:

1. introducing the students to computational think-

ing by enhancing their abilities in music analysis

and abstraction of musical concepts

2. fostering the potentialities of music creativity

through the manipulation and numeric control of

simple music production algorithms

3. offering them an experience related to the ”Four

C’s” (critical thinking, creativity, collaboration

and communication).

3.2 Material

The course is developed in Pure Data, which is a

free always available software, while MAX requires

to buy a license. MAX is very rich from the graph-

ical point of view and can rely on a lot of support-

ive tools. In spite of this, also if Cycling’74 offers

many facilities (academic licenses, institutional dis-

counts, monthly payments, 30 days free demos), the

advantages of a free software are greater for non pro-

fessional users. Thus, some of the basic algorithms

presented by (Manzo, 2016) have been ported in Pure

Fostering Computational Thinking in Undergraduated Music Conservatory Students

451

Table 1: Course organization and content.

Week Lesson Workshop Home work

Introduction

Computational thinking

The ”Four C’s”

Introduction to Pure Data

Controlling numerical ﬂow

(

+random+,+moses+,+clip+)

Pre-course questionnaires

lab1

assignment (logic)

Audio and MIDI

MIDI events

MIDI production

(noteout, makenote)

MIDI controls

(modulation, volume,

pan and sustain)

lab2 assignment

(exploration)

Counter

(recursivity, reset, loops)

The

+counter+

abstraction.

A pattern of a musical form.

lab3 assignment

(musical form)

4 Scales (midi notes and arrays)

Major and minor scales.

Scale transposition

lab4 assignment

scale fragments

(creativity)

Musical structures

(patterns, polyphony, chords)

Pattern repetition (cycles),

polyphony

lab5 assignment (chords)

6 Melodies

Augmentation,

musical streams

lab6 assignment (creativity)

7 Patch modules

Work group.

Graphical scores

Final group assignment

8 Group assignment discussion Group assignment discussion

Delivery of the ﬁnal project

Post-course questionnaires

Data and further processed to comply the course pro-

gram.

3.3 Organization and Participants

The course is addressed to Music Conservatory stu-

dents at undergraduate level. To access this level a

high school diploma is required, also if exceptions are

allowed in case of particularly gifted students. The

course takes 24 hours, subdivided into 8 weeks start-

ing from February 8, 2022. It is held online through

the institutional platform of the Conservatory

. All

the activities are recorded and made available for the

students until about two weeks after the end of the

course, expected for March 29, 2022. The credits

for each lesson are assigned only after delivery of

the assignments contained in the videos. Currently

take part in the class 55 students (24 females), aged

Mean = 23.43 years, StandardDeviation = 7.75.

3.4 Contents

The program of the course is reported in detail in Ta-

ble 1

. Course activities are subdivided into lessons -

where each topic is presented in detail by the teacher

-, and workshop activities - where each topic is put

in practice through the realization of exercises with

the participation of the whole class -. Each lesson

has its own home assignment, where the students are

https://en.wikipedia.org/wiki/Google

Classroom

The patches used in the course are available at https://

github.com/marmanda/CompT

required to develop autonomously the topics experi-

enced during the lesson. The course activities are in-

spired by the ”Four C’s” abilities, whose ﬁnalization

is described in the following Sections 3.4.1, 3.4.2, and

3.4.3.

3.4.1 Problem Solving and Abstraction

The ability of solving a problem is linked to critical

thinking and to out of the box reasoning. Here the fo-

cus is not only on simple problem solving, but rather

on the ability of formulating the solution in a gen-

eral way, such to be reused in different conditions (ab-

straction). To show an example of this process, let’s

look at the activities of week 4, which focus on the

building of a musical scale. The ﬁrst step shows an

algorithm for the production of a C major scale, start-

ing from MIDI pitch 60 (see Figure 2).

Figure 2: The basic algorithm for the production of a C

major scale.

To allow the building of the scale on different fun-

damental pitches, the algorithm may be changed as in

Figure 3, where the concept of the use of a variable

(the fundamental pitch of the scale) is introduced.

CSME 2022 - 3rd International Special Session on Computer Supported Music Education

452

Figure 3: The algorithm for the production of a C major

scale with the use of the fundamental pitch variable.

The ﬁnal solution proposed is depicted in Figure 4

where the use of an

+array+

containing the interval

information related to each scale provides a good de-

gree of ﬂexibility and generalization. The contents of

the

+array+

may be changed with a message; the in-

tervals to be summed to the fundamental of the scale

are available as the output of the

+tabread+

object af-

ter it receives the index number.

The algorithm of Figure 5 produces a scale fol-

lowed by its transpositions one fourth and one ﬁfth up.

The patch is composed by different modules aimed

respectively at:

• music information management

• time control

• musical form management

• transposition

• sound production

The music information module is depicted in Fig-

ure 4. It is put into action by the time control mod-

ule (

+metro+

and

counter

). The

+counter+

produces

the sequence of indices to be sent at timed intervals

to the

+tabread+

object. The

+module+

(

+%+)

object

keeps the count inside the size limits of the

+array+,

producing thus a continuouscycle of scales.

The module that controls the musical form keepstrack

of the output of the

counter

object and through a se-

lector (the

sel

object) provides the transposition of

the scales. This is realized by adding to the funda-

mental the quantity of semitones of the transposition

interval. The same mechanism is used to stop the per-

formance. At least the sound production module re-

ceives the MIDI data (

makenote

) and outputs them to

an external virtual synthesizer (

noteout

3.4.2 Creativity

During the workshop the students become familiar

with all the modules contained in the patch and then

receive an assignment where the same patch struc-

ture is employed to create something that looks and

sounds very different. The assignment is shown in

Figure 6 in the form of a possible desired output.

Consider the possibility of assigning a random fun-

damental pitch (range 30-80) each time the scale cy-

cle begins and also to assign a random value (range

1-8) to the argument of the

module

object. This pro-

duces scale fragments of different length starting al-

ways from different fundamental pitches. The aim of

this assignment is to stress the creative possibilities

offered by a simple scale when its production algo-

rithm reaches a level of abstraction that allows nu-

merical manipulation. It also evidences that the tra-

ditional musical scale is only a particular case of a

much wider musical universe, which can be explored

with the use of these very simple programming tools.

Further musical development can be obtained by pro-

gramming musical streams (note bands with common

timbre constrained inside height and duration ranges),

impulsive events (clusters or chords), and polyphony

(i.e. piping events), and so on. Such creative activities

may also be inspired by the use of graphical scores,

where visual elements can be freely interpreted by the

students.

3.4.3 Collaboration and Communication

Weeks 7 and 8 are devoted to group activities. Each

group is formed by 5-6 people. These activities aim

at preparing a creative patch responding to a precise

composition plan (descending from a graphical score

or other organizationcriteria). The patch mustcontain

the instructions for the performance of the composi-

tion, a general description of the composition plan as

well as the comments explaining the functions of the

objects employed. These activities involve group or-

ganization, communication among the members, cre-

ativity and the ability of negotiating with others about

the best solutions to be chosen.

4 ASSESSMENT

Greher and Heines (Greher and Heines, 2014) have

prepared a pre and post-course questionnaire for the

assessment of course outcomes. It is divided into 4

sections:

1. reasons for taking the course

2. expectations for the course

3. self perception and

4. opinions about computing and music

The aim of this questionnaire is to take a picture as

accurate as possible of the ideas of the students and

Fostering Computational Thinking in Undergraduated Music Conservatory Students

453

Figure 4: The music information module.

Figure 5: The complete algorithm for the production a major scale with transpositions: the fundamental pitch variable, the

timing and cycle module, the control of musical form and transpositions and the sound production module.

Figure 6: A possible desired output example for the home

assignment of lesson 4.

of how these may be changed after course activi-

ties. Many questions concern the ”Four C’s” abilities,

and try to provoke a reﬂection in the students about

their relationship with computers, music composition

and creativity. For the present course the original

questionnaire has been slightly adapted and integrated

with further questions concerning basic music and

music technology knowledge. The main challenge in

the preparation of this part of the questionnaire has

been how to measure the logical, abstraction and an-

alytical abilities of the students before the beginning

of the teaching activities. As the great majority of the

students (about the 85%) has never used any music

programming language before, the assessment can-

not be made through language speciﬁc questions, but

rather involve more general concepts. These are:

• music analysis

• patch logic and

• ﬂow diagram.

In the pre-course questionnaire there are 2 ques-

tions for music analysis and one question for each of

the remaining items. Similar questions will be pre-

pared for the post-course questionnaire.

4.1 Music Analysis

For testing the music analysis abilities a melody is

presented to the students with some examples of

pattern repetition and pattern transposition (see Fig-

ure 7). In the ﬁrst question the students are required

to identify how many patterns they could ﬁnd in the

melody. In the second question they must identify

the pattern repetitions and transpositions in the same

melodic excerpt.

4.2 Patch Logic

This test is to check what kind of functions students

consider as the most important for the automatic per-

formance of a melody. The test is presented in the

CSME 2022 - 3rd International Special Session on Computer Supported Music Education

454

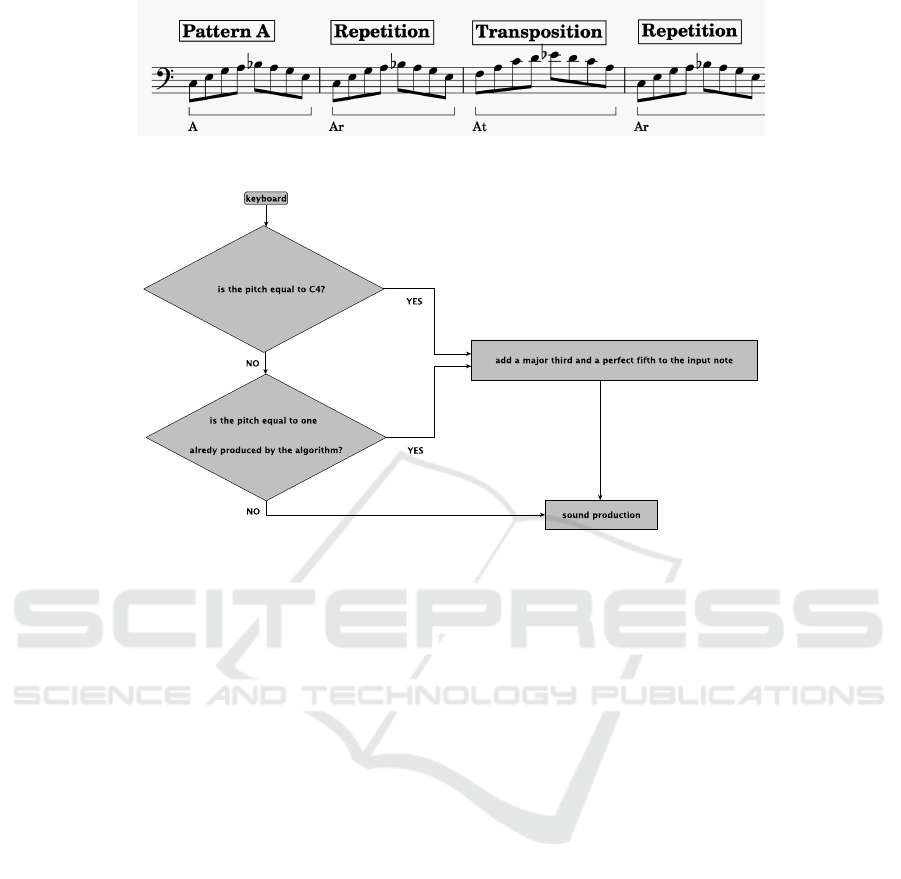
Figure 7: An example of pattern repetition and transposition.

Figure 8: A ﬂow diagram of a music production algorithm.

form of a ﬁve point Likert scale matrix (1 not impor-

tant – 5 very important) with the following 15 items:

1. A sound production system

2. Start and stop controls

3. An information storage system

4. A way for controlling the number of voices for the

performance

5. A control for pattern repetition

6. A list of possible note durations

7. A time control mechanism

8. A list of available note timbres

9. A control for pattern transposition

10. An external electronic keyboard

11. A way to express the pitches of the notes

12. A counter

13. A way to introduce a variable

14. A list of possible keys

15. A way to control the speed of the performance

This list has been ﬁlled in with modules actually used

in the patches as well as with other musical elements

that are the output of the same modules. At the end

of the course students will be presented with the same

matrix to verify if they can identify such dependen-

cies.

4.3 Flow Diagram

The students are presented with the ﬂow diagram de-

picted in Figure 8. They are asked to identify what

can be the output if a short sequence of notes is used

as input. This test checks accurately if the students

understand how the algorithm works and how the sys-

tem output changes after the input has been processed.

A similar question will be inserted in the post-course

questionnaire to see if some improvement has been

achieved.

4.4 Expected Results

The main expected results for this music technology

course may be grouped into two main areas: improve-

ment of computer literacy/programming skills; en-

hancement of musical creativity.

4.4.1 Improvement of Computer and

Programming Skills

The 6 pre-course questions about computers and pro-

gramming are outlined in Table 2. The answers were

collected as ratings on a Likert scale ranging from 1

(false) to 5 (true). Results are reported in Figure 9.

Although a good number of students seem to be

interested in learning something more about comput-

ers and programming (Q1 and Q2), a smaller number

Fostering Computational Thinking in Undergraduated Music Conservatory Students

455

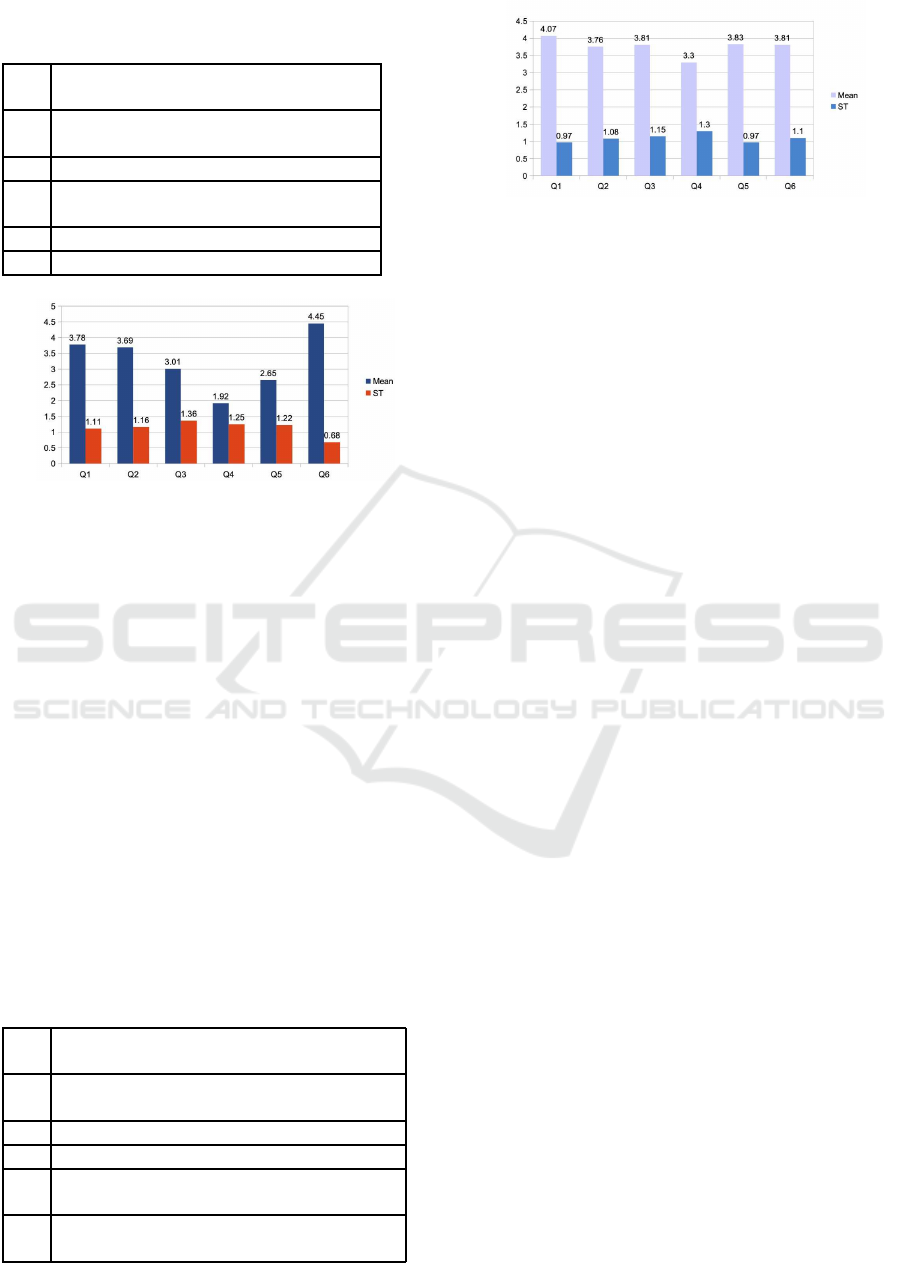
Table 2: The 6 pre-course questions about computers and

programming.

I want to learn something more about

computers

I want to learn something more about

computers and programming

Q3 I enjoy working with computers

I am conﬁdent using a computer

language to accomplish complex tasks

Q5 Computer programming is fun

Q6 Programming a computer is difﬁcult

Figure 9: Results of the 6 pre-course questions about com-

puters and programming, with answers mean and standard

deviation.

enjoys working with computers (Q3) and a very small

number is conﬁdent in dealing with programming lan-

guages (Q4). Moreover computer programming is not

considered to be a very funny activity (Q5), while it is

for sure very difﬁcult for the majority of the students

(Q6). These results depict a not very promising start-

ing point for the course activities, also if Q1 and Q2

seem to show some room for improvement. A great

result should be a higher mean in Q3, 4 and 5, and a

decrease in Q6, showing that actually some students

have earned a major level of computer literacy and

have become more conﬁdent in the use of computers.

4.4.2 Enhancement of Musical Creativity

In the pre-course questionnaire there are 6 questions

addressing the topic of musical creativity, particularly

Table 3: The 6 pre-course questions about musical creativ-

ity and composition.

I want to learn more about the integration

of computers and music

I want to learn more about music and

composing

I want to learn to be more creative

Q4 I enjoy creating my own music

I am conﬁdent in my ability to express

myself through music

Computers can be used to create cool

music

Figure 10: Results of the 6 pre-course questions about mu-

sical creativity, with answers mean and standard deviation.

music composition. The questions are outlined in Ta-

ble 3 and results reported in Figure 10. Here the start-

ing situation seems to be more promising, showing

that students feel much more comfortable with cre-

ativity than with computer programming. They seem

to be particularly curious about the relationship be-

tween music and computers (Q1) and show a pos-

itive attitude towards music created with computers

(Q5), also if a lower number enjoys creating music

(Q4). The link between computational thinking and

creativity is one of the main objectives of the course

(see Section 3.1). Hence an increase of the mean of

Q4 and Q6 could indicate a positive evaluation of the

computer–mediated creative activities proposed dur-

ing the course.

5 CONCLUSION AND FURTHER

WORK

In this paper a music technology course program has

been presented. The contents of the course have been

discussed in the light of the enhancement of the ”Four

C’s” abilities (critical thinking, creativity, collabora-

tion and communication). A road from a basic, stiff

and not reusable algorithm (Figure 2) to a more gen-

eral and ﬂexible production module (Figure 4) has

been shown, and the possibilities of creative use of

the same algorithm have been suggested. The aim

of this work is to demonstrate the connection be-

tween computational thinking and creativity as one of

the most powerful expressions of contemporary art.

Finally, some ideas for the assessment of computa-

tional thinking abilities in pre and post-course ques-

tionnaires have been developed and presented. At the

conclusion of the course many important data will be

available for analysis:

• quantitative data from pre and post-course ques-

tionnaires

• the ﬁnal course assignments where students will

produce and comment an original music creation

algorithm

CSME 2022 - 3rd International Special Session on Computer Supported Music Education

456

• the lesson-by-lesson assignments, which will

show the road that each student has followed to

reach the course objectives.

Also if some results have been speculated in Sec-

tion 4.4, only a global analysis of all these data will

provide signiﬁcant elements for the evaluation of the

course design, if it is successful in reaching the im-

portant goals listed in Section 3.1 and, mainly, if it is

useful in contributing to the progress of the students.

ACKNOWLEDGEMENTS

The present research has been funded by Fondazione

ASM

, Brescia (Italy).

REFERENCES

Aaron, S., Blackwell, A. F., and Burnard, P. (2016). The de-

velopment of sonic pi and its use in educational part-

nerships: Co-creating pedagogies for learning com-

puter programming. Journal of Music, Technology &

Education, 9(1):75–94.

Aho, A. V. (2012). Computation and computational think-

ing. The computer journal, 55(7):832–835.

Avanzini, F., Barate, A., Ludovico, L. A., and Marcella,

M. (2021). Songs in music education: Design and

early experimentation of a web tool for the recogni-

tion of harmonic changes. In International Confer-

ence on Computer Supported Education, pages 709–

720. SCITEPRESS.

Barat`e, A., Ludovico, L. A., and Malchiodi, D. (2017).

Fostering computational thinking in primary school

through a lego®-based music notation. Procedia com-

puter science, 112:1334–1344.

Bell, J. and Bell, T. (2018). Integrating computational think-

ing with a music education context. Informatics in

Education, 17(2):151–166.

Bellettini, C., Lonati, V., Malchiodi, D., Monga, M., Mor-

purgo, A., Torelli, M., and Zecca, L. (2014). Extracur-

ricular activities for improving the perception of infor-

matics in secondary schools. In International Confer-

ence on Informatics in Schools: Situation, Evolution,

and Perspectives, pages 161–172. Springer.

Collins, N., Collins, N., Schedel, M., and Wilson, S. (2013).

Electronic music. Cambridge University Press.

Copeland, B. J. and Long, J. (2017). Turing and the history

of computer music. In Philosophical Explorations of

the Legacy of Alan Turing, pages 189–218. Springer.

Cuny, J., Snyder, L., and Jeannette, M. (2010).

Wing. Demystifying Computational Thinking for Non-

Computer Scientists, work in progress.

Engelman, S., Magerko, B., McKlin, T., Miller, M., Ed-

wards, D., and Freeman, J. (2017). Creativity in au-

thentic steam education with earsketch. In Proceed-

https://fondasm.it/

ings of the 2017 ACM SIGCSE Technical Symposium

on Computer Science Education, pages 183–188.

Gorson, J., Patel, N., Beheshti, E., Magerko, B., and Horn,

M. (2017). Tunepad: Computational thinking through

sound composition. In Proceedings of the 2017 Con-

ference on Interaction Design and Children, pages

484–489.

Greher, G. R. and Heines, J. M. (2014). Computational

thinking in sound: Teaching the art and science of mu-

sic and technology. Oxford University Press.

Hamilton, E. R., Rosenberg, J. M., and Akcaoglu, M.

(2016). The substitution augmentation modiﬁcation

redeﬁnition (samr) model: A critical review and sug-

gestions for its use. TechTrends, 60(5):433–441.

Hancock, O. (2014). Play-based, constructionist learning of

pure data: A case study. Journal of Music, Technology

& Education, 7(1):93–112.

Israel-Fishelson, R. and Hershkovitz, A. (2022). Studying

interrelations of computational thinking and creativ-

ity: A scoping review (2011–2020). Computers &

Education, 176:104353.

Jenkins, H. (2009). Confronting the challenges of partici-

patory culture: Media education for the 21st century.

The MIT Press.

Krathwohl, D. R. (2002). A revision of bloom’s taxonomy:

An overview. Theory into practice, 41(4):212–218.

Maloney, J., Resnick, M., Rusk, N., Silverman, B., and

Eastmond, E. (2010). The scratch programming lan-

guage and environment. ACM Transactions on Com-

puting Education (TOCE), 10(4):1–15.

Manzo, V. J. (2016). Max/MSP/Jitter for music: A practi-

cal guide to developing interactive music systems for

education and more. Oxford University Press.

Resnick, M., Ocko, S., and Papert, S. (1988). Lego, logo,

and design. Children’s Environments Quarterly, pages

14–18.

Selby, C. C. and Woollard, J. (2014). Reﬁning an under-

standing of computational thinking.

Shute, V. J., Sun, C., and Asbell-Clarke, J. (2017). Demys-

tifying computational thinking. Educational Research

Review, 22:142–158.

Trower, J. and Gray, J. (2015). Blockly language creation

and applications: Visual programming for media com-

putation and bluetooth robotics control. In Proceed-

ings of the 46th ACM Technical Symposium on Com-

puter Science Education, pages 5–5.

Wing, J. (2011). Research notebook: Computational think-

ing—what and why. The link magazine, 6:20–23.

Wing, J. M. (2008). Computational thinking and thinking

about computing. Philosophical Transactions of the

Royal Society A: Mathematical, Physical and Engi-

neering Sciences, 366(1881):3717–3725.

Fostering Computational Thinking in Undergraduated Music Conservatory Students

457