Biodegradation Prediction and Modelling for Decision Support

David F. Nettleton

, Cristina Fernandez-Avila

, Sara Sánchez-Esteva

, Steven Verstichel

Maria Beatrice Coltelli

, Helena Marti-Soler

, Laura Aliotta

and Vito Gigante

IRIS Technology Solutions, Ctra. d'Esplugues, 39-41, 08940 Cornellà de Llobregat, Barcelona, Spain

OWS, Dok-Noord 5, 9000 Gent, Belgium

Dipartimento di Ingegneria Civile ed Industriale, Università di Pisa, Largo Lucio Lazzarino 56122 Pisa PI, Italy

{laura.aliotta, vito.gigante}@dici.unipi.it

Keywords: Modelling, Simulation, Interpolation, Multi-agent System, Case based Reasoning, Time-Series,

Biodegradation, Bioplastics.

Abstract: In this paper we describe the functionality of a decision support modelling approach to select appropriate

biomaterial blends depending on their mechanical/chemical properties on the one hand, and their

biodegradation behaviour, on the other. Firstly, a Case Based Reasoning (CBR) approach is applied to predict

expected biodegradation behaviour over time, based on historical examples and using a weighted distance

metric on the material properties in order to calculate the trend curve of the new case. Secondly, a Multi-

Agent System (MAS) is applied to dynamically simulate the biodegradation curve, in which the two main

agents, bacteria and plastic, interact to reproduce the biodegradation kinetics over time. The results of the

interpolation are very promising with a good approximation to the real curve time series and % biodegradation,

and the Multi-Agent System successfully simulates the different trend curves over time. The system has been

confirmed as useful by materials expert end-users, who participated in the project, in order to evaluate a priori

new blends “in silico”, and identify and select the most promising, before conducting the long duration

biodegradation experiments in the real environment.

1 INTRODUCTION

Developing biodegradable materials which are fit for

purpose in the future circular economy is a critical

task if we wish to make the transition from fossil fuel

plastics. However, finding an equilibrium between

mechanical properties of the different potential bio-

material blends and their biodegradation

requirements can be a complex, trial and error, and

lengthy process (due to the long experimental time

required for biodegradation testing).

Hence, it is of great interest to be able to

accurately model and predict the biodegradation

process of potential material blends, in order to focus

on the most promising and reduce experimental

https://orcid.org/0000-0002-5852-7716

https://orcid.org/0000-0002-2678-4347

https://orcid.org/0000-0002-4581-6084

https://orcid.org/0000-0002-0418-8974

https://orcid.org/0000-0002-7127-205X

https://orcid.org/0000-0003-1876-5995

https://orcid.org/0000-0003-3896-9629

testing time.

In this paper, we show that Case Based Reasoning

and Multi-Agent System modelling approaches can

be useful to generate the biodegradation prediction of

a new blend based on material properties, and

simulate the corresponding biodegradation curve.

The results are very promising, although on a limited

set of cases, for predicting best and worst performers.

First, the CBR obtains the closest historical cases

to a new one, interpolates and expected trend curve,

and then passes this information to the MAS to

simulate in a kinetic and stochastic solution space.

The motivation of using CBR and MAS for

predicting and simulating the biodegradation process,

comes from the shortcomings of existing approaches,

Nettleton, D., Fernandez-Avila, C., Sánchez-Esteva, S., Verstichel, S., Coltelli, M., Marti-Soler, H., Aliotta, L. and Gigante, V.

Biodegradation Prediction and Modelling for Decision Suppor t.

DOI: 10.5220/0011136200003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 26-35

ISBN: 978-989-758-578-4; ISSN: 2184-2841

such as the need for complex representations of large

amounts of low level chemical knowledge, and the

lack of representation of stochastic and kinetic

features.

The system is defined “as a service”, where

material designers and testers provide the material

characteristics and the system returns the predicted

biodegradation behaviour (curve over time).

The paper is organized as follows: in Section 2

related work is presented, in Section 3 the data used

and pre-processing is summarized, in Section 4 the

Case Based Reasoning processing and matching

approach is described with examples, in Section 5 the

Multi-Agent System based simulation is described

and Section 6 summarizes the work. Also, a Dynamic

System Model definition of the biodegradation

process is given in the Annex.

2 RELATED WORK AND

BACKGROUND

There is an extensive literature of chemical based

biodegradation modelling, using traditional statistical

techniques together with detailed chemical

knowledge (Pavan and Worth, 2006;2008), as well as

more recent approaches based on kinetic

modelling(Farzi et al., 2019; Sonwani et al., 2020;

Sable et al., 2019). However, data modelling using a

simple set of descriptive parameters including

chemical and mechanical properties and using

artificial intelligence techniques is more difficult to

find in the literature. Hence, this is one of the key

motivations and advantages for our current work.

Purely chemical based approaches for the

biodegradability of material require highly

specialized parameterisations, such as in (Alalayah,

2017) (Dragomir et al, 2021), which require deep

chemical knowledge.

Furthermore, sets of ordinary differential

equations (ODEs) have limitations when representing

problems which involve spatial interactions or

emerging properties (Borshchev and Filippov, 2004),

and present difficulties for embodying emergent and

stochastic behaviour. (Pavan and Worth, 2006;2008)

consider QSAR (Quantitative Structure-Activity

Relationship) which is an important family of models

for chemical modelling. QSARs are mathematical

models that can be used to predict different properties

of compounds from the knowledge of their chemical

structure.

In terms of AI techniques applied specifically to

biodegradation modelling, neural networks and rule

induction are two examples. (Gamberger, et al., 1996)

used a rule induction technique and chemical feature

sets as inputs. The biodegradation data from both

data-bases are discrete values, i.e. those chemicals are

classified as biodegradable or non-biodegradable.

The work of (Baker et al., 2004), uses rule induction

and as input includes complex low level chemical

information. Binary output variables are assigned to

each chemical with a 1 for fast biodegradability and 0

for slow biodegradability. (Arranz, et al., 2008) used

neural networks to model biodegradation processes,

requiring a high number of samples to train the

network. Note that in the case of (Gamberger et al.,

1996) and (Baker et al., 2004), their models are

limited to producing a binary classification as output.

In contrast, our solution produces the trend curve with

quantified values for % biodegradation and time.

In their review paper, (Baker et al., 2004)

indicated the use of multiple linear regression and

artificial neural networks, Partial least squares

discriminant analysis and Inductive machine learning

(rule based), among others, however the focus was on

a lower level chemical analysis. Also from (Baker et

al., 2004), a Knowledge-based learning system was

described as a method using machine learning

techniques to determine relevant descriptors

mathematically from data on activity and basic

chemical structure. Furthermore, Multi-Agent based

systems (MAS) (Ferber and Weiss, 1999) and

Dynamic System Models (DSM) (Radzicki and

Taylor, 2008) have been used for stochastic system

modelling in different fields. As recent examples,

(Nettleton et al., 2020) and (Estivill-Castro et al.,

2021) have applied and contrasted the utility of MAS

and DSM for clinical applications, simulating

multiple trend curves over time for modelling

complex kinetic interactions and behaviours between

the human immune system and cancer cells.

The case for using MAS in preference to

mathematical models and DSMs is supported by the

ability of the former to more easily simulate kinetic

and stochastic behaviour, as well as being data driven

so requiring less theoretical know-how to be pre-

defined.

The current work takes (Nettleton et al., 2020) and

(Estivill-Castro et al., 2021) as starting point to apply

the MAS approach to the novel application of

bioplastic blend biodegradation over time. Case

Based Reasoning (CBR) (Aamodt and Plaza, 1994) is

also an approach taken from artificial intelligence

which essentially uses a set of historical cases as a

reference in order to find the closest match to a new

case. In the current work we use CBR as pre-

processing for the MAS, in order to match the

material properties of a new blend to find the closest

Biodegradation Prediction and Modelling for Decision Support

historical blends, and hence their corresponding

biodegradation trend curves.

The EU Horizon 2020 project Biontop, of which

the current work forms a part, is aimed at developing

novel packaging films and textiles with tailored end

of life and performance based on bio-based polymers.

In the framework of the project bioplastics blends

based on biobased and industrially compostable

Poly(lactic acid) (PLA) were considered (Narancic et

al., 2018). The blending with other bio-polyesters

resulted successful for modulating the mechanical

properties of this polymer in a wide range of values

(Aliotta et al., 2021;2021). One key aim of the project

is to find bioplastics which are ‘home-compostable’,

which means they are biodegradable at a lower

temperature and in milder conditions than those

typical of ‘industrial composting’.

Hence, the biodegradation testing of blends was

performed for home-composting conditions,

executed according to ISO 14855 but at ambient

temperature (28°C). The tests were carried out using

pellets produced by twin screw extrusion in a Comac

EBC 25 HT extruder (Comac, Milan, Italy).

In the Appendix can be found a dynamic system

model (DSM) simplified representation of the

bioreactor set-up. A DSM typically consists of a stock

and flow diagram (Figure 7), a set of differential

equations to represent the behaviour of the stocks

over time (Table 6), a set of algebraic equations to

define the flows (Table 7), and a set of control

parameters used by the system (Table 8). In Figure 7,

five stocks are defined: bioplastic, compost, Reactor,

and CO

. The flow on the top right indicates the

bioplastic formulation (blend) which is input at the

process start as a batch. The flows below are O

which

oxygenated the Reactor and compost, which is input

at the process start as a batch and is the source of the

bacteria. On the right is the CO

stock produced as

output (by the biodegradation process) inside the

Reactor stock which is located in the middle. The

degree is biodegradation is quantified from the CO

readings.

3 DATA AND PRE-PROCESSING

The data used for prediction and modelling is based

on the materials properties (chemical and

mechanical) as shown in Table 1, and the

biodegradation results of each material, as shown in

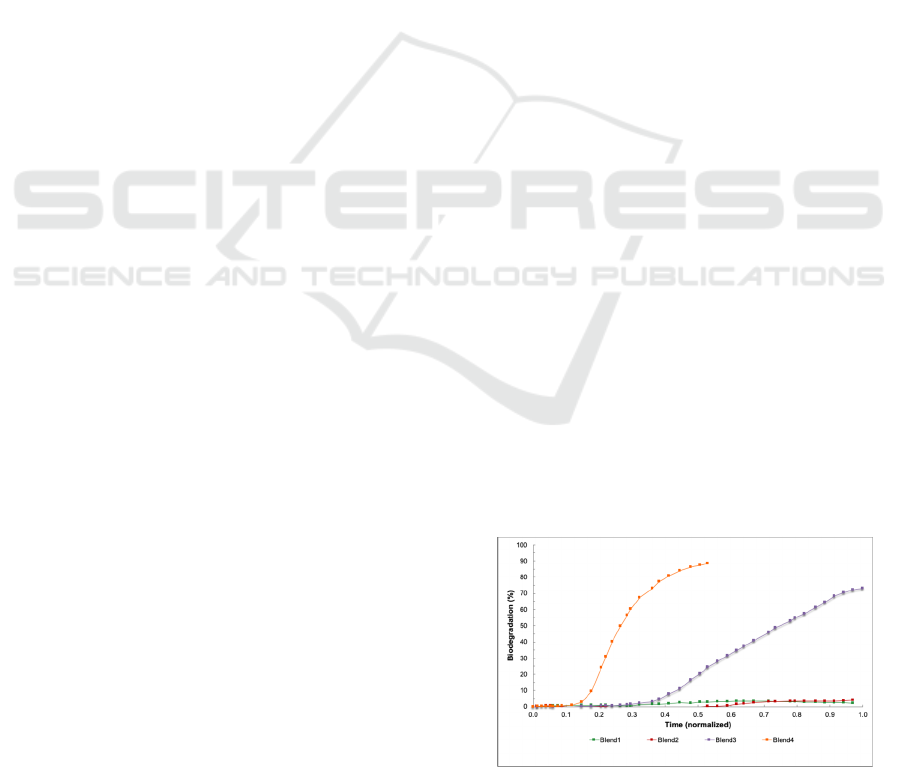
Table 2 and Figures 1 and 2. Eight material blends

were used for biodegradation testing, as part of the

Biontop project (see background Section). Note that

for confidentiality reasons and intellectual property

protection of the Biontop project, the data has been

normalized or rescaled, and the material names

anonymized. However, this has been done in a way

so as to maintain the relative values and

interpretability of the data with the results.

Table 1 shows a summary of the chemical and

mechanical properties of the eight main bioplastic

materials, named as blends 1 to 8. For confidentiality

reasons, all material property values are normalized

in a range between 0.5 and 1.5, and the

biodegradation times are scaled between 0 and 1. It

can be seen that in terms of chemical properties, blend

7 has a low molecular weight and medium polarity

and crystallinity; in terms of mechanical properties, it

has a low Young’s Modulus, a low elongation at

break and a high tensile strength.

Table 2 shows a summary of the biodegradation

results for the eight material blends whose

characteristics were given in Table 1. It can be seen

that blend 7 gives the best biodegradation results,

reaching 100% biodegradation in a scaled time of 0.6.

On the other extreme, the blend 5 material gives the

worst biodegradation results, achieving only 1.2%

biodegradation in a scaled time of 1.0 (highest value).

From the material characteristics of Table 1 and

the biodegradation results of Table 2, a strong

correlation is evident between the two. For example,

a low molecular weight and high crystallinity give a

propensity for the material to biodegrade.

We note that only eight cases (i.e. blends) were

available from the Biontop project with their full

material properties data and biodegradation results.

However, they were chosen, by the materials experts

involved in the project, to cover a realistic and

representative distribution of scenarios from good

biodegradation (blends 4 and 6 to 8), medium (blend

3) and poor (blends 1, 2 and 5).

Figures 1 and 2 show all the biodegradation trend

curves for the eight blends which were empirically

tested.

Figure 1: Biodegradation curves for blends 1 to 4.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

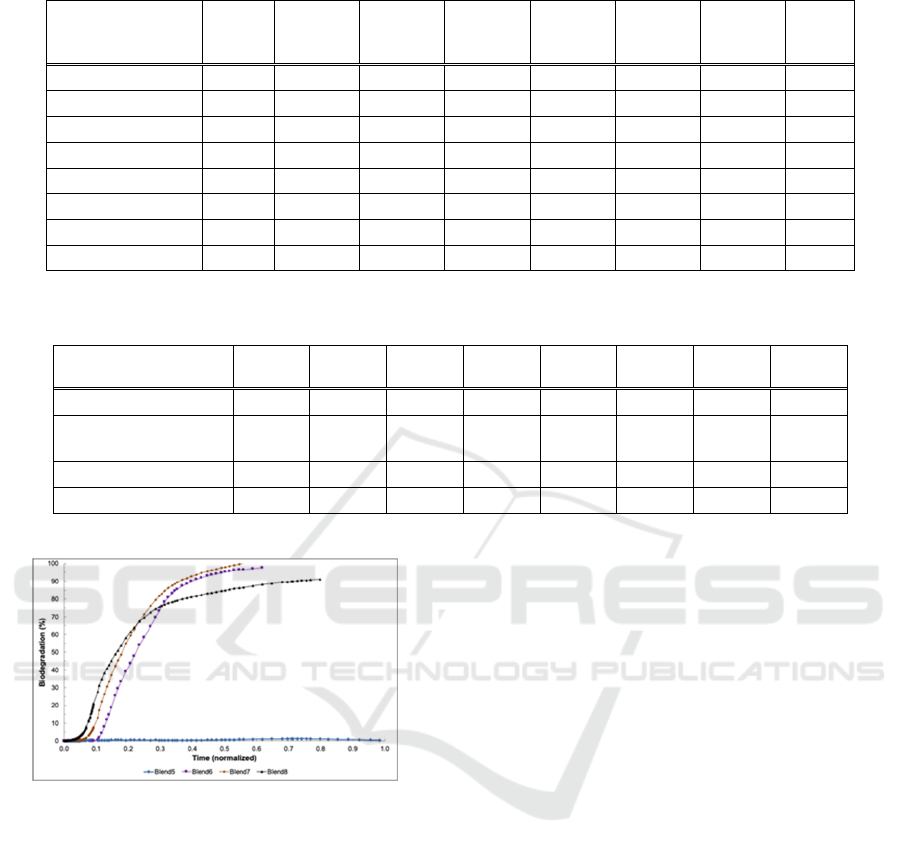
Table 1: Chemical and mechanical properties of blends 1 to 8*.

Chemical and

Mechanical

Properties

Blend1 Blend2 Blend3 Blend4 Blend5 Blend6 Blend7 Blend8

Polarity 0.7 0.7 1.4 1.5 0.8 1.3 1.2 1.1

Molecular weights 1.5 1.4 0.9 0.7 1.3 0.6 0.6 0.5

Crystallinity 1.5 1.2 0.9 0.7 1.5 0.7 0.8 0.5

MFR 0.5 0.6 0.6 0.7 1.3 1.4 1.4 1.5

Impact strength 0.7 0.8 0.9 1.5 0.7 1.4 1.4 1.5

Tensile strength 1.2 1.1 0.5 0.9 1.5 0.5 0.6 0.8

Young's Modulus 1.5 1.3 1.0 0.8 1.5 0.5 0.5 0.6

Elongation at break 0.5 0.7 1.1 1.5 0.5 1.2 1.2 1.2

*All values are normalized to a range between 0.5 and 1.5.

Table 2: Biodegradation results of blends 1 to 8*.

Biodegradation

Criteria

Blend1 Blend2 Blend3 Blend4 Blend5 Blend6 Blend7

Blend8

Time to 50% 0.8 0.3 0.2 0.2 0.2

Time to 100% or

MAX

0.6 1.0 1.0 0.5 1.0 0.6 0.6 0.7

Max% 3.5 4.2 73 88 1.2 97.7 100 90.3

Rank biodegradability 6 7 5 4 8 2 1 3

*All values (except max%) are scaled to a range between 0 and 1.0.

Figure 2: Biodegradation curves for blends 5 to 8.

4 CASE BASED MATCHING

In this section we explain how the Case Based

Matching approach with an appropriate distance

metric, is applied to the material properties and

biodegradation data in order to predict the

biodegradation of new blends.

4.1 Modus Operandi and Example

Applying CBM to Material

Properties and Blend

Biodegradation Data

The data processing of the CBM approach has the

following four steps, with reference to Table 3, Figure

3 and Equation (1): (i) choose one blend as “new

blend” (e.g. blend8); (ii) calculate “distance” between

new blend and all remaining historical blends using

only material properties data (i.e. only a priori

information); (iii) identify two “closest” historical

blends in terms of distance (e.g. blends 6 and 7); (iv)

use the two “closest” historical blends to interpolate

curve of “new blend” (Figure 3).

The distance D is calculated by applying a

Euclidean metric to the respective material properties

(Table 1) and summing over n, the number of

properties, which are previously normalized and have

equal weighting:

D 

∑

|𝑝



𝑝



|





(1)

where 𝑝



is property i of material 1 and 𝑝



property i of material 2.

Table 3 shows the seven blends used as the

historical case base and blend 8 considered as a “new”

blend (but whose biodegradation results are known).

Blends 6 and 7 are found to be the “closest” to blend

8 (from all 7 available historical blends) using the

distance metric calculation. This gives a distance of

0.7 and 0.6, respectively for blends 6 and 7.

Biodegradation Prediction and Modelling for Decision Support

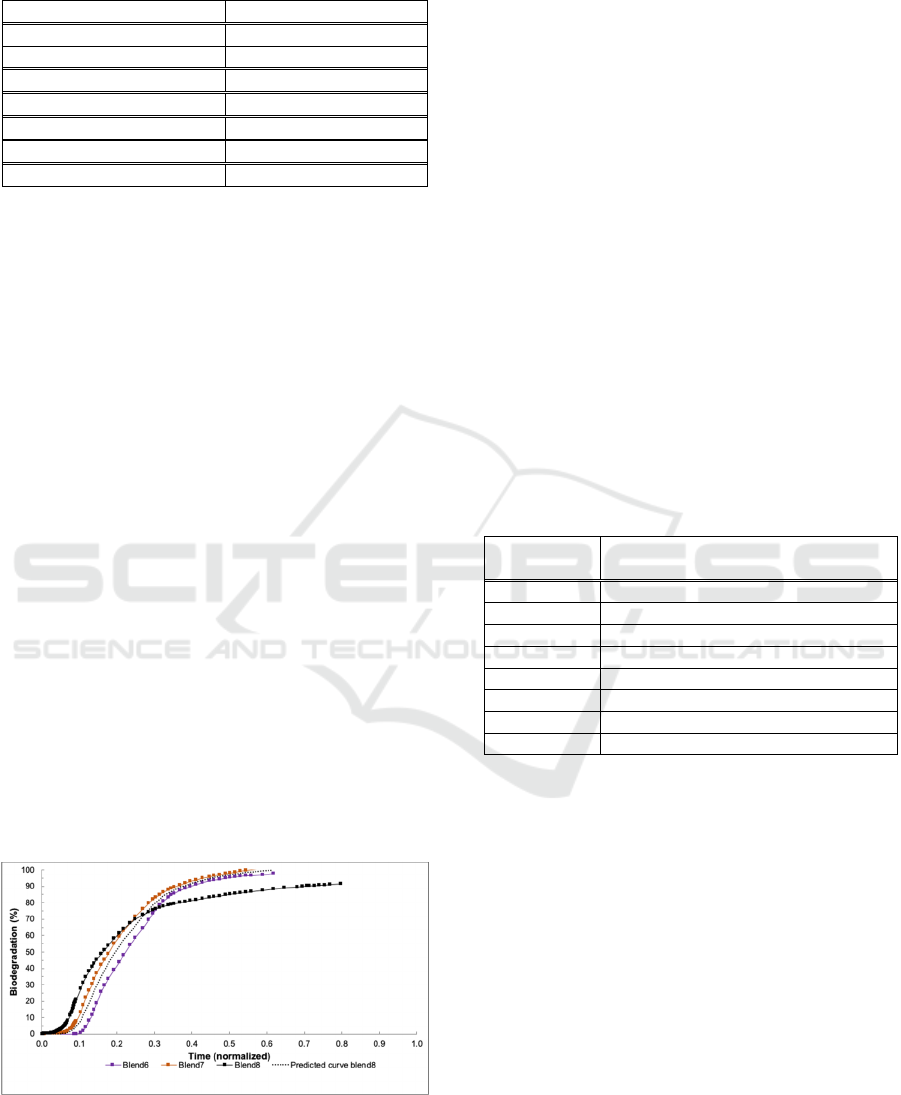
Table 3: Blends selected as historical examples and new

blend.

Historical examples Distance to Blend 8

Blend1 1.5

Blend2 1.5

Blend3 1.0

Blend4 0.8

Blend5 1.5

Blend6 0.7

Blend7 0.6

Now, using the curve points 𝑦



and 𝑦



of existing

blends 6 and 7, respectively, the corresponding curve

point approximation 𝑦



for the new blend is obtained:

first the distances of Table 3 are normalized and then

the two smallest values used as weights

𝑤



and 𝑤



interpolate. From this, the polynomial equation is

estimated which best fits the curves 𝑌



and 𝑌



and the

individual points 𝑦



(% biodegradation over time)

are calculated thus:

∀𝑦  0, 𝑤∈



0. .1



𝑦′



 𝑦





𝑤



(2)

𝑦′



 𝑦





𝑤



𝑦



 𝑦′



 𝑦′



Hence, the overall result of the case matching of a

new blend with historical blends, is to obtain a new

interpolated biodegradation trend curve over time. In

Figure 3 it is shown that blends 6 and 7 are identified

as the closest blends to the “new” blend 8, based on

chemical and mechanical properties. Also in Figure 3

is seen how the blend 8 curve is interpolated from the

curves of blends 6 and 7, using the weighted distance

metric (Equation 2) to generate the points. In the case

of blend 8, the fit of the interpolated curve to the real

blend 8 curve is relatively lower (0.75, see Table 4).

Figure 3: Closest historical curves and new curve

interpolation.

This is because the trend of the real curve for blend 8

flattens out from time 0.3 onwards, diverging from

the trends of blend curves 6 and 7. However, at this

point it has already reached almost 80%

biodegradation (Figure 2).

4.2 Results of Applying CBM to Predict

Biodegradation Curve of Blends

The process described in Section 4.1 with blend 8 as

the “new blend”, was repeated for blends 1 to 7. Table

4 shows the results of comparing the trend curves

predicted by CBM with the real curves, for each of

the blends. It can be seen that all the R

values of the

matches were over 0.81, with the exception of blends

3 and 8, with R

values of 0.68 and 0.75, respectively.

The lower performance for blends 3 and 8 was

expected as they have intermediate biodegradation

performance with respect to the best blends for

biodegradation and the worst ones (see Figures 1 and

2). In summary, estimated blend curves 1, 2 and 5 are

fitting closely together, also blends 4, 6 and 7, while

blends 3 and 8 are relative ‘outliers’. This is

supported by the R

values shown in Table 4.

Table 4: Matching of simulated data trend curve (simulated

data) with real trend curve - R

value.

Composition

/Blen

Trend curve (simulated data) vs trend

curve (real data)

–

value

Blend1 0.9440

Blend2 0.9379

Blend3 0.6830

Blend4 0.8174

Blend5 0.9373

Blend6 0.9002

Blend7 0.8907

Blend8 0.7506

Furthermore, two aspects are of interest to the

material experts: what is the % degradation at time

0.6 (or less) and how long does it take to reach a given

biodegradation %. In general, the estimated curves

provide a good approximation of this information.

Note that for blends 3 and 8, the matching is with

curves of shorter duration (0.6) and so the estimated

curves get truncated at this limit. Hence, in

conclusion, special attention has to be made to

defining similar experimental conditions (time

duration) for blend testing and having sub-groups of

similar blends for comparison proximity. The

accuracy for % at time 0.6 was generally within 15%

for blends 3 and 8, 10% for blends 4, 6 and 7, and

within 5% for blends 1,2 and 5. For the former, this

was more dependent on the cut-off time of the closest

blends chosen.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

5 MULTI-AGENT SIMULATION

In this section we use a Multi-Agent System (MAS)

to simulate the blend biodegradation behaviour, based

on the trend curves. This requires the adjustment of

the MAS control parameters (biodegrade chance,

biodegrade distance, detect distance, speed) which act

in a 2D solution space during the process.

As a starting point, the control parameters are

assigned as a generic “predator-prey” model (Bădică

et al., 2018; Karsai et al., 2016) which is interpreted

in the current context as a kinetic model where the

predator is the bacteria and the prey is the plastic.

Furthermore, a plastic agent remains fairly static

whereas a bacterium is more mobile, performing a

random walk at a given “speed” (SP) until a plastic

agent comes within its “detect distance” (DD). Once

this happens the bacteria agent moves directly

towards the plastic agent until it reaches the

“biodegrade distance” (BD), and then, depending on

the “biodegrade chance” (BC), it will biodegrade the

plastic agent (i.e. the plastic agent is consumed and

disappears). This apparently simple individual

behaviour can give rise to a complex collective

system, and more advanced interaction rules can be

programmed into the agents. Figure 4 illustrates the

concept of the two dimensional state space and

respective action distances between the agents.

Figure 4: State space definition for agent interactions.

5.1 Modus Operandi

It is recalled that the CBM processing approach

applied in Section 4 obtains the polynomial trend

curve for the new blend. Now, we provide the trend

curve (polynomial equation) to the MAS, and as it

runs the agent system control parameters adapt in

order to keep the population (of plastic) as close as

possible to the trend curve. A weighting is also used

for each control parameter.

The process is repeated ad-hoc for several trend

curves, until a historical of results (trend curves with

their corresponding agent control parameters) is

accumulated. Once sufficient historical examples are

available, the agent control parameter initial values

and weighting can be automatically estimated for a

new trend curve, without having to perform ad-hoc

testing (thus significantly reducing the testing and

refinement cycles to obtain the settings).

The control parameters are updated as follows: let

be the expected plastic biodegradation percentage

calculated from the trend curve and P

the current

plastic agent population percentage in the MAS.

Then, the percentage difference 𝑃

∆

between the two

will be:

𝑃

∆



















Next, a multiplier coefficient is defined as:

𝑚𝑢  1.0  𝑃

∆

Then, the update rules are defined as:

𝐵𝐶  𝑚𝑖𝑛



1, 𝐵𝐶  𝑚𝑢



𝐵𝐷  𝐵𝐷 𝑚𝑖𝑛



1, 𝑚𝑢



𝑆𝑃  𝑆𝑃 𝑚𝑢

𝐷𝐷  𝐷𝐷 𝑚𝑢 (3)

where BC = biodegrade chance, BD = biodegrade

distance, SP = speed and DD = detect distance.

5.2 Results of Applying MAS to Blend

Biodegradation Data

Figure 5 shows the results for the agent simulation

processing the blend 3 trend curve. On the left are the

Multi-Agent user interface screens where the blue

dots represent the “plastic agents” and the green dots

represent the “bacteria agents”. The initial state is

seen on the top left (with an equal amount of blue and

green dots) and the final state is on the bottom left

(with many more green and less blue). That is, the

biodegradation process has worked, the bacteria have

biodegraded the plastic. The right side of Figure 5

shows the corresponding simulation over time

(accelerated time which processes a long time period

in just a few minutes). On the top right is the real

biodegradation curve for the new blend 3, and on the

bottom right (green line) is the Multi-Agent

simulation result. It can be seen that the simulated

curve (bottom right) is a good approximation of the

real curve (top right) in final percentage reached

(70%) and normalized time duration of 1.0, as well as

the gradient and general trend of the curve.

Biodegradation Prediction and Modelling for Decision Support

Figure 5: Agent simulation (Blend 3).

Figure 6: Agent simulation (Blends 1 and 4).

Having successfully simulated blend 3, we now

perform the same process for blends 1 and 4, as

shown in Figure 6. These blends represent the best

performer and the worst, respectively, in terms of

biodegradation behaviour. On the left of Figure 6 are

shown the real trend curves over time, where it can be

seen that blend 4 reaches 90% biodegradation with a

normalized time duration of 0.6, whereas the blend 1

only achieves a max. of 5% with a normalized time

duration of 0.8. On the right of Figure 6 it can be seen

that the Multi-Agent system successfully models both

trend curves over time and % end point, with the

green curve of blend 4 shown on the top right and the

green curve of blend 1 shown on the bottom right.

Table 5: Multi-agent system control parameters for three

different biodegradation simulations*.

Bio-degrade

chance

Bio-degrade

distance

Detect

distance

Speed

Blend 1 0.08 0.8 1.5 0.03

Blend 3 0.8 1.0 3.0 0.1

Blend 4 2.4 1.6 8.0 0.3

*Values have been anonymized while maintaining their relative magnitudes.

Table 5 shows the control parameters used for the

simulations of biodegradation for blends 1, 3 and 4,

which are depicted in Figures 5 and 6. The four

control parameters are given which relate to the

bacteria and plastic agents: distance in which a

bacteria agent can detect and “biodegrade” a plastic

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

agent, and the speed of movement for the bacteria

agent.

It can be seen that blend 4, which has one of the

best biodegradation behaviours (in terms of time and

%, see Table 2) has the highest relative values for all

four control parameters. On the other hand, blend 1,

which has the worst biodegradation, has the lowest

values, also for all four control parameters. This is

explained by the degree of “excitation” of the system

necessary in order to replicate the biodegradation

curves (see Figures 5 and 6) in terms of agent

populations. It could be interpreted as a degree of

“kinetic energy” of the bacteria and the plastic. Blend

3, which displays an intermediate level of

biodegradation, shows intermediate values for its

control parameters, relative to blends 1 and 4,

however the relation between the control parameters

of the blends is non-linear. For example, the

“biodegrade chance” for blend 1 is 10 times less than

blend 3, whereas the “biodegrade chance” of blend 4

is only three times that of blend 3. It can be

interpreted also in terms of the “distance” between the

trend curves (Figures 5 and 6) and also between the

respective material properties (Table 1).

In each case, the MAS control parameters have

been optimized manually for each blend. However, as

we progressively obtain a set of historical settings,

they can be used to approximate settings (at least as

an initial starting point) for new blends, in a similar

way to the CBR, based on some distance function

related to the material properties.

6 CONCLUSIONS

In this paper we have explained how a Case Based

Reasoning (CBR) approach can be used to predict a

biodegradation trend curve over time and how a

Multi-Agent System can be applied to simulating the

biodegradation process.

The CBR approach has been demonstrated to be

able to generate a biodegradation prediction and trend

curve for a blend, which is a good fit to real data,

using the chemical/mechanical properties for

matching closest historical cases, which is calculated

using a weighted distance function. The results in

Table 4 show all R

fitting values of predicted vs real

curves to be over 0.81, with the exception of outlier

blends 3 and 8 (refer to Section 4.2 for explanation).

Furthermore, we have demonstrated how a MAS

can be used to simulate the corresponding

biodegradation curves, with dynamic weighted MAS

control parameter calculation (Table 5) tuned for each

trend curve.

The results are clearly promising and verified as

useful by the materials experts who design blends

which must comply with given chemical and

mechanical properties on the one hand, and

biodegradation characteristics on the other.

The choice of material properties provided a

strong set of descriptors with a good correlation

between chemical and mechanical properties and

their biodegradation behaviour. However, in order to

obtain a good predictive capability from the CBR, a

combination of a non-trivial weighted distance

calculation and an interpolation method were

necessary. In the case of the MAS, the real-time

control parameter optimization also used a set of non-

trivial updating formulas including weighting factors.

Overall, the approaches appear to offer promising

solutions for a variety of bioplastic blends, for their

biodegradation trend prediction and dynamic

simulation, respectively.

Also, the MAS offers a simulation solution which

is relatively easy to implement and calibrate, in

contrast with DSM and mathematical modelling

approaches. Furthermore, the MAS is able to embody

stochastic and noisy features present in real systems,

As future work, as part of the ongoing Biontop

project, we expect to incorporate new blends into the

modelling. Also, we plan to develop further the MAS

modelling, by improving the induction of the MAS

control parameters from the material properties, thus

generating the trend curve automatically.

Furthermore, the MAS control parameters, which

were initially optimized manually for the different

blends, can be used to find settings for new blends, in

a similar way to the CBR approach.

ACKNOWLEDGEMENTS

The BIONTOP project has received funding from the

Bio Based Industries Joint Undertaking under the

European Union’s Horizon 2020 research and

innovation programme under grant agreement No

837761.

REFERENCES

Aamodt, A., Plaza, E. (1994). "Case-Based Reasoning:

Foundational Issues, Methodological Variations, and

System Approaches," Artificial Intelligence

Communications 7 (1994): 1, 39-52.

Alalayah, W. M. (2017). Simulation of the biodegradation

of petroleum hydrocarbons utilizing Artificial Neural

Networks. International Journal of Engineering

Development and Research, 5(4), 891-896.

Biodegradation Prediction and Modelling for Decision Support

Aliotta, L., Vannozzi, A., Canesi, I., Cinelli, P., Coltelli,

M.-B., Lazzeri, A. (2021). Poly(lactic acid)

(PLA)/Poly(butylene succinate-co-adipate) (PBSA)

Compatibilized Binary Biobased Blends: Melt Fluidity,

Morphological, Thermo-Mechanical and Micro-

mechanical Analysis. Polymers 2021, 13, 218.

https://doi.org/10.3390/polym13020218.

Aliotta, L., Gigante, V., Coltelli, M.-B., Lazzeri, A. (2021).

Volume Change during Creep and Micromechanical

Deformation Processes in PLA–PBSA Binary Blends.

Polymers 2021, 13, 2379. https://doi.org/10.3390/

polym13142379.

Arranz, A., Bordel, S., Villaverde, S., Zamarreño, J. M.,

Guieysse, B., & Muñoz, R. (2008). Modeling

photosynthetically oxygenated biodegradation

processes using artificial neural networks. Journal of

hazardous materials, 155(1-2), 51-57.

Bădică, A., Bădică, C., Ivanović, M., & Dănciulescu, D.

(2018). Multi‐agent modelling and simulation of graph‐

based predator–prey dynamic systems: A BDI

approach. Expert Systems, 35(5), e12263.

Baker, J. R., Gamberger, D., Mihelcic, J. R., Sabljić, A.

(2004). Evaluation of Artificial Intelligence Based

Models for Chemical Biodegradability Prediction,

Molecules. 2004 Dec; 9(12): 989–1003.

Borshchev, A. and Filippov, A. (2004). From system

dynamics and discrete event to practical agent based

modeling: Reasons, techniques, tools. 22nd Int. Conf.

of the System Dynamics Society.

Dragomir, T. L., Pană, A. M., Ordodi, V., Gherman, V.,

Dumitrel, G. A., & Nanu, S. (2021). An Empirical

Model for Predicting Biodegradation Profiles of

Glycopolymers. Polymers, 13(11), 1819.

Estivill-Castro, V., Hernández-Jiménez, E., Nettleton, D. F.

(2021). A system dynamics model approach for

simulating hyper-inflammation in different COVID-19

patient scenarios. In 11th International Conference on

Simulation and Modeling Methodologies, Tech-

nologies and Applications, SIMULTECH 2021 (pp.

141-143).

Farzi, A., Dehnad, A., Fotouhi, A. F. (2019).

Biodegradation of polyethylene terephthalate waste

using Streptomyces species and kinetic modeling of the

process. Biocatalysis and agricultural biotechnology,

17, 25-31.

Ferber, J., Weiss, G. (1999). Multi-agent systems: an

introduction to distributed artificial intelligence (Vol.

1). Reading: Addison-Wesley.

Gamberger, D., Sekušak, S., Medven, Ž., & Sabljić, A.

(1996). Application of artificial intelligence in

biodegradation modelling. In Biodegradability

Prediction (pp. 41-50). Springer, Dordrecht.

Karsai, I., Montano, E., and Schmickl, T. (2016). Bottomup

ecology: an agent-based model on the interactions

between competition and predation. Letters in

Biomathematics, 3(1):161–180.

Narancic, T., Verstichel, S., Reddy Chaganti S., Morales-

Gamez, L., Kenny, S.T., De Wilde, B,, Babu Padamati,

R., O'Connor, K. E. (2018). Biodegradable Plastic

Blends Create New Possibilities for End-of-Life

Management of Plastics but They Are Not a Panacea

for Plastic Pollution. Environ Sci Technol. 2018 Sep

18;52(18):10441-10452. doi: 10.1021/acs.est.8b02963.

Epub 2018 Aug 29. PMID: 30156110.

Nettleton, D. F., Estivill-Castro, V., Jiménez, E. H. (2020).

Multi-agent Modeling Simulation of In-vitro T-cells for

Immunologic Alternatives to Cancer Treatment. In

ICAART (1) (pp. 169-178).

Pavan, M., Worth, A. (2006). Review of QSAR Models for

Ready Biodegradation.

Pavan, M., Worth, A.P. (2008). Review of Estimation

Models for Biodegradation, QSAR & Combinatorial

Science, Vol. 27, Issue 1, Special Issue: Computational

Assessment of Toxicity and Environmental Fate,

January 2008, Pages 32-40.

Radzicki, M.J., Taylor, R.A. (2008). Origin of System

Dynamics: Jay W. Forrester and the History of System

Dynamics. In: U.S. Department of Energy's

Introduction to System Dynamics. Retrieved 23

October 2008.

Sable, S., Mandal, D. K., Ahuja, S., & Bhunia, H. (2019).

Biodegradation kinetic modeling of oxo-biodegradable

polypropylene/polylactide/nanoclay blends and

composites under controlled composting conditions.

Journal of environmental management, 249, 109186.

Sonwani, R. K., Swain, G., Giri, B. S., Singh, R. S., Rai, B.

N. (2020). Biodegradation of Congo red dye in a

moving bed biofilm reactor: Performance evaluation

and kinetic modeling. Bioresource Technology, 302,

122811.

APPENDIX

The following defines the Dynamic System Model

representation of the biodegradation process. Figure

7 shows the overall schema of stocks and flows,

Tables 6 and 7 show the differential and algebraic

equations, respectively, and Table 8 shows the

systemic variables and parameters. See Section 2 of

the paper for further explanation.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

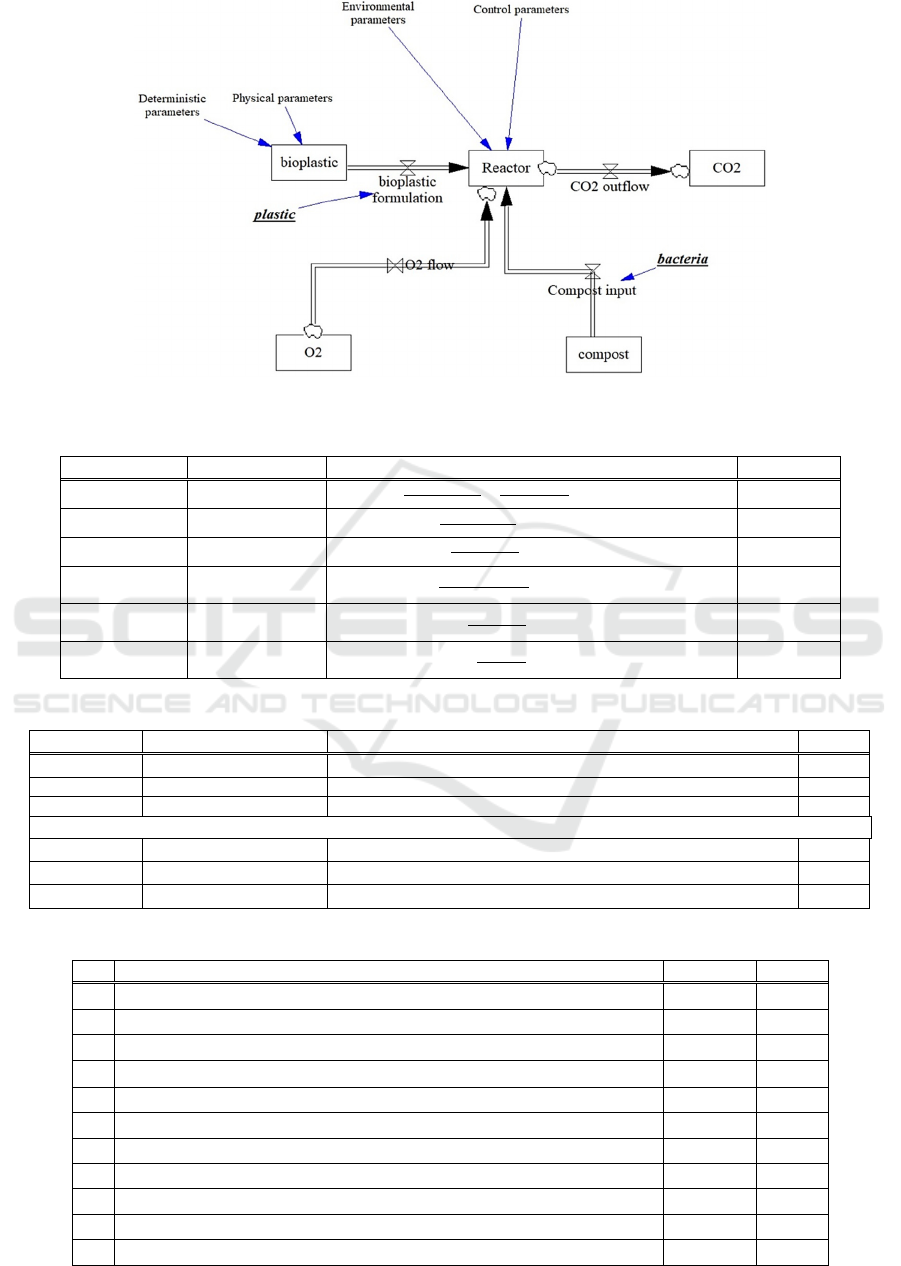
Figure 7: Stocks and Flows.

Table 6: Differential Equations.

Equation no. Stoc

Differential equations Units

1 Reactor











𝑟𝑒𝑎𝑐𝑡𝑜𝑟(t)

kg/d

2 Bioplastic





 𝑏𝑖𝑜𝑝𝑙𝑎𝑠𝑡𝑖𝑐(t)

kg/d

3 Compost





 compost(t)

kg/d

4 Bacteria

𝑑𝑏𝑎𝑐𝑡𝑒𝑟𝑖𝑎𝑡

𝑑𝑡

 bacteriat

5 CO2

𝑑𝐶𝑂2𝑡

𝑑𝑡

𝐶𝑂2𝑡

6 O2

𝑑𝑂2𝑡

𝑑𝑡

𝑂2𝑡

Table 7: Algebraic Equations.

Equation no. Flow Algebraic equations Units

1 Biodecomposition material Biodegradation material(t) = bioplastic(t) + compost(t) + O2(t) – CO2(t) kg/h

2 O2 O2(t) = O2 cm

3 CO2 CO2(t) = CO2 cm

Quality criteria

Quality 1 Decomposition time days

Quality 2

% decomposition

achieved (absolute and/or relative)

Quality 3

Time to reach a target decomposition

days

Table 8: Systemic variables and parameters.

Nº. Paramete

Value

(

)

Units

Amount of bioplastic

Amount of compost

Bioplastic formulation

Average absolute humidity

g/M

CO2

Cut off time

days

Cut off %

Mechanical properties of bioplastics

, p

Chemical properties of bioplastics (DETERMINISTIC)

, d

11 Composting conditions (ENVIRONMENTAL, less DETERMINISTIC) e

, e

Biodegradation Prediction and Modelling for Decision Support