
Assessment of the RSS Model Suitability using Graph Neural Network
based on a Naturalistic Driving Dataset
Sungmoon Ahn
a
and Shiho Kim
b
School of Integrated Technology, Yonsei University, Incheon, 21983, Republic of Korea
Keywords:
Neural Nets and Fuzzy Systems, Data Analytics and Simulation, Intelligent Transportation.
Abstract:
We propose a method to evaluate the RSS model using data obtained from real roads. Recently, the
Responsibility-Sensitive Safety (RSS) model representing the minimum safety distance has been proposed.
After that, there were studies to evaluate the RSS model using simulators. Most virtual simulation studies
showed that the RSS model guarantees safety but adversely affects traffic flow by estimating the distance too
long than necessary. We evaluated the RSS model using data obtained in natural situational environments, un-
like previous studies. First, we found correlations representing distances between vehicles from the data using
Graph Neural Networks. Using the obtained correlations, we expressed it as a mathematical model through
symbolic regression. As a result of comparing the model we found with the RSS model, we verified that the
RSS model has a significant trade-off between safety and traffic flow.
1 INTRODUCTION
Although many research efforts on autonomous driv-
ing have not yet been perfect for fully autonomous
driving, advanced driving assistant systems (ADAS),
which require lower technologies than fully au-
tonomous driving, have already been commercialized
(Chai et al., 2020; Mishra et al., 2021; Mishra et al.,
2022). Among ADAS, adaptive cruise control (ACC)
is a typical longitudinal control system and is a tech-
nology that maintains a safe distance between the sub-
ject vehicle and the leading vehicle. The ACC system
might not work correctly if the front vehicle suddenly
decelerates or another vehicle abruptly cuts in front of
the subject vehicle (Magdici and Althoff, 2017; Bae
et al., 2020).
There have been many studies to set the safety dis-
tance standard between a leading vehicle and a subject
vehicle to improve the safety of ACC against these
worst conditions. Intel Mobileye proposed the Re-
sponsibility Sensitive Safety (RSS) model associated
with NHTSA and IEEE SA (Shashua et al., 2018).
RSS model suggests a safety distance model through
mathematical methodologies using the subject vehi-
cle’s response time, velocity, and acceleration and the
velocity and deceleration of the leading vehicle.
a
https://orcid.org/0000-0002-6209-7309
b
https://orcid.org/0000-0001-9935-1721
In particular, since it is a safe distance calculated
based on the worst-case, it is a model that emphasizes
that a collision does not occur if this distance is main-
tained within the RSS model (Shalev-Shwartz et al.,
2017).
A simple mathematical model can express the cor-
relation between the leading vehicle and the subject
vehicle. Most safety-distance studies have proposed
slightly modified models of the RSS model based on
theoretical analysis or evaluated the suitability of the
RSS model through simulations.
In this work, we propose a new method to evaluate
the safety distance margin of the RSS model through
artificial intelligence (AI) approach based on actual
road data. First, we identified the correlations be-
tween vehicles with Neural Networks using accident-
free vehicle data obtained from the natural road en-
vironments. Second, the correlations found through
Neural Networks were expressed in a formula us-
ing symbolic regression. We propose a new model
representing the safety distance between the leading
vehicle and the subject vehicle through this process.
This study aims to demonstrate that the proposed
model could reduce the trade-off between safety dis-
tance and improving traffic flow compared to the RSS
model. We also verified that the RSS model could af-
fect the traffic flow by estimating more space than the
required minimum distance for safety.
210
Ahn, S. and Kim, S.
Assessment of the RSS Model Suitability using Graph Neural Network based on a Naturalistic Driving Dataset.
DOI: 10.5220/0011139800003274
In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 210-217
ISBN: 978-989-758-578-4; ISSN: 2184-2841
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

2 RELATED WORK
2.1 Car-Following Model
The Car-Following Model refers to an analysis tech-
nique developed to define the correlation through
changes in acceleration, velocity, and headway dis-
tance between two consecutively driving vehicles.
The purpose is to predict the response of the sub-
ject vehicle according to the movement of the leading
vehicle. We can divide the car-following model into
three main domains: Gazis-Herman-Rothery (GHR),
safety distance or collision avoidance (CA), and psy-
chophysical or behavioral points (AP) (Brackstone
and McDonald, 1999). This paper utilizes the CA
field approach. There have been many studies in the
field of CA. Lefevre et al. proposed a model that cre-
ates a model from the driver’s actual driving trajec-
tory and mixes a controller that restricts driving for
safety (Lefevre et al., 2015). Wen-Xing and Li-Dong
proposed a safety distance model using the expected
average velocity (Wen-Xing and Li-Dong, 2018). It
is similar to our methodology because it uses the pre-
dicted velocity. Still, the difference is that we propose
the formula through correlations predicted through
GNNs based on data obtained from the actual envi-
ronments rather than using mathematical approaches.
And there is the RSS model that has been evaluated
and used a lot recently. The RSS model is divided
into five cases as follows;
• Safe longitudinal distance — same directions
• Safe longitudinal distance — opposite directions
• Safe Lateral Distance
• Longitudinal Safe Distance for Two Routes of
Different Geometry
• Lateral Safe Distance for Two Routes of Different
Geometry
Since our purpose is to evaluate using data obtained
from the natural environment, only the safety distance
model for the same direction can be obtained from the
referred database. Equation (1) shows the Safe longi-
tudinal distance formula of the RSS model (Shashua
et al., 2018).
d
min
=
[v
r
ρ +
1
2
a
max,accel
ρ
2
+
(v
r
+ ρa
max,accel
)
2
2a
min,brake
−
v
2
f
2a
max,brake
]
+
(1)
where [x]
+
= max{x,0}.
v
r
indicates the subject vehicle and v
f
indicates
the leading vehicle. This is a formula considering
the worst-case scenario in which the subject vehicle
accelerates to α
max,accel
for ρ time when the leading
vehicle rapidly decelerates to α
max,brake
. It may not
always be proper to consider the worst-case scenario.
For this reason, numerous studies evaluating the ad-
equacy of RSS have been conducted. Among them,
there were studies that RSS improves the safety per-
formance of ACC, but it can reduce traffic flow effi-
ciency in terms of the traffic flow by maintaining a
distance longer than necessary (Mattas et al., 2019).
There were several studies to solve this problem. Li
et al. proposed a modified model that can reduce the
safety gap and make traffic flow more efficient at the
same time based on the RSS through a theoretical
analysis method (Li et al., 2018). Chai et al. pro-
posed an efficient model that can reduce the trade-off
between safety and traffic flow by dividing the inter-
val between the leading vehicle and the subject vehi-
cle into three sections and slightly modifying the RSS
depending on the situation (Chai et al., 2020). Nau-
mann et al. proposed a methodology to find reason-
able parameters of RSS based on physical limitations
(Naumann et al., 2021). Kim et al. extracted and ver-
ified the safety distance for each velocity by applying
the actual vehicle spec to the RSS model (Kim et al.,
2021).
Previous papers have proposed methodologies
that verify the RSS through simulation or slightly
modify the existing model through mathematical
analysis. The RSS model was created by combin-
ing widely known physical and mathematical theo-
ries. Cranmer et al. showed that the formula derived
through artificial intelligence (AI) expresses the ac-
tual motion of atoms better than the formula used in
the existing atomic motion theories (Cranmer et al.,
2020). Based on the results of Cranmer et al., the
purpose of this paper is not to slightly modify the ex-
isting model or verify it through simulations but to
find a new formula using the results of extracting cor-
relations between vehicles through AI based on data
obtained from natural road environments (Cranmer
et al., 2020).
2.2 Graph Neural Networks
First, we need to figure out the correlations repre-
senting the distance between vehicles. The vehi-
cle data obtained from the natural road environments
we want to use is not structured data such as im-
ages. Graph Neural Networks (GNN) are Neural Net-
works structures suitable for analyzing unstructured
data. The advantage of GNN is that GNN can work
with unstructured data such as images without pre-
processing. Therefore, compared to other types of
Neural Networks, GNNs are relatively more robust
Assessment of the RSS Model Suitability using Graph Neural Network based on a Naturalistic Driving Dataset
211

to inductive bias compared with Convolution Neu-
ral Networks (CNNs) and Recurrent Neural Networks
(RNNs) (Battaglia et al., 2018). An additional advan-
tage of GNN is that the correlations between nodes
can be found via the edges between each node. For
these reasons, we used GNNs to find the safety dis-
tance between vehicles in this work. In this paper, the
nodes of GNNs will be each vehicle, and the edges
represent the distance between the vehicles, which are
the correlations between the nodes we want to find.
GNNs started by applying Neural Networks to
acyclic graphs proposed in Sperdui and Starita, and
many studies were conducted until the late 2000s
(Sperduti and Starita, 1997). They aimed to learn the
target node’s representation by iteratively propagat-
ing neighbor information. However, these method-
ologies required too much computation. Since then,
ConvGNNs studies have applied many CNN’s meth-
ods that can compute in parallel to solve various prob-
lems (Wu et al., 2020).
We can classify ConvGNNs into two spectral-
based and spatial-based architectures. Spectral-based
ConvGNNs are trained to learn filter parameters using
the concept of Graph Fourier Transform throughout
the graph signal processing.
However, in spectral-based, the eigenbasis prob-
lem changes when graph perturbation occurs. The is-
sue is that the learned filters are domain-dependent
and cannot apply to other structures, and the eigen-
decomposition O(n
3
) computational complexity (Wu
et al., 2020). In particular, to solve the compu-
tational complexity problem, ChebNet (Defferrard
et al., 2016) and GCN (Kipf and Welling, 2016) re-
duced the amount of computation through several ap-
proximations and simplifications. Nevertheless, there
are still issues such as per- forming eigendecomposi-
tion on a spectral basis or processing the entire graph
at once (Wu et al., 2020). Many other studies have
been done to solve hard problems based on GCN
(Chen et al., 2018; Chen et al., 2017; Chiang et al.,
2019).
There are also spatial-based ConvGNNs studies
to solve the aforementioned spectral-based problems.
Spatial-based ConvGNNs are derived from the con-
cept of existing CNNs that set the representation of a
specific node and the representation of adjacent nodes
as one patch and update it through convolution. It is
the same concept as the initial GNNs but differs in
performing a convolution operation.
Compared to spectral-based ConvGNNs, it does
not require expensive operations such as eigendecom-
position and is easy to generalize to new graphs be-
cause it does not rely on Fourier-based. And it has
the advantage of solving the problem that can only
be computed on the undirected graph, which is a
disadvantage of spectral-based. Many studies have
used performance development using these advan-
tages (Micheli, 2009; Li et al., 2017; Masci et al.,
2015).
In particular, the performance of inductive data
has been greatly improved due to Graph Attention
Networks (GAT) (Veli
ˇ
ckovi
´
c et al., 2017). They
applied a self-attentional layer that applies attention
mechanisms to learning the relative weights of two
connected nodes, allowing us to generalize the unseen
graph. In general, the adjacency matrix, which means
Graph Structure, is used as an input for GNNs. The
adjacency matrix refers to a matrix indicating the cor-
relations between each node. In particular, GCN is
fixed with the given Adjacency Matrix values as the
features of edges, which mean the connections be-
tween nodes. However, GAT does not fix these val-
ues but applies attention mechanisms to learn the cor-
relation between nodes. Therefore, it can adapt to
a new graph more efficiently with a bit of training.
Since the data used in this paper is realtime vehicle
data at a fixed location, it is necessary to repeatedly
train the unseen graph in which vehicle information
changes continuously. Therefore, attention mecha-
nisms, which are the core of GAT, are essential for
finding the correlations between two vehicles, which
is the most important part of this paper. More details
on data are described in the Method.
In addition to finding correlations between the cur-
rent data of each vehicle, we can find more sophis-
ticated correlations if historical data can be used to-
gether.
We used Spatio-Temporal Graph Neural Networks
(STGNNs) to get more accurate correlations, which
added the concept of time to the spatial-based Con-
vGNNs. Based on STGNNs, many studies have im-
proved the performance in various fields such as rec-
ommendation system and traffic prediction (Li et al.,
2017; Guo et al., 2019; Wu et al., 2019; Roy et al.,
2021; Tian and Chan, 2021).
We found that the structure of STAWNet (Tian and
Chan, 2021) is most suitable for our purposes. The
first reason is that most GNNs required an Adjacency
Matrix, which is graph structure information, as input.
However, it is difficult to understand the connection
structures between all vehicles with the data obtained
from the real environments we want to use.
To solve this problem, STAWNet did not use an
adjacency matrix but applied the self-attentional layer
used in GAT to obtain the adjacency edge weights.
As a result, we can find that the self-learned relation-
ship showed a similar relationship found in the actual
data. At the same time, it was possible to find a hid-
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
212

den relationship between the remaining nodes that did
not appear. We thought it was appropriate for the part
where we wanted to see the correlations between the
leading vehicle and the subject vehicle. And since it
is the architecture that includes the concept of tempo-
ral, a more sophisticated correlation can be inferred
by using past data simultaneously as the present.
We utilized STAWNet, which uses a Spatio-
Temporal architecture without requiring an adjacency
matrix as input, to find the correlations between the
two vehicles by training it after modifying it for our
data set and purpose.
2.3 Symbolic Regression
Symbolic regression is an analysis method that di-
rectly creates a function that can explain the re-
relationship between dependent and independent vari-
ables for given data. A lot of studies have been
done based on (Sampson, 1976), which is one of the
techniques to solve the optimization problem. Sym-
bolic regression has been generally studied based
on genetic algorithms (GA), genetic programming
(GP), and Neural Networks (NN) (Mundhenk et al.,
2021). We used GA based Eureq (Schmidt and Lip-
son, 2009). Eureqa stochastically combines algebraic
expressions to create an optimized closed-form equa-
tion. The criteria for optimization are computational
complexity and accuracy. In the problem of find-
ing the safety distance in realtime, if the realtime
is not guaranteed through complex calculations, it
may cause a collision, so we used only simple +,-,/,*
among many operators. For example, suppose a com-
plex operation such as power appears in an expression
obtained through symbolic regression. In that case,
realtime performance may not be guaranteed as the
time complexity is O(n) or more.
3 METHOD
Our process can be summarized as follows.
• First, the Graph Neural Network is trained using
vehicle data obtained from the real road environ-
ments to find the edge embedding features and
correlations between each vehicle.
• Second, we apply symbolic regression using the
found correlations (edge embedding features) to
find the optimal formula to describe the relation-
ships.
• Finally, the optimal formula found is applied to
the dataset to calculate the error from the real val-
ues and validate the formula.
Figure 1: Proposed process for extracting the safety dis-
tance model using Graph Neural Network based on the nat-
uralistic driving dataset.
Our overall process is shown in Figure 1.
3.1 Dataset
We used the highD dataset as data obtained from nat-
ural real road environments. The highD dataset is
the data captured using a drone on German Highways
(Krajewski et al., 2018). Other naturalistic datasets
(Geiger et al., 2013; Yu et al., 2020; Caesar et al.,
2020; Lee et al., 2014; Houston et al., 2020) are those
typically obtained via vehicles. We needed data that
could get information about multiple vehicles simul-
taneously. Using a drone’s data observed with a bird-
eye view was suitable for our purpose. The highD
dataset has data on the current velocity and accelera-
tion of the subject vehicle, the ID of the sur- rounding
vehicle, the velocity and acceleration of the leading
vehicle, the distance to the vehicle in front, headway
distance, time-to-collision.
We can see that this dataset contains information
that can be utilized to compare the RSS model. This
allowed us to select only the data from the highD
dataset and use it to input the GNNs. The informa-
tion we used is as below.
• Subject vehicle Velocity & Acceleration
• Leading vehicle Velocity & Acceleration
• The initial distance between two vehicles
Since our purpose is to compare the natural driving
pattern with the RSS, only the information used in the
RSS was extracted from the dataset and used. Next,
we trained the GNN using the data.
3.2 Graph Neural Network Training
We used a modified structure of STAWNet. First, we
defined each input feature as a temporal data frame.
Second, the final input features were characterized by
Assessment of the RSS Model Suitability using Graph Neural Network based on a Naturalistic Driving Dataset
213

concatenating all input information. While the train-
ing phase, the output is trained to predict the velocity
of each vehicle. GNNs have the advantage of being
able to derive the results of all nodes at once. This set-
ting of GNN helps find the correlations between ve-
hicles by predicting the velocity, which is the move-
ment of all vehicles. The feature maps of the self-
attentional layers indicating the correlations of each
node were extracted by the training. Based on the
feature maps, the embedding space with significant
variance mentioned in Cranmer et al. can general-
ize well and have high performance (Cranmer et al.,
2020). Only the feature map with the largest vari-
ance was extracted among many self-attention feature
maps. The results are shown in Figure 2. Figure 2.(a)
shows the 2-hops adjacency matrix from the highD
dataset. It is the result of normalization with the fol-
lowing equation in order to represent it on the same
scale as Figure 2.(b).
W
d
i j
= exp(−
dist(v
i
,v
2
j
σ
2
) i f dist(v
i
,v
j
) ≤ κ
d
(2)
W
d
i j
represents the correlation between each node
calculated by dist(v
i
,v
j
), which denotes the euclidean
distance between node v
i
and v
j
, σ is the standard de-
viation of the distances and κ
d
means distance thresh-
old (Li et al., 2017).
Next, Figure 2.(b) shows the test result with the
largest variance among self-attentional feature maps.
The result of the corresponding feature map was ex-
tracted through the equation shown below.
W
s
i j
=
e
i
e
j
k
e
i
k
e
j
i f W
i j
≥ κ
s
(3)
W
s
i j
can determine the correlation between node
embeddings based on cosine similarity. That is, it is
possible to know the edge weights between each node
(Tian and Chan, 2021).
Looking at the thick red line, we can see the cor-
relation similarity between the real adjacency matrix
and the edge weights of the prediction results is sim-
ilarly well expressed. Therefore, we can extract the
self-learned adjacency matrix, which is the distance
between vehicles obtained through training, In addi-
tion, the relationship between vehicles with unknown
correlations in the dataset was able to find hidden re-
lationships through self-learned to some extent. So,
we used the correlations extracted through GNNs as
the y value of symbolic regression.
3.3 Symbolic Expression
The extracted edge correlations were set to y, and the
information used as input to the GNN was set to x,
Figure 2: The comparison between (a) the real adjacency
relationship from dataset and (b) the self-learned relation-
ship on the training.
and applied to Eureqa, a symbolic regression pack-
age. The advantage of Eureqa is that it provides vari-
ous information, such as accuracy and computational
complexity, and at the same time finds the optimal
formula through ranking. Since our goal is to find the
required safety distance formula for vehicles in real-
time, we chose an equation that exhibits relatively low
computational complexity and high accuracy.
4 RESULTS & DISCUSSION
Using the learned results, the optimal formula was
derived through symbolic regression. We obtained
safety distance from the naturalistic driving dataset,
which shows that the safety distance was relatively
small compared to the RSS model. And as a result
of applying the formula to accident-free data used for
learning and checking the error with the real value, it
was confirmed that there was almost no error.
It can be a formula that can reduce the trade-off
between the safety distance and the traffic flow. The
best matching formula found through symbolic re-
gression is as follows;
d
min
=
v
2
r
+ v
f
+ a
v
r
+ v
r
α × v
f
(4)
where v
r
indicates the subject vehicle, v
f
indicates the
leading vehicle and a
v
r
means acceleration of the sub-
ject vehicle. α is hyper-parameter.
Correlations extracted from GNN appear as values
between 0 and 1 due to soft-max knowing the impor-
tance of each other. So, after performing symbolic re-
gression, we additionally proceeded to find α that can
reduce the error with the data. As a result, α becomes
approximately 2.0.
Comparing the number of parameters required for
the RSS model with the number of necessary param-
eters for our model, we can see that few are required.
Table 1 shows the parameter comparison. In Table 1,
SV means the subject vehicle and LV means the lead-
ing vehicle.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
214
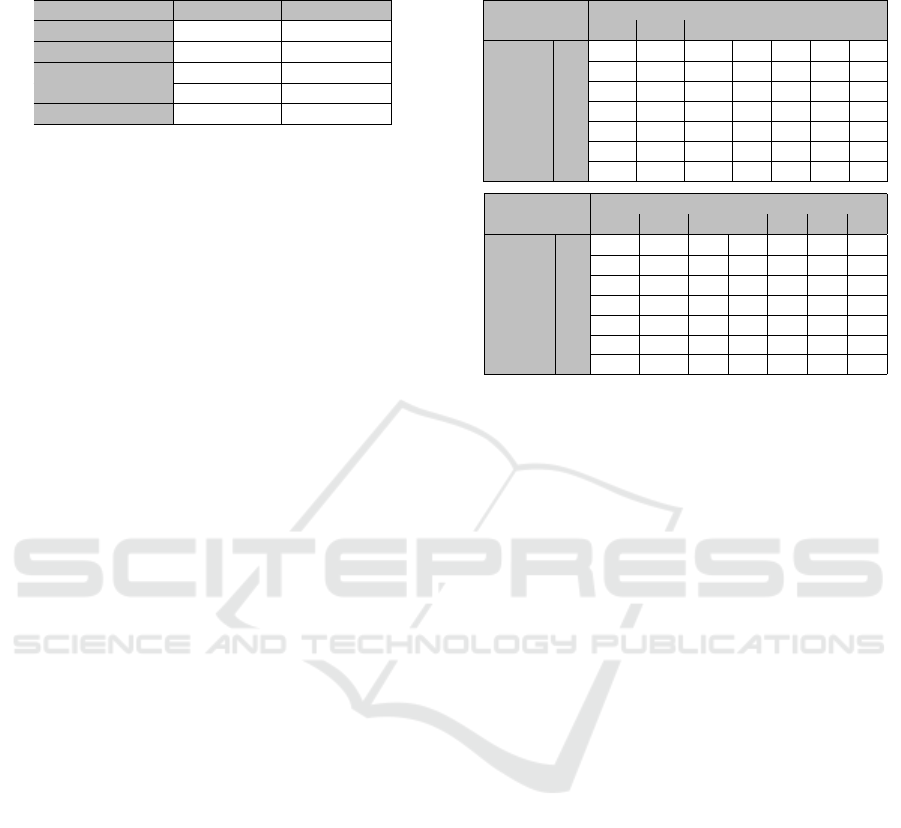
Table 1: Comparison of the number of parameters in our
model and RSS model.
Our Model RSS Model
SV Velocity Yes Yes
SV Accel Yes Yes
LV Accel No Yes
LV Velocity Yes Yes
Response Time No Yes
Using parameters such as the RSS model can
be more conservative due to unnecessary parameter
combinations. The model with more considerable
margins for the necessary distance may impede the
traffic flow while autonomous vehicles drive in the
actual road environment (Chai et al., 2019). So we
can see that our model with fewer parameters is more
efficient. Finally, we compared the number of vari-
ous cases according to the velocity change between
the leading vehicle and the subject vehicle. The re-
sults are shown in Table 2. At this time, the RSS
model needs a response time of ρ. Since we trained
the GNNs assuming the data period is 1 second, we
set ρ to compare it to the same environments. In ad-
dition, For the maximum acceleration/deceleration of
the vehicle, we put a value of 4m/s
2
for maximum
acceleration and of -4.9m/s
2
for maximum decelera-
tion, respectively, as defined by the FSRA (Full Speed
Range Adaptive Cruise Control) system of the inter-
national standard ISO-22179 (Park et al., 2018). The
results can be divided into three cases. First, assuming
that the subject vehicle is driving faster than the lead-
ing vehicle by more than 20km/h, the RSS model re-
sults show that the distance should maintain a distance
from 1.2 to 1.4 times greater than our model. Sec-
ond, assuming that the subject vehicle and the lead-
ing vehicle drive at the same velocity, our model esti-
mates the safety distance to be about 9m smaller than
the RSS model. Finally, when the leading vehicle is
driving faster than the subject vehicle by more than
40km/h, the RSS model showed that the safety dis-
tance was 0, indicating no need to keep the safety dis-
tance.
In contrast, our model showed that a smaller dis-
tance than the required distance of the RSS had to
be maintained. And to validate the safety of our
model, we compared using the highD dataset, which
is accident-free data. As a result of substituting the ac-
tual values of the dataset, the RSS model estimated a
distance 10 to 30m larger than the actual inter-vehicle
distance, and our model estimated a distance of 0
to 10m larger than the real inter-vehicle distance. It
shows that both the RSS and our models are safe mod-
els that prevent crashes. Therefore, although the RSS
model has a low accident probability, we could affirm
that the trade-off between traffic flow and safety is
Table 2: Comparison of our model and RSS model for var-
ious situations.
Subject Vehicle(km/h)RSS
Model 120 110 100 90 80 70 60
120 70.9 47.7 26.1 6.1 - - -
110 89.0 65.8 44.3 24.2 5.8 - -
100 105.5 82.4 60.8 40.8 22.4 5.5 -
90 120.5 97.3 75.7 55.7 37.3 20.5 5.2
80 133.9 110.7 89.1 69.1 50.7 33.8 18.6
70 145.7 122.5 100.9 80.9 62.5 45.7 30.4
Leading
Vehicle
(km/h)
60 155.9 132.8 111.2 91.2 72.7 55.9 40.6
Subject Vehicle(km/h)Our
Model 120 110 100 90 80 70 60
120 61.0 51.4 42.6 34.6 27.5 21.2 15.8
110 66.5 56.0 46.4 37.7 30.0 23.1 17.2
100 73.1 61.6 51.0 41.5 32.9 25.4 18.8
90 81.2 68.4 56.6 46.0 36.5 28.1 20.9
80 91.3 76.8 63.7 51.7 41.0 31.6 23.4
70 104.2 87.7 72.7 59.0 46.8 36.0 26.7
Leading
Vehicle
(km/h)
60 121.5 102.3 84.7 68.8 54.5 41.9 31.0
significant by estimating a relatively large safety dis-
tance.
5 CONCLUSIONS & FUTURE
WORK
This paper evaluated the RSS model by comparing
the RSS model with the safety distance model found
through Graph Neural Networks (GNNs) based on a
real road dataset. In the previous safety distance mod-
els, there is a representative RSS model. However,
it is inefficient for traffic flow to estimate the safety
distance longer than necessary. Most studies have
evaluated the RSS model through simulations or pro-
posed a model with a slight modification of the RSS
model to solve the problem. Unlike previous stud-
ies, we proposed a new model through machine learn-
ing rather than a mathematical car-following model.
First, we trained GNNs using data obtained from real
road environments. After that, edge weights, which
are the correlations of nodes representing each vehi-
cle obtained through GNNs learning, were extracted.
Finally, the optimized formula was derived through
symbolic regression using the extracted edge weights.
The formula we found estimates a relatively short
safety distance compared to the RSS model when the
velocity of the leading vehicle is comparable to or
slower than the velocity of the subject vehicle. Con-
versely, the results showed that the minimum safety
distance should be maintained even when the speed
of the leading vehicle is significantly faster than that
of the subject vehicle. In addition, compared with
accident-free data to verify safety, there was little er-
Assessment of the RSS Model Suitability using Graph Neural Network based on a Naturalistic Driving Dataset
215

ror between our safety distance and the actual dis-
tance. As a result, our model can reduce the safety
margin between safety and traffic flow compared to
the RSS model. Therefore, we conclude that the RSS
model needs improvement.
Like the follow-up studies on the RSS model, we
will verify our model through various additional sim-
ulations (Chai et al., 2020; Xu et al., 2021).
ACKNOWLEDGEMENTS
This work was supported by Institute for Infor-
mation & communications Technology Planning &
Evaluation(IITP) grant funded by the Korea gov-
ernment(MSIT) (No.2021-0-01352, Development of
technology for validating the autonomous driving ser-
vices in perspective of laws and regulations)
REFERENCES
Bae, I., Moon, J., Jhung, J., Suk, H., Kim, T., Park, H., Cha,
J., Kim, J., Kim, D., and Kim, S. (2020). Self-driving
like a human driver instead of a robocar: Personalized
comfortable driving experience for autonomous vehi-
cles. arXiv preprint arXiv:2001.03908.
Battaglia, P. W., Hamrick, J. B., Bapst, V., Sanchez-
Gonzalez, A., Zambaldi, V., Malinowski, M., Tac-
chetti, A., Raposo, D., Santoro, A., Faulkner, R., et al.
(2018). Relational inductive biases, deep learning, and
graph networks. arXiv preprint arXiv:1806.01261.
Brackstone, M. and McDonald, M. (1999). Car-following:
a historical review. Transportation Research Part F:
Traffic Psychology and Behaviour, 2(4):181–196.
Caesar, H., Bankiti, V., Lang, A. H., Vora, S., Liong, V. E.,
Xu, Q., Krishnan, A., Pan, Y., Baldan, G., and Bei-
jbom, O. (2020). nuscenes: A multimodal dataset for
autonomous driving. In Proceedings of the IEEE/CVF
conference on computer vision and pattern recogni-
tion, pages 11621–11631.
Chai, C., Zeng, X., Wu, X., and Wang, X. (2019). Safety
evaluation of responsibility-sensitive safety (rss) on
autonomous car-following maneuvers based on sur-
rogate safety measurements. In 2019 IEEE In-
telligent Transportation Systems Conference (ITSC),
pages 175–180.
Chai, C., Zeng, X., Wu, X., and Wang, X. (2020). Eval-
uation and optimization of responsibility-sensitive
safety models on autonomous car-following maneu-
vers. Transportation research record, 2674(11):662–
673.
Chen, J., Ma, T., and Xiao, C. (2018). Fastgcn: fast learn-
ing with graph convolutional networks via importance
sampling. arXiv preprint arXiv:1801.10247.
Chen, J., Zhu, J., and Song, L. (2017). Stochastic training of
graph convolutional networks with variance reduction.
arXiv preprint arXiv:1710.10568.
Chiang, W.-L., Liu, X., Si, S., Li, Y., Bengio, S., and Hsieh,
C.-J. (2019). Cluster-gcn: An efficient algorithm for
training deep and large graph convolutional networks.
In Proceedings of the 25th ACM SIGKDD Interna-
tional Conference on Knowledge Discovery & Data
Mining, pages 257–266.
Cranmer, M., Sanchez Gonzalez, A., Battaglia, P., Xu, R.,
Cranmer, K., Spergel, D., and Ho, S. (2020). Discov-
ering symbolic models from deep learning with induc-
tive biases. Advances in Neural Information Process-
ing Systems, 33:17429–17442.
Defferrard, M., Bresson, X., and Vandergheynst, P. (2016).
Convolutional neural networks on graphs with fast lo-
calized spectral filtering. Advances in neural informa-
tion processing systems, 29.
Geiger, A., Lenz, P., Stiller, C., and Urtasun, R. (2013).
Vision meets robotics: The kitti dataset. The Inter-
national Journal of Robotics Research, 32(11):1231–
1237.
Guo, S., Lin, Y., Feng, N., Song, C., and Wan, H. (2019).
Attention based spatial-temporal graph convolutional
networks for traffic flow forecasting. In Proceedings
of the AAAI conference on artificial intelligence, vol-
ume 33, pages 922–929.
Houston, J., Zuidhof, G., Bergamini, L., Ye, Y., Chen,
L., Jain, A., Omari, S., Iglovikov, V., and Ondruska,
P. (2020). One thousand and one hours: Self-
driving motion prediction dataset. arXiv preprint
arXiv:2006.14480.
Kim, M.-J., Yu, S.-H., Kim, T.-H., Kim, J.-U., and Kim, Y.-
M. (2021). On the development of autonomous vehi-
cle safety distance by an rss model based on a variable
focus function camera. Sensors, 21(20):6733.
Kipf, T. N. and Welling, M. (2016). Semi-supervised clas-
sification with graph convolutional networks. arXiv
preprint arXiv:1609.02907.
Krajewski, R., Bock, J., Kloeker, L., and Eckstein, L.
(2018). The highd dataset: A drone dataset of natural-
istic vehicle trajectories on german highways for val-
idation of highly automated driving systems. In 2018
21st International Conference on Intelligent Trans-
portation Systems (ITSC), pages 2118–2125. IEEE.
Lee, S., Kim, J., Song, H., and Kim, S. (2014). A 3-
dimensional real-time traffic simulator considering the
interaction among autonomous and human-driven ve-
hicles. In 17th International IEEE Conference on In-
telligent Transportation Systems (ITSC), pages 1917–
1918. IEEE.
Lefevre, S., Carvalho, A., and Borrelli, F. (2015). Au-
tonomous car following: A learning-based approach.
In 2015 IEEE Intelligent Vehicles Symposium (IV),
pages 920–926. IEEE.
Li, L., Peng, X., Wang, F.-Y., Cao, D., and Li, L. (2018).
A situation-aware collision avoidance strategy for car-
following. IEEE/CAA Journal of Automatica Sinica,
5(5):1012–1016.
Li, Y., Yu, R., Shahabi, C., and Liu, Y. (2017). Diffusion
convolutional recurrent neural network: Data-driven
traffic forecasting. arXiv preprint arXiv:1707.01926.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
216

Magdici, S. and Althoff, M. (2017). Adaptive cruise con-
trol with safety guarantees for autonomous vehicles.
IFAC-PapersOnLine, 50(1):5774–5781.
Masci, J., Boscaini, D., Bronstein, M., and Vandergheynst,
P. (2015). Geodesic convolutional neural networks on
riemannian manifolds. In Proceedings of the IEEE in-
ternational conference on computer vision workshops,
pages 37–45.
Mattas, K., Makridis, M., Raposo, M., and Ciuffo, B.
(2019). How the responsibility-sensitive safety frame-
work affects traffic flows on a freeway microsimula-
tion scenario. In 98th Annual Meeting of the Trans-
portation Research Board, Washington, DC.
Micheli, A. (2009). Neural network for graphs: A con-
textual constructive approach. IEEE Transactions on
Neural Networks, 20(3):498–511.
Mishra, A., Cha, J., and Kim, S. (2022). Privacy-preserved
in-cabin monitoring system for autonomous vehicles.
Computational Intelligence and Neuroscience, 2022.
Mishra, A., Kim, J., Cha, J., Kim, D., and Kim, S. (2021).
Authorized traffic controller hand gesture recogni-
tion for situation-aware autonomous driving. Sensors,
21(23):7914.
Mundhenk, T. N., Landajuela, M., Glatt, R., Santiago, C. P.,
Faissol, D. M., and Petersen, B. K. (2021). Symbolic
regression via neural-guided genetic programming
population seeding. arXiv preprint arXiv:2111.00053.
Naumann, M., Wirth, F., Oboril, F., Scholl, K.-U., Elli,
M. S., Alvarez, I., Weast, J., and Stiller, C. (2021).
On responsibility sensitive safety in car-following
situations-a parameter analysis on german highways.
In 2021 IEEE Intelligent Vehicles Symposium (IV),
pages 83–90. IEEE.
Park, S., Park, S., Hong, Y., Ryu, S., and Yun, I. (2018).
Comparison of rss safety distance for safe vehicle
following of autonomous vehicles. The Journal of
The Korea Institute of Intelligent Transport Systems,
17(6):84–95.
Roy, A., Roy, K. K., Ahsan Ali, A., Amin, M. A., and Rah-
man, A. (2021). Sst-gnn: Simplified spatio-temporal
traffic forecasting model using graph neural network.
In Pacific-Asia Conference on Knowledge Discovery
and Data Mining, pages 90–102. Springer.
Sampson, J. R. (1976). Adaptation in natural and artificial
systems (john h. holland).
Schmidt, M. and Lipson, H. (2009). Distilling free-
form natural laws from experimental data. science,
324(5923):81–85.
Shalev-Shwartz, S., Shammah, S., and Shashua, A. (2017).
On a formal model of safe and scalable self-driving
cars. arXiv preprint arXiv:1708.06374.
Shashua, A., Shalev-Shwartz, S., and Shammah, S. (2018).
Implementing the rss model on nhtsa pre-crash sce-
narios. tech. rep.
Sperduti, A. and Starita, A. (1997). Supervised neural net-
works for the classification of structures. IEEE Trans-
actions on Neural Networks, 8(3):714–735.
Tian, C. and Chan, W. K. (2021). Spatial-temporal atten-
tion wavenet: A deep learning framework for traffic
prediction considering spatial-temporal dependencies.
IET Intelligent Transport Systems, 15(4):549–561.
Veli
ˇ
ckovi
´
c, P., Cucurull, G., Casanova, A., Romero, A., Lio,
P., and Bengio, Y. (2017). Graph attention networks.
arXiv preprint arXiv:1710.10903.
Wen-Xing, Z. and Li-Dong, Z. (2018). A new car-following
model for autonomous vehicles flow with mean ex-
pected velocity field. Physica A: Statistical Mechanics
and its Applications, 492:2154–2165.
Wu, Z., Pan, S., Chen, F., Long, G., Zhang, C., and Philip,
S. Y. (2020). A comprehensive survey on graph neural
networks. IEEE transactions on neural networks and
learning systems, 32(1):4–24.
Wu, Z., Pan, S., Long, G., Jiang, J., and Zhang, C. (2019).
Graph wavenet for deep spatial-temporal graph mod-
eling. arXiv preprint arXiv:1906.00121.
Xu, X., Wang, X., Wu, X., Hassanin, O., and Chai,
C. (2021). Calibration and evaluation of the
responsibility-sensitive safety model of autonomous
car-following maneuvers using naturalistic driving
study data. Transportation research part C: emerging
technologies, 123:102988.
Yu, F., Chen, H., Wang, X., Xian, W., Chen, Y., Liu, F.,
Madhavan, V., and Darrell, T. (2020). Bdd100k: A
diverse driving dataset for heterogeneous multitask
learning. In Proceedings of the IEEE/CVF conference
on computer vision and pattern recognition, pages
2636–2645.
Assessment of the RSS Model Suitability using Graph Neural Network based on a Naturalistic Driving Dataset
217
