Robust Neural Network for Sim-to-Real Gap in End-to-End Autonomous

Driving

Stephan Pareigis

and Fynn Luca Maaß

Department of Computer Science, HAW Hamburg, Berliner Tor 7, 20099 Hamburg, Germany

Keywords:

Sim-to-Real Gap, End-to-End Learning, Autonomous Driving, Artiﬁcial Neural Network, CARLA

Simulator, Robust Control, PilotNet.

Abstract:

A neural network architecture for end-to-end autonomous driving is presented, which is robust against discrep-

ancies in system dynamics during the training process and in application. The proposed network architecture

presents a ﬁrst step to alleviate the simulation to reality gap with respect to differences in system dynamics.

A vehicle is trained to drive inside a given lane in the CARLA simulator. The data is used to train NVIDIA’s

PilotNet. When an offset is given to the steering angle of the vehicle while the trained network is being ap-

plied, PilotNet will not keep the vehicle inside the lane as expected. A new architecture is proposed called

PilotNet∆, which is robust against steering angle offsets. Experiments in the simulator show that the vehicle

will stay in the lane, although the steering properties of the vehicle differ.

1 INTRODUCTION

The motivation for this particular research question

is based upon a laboratory experiment with minia-

ture autonomous vehicles (Tiedemann et al., 2019).

Vehicles in the scale 1 : 87 as shown in Figure 1

shall be constructed to drive autonomously in a model

city. The vehicles use a small camera and a mi-

croprocessor to do on-board image based feature ex-

traction of the environment. The microprocessor al-

lows a TPU (google coral) to be connected for faster

ML inference. The experimental setup provides for

different technological approaches to be applied, in-

vestigated, and tested: Up to date several regres-

sion networks have been applied, conventional lane

recognition, various kinds of semantic lane segmen-

tation, imitation learning and reinforcement learn-

ing approaches. Some of these approaches combine

both image interpretation and steering control, e.g.

reinforcement learning, and end-to-end approaches.

Other algorithms like lane segmentation require an

additional control method for steering to be applied

on top of the image recognition. In these latter cases,

usually pure pursuit methods are used for steering

control.

Many of the above mentioned approaches are very

sensitive to small deviations in the vehicle dynamics

https://orcid.org/0000-0002-7238-0976

https://orcid.org/0000-0002-4555-4870

Figure 1: Miniature Autonomous Vehicle. The steering me-

chanics are sensitive and difﬁcult to adjust precisely. Con-

trol algorithms have to account for small deviations.

between training and inference. In the particular case

of very small model vehicles, the mechanical preci-

sion plays an important role in the success of a control

algorithm. Generally, in robotics, the availability of

methods which are robust against imprecise calibra-

tion is of advantage, as mechanical adjustments may

be subject to change during operation.

This leads to the question of a control method

which is robust against small deviations in system dy-

namics of the vehicle. As some of the above men-

tioned algorithms are trained using a simulation, the

problem setting can be regarded as a simulation to re-

ality gap problem. A simulation builds on a perfectly

calibrated system. The resulting algorithms will not

work when applied to a falsely calibrated system in

reality.

Pareigis, S. and Maaß, F.

Robust Neural Network for Sim-to-Real Gap in End-to-End Autonomous Driving.

DOI: 10.5220/0011140800003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 113-119

ISBN: 978-989-758-585-2; ISSN: 2184-2809

113

However, our interest is not only to overcome the

simulation to reality gap, but to ﬁnd a general ap-

proach for robustness with regard to vehicle steering

mechanics. Of particular interest is an offset in the

steering angle. This means that with a value of 0 to the

steering servo, the vehicle will not drive in a straight

line but in a slight curve. This steering offset may

be very sensitive and may change when picking the

miniature vehicle up and putting it back down. The

offset of the steering angle may therefore practically

change during operation.

As mentioned above, different paradigms exist

for autonomous driving. (Chen et al., 2015) present

an overview: Mediated perception, direct perception,

and behaviour reﬂex. The end-to-end approach in this

experiment belongs to the behaviour reﬂex paradigm.

To approach this question, a simple simulation us-

ing the autonomous driving simulator CARLA (Doso-

vitskiy et al., 2017) was set up. An end-to-end

approach using NVIDIA’s PilotNet (Bojarski et al.,

2016) (Bojarski et al., 2017) was implemented and

trained. See (Bojarski et al., 2020) for current work

on PilotNet.

Training was performed using perfect system dy-

namics. The approach requires learning steering an-

gles in a supervised learning setting based on state in-

formation. When the trained neural network is being

applied (inference phase) to a vehicle with the same

perfect system dynamics as during the training pro-

cess, the vehicle behaves as desired and stays in the

lane.

When a steering angle offset is applied to the ve-

hicle system dynamics during the inference phase, the

vehicle will follow the road, however, it will drive

with an offset either closer to the right boundary line

of the lane, or closer or on top of the middle line, de-

pending on the angle offset.

The proposed network architecture PilotNet∆ cor-

rects angle offsets. The steering properties of

PilotNet∆ prove to be independent of mechanical

steering offsets. Experiments show that the proposed

correction method works for a wide range of offset

values. It can be seen in the experiments that the

impulse response of the vehicle with a steering off-

set slightly differs from the original impulse response

used during training.

The special idea of PilotNet∆ is that it takes three

consecutive images as an input and learns an angu-

lar difference, as opposed to the absolute angle as in

PilotNet. To process three input images, an LSTM

architecture is used in PilotNet∆. Other similar archi-

tectures have been proposed using LSTMs, e.g. (Er-

aqi et al., 2017), in which the focus is on detecting

temporal dependencies. Other extensions to PilotNet

have been made as e.g. in (Hecker et al., 2018) using

a 360° camera, or in (Codevilla et al., 2017) where

extensions to PilotNet on a feature level were made.

Also the problem of class imbalance, which oc-

curs in the proposed experimental setup, has been ad-

dressed by various authors, e.g. (Chawla et al., 2011)

who solve the problem using over/under sampling,

and (Ling and Sheng, 2010) who use cost sensitive

loss functions. The latter approach is used in the pro-

posed experiment.

Section 2 describes the experimental setup inside

the simulator CARLA. Section 3 introduces the pro-

posed neural network architecutre PilotNet∆ . Section

4 contains the experimental results and comparisons

between PilotNet and PilotNet∆ and section 5 con-

cludes the results.

2 EXPERIMENTAL SETUP

The experimental setup consists of a CARLA envi-

ronment (Dosovitskiy et al., 2017) to collect training

data. The data is used to train NVIDIA’s PilotNet (Bo-

jarski et al., 2016) and the here proposed PilotNet∆.

Two maps have been created inside CARLA using

the RoadRunner tool (Mathworks, 2021). The map in

Figure 2 is used to collect training data. The map in

Figure 3 is used for testing.

Figure 2: Map for collecting training data. Curves with dif-

ferent curvature and length were created. A PID controller

provided by CARLA’s trafﬁc manager keeps the vehicle in-

side the lane. Steering angles created in this way are used

to label images of the front facing camera as in Figure 4.

CARLA provides a tool called trafﬁc manager

(CARLA, 2021). The trafﬁc manager allows vehi-

cles to drive inside the simulation according to traf-

ﬁc rules. The trafﬁc manager uses a PID controller

to keep the vehicles inside their lanes. The trafﬁc

manager is used in this experimental setup to steer the

vehicle and create training data. CARLA provides a

simulated image of a front facing camera inside the

vehicle. The environment in this experimental setup

is deliberately kept simple. The focus of the setup

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

114

Figure 3: Map for testing the behaviour of the vehicle in a

right and left curve.

is to understand control theoretical behaviour of the

neural network. See Figure 4 for an example of the

images which have been produced by the simulation.

In addition to the images of the front facing cam-

era, CARLA also provides steering angles of the vehi-

cle, which have been calculated by the PID controller.

The images (as input to the neural network), together

with the corresponding steering angles (as labels), are

used as training data in this experimental setup.

2.1 Data Creation

Training data is generated using two principles. First,

the vehicle is driven on the map in Figure 2 using the

trafﬁc manager. Images and steering angles are col-

lected. Figure 8 shows a distribution of the collected

steering angles in this setting. Second, the vehicle is

initially put on the lane with a lateral offset. The traf-

ﬁc manager then guides the vehicle back to the correct

lateral position of the lane in an S-shaped curve. Also

in this case, images and corresponding steering an-

gles are collected. Figure 9 shows the distribution of

steering angles for this case.

It shall be mentioned that the images are cropped

above the horizon before being used as training data.

This allows a faster training process, as the input im-

ages are smaller. It also provides independence of the

outcome upon any kind of simulated clouds above the

horizon.

2.2 Evaluation Methods

Evaluation of NVIDIA’s PilotNet and PilotNet∆ is

done in the CARLA simulator in a driving test. The

vehicle is placed on the test map with the trained

model steering the vehicle. The position of the ve-

hicle throughout the map is compared to the ground

truth trajectory generated by the vehicle steered with

CARLA’s trafﬁc manager. Given this, the error in lat-

eral position is calculated at any simulation time step.

Further, the mean absolute error in lateral position is

calculated. A mean absolute error in the lateral po-

sition of zero would mean that the vehicle’s trajec-

tory is identical to the ground truth trajectory of the

trafﬁc manager, which is a best-case scenario. Pilot-

Net and PilotNet∆ are evaluated twice. First, with no

changes in system dynamics of the vehicle. Second,

with changes in system dynamics of the vehicle in the

form of a steering offset of -7.5 degree (left). In the

latter, if the model steers the vehicle straight ahead, it

constantly drives 7.5 degrees to the left.

2.3 Training and Results of PilotNet

The data, as described above, is used to train

NVIDIA’s PilotNet (Bojarski et al., 2020). As ex-

pected, the vehicle stays perfectly inside the lane, pro-

vided that the vehicle has the same steering properties

as during generation of the training data. Figure 4

shows an image of the front facing camera inside the

vehicle, when its lateral position is as desired. The red

circle indicates the position of the right lane boundary

with respect to the vehicle. This helps the viewer to

acknowledge the correct lateral position.

Figure 4: Front facing camera inside the CARLA simula-

tion. The environment is deliberately kept simple to focus

on control theoretical aspects of the setup. The red circle

helps the viewer to identify the lateral position of the vehi-

cle. This case shows the car with the desired lateral position

on the lane.

In the next experiment, an offset is added to the

steering angle. This shall simulate an incorrect zero-

adjustment of the steering mechanics. The experi-

ment shows that the vehicle coarsely follows the lane.

However, the lateral position of the vehicle is closer

or on top of the middle lane, leading to unacceptable

driving behavior. Figure 5 shows an image from in-

side the vehicle. In curves, the vehicle behaves errat-

ically and may also leave the lane.

3 PilotNet∆

A new end-to-end architecture called PilotNet∆ (Pi-

lotNet Delta) is proposed in this paper. The architec-

ture has increased robustness against different steer-

Robust Neural Network for Sim-to-Real Gap in End-to-End Autonomous Driving

115

Figure 5: In this case, the vehicle is positioned to the left

of the desired lateral position. Looking at the red circle,

which indicates the position of the right lane boundary with

respect to the vehicle, helps to see this. See Figure 4 for

comparison. This is the behaviour which is received when

the vehicle has been trained with perfect steering mechan-

ics, and an offset is added to the steering angle during the

inference phase.

ing offsets, characterized by a lower mean absolute

error in positioning compared to the original PilotNet

driving under same conditions.

3.1 Neural Network Architecture

Table 1 illustrates the new CNN-LSTM architecture

of PilotNet∆.

Table 1: PilotNet∆ Architecture including a ConvLSTM

Layer - 315,291 Parameters.

Layer Type Stride Activation Output Shape Params

Input Sequence - - 3x66x200x3 -

Standardization - - 3x66x200x3 -

ConvLSTM2D 5x5 2x2 ELU 24@31x98 64896

Dropout 0.2 - - 24@31x98 -

Conv2D 5x5 2x2 ELU 36@14x47 21636

Conv2D 5x5 2x2 ELU 48@5x22 43248

Conv2D 3x3 1x1 ELU 64@3x20 27712

Dropout 0.2 - - 64@3x20 -

Conv2D 3x3 1x1 ELU 64@1x18 36928

Flatten - - 1152 -

Dropout 0.2 - - 1152 -

Dense - ELU 100 115300

Dense - ELU 50 5050

Dropout 0.2 - - 50 -

Dense - ELU 10 510

Output - - 1 11

315,291

The general structure of PilotNet∆ is very similar

to the original PilotNet from NVIDIA. PilotNet∆ in-

cludes one major difference in regard to the input and

output of the neural network. Originally, NVIDIA’s

PilotNet operates on single images at a time (image

)

labeled with the corresponding absolute steering an-

gle (α

), creating the mapping as depicted in Figure

PilotNet Input → Output Behaviour

image

7→ α

Figure 6: PilotNet takes a single image as input and learns

the corresponding absolute steering angle α

PilotNet∆ follows a different approach. The archi-

tecture takes the last three frames at a time t: image

image

t−1

, image

t−2

, labeled with the amount the an-

gle (α

) has to change compared to the previous angle

(α

t−1

), referred to as relative angle, creating the fol-

lowing mapping:

PilotNet∆ Input → Output Behaviour

(image

, image

t−1

, image

t−2

) 7→ α

− α

t−1

Figure 7: PilotNet∆ takes three consecutive images as input

and learns the corresponding relative steering angle ∆α

− α

t−1

Compared to NVIDIA’s PilotNet, PilotNet∆ im-

plements a convolutional LSTM layer to process the

sequence of three images (for a similar approach us-

ing an LSTM layer see (Eraqi et al., 2017)). Each

sequence has a shape of 3 by 66 by 200 by 3 pix-

els (sequence x height x width x channels), encoded

in the YUV color space. Each image is spatially 0.5

m apart from the next one. Compared to the orig-

inal architecture from NVIDIA, the PilotNet∆ net-

work contains 4 dropout layers throughout the model.

Besides the ﬁrst ConvLSTM Layer, the dropout lay-

ers in between, and the different output, PilotNet∆

matches NVIDIA’s PilotNet in regard to layer number

and shapes. Due to the additional ConvLSTM layer,

PilotNet∆ contains 315,000 parameters and therefore

roughly 65.000 more than NVIDIA’s PilotNet.

3.2 Training Details

PilotNet∆ is trained in a supervised manner given

roughly 12.000 images (20 minutes of driving se-

quences) collected by the two principles introduced

in section 2.

Figure 8 shows the distribution of data that was

gathered by the trafﬁc manager driving on the map

in Figure 4. Figure 9 shows the distribution of data

gathered by the trafﬁc manager driving with an initial

lateral offset. Both data sets have nearly the same size

and are combined during training.

NVIDIA’s PilotNet is trained using single images

image

and respective absolute steering angles α

shown in Figure 6. The training data for PilotNet∆ is

based on the same data set. However, three consec-

utive images and relative steering angles are used as

training data as shown in Figure 7.

The unfavorable data distributions complicates the

training for PilotNet∆ and requires further actions to

ensure a successful training. Cost-sensitive loss func-

tions are a way to deal with class imbalance problems

(Ling and Sheng, 2010). A prototype cost-sensitive

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

116

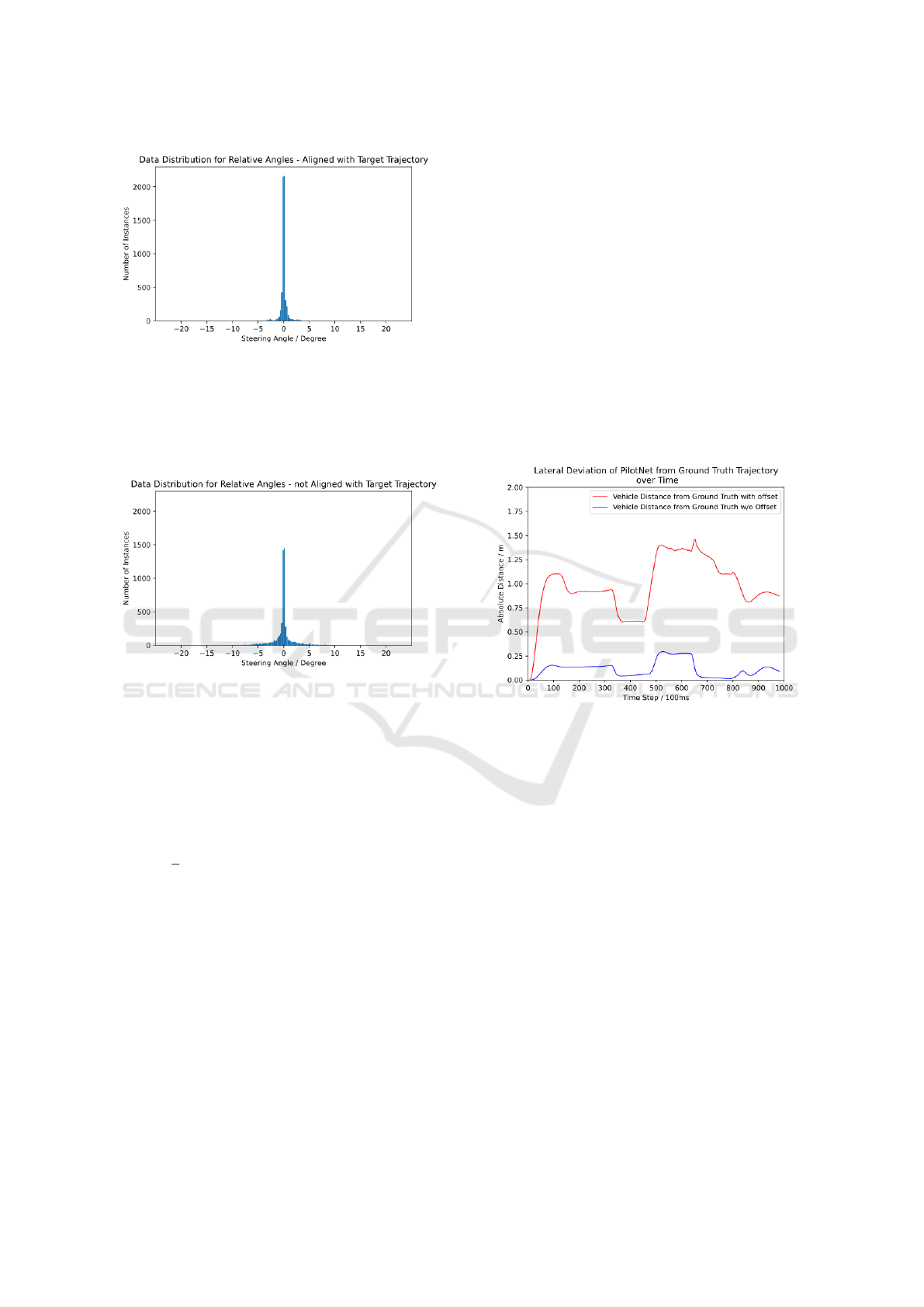
Figure 8: The diagram shows the distribution of gathered

data by the vehicle driving in the map in Figure 2 using

the trafﬁc manager. The histogram with bins of 0.25 degree

width shows the distribution for relative angles while the

vehicle was driving inside its lane. 6,054 Images - Mean:

-0.0001 - Standard Deviation: 0.84. Most of the collected

relative steering angels are small, i.e. close to zero.

Figure 9: The diagram shows the distribution of gathered

data by the vehicle when it is initially put on the lane with

a lateral displacement. The histogram with bins of 0.25 de-

gree width shows the distribution for relative angles. 5,920

Images - Mean: 0.0004 - Standard Deviation: 04.16. It can

be seen that more data from curves has been collected in

this case. The peak at 0 is smaller (less data) and more data

from nonzero relative angles is available for training.

variation of the MSE loss function is proposed:

∑

t=1

pred

−Y

true

)

∗ (|Y

true

| + 0.1) (1)

It calculates the Mean Squared Error between the

model’s prediction (Y

pred

) to the ground truth steer-

ing angle (Y

true

). It then re-weights the MSE depend-

ing on the probability of the ground truth in the data

set. This loss functions beneﬁts from the fact that the

amount of the ground truth correlates to its probabil-

ity. Ground truths with the value 0 are re-weighted

with a factor of 0.1. In contrast to over/under sam-

pling techniques (Chawla et al., 2011) that were tried,

the proposed cost-sensitive loss function in combina-

tion with a batch size of 200 leads to a good training

result.

4 EXPERIMENTAL RESULTS

For the following results, NVIDIA’s PilotNet and

PilotNet∆ drove on the test map in Figure 3 with

and without changed steering mechanics in the form

of a steering offset of -7.5 degrees (left). The fol-

lowing ﬁgures 10 and 11 illustrate the absolute error

in position from the ground truth trajectory given by

CARLA’s trafﬁc manager over time.

4.1 Results for NVIDIA’s PilotNet

As mentioned previously, NVIDIA’s PilotNet perfor-

mance when driving without a change in steering me-

chanics was good. However, when an offset in the

steering is present, the driving performances was un-

acceptable.

Figure 10: Error in lateral position over time (red - driv-

ing with offset, blue - driving without offset) for PilotNet

when driving on the test map in Figure 3. The right curve is

approximately at [350, 480], the left curve at [650, 800].

Figure 10 illustrates the two different scenarios.

The blue function describes the lateral deviation from

the ground truth trajectory (i.e. CARLA’s trafﬁc man-

ager) when NVIDIA’s PilotNet drove with no changes

in the steering mechanics. The right curve is be-

tween time steps [350, 480], the left curve between

[650, 800]. PilotNet shows the largest lateral displace-

ment of 25cm after the right curve. During the left

and during the right curve the lateral displacement is

minimal.

The red function shows the lateral deviation from

the ground truth trajectory when NVIDIA’s PilotNet

drove with a steering offset. The lateral deviation

is signiﬁcantly higher throughout the whole test run.

The vehicle was pushed to the left side, driving close

or on the center mark of the lane, but managed to drive

successfully until the end.

Robust Neural Network for Sim-to-Real Gap in End-to-End Autonomous Driving

117

4.2 Results for PilotNet∆

Figure 11: The functions show the lateral deviation of the

PilotNet∆-driven vehicle with respect to the trajectory of

CARLA’s trafﬁc manager over time (red - driving with off-

set, blue - driving without offset) on the test map. Apart

from the overshoot in the beginning, PilotNet∆ shows al-

most identical driving behaviour without and with a me-

chanical steering offset.

Figure 11 shows the error in positioning from the

ground truth trajectory of PilotNet∆ while driving

with changed system dynamics (red) compared to

driving without changed system dynamics (blue). In

contrast to NVIDIA’s PilotNet, both test runs for

PilotNet∆ show nearly identical results. This il-

lustrates the advantage of PilotNet∆ over NVIDIA’s

PilotNet and its abilities to compensate mechanical

steering offsets. When the vehicle drove with an off-

set in the steering (red), a difference in the start up

phase can be seen. Due to the offset, the vehicle de-

viated 0.75 m from the center of its lane for the ﬁrst

100 time steps. After time step 100, both test runs are

identical.

The error in lateral position in the test run when

the vehicle drove without changed system dynamics

(blue) is larger than with PilotNet. It is seen, that

there is a measurable error in lateral position of about

0.5 m in the ﬁrst segment of the test map. When the

vehicle was entering the ﬁrst right turn at time step

300, the lateral displacement fell from 0.55 m to 0 m

and then rose again to 0.2 m. At this point, the ve-

hicle transitioned from the left side to the right side

relative to the ground truth trajectory. When the ve-

hicle entered the left curve at time step 480 the same

happened once again, but vice versa. On the second

straight road segment between time step 500 and 650

the error in positioning was about 0.6 m with small

oscillations present. In the left curve at time step 650

to 850 the vehicle deviated 1.2 m from the center of

its lane.

Table 2 concludes information already present in

the Figures 10 and 11 in a compact form. It shows the

mean absolute error in positioning across the whole

test runs and the maximum errors in positioning for

PilotNet and PilotNet∆ either with or without changed

system dynamics. The table concludes, that the base-

line performance of NVIDIA’s PilotNet is better than

the baseline performance of PilotNet∆ in regard to the

lateral positioning. However, the table clearly shows

once again the robustness of PilotNet∆ against chang-

ing system dynamics in the form of a steering off-

set. In a direct comparison from NVIDIA’s Pilot-

Net to PilotNet∆, both driving with a steering offset,

PilotNet∆’s mean absolute error in positioning is with

0.57 m signiﬁcantly lower than NVIDIA’s PilotNet

with 0.98 m.

Table 2: MAE of PilotNet and PilotNet∆ during the eval-

uation process, driving with and without an offset, contra-

dicted.

Architecture MAE Max MAE with Max Error

Error with Offset with Offset

NVIDIA’s PilotNet 0.11 m 0.29 m 0.98 m 1.46 m

PilotNet∆ 0.55 m 1.18 m 0.57 m 1.19 m

5 DISCUSSION AND

CONCLUSION

It can be shown that the proposed neural network ar-

chitecture PilotNet∆ has the capability of compen-

sating deviations in steering mechanics. The exper-

iments are focused on an offset in the steering angle.

Other deviations in the steering mechanics, like vari-

ations in the conversion function from servo settings

to steering angle, have not yet been experimentally

investigated. Also, experiments with the real model

vehicle are pending.

PilotNet∆’s steering capabilities with respect to

the absolute derivation from the given path is inferior

to PilotNet. In our opinion, the proposed architecture

must be developed further to achieve the same accu-

racy as PilotNet.

The feature complexity of the simulation environ-

ment is intentionally reduced to a minimum for the

purpose of this paper. Generally, End-to-End solu-

tions are capable of learning complex image features,

capable of driving in the real world, including difﬁ-

cult scenarios such as parking lots and on unpaved

roads (Bojarski et al., 2016), (Wang. et al., 2019),

(Hoveidar-Seﬁd. and Jenkin., 2018).

There were major difﬁculties in preparing the data

to achieve robust training in the case of PilotNet∆.

When collecting data in an imitation learning setting,

too little information is collected to describe the be-

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

118

haviour in curves, especially when relative steering

angles instead of absolute steering angles are used.

This is due to the fact that the vehicle mostly drives

with small steering angles. This results in the be-

haviour of the desired controller not being represented

adequately by the samples.

The use of a simulation offers great possibilities

for collecting sufﬁcient data in the whole working

range of the controller. In the described setup, a PID-

controller was provided inside the simulation, which

was used as a role model from which the samples

have been taken. It may be asked if an existing PID-

controller is really necessary to train a neural network

to achieve a controller with a desired behaviour. Other

than a desired behaviour of the steering controller, a

cost function may be provided to be minimized and

reinforcement learning techniques can be applied. In

either case, the question of an exact formulation of

the requirements for vehicle steering and its control

properties has to be answered.

REFERENCES

Bojarski, M., Chen, C., Daw, J., De

girmenci, A., Deri, J.,

Firner, B., Flepp, B., Gogri, S., Hong, J., Jackel, L.,

Jia, Z., Lee, B., Liu, B., Liu, F., Muller, U., Payne, S.,

Prasad, N. K. N., Provodin, A., Roach, J., Rvachov,

T., Tadimeti, N., van Engelen, J., Wen, H., Yang, E.,

and Yang, Z. (2020). The nvidia pilotnet experiments.

Bojarski, M., Del Testa, D., Dworakowski, D., Firner, B.,

Flepp, B., Goyal, P., Jackel, L. D., Monfort, M.,

Muller, U., Zhang, J., Zhang, X., Zhao, J., and Zieba,

K. (2016). End to End Learning for Self-Driving Cars.

arXiv e-prints, page arXiv:1604.07316.

Bojarski, M., Yeres, P., Choromanska, A., Choromanski,

K., Firner, B., Jackel, L., and Muller, U. (2017). Ex-

plaining How a Deep Neural Network Trained with

End-to-End Learning Steers a Car. arXiv e-prints,

page arXiv:1704.07911.

CARLA (2021). trafﬁcmanager. //carla.readthedocs.io/

en/latest/adv trafﬁc manager. Accessed: 2021-10-03.

Chawla, N. V., Bowyer, K. W., Hall, L. O., and

Kegelmeyer, W. P. (2011). SMOTE: Synthetic Mi-

nority Over-sampling Technique. arXiv e-prints, page

arXiv:1106.1813.

Chen, C., Seff, A., Kornhauser, A., and Xiao, J. (2015).

Deepdriving: Learning affordance for direct percep-

tion in autonomous driving. In 2015 IEEE Interna-

tional Conference on Computer Vision (ICCV), pages

2722–2730.

Codevilla, F., M

uller, M., L

opez, A., Koltun, V., and Doso-

vitskiy, A. (2017). End-to-end Driving via Con-

ditional Imitation Learning. arXiv e-prints, page

arXiv:1710.02410.

Dosovitskiy, A., Ros, G., Codevilla, F., Lopez, A., and

Koltun, V. (2017). Carla: An open urban driving sim-

ulator.

Eraqi, H. M., Moustafa, M. N., and Honer, J. (2017). End-

to-End Deep Learning for Steering Autonomous Ve-

hicles Considering Temporal Dependencies. arXiv e-

prints, page arXiv:1710.03804.

Hecker, S., Dai, D., and Van Gool, L. (2018). End-to-

End Learning of Driving Models with Surround-View

Cameras and Route Planners. arXiv e-prints, page

arXiv:1803.10158.

Hoveidar-Seﬁd., M. and Jenkin., M. (2018). Autonomous

trail following using a pre-trained deep neural net-

work. In Proceedings of the 15th International Con-

ference on Informatics in Control, Automation and

Robotics - Volume 1: ICINCO,, pages 103–110. IN-

STICC, SciTePress.

Ling, C. and Sheng, V. (2010). Cost-sensitive learning and

the class imbalance problem. Encyclopedia of Ma-

chine Learning.

Mathworks (2021). Roadrunner. //de.mathworks.com/pro

ducts/roadrunner.html. Accessed: 2021-10-03.

Tiedemann, T., Fuhrmann, J., Paulsen, S., Schnirpel, T.,

Sch

onherr, N., Buth, B., and Pareigis, S. (2019).

Miniature autonomy as one important testing means in

the development of machine learning methods for au-

tonomous driving : How ml-based autonomous driv-

ing could be realized on a 1:87 scale. In Interna-

tional Conference on Informatics in Control, Automa-

tion and Robotics 2019, ICINCO 2019 : proceedings

of the 16th International Conference on Informatics in

Control, Automation and Robotics, pages 483–488.

Wang., Y., Liu., D., Jeon., H., Chu., Z., and Matson.,

E. (2019). End-to-end learning approach for au-

tonomous driving: A convolutional neural network

model. In Proceedings of the 11th International Con-

ference on Agents and Artiﬁcial Intelligence - Volume

2: ICAART,, pages 833–839. INSTICC, SciTePress.

Robust Neural Network for Sim-to-Real Gap in End-to-End Autonomous Driving

119