
Constructive Model Inference: Model Learning
for Component-based Software Architectures
Bram Hooimeijer
1 a
, Marc Geilen
2 b
, Jan Friso Groote
3,4 c
,
Dennis Hendriks
5,6 d
and Ramon Schiffelers
4,3 e
1
Prodrive Technologies, Eindhoven, The Netherlands
2
Department of Electrical Engineering, Eindhoven University of Technology, Eindhoven, The Netherlands
3
Department of Mathematics and Computer Science, Eindhoven University of Technology, Eindhoven, The Netherlands
4
ASML, Veldhoven, The Netherlands
5
ESI (TNO), Eindhoven, The Netherlands
6
Department of Software Science, Radboud University, Nijmegen, The Netherlands
Keywords:
Model Learning, Component-based Software, Industrial Application.
Abstract:
Model learning, learning a state machine from software, can be an effective model-based engineering tech-
nique, especially to understand legacy software. However, so far the applicability is limited as models that can
be learned are quite small, often insufficient to represent the software behavior of large industrial systems.
We introduce a novel method, called Constructive Model Inference (CMI). It effectively allows us to learn
the behavior of large parts of the industrial software at ASML, where we developed the method and it is now
being used. The method uses observations in the form of execution logs to infer behavioral models of concur-
rent component-based (cyber-physical) systems, relying on knowledge of their architecture, deployment and
other characteristics, rather than heuristics or counter examples. We provide a trace-theoretical framework,
and prove that if the software satisfies certain architectural assumptions, our approach infers the correct re-
sults.
We also present a practical approach to deal with situations where the software deviates from the assump-
tions. In this way we are able to construct accurate and intuitive state machine models. They provide practi-
tioners with valuable insights into the software behavior, and enable all kinds of behavioral analyses.
1 INTRODUCTION
Model-based systems engineering can cope with the
increasing complexity of software (Akdur et al.,
2018). However, for most software, especially legacy
software, no models exist and constructing models
manually is laborious and error-prone.
A solution is to learn the models automatically
from logs of the software. Model inference has been
studied in the fields of model learning (de la
Higuera, 2010) and process mining (van der Aalst,
2016). Both encompass a vast body of research, and
do not focus specifically on software systems. Still,
a
https://orcid.org/0000-0003-0152-4909
b
https://orcid.org/0000-0002-2629-3249
c
https://orcid.org/0000-0003-2196-6587
d
https://orcid.org/0000-0002-9886-7918
e
https://orcid.org/0000-0002-3297-2969
the techniques have been applied to software compo-
nents in general (Heule and Verwer, 2013; van der
Aalst et al., 2003), and specifically to legacy compo-
nents (Schuts et al., 2016; Leemans et al., 2018; Bera
et al., 2021).
There are known fundamental limitations to the
capabilities of model inference: Mark Gold has
proven that accurately generalizing a model beyond
observations (logs) is impossible based on observa-
tions alone (Mark Gold, 1967). Accurate learning
from logs requires additional information, such as for
instance counter examples, i.e., program runs that
can never be executed. In practice, often heuristics
are used, based on the input observations (e.g., con-
sidering only the last n events) or the resulting model
(e.g., limiting the number of resulting states).
Alternative to counter examples, active automata
learning queries (parts of) the system (Angluin,
146
Hooimeijer, B., Geilen, M., Groote, J., Hendriks, D. and Schiffelers, R.
Constructive Model Inference: Model Learning for Component-based Software Architectures.
DOI: 10.5220/0011145700003266
In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 146-158
ISBN: 978-989-758-588-3; ISSN: 2184-2833
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

1987). It guarantees that the inferred models exactly
match the software implementation. But it suffers
from scalability issues (Howar and Steffen, 2018;
Yang et al., 2019; Aslam et al., 2020), limiting the
learned models to a few thousand states at most.
We aim to infer models for large industrial sys-
tems. Our approach therefore learns models from
software execution logs, which are interpreted using
knowledge of the software architecture, its deploy-
ment and other characteristics. It does not rely on
queries or counter examples. It also has no heuristics
that would be hard to configure correctly, especially
if they do not directly relate to system properties.
We instead inject our knowledge of the system’s
component structure, and the services each compo-
nent provides, which it can implement by invoking
services provided by other components. After a com-
ponent executes a service, it returns a response and is
ready to again provide its services. This knowledge
of the components and their services is essential to
cope with the complexity of the industrial systems
we deal with. It allows us to learn multi-level models
that are small enough for engineers to interpret, while
capturing the complex system behavior of actual
software systems at company ASML, consisting of
dozens of components, with states spaces that are too
large to interpret (i.e., 10
10
states and beyond). To
the best of our knowledge no similar approach exists.
To demonstrate that our learning approach is ade-
quate, we prove that if a component-based software
architecture satisfies our assumptions, our learning
approach returns the correct result, both in settings
with synchronous and asynchronous commu-
nication between the concurrent components. While
the actual software largely adheres to our structural
and behavioral assumptions, there are however parts
that do not. We deal with this by analyzing the
learned models, e.g., by searching for deadlocks. Part
of the approach is a systematic method to add addi-
tional knowledge, to exclude from the models any
behavior known to not be exhibited by the system.
Inspection of the learned models by experts led
to the judgment that the models are very adequate,
and provide them the software behavior abstractions
that they currently lack (Yang et al., 2021). Learning
larger models is limited not by the software size, but
by the capability to analyze those models.
This paper is organized as follows. Section 2
presents an overview of the approach. Section 3 re-
calls basic definitions. The novel Constructive Model
Inference (CMI) approach, our main contribution, is
described and analyzed, for synchronously and asyn-
chronously composed component-based systems, in
Sections 4 and 5, respectively. Section 6 outlines a
method to apply the approach, using a case study at
ASML as example. Section 7 draws conclusions.
2 CMI OVERVIEW
We present a high-level outline of the method before
discussing the detailed steps in the following sec-
tions. Figure 1 illustrates the overall approach and
the steps involved. The left column shows the as-
sumed system architecture. A system (S) consists of
a known set of components (C
1
, C
2
, C
3
) that collabo-
rate, communicate and use each other’s services. A
component, in turn, consists of the services it offers
(F
1
, F
2
). We refer to different functions in the com-
ponent’s implementation that together implement a
service (F
1,1
, F
1,2
, F
1,3
) as service fragments. They
handle incoming communications, e.g., client re-
quests and server responses. We use this architecture
to decompose observations, downwards in the mid-
dle column, and compose models, upwards in the
right column, to reconstruct the system behavior.
The inference method requires observing system
executions (Preparation). The resulting runtime ob-
servations in the form of execution logs, consisting of
events, are the input to our method. Using knowledge
of the system architecture, the observations are first
(Step 1) decomposed into observations pertaining to
individual components. Assuming that the beginning
and the end of each service fragment can be identi-
fied, we decompose observations further into
observations of individual service fragments (Step 2).
Then, we infer finite state automata models of
service fragments from their observations (Step 3),
assuming that offered services may be repeatedly re-
quested, and executed from start to end. The service
fragment models are combined to form component
models (Step 4), where each component repeatedly
executes its services, non-preemptively, one at a
time. These component models are put in parallel to
form the behavior of the system (Step 6).
The learned system model may exhibit behavior
that the real system does not, e.g., due to missing de-
pendencies between service fragments. The method
provides for optional refinement (Step 5), whereby
behavioral constraints derived from the software ar-
chitecture and expert knowledge can be added to the
component models, in a generic and structured way.
Injecting such behavior allows turning stateless ser-
vices into stateful ones, removing non-system
behavior from the models.
The composition in Step 6 can be performed in
various ways, depending on assumptions about the
way the system is composed of components, i.e., ei-
Constructive Model Inference: Model Learning for Component-based Software Architectures
147

System
level
Component
level
Service
(fragment)
level
Architecture
Observations
Behavioral models
S
C
1
C
2
C
3
... ...
F
1
F
2
F
1.1
F
1.2
F
1.3
System observations
S S
...
Component observations
C
1
C
1
C
2
... ...
Service fragment observations
F
1.1
F
1.1
F
2
... ...
Service fragment models
F
1.1
F
1.1
F
1.1
F
1.2
F
1.2
F
1.2
F
2
F
2
F
2
... ...
Component models (stateless
across service fragments)
C
1
C
2
...
Component models
(stateful)
C
1
...
System model
∥ B
1
∥ B
2
∥ ∥
C
1
C
2
...
Preparation: Observe
system execution
Step 1: System
decomposition
Step 2: Component
decomposition
Step 3: Service fragment
model inference
Step 4: Service
fragment generalization
Step 5: Stateful
behavior injection
Step 6: Component
composition
Figure 1: Constructive Model Inference (CMI): Overview and its six steps, positioned along abstraction levels (rows) and
conceptual views (columns).
ther synchronously or asynchronously, with varying
buffering and scheduling policies. In the figure, this
is visualized as the composition of component
models with explicit buffer models (B
1
, B
2
).
Running Example. Figure 2 shows two examples of
observations of the behavior of a component-based
system on a horizontal time axis. The system con-
sists of three components, C
1
, C
2
and C
3
, shown on
the vertical axis. In Figure 2a, component C
1
receives an incoming request req
f
from the environ-
ment, and in response executes its service fragment
(function) f , illustrated by the horizontal bar, ulti-
mately leading to a reply rep
f
. During the execution
of function f , component C
1
executes function g and
component C
3
handles it. This involves a remote pro-
cedure call (arrow in the figure), with request req
g
being sent to component C
3
, and after C
3
has exe-
cuted function g, its reply rep
g
being received by C
1
.
C
1
similarly calls h on component C
2
. After C
1
be-
comes idle again, a second request req
z
is received,
and handled in service fragment z, leading to a reply
rep
z
, this time without involving other components.
In the figure, the stacked bars for each component
represent call stacks of nested function calls. The
bottom bars represent service fragment function exe-
cutions. Complete call stacks are visualized in the
figure by enclosing them in blue dashed rectangles.
C
1
f
g h
z
C
2
h
C
3
g
req
f
rep
f
req
g
rep
g
req
h
rep
h
req
z
rep
z
(a)
C
1
f
g h
z hr gr
f r
C
2
h
C
3
g
req
f
rep
f
req
g
rep
h
req
h
rep
g
req
z
rep
z
(b)
Figure 2: Observations showing client request req
f
be-
ing handled by component C
1
through calls g and h to its
servers, (a) synchronously and (b) asynchronously.
From the start of a service fragment’s call stack, until
its end where it is idle again, this represents a single
observation of its behavior.
Figure 2b shows a different observation of the
system, where request req
f
is handled asyn-
chronously. Again, services from components C
3
and
C
2
are requested, but now the system does not wait
for their replies. Instead, it completes service frag-
ment f and proceeds to handle request req
z
. When the
responses from the other components come in (rep
h
and rep
g
), it handles these in separate service frag-
ments (hr and gr). Having received both responses, it
sends reply rep
f
as part of the last service fragment.
Here service fragments f, hr and gr together
implement a service of C
1
, offered via req
f
.
Such system behaviors can be observed in the
form of an execution log, sequences of events in the
order in which they occur in the system. Each start
and end of a function execution (bars in Figure 2) has
an associated event. We identify an event by its exe-
cuting component, the related function, and whether
it represents the start (↑) or the completion (↓) of its
execution. E.g., event f
↑
C
1
, abbreviated to f
↑
1
, denotes
the start of function f on component C
1
. Where ap-
propriate, we identify service fragments by their start
events, e.g., f
↑
1
, z
↑
1
, hr
↑
1
, gr
↑
1
, h
↑
2
and g
↑
3
for Figure 2.
Our running example has two observations. The
first one is the behavior from Figure 2b, i.e., w
1
= ⟨ f
↑
1
,
g
↑
1
, g
↑
3
, g
↓
1
, h
↑
1
, h
↑
2
, h
↓
1
, f
↓
1
, z
↑
1
, z
↓
1
, h
↓
2
, hr
↑
1
, hr
↓
1
, g
↓
3
, gr
↑
1
,
f r
↑
1
, f r
↓
1
, gr
↓
1
⟩. The second one is a variation of w
1
,
where the calls to g and h are reversed, and z handled
last, i.e., w
2
= ⟨ f
↑
1
, h
↑
1
, h
↑
2
, h
↓
1
, g
↑
1
, g
↑
3
, g
↓
1
, f
↓
1
, h
↓
2
, hr
↑
1
,
hr
↓
1
, g
↓
3
, gr
↑
1
, f r
↑
1
, f r
↓
1
, gr
↓
1
, z
↑
1
, z
↓
1
⟩. The figure for w
2
is omitted for brevity.
ICSOFT 2022 - 17th International Conference on Software Technologies
148

3 PRELIMINARY DEFINITIONS
This section introduces basic definitions that we build
upon to place our CMI method in a framework based
on finite state automata and regular languages.
3.1 Finite State Automata
Let Σ be a finite set of symbols, called an alphabet. A
word (or string) w over Σ is a finite concatenation of
symbols from Σ. The Kleene star closure of Σ, Σ
∗
, is
the set of all finite words over Σ, including the empty
word denoted as ε. The Kleene plus closure of Σ is
defined as Σ
+
= Σ
∗
\ {ε}.
Given a word w, we denote its length as |w|, and
its i
th
symbol as w
i
. If words u and v are such that
uv = w, then u is a prefix of w and v a suffix of w.
We represent inferred models using DFAs:
Definition 3.1 (DFA) A deterministic finite automa-
ton (DFA) A is a 5-tuple A = (Q,Σ, δ,q
0
,F), with Q a
finite set of states, Σ a finite alphabet, δ : Q × Σ → Q
the partial transition function, q
0
∈ Q the initial state
and F ⊆ Q a set of accepting states.
The transition function is extended to words such
that δ : Q × Σ
∗
→ Q, by inductively defining δ(q,ε) =
q and δ(q, wa) = δ(δ(q,w), a), for w ∈ Σ
∗
, a ∈ Σ. DFA
A = (Q,Σ, δ,q
0
,F) accepts word w iff state δ(q
0
,w) ∈
F. If w is not accepted by A, it is rejected. Set L (A) =
{w ∈ Σ
∗
| A accepts w} is the language of A.
A DFA is minimal iff every two states p, q ∈ Q
(p ̸= q) can be distinguished, i.e. there is a w ∈ Σ
∗
such that δ(p,w) ∈ F and δ(q,w) /∈ F, or vice versa.
Given a set of words W ⊆ Σ
∗
, a Prefix Tree Au-
tomaton PTA(W ) is a tree-structured acyclic DFA
with L(PTA(W )) = W , where common prefixes of W
share their states and transitions.
Given two languages K, L over the same alphabet,
concatenation language KL is {uv | u ∈ K,v ∈ L}. The
repetition of a language L is recursively defined to be
L
0
= {ε}, L
i+1
= L
i
L. Similarly, the repetition of a
word w is w
0
= ε, w
i+1
= w
i
w. The Kleene star and
plus closures of L are defined as L
∗
=
S
∞
n=0
L
n
and
L
+
=
S
∞
n=1
L
n
, respectively.
Given two DFAs A
1
, A
2
we define operations on
DFAs with notations that reflect the effect on their re-
sulting languages, i.e., A
1
∩ A
2
, A
1
∪ A
2
, and A
1
\ A
2
result in DFAs with languages L(A
1
) ∩ L(A
2
),
L(A
1
) ∪ L(A
2
), and L(A
1
) \ L(A
2
), respectively. In
addition, we define synchronous composition:
Definition 3.2 (Synchronous Composition) Given
two DFAs A
1
= (Q
1
,Σ
1
,δ
1
,q
0,1
,F
1
), A
2
= (Q
2
,Σ
2
,
δ
2
,q
0,2
,F
2
), their synchronous composition, denoted
A
1
∥A
2
, is the DFA:
A = (Q
1
× Q
2
,Σ
1
∪ Σ
2
,δ,(q
0,1
,q
0,2
),F
1
× F
2
),
with δ((q
1
,q
2
),a) defined as:
(δ
1
(q
1
,a),δ
2
(q
2
,a)) if δ
1
(q
1
,a),δ
2
(q
2
,a) are defined,
(δ
1
(q
1
,a),q
2
) if δ
1
(q
1
,a) is defined, and a /∈ Σ
2
,
(q
1
,δ
2
(q
2
,a)) if δ
2
(q
2
,a) is defined, and a /∈ Σ
1
,
undefined otherwise.
Two DFAs A
1
,A
2
are language equivalent, A
1
⇔
L
A
2
, iff L (A
1
) = L (A
2
). Under language equivalence,
each of the operators ⋄ ∈ {∥, ∪,∩} is both commuta-
tive and associative, i.e. A
1
⋄ A
2
⇔
L
A
2
⋄ A
1
and (A
1
⋄
A
2
) ⋄ A
3
⇔
L
A
1
⋄ (A
2
⋄ A
3
).
To reason about components of a synchronous
composition, we define word projection:
Definition 3.3 (Word Projection) Given a word w
over alphabet Σ, and a target alphabet Σ
′
, we define
the projection π
Σ
′
(w) : Σ
∗
→ Σ
′∗
inductively as:
π
Σ
′
(w) =
ε if w = ε,
π
Σ
′
(v) if w = va with v ∈ Σ
∗
,a ̸∈ Σ
′
,
π
Σ
′
(v)a if w = va with v ∈ Σ
∗
,a ∈ Σ
′
.
This definition is lifted to sets of words:
π
Σ
′
(L) = {π
Σ
′
(w) | w ∈ L}.
With word projection, we define synchronization
of languages, which is commutative and associative:
Definition 3.4 (Synchronization) Given languages
L
1
⊆ Σ
∗
1
,L
2
⊆ Σ
∗
2
, the synchronization of L
1
and L
2
is
the language L
1
∥L
2
over Σ = Σ
1
∪ Σ
2
such that
w ∈ (L
1
∥L
2
) ⇔ π
Σ
1
(w) ∈ L
1
∧ π
Σ
2
(w) ∈ L
2
.
From the definitions we derive:
Proposition 3.5 Given DFAs A
1
, A
2
, their syn-
chronous composition is homomorphic with the
synchronization of their languages: L(A
1
∥A
2
) =
L(A
1
)∥L(A
2
).
Proof. For proofs, see (Hooimeijer, 2020).
Corollary 3.6 Given DFAs A, A
1
, A
2
such that A =
A
1
∥ A
2
, over alphabets Σ, Σ
1
, Σ
2
, respectively, then
w ∈ L(A) ⇔ π
Σ
1
(w) ∈ L(A
1
) ∧ π
Σ
2
(w) ∈ L(A
2
).
3.2 Formalizing Concurrent Behavior
Automata model behavior. To represent concurrent
behavior, Mazurkiewicz Trace theory is introduced
briefly (Mazurkiewicz, 1995). Intuitively, symbols in
the alphabets of multiple automata synchronize in
the synchronous composition (are dependent), while,
e.g., internal non-communicating symbols and
communications involving different components in-
terleave (are independent), and can thus be reordered
or commuted.
Formally, let dependency D ⊆ Σ
D
× Σ
D
be a sym-
metric reflexive relation over dependency alphabet
Constructive Model Inference: Model Learning for Component-based Software Architectures
149

Σ
D
. Relation I
D
= (Σ
D
× Σ
D
) \ D is the independency
induced by D. Mazurkiewicz trace equivalence for D
is defined as the least congruence ≡
D
in the monoid
Σ
∗
D
such that for all a, b ∈ Σ
D
: (a, b) ∈ I
D
⇒
ab ≡
D
ba, i.e., the smallest equivalence relation that,
in addition to the above, is preserved under
concatenation: u
1
≡
D
u
2
∧ v
1
≡
D
v
2
⇒ u
1
v
1
≡
D
u
2
v
2
.
Equivalence classes over ≡
D
are called traces. A
trace [w]
D
for a word w is the set of words equivalent
to w under D. This definition is lifted to languages:
[L]
D
= {[w]
D
| w ∈ L}. We drop subscript D if it is
clear from the context. Language iteration is ex-
tended to traces by defining concatenation of
[u]
D
, [v]
D
∈ [Σ
∗
D
]
D
as [u]
D
[v]
D
= [uv]
D
, with [u]
D
a
prefix of [uv]
D
and [v]
D
a suffix of [uv]
D
.
Given a set T of traces, linT is the linearization of
T , i.e., the set {w ∈ Σ
∗
D
| [w]
D
∈ T }. For any string
language L, if L = lin[L]
D
then L is consistent with
D, as opposed to when L ⊂ lin[L]
D
. If the language
L(A) of automaton A is consistent with D, A has trace
language T (A) = [L (A)]
D
.
Take e.g. Σ
D
= {a,b,c} and D = {a,b}
2
∪ {a,c}
2
= {(a,a),(a, b),(a, c),(b, a),(b,b),(c,a), (c,c)}. As
b and c can then occur independently, I
D
=
{(b,c),(c,b)}. Word abbca is part of trace [abbca]
D
= {abbca, abcba,acbba}, which confirms that
commuting b and c results in the same trace.
The commutation of symbols is captured by bi-
nary relation ∼
D
, with u ∼
D
v iff there are x,y ∈ Σ
∗
D
and (a, b) ∈ I
D
such that u = xaby and v = xbay.
Clearly, ≡
D
is the reflexive transitive closure of
∼
D
, i.e. u ≡
D
v iff there exists a sequence
(w
0
,...,w
n
) such that w
0
= u, w
n
= v and w ∼
D
w
i+1
for 0 ≤ i < n.
We rely on an additional result from
Mazurkiewicz (Mazurkiewicz, 1995):
Proposition 3.7 Given dependency D and words
u,v ∈ Σ
∗
D
, we have u ≡
D
v ⇒ π
Σ
(u) ≡
D
π
Σ
(v) for any
alphabet Σ.
3.3 Asynchronous Compositions
In addition to synchronous composition, we intro-
duce asynchronous composition (Akroun and Sala
¨
un,
2018; Brand and Zafiropulo, 1983). This makes use
of explicit buffers to pass messages from a sender to
a receiver. For an asynchronous composition of
DFAs A
1
,...,A
n
, we assume component A
i
,
1 ≤ i ≤ n, has alphabet Σ
i
, partitioned in sending-,
receiving- and internal-symbols, Σ
!
i
, Σ
?
i
and Σ
τ
i
, re-
spectively. Each message has a unique sender and
receiver, Σ
!
i
∩ Σ
!
j
=
/
0, Σ
?
i
∩ Σ
?
j
=
/
0, i ̸= j. The receiver
is assumed to exist, and to be different from the
sender, a ∈ Σ
!
i
⇒ ∃
j̸=i
: a ∈ Σ
?
j
. Finally, we assume
internal actions are unique to a component,
Σ
τ
i
∩ Σ
j
=
/
0,i ̸= j. We denote an alphabet under these
assumptions as Σ
!,?,τ
i
.
The components communicate via buffers, de-
noted B
i
, which represent, e.g., a FIFO buffer or a
bag buffer. FIFO buffers are modeled as a list of
symbols over Σ
?
i
, with ε the empty buffer, where mes-
sages are added to the tail of the list and consumed
from the head of the list. We define the asynchronous
composition using FIFO buffers as follows:
Definition 3.8 Consider n DFAs A
1
,...,A
n
, with
A
i
= (Q
i
,Σ
!,?,τ
i
,δ
i
,q
0,i
,F
i
), 1 ≤ i ≤ n. The asyn-
chronous composition A of A
1
,...,A
n
using FIFO
buffers B
i
,...,B
n
, denoted A = ∥
n
i=1
(A
i
∥B
i
), is given
as the (typically infinite) state machine:
A = (Q,Σ,δ, (q
0,1
,ε,...,q
0,n
,ε),F
1
× ··· × F
n
)
with Q = Q
1
× (Σ
?
1
)
∗
× ·· · × Q
n
× (Σ
?
n
)
∗
, Σ =
S
i
{a!|a ∈ Σ
!
i
} ∪
S
i
{a?|a ∈ Σ
?
i
} ∪
S
i
Σ
τ
i
, and
δ ⊆ Q × Σ × Q such that for q = (q
1
,b
1
,...,q
n
,b
n
)
and q
′
= (q
′
1
,b
′
1
,...,q
′
n
,b
′
n
) we have:
(send) (q, a!,q
′
) ∈ δ if ∃
i, j
: (i) a ∈ Σ
!
i
∩ Σ
?
j
, (ii)
(q
i
,a,q
′
i
) ∈ δ
i
, (iii) b
′
j
= b
j
a, (iv) ∀
k̸=i
q
′
k
=
q
k
, (v) ∀
k̸= j
b
′
k
= b
k
.
(receive) (q,a?, q
′
) ∈ δ if ∃
i
: (i) a ∈ Σ
?
i
, (ii)
(q
i
,a,q
′
i
) ∈ δ
i
, (iii) b
i
= ab
′
i
, (iv)
∀
k̸=i
q
′
k
= q
k
, (v) ∀
k̸=i
b
′
k
= b
k
.
(internal) (q, a,q
′
) ∈ δ if ∃
i
: (i) a ∈ Σ
τ
i
, (ii)
(q
i
,a,q
′
i
) ∈ δ
i
, (iii) ∀
k̸=i
q
′
k
= q
k
, (iv)
∀
k
b
′
k
= b
k
.
Bag buffers are defined as a multiset over Σ
?
i
. To
use bags instead of FIFOs, we change: ε to
/
0 for A,
list type to multiset type for Q, send rule clause (iii)
to b
′
j
= b
j
∪ {a}, and receive rule clause (iii) to a ∈
b
i
∧ b
′
i
= b
i
− {a}.
With unbounded buffers, asynchronous composi-
tions can have infinite state spaces. When buffers are
bounded, the buffer models can be represented by a
(finite) DFA (Muscholl, 2010), and hence the compo-
sition as well. We bound buffer B
i
to k places,
denoted B
k
i
, by adding requirement |b
j
| < k (such
that |b
′
j
| ≤ k) to the send rule.
We do not discuss the construction of a DFAs for
B
k
i
, as it follows from the definition above. Then, the
synchronous composition of such constructed DFAs
A
i
∥B
k
i
is equivalent to asynchronous composition
A
i
∥B
k
i
as in Definition 3.8, if for synchronous com-
position we differentiate a! and a? to prevent
synchronization of communications to and from
buffers, respectively.
The question whether there is a buffer capacity
bound such that every accepted word of the un-
bounded composition is also accepted by the
ICSOFT 2022 - 17th International Conference on Software Technologies
150

bounded composition is called boundedness and is
generally undecidable (Genest et al., 2007). How-
ever, if the asynchronous composition is ‘deadlock
free’, i.e. a final state can be reached from every
reachable state (Kuske and Muscholl, 2019), then it
is decidable for a given k whether the asynchronous
composition is bounded to k (Genest et al., 2007).
4 CONSTRUCTIVE MODEL
INFERENCE (SYNCHRONOUS
COMPOSITION)
In this section, we detail our method, considering a
system with a synchronous composition of compo-
nents. We later lift the restriction in Section 5, where
we discuss asynchronous compositions.
Recall the CMI method introduced in Section 2,
and its overview in Figure 1. In the previous sections
we introduced the definitions and the results with
which we can now detail the CMI method.
We assume system execution observations are
available (Preparation step). They are decomposed
following the system architecture (Steps 1 and 2).
Models are then inferred at the most detailed level,
for service fragments (Step 3). Again following the
architecture, inferred models are composed to obtain
models at various levels of abstraction (Steps 4 – 6).
Formally, in this section, we assume the system
under study is a DFA A = (Q,Σ,δ,q
0
,F), Σ consists
of observable events, A is synchronously composed
of n component DFAs, A = A
1
∥...∥A
n
, and that ob-
servations W ⊆ L (A) are available to infer an
approximation A
′
of A. We use subscripts for compo-
nent and service fragment instances, and prime
symbols for inferred instances.
4.1 Step 1: System Decomposition
Informal Description: We assume a fixed and known
deployment of services on components, such that we
can project the observations onto each component.
Formalization: We assume component alphabets Σ
i
are known a-priori. W is projected to π
Σ
i
(W ) for each
component, 1 ≤ i ≤ n. Recall that we denote events
in Σ as f
s
i
, with f a function, C
i
a component, and s ∈
{↑,↓} denoting the start or completion of a function
execution, e.g., f
↑
1
. Hence, alphabet Σ
i
for component
C
i
contains the events with subscript i.
Example: Consider again the running example from
Section 2, with W = {w
1
,w
2
}. By projection on, e.g.,
component C
3
, we obtain for both words the projected
word ⟨g
↑
3
, g
↓
3
⟩, i.e., π
Σ
3
(W ) = {⟨g
↑
3
, g
↓
3
⟩}.
4.2 Step 2: Component Decomposition
Informal Description: We assume that, 1) compo-
nents are sequential (e.g., corresponding to a single
operating system thread), 2) client requests (and
server responses) can only be handled once the com-
ponent is idle, and prior requests are finished, i.e.,
service fragments are executed non-preemptively,
and 3) symbols that start or end a service fragment
can be distinguished. These assumptions enable us to
decompose component observations into service
fragment observations.
Formalization: A task or task word captures a possi-
ble execution behavior of a service fragment:
Definition 4.1 (Task) Let Σ be a partitioned alphabet
Σ
s,o,e
= Σ
s
∪ Σ
o
∪ Σ
e
, with service fragment execution
start events Σ
s
, its corresponding end events Σ
e
, and
other events Σ
o
. Word w ∈ Σ
∗
is a task on component
C
i
iff w = f
↑
i
v f
↓
i
with f
↑
i
∈ Σ
s
, v ∈ Σ
o∗
, and f
↓
i
∈ Σ
e
.
We also define task sequence and task set:
Definition 4.2 (Task Sequence/Set) Given alphabet
Σ
s,o,e
, a word w ∈ Σ
∗
is a task sequence iff
w = w
1
...w
n
with each w
i
, 1 ≤ i ≤ n, a task. The set
T (w) = {w
i
|1 ≤ i ≤ n} is the task set corresponding
to w. Similarly T (W ) =
S
w∈W
T (w) for W ⊆ Σ
∗
.
Identifying a service fragment by its start event
f ∈ Σ
s
, its task set is T
f
(w) = {v | v ∈ T (w) ∧
w
1
= f }. T
f
(W ) ⊆ T (W ) is similarly defined.
For each component C
i
, given its component
observations π
Σ
i
(W ), we obtain for each service frag-
ment f ∈ Σ
s
its task set T
f
(π
Σ
i
(W )), containing the
various observed alternative executions of f .
Example: We get for service fragments f
↑
1
, z
↑
1
, hr
↑
1
,
gr
↑
1
, h
↑
2
, and g
↑
3
, their respective task sets: {⟨ f
↑
1
, g
↑
1
,
g
↓
1
, h
↑
1
, h
↓
1
, f
↓
1
⟩, ⟨ f
↑
1
, h
↑
1
, h
↓
1
, g
↑
1
, g
↓
1
, f
↓
1
⟩}, {⟨z
↑
1
, z
↓
1
⟩},
{⟨hr
↑
1
, hr
↓
1
⟩}, {⟨gr
↑
1
, f r
↑
1
, f r
↓
1
, gr
↓
1
⟩}, {⟨h
↑
2
, h
↓
2
⟩}, {⟨g
↑
3
,
g
↓
3
⟩}.
4.3 Step 3: Service Fragment Model
Inference
Informal Description: We infer a DFA per service
fragment. Assuming services may be requested re-
peatedly, each DFA allows its service fragment to
repeatedly be completely executed from start to end.
Formalization: For service fragment f ∈ Σ
s
, TDFA
f
constructs a Task DFA (TDFA) from T
f
(π
Σ
i
(W )), i.e.,
TDFA
f
(W,Σ
s,o,e
, f ) = A
′
f
= (Q,Σ
i
,δ,q
0
,{q
0
}). Its
has language L(A
′
f
) = T
f
(π
Σ
i
(W ))
∗
, with repeated
executions of its observed set of tasks. An efficient
way to implement TDFA
f
is to build
Constructive Model Inference: Model Learning for Component-based Software Architectures
151
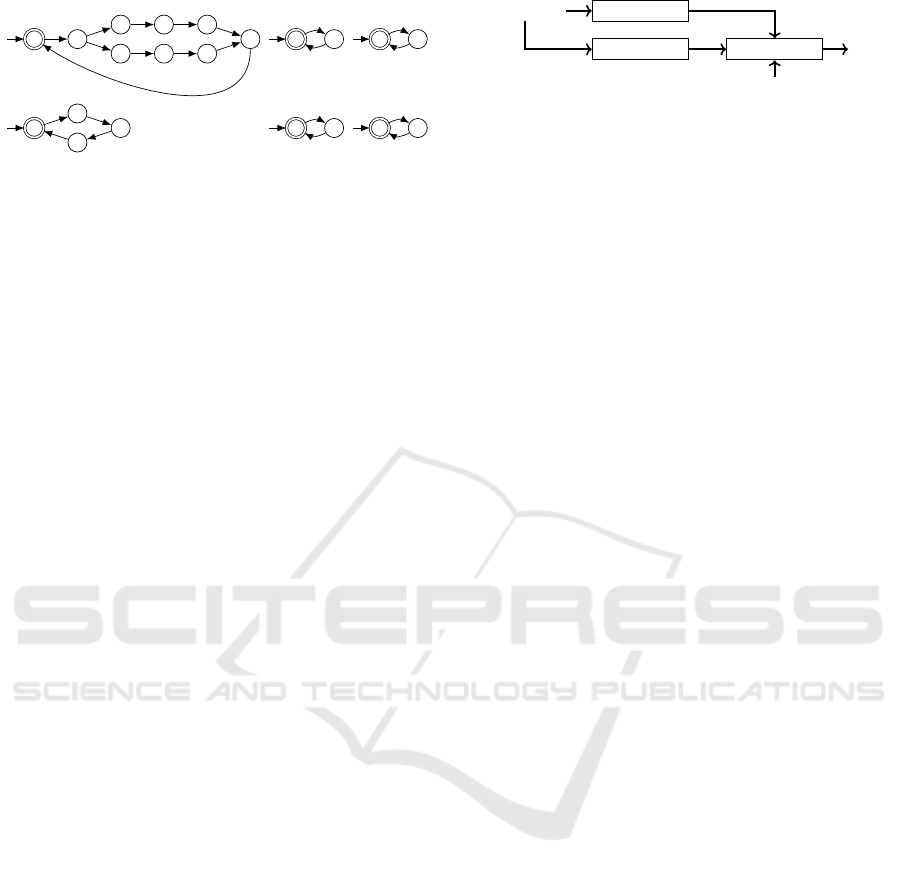
f
↑
1
g
↑
1
g
↓
1
h
↑
1
h
↓
1
h
↑
1
h
↓
1
g
↑
1
g
↓
1
f
↓
1
z
↑
1
z
↓
1
hr
↑
1
hr
↓
1
h
↑
2
h
↓
2
g
↑
3
g
↓
3
gr
↑
1
f r
↑
1
f r
↓
1
gr
↓
1
Figure 3: Task DFAs for the service fragments of the run-
ning example.
PTA(T
f
(π
Σ
i
(W ))) with root q
0
. Then, optionally,
minimize the PTA to reduce any redundancy. Finally,
merge all accepting states into initial state q
0
, which
is then the one and only accepting state.
Example: The inferred Task DFAs for the running
example’s service fragments are shown in Figure 3.
4.4 Step 4: Service Fragment
Generalization
Informal Description: We assume components can
repeatedly handle requests of their services. We also
assume (for now, but we revisit this assumption in
Section 4.5) that service executions carry no observ-
able state and are therefore mutually independent.
We infer component models from service fragment
models, generalizing the component behavior to re-
peated non-preemptive executions of the various
service fragments. A component is thus assumed to
be able to execute any number of any of its service
fragments in arbitrary order.
Formalization: For a component C
i
, its service frag-
ments are Σ
s
i
= Σ
i
∩ Σ
s
. TDFA
i
constructs TDFA A
i
for component C
i
, i.e., TDFA
i
(W,Σ
s,o,e
,Σ
s
i
) = A
′
i
. It
does so by merging the initial states of all TDFAs
A
′
f
= TDFA
f
(W,Σ
s,o,e
, f ) for service fragments
f ∈ Σ
s
i
. Then L(A
′
i
) = T (π
Σ
i
(W ))
∗
. A
′
i
is determinis-
tic, as all outgoing transitions from the initial states
of TDFAs A
′
f
, i.e., f
↑
i
, are unique.
Example: The component models for C
2
and C
3
are
identical to their service fragment models, for h
↑
2
and
g
↑
3
, respectively, in Figure 3. For C
1
, the initial states
of its four service fragment models are merged.
4.5 Step 5: Stateful Behavior Injection
Informal Description: In Step 4 we assumed service
fragments to be mutually independent. This is not
always the case in practice. Consider our running ex-
ample (Figure 2b in Section 2). Service fragment f
handles the responses for asynchronous calls g and h
Observations
Steps 1-4
Mining Composition
Model
Manually specified automata
Figure 4: Generic approach to inject specific domain knowl-
edge in Step 5.
in service fragments gr and hr, respectively. There-
fore, handling gr always comes after call g in f . This
is ensured by the interaction with C
3
, but it is not
captured in the model for C
1
.
Optional Step 5 allows to inject stateful behavior
to obtain stateful models that exclude behavior that
cannot occur in the real system. As many varieties of
component-based systems exist, our structured ap-
proach allows to improve the inferred models based
on injection of domain knowledge. This allows cus-
tomization to fit a certain architecture or target
system, and is not specific to our case of Section 6.
E.g., it allows to capture the general property that ‘a
response must follow a request’ (gr after g).
Figure 4 visualizes the approach. We compose
TDFAs inferred in Steps 1 – 4 with additional, typi-
cally small, automata, which specify explicitly which
behavior we add, constrain or remove. Multiple dif-
ferent composition operators are supported: union,
intersection, synchronous composition and (symmet-
rical) difference (see Section 3). The injected
automata are manually specified, or obtained by a
miner (Beschastnikh et al., 2013), an automated
procedure on the observations.
Additional properties that should be added often
apply in identical patterns across the whole system.
To allow modeling them only once, DFAs with pa-
rameters are used, e.g., for the pattern of a request
and reply. The parameterized DFA (template) is in-
stantiated for specific symbols, e.g. user-provided
request/reply pairs, to obtain the DFAs to inject.
Formalization: We define substitution:
Definition 4.3 (Substitution) Given a parameterized
DFA A = (Q,Σ, δ,q
0
,F), and symbols p ∈ Σ, a /∈ Σ,
the substitution of a for p in A, denoted A[p := a],
is defined as A[p := a] = (Q,(Σ \ {p}) ∪ {a},δ[p :=
a],q
0
,F), with δ[p := a](q,c) = δ(q, p) if c = a, and
δ(q,c) otherwise.
In general the order of substitutions matters. We
apply them in the given order, and only replace pa-
rameter symbols by concrete symbols, assuming
both sets are disjoint.
Example 1 (Request before Reply): For asynchronous
calls, a reply must follow a request, e.g., gr after g.
We model this property as DFA P
1
in Figure 5a. Pa-
rameter Req represents a request, Reply a reply. To
ICSOFT 2022 - 17th International Conference on Software Technologies
152

Req
Reply
(a)
1 2
3
cReq
cReply
sReq
sReply
(b)
Figure 5: Parameterized property automata: (a) request be-
fore reply (P
1
), (b) server replies before client reply (P
2
).
enforce the property, we compose the inferred
TDFAs A
′
i
with P
1
, for every request and its corre-
sponding reply in the system being considered:
A
′′
i
= A
′
i
∥ (∥
a∈reqs
P
1
[Req := a][Reply := R(a)]),
where reqs is the set of requests, and R : Σ
i
→ Σ
i
maps requests to their replies. E.g., for our example,
g
↓
1
∈ reqs and (g
↓
1
,gr
↑
1
) ∈ R. By Corollary 3.6, for any
a ∈ reqs: π
{a,R(a)}
(L(A
′′
)) = {(a.R(a))
n
| n ∈ N}.
This correctly models the informally given property,
assuming at most one outstanding request for each a.
Example 2 (Server Replies before Client Reply): For
a service execution, often nested requests should have
been replied before finishing the service. We model
this property as DFA P
2
in Figure 5b. Upon receiving
a client request cReq, P
2
goes to state 2. If during this
service, a request sReq is sent to a server, it must be
met with reply sReply to get out of state 3 and allow
the original service to reply to its client (cReply).
The examples show that domain knowledge can
be added explicitly, straightforwardly, and with
parameterized DFAs and miners also scalably.
4.6 Step 6: Component Composition
Informal Description: The last step is to form system
models by composing the obtained stateless and/or
stateful component models (from Steps 4 and 5).
Formalization: So far we have used unique symbols
per component, such as, e.g., f
↑
1
. Properly capturing
component synchronization requires that we ensure
the correct communications when one components
uses the services of another component. For our
running example (see Figure 2b), we have a commu-
nication (arrow) from g
↑
1
to g
↑
3
. To ensure correct
synchronization, we use the same symbol for both of
them. We combine g
↑
1
and g
↑
3
to the synchronization
action g
↑,↑
1,3
, representing the start of call g on C
1
lead-
ing to the immediate start of a handler for g on C
3
.
Then synchronous composition can be applied to di-
rectly obtain A
′
= A
′
1
∥A
′
2
∥...∥A
′
n
as per
Definition 3.2.
Example: We omit the resulting system model
automaton for brevity.
4.7 Analysis of the CMI Method
Steps 1 and 6: These steps together reduce the
problem of inferring system models from system ob-
servations to inferring component models from
component observations. We first analyze four as-
pects purely for this reduction, without considering
that, e.g., other steps allow repeated (task) execution.
Hence, for now we consider PTAs, not TDFAs. And
word length of observations is preserved, even after
commutations for Mazurkiewicz trace equivalence.
1) We prove that composition A
′
= A
′
1
∥...∥A
′
n
of in-
ferred components A
′
i
accepts the original system
observations W from which it was inferred, i.e.,
W ⊆ L (A
′
). By definition, if A
′
= PTA(W ) then
L(A
′
) = W . We have A
′
i
= PTA(π
Σ
i
(W )) instead, for
each i. Then by Corollary 3.6 this follows directly.
2) We show that composition A
′
generalizes to traces,
using Mazurkiewicz trace theory. That is, it properly
uses concurrency between components to accept all
valid alternative interleavings that were not directly
observed, i.e., learning a PTA per component
generalizes L(A
′
) from W to lin[W ]
D
.
Proposition 4.4 If dependency D =
S
n
i=1
(Σ
2
i
), u,v ∈
Σ
∗
, Σ =
S
n
i=1
Σ
i
, then u ≡
D
v ⇔ ∀
i
: π
Σ
i
(u) = π
Σ
i
(v).
Corollary 4.5 For a synchronous composition A =
A
1
∥...∥A
n
and D =
S
n
i=1
(Σ
2
i
), L(A) = lin[L (A)]
D
.
Per Proposition 4.4 and Corollary 4.5, decompos-
ing the system to components preserves commuta-
tions, and all commutated words are indeed in L(A
′
).
3) We show A
′
does not over-generalize A. That is,
the inferred model has no behavior that the original
system does not have, i.e., L(A
′
) ⊆ L (A). As A and A
′
both generalize to traces per Corollary 4.5, and given
W ⊆ L (A), this follows directly. Together this leads
to the following theorem:
Theorem 4.6 Consider DFA A = ∥
n
i=1
A
i
, W ⊆ L (A),
DFA A
′
= ∥
n
i=1
A
′
i
with A
′
i
= PTA(π
Σ
i
(W )), and D =
S
n
i=1
(Σ
2
i
). Then L (A
′
) = lin[W ]
D
and L(A
′
) ⊆ L(A).
Generally, it is sufficient to show this per component:
Proposition 4.7 If L(A
′
1
) ⊆ L(A
1
) and
L(A
′
2
) ⊆ L(A
2
), then L(A
′
1
∥ A
′
2
) ⊆ L(A
1
∥ A
2
).
4) A
′
is robust under additional observations, i.e., if
inference uses additional observations, then the
language of the inferred model can only grow:
Theorem 4.8 Consider DFA A
′
= ∥
n
i=1
A
′
i
with
A
′
i
= PTA(π
Σ
i
(U)), obtained from observations U ,
and DFA A
′′
, similarly composed and obtained from
observations V , with U ⊆ V . Then L(A
′
) ⊆ L(A
′′
).
Steps 2 – 4: Steps 2 and 4 together reduce the prob-
lem of inferring component models from component
Constructive Model Inference: Model Learning for Component-based Software Architectures
153

∥
=
a
b b
c a
b
c
a
c
(a)
∥
a a
d
a
c
b
c
(b)
Figure 6: (a) TDFAs X
′
1
∥X
′
2
= X
′
, (b) TDFAs Y
′
1
||Y
′
2
.
observations to inferring service fragment models
from service fragment observations, which is real-
ized by Step 3. We analyze the four aspects as
before, plus an extra one. Unlike before, we now do
consider repeated (task) executions and TDFAs.
1) We show that our approach produces correct com-
ponent Task DFAs A
′
i
, and that composition
A
′
= A
′
1
∥...∥A
′
n
then still accepts W :
Proposition 4.9 Consider DFA A with Σ
s,o,e
com-
posed of Task DFAs, A = ∥
n
i=1
A
i
with each a Σ
s
i
=
Σ
i
∩ Σ
s
, observations W ⊆ L(A), and DFAs A
′
i
=
TDFA
i
(W,Σ
s,o,e
,Σ
s
i
). Then L (A
′
i
) = T (π
Σ
i
(W ))
∗
.
Proposition 4.9 follows by construction. Then, by
Corollary 3.6, also W ⊆ L (A
′
) still holds.
2) We consider how A
′
generalizes observations. A
composition A
′
of TDFAs A
′
i
is not generally a Task
DFA. Even if a symbol is only in Σ
e
for all compo-
nents, transitions for that symbol might not go to the
accepting state (e.g. abac over Figure 6a). Yet, by
Proposition 3.5, we know that any word in the
language of A represents executions of tasks on com-
ponents. Hence, we extend tasks to task traces and
task sequences to task sequence traces:
Definition 4.10 (Task (Sequence) Trace) Consider a
dependency D =
S
n
i=1
Σ
2
i
and alphabet Σ
s,o,e
. A trace
[t] ∈ [Σ
∗
D
] is a task sequence trace iff ∀
n
i=1
π
Σ
i
(t) is a
task sequence for Σ
s,o,e
. Its task set T([t]), is given
as {[t
j
] | [t
1
... t
m
] = [t] and t
j
a task for 1 ≤ j ≤ m}.
If additionally, no task sequences [u],[v] ∈ [Σ
+
D
] exist
such that [uv] = [t], then [t] is not a concatenation of
multiple task traces, but a single task trace.
Using task traces, we define how a composition of
concurrently executing components generalizes, i.e.,
what commutations are possible:
Proposition 4.11 Consider a composition A = ∥
n
i=1
A
i
of n Task DFAs, with dependency D =
S
n
i=1
Σ
2
i
. Then
any [t] ∈ T (A) is a task sequence, and furthermore
[t] ∈ T (A) ⇔ T ([t]) ⊆ T (A), and T (A) = T (T (A))
∗
.
For the TDFAs in Figure 6a, Mazurkiewicz traces
allow us to define T (X
′
) = T([abacbc])
∗
= {abc,
abacbc}
∗
. Clearly, T (X
′
) allows commutations, as
abc ∈ T (X
′
), while abc /∈ T (abacbc)
∗
.
Corollary 4.5 earlier showed that A
′
generalizes
to trace equivalence, [W ] ∈ T (A
′
). Proposition 4.11
proves even more generalization: all task traces in W
can be repeated in any order T ([W ])
∗
⊆ T (A
′
).
However, A
′
generalizes beyond T ([W ])
∗
. For
Figure 6a, L (X
′
) = ab(acb)
∗
c, beyond T (X
′
). Con-
sider also Y
′
1
and Y
′
2
in Figure 6b, inferred from
W = {abcacd} for Σ
1
= {a,d} and Σ
2
= {a,b, c}.
Here, [w] is a task, as aad cannot be split. Yet
Y
′
= Y
′
1
∥Y
′
2
also accepts w
′
= abcabcd and
w
′′
= acacd, outside T ([W ])
∗
. Y
′
2
accepts tasks ac
and abc that synchronize equally with Y
′
1
and can
thus be interchanged. Therefore, characterizing the
full generalization remains an open problem.
3) The inferred component models A
′
i
do not over-
generalize, i.e., L (A
′
i
) ⊆ L (A
i
), per Proposition 4.9
and since π
Σ
i
(W ) ⊆ T (π
Σ
i
(W ))
∗
. Then for A
′
also
still L(A
′
) ⊆ L(A), per Proposition 4.7.
4) Allowing for repeated task executions, A
′
is still
robust under additional observations:
Theorem 4.12 Consider DFA A
′
= ∥
n
i=1
A
′
i
, with A
′
i
=
TDFA
i
(U,Σ
s,o,e
,Σ
s
i
) obtained from observations U,
and DFA A
′′
similarly composed and obtained from
observations V , with U ⊆ V . Then L(A
′
) ⊆ L(A
′′
).
5) Finally, we consider completeness. To infer the
complete behavior of system A, its component task
sets T (L(A
i
)) should at least be finite, as we enumer-
ate these tasks in approximations A
′
i
. If all tasks of A
are observed, the full system behavior is inferred.
5 CONSTRUCTIVE MODEL
INFERENCE
(ASYNCHRONOUS
COMPOSITION)
In Section 4 we considered systems consisting of
synchronously composed components. This section
considers the CMI approach applied to systems with
asynchronously composed components.
We now assume the system is a DFA A, asyn-
chronously composed of components A
i
, using
buffers B
i
bounded to capacity b
i
. Per Section 3.3 we
model this as a synchronous composition with buffer
automata, A = ∥
n
i=1
(A
i
∥B
b
i
i
). Then A
i
has alphabet
Σ
!,?,τ
i
, Σ
B
i
= Σ
?
B
i
∪ Σ
!
B
i
, Σ
?
B
i
= {a! | a? ∈ Σ
?
i
}, and
Σ
!
B
i
= Σ
?
i
. We assume system observations W ⊆ L (A)
as before.
To infer A
′
, we first infer the components A
′
i
,
reusing Steps 1–5 from the synchronous case of Sec-
tion 4. Then, we model DFA buffers B
′b
i
i
as in
Section 3.3, according to the buffer type (FIFO or
bag) and capacity bound b
i
. A capacity lower bound
ICSOFT 2022 - 17th International Conference on Software Technologies
154
C
1
f
C
2
f
C
3
f
g
C
4
g
req
f
rep
f
req
g
rep
g
req
C
2
Figure 7: Example of limited commutations for FIFO
buffers.
b
i,w
for each buffer B
i
is inferred from W, by consid-
ering the maximally occupied buffer space along
each observed word w ∈ W . That is b
i,w
=
max
1≤i≤|w|
(|π
Σ
?
B
i
(w
1
...w
i
)| − |π
Σ
!
B
i
(w
1
...w
i
)|).
Then, the overall lower bound b
i
for B
i
is inferred, as
b
i
= max
w∈W
b
i,w
. Finally, A
′
is given as synchronous
composition A
′
= ∥
n
i=1
(A
′
i
∥B
′b
i
i
).
Just as for the synchronous case, we prove for
this asynchronous version of Step 6, that A
′
accepts
W , does not over-generalize, and is robust under
additional observations:
Proposition 5.1 Consider DFA A = ∥
n
i=1
(A
i
∥B
i
)
with B
i
a FIFO (or bag) buffer, W ⊆ L (A), DFA A
′
=
∥
n
i=1
(A
′
i
∥B
′b
i
i
) with A
′
i
= TDFA
i
(W,Σ
s,o,e
,Σ
s
i
), and
B
′b
i
i
a FIFO (or bag) buffer with b
i
= max
w∈W
b
i,w
.
Then W ⊆ L (A
′
) ⊆ L(A). For DFA A
′′
, similarly
composed and obtained from observations V , with
W ⊆ V , then holds L(A
′
) ⊆ L(A
′′
).
With this approach we need to know a-priori the
kind of buffers used in our system. To understand
whether our choices were correct we experimented
with various buffer types. For instance, using a sin-
gle FIFO buffer between each pair of components
can lead to an issue shown in Figure 7. If req
C
2
is
sent before rep
g
, the FIFO order enforces reception
of req
C
2
before rep
g
, while the TDFA for C
3
has to
handle rep
g
before starting a new service with req
C
2
,
leading to a deadlock. In order to resolve this
problem, and other mismatches with ASML’s mid-
dleware, we use a FIFO buffer per client that a
component communicates with, and a bag per server.
6 CMI IN PRACTICE
We demonstrate our CMI approach by applying it to
a case study at ASML. ASML designs and builds
machines for lithography, which is an essential step
in the manufacturing of computer chips.
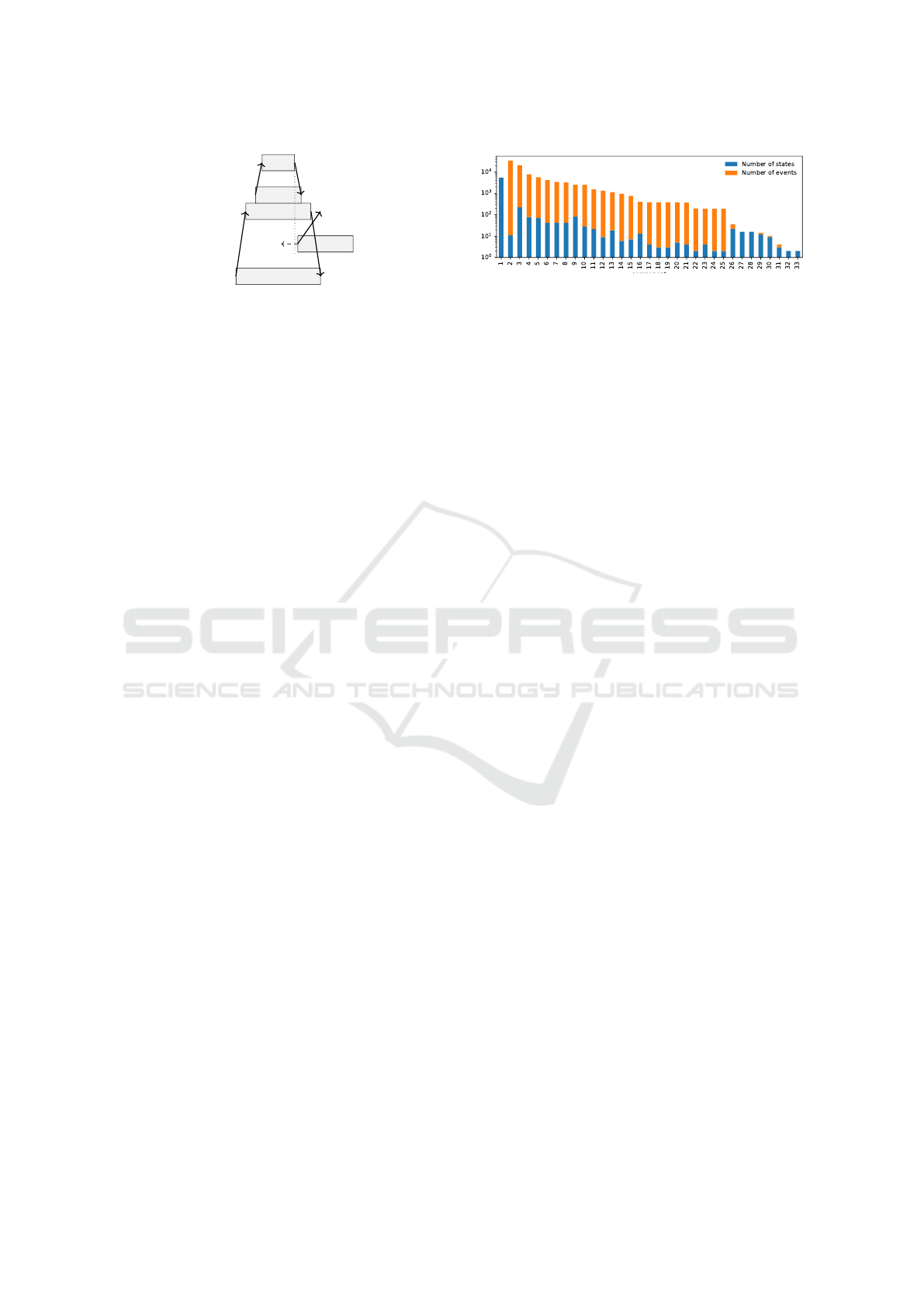
Figure 8: Per component, the number of states in its compo-
nent model after Step 4, compared to the number of events
in its observations.
6.1 System Characteristics
Our CMI approach requires as input system observa-
tions. The middleware in ASML’s systems has been
instrumented to extract Timed Message Sequence
Charts (TMSCs) from executions. A TMSC (Jonk
et al., 2020) is a formal model for system observa-
tions, akin to what we described in Section 2. The
TMSC formalism implies that the system can be
viewed as a composition of sequential components
bearing nested, fully observed, non-preemptive
function executions. We can therefore obtain obser-
vations W , component alphabets Σ
i
, and partitioned
alphabet Σ
s,o,e
, from TMSCs, to serve as inputs to
our method.
For this case study, we infer a model of the expo-
sure subsystem, which exposes each field (die) on a
wafer. By executing a system acceptance test, and
observing its behavior during the exposure of a sin-
gle wafer, which spans about 11 seconds, a TMSC is
obtained that consists of around 100,000 events for
33 components.
6.2 Model Inference Steps 1 – 4
We apply Steps 1 – 4 for our case study. Figure 8
shows the sizes of the resulting component models in
terms of the number of events in the observations and
the number of states of the inferred models. For most
components the inferred model is two orders of mag-
nitude more compact than its observations, showing
repetitive service fragment executions in these
components.
Component 1 orchestrates the wafer exposure. Its
model has the same size as its observation, as it spans
a single task with over 5,000 events. For components
26 – 33, the small reduction is due to their limited ob-
servations.
6.3 Model Inference Step 5
We analyze the inferred models, assessing whether
their behavior is in accordance with what we expect
Constructive Model Inference: Model Learning for Component-based Software Architectures
155

C
7
f
h g
gr hr
f r
S
1
g
S
2
h
req
f
rep
f
req
h
rep
g
req
g
rep
h
(a)
C
7
f
h g
hr gr
f r
S
1
g
S
2
h
req
f
rep
f
req
h
rep
g
req
g
rep
h
(b)
Figure 9: Component C
7
requires both rep
g
and rep
h
to re-
ply to its client. (a) gr before hr, with fr in hr, and (b) hr
before gr, with fr in gr.
from the actual software and if not, what knowledge
must be added (according to Step 5).
Although the system matches an asynchronous
composition of components as discussed in Sec-
tion 5, we first apply our CMI approach for
synchronous systems (Step 6 from Section 4). A syn-
chronous composition has more limited behavior
compared to an asynchronous composition, and
hence a smaller state space. The resulting model can
therefore be analyzed for issues more easily, while
many such issues apply to both the synchronous and
the asynchronous compositions.
We observe that component model 1, A
′
1
, has over
5,000 states, in a single task w. To reduce the model
size, we analyze w for repetitions and reduce it
(Nakamura et al., 2013). We look for short
x,y, z ∈ Σ
∗
1
such that w = xy
n
z for some n. Then, we
create reduced model A
′′
1
, with L(A
′′
1
) = (xyz)
∗
. This
reduces the model size by |y| ∗ (n − 1) states to about
600 states for Component 1, without limiting its
synchronization with the other components.
As a second reduction, we remove DFA transi-
tions that do not communicate and originate from a
state which has a single outgoing transition, i.e. does
not allow for a choice in the process. This is akin to
process algebra axiom a.τ.b = a.b, where τ is a non-
synchronizing action (Milner, 1989). Examples in
Figure 9 are g
↓
7
and f
↓
7
. This further reduces A
′′
1
from
about 600 to about 300 states. Other components are
reduced as well.
With these two reductions, exploring the resulting
state space becomes feasible, being approximately
10
10
states. We look for deadlocks: states without
outgoing transitions. As our learned model repre-
sents actual software, we expect no deadlocks. If a
deadlock arises, it is due to a synchronizing symbol,
the counterpart of which cannot be reached.
A first issue is illustrated in Figure 9. Component
C
7
requests services g and h concurrently. Both are
called asynchronously and can return in either order,
with only the last reply leading to rep
f
. The inferred
‘stateless’ model does not capture the dependency
between replies rep
g
, rep
h
and rep
f
. When in the
learned model both, or neither, incoming replies are
followed by rep
f
, the system deadlocks, as the call-
C
14
f
g
k e
2
kr
S
∗
1
g e
2
req
f
rep
f
req
k
rep
k
n
2
req
g
rep
g
(a)
C
14
f
g
k e
2
kr
S
∗
1
g
h
e
1
e
2
S
∗
2
h
e
1
req
f
rep
f
req
k
rep
k
n
2
n
1
req
g
rep
g
trg
h
(b)
Figure 10: Component C
14
communicates with components
outside the observations, causing missing dependencies.
ing environment expects exactly one reply. This is
solved by enforcing nested services to be finished be-
fore finishing f , as in Example 2 from Step 5 of
Section 4.5.
A second issue is illustrated in Figure 10, where
component C
14
deals with server S
∗
1
. However, we do
not observe S
∗
1
directly, but merely through the mes-
sages obtained at C
14
. The server S
∗
2
, which S
∗
1
uses,
is not observed at all. The observation is shown in
Figure 10a, and a possible perspective of the actual
system is shown in Figure 10b.
Since we do not observe S
∗
1
and S
∗
2
, the model
misses the dependency between functions g and e
2
.
Now, e
2
has no incoming message and it is able to
start ‘spontaneously’. The actual system relies on the
dependency, and as it is missing in the learned be-
haviour, it has deadlocks. Knowing the missing
dependency from domain knowledge, we inject it
through Step 5 as a one-place buffer similar to
Figure 5a, extended to multiple places as needed.
After resolving these issues, we analyze choices.
From other observations we know that g is optional
when performing f in component C
7
of Figure 9a.
The inferred model thus contains tasks which have a
common prefix, i.e. ⟨ f
↑
7
,h
↑
7
,h
↓
7
, f
↓
7
⟩ (g is skipped),
and ⟨ f
↑
7
,h
↑
7
,h
↓
7
,g
↑
7
,g
↓
7
, f
↓
7
⟩ (g is called). After h
↓
7
a
choice arises, to either call g by g
↑
7
or finish f by f
↓
7
.
Such choices can enlarge the state space, and may
not apply in all situations. We therefore asked do-
main experts on which information in the software
such a choice could depend. Together, we concluded
that g is only skipped once, and this relates to the
repetitions we observed for C
1
, as g is skipped for
one particular such iteration. We ensured the correct
choice is made, by constraining the two options to
their corresponding iterations on C
1
, thus removing
some non-system behavior from the inferred model.
6.4 Model Inference Step 6
To the result of Step 5, we apply asynchronous com-
position (Step 6, Section 5). Using FIFO and bag
buffers as described in that section, service fragments
ICSOFT 2022 - 17th International Conference on Software Technologies
156

are allowed to commute due to execution and
communication time variations.
For our case study, all inferred buffer capacities
are either one or two, except component C
2
, which has
buffers with capacities up to 24. The low number of
buffer places is due to the extensive synchronization
on replies. C
2
, the log component, only receives ‘fire-
and-forget’-type logging notifications without replies.
We verified that the resulting, improved, asyn-
chronously composed model indeed accepts its input
TMSC, i.e., the inferred model accepts the input ob-
servation from which it was inferred. This gives trust
that the practically inferred model is in line with that
observation. The inferred models were confirmed by
domain experts as remarkably accurate, allowing
them to discuss and analyze their system’s behavior.
This in stark contrast to models that were previously
inferred using process mining and heuristics-based
model learning, where they questioned the accuracy
of the models instead.
7 CONCLUSIONS AND FUTURE
WORK
We introduced our novel method, Constructive
Model Inference (CMI), which uses execution logs
as input. Relying on knowledge of the system archi-
tecture, it allows learning the behavior of large
concurrent component-based systems. The trace-
theoretical framework provides a solid foundation.
ASML considers the state machine models resulting
from our method accurate, and the service fragment
models in particular also highly intuitive. They see
many potential applications, and are already using
the inferred models to gain insight into their software
behavior, as well as for change impact analysis.
Future work includes among others extending the
CMI method to inferring Extended Finite Automata
and Timed Automata, further industrial application
of the approach, and automatically deriving interface
models from component models.
ACKNOWLEDGEMENTS
This research is partly carried out as part of the
Transposition project under the responsibility of ESI
(TNO) in co-operation with ASML. The research ac-
tivities are partly supported by the Netherlands
Ministry of Economic Affairs and TKI-HTSM.
REFERENCES
Akdur, D., Garousi, V., and Demir
¨
ors, O. (2018). A survey
on modeling and model-driven engineering practices
in the embedded software industry. Journal of Systems
Architecture, 91(October):62–82.
Akroun, L. and Sala
¨
un, G. (2018). Automated verification
of automata communicating via FIFO and bag buffers.
Formal Methods in System Design, 52(3):260–276.
Angluin, D. (1987). Learning regular sets from queries
and counterexamples. Information and Computation,
75(2):87–106.
Aslam, K., Cleophas, L., Schiffelers, R., and van den Brand,
M. (2020). Interface protocol inference to aid under-
standing legacy software components. Software and
Systems Modeling, 19(6):1519–1540.
Bera, D., Schuts, M., Hooman, J., and Kurtev, I. (2021).
Reverse engineering models of software interfaces.
Computer Science and Information Systems.
Beschastnikh, I., Brun, Y., Abrahamson, J., Ernst, M. D.,
and Krishnamurthy, A. (2013). Unifying FSM-
inference algorithms through declarative specifica-
tion. Proceedings - International Conference on Soft-
ware Engineering, pages 252–261.
Brand, D. and Zafiropulo, P. (1983). On Communicating
Finite-State Machines. Journal of the ACM (JACM),
30(2):323–342.
de la Higuera, C. (2010). Grammatical Inference. Cam-
bridge University Press, New York, 1st edition.
Genest, B., Kuske, D., and Muscholl, A. (2007). On com-
municating automata with bounded channels. Funda-
menta Informaticae, 80(1-3):147–167.
Heule, M. J. and Verwer, S. (2013). Software model syn-
thesis using satisfiability solvers. Empirical Software
Engineering, 18(4):825–856.
Hooimeijer, B. (2020). Model Inference for Legacy Soft-
ware in Component-Based Architectures. Master’s
thesis, Eindhoven University of Technology.
Howar, F. and Steffen, B. (2018). Active automata learning
in practice. In Bennaceur, A., H
¨
ahnle, R., and Meinke,
K., editors, Machine Learning for Dynamic Soft-
ware Analysis: Potentials and Limits: International
Dagstuhl Seminar 16172, Dagstuhl Castle, Germany,
April 24-27, 2016, Revised Papers, pages 123–148,
Cham. Springer International Publishing.
Jonk, R., Voeten, J., Geilen, M., Basten, T., and Schiffelers,
R. (2020). SMT-based verification of temporal proper-
ties for component-based software systems. Technical
Report ES Reports, Eindhoven University of Technol-
ogy, Department of Electrical Engineering, Electronic
Systems Group, Eindhoven.
Kuske, D. and Muscholl, A. (2019). Communicat-
ing Automata. Submitted for peer review (Jour-
nal unknown) Retrieved from http://eiche.theoinf.tu-
ilmenau.de/kuske/Submitted/cfm-final.pdf.
Leemans, M., van der Aalst, W. M., van den Brand, M. G.,
Schiffelers, R. R., and Lensink, L. (2018). Soft-
ware Process Analysis Methodology – A Methodol-
ogy based on Lessons Learned in Embracing Legacy
Software. In 2018 IEEE International Conference on
Constructive Model Inference: Model Learning for Component-based Software Architectures
157

Software Maintenance and Evolution (ICSME), pages
665–674. IEEE.
Mark Gold, E. (1967). Language identification in the limit.
Information and Control, 10(5):447–474.
Mazurkiewicz, A. (1995). Introduction to Trace Theory. In
Diekert, V. and Rozenberg, G., editors, The Book of
Traces, chapter 1, pages 3–41. World Scientific, Sin-
gapore.
Milner, R. (1989). Communication and Concurrency.
Prentice-Hall, Inc., River, NJ, United States.
Muscholl, A. (2010). Analysis of communicating automata.
In LATA 2010: Language and Automata Theory and
Applications, pages 50–57.
Nakamura, A., Saito, T., Takigawa, I., and Kudo, M. (2013).
Fast algorithms for finding a minimum repetition rep-
resentation of strings and trees. Discrete Applied
Mathematics, 161(10-11):1556–1575.
Schuts, M., Hooman, J., and Vaandrager, F. (2016). Refac-
toring of Legacy Software using Model Learning and
Equivalence Checking: an Industrial Experience Re-
port. In Integrated Formal Methods: 12th Interna-
tional Conference, pages 311–325.
van der Aalst, W. (2016). Process Mining. Springer-Verlag
Berlin Heidelberg, Berlin Heidelberg, 2nd edition.
van der Aalst, W. M., van Dongen, B. F., Herbst, J.,
Maruster, L., Schimm, G., and Weijters, A. J. (2003).
Workflow mining: A survey of issues and approaches.
Data and Knowledge Engineering, 47(2):237–267.
Yang, N., Aslam, K., Schiffelers, R., Lensink, L., Hendriks,
D., Cleophas, L., and Serebrenik, A. (2019). Improv-
ing Model Inference in Industry by Combining Active
and Passive Learning. SANER 2019 - Proceedings of
the 2019 IEEE 26th International Conference on Soft-
ware Analysis, Evolution, and Reengineering, pages
253–263.
Yang, N., Schiffelers, R., and Lukkien, J. (2021). An in-
terview study of how developers use execution logs in
embedded software engineering. In 2021 IEEE/ACM
43rd International Conference on Software Engineer-
ing: Software Engineering in Practice (ICSE-SEIP),
pages 61–70.
ICSOFT 2022 - 17th International Conference on Software Technologies
158
