
An Ensemble Classifier based Method for Effective Fault Localization
Arpita Dutta
1 a
and Rajib Mall
2 b
1
School of Computing, National University of Singapore, Computing Dr, Singapore
2
Dept. of Computer Science and Engineering, Indian Institute of Technology, Kharagpur, India
Keywords:
Software Fault Localization, Debugging, Ensemble Classifier, Program Analysis.
Abstract:
Fault localization (FL) is one of the most difficult and tedious task during software debugging. It has been
reported in literature that different FL techniques show superior results under different circumstances. No
reported technique always outperforms all existing FL techniques for each type of bug. On the other hand,
it has been reported that ensemble classifiers combine different learning methods to obtain better predictive
performance that may not be obtained from any of the constituent learning algorithms alone. This has mo-
tivated us to use an ensemble classifier for effective fault localization. We focus on three different families
of fault localization techniques, viz., spectrum based (SBFL), mutation based (MBFL), and neural-network
based (NNBFL) to achieve this. In total, we have considered eleven representative methods from these three
families of FL techniques. Our underlying model is simple and intuitive as it is based only on the statement
coverage data and test execution results. Our proposed ensemble classifier based FL (EBFL) method classifies
the statements into two different classes viz., Suspicious and Non-Suspicious set of statements. This helps
to reduce the search space significantly. Our experimental results show that our proposed EBFL technique
requires, on an average, 58% of less code examination as compare to the other contemporary FL techniques,
viz., Tarantula, DStar, CNN, DNN etc.
1 INTRODUCTION
With the increasing complexity and size of software
systems, bugs are inevitable (Wong et al., 2016). In
the complete process of debugging, fault localization
(FL) is the most time-consuming and tiresome. Any
improvement in this task lead to a huge reduction in
total software development cost. Hence, several FL
methods were reported in last two-to-three decades
(Choi et al., 2010; Wong et al., 2016; Dutta et al.,
2019a; Dutta et al., 2021; Dutta et al., 2019b).
Weiser (Weiser, 1984) introduced the concept of
program slicing. Later, Lyle et al.(Lyle, 1987) and
others (Krinke, 2004; Sridharan et al., 2007) extended
the Weiser’s static slicing with program execution in-
formation and proposed dynamic slicing, thin slic-
ing, hybrid slicing etc. However, these techniques
most often returns a considerably large size of pro-
gram slice without any ranking. To solve these is-
sues, different spectrum based and machine learn-
ing techniques are used for FL. SBFL techniques
take program spectra info and test execution results
a
https://orcid.org/0000-0001-7887-3264
b
https://orcid.org/0000-0002-2070-1854
as input and generate ranked list of statements. Fa-
mous SBFL techniques are Ochiai, Jaccard, Taran-
tula, DStar (Wong et al., 2013; Jones et al., 2002)etc.
Using the same input information as SBFL tech-
niques, different neural network models are also
trained to identify the faulty locations. Most com-
monly used NN models are BPNN(Wong and Qi,
2009), DNN(Zhang et al., 2017), CNN(Zhang et al.,
2019) etc. Mutation testing(Wong et al., 2016) is also
used for FL. MUSE(Moon et al., 2014) and Metal-
laxis(Papadakis and Le Traon, 2015) are two most
popular MBFL techniques.
Even though a large number of FL techniques
have been reported but none of these outperforms all
FL techniques in all circumstances. For example,
some of the techniques work very well for logical and
relational operator related faults whereas some other
technique work for arithmetic-operator related bugs.
It has been reported that ensemble classifier combines
different learning methods to obtain better predictive
performance that may not be obtained from any of the
constituent learning algorithms alone. This motivated
us to use an ensemble classifier for effective FL. Be-
sides, the existing techniques are not effective enough
Dutta, A. and Mall, R.
An Ensemble Classifier based Method for Effective Fault Localization.
DOI: 10.5220/0011166800003266
In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 159-166
ISBN: 978-989-758-588-3; ISSN: 2184-2833
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
159
for large size programs.
In order to address these stated problems, we pro-
pose an ensemble classifier based FL method. We
focus on three different families of fault localiza-
tion techniques, viz., SBFL, MBFL, and NNBFL to
achieve this. In total, we have considered eleven
representative techniques from these three families.
We further discuss the extension of our proposed ap-
proach to localize multiple-fault programs.
Rest of the chapter is organized as follows: Pro-
posed method is discussed in Section 2. In Sec-
tion 3, empirical evaluation and obtained results are
discussed. We present the comparison with related
works in Section 4. We finally conclude in Section 5.
2 PROPOSED APPROACH: EBFL
Ensemble classifier is a well accepted machine learn-
ing model which has better predictive performance
than each of the base classifier (Mitchell et al., 1997).
To take advantage of this, we proposed an Ensemble
classifier Based Fault Localization (EBFL) method.
In our proposed EBFL method, we use three differ-
ent fault localization families viz., SBFL, MBFL, and
NNBFL. Our proposed model first classifies the state-
ments into two different classes: suspicious or non-
suspicious. Further, the fault is localized among the
suspicious set of statements.
In EBFL model, we have considered three promi-
nent fault localization techniques: Tarantula(Jones
et al., 2002), Ochiai(Abreu et al., 2007), and D
∗
(Wong et al., 2013) from SBFL family. From mu-
tation based techniques, Metallaxis (Papadakis and
Le Traon, 2015) has been selected. Metallaxis maps
the mutation kill and alive information with statement
coverage information of SBFL techniques and uses an
SBFL formula to compute the suspiciousness scores
of the statements. We have used the suspiciousness
score computation formulas of Tarantula, Ochiai, and
D
∗
with Metallaxis-FL. Five popular neural network
models, BPNN(Wong and Qi, 2009), RBFNN(Wong
et al., 2011), DNN(Zheng et al., 2016), CNN(Zhang
et al., 2019), and RNN(Sherstinsky, 2020) are also
considered to compute the suspiciousness scores of
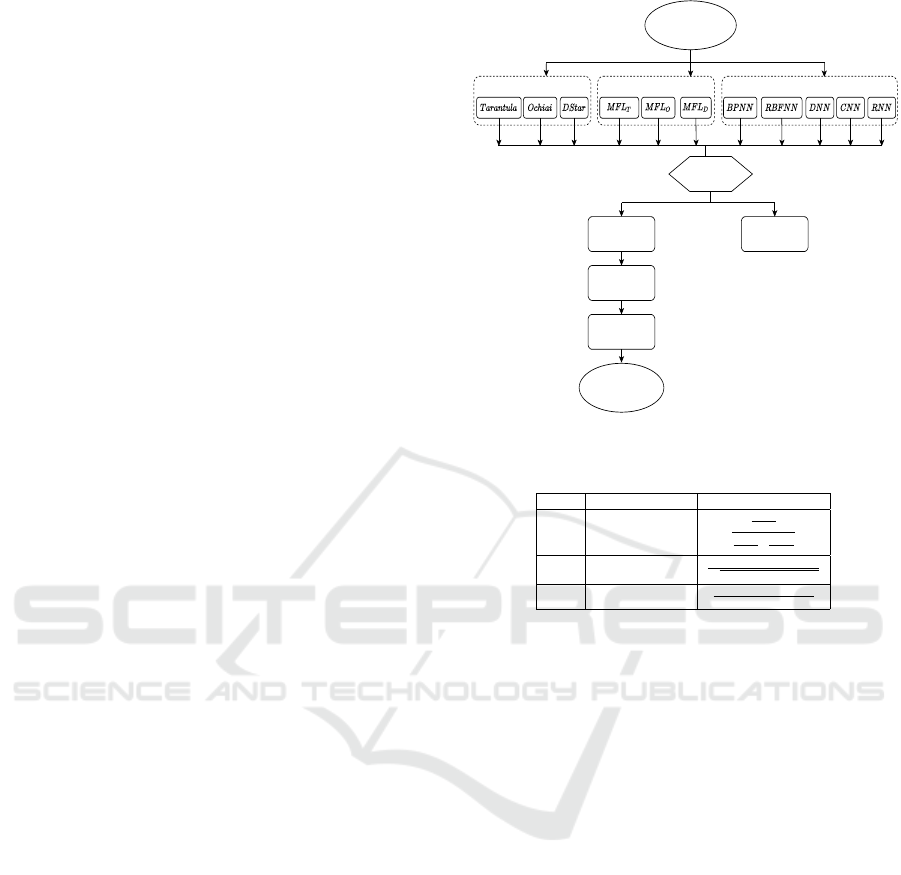
the statements. Figure 1 shows the flow diagram of
our proposed EBFL technique. EBFL takes program
spectra and test execution results as inputs and gener-
ates a ranked list of statements as output.
2.1 Spectrum Based Fault Localization
In SBFL techniques, invocation information of pro-
gram elements and execution results for a number of
Program Spectra and Test
Execution Results
SBFL MBFL NNBFL
Voting to classify
statements
Suspicious
Statements
Non-Suspicious
Statements
Score
Normalization
Combining scores
with Learning to
Rank
Prioritized list of
suspicious statements
Figure 1: Flow diagram of EBFL.
Table 1: SBFL techniques and their formulas.
S.No. SBFL Technique Formula
1 Tarantula
N
e f
(s)
N
f
N
e f
(s)
N
f
+
N
ep
(s)
N
p
2 Ochiai
N
e f
(s)
√
(N
f
)×(N
e f
(s)+N
ep
(s))
3 DStar(D
∗
)
(N
e f
(s))
∗
(N
ep
(s))×(N
f
−N
e f
(s))
test cases are used as input. With these information,
suspiciousness scores of program elements are com-
puted using a mathematical formula. We now briefly
review the important SBFL techniques that have been
proposed by researchers.
Tarantula(Jones et al., 2002): Tarantula is consid-
ered to be a classic SBFL technique. It was introduced
based on the fact that the statements mainly invoked
by failed test cases are more susceptible to contain a
bug as compared to the statements that are invoked by
mainly passed test cases.
Ochiai(Abreu et al., 2007): Ochiai was motivated
from molecular biology field. Other SBFL techniques
e.g., Ample (Wong et al., 2016), Jaccard (Wong et al.,
2010), etc. uses only the information in failed and
passed runs. Whereas, Ochiai also considers the count
of failed test cases which have not executed the state-
ment while computing suspiciousness value.
DStar (D
∗
) (Wong et al., 2013): DStar uses a mod-
ified form of the Kulczynski coefficient (Choi et al.,
2010). It assigns suspiciousness value to a statement
directly proportional to the number of failed tests that
executed it. Table 1 shows the formulas used to cal-
culate suspiciousness score using SBFL techniques.
ICSOFT 2022 - 17th International Conference on Software Technologies
160

Table 2: Symbols used in SBFL techniques in Table 1.
Notation Meaning
N
p
# passed test cases present
N
f
# failed test cases present
N
ep
(s) # passed test cases invoked statement s
N
e f
(s) # failed test cases invoked statement s
Table 3: MBFL techniques and their formulas.
MBFL Technique Abbv. Formula
M-FL with Tarantula MFL
T
max
m∈M(s)
(
N
k f
(s)
N
f
N
e f
(s)
N
f
+
N
ep
(s)
N
p
)
M-FL with Ochiai MFL
O
max
m∈M(s)
(
N
k f
(s)
√
(N
f
)×(N
k f
(s)+N
kp
(s))
)
M-FL with DStar(D
∗
) MFL
D
max
m∈M(s)
(
(N
k f
(s))
∗
(N
kp
(s))×(N
f
−N
k f
(s))
)
Table 4: Symbols used in MBFL techniques in Table 3.
Notation Meaning
M(s) Set of mutants created for statement s
m A mutant from set M(s)
N
kp
(s) Total passed test cases killed by mutant m
N
k f
(s) Total failed test cases killed by mutant m
2.2 Mutation Based Fault Localization
Though SBFL techniques have been intensively stud-
ied but they have limitations. Key reason is that many
times a fault-free statement is executed by all the
failed test cases and also passed test cases may exe-
cute the faulty statement coincidentally. To mitigate
this problem, MBFL was introduced. In MBFL tech-
niques, a number of mutants for each statement are
created. Based on these, FL is done. We briefly re-
view an important MBFL technique in the following.
Metallaxis-FL (Papadakis and Le Traon, 2015): It is
a well-known MBFL technique and has been reported
to outperform many prominent SBFL techniques. Pa-
padakis et al. map the statement coverage informa-
tion used in SBFL techniques with the number of
pass and fail test cases that kill a mutant. Subse-
quently, they used an SBFL formula to compute the
suspiciousness score of a statement. In EBFL, we use
the same formulas as Tarantula, Ochiai, and D
∗
with
Metallaxis-FL to generate the suspiciousness scores
of the statements. Table 3 shows the formulas used
to calculate the suspuciousness score of a statement
using Metallaxis-FL.
2.3 Neural Network Based Fault
Localization
MBFL techniques are effective, but their effectiveness
gets considerably reduced either when all or none of
the mutants are killed by the failed test cases. Another
drawback of these techniques is that, they are com-
pute intensive. Neural network models can be used
to minimize these limitations. Statement coverage in-
formation along with the test results have been con-
sidered as training samples and labels of training data
respectively for NN models. Subsequently, a virtual
test suite is used to test the trained model and com-
pute the suspiciousness scores of each statement. We
use five representative neural network models in our
ensemble classifier EBFL.
BPNN-FL (Duda and Hart, 1973): Back propaga-
tion neural network (BPNN) is the simplest and eas-
iest to implement. We use the same architecture as
discussed by Wong et al.(Wong and Qi, 2009).
RBFNN-FL (Mitchell et al., 1997): RBFNN easily
maps the complex functions and free from the prob-
lems like local minima(Duda and Hart, 1973) and
paralysis (Wasserman, 1993). The RBFNN model
used in EBFL is as same as in (Wong et al., 2011).
DNN-FL (Mitchell et al., 1997): DNNs are pow-
erful enough to correctly approximate considerably
complex functions. It achieves this by the distributed
representation for input data which can be learnt by
the non-linear network structures in presence of lim-
ited samples also. Other than the input and output
layers, three hidden layers are present in the DNN
model that we use. Other optimizations and network
settings used in DNN are the as same as in (Zheng
et al., 2016).
CNN-FL (Ketkar, 2017): Convolutional neural net-
work (CNN) is an important class of deep neural net-
works. It can efficiently work with large-sized data
sets using its parameter sharing and down sampling
features. Also, CNNs have good generalization capa-
bility. In the CNN model which we have used, there
are two convolutional layers, two pooling layers, and
two rectified linear units (ReLu) to connect the con-
volutional layer and pooling layer. A fully connected
three layered NN has been discussed subsequently.
RNN-FL (Sherstinsky, 2020): Another popular deep
neural network architecture is recurrent neural net-
work (RNN). RNNs have memory which stores pre-
viously computed information. RNN uses same pa-
rameters for each of the inputs on which it has per-
form the similar functions on all hidden as well as
input layers to generate the output. RNN model used
in EBFL contains one input, three recurrent and one
output layers in complete.
2.4 Ensemble Classifier Based Fault
Localization (EBFL)
We first generate the suspiciousness scores of all
statements using each FL technique considered. Fur-
ther, the medians of the suspiciousness scores gen-
An Ensemble Classifier based Method for Effective Fault Localization
161

erated by each technique are computed. We apply a
voting strategy to classify the program statements into
two classes viz., non-suspicious and suspicious. Ac-
cording to our voting strategy, if a statement’s suspi-
ciousness scores for six or above number of FL tech-
niques, are higher than or equal to that particular FL
technique’s median value, then the statement is con-
sidered into the suspicious class otherwise it is con-
sidered into the non-suspicious class.
After separating the statements into two classes,
we normalize the suspiciousness scores generated by
different techniques. Suspiciousness scores generated
by RBFNN, BPNN and Tarantula are always between
0 to 1, whereas, DStar generates scores any positive
values. We then normalize the suspiciousness val-
ues generated by all the FL techniques in range of
0 to 1 to maintain a uniformity among all the tech-
niques. To achieve this, the suspicious value of each
statement is divided by the summation of the suspi-
ciousness scores of all the statements for the respec-
tive FL technique.
Subsequently, we combine the suspiciousness
scores generated by all the FL techniques to assign
a single suspiciousness score to a statement. We
use learning to rank algorithm (Xuan and Monper-
rus, 2014) to add weights to each FL technique. The
combined suspiciousness score of statement e is cal-
culated using Equation 1.
susp(e) =
m
∑
i=1
w
i
(e) ∗ss
i
(e) (1)
where, w
i
(e) and ss
i
(e) denote the weight of the i
th
FL technique and suspiciousness score for statement
e generated by the same FL technique respectively.
Learning-to-Rank algorithm learns the order be-
tween non-faulty and faulty statements such that the
faulty statements always have higher suspiciousness
score than the non-faulty ones. The loss function used
by the algorithm is given in Equation 2.
loss =
∑
<e
+
,e
−
>
||susp(e
+
) ≤ susp(e
−
)|| (2)
Where, < e
+
, e
−
> denotes a pair of faulty and cor-
rect statements and loss function computes the num-
ber of pairs for which the suspiciousness score of
faulty statement is less than the correct statements.
The input data required for learning-to-rank (LTR)
algorithm is given in Table 5. In the table, Column
1 (SID) shows the statement number and and Column
2 (VID) shows the version number of faulty program
considered. Column 3 (FT) represents whether the
statement is faulty or not. If it contains ‘1’, then the
statement of that version is faulty otherwise not. Re-
maining columns contains the suspiciousness scores
Table 5: Sample training data for LTR algorithm.
SID VID FT Susp
1
Susp
2
Susp
3
···
S
1
1 0 SS
(1,1)
1
SS
(1,1)
2
SS
(1,1)
3
···
S
1
2 1 SS
(1,2)
1
SS
(1,2)
2
SS
(1,2)
3
···
S
2
1 0 SS
(2,1)
1
SS
(2,1)
2
SS
(2,1)
3
···
S
2
2 0 SS
(2,2)
1
SS
(2,2)
2
SS
(2,2)
3
···
··· ··· ··· ··· ··· ··· ···
generated by different FL techniques. For exam-
ple, SS
(1,2)
3
contains the suspiciousness score gener-
ated by FL technique 3 for the 1
st
statement of 2
nd
faulty version. Different pairwise Learning-to-Rank
approaches can be applied for fault localization, e.g.,
RankBoost, RankNet and FRank etc. We have used
RankBoost algorithm in EBFL. RankBoost (Freund
et al., 1998) is classic and efficient approach based on
Adaboost.
2.5 Multiple Fault Localization
Till now we have discussed our localization method
for single-fault programs. However, in practice, a pro-
gram may contain multiple faults. We extend our pro-
posed technique Combi-FL to handle multiple-fault
programs using the concept of parallel debugging
(Jones et al., 2007). For parallel debugging, failed
test cases are divided into different fault focused clus-
ters. Subsequently, each of these clusters is used to lo-
calized the bugs in parallel. These steps are repeated
until all the test cases are pass.
2.5.1 Creation of Fault-focused Cluster
Let us consider that there are p
u
and f
u
number of
unique pass and unique failed test cases are present
in the test suite. Here, the term ‘unique’ stands in
terms of unique statement coverage vectors. Initially,
we create f
u
number of test suites by combining one
failed test case with all the p
u
test cases. Subse-
quently, we apply the EBFL technique over each of
the f
u
test suites to generate f
u
statement ranking se-
quences corresponding to each failed test case vector.
We further compute the similarity among different
statement ranking sequences using revised Kendall’s
tau correlation coefficient defined by Gao et al. (Gao
and Wong, 2017). In revised Kendall’s tau coeffi-
cient (Knight, 1966) computation, high weights are
assigned to the statements holding higher ranks and
low weights to the lower ranking statements. The ob-
tained ranking sequences are combined based on their
similarity using the agglomerative hierarchical clus-
tering method (Davidson and Ravi, 2005). This pro-
cess continues until a single cluster formed. It results
in a f
u
-level hierarchical tree.
ICSOFT 2022 - 17th International Conference on Software Technologies
162
2.5.2 Stopping Criterion
Our stopping criterion is based on a measure the simi-
larity between the top-25% of ranking sequences gen-
erated by the clusters present at the k
th
and (k −1)
th
levels of the hierarchical tree. We use Jaccard simi-
larity metric to compute the similarity between rank-
ing sequences. If the Jaccard similarity is more than
85%, we consider the faulty location indicated by the
test cluster at k
th
and (k −1)
th
levels are same. On the
other hand, if the similarity score is less than 85%,
then the buggy locations indicated are different and
clusters are further broken up to find the correct loca-
tion. This process is repeated until all the bugs have
been located in the code.
3 EXPERIMENTAL RESULTS
In this section, we present the used setup and pro-
grams for our experiments. Followed by this, we
discuss the obtained experimental results. The sec-
tion is completed by discussing some of the important
threats to the validity of experimental results.
3.1 Setup
The experiments were performed on a 64-bit Ubuntu
machine with 16 Giga Bytes RAM and Intel core
processor. The input C-programs are complied us-
ing GCC-7.4.0 compiler. Information of program
spectra and test execution results were obtained us-
ing GCOV(gcov, 2002) tool. Since, Defects4j pro-
gram suite contains Java programs, we used open-
source available coverage results and other required
resources in our experiment are taken from (De-
fects4J, 2014). We have developed a mutator to create
the mutants and it is available online (Mutator, 2019)
for use.
3.2 Subject Programs
To evaluate the effectiveness of EBFL, we have ex-
perimented with four program suites comprising of
eleven different programs. We have used three bench-
mark suites: Siemens suite, Space
2.0, and Gzip 1.50
downloaded from SIR repository(SIR, 2005). Last
two programs are taken from Defects4j (Defects4J,
2014). The benchmark program suites also accompa-
nied by faulty versions and test cases. Table 6 shows
some of the important characteristics of the programs
used in our experimental study. Columns 2-5 present
the program name, number of faulty versions, number
of executable statements, total number of test cases
Figure 2: Effectiveness of EBFL, D
∗
and Tarantula for the
Siemens suite.
and number of mutants generated respectively. For
the last two programs, we have used the statement
coverage information and test execution results al-
ready available in their respective website (Defects4J,
2014).
3.3 Results
We compare the results of EBFL with two SBFL
techniques: Tarantula (Jones et al., 2002) and DStar
(Wong et al., 2013) and two NNBFL techniques:
DNN(Zheng et al., 2016) and CNN(Zhang et al.,
2019). Since, SBFL techniques sometimes allot the
same suspiciousness value to two or more number
of program statements, which leads to two different
types of effectiveness, the worst effectiveness and the
best effectiveness. On the other hand, EBFL, CNN
(Zhang et al., 2019), and DNN (Zheng et al., 2016) as-
sign unique suspiciousness scores to each statement.
For this reason, in the line graphs 2 to 7, the effective-
ness of SBFL techniques are represented with two dif-
ferent line plots and other techniques are represented
with a single line plot.
Table 6: Program characteristics.
Program No. of No. of No. of No. of
Name Flty. Ver. Ex. LOC Tests Mutants
Print Tokens 7 195 4130 285
Print Tokens2 10 200 4115 314
Schedule 9 152 2650 406
Schedule2 10 128 2710 350
Replace 32 244 5542 508
Tcas 41 65 1608 216
Tot info 23 122 1052 571
Space 2.0 38 3656 13585 17521
Gzip 1.50 13 1720 195 8250
Time 27 40.1K 4130 416
Lang 65 30.2K 2245 775
Figure 2 represents the effectiveness comparison
of EBFL, DStar and Tarantula for the Siemens suite
programs. It can be observed from the figure that
An Ensemble Classifier based Method for Effective Fault Localization
163
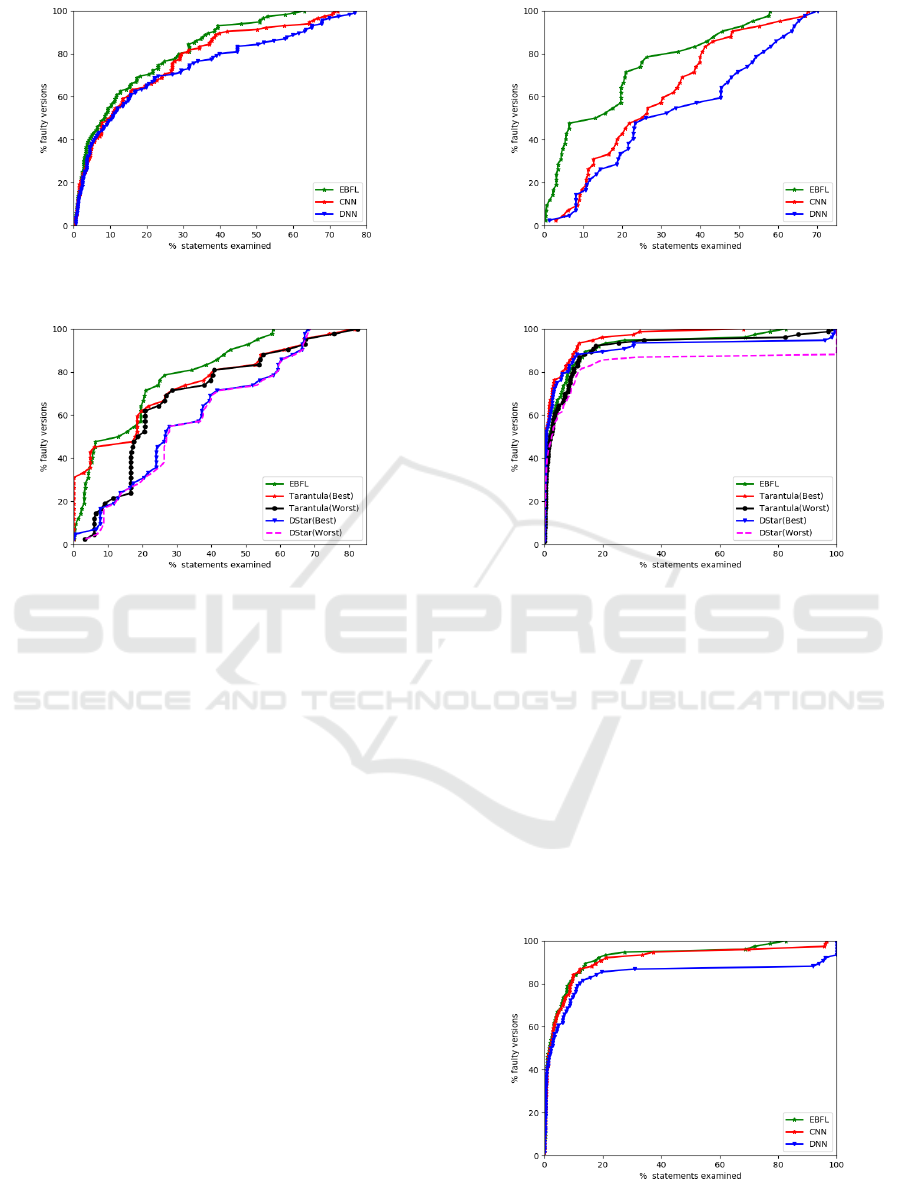
Figure 3: Effectiveness of EBFL, CNN and DNN for the
Siemens suite.
Figure 4: Effectiveness of EBFL, D
∗
and Tarantula for Gzip
and Space.
by examining 10% of statements, Tarantula(Best)
and Tarantula(Worst), and DStar(Worst) localize bugs
in 46.08%, 39.13%, and 45.21% of faulty versions.
Whereas, by examining the same percentage of state-
ments, EBFL localized bugs in 58.48% of faulty pro-
grams. On an average, when using EBFL it is neces-
sary to examine 20.44% and 35.50% less statements
than DStar and Tarantula respectively.
Figure 3 shows the experimental results of EBFL,
CNN, and DNN for the Siemens suite. It can be ob-
served that EBFL outperforms both CNN and DNN.
In the worst case, EBFL requires 3% and 6% less code
analysis than CNN and DNN. On an average, EBFL
performs 16.53% and 28.73% more effectively than
both CNN and DNN models respectively for fault lo-
calization.
Figure 4 presents the effectiveness comparison of
EBFL, DStar and Tarantula for the Gzip and Space
suites. We can observe from the line graphs in Fig. 4
that by analysing only 12% of program code, faults
are localized in 50% of faulty versions by EBFL.
However, with the same amount of code analysis,
faults are localized in only 45.23%, 21.42%, 21.42%,
and 19.04% of faulty programs by Tarantula(Best),
Tarantula(Worst), DStar(Best), and DStar(Worst) re-
spectively. Moreover, in the worst case, EBFL is
Figure 5: Effectiveness of EBFL, CNN and DNN for Gzip
and Space.
Figure 6: Effectiveness of EBFL, D
∗
and Tarantula for De-
fects4j.
24.62% and 10.92% better than Tarantula(Best) and
DStar(Best). Therefore, for the Space and Grep suites
of programs, EBFL is, on an average, 46.70% and
25.56% better than DStar and Tarantula respectively.
Figure 5 shows performance results for EBFL,
DNN, and CNN using the Gzip and Space programs.
We can observe from the figure 5 that for almost all
the faulty programs, EBFL performs more effectively
than both DNN and CNN. By analysing only 10% of
the program code, EBFL localizes bugs in 47.61%
of faulty versions whereas, DNN and CNN localize
bugs in only in 16.67% and 19.04% of versions for
Figure 7: Effectiveness of EBFL, CNN and DNN for De-
fects4j.
ICSOFT 2022 - 17th International Conference on Software Technologies
164

Table 7: Relative improvement using EBFL over existing
FL techniques.
Programs Tarantula DStar DNN CNN
Siemens 64.59 79.59 71.29 83.50
Space 69.74 49.87 49.37 60.61
Gzip 85.01 76.11 83.83 89.06
Defects4j 87.05 58.82 47.12 85.15
the same amount of code examination. Further, in
the worst case, EBFL performs 12.22% and 9.88%
more effectively than DNN and CNN respectively. On
an average, EBFL examines respectively 47.36% and
35.03% less code than DNN and CNN.
Figure 6 presents the effectiveness comparison of
EBFL, DStar and Tarantula for the Defects4j pro-
grams. We can observe from the figure that by exam-
ining only 1% of program code EBFL localizes faults
in 44.73% of buggy versions of Defects4j. Whereas,
Tarantula(Worst), and DStar(Worst) require to exam-
ine at least 1.36%, and 1.53% of code. In the worst
case, EBFL is 33.69% better than DStar and Taran-
tula. EBFL is, on an average, 8.63% and 39.62%
more effective than Tarantula and DStar respectively.
Figure 7 shows effectiveness comparison of re-
sults of EBFL, DNN, and CNN for Defects4j pro-
gram suite. By checking 0.03% of program code,
EBFL localizes bugs in 23.68% of the faulty ver-
sion. Whereas, with the same EXAM
Score, CNN
and DNN are able to localize bugs in only 18.42%
and 17.10% of faulty program versions respectively.
EBFL is, on an average, 60.68% more effective than
DNN; and 28.93% more effective than CNN in local-
izing software faults.
Table 7 shows the relative improvement achieved
using EBFL over the existing FL techniques. It can
be observed that for almost all the considered pro-
grams, EBFL performs better than Tarantula, DStar,
DNN and CNN.
3.4 Threats to Validity
We present a few important threats to the validity of
our obtained experimental results.
• We have experimented our EBFL approach over
limited set of programs. It may possible that the
results are not similar for other set of programs.
However, to mitigate this risk, we have examined
program from different application domains and
variable complexities, LOCs etc.
• Effectiveness of EBFL technique lies on proper
combination of passed and failed test cases. If the
test suite is biased, for example, either all the test
cases are passed or failed, then it will not perform
effectively.
4 COMPARISON WITH
RELATED WORK
We have experimentally compared our proposed
EBFL technique with two prominent SBFL tech-
niques: DStar (Wong et al., 2013), and Tarantula
(Jones et al., 2002). Our results indicate that EBFL
performs, on an average, 37.88%, and 25.43% bet-
ter than DStar and Tarantula respectively for the con-
sidered programs. Also, EBFL assigns a unique sus-
piciousness score to each statements. This is unlike
SBFL techniques which may assign the same suspi-
ciousness scores to two or more statements.
Different slicing based fault localization tech-
niques have been proposed and reported (Agrawal
and Horgan, 1990; Lyle, 1987; Weiser, 1984). These
techniques yields a set of suspected statements only.
They do not assign any ranking to the statements even
which hampers the effectiveness of a FL technique.
Also, sometimes a slice may contain all or most of
the statements present in the program. On the other
hand, EBFL assigns unique suspiciousness values to
each of the executable statement present in the suspi-
cious class.
Renieris et al. (Renieres and Reiss, 2003) pro-
posed a FL technique based nearest neighbor con-
cept. This technique discovers the most similar ex-
ecution trace covered by a failed test case with that
covered by different passed test cases. Subsequently,
they have used set difference to remove the irrele-
vant statements and reports the suspicious set of state-
ments. Their approach sometimes returns a empty
set of suspicious statements too. Whereas, EBFL
first classifies the statements into two separate groups:
non-suspicious and suspicious using a voting-scheme
based on the suspiciousness scores generated by dif-
ferent techniques. Our proposed EBFL method will
never return an empty set of suspicious statements.
Xuan et al. (Xuan and Monperrus, 2014) pro-
posed a technique to merge different spectrum based
fault localization methods using learning-to-rank al-
gorithm to generate effective prioritized list of state-
ments. On the other hand, in EBFL, we have consid-
ered three different domains of fault localization tech-
niques: spectrum based, mutation based and neural
network techniques for better localization of faults.
5 CONCLUSION
Fault localization is an important part of debugging.
To make bug localization easier and effective, we
have proposed an ensemble classifier based tech-
nique. We have combined three different families of
An Ensemble Classifier based Method for Effective Fault Localization
165

FL techniques viz., SBFL, MBFL, and NNBFL. Our
method is able to effectively localize common as well
as instrinsic bugs present in the program. Empirical
evaluation shows that, on an average, EBFL performs
58% more effectively in terms of less code examina-
tion than cntemporary FL techniques.
In future, we make use of the individual bug ex-
posing capabilities of test cases to improve the effec-
tiveness of EBFL.
REFERENCES
Abreu, R., Zoeteweij, P., and Van Gemund, A. J. (2007). On
the accuracy of spectrum-based fault localization. In
TAICPART-MUTATION 2007, pages 89–98.
Agrawal, H. and Horgan, J. R. (1990). Dynamic program
slicing. ACM SIGPlan Notices, 25(6):246–256.
Choi, S.-S., Cha, S.-H., and Tappert, C. C. (2010). A survey
of binary similarity and distance measures. Journal of
Systemics, Cybernetics and Informatics, 8(1):43–48.
Davidson, I. and Ravi, S. (2005). Agglomerative hierarchi-
cal clustering with constraints: Theoretical and empir-
ical results. In European Conference on Principles of
Data Mining and Knowledge Discovery, pages 59–70.
Defects4J (2014). github.com/rjust/defects4j.
Duda, R. O. and Hart, P. E. (1973). Pattern recognition and
scene analysis.
Dutta, A., Kunal, K., Srivastava, S. S., Shankar, S., and
Mall, R. (2021). Ftfl: A fisher’s test-based approach
for fault localization. Innovations in Systems and Soft-
ware Engineering, pages 1–25.
Dutta, A., Manral, R., Mitra, P., and Mall, R. (2019a). Hier-
archically localizing software faults using dnn. IEEE
Transactions on Reliability, 69(4):1267–1292.
Dutta, A., Pant, N., Mitra, P., and Mall, R. (2019b). Effec-
tive fault localization using an ensemble classifier. In
QR2MSE, pages 847–855. IEEE.
Freund, Y., Iyer, R., Schapire, R. E., and Singer, Y. (1998).
An e cient boosting algorithm for combining prefer-
ences. In ICML. Citeseer.
Gao, R. and Wong, W. E. (2017). Mseer—an advanced
technique for locating multiple bugs in parallel. IEEE
Transactions on Software Engineering, 45(3):301–
318.
gcov (2002). man7.org/linux/man-pages/man1/gcov-tool.
1.html.
Jones, J. A., Bowring, J. F., and Harrold, M. J. (2007). De-
bugging in parallel. In Proceedings of the 2007 inter-
national symposium on Software testing and analysis,
pages 16–26.
Jones, J. A., Harrold, M. J., and Stasko, J. (2002). Visual-
ization of test information to assist fault localization.
In ICSE, pages 467–477. IEEE.
Ketkar, N. (2017). Convolutional neural networks. In Deep
Learning with Python, pages 63–78. Springer.
Knight, W. R. (1966). A computer method for calculat-
ing kendall’s tau with ungrouped data. Journal of the
American Statistical Association, 61(314):436–439.
Krinke, J. (2004). Slicing, chopping, and path conditions
with barriers. Software Quality Journal, 12(4).
Lyle, R. (1987). Automatic program bug location by pro-
gram slicing. In 2nd international conference on com-
puters and applications, pages 877–883.
Mitchell, T. M. et al. (1997). Machine learning.
Moon, S., Kim, Y., Kim, M., and Yoo, S. (2014). Ask the
mutants: Mutating faulty programs for fault localiza-
tion. In 7th STVV, pages 153–162.
Mutator (2019). github.com/ArpitaDutta/Mutator .
Papadakis, M. and Le Traon, Y. (2015). Metallaxis-
fl: mutation-based fault localization. STVR, 25(5-
7):605–628.
Renieres, M. and Reiss, S. P. (2003). Fault localization with
nearest neighbor queries. In 18th ASE, pages 30–39.
Sherstinsky, A. (2020). Fundamentals of rnn and
lstm network. Physica D: Nonlinear Phenomena,
404:132306.
SIR (2005). sir.unl.edu/portal/index.php.
Sridharan, M., Fink, S. J., and Bodik, R. (2007). Thin slic-
ing. In 28th PLDI, pages 112–122.
Wasserman, P. D. (1993). Advanced methods in neural com-
puting. John Wiley & Sons, Inc.
Weiser, M. (1984). Program slicing. IEEE Transactions on
software engineering, (4):352–357.
Wong, W. E., Debroy, V., and Choi, B. (2010). A family
of code coverage-based heuristics for effective fault
localization. JSS, 83(2):188–208.
Wong, W. E., Debroy, V., Gao, R., and Li, Y. (2013). The
dstar method for effective software fault localization.
IEEE Transactions on Reliability, 63(1):290–308.
Wong, W. E., Debroy, V., Golden, R., Xu, X., and Thurais-
ingham, B. (2011). Effective software fault localiza-
tion using an rbf neural network. IEEE Transactions
on Reliability, 61(1):149–169.
Wong, W. E., Gao, R., Li, Y., Abreu, R., and Wotawa, F.
(2016). A survey on software fault localization. IEEE
TSE, 42(8):707–740.
Wong, W. E. and Qi, Y. (2009). Bp neural network-based
effective fault localization. IJSEKE, 19(04):573–597.
Xuan, J. and Monperrus, M. (2014). Learning to combine
multiple ranking metrics for fault localization. In 2014
IEEE ICMSE, pages 191–200.
Zhang, Z., Lei, Y., Mao, X., and Li, P. (2019). Cnn-fl: An
effective approach for localizing faults using convolu-
tional neural networks. In SANER, pages 445–455.
Zhang, Z., Lei, Y., Tan, Q., Mao, X., Zeng, P., and Chang,
X. (2017). Deep learning-based fault localization with
contextual information. IEICE Transactions on Infor-
mation and Systems, 100(12):3027–3031.
Zheng, W., Hu, D., and Wang, J. (2016). Fault localization
analysis based on deep neural network. Mathematical
Problems in Engineering.
ICSOFT 2022 - 17th International Conference on Software Technologies
166
