Comparative Study of a Vacuum Powered Upper Limb Exoskeleton

Dimitar Chakarov

, Ivanka Veneva

and Pavel Venev

Institute of Mechanics, Bulgarian Academy of Sciences, “Acad. G. Bonchev” str., Block 4, Sofia 1113, Bulgaria

Keywords: Exoskeleton, Pneumatic Drive, Positive Pressure, Vacuum Pressure, Simulations, Harmonic Motion,

Interaction Force, Safety, Transparency.

Abstract: In the present work, an exoskeleton of upper limb intended for rehabilitation and training is studied. The aim

of the work is to find and evaluate an appropriate design solution that provides performance on the one hand

and transparency and natural safety on the other. Therefore, a pneumatic drive is proposed and transparency

of the exoskeleton is investigated, where positive pressure actuation is compared with vacuum pressure

actuation. To assess transparency, the interaction force between the patient and the exoskeleton in passive

mode is examined. Simulations and estimates of the interaction force between the patient and the exoskeleton

as a result of exoskeleton gravity and the elastic forces from the pneumatic actuation are performed. In this

case, the forces in the closed chambers of the pneumatic actuators are used to compensate for the gravitational

forces. Simulations are performed with harmonic motion imposed by the patient at one joint of the

exoskeleton. The interaction force at the end effector is evaluated in two cases of pneumatic actuation: at

pressures higher than atmospheric pressure and at vacuum pressure. The simulation results are shown

graphically. A discussion is presented as well as conclusions and directions for future work.

1 INTRODUCTION

The use of exoskeletons for robotic rehabilitation

provides an alternative to conventional manual

therapy to improve motor function in post-stroke

patients (Manna, 2018). Rehabilitation exoskeleton

should be able to create great power to support, assist

and direct the patient's hand in the early stages of

recovery as well as to follow the human arm without

opposition or be able to respond to the movement

made by the patient in the full recovery stage.

(Jarrasse, 2014). For this reason, in the control design

of the rehabilitation exoskeletons in general, two

"extreme" ideal modes can be defined that cover the

whole spectrum of therapeutic interventions: "robot

in charge" and "patient in charge" (Veneman, 2006).

In the 'robot in charge' mode, it is important that the

robot has sufficient force and power to realize the

desired motion with relatively high impedance. In the

"patient in charge" manner, it is important that the

interaction forces between the exoskeleton and the

human are low; in other words, the perceived

https://orcid.org/0000-0002-2312-5725

https://orcid.org/0000-0001-5501-7668

https://orcid.org/0000-0001-7809-3540

impedance of the robot should be low. The key

feature here is transparency.

To provide security and transparency in the

interaction, there are two main approaches to change

the mechanical impedance of the structure: active and

passive. Electric motors and other active actuators are

used to control the impedance of rehabilitation

exoskeletons through an active approach. This control

is based on sensors and motor control algorithms. For

example, impedance control successfully manages

the interaction between the patient and the

exoskeleton in all regimens of therapeutic

interventions (Courtois G., 2021).

The passive approach involves natural and

inherently safe actuators. Pneumatic actuation has the

inherent flexibility and allows in a passive manner to

achieve inherent safety and transparency in all stages

of the rehabilitation process (Morales, 2011). There

are different types of pneumatic actuators. The most

widely known are conventional pneumatic cylinders

and rotary pneumatic motors. They are characterized

by large dimensions, high weight and rigidity of

construction, therefore they are not suitable for

Chakarov, D., Veneva, I. and Venev, P.

Comparative Study of a Vacuum Powered Upper Limb Exoskeleton.

DOI: 10.5220/0011260100003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 403-410

ISBN: 978-989-758-585-2; ISSN: 2184-2809

403

wearable devices. One of the oldest approaches to

implement inherent safety and natural compliance is

the use of pneumatic artificial muscles (PAMs)

(Daerden Fr., 2002). These have good power-to-

weight (volume) ratios for wearable systems. The

impedance is low over a wide frequency range due to

the low inertia and compliance of the gas. The

problem is that performance is reduced by poor

dynamic force response and poor positioning.

Various pneumatic actuators are known to be

used in the field of soft robotics, which stretch and

bend by inflating or deforming elastic chambers to

produce useful mechanical work (Nikolov S., 2016).

All of the pneumatic actuators discussed so far are

activated at pressures higher than atmospheric

pressure. Recently, some soft pneumatic actuators

have been developed that are activated by vacuum

(Yang D., 2017). Using the effect of mechanical

deformation to generate controlled force, vacuum

actuated mechanisms have been successfully

developed and used for soft robotic systems with

redundancy (Matthew A., 2017). Soft vacuum

actuators have many advantages over positive

pressure actuators. First, this type of actuator offers

implicitly safe operation where the actuation force is

limited by the magnitude of the atmospheric pressure.

Thus, in (Mendoza, 2021) a low-profile vacuum-

actuated artificial muscle has been developed and

proposed for infant rehabilitation. Second, vacuum

actuators contract upon activation similar to

biological muscle (Tawk Ch., 2019). This makes

them suitable for a bionic approach of actuation,

through the opposing action of antagonist actuators.

Finally, this actuation method improves the lifetime

and durability of actuators.

A pneumatically driven upper limbs exoskeleton

has been developed by the authors, which is designed

for training and rehabilitation assisted by interactions

in virtual scenes. Experiments on exoskeleton

propulsion have been performed using PAM bundles

included in an antagonistic scheme (Chakarov D.,

2019), as well as propulsion units integrating

pneumatic cylinders and parallel electric motors

(Chakarov D., 2021).

The aim of this article is to continue the previous

work by studying the case in which the exoskeleton is

driven by pneumatic cylinders with vacuum pressure

and to compare this approach with positive pressure

actuation. The aim of the work is to evaluate the

exoskeleton actuation in terms of transparency and

natural safety on the one hand, and in terms of

performance on the other.

2 MATERIALS AND METHODS

OF THE STUDY

As presented in our previous studies (Chakarov D.,

2019), (Chakarov D., 2021) a prototype of a

lightweight upper limb exoskeleton has been created

in which all the heavy components are added in a

fixed base. The exoskeleton mechanical structure

includes two identical arms. Each arm includes pairs

of identical rotational joints for clavicle movements

J1, J2, shoulder movements J3, J4 and elbow

movements J5, J6 respectively, as shown in Figure 1

a), b). Each arm has a total of 6 degrees of mobility,

mimicking the natural movement of the human arm

from back to elbow. The structure of Figure 1 was

selected for designing the arm exoskeleton using

uniform universal joints and thus more complex

solutions involving circular guide and triaxial joints

are avoided.

J4 J5

Figure 1: Exoskeleton right arm: a) prototype; b) structural

scheme.

Each arm of the exoskeleton consists of six

movable segments (1, 2, 3, 4, 5 and 6) made primarily

of aluminum alloy. Plastic shells with straps are

placed on the segments for attachment to the human

limb (Figure 1a). The generalized masses of the six

segments of the arm are M

= 0.463 kg, M

= 0.321

kg, M

= 0.497 kg, M

= 0.782 kg, M

= 0.510 kg and

= 0.793 kg. The arm and forearm lengths of the

exoskeleton were set with initial values L

= 0.286 m

and L

= 0.370 m. The range of motion in the joints is

as follows: J

(15°),J

(120°), J

(120 °), J

(150 °), J

(135 °). The range of movements in the

joints is tailored to that in the joints of the human arm,

as shown in (Abane, 2016).

Light drive units integrating pneumatic cylinders

and cable transmissions are used to drive the

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

404

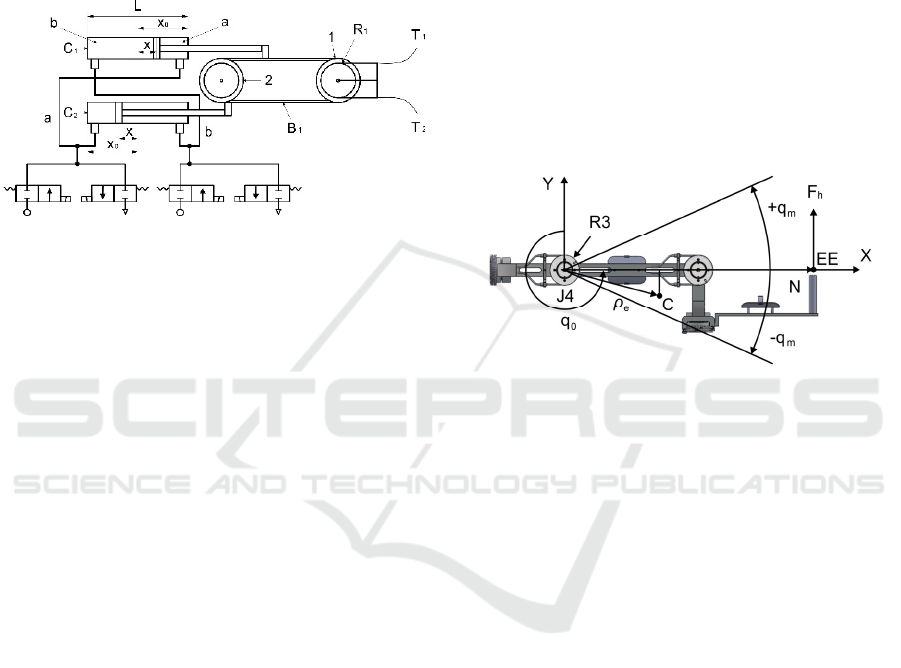
exoskeleton joints. The drive unit of each exoskeleton

joint is built as a separate unit located in the fixed

base. A diagram of the drive unit is shown in Figure

2. The base has a bearing wheel 1 with a cable reel R1

mounted thereon. Bowden cables T1, T2 are used to

connect the reel R1 and a similar reel R3, located in

the exoskeleton joint. A high-precision rotary sensor

is installed in the joint to measure the effective

deviation.

Figure: 2: Scheme of pneumatic drive of the exoskeleton

joints.

The pneumatic actuator consists of a pair of

pneumatic cylinders, C1 and C2, mounted in the base

as shown in Figure 2. Pneumatic cylinders with

diameter D = 0,02 m were used. A transmission was

used, including timing belt B1 and additional wheel 2

to transmit movement from pneumatic cylinders to

wheel 1. The cylinders simultaneously drive opposite

sides of the belt B1. The left-hand chamber of one

cylinder is connected to the right-hand chamber of the

other cylinder by piping, and the other right-hand and

left-hand chambers are connected by other piping

(Figure 2). The piping of each pair is connected to two

parallel valves, one of which supplies pressure air to

the chambers and the other of which connects the

chambers to atmospheric pressure. Pressure sensors

are mounted on each line.

In the work, the interaction between the patient

and the exoskeleton is evaluated in the so-called

"patient in charge" modes, when the patient is able to

initiate complex independent movement in a

relatively safe manner, where it is important that the

interaction forces between the exoskeleton and the

patient are low.

Different approaches are used to study human-

robot interaction. They are all built on the connection

between human behavior and the abilities of the

robot. For example, in (Melchiorre M., 2018) the

robot monitors the position of the human operator's

hand and moves its end effector to reach the operator's

hand.

To assess the interaction forces, experiments are

performed with motion in one joint of the

exoskeleton, similar to the approach used in (Bembli

S., 2019). All joints are locked and the J4 joint is

mobile where flexion-extension is performed in the

shoulder. The patient moves the arm on the

exoskeleton applying force in the end effector (EE)

normal to the arm. This force is the subject of

assessment in the present work.

The patient performs harmonic motions from an

initial position q

with uniform amplitude q

and

constant oscillation frequency ω. The angle q at joint

J4 determines the arm position, assuming q = 0 when

the arm is coincident with the y-axis (Figure 3). The

following law of motion is used to model the

harmonic motions

q)tsin(qq







(1)

Figure: 3: Exoskeleton joint J4 performing harmonic

motion with amplitude q

from starting position q

The assessment of the interaction forces is carried

out in a passive regime. In passive mode, the

exoskeleton does not generate active forces. The

resisting forces are determined only by the

mechanical impedance of the exoskeleton. The EE

force applied to the operator's arm, which overcomes

the mechanical impedance of the exoskeleton, is

determined by the inertial, frictional and gravitational

forces as well as the elastic forces of the pneumatic

actuation. In the present study, a low dynamic mode

is applied in which only the influence of gravitational

and elastic forces is considered. The EE force F

applied to the patient's arm is the sum of the forces

from gravity F

and the forces from the pneumatic

actuation F

applied to the end effector according to

equation:

pgh

FFF 

(2)

where

N/QF



  (3)

N/QF



.   (4)

Above:

is the torque created by the exoskeleton

gravity according to the equation

Comparative Study of a Vacuum Powered Upper Limb Exoskeleton

405

)qcossinqg(MQ

e2e1e





(5)

where: M

represents the mass of exoskeleton moving

parts 4, 5, 6; ρ

=[ρ

; ρ

]

represents the radius

vector of the mass center C in а local frame and g is

the gravity acceleration coefficient;

is the torque produced by the forces in the two

pneumatic cylinders, represented by the sum

r))s(sp-)s(sp(Q

21b21ap



(6)

where p

and p

are the supply pressures in both

chambers, r is the radius of reel R1 and s

and s

are

the areas on both sides of the piston;

N is the value of the radius vector of the EE.

In the passive mode, to provide transparency of

gravity, the torque generated by the pneumatic

cylinder forces Q

is used to compensate the torque

from the gravitational forces Q

. For this reason, one

of the chambers of the pneumatic cylinders is

supplied with an appropriate pressure, after which the

inputs and outputs of this chamber are closed. The

second chamber of the pneumatic cylinders is open to

the atmosphere. In this case, the torque Q

determined by the elastic forces in the closed chamber

due to air compression.

Assuming that air is an ideal gas undergoing an

isothermal process (Czmerk, A., 2017), the rate of

pressure change p and volume change V in a closed

chambers of the cylinder can be expressed by the

polytrophic process equation

CVp 

(7)

where C is a constant.

Once in the starting position of the cylinders X

(Figure 2), chamber a of the pneumatic cylinders is

closed with a pressure p

(a)

and the volume V

(a)

of the

chamber is represented as a function of piston area

and chamber length, equation (7) takes the form:

a210

(a)

C)ss(Xp 

  (8)

where s

and s

are the areas on both sides of the

piston and C

is a constant.

After the patient performs motions according to

the scheme of Figure 3, the piston makes a deviation

x from starting position X

(Figure 2) and the pressure

in the closed chamber changes. Then equation (8)

allows the new equality to be displayed:

a210a210

(a)

C)ss)(xX(p)ss(Xp 

(9)

Then, equality (9) give the equation for the variation

of the pressure p

depending on the piston deviation x





   (10)

When chamber a is closed and chamber b open to

the atmosphere or p

= p

atm

, according to (6) and (10),

the equality of elastic actuator torque as a result of the

pistons deviation x from the starting position X

derived

)rs](sp-

21atm







(11)

When in the starting position of the cylinders X

chamber b is closed with a pressure p

(b)

and chamber

a is open to the atmosphere, after that the patient

performs motions and the piston makes a deviation x

from starting position X

, (Figure 2), еquation (7)

allows the following equalities to be compiled

b210

210

C)ss)(xXL(p

)ss)(XL(p





(12)

xX-L

)X-(Lp





(13)

where L is the cylinder length and C

is a constant.

In this case where p

= p

atm

according to (6) and

(13) the equality of elastic actuator torque is as

follows

)rs](s

xX-L

)X-(Lp

-p[Q

atmpb





(14)

As the initial position of the arm q

corresponds to

the starting position X

of the cylinders, the piston

deviation x, is determined by the deviation q of the

joint angle, as follows



(15)

The behavior of closed pneumatic cylinders

according to (11) and (14) behaves like a variable

compliance spring. The stiffness of the joint driven

by pneumatic cylinders can be determined as a

derivative of the joint torques (11) and (14) about the

joint deviation, according to the equality:

)b,a(p)b,a(p

)b,a(









( 1 6 )

After differentiating equations (11) and (14),

taking into account that p

atm

=const, p

=const,

=const and that piston displacement x is a linear

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

406

function (15) of the articular displacements q, it

follows

)rs(s

x)(X

K 



 (17)

)rs(s

)xX-(L

)X-(Lp

K 





(18)

The stiffness of the joint when a chamber is

closed and the other is open to the atmosphere

according to (17) and (18), represents a linear

function of the initial pressure in the closed chamber

and a nonlinear function of the piston displacements.

In the present study, the objective is to evaluate

the interaction force at the end effector as a result of

pneumatic actuation with pressures higher and lower

than atmospheric pressure. Therefore, two cases are

considered: first, when the pressure p

(a)

in chamber

a is greater than atmospheric pressure, and chamber b

is open to the atmosphere (p

= p

atm)

; second, when

chamber а is open to the atmosphere (p

= p

atm

), and

the pressure p

(b)

in chamber b is less than

atmospheric pressure or vacuum pressure.

3 RESULTS

3.1 Interaction Force at the End

Effector as a Result of Pneumatic

Actuation with Pressure Higher

than Atmospheric Pressure

In this experiment, the initial pressure in chamber a

takes on the following values equal to or greater than

atmospheric pressure: p

(a)

= 100, 150, 250, 350 kPa.

Chamber b is open to the atmosphere and has a

constant pressure p

= p

atm

=100kPa. The other

parameters of the pneumatic drive are shown in Table

1. Since chamber a is closed, it is a generator of

elastic force. The initial position of the arm is q

270

(Figure 3) and the selected starting position of

the piston is X

= 0.0625 m. The maximum deviations

of the arm from the starting position equal to q

= 25

correspond to the deviations of the piston from the

starting position equal to x = 0.014 m. When the arm

oscillates according to (1), the elastic moment (11) is

calculated and is brought to the end effector, where it

forms the resistance force from the pneumatics (4).

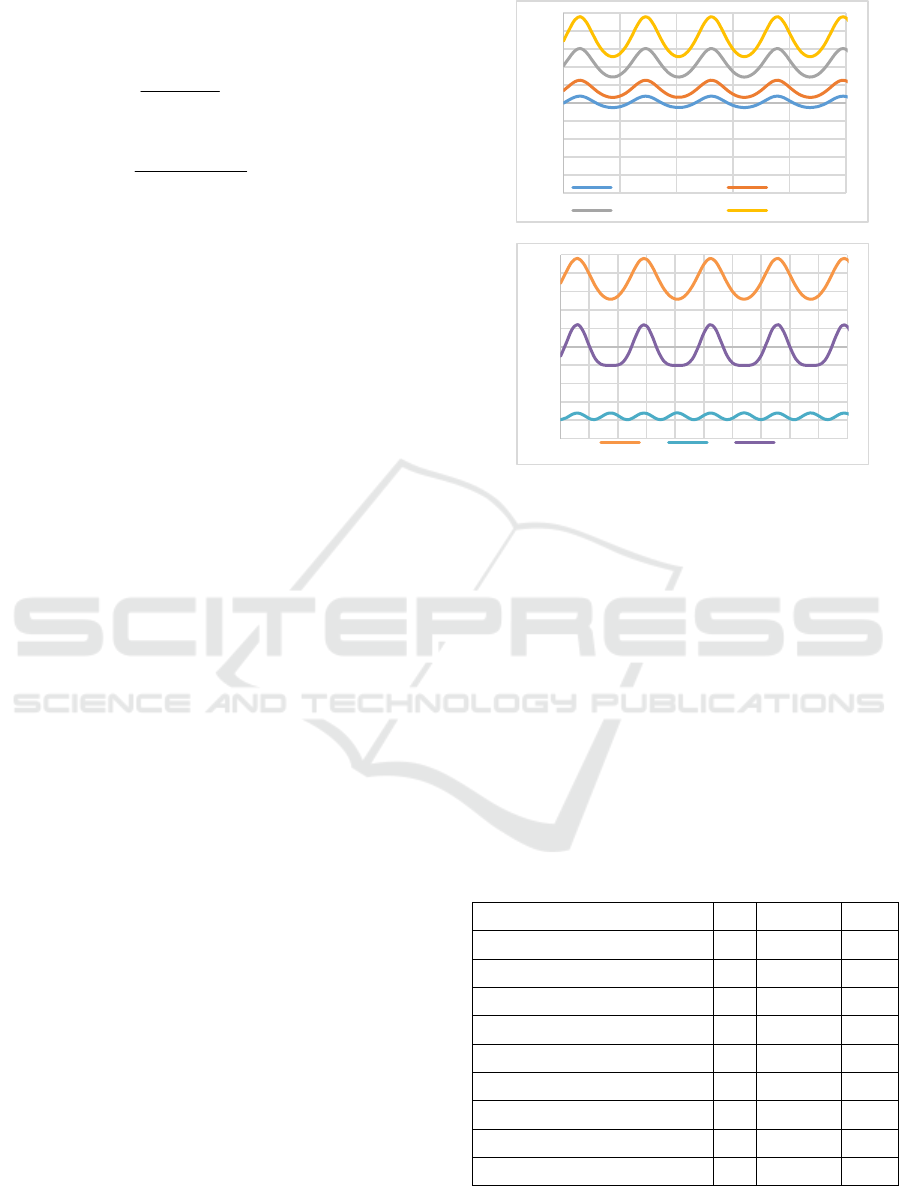
The results of this experiment are shown graphically

in Fig.4 a).

Figure 4: Interaction force at the end effector as a result of:

a) pneumatic (F

) with pressures p

(a)

= 100, 150, 250, 350;

b) gravity (F

); pneumatic (F

) with pressure p

(a)

= 350

kPa and resulting force (F

+ F

In order to use the force from the pneumatic drive

as a balancer of the force from the exoskeleton gravity

according to (2), a pressure in chamber a equal to p

= 350 kPa is selected. The aim is to increase the

transparency or to bring the force applied to the

operator's arm closer to 0. At the same starting

position and the same arm movements as in the

previous experiment, the change in gravitational force

(3) and pneumatic force (4) was calculated. Graphs

with the variation of these forces, as well as with the

resulting force (2), are shown in Fig.4 b).

Table 1: Pneumatic drive parameters.

Piston area side 1

314 10

-6

Piston area side 2 s

264 10

-6

Pneumatic cylinder diameter D 0.020 m

Pneumatic cylinder stroke L 0.125 m

Piston starting position X

0.0625 m

Exoskeleton mass M

2.085 kg

Radius of EE N 0.660 m

Radius of pulley 1 r 0.0315 m

Coordinate 1 of mass center ρ

0.256 m

Coordinate 2 of mass center ρ

0.031 m

‐10

‐8

‐6

‐4

‐2

0246810

[N]

[s]

pa=100kPa pa=150kPa

pa=250kPa pa=350kPa

‐10

‐8

‐6

‐4

‐2

012345678910

[N]

[s]

Fp Fg Fp+Fg

Comparative Study of a Vacuum Powered Upper Limb Exoskeleton

407

3.2 Interaction Force at the End

Effector as a Result of Pneumatic

Actuation with Pressures Lower

than Atmospheric Pressure

In the experiment, the chamber a of the pneumatic

cylinders is connected to the atmosphere, therefore it

has a constant pressure p

= p

atm

=100 kPa. The initial

pressure in chamber b acquires the following values

less than or equal to atmospheric pressure: p

(b)

= 0,

14, 40, 70, 100 kPa. Since chamber b is closed, it is a

generator of elastic force. When p

(b)

= 0 (vacuum),

according to (14) the actuator torque reaches its

maximum value Q

max

which is constant and does not

depend on the deviations of the piston position.

.constr))s(spQ

21atm

max



(19)

The maximum torque determined by the constant

atmospheric pressure may not be sufficient to drive

the designed device. For this reason, the vacuum-

powered exoskeleton needs to change some of the

other parameters, such as the face of the pistons.

Thus, larger pneumatic cylinders with diameter D

= 0.035 m and piston area (s1 + s2) = 0.001840 m

were selected for vacuum pressure drive. The values

of the other parameters of the pneumatic drive are

those of Table 1.

The experiment was performed with the same arm

movements: starting position q

= 270

and maximum

deviations q

= 25

. When the arm oscillates

according to (1), the elastic moment (14) is

calculated, which is reduced to the end effector as the

interaction force from the pneumatic actuation (4).

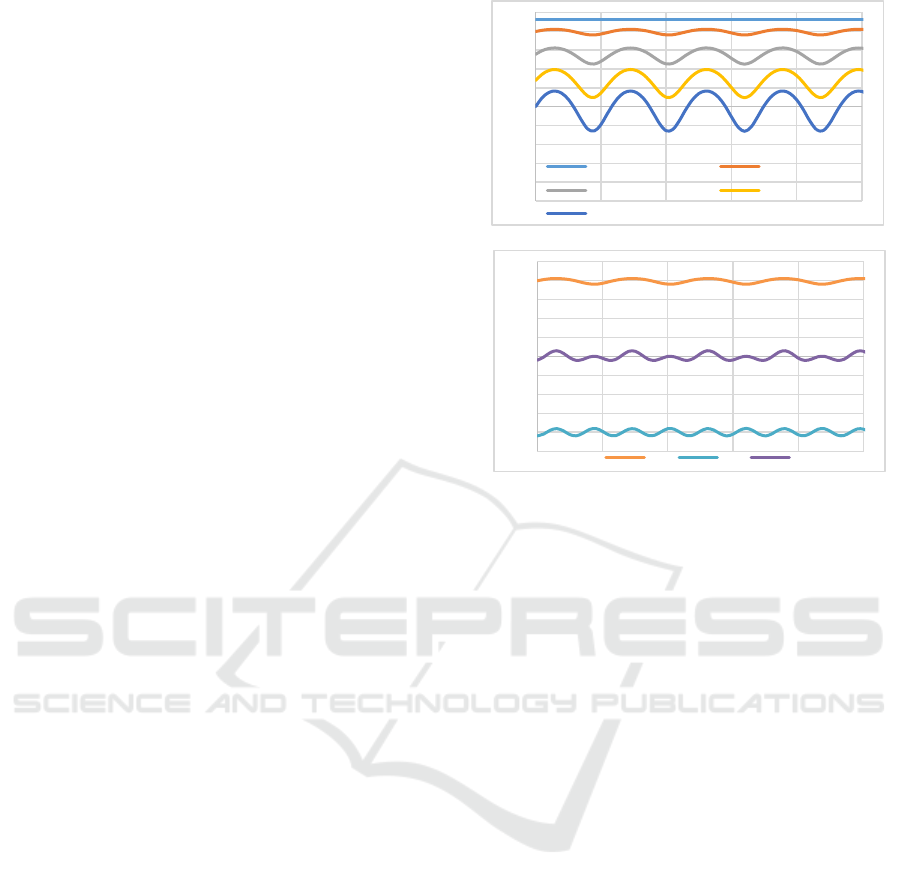
The results of this experiment are shown graphically

in Fig.5 a).

In order to balance the gravity of the exoskeleton

with the pneumatic drive according to (2), chamber

pressure, p

=14 kPa is chosen, so that the force

applied to the operator's arm is equal to 0. At the same

starting position and arm movements the force (2) is

calculated. The change of this force, as well as of the

gravitational force (3) and of the pneumatic drive

force (4) are shown in the graph in Fig.5 b).

4 DISCUSSION

In the experiments performed, the interaction force in

the passive mode of interaction is evaluated, as this

force represents the initial reaction of the

exoskeleton, which can then be changed by the active

mode. Static forces in the interaction such as gravity

resistance and propulsion resistance are evaluated.

)

Figure 5: Interaction force at the end effector as a result of:

a) pneumatic actuation (F

) with vacuum pressures p

(b)

= 0,

14, 40, 70, 100 kPa ; b) gravity (F

); pneumatic (F

) with

pressure p

(b)

= 14 kPa and resulting force (F

+ F

When the pneumatic drive uses positive pressure,

the compressed gas creates an elastic resistance force,

which is greater at higher pressures and is close to 0

when the pressure in the closed chamber is equal to

atmospheric (Fig. 4a). Pneumatic actuation can

compensate for gravity by appropriate pressure in the

chambers, but deviations from the equilibrium

position lead to resistance fluctuations due mainly to

the increased pressure and increased stiffness of the

compressed gas (Fig. 4b). The advantage here is the

theoretically unlimited magnitude of the driving

force.

When the pneumatic drive uses vacuum pressure,

the resistance force depends less on the imposed

deviations. In this case, when the vacuum pressure

approaches zero, the drive force increases, and the

stiffness of the drive decreases (Fig.5a). This leads to

a constant resistance force, independent of the

imposed deviations. If gravity is compensated by a

vacuum pressure close to 0, in the case of deviations

from the equilibrium position, the force of interaction

remains almost constant, and small deviations are the

result of changes in the moment of gravity (Fig.5b).

The main advantage of the vacuum drive is the low

stiffness of the drive, which reaches its minimum

when the driving force is highest. The disadvantage

of this approach is the limitation in the maximum

value of driving force. This can be corrected by

‐10

‐8

‐6

‐4

‐2

0246810

[N]

[s]

pb=0 pb=14kPa

pb=40kPa pb=70kPa

pb=100kPa

‐10

‐8

‐6

‐4

‐2

0246810

[N]

[s]

Fp Fg Fp+Fg

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

408

increasing the active area of the pneumatic actuator

on which the atmospheric pressure acts. However, the

increased area leads to a change in other mechanical

parameters.

5 CONCLUSION

In the present work, an exoskeleton of the upper limb

intended for rehabilitation and training is studied. The

aim of the work is to find and evaluate an appropriate

exoskeleton solution that provides performance on

the one hand and transparency and natural safety on

the other. Therefore, a pneumatic drive is proposed in

the work, which is evaluated by comparing the

positive pressure drive with the vacuum pressure

drive. To assess transparency, the interaction force

between the patient and the exoskeleton in passive

mode is examined.

Simulations were performed with harmonic

movement imposed by the patient in one joint of the

exoskeleton. The interaction force between the

patient and the exoskeleton was assessed as a result

of the gravity of the exoskeleton and the pneumatic

force. In this case, the torque generated by the elastic

forces in the closed chamber of the pneumatic

actuators is used to compensate for the torque due to

gravity. The interaction force at the end effector is

estimated for cases of pneumatic propulsion with

pressure higher than atmospheric and with vacuum

pressure.

Assessments show that an increase in positive

pressure leads to increased stiffness and higher values

of the interaction forces. This allows for better

efficiency when performing operations in "robot in

charge" mode. Vacuum pressure reduces stiffness and

leads to small deviations in the interaction force and

from there to higher transparency and patient safety.

However, low stiffness is associated with a weak

force response and low efficiency.

The combination of safety requirements on the

one hand and the efficiency requirements on the other

can be achieved through pneumatic actuators that

allow a wide range of control pressures. The subject

of the future work of the authors is the development

and experimentation of pneumatic drive, which

allows adjusting the stiffness in a wide range.

ACKNOWLEDGEMENTS

This work has been accomplished with the financial

support by the Grant No BG05M2OP001-1.002-

0011-C02 financed by the Science and Education for

Smart Growth Operational Program (2014-2020) and

co-financed by the European Union through the

European structural and Investment funds.

REFERENCES

Manna S. K., Dubey V. N., (2018). Comparative study of

actuation systems for portable upper limb exoskeletons,

Medical Engineering and Physics, 60, 1–13.

Jarrasse, N., T. Proietti, et al., (2014). Robotic

Exoskeletons: A Perspective for the Rehabilitation of

Arm Coordination in Stroke Patients, Frontiers in

Human Neuroscience, Vol.8, Art.947, 1-13.

Veneman, J.F., R. Ekkelenkamp, et al., (2006). A series

elastic- and bowden-cable-based actuation for use as

torque actuator in exoskeleton-type robots, The Int.

Journ. of Rob. Research, vol. 25(3), 261-281.

Courtois G., Chevrie J., Dequidt A., Bonnet X. and Pudlo

P. (2021). Design of a Rehabilitation Exoskeleton with

Impedance Control: First Experiments. Proc.of the

18th Int. Conf. on Informatics in Control, Automation

and Robotics – ICINCO 2021, 469-476. DOI:

10.5220/0010580004690476.

Morales R., et al., (2011). Pneumatic robotic systems for

upper limb rehabilitation, Med. Biol. Eng. Comput. 49,

1145–1156.

Daerden Fr. and Lefeber D., (2002). Pneumatic Artificial

Muscles: actuators for robotics and automation. Europ.

J. of Mech. and Environmental Engineering; 47,1:1–11.

Nikolov S., V. Kotev, K. Kostadinov, F. Wang, C. Liang,

and Y. Tian, (2016). Model-based design optimization

of soft fiber-reinforced bending actuators," in Proc.

IEEE Int. Conf. Manipulation, Manuf. Meas.

Nanoscale, pp. 136-140.

Yang D., M. S. Verma, E. Lossner, D. Stothers, G. M.

Whitesides, (2017). Negative-pressure soft linear

actuator with a mechanical advantage. Adv. Mater.

Technol., vol.2, issue 1, pp.1600164 1-6.

Matthew A., Robertson and Jamie Paik, (2017). New soft

robots really suck: Vacuum-powered systems empower

diverse capabilities. Science Robotics, vol. 2, no.9, 30.

August 2017, doi: 10.1126/scirobotics.aan6357.

Mendoza Mijaíl Jaén, Samuel Dutra Gollob, Diego Lavado,

Bon Ho Brandon Koo, Segundo Cruz, Ellen T. Roche

and Emir A. Vela, (2021). A Vacuum-Powered

Artificial Muscle Designed for Infant Rehabilitation.

Micromachines, 12 (8), 971. doi: 10.3390/mi12080971.

Tawk, C., Spinks, G. M., in het Panhuis, M. & Alici, G.

(2019). 3D Printable Linear Soft Vacuum Actuators:

Their Modeling, Performance Quantification and

Application in Soft Robotic Systems. IEEE/ASME

Transactions on Mechatronics, 24 (5), 2118-2129.

Chakarov D., Veneva I., Tsveov M., Mitrouchev P., Venev

P. (2019), Design of a Two Arms Exoskeleton as Haptic

Device for Virtual Reality Applications, Lecture Notes

in Mech. Eng., Springer Nature, Chapter 25, 252-262.

Comparative Study of a Vacuum Powered Upper Limb Exoskeleton

409

Chakarov, D., Veneva, I., Venev, P., Tsveov M, (2021).

Evaluation of the capabilities of a hybrid driven

exoskeleton in passive mode of interaction. Pros of the

18th Int. Conf. on Informatics in Control, Automation

and Robotics, ICINCO 2021, 442-449. DOI:

10.5220/0010569004420449

Abane A., Guiatni M., Fekrache D., Merouche S., Otmani

A., Tair M. and Ababou N. (2016). Mechatronics

Design, Modeling and Preliminary Control of a 5 DOF

Upper Limb Active Exoskeleton. Proc. of the 13th Int.

Conf. on Informatics in Control, Automation and

Robotics – Vol. 2: ICINCO 2016, 398-405. DOI:

10.5220/0005984203980405.

Melchiorre M., Sabatino Scimmi L., Mauro S. and

Pastorelli S. (2018). Influence of Human Limb Motion

Speed in a Collaborative Hand-over Task. Proc. of the

15th Int. Conf. on Informatics in Control, Automation

and Robotics – Vol. 2: ICINCO 2018, 349-356. DOI:

10.5220/0006864703490356

Bembli, S., Haddad, N. and Belghith, S., (2019). A

Terminal Sliding Mode Control using EMG Signal:

Application to an Exoskeleton- Upper Limb System.

Proc. of the 16th Int. Conf. on Informatics in Control,

Automation and Robotics, Vol.2: ICINCO 2019, 559-

565. DOI: 10.5220/0008071905590565

Czmerk, A., A. Bojtos, (2017). Stiffness investigation of

pneumatic cylinders, 59th Ilmenau Scientific

Colloquium, Technische Universität Ilmenau, 11 – 15

September, 2017, 1-7, URN: urn:nbn:de:gbv:ilm1-

2017iwk-148:6.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

410