Mutual Relative Localization in Heterogeneous Air-ground Robot Teams

Samet G

uler

I. Emre Yıldırım

and H. Halid Alabay

Dept. Electrical and Electronics Eng., Abdullah G

ul University, Barbaros, Kayseri, 38080, Turkey

Keywords:

Heterogeneous Multi-robot Systems, Relative Localization, Bayesian Filtering.

Abstract:

Air and ground robots with distinct sensing characteristics can be combined in a team to accomplish de-

manding tasks robustly. A key challenge in such heterogeneous systems is the design of a local positioning

methodology where each robot estimates its location with respect to its neighbors. We propose a ﬁltering-

based relative localization algorithm for air-ground teams composed of vertical-take-off-and-landing drones

and unmanned aerial vehicles. The team members interact through a sensing/communication mechanism rely-

ing on onboard units, which results in a mutual connection between the air and ground components. Exploiting

the supplementary features of omnidirectional distance sensors and monocular cameras, the framework can

function in all environments without ﬁxed infrastructures. Various simulation and experiment results verify

the competency of our approach.

1 INTRODUCTION

Heterogeneous multi-robot systems (HMRS) offer

unparalleled advantages in various tasks which re-

quire a collection of distinct sensing and manipulation

capabilities such as area coverage, search and rescue,

collaborative transportation, and signal source local-

ization (Kushleyev et al., 2013; Staub et al., 2017;

Tokekar et al., 2016; Manyam et al., 2016; Grochol-

sky et al., 2006; Vidal et al., 2002; Yu et al., 2015).

In a HMRS, each individual robot acquires a local

sensory information from the environment with its

unique sensing capabilities. For instance, for a map-

ping objective, a set of aerial robots can collect vi-

sual representation of the environment while the lo-

cal occupancy properties can be sensed by a group of

ground robots. Then, the acquired data can be fused

online to build a uniﬁed map, improving the efﬁciency

and robustness compared to the homogeneous MRS

approaches (Li et al., 2016; Mueggler et al., 2014;

Kaslin et al., 2016).

Estimation of relative positions between team

members in a MRS has been an active research area

in the last decade. Traditional localization methods

for HMRS rely on the existence of infrastructures

which provide an absolute frame such as GPS and

motion capture (mocap) systems. Such approaches

lose validity in several real-life conditions, e.g., in

GNSS-denied environments or rooms without mocap

https://orcid.org/0000-0002-9870-166X

https://orcid.org/0000-0001-8035-0569

https://orcid.org/0000-0001-5360-3655

Figure 1: A sample heterogeneous team composed of ﬁve

UGVs and a drone.

systems. To remove this fundamental necessity, the

relative quantities between the team members should

be estimated with the onboard perception capabili-

ties. A common approach is to fuse distance sensors

with proprioceptive onboard sensors such as IMU

(Kia et al., 2016; Wallar et al., 2018; Prorok et al.,

2011; Hepp et al., 2016; Kim and Kim, 2013; Nguyen

et al., 2021). Since most distance sensors (e.g., ultra-

sonic and laser-based) provide one-directional mea-

surement data with limited FOV, a collection of those

sensors are implemented on the robots or in the en-

vironment to enlarge the operation zone of the robots

in a MRS (Kim and Kim, 2013). On the other hand,

ultrawideband (UWB) sensors offer unparalleled ad-

vantages in mobile robot localization thanks to their

omnidirectional distance measurement with high ac-

curacy and precision (Hepp et al., 2016; Wallar et al.,

2018). However, one may lose the observability of

304

Güler, S., Yıldırım,

I. and Alabay, H.

Mutual Relative Localization in Heterogeneous Air-ground Robot Teams.

DOI: 10.5220/0011267800003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 304-312

ISBN: 978-989-758-585-2; ISSN: 2184-2809

the relative position with the distance only approaches

in leader-follower formations (van der Helm et al.,

2019).

Several works employed vision-based approach

for relative localization in MRSs. Early works in this

direction used tags with speciﬁc patterns mounted on

robots to discriminate the robots from the background

in camera images (Krajn

ık et al., 2014; Saska et al.,

2016; Roelofsen et al., 2015). With the recent devel-

opments in computer vision methods and computa-

tional units, the time required to detect sophisticated

object models has reduced signiﬁcantly, which en-

abled onboard detection of drones with deep learn-

ing techniques (Vrba and Saska, 2020). Although

high detection rates for onboard drone detection using

convolutional neural network (CNN) methods are re-

ported in several tasks, the distance estimation mech-

anisms show poor performance with vision-only ap-

proaches. These results call for the need for an inte-

gration of the distance and vision sensors for reliable

relative localization.

We address the relative localization objective in an

air-ground team which consists of a team of drones

and unmanned ground vehicles (UGV). We develop

a ﬁltering algorithm to estimate online the relative

positions between the UGVs by utilizing the percep-

tion feedback of the drones. Our algorithm relies

on the mutual interaction between the drone and the

UGVs, established by the robots’ onboard perception

and local inter-robot communication. Particularly, the

drones are commanded to hover around the desig-

nated locations on the UGV formation to provide the

UGVs with the bearing measurements required to per-

form estimation. We performed several simulations

and experiments with varying number of drones and

UGVs. The main contributions of the work are as fol-

lows. We propose a complete localization and co-

ordination framework for an air-ground robot team

by integrating the onboard distance and vision sens-

ing capabilities. Second, we propose a multi-rate ex-

tended Kalman ﬁltering (EKF) algorithm which man-

ages three measurement cases which occur as a re-

sult of the varying formation geometry of the HMRS.

Finally, we illustrate several simulation and exper-

iment results for the externally commanded UGVs

case and formation control case. Our work differs

from the previous HMRS applications (Staub et al.,

2017; Tokekar et al., 2016; Grocholsky et al., 2006;

Manyam et al., 2016; Vidal et al., 2002; Yu et al.,

2015) in two aspects. First, the main objectives in the

aforementioned works are path planning, map build-

ing or target tracking objectives with several infras-

tructure aids. Since our ultimate goal is to build safe

and efﬁcient swarms with arbitrary number of robots,

we aim at improving the situational awareness of the

robots in the swarm and focus on relative localization.

Second, we utilize communication and sensor fusion

by incorporating a visual sensor, UWB distance sen-

sors, and IMUs onboard of the robots for an improved

coordination between the air and ground entities. In

(Cognetti et al., 2014), a drone equipped with vision

sensors localizes a team of UGVs without any on-

board tags exploiting the vertical motion capability

of the drone. However, drones may lose tracking of

the UGVs in an operation. In our framework, UWB

sensors on board of the UGVs adds resiliency to the

HMRS by pursuing the localization when the drones

lose the UGVs in their image views.

The rest of the work is organized as follows. In

Section 2, we deﬁne the HMRS model and formulate

the localization problem. In Section 3, we propose

the ﬁltering and motion control algorithms. Section 4

demonstrates the simulation and experimental results

as well as a discussion on the applications. Finally,

Section 5 concludes the work.

2 OBJECTIVE

We consider a heterogeneous multi-robot system

(HMRS) of N + M + 1 robots, comprised of N +

1 non-holonomic UGVs R

, i ∈ {0,...,N} and M

drones D

, j ∈ {1, ... ,M}. The robots are desired

to move in coordination to accomplish a given ob-

jective. We focus on the design of a practical coor-

dination mechanism between the robots. Designing

such mechanisms in the absence of an infrastructure

such as motion capture (mocap) systems remains a

big challenge. Our goal is to devise a scalable and ro-

bust localization algorithm for the swarm that enables

the realization of the typical practical distributed for-

mation control algorithms.

To realize such a scheme without the aid of a GPS

or mocap system, each robot should utilize its on-

board capabilities and achieve a certain level of sit-

uational awareness. We assume that each UGV R

is equipped with UWB sensors to acquire the inter-

UGV distance measurements. Consider the common

motion model for a non-holonomic UGV R

as fol-

lows:

k+1

= p



cos(θ

),sin(θ

)



, (1)

k+1

= θ

+ ω

, (2)

where p





∈ ℜ

is the 2D position, θ

is the

heading angle, v

,ω

are the linear and angular speed

commands of R

, i ∈ {0,. .., N}, k ∈ N

is the time

step, and T

is the sampling time constant.

Mutual Relative Localization in Heterogeneous Air-ground Robot Teams

305

We assume that each drone D

is equipped with a

monocular camera together with a ﬂight control unit

for the low-level control. Assuming that the motion

in the roll and pitch axes are stabilized by the low-

level controller, we denote by ζ =



,ψ



∈ ℜ

the state vector of a drone D

, where x

are the 2D

coordinates and ψ

is the heading angle with respect

to a ﬁxed frame F

Our main objective is to design a robust localiza-

tion algorithm for the system components such that

each robot will be able to estimate or receive by com-

munication the relative quantities required for a coor-

dinated motion. We deﬁne the localization objective

as follows. A UGV R

, i = (1,. .., N) should esti-

mate the relative positions r

to its neighbors deﬁned

by an underlying constraint graph in the UGV team

in the ﬁxed frame F

. Simultaneously, the drones

should move in coordination with the UGVs and pro-

vide them with a perspective view and absolute sensor

measurements to be used in the relative position esti-

mations. Therefore, we aim at designing a Bayesian

ﬁltering algorithm and a formation control algorithm

for the UGVs so that they can estimate their relative

positions to their neighbors to move in coordination.

3 APPROACH

Our approach is divided in two parts below. First, we

design the localization algorithm for the UGVs stating

the assumptions on the drones’ motion. Second, we

present the drones’ formation control mechanisms.

3.1 Ground Robot Localization

We assign UGV R

as the leader which moves with

external commands or based on a path planning al-

gorithm. Typically, the leader UGV is equipped with

a better sensor suite than the other UGVs and deter-

mines suitable paths or waypoints for the entire team.

For instance, it can build a collision-free path for the

team with an onboard LIDAR sensor by assuming the

entire team constructs a disc with certain radius. Not-

ing that various path planning algorithms can be inte-

grated, we focus on the design of our relative local-

ization framework below.

Each follower UGV, R

, i ∈ {1,..., N}, uses the

inter-robot distance measurements and the feedback

signal received from the drones D

to estimate its rel-

ative position r

towards R

. Assuming that all UGVs

move on a 2D plane, we deﬁne the relative position

system model between R

and R

, i ∈ {1,..., N}, as

follows:

k+1

= x







cos(x

) − u

cos(x

)

sin(x

) − u

sin(x

)







, (3)

where x



)

,θ



is the state vector, u =



,ω



is the input vector for the two-robot

system

{

}

, and r





∈ ℜ

is the rela-

tive position seen by R

in the ﬁxed frame F

Furthermore, the objective of a drone

, j ∈ {1,...,M}, is to detect and follow the

pair {R

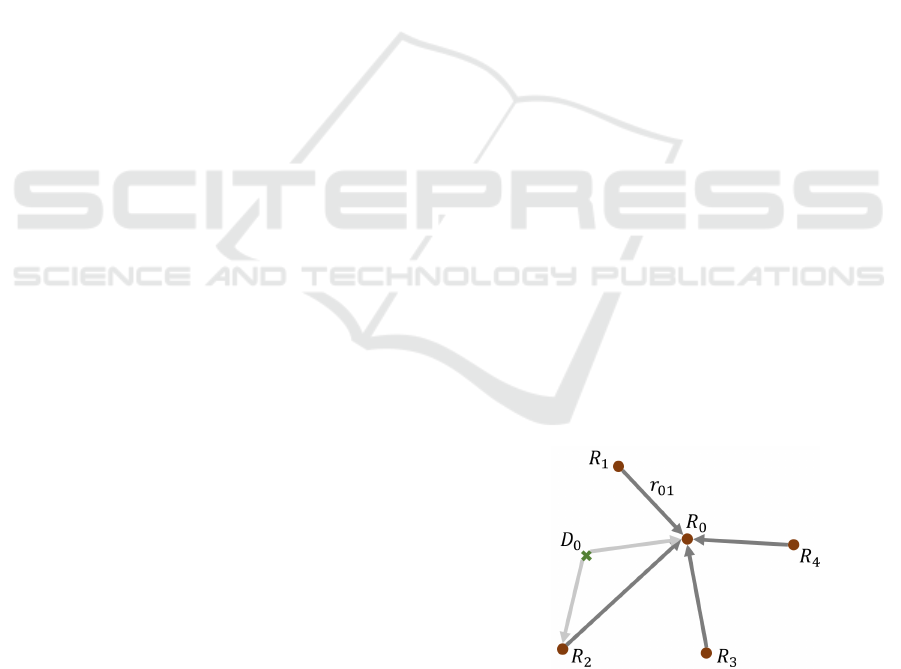
} where i ∈ {1, ...,N} (Fig. 2).

Drone D

changes the index i in its leader

list {R

} with a certain time period such as

({R

},{R

},. .., {R

N−1

},{R

},. ..)

based on a schedule which will be designed in

Section 3.2. During an operation, all drones ﬂy with

a ﬁxed heading in the ﬁxed frame F

, i.e., ψ

for some arbitrary constant

ψ. Thus, the constant

orientation of the drones serves as the absolute

coordinate frame provider for the entire MRS. That

is, the x − y plane of the drone’s body coordinate

frame is utilized as the global frame. To maintain

the constant heading during an operation, the drones

may utilize their onboard magnetometers or a set

of patterns in the environment. For instance, if the

team is intended to operate in a certain environment

with low magnetic deviation, the drones may trust

their magnetometers which are available in most

commercial ﬂight control units.

Denote the bearing angles between R

and R

, i ∈

{1,..., N}, by φ

= atan(r

). A drone D

aims at

calculating and broadcasting the bearing angles φ

and

heading angles θ

of the UGVs. For this purpose, the

ground robots are equipped with certain patterns over-

Figure 2: The proposed localization graph among a team of

ﬁve UGVs and a drone projected onto a 2D plane. UGV

serves as the leader for the team while each of the other

UGVs R

, i ∈ {1,...,N}, acts as the ﬁrst follower and de-

tects and estimates their relative positions toward R

. Each

drone D

, j ∈ {1,..., M}, acts as the second follower and

estimates its relative positions toward R

and a follower

, i ∈ {1, ..., N} at any time.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

306

head, e.g., qr code, so that their heading and bear-

ing angles can be acquired by the drone’s camera

(Fig. 1). For convenience, drone D

is assumed to

ﬂy at a sufﬁciently high altitude ¯z so that it can de-

tect a pair of robots {R

} by its camera. Such a

suitable margin for ¯z can be found empirically. More-

over, each follower UGV R

, i ∈ {1,...,N}, measures

the distances d

= kr

k and the inter-UGV distances

= kr

i j

k = kp

− p

k from the onboard UWB sen-

sors. Therefore, the observed variables are the dis-

tances d

, the heading angles θ

, and the bearing an-

gles φ

To estimate r

by robot R

, i ∈ (1,...,N), we use

a multi-rate EKF algorithm with three measurement

models. Based on the availability of the measure-

ments broadcast by drone D

, robot R

performs the

update stage using one of the following models:













,φ

,θ



, if sw = 1



,θ



, if sw = 2

, if sw = 3

(4)

where the switching signal sw denotes the drone’s

measurement mode. Denote the set of the pairs of

UGVs detected by the drones at any time instant by

S =

{

.. .{R

}. ..

}

, i ∈ {1, ...,N}. Then, the mea-

surement model of UGV R

, i ∈ {1,..., N}, at that

time instant is determined based on the following

rules:

• (sw=1) If {R

} ∈ S , we set sw = i, which im-

plies the bearing φ

is measured. Thus, the de-

tected robot R

uses the ﬁrst measurement model

which includes the distance d

and bearing φ

to-

ward R

, the self heading θ

, and the heading θ

of R

• (sw=2) If {R

} /∈ S and S 6=

0, the UGV

uses the second measurement model where

the bearing

toward R

is calculated artiﬁ-

cially by using the formation geometry as fol-

lows. Consider Fig. 3 where two UGVs R

follow a leader UGV R

. Denote the internal

angles formed by the triangles T





and





by α

and α

, respectively. By as-

sumption, we exclude the collinear robots case,

thus α

,α

are well-deﬁned. If {R

} ∈ S and

thus β

is measured at a given time instant, then

the bearing angle β

for all robots R

,i 6= j that

are on the right half plane of the line l

(the green-

shaded area in Fig. 3) can be calculated as follows:

= β

+ π − α

− α

where

= arctan(

1 − γ

,γ), γ =

+ d

− d

Figure 3: Calculation of the bearing angles for the UGVs

not detected by the drones.

Similarly, α

can be calculated. Likewise, the

bearing angles which lie on the left-half-plane

of the line l

can be calculated using the same

method.

• (sw=3) If S ≡

0, i.e., none of the drones can

see a UGV pair {R

} for any i ∈ {1, ...,N},

then all drones broadcast a Null message, mean-

ing that all UGVs perform the iteration with the

third measurement model by using the UWB dis-

tances only.

A pseudocode for the estimation algorithm of

robot R

is given in Algorithm 1. This algorithm har-

monizes the sensing, communication, and ﬁltering ca-

pabilities of the robots. To summarize, each UGV

performs the usual EKF prediction step followed by

the selection of the measurement model at the time

instant k which determines the update step. Particu-

larly, the linearized measurement model matrix is up-

dated based on the measurement model of the UGV.

We omit the details of the EKF algorithm for the sake

of space, which can be found in (Thrun et al., 2005).

In the proposed system, each UGV R

estimates its

relative position to R

independently. In this sense,

our application differs from the collaborative local-

ization in which all team members update the same

state vector estimate in a centralized manner.

Algorithm 1: EKF for robot R

Require: Previous state and covariance estimate

Ensure: Current state and covariance estimate

1: Prediction step

2: if Measurement model 1 then

3: y



,φ

,θ



4: else if Measurement model 2 then

5: y



,θ



6: else if Measurement model 3 then

7: y

= d

8: end if

9: Update step

10:

← New state estimate

11: Σ

← New covariance estimate

Mutual Relative Localization in Heterogeneous Air-ground Robot Teams

307

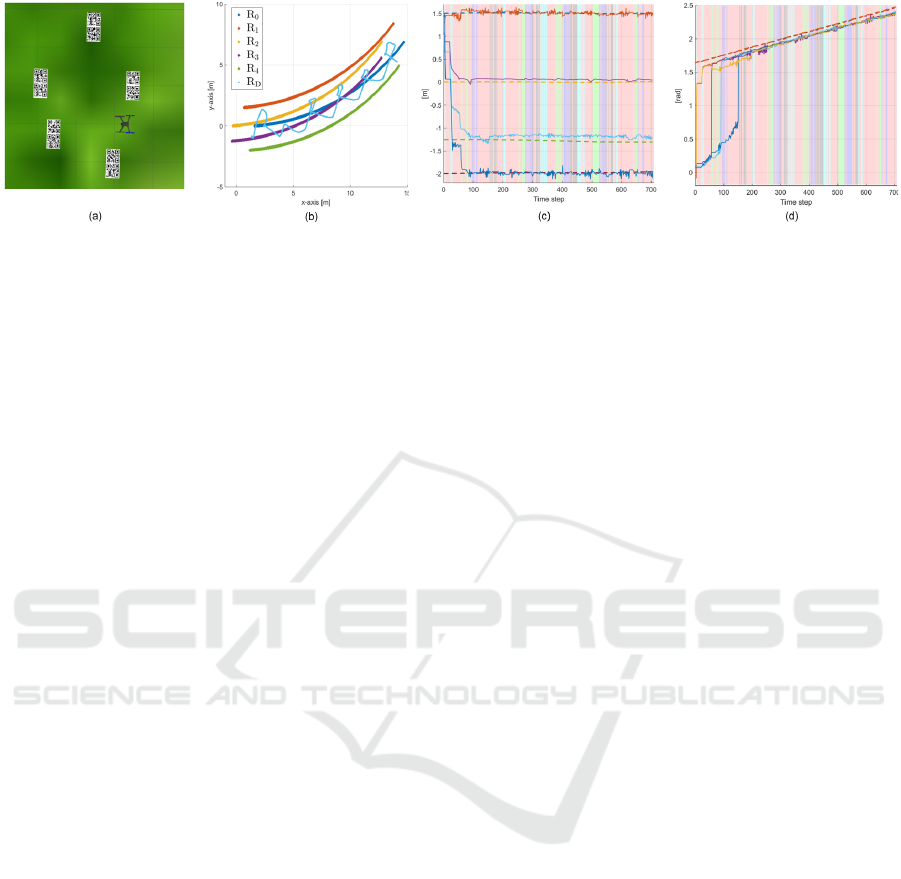
Figure 4: (a) A top view of the simulation setup; (b) traces of the robots; (c) relative position estimate; (d) heading angle

estimations.

3.2 Drone Localization and Control

Each drone D

, j ∈ {1,..., M} estimates its planar po-

sition with respect to the UGVs by using its onboard

camera sensor. As the second follower in the un-

derlying graph, a drone D

aims at hovering on the

midpoints m

between the pair of UGVs {R

}, i ∈

{1,..., N} with respect to the following schedule. At

the initial time step k = 0, the drones are commanded

to track the midpoints m

,. .., m

. To provide ev-

ery R

with its bearing toward R

, it is desired to visit

all midpoints m

, i ∈ {1,...,N} periodically by the

drones. We denote the time spent at a midpoint by

and set it as a design constant. Therefore, at the

time instants k = bk

, b ∈ N

, the drones switch their

commanded midpoints to m

b+1

b+2

,. .., m

b+M

until

N = b+ M, where N is the total number of the UGVs.

When N = b + M + 1, the commanded midpoints for

the drones is switched back to m

,. .., m

When hovering on the midpoints m

, the drones

uses computer vision techniques to detect the spe-

cial patterns on the UGVs. When the drone detects

a pair {R

}, it calculates and broadcasts the head-

ing angles θ

,θ

and the bearing angle φ

and sets

the parameter sw accordingly. Remarkably, since the

drone maintains a constant heading

ψ during an oper-

ation, the bearing angle φ

is calculated with respect

ψ which serves as the absolute north for the entire

team. Furthermore, the drones use the desired forma-

tion geometry to calculate the control signal required

to move between the midpoints. In the next section,

we apply the typical proportional controller to control

the drones’ motions on the horizontal plane, noting

that more advanced control algorithms can be applied

to control the drones’ motions with higher precision.

4 RESULTS

We evaluated the proposed framework both in simula-

tions and real experiments. We aimed at demonstrat-

ing the applicability of the framework and its integra-

tion into formation control algorithms.

4.1 Simulations

We used a Gazebo environment including Rosbot

UGVs and Iris drones integrated to the ROS inter-

face. We mounted two qr code patterns on each

Rosbot to be able to detect its heading angle by a

mono camera attached at the bottom of the drone.

The UGVs were accepting linear and angular veloc-

ity inputs and placed in a hexagon formation with

the leader (R

) in the front (Fig. 4a). Each follower

UGV performed relative position estimation indepen-

dently obeying the state and observation models given

in Section 3.1. The drone implemented the px4 soft-

ware which accept the high-level planar velocity and

yaw commands by handling the low-level control. All

robots ran their estimation code at 20 Hz. We ac-

quired the inter-UGV distances from the simulation

model, emulating the UWB distance measurements.

We show the traces of the robots and the relative

position and heading estimation results of a simula-

tion in Fig. 4. In this simulation, the UGVs moved

on an arc with constant linear and angular veloci-

ties, and the drone followed the midpoints periodi-

cally for t

= 8 seconds per robot with the sequence

,. ..) by utilizing a custom control

algorithm. In Fig. 4b and Fig. 4c, the green back-

ground shows the time instants where the drone ob-

serves the pair {R

}, the blue background for

}, the black background for {R

}, and the

cyan background for {R

}. The UGV R

cor-

rected its relative position estimation to the leader

(green colored robot) successfully when the drone de-

tected the robot pair {R

} and broadcast φ

the start of the operation (Fig. 4c). Meanwhile, the

other UGVs R

, and R

calculated their bearing

angles φ

,φ

, and φ

, respectively, by using the for-

mation geometry (as given in Section 3.1) and cor-

rected their relative position estimations accordingly.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

308

Figure 5: (a) A simulation setup with two drones; (b) Paths

of the robots in an arc motion test.

On the other hand, every follower UGV corrects its

own heading estimation once the drone visits its cor-

responding midpoint (Fig. 4d). The main reason for

the undetected time zones (red background) was the

switching motion of the drone between the midpoints.

Remarkably, although the total time without UGV de-

tection was almost half of the simulation time, the

framework showed high performance in estimating

the actual relative positions.

Next, we used two drones and ﬁve UGVs in 11

simulations to demonstrate the scalability of our ap-

proach (Fig. 5). The ﬁrst drone is assigned to de-

tect the UGVs R

, and R

, and the second drone

aims at detecting the UGVs R

, and R

. The fol-

lower UGVs R

, i ∈ {1, ...,4}, used the EKF outcome

to maintain their desired relative positions toward the

leader R

in a hexagon formation. We deﬁne the esti-

mation root mean square errors (RMSE) by

∑

k=1



i j

− r

i j



, (5)

where K is the total time steps during an experi-

ment,

are the relative pose estimations of the

ith UGV’s EKF for the x and y axes, respectively,

with j ≡ {x,y} denoting the coordinate axis. We ob-

served that e

remained below 0.1 meters for all i, j

in all tests. We did not observe signiﬁcant perfor-

mance variation with the change in the drone’s fol-

low time t

. Compared to the ﬁrst set of simulations,

the lower estimation errors stemmed from the fact that

each drone is responsible for two UGVs, which in-

creased the time duration spent on top of each UGV.

4.2 Experiments

The experimental setup consisted of a custom-built

drone with an F450 frame and three non-holonomic

UGVs (two Rosbots and a Turtlebot) (Fig. 6). A Ros-

bot was assigned as the leader (R

), and the other

Figure 6: The experimental setup consisted of a custom-

built drone of diameter 45cm equipped with a Pixhawk

ﬂight controller together with two Rosbot and a Turtlebot

UGVs.

UGVs were to estimate the relative positions r

Each UGV was equipped with calibrated Decawave

ultrawideband distance sensors at the center and two

qr code patterns on the top. A Raspberry Pi4 with

a camera performed UGV detection and high-level

computations on the drone while the low-level con-

trol was handled by a Pixhawk 4 ﬂight controller.

We collected the ground truth position data and con-

trolled the drone’s low-level motion with a Vicon mo-

tion capture system. We used the traditional com-

puter vision techniques and packages to detect the

qr code patterns. We observed that the camera de-

tected reliably the patterns at the distance interval

1.4 < h < 1.85 meters, and thus we ﬂew the drone

at the altitude h = 1.75 m.

In the ﬁrst set of experiments, the UGVs were

steered with exogenous velocity commands, and the

drone was controlled to follow the midpoints m

An experiment’s result is given in Fig. 7 where the

UGVs followed a straight path with v

= 0.05 m/s and

= 0 rad/s. The drone was commanded to follow

each midpoint for t

= 4 seconds before switching

to the other midpoint. In Fig. 7b and Fig. 7c, the

green background shows the time instants where the

drone observes both R

and R

, the blue background

for both R

and R

, and the black background for

all R

and R

. Finally, the light red background

shows that the drone cannot detect any UGV. Once

the drone detected the pair {R

} for the ﬁrst time

(the ﬁrst green time instant), the EKF of UGV R

uses

the ﬁrst measurement model in (4) which corresponds

to the locally observable instant, and the correct rela-

tive position and heading

are estimated. However,

could not be estimated until the drone could detect

the heading of R

at the time step 400 (the ﬁrst time

instant the blue background is seen in Fig. 7d). No-

tably, this time instant corresponds to the unobserv-

able mode, which we aim at studying in our future

Mutual Relative Localization in Heterogeneous Air-ground Robot Teams

309

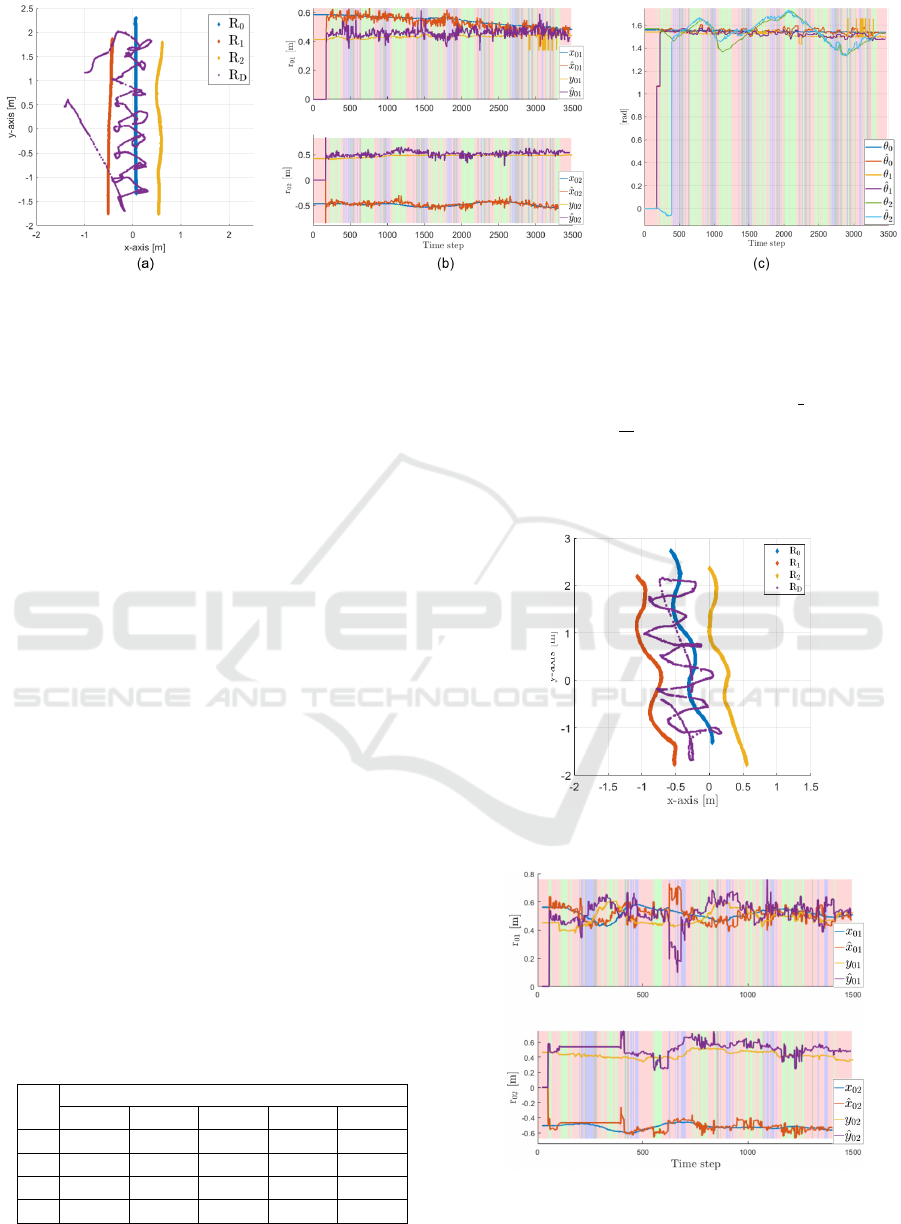
Figure 7: Results of an experiment with externally commanded UGVs: (a) Traces of the robots; (b) relative position estimates

; (c) heading angle estimations

. Background color codes: Green: {R

} detected; Blue: {R

} detected; Black:

} detected; Red: No pair detected.

works. We emphasize that the relative position and

heading estimations were initiated far from their cor-

rect values in this experiment. Nevertheless, the ﬁl-

ter succeeded to approach the correct values. Table 1

shows the RMSE for the relative position estimations

(5) in ﬁve experiments. We observed that the aver-

age error remained below 0.16 meters in all experi-

ments. We note that the drone’s high-level controller

was tuned to follow smoothly the midpoints m

In the second set of experiments, we used the per-

ception layer output as feedback to a formation con-

trol layer. Particularly, the follower UGVs tried to

maintain the desired relative positions r

des

to-

ward the leader R

by using the estimation outcomes

. We illustrate a formation control experiment in

Fig. 8 and Fig. 9 where R

and R

use custom con-

trol algorithms to maintain the desired relative poses

des

= [0.5,0.5]

des

= [−0.5,0.5]

m toward the

leader R

which is commanded externally to follow an

S-shaped path. Similar to the previous case, the drone

was controlled to switch between the midpoints m

and m

. We observed that the estimation performance

sufﬁced to maintain the desired formation as long as

the drone tracks the midpoints smoothly. We provide

further insights and a detailed discussion in the next

part.

In Fig 10, we show the RMSE for the formation

errors in eight experiments, which are deﬁned as fol-

Table 1: Relative position estimation RMSEs of ﬁve exper-

iments in meters.

Experiment No

1 2 3 4 5

0.133 0.132 0.135 0.104 0.157

0.099 0.188 0.115 0.089 0.137

0.109 0.098 0.105 0.106 0.135

0.110 0.191 0.115 0.120 0.155

lows:

i, j

∑

k=1



i j

− r

i j,des



where K is the total time steps during an experiment,

i is the follower UGV identity, and j ≡ {x,y} denotes

Figure 8: Traces of the robots in a formation control exper-

iment.

Figure 9: Relative position estimates

in a for-

mation control experiment. Background color codes:

Green: {R

} detected; Blue: {R

} detected; Black:

} detected; Red: No pair detected.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

310

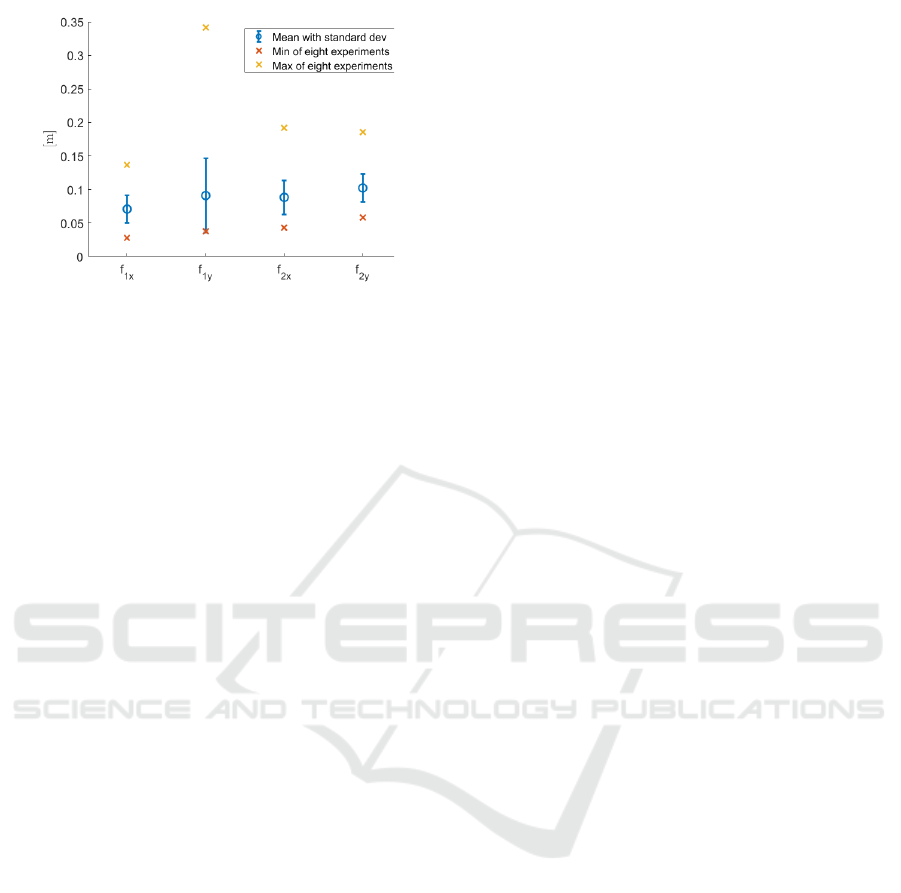
Figure 10: RMSE of eight formation control experiments.

the coordinate axis. Although we did not observe a

direct correlation between the error levels and the co-

ordinate axes or robots’ identities, we observed that

the average error in each axis remained below 0.12

meters, which proves the efﬁciency of the proposed

method.

We emphasize the unique difﬁculty of the relative

localization problem in a HMRS, particularly when

combined with a formation control algorithm. In con-

trast to the traditional localization objective where a

set of anchors located at known locations serve as bea-

cons to ﬁnd the location of a group of tag sensors, rel-

ative localization systems try to generate hypothesis

in the absence of an anchor. For this reason, the rel-

ative position estimators usually cannot generate cen-

timeter level accuracy as in the case of the traditional

estimators (Vrba and Saska, 2020). Nevertheless, we

observed satisfactory results both in the localization

and formation control simulations and experiments.

To overcome the issue of deviating drones due

to unobserved patterns, we developed a custom con-

trol algorithm for the UGVs that make use of the

leader velocity, which proved useful when the forma-

tion moved on arcs. In our primary tests, the drone

tended to deviate from the midpoints of the UGV

pairs, which we overcame by designing a control law

for the drone that utilized the single UGV detection as

well. Therefore, we emphasize that a designer should

ﬁne tune the drone controller before implementing the

proposed framework.

5 CONCLUSIONS AND FUTURE

WORK

We have addressed the relative localization in het-

erogeneous multi-robot systems, a key challenge for

the realization of such systems in a variety of ap-

plications. We have proposed a Bayesian ﬁlter

which estimates the relative positions among the

UGVs in certain conﬁgurations by utilizing their on-

board sensing and communication mechanisms to-

gether with the drones’ perception. We have demon-

strated through simulations and experiments that the

proposed method yields sufﬁcient estimation perfor-

mance under the case of intermittent perception feed-

back acquired from the aerial vehicle. A comprehen-

sive set of simulations and experiments have proven

that the estimation outcome yield sufﬁcient accuracy

for the formation maintenance without external in-

frastructures.

Future work may include a realization of the pro-

posed model with more UGVs and drones both in-

doors and outdoors. Also, a more robust control algo-

rithm design for the drone can improve the estimation

performance. Furthermore, we aim at carrying out

a detailed observation analysis for the system model

to investigate the observable and unobservable modes

for the varying cases of drone detection.

ACKNOWLEDGEMENTS

This paper has been produced beneﬁting from

the 2232 International Fellowship for Outstanding

Researchers Program of T

ITAK (Project No:

118C348). However, the entire responsibility of the

paper belongs to the owner of the paper. The ﬁnancial

support received from T

ITAK does not mean that

the content of the publication is approved in a scien-

tiﬁc sense by T

ITAK.

REFERENCES

Cognetti, M., Oriolo, G., Peliti, P., Rosa, L., and Stegagno,

P. (2014). Cooperative control of a heterogeneous

multi-robot system based on relative localization. In

2014 IEEE/RSJ International Conference on Intelli-

gent Robots and Systems. IEEE.

Grocholsky, B., Keller, J., Kumar, V., and Pappas, G.

(2006). Cooperative air and ground surveillance.

IEEE Robotics & Automation Magazine, 13(3):16–25.

Hepp, B., N

ageli, T., and Hilliges, O. (2016). Omni-

directional person tracking on a ﬂying robot using

occlusion-robust ultra-wideband signals. In 2016

IEEE/RSJ International Conference on Intelligent

Robots and Systems (IROS), pages 189–194.

Kaslin, R., Fankhauser, P., Stumm, E., Taylor, Z., Mueg-

gler, E., Delmerico, J., Scaramuzza, D., Siegwart, R.,

and Hutter, M. (2016). Collaborative localization of

aerial and ground robots through elevation maps. In

2016 IEEE International Symposium on Safety, Secu-

rity, and Rescue Robotics (SSRR). IEEE.

Mutual Relative Localization in Heterogeneous Air-ground Robot Teams

311

Kia, S. S., Rounds, S., and Martinez, S. (2016). Coopera-

tive localization for mobile agents: A recursive decen-

tralized algorithm based on kalman-ﬁlter decoupling.

IEEE Control Systems, 36(2):86–101.

Kim, S. J. and Kim, B. K. (2013). Dynamic ultra-

sonic hybrid localization system for indoor mobile

robots. IEEE Transactions on Industrial Electronics,

60(10):4562–4573.

Krajn

ık, T., Nitsche, M., Faigl, J., Van

ek, P., Saska, M.,

reu

cil, L., Duckett, T., and Mejail, M. (2014). A

practical multirobot localization system. Journal of

Intelligent & Robotic Systems, 76(3-4):539–562.

Kushleyev, A., Mellinger, D., Powers, C., and Kumar, V.

(2013). Towards a swarm of agile micro quadrotors.

Autonomous Robots, 35(4):287–300.

Li, J., Deng, G., Luo, C., Lin, Q., Yan, Q., and Ming,

Z. (2016). A hybrid path planning method in un-

manned air/ground vehicle (UAV/UGV) cooperative

systems. IEEE Transactions on Vehicular Technology,

65(12):9585–9596.

Manyam, S. G., Casbeer, D. W., and Sundar, K. (2016). Path

planning for cooperative routing of air-ground vehi-

cles. In 2016 American Control Conference (ACC).

IEEE.

Mueggler, E., Faessler, M., Fontana, F., and Scaramuzza,

D. (2014). Aerial-guided navigation of a ground

robot among movable obstacles. In 2014 IEEE Inter-

national Symposium on Safety, Security, and Rescue

Robotics (2014), pages 1–8.

Nguyen, T. H., Nguyen, T.-M., and Xie, L. (2021). Range-

focused fusion of camera-IMU-UWB for accurate and

drift-reduced localization. IEEE Robotics and Au-

tomation Letters, 6(2):1678–1685.

Prorok, A., Tom

e, P., and Martinoli, A. (2011). Accom-

modation of nlos for ultra-wideband tdoa localization

in single- and multi-robot systems. In 2011 Interna-

tional Conference on Indoor Positioning and Indoor

Navigation, pages 1–9.

Roelofsen, S., Gillet, D., and Martinoli, A. (2015). Recipro-

cal collision avoidance for quadrotors using on-board

visual detection. IEEE.

Saska, M., Baca, T., Thomas, J., Chudoba, J., Preucil,

L., Krajnik, T., Faigl, J., Loianno, G., and Kumar,

V. (2016). System for deployment of groups of un-

manned micro aerial vehicles in GPS-denied environ-

ments using onboard visual relative localization. Au-

tonomous Robots, 41(4):919–944.

Staub, N., Mohammadi, M., Bicego, D., Prattichizzo, D.,

and Franchi, A. (2017). Towards robotic MAGMaS:

Multiple aerial-ground manipulator systems. In 2017

IEEE International Conference on Robotics and Au-

tomation (ICRA). IEEE.

Thrun, S., Burgard, W., and Fox, D. (2005). Probabilistic

Robotics. MIT press.

Tokekar, P., Hook, J. V., Mulla, D., and Isler, V. (2016).

Sensor planning for a symbiotic UAV and UGV sys-

tem for precision agriculture. IEEE Transactions on

Robotics, 32(6):1498–1511.

van der Helm, S., Coppola, M., McGuire, K. N., and

de Croon, G. C. H. E. (2019). On-board range-based

relative localization for micro air vehicles in indoor

leader–follower ﬂight. Autonomous Robots, 44(3-

4):415–441.

Vidal, R., Shakernia, O., Kim, H., Shim, D., and Sastry, S.

(2002). Probabilistic pursuit-evasion games: theory,

implementation, and experimental evaluation. IEEE

Transactions on Robotics and Automation, 18(5):662–

669.

Vrba, M. and Saska, M. (2020). Marker-less micro aerial

vehicle detection and localization using convolutional

neural networks. IEEE Robotics and Automation Let-

ters, 5(2):2459–2466.

Wallar, A., Araki, B., Chang, R., Alonso-Mora, J., and Rus,

D. (2018). Foresight: Remote sensing for autonomous

vehicles using a small unmanned aerial vehicle. In

Hutter, M. and Siegwart, R., editors, Field and Ser-

vice Robotics, pages 591–604, Cham. Springer Inter-

national Publishing.

Yu, H., Meier, K., Argyle, M., and Beard, R. W. (2015).

Cooperative path planning for target tracking in ur-

ban environments using unmanned air and ground ve-

hicles. IEEE/ASME Transactions on Mechatronics,

20(2):541–552.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

312