A Hybrid Complexity Metric in

Automatic Software Defects Prediction

Laura Diana Cern

, Laura Dios

and Camelia S

erban

Faculty of Mathematics and Computer Science, Babes

Bolyai University, Cluj-Napoca, Romania

Keywords:

Complexity, Automatic Defect Prediction, Software Metrics.

Abstract:

Nowadays, software systems evolve in vast and complex applications. In such a complex system, a minor

change in one part may have unexpected degradation of the software system design, leading to an unending

chain of bugs and defects. Therefore, to keep track of implications that could appear after a change has been

applied, the assessment of the software system is of utmost importance. As a result, in this direction, software

metrics are suitable for quantifying various aspects of system complexity and predicting as early as possible

those parts of the system that could be error-prone. Thus, in this paper, we propose a comparative study of two

complexity metrics, Weighted Method Count and Hybrid Cyclomatic Complexity, regarding the prediction

of software defects. Speciﬁcally, the objective is to investigate whether using a hybrid metric that measures

the complexity of a class improves the performance of the fault prediction model. We conduct a series of

several experiments on ﬁve open source projects datasets. The preliminary results of our research indicate that

the proposed metric performs better than the standard complexity metric of a class, Weighted Method Count.

Moreover, the Hybrid Cyclomatic Complexity metric can be seen as a base for building a more complex and

robust complexity metric.

1 INTRODUCTION

Software systems became more and more complex,

and their size exponentially increased from one ver-

sion to another. Time constraints and resources of-

ten force some technical debt to be tolerated, thus

affecting in time the system quality (Holvitie et al.,

2018). Furthermore, any change comes with an un-

ending chain of adjustments in multiple places, which

hampers the maintenance and evolution of the sys-

tems. Trying to mitigate these, early detection and

prediction of software defects play an essential role

in the software industry in terms of quality measure-

ment.

It is well known that a good internal design struc-

ture has a strong positive impact on external quality

attributes (Fenton, 1994). Therefore, a desideratum

in designing a software system is to obtain ﬂexible

and easily adaptable software design to extend the

system’s functionality, with limited alteration to ex-

isting modules (Coad and Yourdon, 1991). A quanti-

https://orcid.org/0000-0002-6876-9065

https://orcid.org/0000-0002-6339-1622

https://orcid.org/0000-0002-5741-2597

tative examination of the software system’s internal

structure is of utmost importance to assure this re-

silience and malleability. As a result, software metrics

are beneﬁcial for quantifying essential aspects of the

assessment in this direction. By linking these met-

rics to those aspects that characterize a good inter-

nal structure of the software systems, we can predict

those design entities that are error-prone or defective.

Predicting and detecting software defects as early as

possible could overcome critical problems from ap-

pearing later in the software development lifecycle,

reduce (Holvitie et al., 2018) and thus guarantee a

good quality of the system. All these actions strongly

impact software testing activity and assure high main-

tainability of the software system in the cause.

Considering the aspects mentioned above regard-

ing the importance of automatic prediction of soft-

ware defects as early as possible in the development

cycle of the software systems, the pillars of this re-

search investigation are a metric proposal - Hybrid

cyclomatic complexity (CC). This metric aims to im-

prove the defect prediction accuracy and validate this

metric through an empirical approach. The initial re-

sults reveal that the HCC metric performs better than

the Weighted Methods Count (WMC), the metric used

Cern

au, L., Dios

an, L. and S

erban, C.

A Hybrid Complexity Metric in Automatic Software Defects Prediction.

DOI: 10.5220/0011269700003266

In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 433-440

ISBN: 978-989-758-588-3; ISSN: 2184-2833

433

to measure a class’s complexity. Moreover, the HCC

metric can be considered a more complex and robust

metric, which considers more aspects regarding the

complexity of a class.

To study the performance of this hybrid metric,

we used it for predicting the existence of bugs in

source code based on different combinations of soft-

ware metrics. We used a public data set containing

source code ﬁles from Java projects together with in-

formation and correlation with bugs for this predic-

tion. Our approach is platform agnostic (desktop/mo-

bile/web), meaning that the algorithm should perform

the same no matter what type of source code ﬁles are

analyzed.

The paper is organized as follows: Section 2 con-

tains related work. Section 3 describes the proposed

approach based on metrics, along with the Support

Vector Machine method. Section 4 describes the pro-

posed experiments of our investigation and the ob-

tained results. Section 5 discusses threats to validity

that can affect the results of our study. Finally, the

conclusions of our paper and further research direc-

tions are outlined in Section 6.

2 RELATED WORK

Numerous papers in the literature address the issue of

an automatic prediction of software defects. In the

following, we will brieﬂy describe some of these that

are similar to our approach.

In their article, (Ferzund et al., 2008) use ma-

chine learning to ﬁnd a predictor that will label a

ﬁle as clean or containing bugs. In order to accom-

plish their goal, they used the decision tree algo-

rithm. The data used for training the classiﬁer con-

sisted of a set of static code metrics and the bugs re-

lated to each ﬁle. The metrics that were used in this

study are the following: NEL(Number of Executable

Lines), CD(Control Density), CC(Cyclomatic Com-

plexity), PC (Parameter Count), RP(Return Points),

LVC(Local Variable Count) and ND(Nesting Depth).

Another example would be (Alshehri et al., 2018),

where the authors analyze the performance of a re-

duced set of change metrics, static metrics and a com-

bination of both categories as the predictors for fault-

prone code. Among the static code metrics they used

are LOC(lines of code), Max Complexity, Methods

per Class. At the same time, some of the change met-

rics used are Ave-LOC Added, LOC-Deleted, Refac-

torings(how many times a ﬁle was refactored) and

code churn. Their analysis used three machine learn-

ing algorithms: Logistic Regression, Naive Bayes,

and Decision Tree J48.

A comparison between multilayer deep feedfor-

ward networks and traditional machine learning al-

gorithms (decision tree, random forest, naive Bayes

and support vector machines) for predicting security-

related faults using software quality metrics was pre-

sented in (Clemente et al., 2018). According to their

ﬁndings, the deep learning algorithm performed bet-

ter in predicting security bugs. According to the au-

thors, the metrics used in this research are part of

three categories: object-oriented, complexity and vol-

ume, and among them are Cyclomatic Complexity,

Executable Statements, Declarative Statements, Com-

ment to Code Ratio.

A fault prediction model developed on a combi-

nation of three different ensemble methods learning

algorithms is proposed in (Kumar et al., 2017). The

authors used a heterogeneous ensemble method with

three rule combinations, one nonlinear and two lin-

ear, in the model’s development process. One of

the conclusions of their research is that a subset of

code metrics has a signiﬁcant impact on the accuracy

of the prediction rather than the whole set of code

metrics. This subset includes DIT(depth of inheri-

tence tree), WMC, CBO(Coupling between objects),

LCOM3(Lack of Cohesion of Methods), AVG-CC,

NOC(Number of Children), among other Chidamber

and Kemerer Java Metrics.

Unlike the methods mentioned above, (Erturk and

Sezer, 2016) proposed a solution for the software fault

prediction problem using a Fuzzy Inference System

(FIS) algorithm to build a predictive model. The

authors employed the Mamdani type FIS and the

McCabe code metrics in their research, representing

method-level metrics. According to their study, Er-

turk et al. claim that the FIS algorithm performs bet-

ter than the traditional machine learning algorithms,

which require historical data for the training phase.

3 METRICS BASED DEFECT

PREDICTION

In the following subsections, we resume the ar-

guments supporting our defect prediction approach

starting from the software system’s internal structure.

Furthermore, we survey the most relevant object-

oriented metrics found in literature, select some of

them to support our approach and then justify the se-

lection. For the prediction of software defects, we

will use an automatic algorithm based SVM (Vapnik,

1999), a supervised learning method.

ICSOFT 2022 - 17th International Conference on Software Technologies

434

3.1 Proposed Approach Description

One of the main goal of software assessment is aimed

at verifying whether the built system meets quality

factors such as maintainability, extensibility, scalabil-

ity and reusability. The axiom of (Fenton, 1994) re-

veals that: “a good internal structure of software sys-

tem assures its good external quality”. In this respect,

the main assessment goal is reduced to verifying if

there is conformity between the software system’s in-

ternal structure and the principles and heuristics of

good design, which are related to the internal qual-

ity attributes of the system design (such as coupling,

cohesion, complexity and data abstraction). In (Riel,

1996) is stated that such rules should be deemed as a

series of “warning bells that will ring when violated”

(Marinescu, 2002).

Thus, the software system’s internal structure’s

continuous assessment has to be made throughout the

entire software development lifecycle. As a result, in

this direction, software metrics are suitable for quan-

tifying essential aspects of the assessment. Therefore,

software metrics are suitable in the automation of the

assessment process and, at the same time, are used to

predict software defects earlier in the system devel-

opment. Prediction of software defects in the earli-

est possible phases leads to a reduction of the time in

their correction as well as the value of the technical

debts that were made during the development of the

system.

The Figure 1 describes our proposed approach.

3.2 Selected Metrics

3.2.1 Metrics Deﬁnition

Various metrics have been proposed so far, and new

metrics continue to regularly appear in the literature.

Among these, the metrics proposed by (Abreu, 1993),

(Abreu and Rogerio, 1994), (Chidamber and Ke-

merer, 1994), (Li and Henry, 1993), and the MOOD

metrics proposed by (Abreu, 1995) are the most used.

(Marinescu, 2002) has classiﬁed these metrics accord-

ing to four internal characteristics that are essential to

object-orientation: - i.e. coupling, inheritance, cohe-

sion and structural complexity.

In the current study, we are using the CC pro-

posed by (McCabe, 1976) to measure the complexity

of a method, DIT, and LCOM metrics proposed by

(Chidamber and Kemerer, 1994). These metrics are

related to inheritance, cohesion and structural com-

plexity as internal characteristics of a previously men-

tioned class.

In what follows, we provide the deﬁnitions of the

metrics used in our investigation:

• Weighted Methods per Class (WMC) metric is de-

ﬁned as the sum of the complexity of all methods

of a given class. The complexity of a method is

the cyclomatic complexity metric.

Cyclomatic complexity (CC) (McCabe, 1976) is

a measure of a module control ﬂow complexity

based on graph theory. A control ﬂow graph de-

scribes the logical structure of a software mod-

ule. Each ﬂow graph consists of nodes and edges.

The nodes represent computational statements or

expressions, and the edges represent the transfer

of control between nodes (Watson and McCabe,

1996).

Cyclomatic complexity is deﬁned for each mod-

ule to be e − n + 2, where e are the number of

edges and n are the number of nodes in the control

ﬂow graph.

• New Proposed Metric: Hybrid Cyclomatic Com-

plexity (HCC) is deﬁned by adding to the WMC

metric value the sum of the complexity of all in-

herited methods of a given class.

We recall here that one of this paper’s main goals

is to study the impact of a new metric in bug pre-

diction. This is deﬁned by an aggregated measure

quantifying complexity based on inheritance.

• Lack of Cohesion in Methods (LCOM) is deﬁned

by the difference between the number of method

pairs using common instance variables and the

number of method pairs that do not use any com-

mon variables.

• Depth of Inheritance Tree (DIT) is deﬁned as the

length of the longest path of inheritance from a

given class to the root of the tree;

3.2.2 Motivation for the Selected Metrics

In what follows, we bring forth our arguments for

metrics selection. These arguments are based on the

four internal characteristics of object-orientated pro-

gramming mentioned before on the impact of metrics

values on software quality.

Regarding the cyclomatic complexity metric, it is

tightly correlated to the number of alternative paths

the execution of one module can go through. Conse-

quently, a high cyclomatic complexity for a method

could imply that the method breaks the single respon-

sibility principle, has a low readability level and can

be hard to maintain. Another aspect that is mentioned

by (McCabe, 1976) is that this metric can be used as

a testing methodology where the number of test cases

for a module must be equal to the value of the cyclo-

matic complexity for that module. Thus, a high value

for the cyclomatic complexity metric indicates a low-

A Hybrid Complexity Metric in Automatic Software Defects Prediction

435

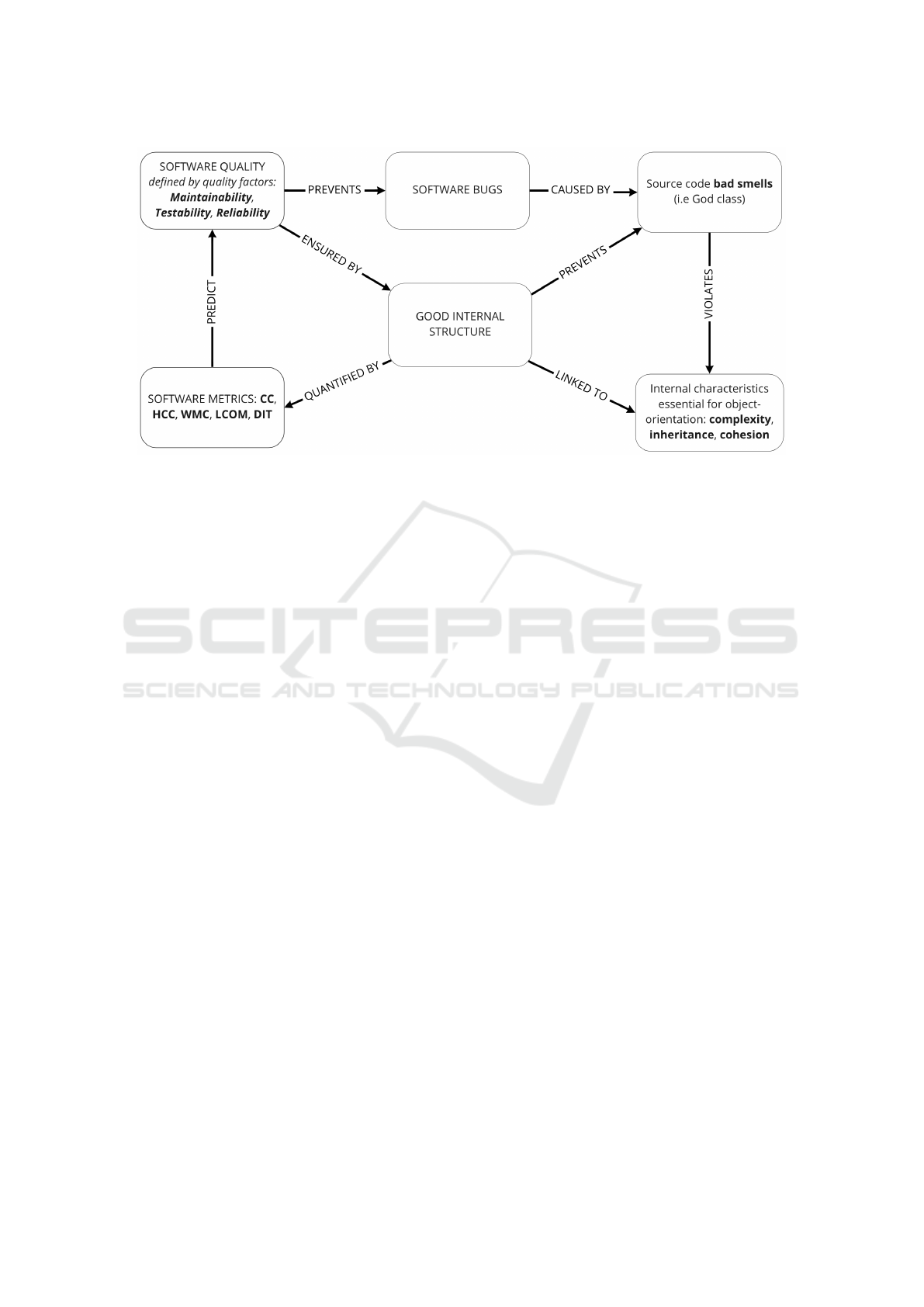
Figure 1: Motivation for our approach in defect prediction.

quality code that might involve difﬁculties in testing

and maintaining.

In order to extend the cyclomatic complexity met-

ric, we chose to use the depth of inheritance tree met-

ric because it is highly correlated to the complexity

of a class. A high value of DIT could have a nega-

tive impact on the understandability of the code be-

cause the logic is spread along in the inheritance path

of one class. In addition, the behaviour of a class

that a higher value of DIT is challenging to predict,

and its complexity should reﬂect the methods it in-

herits. Therefore we chose to study the performance

of a hybrid metric, HCC, a combination of the two

mentioned earlier. Besides these three metrics, we

chose to use LCOM as a feature for the fault predic-

tion model because it is also a cohesion related metric

and reﬂects the degree to which a class respects the

Single Responsibility Principle. Low cohesion may

imply that the complexity of the class is increased,

and therefore the probability for that class to contain

error-prone code is higher.

Moreover, we selected the W MC and DIT metrics

because they are metrics that characterise the com-

plexity degree of a class. In addition to these two,

we chose the LCOM metric because it indicates the

cohesion among a class, which directly impacts the

complexity of the class.

3.3 Machine Learning based Defect

Prediction

The problem of defect prediction is of signiﬁcant

importance during the maintenance and evolution of

software systems. It is essential for software develop-

ers to continuously identify defective software mod-

ules to improve the system’s quality. However, as the

conditions for a software module to have defects are

hard to identify, machine learning-based classiﬁcation

models are still developed to approach the problem

of defect prediction. For our research, we decided

to use the Support Vector Machine classiﬁer. The

main reason for our choice is that the data set is of

small size and it has only a few features. However,

various machine learning algorithms can be used to

detect potentially faulty source code based on soft-

ware quality metrics, including Decision Tree, Ran-

dom Forest, Naive Bayes or Fuzzy Inference System.

The signiﬁcant beneﬁt that these algorithms bring is

that by using them, detecting a bug or signalling a po-

tentially erroneous code becomes automated, without

the need for a human factor to check the metrics and

make judgments based on them.

The proposed approach for defect prediction is

brieﬂy described in Figure 2.

This study aims to explore the relationship be-

tween object-oriented metrics and fault proneness at

the class level. In this paper, a class from an object-

oriented design is labelled as “defect” if it contains at

least one bug related to this class was found by testing

the program. The dependent variable in the SVM al-

gorithm has two values: defect (1) or non-defect (0).

The values of selected metrics HCC, WMC, LCOM

and DIT act as independent variables.

Therefore, having deﬁned dependent variables

and independent variables, we want to investigate

which combination of metrics provides a more ac-

curate prediction. For this, we have deﬁned sev-

eral scenarios with different combinations of metrics:

W MC,DIT

, S

W MC,LCOM

, S

HCC,DIT

, S

W MC,LCOM,DIT

HCC,LCOM,DIT

ICSOFT 2022 - 17th International Conference on Software Technologies

436

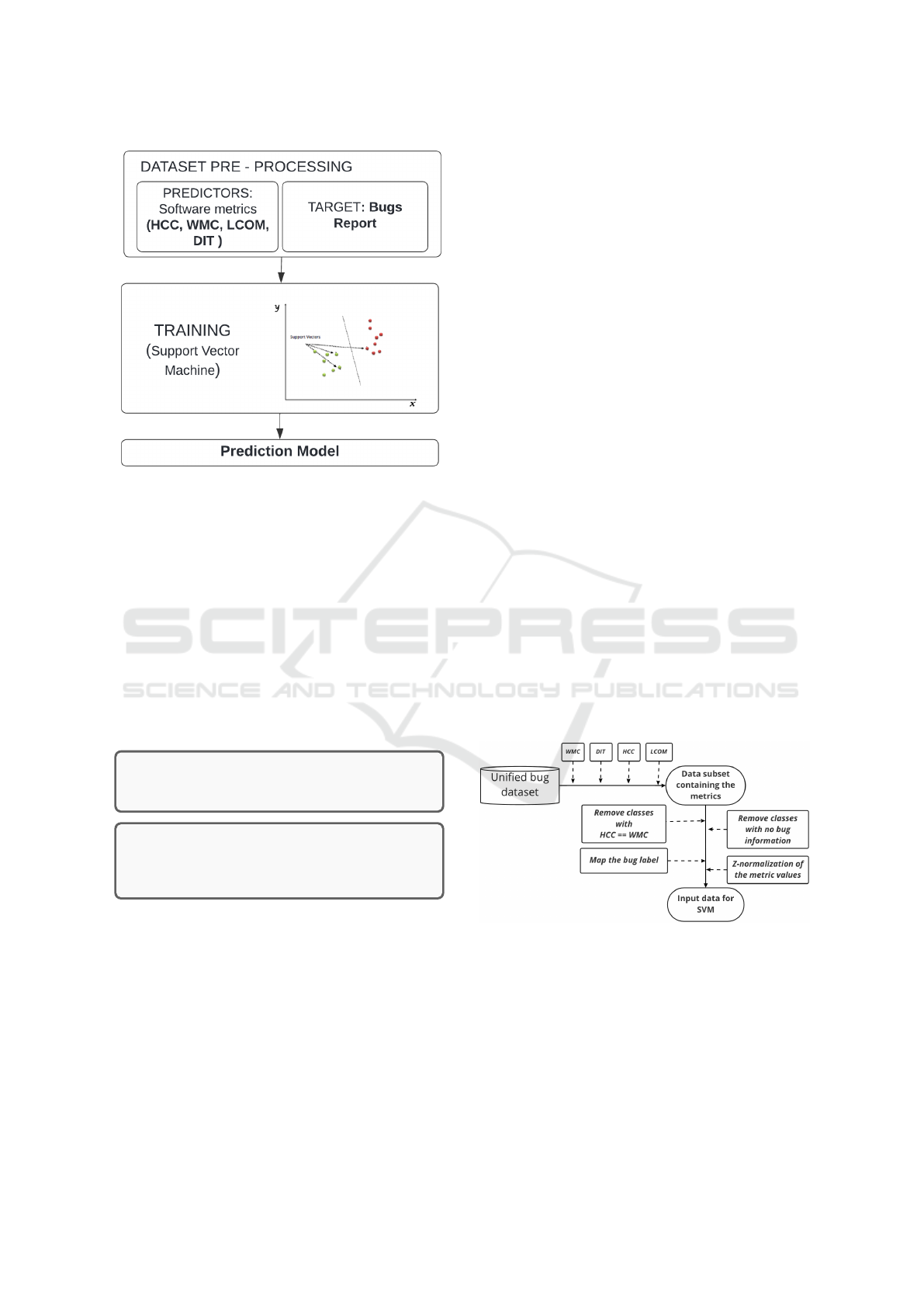
Figure 2: Proposed defect prediction approach.

4 EXPERIMENTS

4.1 Research Questions

Starting from the methodology proposed in Section

3, our empirical analysis aims to address two research

questions.

The proposed research questions aim to support

the understanding of the goals of the study with re-

spect to the methodology steps. Therefore, having

these into consideration, we formulate the following

research questions:

RQ1: How effective is the bug detection

method compared to expert inspections?

RQ2: Which code representation works

better: a representation based on W MC or

one based on HCC?

4.2 Data Set Description

The data set utilised in this paper is part of a more

extensive database collected by (Ferenc et al., 2018).

During this process, the authors computed a set of

source code metrics for source ﬁles from ﬁve public

databases: PROMISE, Eclipse Bug Dataset, Bug Pre-

diction Dataset, Bugcatchers Bug Dataset and Github

Bug Dataset. Consequently, one of the main attributes

of this database is that the deﬁnitions of the code met-

rics are the same amongst all the repositories, and

it can be used as input for building fault prediction

models. The uniﬁed database provided by Ferenc

et al. contains the following information about each

ﬁle: the name of the ﬁle, a set of source code met-

rics calculated using OpenStaticAnalyzer and a label

that speciﬁes the faulty/not-faulty state of the ﬁle (has

no bugs/has a number of bugs/not deﬁned). In build-

ing this data set, the authors assessed a list of elim-

inatory requirements. One example would be that

each project must incorporate information about the

bugs and their association with parts of the source

code. For example, when describing the Eclipse Bug

Dataset, the authors stated the following ”mapped de-

fects from the bug database of Eclipse 2.0, 2.1, and

3.0. The resulting dataset lists the number of pre and

post-release defects on the granularity of ﬁles and

packages that were collected from the BUGZILLA bug

tracking system.”(Ferenc et al., 2018). To obtain the

bug label, the authors merged the information about

the values of the metrics with the information about

the presence of a bug in a particular class. From this

dataset, we utilised a subset of ﬁles randomly selected

and the information about the presence of bugs and

the values of the LCOM code metric. In addition,

we must specify that our approach is an agnostic one

regarding the type of projects of which the analyzed

classes are part. Speciﬁcally, because the granularity

of the chosen software metrics is at the class level, the

analysis results are not impacted by the nature of the

project (mobile/desktop/web).

4.3 Data Set Pre-processing

Figure 3: Data pre-processing.

This section will describe the initial data’s process-

ing phases to become relevant input data for the SVM

algorithm. An overview of the whole process can

be seen in Figure 3. Therefore, in this phase of our

research, we computed the values of the Cyclomatic

Complexity (CC), Depth of Inheritance Tree and the

Hybrid Cyclomatic Complexity (HCC) for the subset

mentioned in the previous section. The Cyclomatic

Complexity metric was calculated using an external

A Hybrid Complexity Metric in Automatic Software Defects Prediction

437

tool, Checkstyle, which helps developers write code

according to a set of coding standards, amongst which

are the values for speciﬁc software quality metrics. In

the next step, after having the Cyclomatic Complexity

deﬁned for each class, we parsed each ﬁle again and

calculated the Hybrid Cyclomatic Complexity and its

DIT. Succeeding these ﬁrst two steps, we had the fea-

tures that were going to be employed in building the

prediction model using the support vector machine al-

gorithm: CC, HCC, DIT, LCOM and the bug label for

each class. The following steps are deﬁned by prepar-

ing the data in order to be suitable for training the

SVM algorithm. Firstly the classes that had no in-

formation about the existence of a bug were removed

from the dataset. Secondly, we removed the classes

with the CC equal to the HCC because our purpose

was to see if the HCC performs as a better predic-

tor for fault prediction. Next, because the SVM al-

gorithm classiﬁes the data in two subsets, in our case

faulty and not-faulty, every value bigger than one for

the bug label was transformed into 1. Therefore, after

these steps, the bug labels for each class would be 0

or 1. The ﬁnal step was to normalize the data, using

a standard scaler (sklearn) that removed the mean and

scaling to unit the variance (Mitchell and Learning,

1997).

4.4 Evaluation Criteria

In the validation stage, to measure the effectiveness of

the classiﬁcation, we compare the results from expert

inspection (that acts as ground truth) to those of our

automatic method.

The ground truth, constructed by experts, was

provided in the uniﬁed bug database, and it is part

of each public dataset (PROMISE, Eclipse Bug-

Dataset, Bug Prediction Dataset, Bugcatchers Bug-

Dataset and Github Bug Dataset). How the pres-

ence of a bug was determined and mapped to a

class/ﬁle depends on each repository. For ex-

ample, the Eclipse Bug Dataset was computed

by (Schr[Pleaseinsertintopreamble]ter et al., 2009).

Then, the authors mapped the defects from the bug

database of Eclipse to ﬁles and classes from the

source code. The information about the defects was

gathered from version archives of the project and bug

tracking systems (BUGZILLA, Jira). Finally, they

correlated the ﬁxes from the logs to the reported bugs.

Another example would be the mapping and fault data

collection presented by Hall et al. (Hall et al., 2014).

The authors used an Apache Ant script in order to col-

lect information about bugs and ﬁxes. Still, the pro-

cess is similar to the one presented before.

During the validation, we are interested in both

the correctness and the integrity of the categorisation

process. Therefore, three evaluation criteria are of in-

terest: precision, recall and speciﬁcity.

The number of items accurately labelled as faulty

(true positive) divided by the total number of items

labelled as possessing defects is the precision of the

positive class in our classiﬁcation problem (i.e. the

sum of true positives and false positives, which are

items without bugs but labelled by the model as be-

longing to the faulty category).

The capacity of a classiﬁcation model to correctly

discover erroneous elements (those items that con-

tain bugs) is referred to as recall (or sensitivity). The

model’s detection rate is the proportion of items pre-

dicted as faulty among those that actually contain

bugs. A negative result in a high-sensitivity classiﬁca-

tion model is beneﬁcial for ruling out problems. On

the other hand, when the answer is negative, a high

sensitivity model is reliable since it seldom misdiag-

noses items with problems.

The model’s ability to correctly classify the

healthy items (without bugs) is referred to as speci-

ﬁcity. The proportion of items that do not have bugs

and are classiﬁed as negative by the model is known

as model speciﬁcity. A positive prediction from a

model with high speciﬁcity is beneﬁcial for determin-

ing whether or not bugs are present. Conversely, a

positive prediction indicates a high likelihood of bug

presence.

4.5 Numerical Experiments

4.5.1 Setup of Experiments

In the data used for training and testing our predic-

tion model, we had the following distribution, 1484

entries for the training set and 1470 for the testing set.

The item distribution in these subsets was a balanced

one. They contain an equal number of source code

classes marked as having bugs and without bugs. For

the data normalization, we used the StandardScaler

from the sklearn Python library (Sta, ) and performed

a Z-normalization (Mitchell and Learning, 1997). We

used the C-Support Vector Classiﬁcation (SVC, ) al-

gorithm from the SVM sklearn module for the data

classiﬁcation. The kernel type used for this algorithm

was the linear one, and the value for the C parameter

was the default one, 1.0.

4.5.2 RQ1 - How Effective Is the Bug Detection

Method Compared to Expert Inspections?

A ﬁrst investigation is aimed to analyse the impact

of data representation how the code features involved

in our automatic classiﬁcation inﬂuence the quality

ICSOFT 2022 - 17th International Conference on Software Technologies

438

of bugs’ detection. Thus, in order to test our clas-

siﬁcation approach, we have considered the expert-

based constructed ground truth for each of the anal-

ysed codebases; afterwards, the proposed system was

run over the analysed applications, and the ﬁndings

were compared against the ground truth.

Table 1 presents our ﬁndings for the ﬁrst three sce-

narios by using the precision, recall and speciﬁcity

metrics. Those performance criteria were used to val-

idate the correctness of our approach from an empiric

point of view.

Table 1: The effectiveness of the classiﬁcation process in

terms of Precision, Recall and Speciﬁcity.

Scenario Precision Recall Speciﬁcity

W MC,LCOM

0.51 0.71 0.32

W MC,DIT

0.57 0.40 0.70

W MC,LCOM,DIT

0.79 0.46 0.88

By considering the precision and speciﬁcity cri-

teria, the best results are obtained in scenario

W MC,LCOM,DIT

, when all three metrics are considered

as features. We noticed that a data representation that

leaves out DIT metric is able of predicting a positive

output (item with bugs) – the classiﬁcation recall in

W MC,LCOM

is quite large – but those items are ac-

tually healthy ones – since the precision obtained in

this scenario is around 0.5, and the model speciﬁcity

is minimal.

We can also notice that by enlarging the feature set

(from S

W MC,LCOM

and S

W MC,DIT

to S

W MC,LCOM,DIT

respectively), both precision and speciﬁcity are im-

proving.

4.5.3 RQ2 - Which Code Representation Works

Better: A Representation based on W MC

or One based on HCC?

By taking into account that a code representation

without DIT metric is not appropriate, in what fol-

lows, just the DIT -based representations will be con-

sidered. We are interested in how HCC metric, in-

stead of the simple W MC one, inﬂuences the qual-

ity of the bug detection. Therefore, Table 2 ﬁgures

out our ﬁndings when the classiﬁer uses as inputs the

HCC, LCOM and DIT metrics.

Table 2: The effectiveness of the classiﬁcation process (in

terms of Precision, Recall and Speciﬁcity) by considering

the HCC-based code representation.

Scenario Precision Recall Speciﬁcity

HCC,DIT

0.72 0.39 0.85

HCC,LCOM,DIT

0.81 0.24 0.94

We can notice that in both scenarios, by using the

HCC metric instead of the simple W MC metric, the

classiﬁer is able to detect the faulty items better.

In the case of HCC and DIT based representa-

tion, the precision of our classiﬁer increases from 0.57

to 0.72. Furthermore, by enlarging the features by

knowledge about LCOM metric, the system’s preci-

sion rises to 0.81, revealing the potential of our novel

metric to contribute to better detection of faulty items.

We also notice an improvement in the model’s

speciﬁcity when the HCC metric is involved as a data

feature for our classiﬁer. The larger speciﬁcity value

indicates a better estimation of how likely the items

without bugs can be correctly ruled out. In both sce-

narios (S

HCC,DIT

and S

HCC,LCOM,DIT

) the number of

false positives is reduced to the corresponding W MC-

based scenarios (S

W MC,DIT

and S

W MC,LCOM,DIT

Regarding the recall value, even if its value is not

so good, the numerical results indicate that even if

there is no signiﬁcant difference between S

W MC,DIT

and S

HCC,DIT

, by involving the hybrid code metric,

the ability of the classiﬁer to detect bug items de-

creases by half. Indeed, a more sensitive model is

desired, but the most important characteristics remain

precision and speciﬁcity.

5 THREATS TO VALIDITY

Threats to Internal Validity. One threat to our ap-

proach’s validity is that we used only a limited num-

ber of metrics, cyclomatic complexity, depth of in-

heritance tree, lack of cohesion in methods and the

extended metric, hybrid cyclomatic complexity. We

chose these metrics because they are part of the same

category, complexity metrics. Another concern is that

the value of the hybrid metric (HCC) relies on the

value of the CC, which is computed using an external

tool, Checkstyle. Also, the algorithm used for these

experiments, SVM, may be considered a threat to the

internal validity of our results.

Threats to External Validity. One weak point of

our approach is the programming language limitation.

More precisely, the dataset contains only Java classes,

and the logic for computing the HCC relies on the

Java syntax when parsing the ﬁles. Another aspect

worth mentioning is that our prediction model was

built based on classes and features from different pub-

lic projects.

Threats to Construct Validity. In the validation

stage, we measure the efﬁcacy of the classiﬁcation

algorithm by comparing the result of the prediction

model with the initial values of the bug labels from the

uniﬁed bug dataset. One threat to this validation’s cor-

A Hybrid Complexity Metric in Automatic Software Defects Prediction

439

rectness is that the defect information from this uni-

ﬁed bug dataset comprises ﬁve public datasets. Each

of these datasets had a different process for mapping

the defects to the source code.

6 CONCLUSIONS AND FUTURE

WORK

One of the main goals of this research was to inves-

tigate whether a hybrid cyclomatic complexity met-

ric is better than the standard cyclomatic complexity

for a class (WMC). Our experiments concluded that

the SVM prediction models that included the hybrid

metric as a feature performed better than the one that

included the standard WMC metric. In addition, we

consider this hybrid metric to be a more complex and

elaborate one because it considers multiple aspects

concerning the complexity of a class.

Based on these preliminary results, we intend to

investigate the efﬁcacy of this metric on larger sets of

data to have a more in-depth analysis and formalise

the deﬁnition of the metric. Moreover, another as-

pect worth studying is the impact of other software

quality metrics combined with the hybrid metric on

the prediction model’s performance. Likewise, we

would like to analyse the sensibility of the results to

the change of the machine learning algorithm.

REFERENCES

StandardScaler. https://scikit-learn.org/stable/modules/

generated/sklearn.preprocessing.StandardScaler.

html/. [Online; accessed 17-February-2022].

SVC. https://scikit-learn.org/stable/modules/generated/

sklearn.svm.SVC.html/. [Online; accessed 17-

February-2022].

Abreu, F. (1993). Metrics for Object Oriented Environment.

In Proceedings of the 3rd International Conference on

Software Quality, Tahoe, Nevada, EUA, October 4th -

6th, pages 67—-75.

Abreu, F. (1995). The MOOD Metrics Set. In 9th Eu-

ropean Conference on Object-Oriented Programming

(ECOOP’95) Workshop Metrics.

Abreu, F. and Rogerio, C. (1994). Candidate Metrics for

Object- Oriented Software within a Taxonomy Frame-

work. In Journal of systems software 26, pages 359–

368.

Alshehri, Y. A., Goseva-Popstojanova, K., Dzielski, D. G.,

and Devine, T. (2018). Applying machine learning to

predict software fault proneness using change metrics,

static code metrics, and a combination of them. In

SoutheastCon 2018, pages 1–7.

Chidamber, S. R. and Kemerer, C. F. (1994). A metrics suite

for object-oriented design. IEEE Trans. Soft Ware

Eng., 20(6):476–493.

Clemente, C. J., Jaafar, F., and Malik, Y. (2018). Is predict-

ing software security bugs using deep learning bet-

ter than the traditional machine learning algorithms?

In 2018 IEEE International Conference on Software

Quality, Reliability and Security (QRS), pages 95–

102.

Coad, P. and Yourdon, E. (1991). Object-Oriented Design.

Prentice Hall, London, 2 edition.

Erturk, E. and Sezer, E. (2016). Software fault predic-

tion using mamdani type fuzzy inference system. In-

ternational Journal of Data Analysis Techniques and

Strategies, 8:14.

Fenton, N. (1994). Software measurement: a necessary sci-

entiﬁc basis. IEEE Transactions on Software Engi-

neering, 20(3):199–206.

Ferenc, R., T

oth, Z., Lad

anyi, G., Siket, I., and Gyim

othy,

T. (2018). A public uniﬁed bug dataset for java. New

York, NY, USA. Association for Computing Machin-

ery.

Ferzund, J., Ahsan, S., and Wotawa, F. (2008). Analysing

Bug Prediction Capabilities of Static Code Metrics in

Open Source Software.

Hall, T., Zhang, M., Bowes, D., and Sun, Y. (2014). Some

code smells have a signiﬁcant but small effect on

faults. ACM Transactions on Software Engineering

and Methodology, 23:1–39.

Holvitie, J., Licorish, S. A., Sp

ınola, R. O., Hyrynsalmi,

S., MacDonell, S. G., Mendes, T. S., Buchan, J., and

Lepp

anen, V. (2018). Technical debt and agile soft-

ware development practices and processes: An in-

dustry practitioner survey. Information and Software

Technology, 96:141–160.

Kumar, L., Rath, S., and Sureka, A. (2017). Using source

code metrics and ensemble methods for fault prone-

ness prediction.

Li, W. and Henry, S. (1993). Maintenance metrics for the

object oriented paradigm. IEEE Proc. First Interna-

tional Software Metrics Symp, pages 52–60.

Marinescu, R. (2002). Measurement and Quality in Object

Oriented Design. PhD thesis, Faculty of Automatics

and Computer Science, University of Timisoara.

McCabe, T. (1976). A Complexity Measure. IEEE Transac-

tions on Software Engineering, 2(4), pages 308–320.

Mitchell, T. M. and Learning, M. (1997). Mcgraw-hill sci-

ence. Engineering/Math, 1:27.

Riel, A. (1996). Object-Oriented Design Heuristics.

Addison-Wesley.

Schr

oter, A., Zimmermann, T., Premraj, R., and Zeller, .

(2009). If your bug database could talk. Empirical

Software Engineering - ESE, page 18.

Vapnik, V. (1999). The nature of statistical learning theory.

Springer science & business media.

Watson, A. H. and McCabe, T. J. (1996). Structured Test-

ing: A Testing Methodology Using the Cyclomatic

Complexity Metric. In National Institute of Standards

and Technology NIST Special Publication, pages 500–

235.

ICSOFT 2022 - 17th International Conference on Software Technologies

440