
Proportional Integral Derivative Decentralized Control vs Linear
Quadratic Tracking Regulator in Vehicle Overtaking within a Platoon
Alessandro Bozzi
a
, Roberto Sacile
b
and Enrico Zero
c
DIBRIS – Department on Informatics, Bioengineering, Robotics and Systems Engineering, University of Genova,
Genova, Italy
Keywords:
Autonomous Vehicles, PID, Linear Quadratic Control, Platooning.
Abstract:
This paper introduces a comparison between a decentralized Proportional Integral Derivative (PID) controller
and a centralized Linear Quadratic Tracking (LQT) controller to automatise the exchange of two inner vehicles
inside a platoon moving on a straight path. Lomonossoff’s model is used to represent vehicle’s longitudinal
dynamics. A case study is presented to demonstrate the effectiveness of both controllers respectively on
nonlinear and linearized model.
1 INTRODUCTION
Autonomous vehicle (AV) is an important research
field of the current century which consists in a car ac-
quiring data and information in real time about the
neighboring environment and driving without the hu-
man interaction for a specified period of time. AVs are
classified accordingly with the vehicle autonomy de-
gree in six levels, from level 0 where there is no driv-
ing automation to level 5 where there is a full driving
automation (SAE, 2014). Equipping cars and light ve-
hicles with this technology will likely reduce crashes,
energy consumption, pollution and congestions (An-
derson et al., 2014). One of the main causes in road
traffic accidents is the human behavior. An applica-
tion of new technologies to monitor driver’s condi-
tion becomes essential to detect anomalous driver be-
havior and prevent near miss accidents has been per-
formed (Zero et al., 2019).
As autonomous vehicles supplant human drivers,
automation’s ability to communicate and cooperate
with people will become more important. Not all ve-
hicles are equipped with sensors for autonomous driv-
ing, so it is also important that the autonomous vehi-
cles interact with the human drivers of other vehicles.
A cooperative maneuver among one autonomous car
and two human-driven vehicles equipped with sensors
and actuators has been tested in (Alonso et al., 2011).
a
https://orcid.org/0000-0002-2436-0946
b
https://orcid.org/0000-0003-4086-8747
c
https://orcid.org/0000-0002-9995-1724
In order to perform this work, the system needs the
position, speed, and intentions of the cars involved
in the maneuver. The authors managed the speed of
human-driven vehicles to make each element arrive at
the intersection at the same time, in order to analyze
the behavior of the unmanned car.
In any urban environment, the vehicle will need
to react safely to each type of unexpected event such
as ill-behaved pedestrians, and pranksters (Koopman
and Wagner, 2017).
In several works, the aim is the management of
vehicle trajectory while driving, in particular the min-
imization of the gap between the planned and the real
trajectory. A novel dynamics controller that consists
of longitudinal and lateral controllers for autonomous
vehicle to simultaneously control it as closer as pos-
sible to the driving limits while following the desired
path has been proposed (Ni and Hu, 2017).
Recent works are not focused on the behavior
management of just one vehicle but they focus on
the behavior of more AVs, namely a platoon of ve-
hicles. This aspect requires more than one sensor em-
bedded in the vehicle. The management of trajectory
of an AVs platoon is fundamental because it is related
to another goal - the reduction of energy consump-
tion. Indeed, it is verified that AV technologies re-
duce fuel consumption by managing better accelera-
tion and deceleration than a human driver (Anderson
et al., 2014).
The management of a trajectory for a vehicle in a
platoon is more complex rather than on a single AV
due to the unexpected events during the transit which
Bozzi, A., Sacile, R. and Zero, E.
Proportional Integral Derivative Decentralized Control vs Linear Quadratic Tracking Regulator in Vehicle Overtaking within a Platoon.
DOI: 10.5220/0011272200003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 427-433
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
427

can affect differently each element of the platoon. In-
deed, vehicle approaching or detachment from neigh-
bors can frequently happen. To generate countermea-
sures for each element of the system, in order to re-
store the correct position, speed and interdistance and
guarantee passengers’ safety, a control system based
on a real-time robust trajectory has been tested (Bozzi
et al., 2021). In order to ensure the safety of ma-
neuvers to let an external vehicle be inserted into the
platoon or alternatively to let a vehicle of the platoon
leave it, a longitudinal Model Predictive Control has
been implemented (Graffione et al., 2020a). The au-
tomation of the overtaking maneuver such as the en-
trance and exit from a platoon is considered to be one
of the hardest challenges in the development of au-
tonomous vehicles. In this direction a fuzzy controller
has been performed to reduce the human interaction
during this maneuver (Naranjo et al., 2008).
This paper proposes a comparison between the
performance of a PID controller on a nonlinear con-
tinuous model and of a Linear Quadratic Tracking
(LQT) controller on a linearized discrete model to
swap the central vehicles of a four-vehicle platoon
moving on a straight path. The former control sys-
tem is decentralized as each vehicle has its own PID
to handle the maneuver, similarly to (Stankovic et al.,
2000), while the latter is computed in a centralized
way, as usually in these cases the leader governs the
vehicle position giving the optimal speed and acceler-
ation to the followers (Graffione et al., 2020b).
The remainder of this work is organized as fol-
lows: Section II reviews the nonlinear and linear
model tested and it shows the driving scenario. In
Section III the case study is analyzed and the results
related to the nonlinear and linear controller simula-
tion. In Section IV conclusions about the comparison
of the two models are reported and the further devel-
opments of this work are proposed.
2 MODELS AND METHODS
In the literature, the longitudinal models are largely
investigated. This happens because the vehicle’s dis-
placement can be often subdivided in longitudinal and
lateral motion and the two are assumed additive. This
paper tackles the problem in the same way but using
a different longitudinal representation for elements of
the platoon. Indeed, they have been modeled through
the Lomonossoff’s equations, mainly used for trains
(as in (Lu et al., 2011)) but easily adaptable for cars
modelization. It faithfully represents vehicle’s evo-
lution overtime and provide the possibility of tak-
ing into accounr vehicle’s parameters such as mass
Table 1: Davis constants.
C
a
9
C
b
0.06
C
c
0.023
W 2
and frictions, that have primary importance especially
when dealing with trucks.
The model chosen is nonlinear due to a quadratic
term function of the speed.
2.1 Nonlinear Model
The Lomonossoff’s equations are:
˙x(t) = v(t)
W
0
˙v(t) = f (t) − (C
a
+C
b
v(t) +C
c
v
2
(t))
−W gsin α(t)
(1)
where:
• x[m] and v[m/s] are state variables, respectively
position and speed of the vehicle
• f [kN] is the control input, corresponding to the
tractive effort
• C
a
[kN], C
b
[
kN
m/s
], C
c
[
kN
m
2
/s
2
] are the Davis con-
stants, related respectively to mechanical resis-
tance, viscous mechanical resistance and aerody-
namic resistance
• W [tonnes] is the vehicle’s tare mass
• W
0
[tonnes] is the vehicle’s effective mass, includ-
ing rotary allowance
• α is the slope angle of the position of the vehicle
They represent the dynamics of the longitudinal mo-
tion for the individual vehicle by prompting a tractive
effort, with a maximum value similarly to what hap-
pens in train modelization.
In the following, it is assumed that α = 0, i.e. ve-
hicles are traveling on a flat road. Vehicles are consid-
ered homogeneous and their parameter estimation for
the case study, which deals with heavy-duty vehicles
(HDVs), is listed on Table 1. The choice of analyzing
HDVs is due to recent literature results, which reveal
that the improvement in their performance is signif-
icant if they are placed in ascending order based on
their braking capabilities (Alam et al., 2014). So, an
algorithm to swap inner vehicles of the platoon can
provide long-term efficiency in fuel consumption and
CO
2
emissions.
2.2 Linear Model
The model presented in (1) can be linearized for each
planned instant t
p
around a working state/control cou-
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
428

ple ( ¯v,
¯
f ), supposing no acceleration in that instant of
time.
The resulting linear approximation that represents
the evolution of the system overtime is:
δ ˙x = A
p
δx + B
p
δ f (2)
where:
δx = [x(t) − ¯x(t) v(t) − ¯v(t)]
T
, δ f =
f (t) −
¯
f (t)
(3)
A
p
=
"
0 1
0 −
C
b
+2C
c
¯v(t)
W
0
#
, B
p
=
0
1/W
0
(4)
It has to be noted that the A
p
matrix is time-variant,
as it depends on the actual speed of the vehicle. In
other words, the matrix A
p
is computed at each sam-
pling instant in order to let the system work around
an operating point that varies overtime and follows
the trend of vehicle’s speed.
The control algorithm is applied to the discretized
system with a sample time, for the case study, of
100ms.
2.3 Driving Scenario
This paper analyzes a driving routine in which two
inner vehicles exchange their position while the pla-
toon is moving on a straight path. Initial positions of
platoon is represented in Fig. 1a.
This kind of maneuver can be seen as an overtak-
ing with space constraints, since the vehicle behind
has to:
• position itself on the fast lane, thus exiting from
the string formation (Fig. 1b)
• overcome the vehicle in front of it in the platoon
formation (that in the meanwhile has to favor the
overtaking with a slow deceleration)
• settle at the correct distance between its neighbor-
ing vehicles (Fig. 1c)
• come back to the platoon lane (Fig. 1d)
The maneuver, graphically represented in Fig. 1 has
to be performed keeping similar speed with respect
to the rest of platoon and in a reasonable time frame.
Moreover, for the whole time, vehicles involved in the
swap have to prevent getting too closer to their neigh-
bors, thus endangering passengers’ safety.
The role of each element can be summarize as fol-
lows:
• Vehicle #1 has to proceed at constant speed and
measure the distance to its follower, in order to
improve the reconstruction of the surroundings
• Vehicle #2 decelerates in order to favor the over-
taking of vehicle #3, while measuring the distance
from the leader and the last element of the platoon
• Vehicle #3 overtakes vehicle #2 and measure the
distance from it and from the leader, in order to
re-enter the string formation in the best position
possible
• Vehicle #4, similarly to vehicle #1, has to proceed
at constant speed and increase the knowledge of
the environment by providing its measurements
(a) (b)
(c) (d)
Figure 1: Overtaking maneuver with position constraints.
3 CASE STUDY
In the following, a four-vehicle platoon is considered
(M = 4). Vehicle #2 and vehicle #3 are involved in
the swap, while the first and the last vehicle of the pla-
toon are assumed to proceed around the regime speed
v
reg
= 22[m/s]. The four-vehicle platoon represents
the most reasonable choice whereas what it happens it
that two trucks exchange their position and they have
to pay attention to adjacent elements of the platoon.
In more numerous platoons, the four-vehicle subset
can be taken into account by the controller only for
the time needed to perform the maneuver, while main-
taining other elements at constant speed.
The maneuver must ensure the safety of the whole
system, so between adjacent elements must intervene
a minimum distance, computed as in (Bozzi et al.,
2021). According to this formulation, the minimum
and the recommended distances are:
d
min
[m] =
3 ∗ v
reg
[km/h]
10
= 23.76m
d
opt
[m] = (
v
reg
[km/h]
10
)
2
= 62.73m
(5)
Proportional Integral Derivative Decentralized Control vs Linear Quadratic Tracking Regulator in Vehicle Overtaking within a Platoon
429
However, these bounds might even be reduced con-
sidering the faster reaction time of unmanned vehi-
cles with respect to human-driven ones. Even if there
are other rules to compute the optimal inter-vehicle
distance, such as the one stated by the Responsibility
Sensitive Safety (RSS) widely used in literature (e.g.
in (Shalev-Shwartz et al., 2017) and (Gassmann et al.,
2019)), it is useful to start with the recommended dis-
tances stated by the traffic regulations which represent
the minimum constraints to satisfy within the road
nowadays. Of course, assuming only unmanned ve-
hicles it can emerge the possibility of taking into ac-
count shorter inter-vehicle distances.
The case study considers an initial inter-vehicle
span of d = 30[m], close to the critical bound (d
min
)
and thus representing a risky situation to perform an
overtaking maneuver between inner element of the
platoon. In the first 5 seconds of the simulation ve-
hicles move at regime and vehicle #3 changes lane in
order to proceed with the overtaking maneuver. Re-
entering the lane is assumed to be done in the last 5
seconds of simulations, without altering the longitu-
dinal displacement.
The inter-vehicle distance should remain un-
changed at the end of the driving routine. Moreover,
vehicles involved in the swap should not get too closer
to other elements of the platoon (i.e. the leader for ve-
hicle #3, the last element for vehicle #2).
The performance of a PID controller on the con-
tinuous nonlinear system are presented and then com-
pared to a control algorithm that deals with the linear
discrete approximation of the Lomonossoff’s model
and makes usage of a LQT problem to compute the
optimal control input.
3.1 Nonlinear System
The control of the nonlinear system is governed by a
PID that acts converting the desired value in position
in a corresponding value in tractive effort. Each ve-
hicle that needs to alter its speed from the regime has
its own PID. The only communication that occurs be-
tween vehicles involves the message with the actual
position, in order for the PID to formulate the proper
control action to pursue the desired value. In fact, the
desired position is expressed in terms of the actual po-
sition, the position of the leader or the position of the
last element of the platoon (respectively for vehicle
#3 and vehicle #2) and the interdistance between ad-
jacent elements, computed as a function of the regime
speed. At each sampling instant k, it can be expressed
as follows:
(
x
d
2
(k) = x
1
(k) − 2d
x
d
3
(k) = x
4
(k) + 2d = x
1
(k) − d
(6)
Table 2: PID coefficients.
Proportional 2.754
Integral 0.484
Derivative 2.986
Filter coefficient 9.300
0 10 20 30 40 50 60
Time[s]
19
20
21
22
23
24
25
Speed[m/s]
v
2
v
3
v
reg
Figure 2: Vehicles’ speed: nonlinear system.
Reference trajectory of vehicle #3 should be written
with respect to the position of the leader, since unex-
pected behavior can arise when dealing with a large
scale platooning, as demonstrated in (Pates et al.,
2017). In this paper, though, considering the small
number of vehicles involved in the platoon, both for-
mulations give the same results.
The parameters of the continuous time PID has been
tuned using the Matlab/Simulink tool and lineariz-
ing the plant near the equilibrium point obtained with
the regime speed. Thus, unexpected behaviour may
emerge at very different speeds from the initial one.
The value used for the simulation are listed in Ta-
ble 2. The filter coefficient is needed to improve the
action of the derivative term, not implemented as a
pure derivative because of its sensitiveness to noise.
Rate limiter has been added to avoid abrupt changes
between consecutive sampling instants, while output
saturation is needed to maintain vehicle around its
equilibrium point and increase the overall realism of
the control input on the virtual environment. Fig. 2
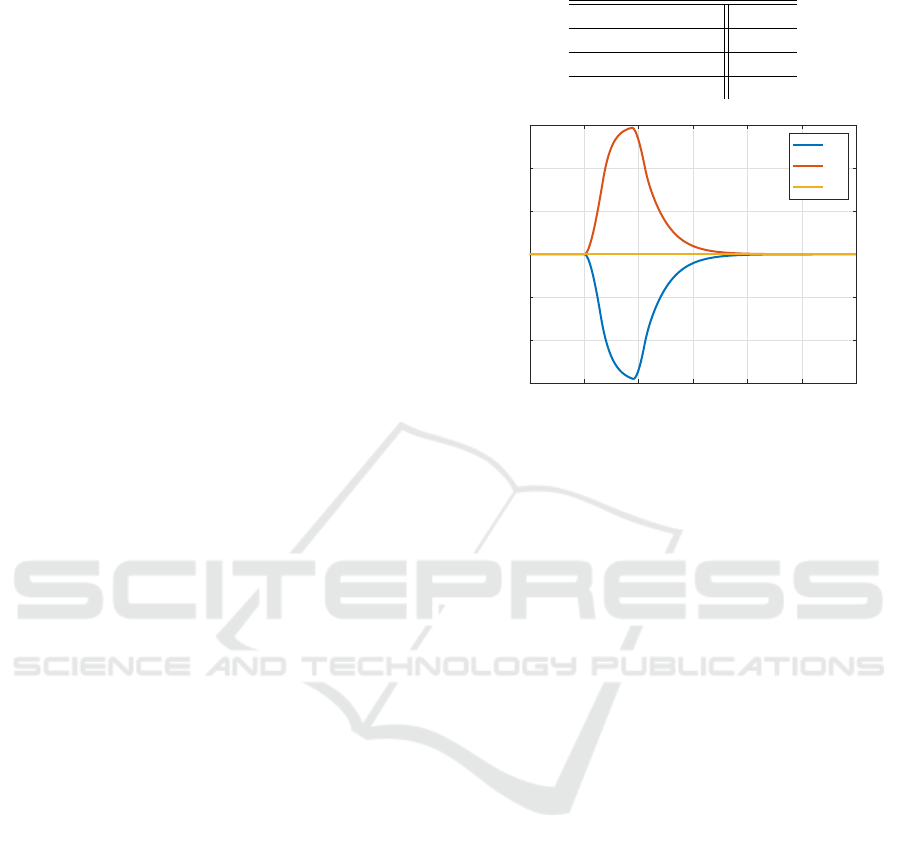
shows the trend of the velocities. As expected, there is
a slight acceleration from the third vehicle, while the
other starts decelerating to favor the overall maneu-
ver. The behavior is almost specular as both vehicles
have the same PID gains and their desired positions
are symmetric with respect to the center of platoon.
Fig. 3 confirms the effectiveness of the nonlinear con-
troller, as the distance between vehicles varies accord-
ing to the expectation and it settles on multiples of 30
meters (based on the pair of vehicles analyzed), en-
suring that the initial inter-vehicle distance is main-
tained.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
430
0 10 20 30 40 50 60
Time[s]
-40
-30
-20
-10
0
10
20
30
40
50
60
Inter-distance[m]
d
12
d
32
d
34
Figure 3: Inter-vehicle distances: nonlinear system.
It can be stated that the objective is achieved
smoothly and fastly, without abrupt changes in accel-
eration and thus preserving passenger’s comfort.
3.2 Linear Controller
The linear controller is more complex to implement
for many factors: first of all, it relies on time-variant
information from the system. Second, it operates on
a discretized model which represents an approxima-
tion of the actual system. As a matter of fact, the state
of the vehicle is used to determine the linearized sys-
tem around the working point
¯
v(t
p
) and to provide the
state for the LQT problem to be solved. For this rea-
son, it is assumed that the trends of the velocities for
the nonlinear evolution is known, as it will be used as
reference signal to be followed by the tracking algo-
rithm.
The knowledge of velocity trends is a strong as-
sumption, but it is reasonable as the behavior depends
on the actual speed of the vehicles. Thus, it is possible
to have a set of different maneuvers based on the ini-
tial regime speed of the other vehicles of the platoon.
The LQT requires a cost function in order to prior-
itize the tracking of certain state variables and the cost
of the control action. For the case study, the overall
cost function for each sampling instant k is:
J =
M
∑
i=1
K
∑
k=1
α
i
(x
i
(k) − x
d
i
(k))
2
+ β
i
(v
i
(k) − v
reg
)
2
+ γ
i
f
i
(k)
+
M
∑
i=1
α
i
(x
i
(K + 1) − x
d
i
(K + 1))
2
+
β
i
(v
i
(K + 1) − v
reg
)
2
(7)
With α, β and γ gains to be tuned to prioritize the re-
spective elements of the summation and K the control
horizon for the LQT problem. The higher the K, the
smoother but less responsive the reaction of the sys-
tem. In the case study it has been chosen K = 10 not to
overburden the computational cost. x
d
i
are retrieved as
in (6) for vehicles involved in swap, and computed as
constant displacement between consecutive sampling
instants for outer vehicles. v
reg
is the regime speed,
in the case study equals to 22m/s for each element of
the platoon.
More in detail the first term is the quadratic devi-
ation from the desired trajectory, which for inner ve-
hicles x
d
i
is computed as in (6) and for outer vehicles
is not considered (i.e. α
1
,α
4
= 0), the second term is
the deviation from the desired speed and their trend is
supposed to be known, and the last term regards the
minimization of the input which translates in the min-
imum tractive effort to be applied to accomplished the
goals. The second summation is needed to represent
the final control instant for the state.
The equivalent of the cost function in matrix form
to be prompted to the LQT is:
Q =
α
3
+ α
2
0 −α
2
0 −α
3
0 0 0 −α
3
d − 2α
2
d
0 β
1
0 0 0 0 0 0 0
−α
2
0 α
2
0 0 0 0 0 2α
2
d
0 0 0 β
2
0 0 0 0 −β
2
v
reg
−α
3
0 0 0 α
3
0 0 0 α
3
d
0 0 0 0 0 β
3
0 0 −β
3
v
reg
0 0 0 0 0 0 α
4
0 0
0 0 0 0 0 0 0 β
4
0
−α
3
d − 2α
2
d 0 2α
2
d −β
2
v
reg
−α
3
d −β
3
v
reg
0 0 0
R =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
(8)
Note that Q ∈ R
2M+1
and R ∈ R
M+1
due to non
quadratic terms present in the cost function that re-
quire to increase the size of the matrix and the state
vector, as explained in (Boyd, 2008).
It is clear that the control technique is centralized,
thus the state of the system is composed by all vehi-
cles belonging to platoon, even the ones that have to
proceed at constant speed. This centralization ensures
the optimal behavior from the platoon’s point of view,
disregarding the individual element favoring the over-
all safety of the system.
In the case study, it has been decided to greatly
privilege the tracking of speeds over the control cost,
setting high β gains. It has to be noted that, if all
α gains are set to zero, the platoon control problem
translates into M control problems concerning the in-
dividual vehicle, as there are no constraints related to
inter-vehicle distance.
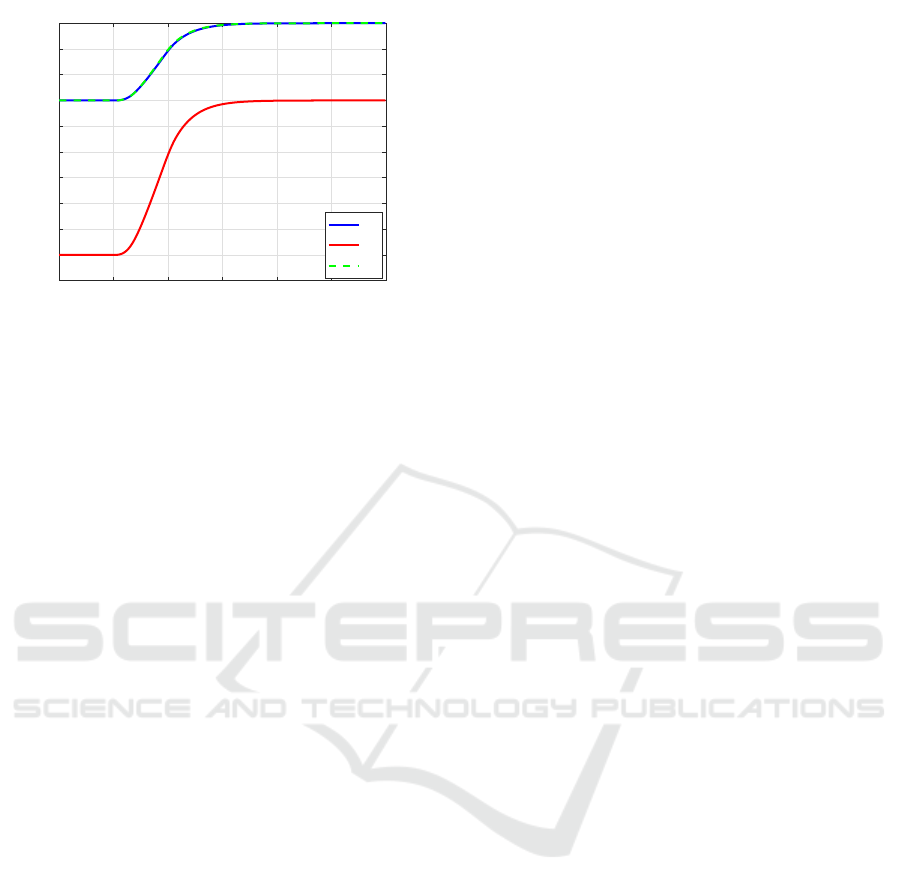
This turned out to be necessary since with unitary
gains the control technique is not able to perform the
swap between vehicles. This is shown in Fig.4 and
happens because, with unitary gains, for the control
algorithm is not convenient to perform the maneuver
due to the cost of the input.
On the other hand, if huge importance is given to
the maneuver (i.e. gains to track velocity trends are
Proportional Integral Derivative Decentralized Control vs Linear Quadratic Tracking Regulator in Vehicle Overtaking within a Platoon
431
0 10 20 30 40 50 60
Time[s]
-50
-40
-30
-20
-10
0
10
20
30
40
50
Distance[m]
(x
2
- x
2
d
)
=1
(x
2
- x
2
d
)
=1000
(x
3
- x
3
d
)
=1
(x
3
- x
3
d
)
=1000
Figure 4: Difference between actual and desired position
with α = 1 and α = 1000.
0 10 20 30 40 50 60
Time[s]
-40
-30
-20
-10
0
10
20
30
40
50
60
Inter-distance[m]
d
12
d
32
d
34
X 59.9
Y 24.2651
X 36
Y 23.3478
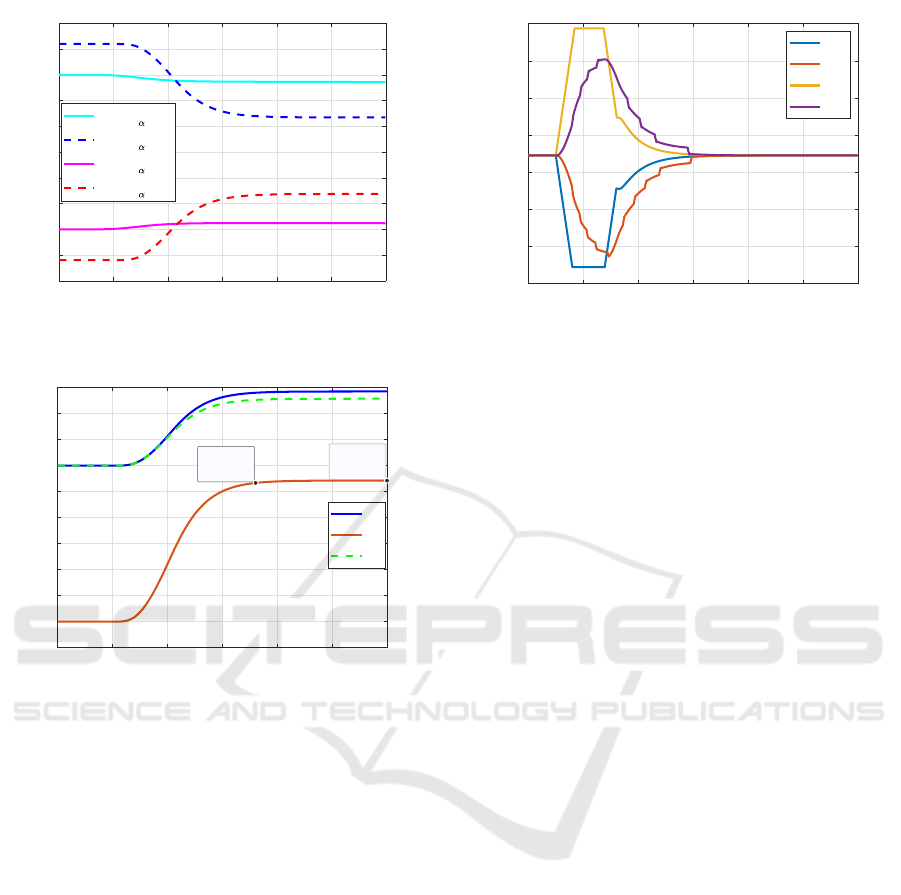
Figure 5: Inter-vehicle distances: linear controller.
significantly higher than gains for the control cost) the
inter-vehicle distance evolves as shown in Fig.5, with
two markers to point out the behaviour in the middle
of the simulation and its final value.
The overall objective is achieved, even if vehicles
experiment little reductions in their interdistances.
This does not affect safety of the whole system, since
each element preserves a distance greater than d
min
with the following vehicle (very close to the mini-
mum bound for the ones involved in the swap). This is
even more valuable considering the high regime speed
and the unfavorable initial conditions that should not
suggest such a maneuver. Increasing the initial span
produces safer results as vehicles have more space in
which to exchange. Moreover, the input prompt re-
ported in Fig. 6 highlights the difference between the
nonlinear case, in which the output reach its satura-
tion, and the linear evolution, closer to the regime and
desired value, improving the fuel consumption over-
time.
0 10 20 30 40 50 60
Time[s]
18
19
20
21
22
23
24
25
Tractive force[kN]
f
2
NL
f
2
L
f
3
NL
f
3
L
Figure 6: Control action for vehicles involved in the swap.
4 CONCLUSION
This paper analyzes the swap of inner elements of a
four-vehicle platoon moving on a straight path. The
work shows a comparison between PID controller on
nonlinear continuous system and LQT controller on
a discretized linear system. A case study for vehi-
cles proceeding at medium speed is presented and an-
alyzed. Even if it is possible, after a correct tuning
of PID and gains, to perform the exchange at higher
velocity, it is not recommended for safety reasons. In
addition, the benefits produced by such driving rout-
ing are detectable mainly on heavy-duty vehicles, that
do not travel at higher speed.
To conclude, it can be asserted that the driving ma-
neuver can be fluently completed by means of the de-
centralized controller. It acts on the nonlinear con-
tinuous system guaranteeing passengers’ comfort and
safety, although it requires an accurate tuning of the
PID parameters to work properly.
Even with the linear controller, though, vehicles
can successfully achieve the swap without endanger-
ing the whole system, also when initial conditions are
not favourable for this maneuver and suggest a more
cautious drive. There still is an offset in the steady
state interdistance, that may be refined by low-level
controllers to be activated once the system is reaching
its regime. Moreover, the tuning can be done more
roughly by prioritizing the velocity constraints over
the position ones. For these reasons and considering
the linearity of the controller and its action on a sim-
plified model of the system, the results obtained on
the nonlinear model are satisfactory.
Its main drawback is the need for a priori informa-
tion that may not be available at the beginning of the
maneuver. For future improvements, we surely aim
to provide a method to dynamically generate velocity
trends to accomplish the driving routine.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
432

It is also worth analyzing an overtaking maneu-
ver that involves more than two vehicles, to fasten the
reaching of the optimal string formation in bigger pla-
toons, though it may require too much time to be ac-
complished even in a free highway road. However, its
feasibility will be studied in further works.
Instead, there is no need to test the algorithm at
much higher speed (> 100km/h), since its advantages
are relevant especially for heavy-duty vehicles that
should not travel and even perform overtaking maneu-
ver at those velocities.
ACKNOWLEDGEMENT
This study is supported by the SysE2021 project
(2021-2023), “Centre d’excellence transfrontalier
pour la formation en ing
´
enierie de syst
`
emes” de-
veloped in the framework of the Interreg V-A
France-Italie (ALCOTRA) (2014 - 2020), Programme
de coop
´
eration transfrontali
`
ere europ
´
eenne entre la
France et l’Italie.
REFERENCES
Alam, A., Gattami, A., Johansson, K. H., and Tomlin, C. J.
(2014). Guaranteeing safety for heavy duty vehicle
platooning: Safe set computations and experimental
evaluations. Control Engineering Practice, 24:33–41.
Alonso, J., Milan
´
es, V., P
´
erez, J., Onieva, E., Gonz
´
alez, C.,
and De Pedro, T. (2011). Autonomous vehicle control
systems for safe crossroads. Transportation research
part C: emerging technologies, 19(6):1095–1110.
Anderson, J. M., Nidhi, K., Stanley, K. D., Sorensen,
P., Samaras, C., and Oluwatola, O. A. (2014). Au-
tonomous vehicle technology: A guide for policymak-
ers. Rand Corporation.
Boyd, S. (2008). Ee363 review session 1: Lqr, control-
lability and observability. https://stanford.edu/class/
ee363/sessions/s1notes.pdf. [Online; accessed 19-
July-2008].
Bozzi, A., Zero, E., Sacile, R., and Bersani, C. (2021). Real-
time robust trajectory control for vehicle platoons: A
linear matrix inequality-based approach. In Proceed-
ings of the 18th International Conference on Infor-
matics in Control, Automation and Robotics, ICINCO
2021, pages 410–415.
Gassmann, B., Oboril, F., Buerkle, C., Liu, S., Yan, S.,
Elli, M. S., Alvarez, I., Aerrabotu, N., Jaber, S., van
Beek, P., et al. (2019). Towards standardization of av
safety: C++ library for responsibility sensitive safety.
In 2019 IEEE Intelligent Vehicles Symposium (IV),
pages 2265–2271. IEEE.
Graffione, S., Bersani, C., Sacile, R., and Zero, E. (2020a).
Model predictive control for cooperative insertion or
exit of a vehicle in a platoon. In ICINCO, pages 352–
359.
Graffione, S., Bersani, C., Sacile, R., and Zero, E. (2020b).
Model predictive control of a vehicle platoon. In 2020
IEEE 15th International Conference of System of Sys-
tems Engineering (SoSE), pages 513–518. IEEE.
Koopman, P. and Wagner, M. (2017). Autonomous vehicle
safety: An interdisciplinary challenge. IEEE Intelli-
gent Transportation Systems Magazine, 9(1):90–96.
Lu, S., Hillmansen, S., and Roberts, C. (2011). A power-
management strategy for multiple-unit railroad vehi-
cles. IEEE Transactions on Vehicular Technology,
60(2):406–420.
Naranjo, J. E., Gonzalez, C., Garcia, R., and De Pedro, T.
(2008). Lane-change fuzzy control in autonomous ve-
hicles for the overtaking maneuver. IEEE Transac-
tions on Intelligent Transportation Systems, 9(3):438–
450.
Ni, J. and Hu, J. (2017). Dynamics control of autonomous
vehicle at driving limits and experiment on an au-
tonomous formula racing car. Mechanical Systems
and Signal Processing, 90:154–174.
Pates, R., Lidstr
¨
om, C., and Rantzer, A. (2017). Control us-
ing local distance measurements cannot prevent inco-
herence in platoons. In 2017 IEEE 56th Annual Con-
ference on Decision and Control (CDC), pages 3461–
3466. IEEE.
SAE (2014). Sae taxonomy and definitions for terms re-
lated to on-road motor vehicle automated driving sys-
tems, j3016, sae international standard. https://www.
sae.org/standards/content/j3016 201806/.
Shalev-Shwartz, S., Shammah, S., and Shashua, A. (2017).
On a formal model of safe and scalable self-driving
cars. arXiv preprint arXiv:1708.06374.
Stankovic, S. S., Stanojevic, M. J., and Siljak, D. D. (2000).
Decentralized overlapping control of a platoon of ve-
hicles. IEEE Transactions on Control Systems Tech-
nology, 8(5):816–832.
Zero, E., Bersani, C., Zero, L., and Sacile, R. (2019). To-
wards real-time monitoring of fear in driving sessions.
IFAC-PapersOnLine, 52(19):299–304.
Proportional Integral Derivative Decentralized Control vs Linear Quadratic Tracking Regulator in Vehicle Overtaking within a Platoon
433
