A New Leakage Resilient Symmetric Searchable Encryption Scheme for

Phrase Search

Samiran Bag

1 a

, Indranil Ghosh Ray

2 b

and Feng Hao

1 c

University of Warwick, U.K.

Queen’s University Belfast, U.K.

Keywords:

Symmetric Searchable Encryption, Encryption Scheme, Security Proof, Symmetric Key, Probabilistic

Trapdoor, Access Pattern, Search Pattern Privacy, Search Index.

Abstract:

Symmetric searchable encryption (SSE) schemes are preferred over asymmetric ones for their lower computa-

tional cost. Owing to the big data size of most of the cloud applications, SSE with keyword search often yields

a large number of search results matching the search criterion, but only a small portion of them is of actual

interest. This results in unnecessary increase of network trafﬁc. A customized search against a phrase instead

of keywords can yield more speciﬁc and relevant search results and can reduce the network trafﬁc. This mo-

tivates the idea of phrase search in SSE. Most of the existing symmetric key searchable encryption schemes

either do not support phrase search or have unwanted leakage associated with them. In this paper, we propose

a symmetric key searchable encryption scheme for phrase search that minimizes the leakage of information

from search pattern and access pattern. We propose a probabilistic trapdoor generation algorithm for phrase

search and thereby prevent the leakage due to search pattern. In earlier SSE based schemes, an honest-but-

curious server could always learn about the position of the sentences and keywords in the encrypted text after

the search operation is performed. This is referred to as the leakage from access pattern. This may turn out to

be a signiﬁcant security concern owing to the prior knowledge of positions of certain sentences and keywords

in certain documents. In this paper, we provide the access pattern secure encryption scheme such that, an

honest-but-curious cloud server could not learn anything about the position of the phrase in the sentence even

after the search. We implement a prototype of our scheme and validate it against commercial data and provide

security and performance analysis to demonstrate its practicality.

1 INTRODUCTION

With the advent of cloud computing, a growing num-

ber of organizations have chosen to outsource stor-

age of data. Resource constrained clients can reliably

store their data on cloud platforms at a reasonable

cost, eliminating the need to procure and maintain ex-

pensive storage equipment. Due to privacy concerns,

these clients need to encrypt their data before they

are stored in the cloud. However, encryption prevents

meaningful processing of the data. For example, if a

client wants to search for a keyword in an encrypted

dataset stored in the cloud, she will need to download

the entire dataset to her local disk, and then decrypt it

for performing the search.

For years, researchers have attempted to explore

an alternative solution called searchable encryption

https://orcid.org/0000-0002-3501-0829

https://orcid.org/0000-0002-4156-8247

https://orcid.org/0000-0002-8664-5074

(SE). SE schemes allow a user to perform searches

on an encrypted ﬁle stored in a cloud using a trap-

door. SE schemes are classiﬁed into two groups,

namely, symmetric searchable encryption (SSE) and

asymmetric searchable encryption (ASE). In SSE, the

entity that encrypts the data is always the same as the

entity that produces trapdoors for enabling searches

on the data. On the other hand, in ASE, the two en-

tities may be distinct. This is because in ASE, en-

crypting a document requires the public key of the

data-receiver which is available to everyone. How-

ever, generation of a trapdoor will require the secret

key of the receiver, and only the receiver has got ac-

cess to it. In spite of this advantage, ASE schemes

are not widely used in practice due to their high com-

putational costs (Salam et al., 2015). Instead, SSE

is becoming popular for its use in applications, like

searching one’s encrypted ﬁles stored at Amazon S3

or Google Drive, without leaking much information

to Amazon or Google.

366

Bag, S., Ray, I. and Hao, F.

A New Leakage Resilient Symmetric Searchable Encryption Scheme for Phrase Search.

DOI: 10.5220/0011273600003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 366-373

ISBN: 978-989-758-590-6; ISSN: 2184-7711

Since most of the cloud applications deal with

huge data sizes, a search against a keyword often re-

sults in many documents, of which only a subset is of

actual interest. Clearly, the search can be further cus-

tomised by specifying the context in a phrase. How-

ever, the majority of SSE constructions that have been

presented in the literature work for keyword search.

This motivates the idea of extending SSE for phrase

search (Poon and Miri, 2019). In an SSE scheme, a

client encrypts the dataset with her own key and stores

it in the cloud. Later, the same client can issue trap-

doors against phrases to be searched in the dataset.

These trapdoors are used by the cloud server to per-

form searches. With our scheme, the index size for an

n-word phrase is O(n

) and the search time is O(n).

It may be noted that for an n-word phrase, one can

achieve phrase search using keyword search function-

ality repetitively just by considering all r-word sub-

strings (r ∈ {1, 2, ·· · , n}) of the phrase and preparing

an index where these substrings are treated as key-

words. In that case, the number of substrings that are

to be considered is

∑

r=1

(n − r) = O(n

), and for this

input size, the size of the index will be

∑

r=1

(n−r)r =

O(n

), however the search time using such index will

be O(n

) as opposed to our search time using our in-

dex, which is O(n ∗ c) where c is the length of the

subphrase to be searched.

In order for the search result to be more compact

and precise, searchable encryption schemes that sup-

port phrase search have been proposed. Such schemes

allow the client to search a string of keywords of ar-

bitrary length in a ciphertext. This mandates preser-

vation of the ordering of keywords in the ciphertext.

That is, the encryption scheme needs to ensure not

only the presence of keywords in the ciphertext, but

also the ordering of the keywords in a suitable for-

mat. Information about the relationship of consecu-

tive keywords is maintained in the form of an addi-

tional data structure called the index table, which is

stored at the server for future search. The index table

needs to be prepared in such a way that it preserves

the adjacency information of the keywords.

There have been a few research works that target

phrase search in textual documents (Li et al., 2015a;

Tang et al., 2012; Poon and Miri, 2019; Uchide and

Kunihiro, 2016; Zittrower and Zou, 2012). Most

of them are not secure as per the deﬁnitions men-

tioned by Curtmola et al. (Curtmola et al., 2006). In

(Curtmola et al., 2006), Curtmola et al. proposed the

ﬁrst efﬁcient SSE construction that achieves sublin-

ear search time. They also introduced notions of non-

adaptive and adaptive indistinguishability for SSE.

Their work introduces the idea of history connected

to a ﬁnite number of consecutive keyword searches.

Ray et al. (Ray et al., 2020) extended that deﬁnition

for string search, and called it history-of-strings. They

proved the scheme to be secure against non-adaptive

indistinguishability. We make necessary changes to

the deﬁnition of non-adaptive indistinguishability for

SSE performing string search to make it adaptive and

prove our scheme secure against the new deﬁnition.

Details of the deﬁnition can be found in the full ver-

sion of the paper.

Motivation. The aim of any searchable encryption

scheme is the protection of privacy of the client. Due

to the ﬂexibility associated with any searchable en-

cryption, it is not always possible to offer full privacy

to a client that stores data in the cloud. Every search

operation is exposed to the risk of leakage of infor-

mation from search pattern and access pattern (Curt-

mola et al., 2006). For example, if the keywords of a

document are encrypted separately and the encrypted

keywords are placed in the same order as they are

in the original document, then an honest-but-curious

cloud server may learn the structure of the plain text

by learning the structure of the ciphertext. Also, in

such cases, the relative position of the phrase in the

document will be revealed to the server for which the

search has been done. On the other hand, if the en-

crypted keywords are not stored in an orderly manner,

the sentences of the document can never be restored

from the ciphertext. Thus, this ciphertext cannot be

used for phrase search. In (Curtmola et al., 2006),

the trapdoor generation algorithm was deterministic

and thus the statistical distribution of the search pat-

tern completely got reﬂected from the distribution of

the trapdoors. In (Ray et al., 2020) authors proposed

search pattern secure SSE scheme by enforcing non-

deterministic trapdoor generation algorithm, however

that scheme suffers leakage from access pattern by re-

vealing adjacency information even before search and

also by revealing the position information of phrases

after the search. Our paper proposes a searchable en-

cryption scheme that is more secure than existing SSE

schemes by minimizing leakages from search pat-

tern and access pattern. The search pattern security

is achieved by enforcing non-deterministic trapdoor

generation algorithm. The access pattern security is

improved in a sense that, unlike existing schemes, our

scheme reveals nothing about the position informa-

tion of a searched phrase and also leaks nothing about

the adjacency information of the already searched

phrases or keywords even after the search. We at-

tain this at the expense of some extra storage space,

which we consider a suitable trade-off owing to the

huge technological advancement in the last decade re-

sulting in cheaper storage cost.

A New Leakage Resilient Symmetric Searchable Encryption Scheme for Phrase Search

367

In this scheme, the encrypted keywords of a sen-

tence are stored in an unordered set. There is an ad-

jacency matrix that stores the ordering information

about consecutive keywords in the sentence, and this

matrix can be used to reconstruct the sentence from

the set of encrypted keywords. In addition, they can

also be used to perform phrase search that does not

give away the position of the searched phrase in the

sentence in case the search outcome is afﬁrmative.

The cloud server only learns the search outcome, and

not the position of the phrase in a sentence.

Contributions.

1. We propose a secure and efﬁcient symmetric

searchable encryption that supports phrase search.

In a naive approach, phrase search can be con-

ducted by applying keyword search techniques

and treating an n-word phrase and all its consec-

utive sub-strings as separate keywords. However,

it will require an index size O(n

) and the search

time O(n

). In our scheme, the index size for an

n-word phrase is only O(n

) and the search time

is O(n).

2. In the full version of the paper, we provide se-

curity proofs to show the security of our scheme.

In particular, previous schemes have various leak-

age issues: e.g., leaking the length of the sentence

before the search, and the adjacency information

about the keywords after the search. Our scheme

stops such leakage.

3. We implement a prototype of our symmetric

phrase search scheme using C and OpenSSL, and

conduct performance evaluation against TIMIT

dataset (dat, 2007) which is presented in the full

version of the paper. Our empirical results indi-

cate that our scheme is feasible for practical use.

Remark 1. Due to space constraint, we move details

of the security proofs along with the experimental re-

sults to the full version of this paper.

Organization. The rest of the paper is organised as

follows. In Section 2, we discuss previous works on

phrase search. In Section 3, we describe our scheme

in detail and prove the correctness of the scheme. In

Section 4, we study the overhead associated with our

scheme. We conclude the paper in Section 5.

https://pure.qub.ac.uk/en/persons/indranil-ghosh-ray

2 RELATED WORK

There are two types of searchable encryption

schemes, namely symmetric searchable encryption

(SSE) and asymmetric searchable encryption (ASE).

SSE schemes were ﬁrst introduced by Song et

al. (Song et al., 2000). In an SSE scheme, the key

is symmetric, hence, only the secret key holder can

produce ciphertexts and perform searches. Their two-

layered encryption scheme leaks information about

access pattern and search pattern, making the scheme

vulnerable to statistical attacks (Curtmola et al.,

2011). Curtmola et al. (Curtmola et al., 2006; Curt-

mola et al., 2011) proposed two schemes for key-

word search. They are based on two security deﬁ-

nitions: non-adaptive and adaptive security models.

In a non-adaptive setting, the adversaries make their

search queries without taking into account the trap-

doors and search outcomes of previous searches. In

an adaptive setting, the adversaries can choose their

queries on the basis of previously queried trapdoors

and search outcomes.

In ASE schemes, the entity that performs search

on encrypted data is different from the one that gen-

erated them. The ﬁrst Public Key Encryption scheme

was proposed by Boneh et al. in (Boneh et al., 2004).

The scheme allows someone to perform keyword

search on an encrypted document using a trapdoor

generated by the user. Encrypting a document re-

quires the public key of the user, whereas the gen-

eration of the trapdoor requires a private key.

Following these works, many researchers focused

on building searchable encryption and several results

were proposed in various aspects of searchable en-

cryption (Zittrower and Zou, 2012; Li et al., 2015b;

Tang et al., 2012; Kissel and Wang, 2013; Cash et al.,

2013; Wang et al., 2014; Cao et al., 2014; Sun et al.,

2013; Naveed et al., 2014; Sun et al., 2016; Ghosh

Ray et al., 2020; Kamara et al., 2012; Stefanov et al.,

2014; Cash et al., 2014). Kamara et al. (Kamara et al.,

2012) proposed a dynamic symmetric searchable en-

cryption scheme. Stefanov et al. (Stefanov et al.,

2014) improved the dynamic encryption scheme of

Kamara et al. Cash et al. (Cash et al., 2014) pro-

posed an encryption scheme that effectively imple-

mented dynamic search on large databases. Wang

et al. (Wang et al., 2014) proposed a fuzzy search

encryption scheme that supports multiple keyword

search. The scheme exploits a locality-sensitive hash-

ing technique and can tolerate typos.

Zittrower et al. (Zittrower and Zou, 2012) pro-

posed the ﬁrst searchable encryption for phrase

search. They employed a strategy to maintain a re-

lational database that stores the keyword location and

SECRYPT 2022 - 19th International Conference on Security and Cryptography

368

the index-data of the encrypted keywords in the doc-

ument. However, the server can learn the frequency

of distinct keywords in different documents, and can

know the ciphertext of likely keywords (Li et al.,

2015b). Tang et al. proposed another construction

in (Tang et al., 2012). This scheme requires an ex-

tra lookup table, and also requires the client to store

a dictionary of keywords for making search possi-

ble. Kissel et al. (Kissel and Wang, 2013) proposed a

two-phrase veriﬁable searchable encryption scheme.

This scheme like all the previous schemes requires

two rounds of communication. Naveed et al. (Naveed

et al., 2014) reduced the leakage of the number of

searched documents by storing documents in blocks.

Chase et al. (Chase and Shen, 2015) proposed an en-

cryption scheme that can perform string search.

Cash et al. (Cash et al., 2013) proposed an efﬁ-

cient symmetric searchable encryption scheme that

supports boolean search queries. Li et al. (Li et al.,

2015b) proposed LPSSE, a symmetric searchable

encryption scheme that supports encrypted phrase

search based on the non-adaptive security deﬁnition

of Curtmola et al (Curtmola et al., 2006).

Cao et al. (Cao et al., 2014) proposed a privacy-

preserving multi-keyword ranked search scheme us-

ing symmetric encryption. Sun et al. (Sun et al.,

2013) proposed an efﬁcient privacy-preserving multi-

keyword supporting cosine similarity measurement.

Sun et al. (Sun et al., 2016) constructed an encryption

scheme that supports multi-user boolean queries.

In (Ghosh Ray et al., 2020), Ray et al. presented

a symmetric key searchable encryption scheme that

supports phrase search. The scheme enables phrase

search by linking consecutive keywords through hash

chains. The hash values that constitute a hash link

are normally masked by the client and can only be

unmasked when a trapdoor is provided by the client.

However, this scheme has a privacy concern. Sup-

pose the server receives two trapdoors t

, and t

, and

successfully ﬁnds corresponding phrases µ

and µ

an encrypted document. If the keywords of µ

, and

are different, the server will learn if µ

and µ

oc-

cur consecutively or not. That is, the server will learn

whether the last keyword of µ

and the ﬁrst keyword

of µ

occur together in the document or not. This leak-

age of information is a limitation of the scheme.

Our SSE scheme proposes to get rid of this leak-

age. This scheme does not allow the cloud server to

learn any extra information other than the existence

of the phrase in the document. Besides, our scheme

produces a probabilistic trapdoor. That is, trapdoors

generated for the same phrase will be different each

time in the view of a third party. Hence, if an eaves-

dropper listens to the channel between the client, and

the server, it would not be able to infer anything about

the search pattern of the client. In other words, if a

phrase is searched multiple times, there is no way for

a third party eavesdropper to learn about it.

3 THE SCHEME

3.1 High Level Idea

Our scheme uses symmetric key cryptography. This

scheme takes as input a document and generates a

ciphertext. The ciphertext consists of two things: a

set of one-dimensional arrays and a set of adjacency

matrices. Our scheme encrypts the sentences of the

document separately. The encryption of a sentence

yields a one-dimensional array of size n and an ad-

jacency matrix of size n × n, n being the number of

keywords in that sentence. So, the encryption of a

document produces as many one-dimensional arrays

and adjacency matrices as there are sentences in the

documents. The one-dimensional array stores the en-

crypted keywords of a sentence in arbitrary order. The

adjacency matrix stores the adjacency information be-

tween the keywords in the sentence. The elements

of an adjacency matrix are random looking, however,

they can be used to ﬁnd if two keywords occur con-

secutively in the sentence or not. That is, the adja-

cency matrix stores the relationship between consec-

utive keywords in the sentence. Thus, the adjacency

matrix can be used to ﬁnd a phrase in the sentence if

sufﬁcient information is available. This information is

what we call trapdoor for phrase search. Our scheme

ensures that only an authorized user can generate a

trapdoor for searching in the sentence. This autho-

rized user is the same entity that holds the secret keys

of the encryption system. This searchable encryption

scheme does not reveal any information about the po-

sition of a phrase in a sentence if there is a successful

search. That is, the cloud server has no way to ﬁnd

the exact position of the phrase in the sentence.

3.2 Description of the Scheme

Let D be a sentence having a total of n keywords. We

show how the different algorithms of the SSE scheme

work.

Setup(1

): This algorithm takes as input, the secu-

rity parameter and outputs two keys K, and k, a keyed

hash function H(·) : {0, 1}

∗

−→ Z

, a symmetric en-

cryption function Enc(·) : {0, 1}

∗

−→ Z

(p being λ

bit prime), and two hash functions Hash

, and Hash

A New Leakage Resilient Symmetric Searchable Encryption Scheme for Phrase Search

369

which take inputs from {0, 1}

∗

and output in {0, 1}

In the subsequent sections, we denote the multiplica-

tion operation on Z

by ‘∗’.

ENC(D, K, k): This algorithm is run by the data

owner. In this algorithm, Enc(.) is applied repeti-

tively over sequence of keywords to achieve sentence

encryption. This algorithm takes as input the sen-

tence D containing n keywords, and the two keys

k, and K. First, the algorithm identiﬁes the key-

words w

, w

, . . . , w

in D. Then the algorithm gen-

erates a 1 × n array J, such that J[i] = Enc

), for

i = 1, 2, . . . , n. The algorithm also generates an n × n

matrix I, such that

I[i][ j] =











||w

) : if w

precedes w

in the sentence D,

R : R

←− Z

, otherwise.

The function outputs J and I.

Trapdoor(l, K, k): This algorithm takes as input a

string of keywords l, and the two keys K, and k. It

generates a trapdoor for l as follows.

(i) First, parse l as hw

, w

, . . . w

(ii) Compute F

= ( f

, f

, . . . , f

), where f

Enc

) for all i ∈ [1, c].

(iii) Compute F

= (

, . . . ,

c−1

), where

||w

i+1

), for all i ∈ [1, c − 1].

(iv) Select r

, r

, . . . , r

←− Z

, and compute M

, r

, . . . , r

), and N

= (h

, h

, . . . , h

), where

= Hash

( f

∗ r

), for i ∈ [1, c].

(v) Select s

, s

, . . . , s

c−1

←− Z

, and compute M

, s

, . . . , s

c−1

), and N

= (

, . . . ,

c−1

where

= Hash

∗

), for all i ∈ [1, c − 1].

(vi) Assign T = (T

, T

), where T

= (M

, N

), and

= (M

, N

). Return T as the trapdoor.

Search(T, J, I): This algorithm is run by the server

which returns ‘yes’ if the match is found, else it re-

turns ‘no’. The server ﬁrst parses the trapdoor T as

, T

). I is parsed as an n × n array, and J is parsed

as a 1 × n array. Then it parses T

as (M

, N

), and

as (M

, N

). Then M

is parsed as (r

, r

, . . . , r

and N

is parsed as (h

, h

, . . . , h

). The algorithm

ﬁnds α

, α

, . . . , α

∈ [1, n], if exist, such that h

Hash

(J[α

] ∗ r

), for all i ∈ [1, c]. If such indices

, α

, . . . , α

can be found, then the algorithm parses

as (s

, s

, . . . , s

c−1

), and N

as (

, . . . ,

c−1

Then the algorithm checks whether or not the follow-

ing relations satisfy.

= Hash

∗ I[α

][α

i+1

]) : ∀i ∈ [1, c − 1]

If the relations satisfy, the algorithm returns ‘yes’,

else it returns ‘no’.

3.3 Correctness

In this section, we show that our symmetric search-

able encryption is correct. First we show that the

search algorithm performed against a correctly gen-

erated trapdoor yields the correct output. That is, if

the trapdoor really exists in the encrypted sentence,

then the search algorithm returns yes, and it returns

no otherwise.

Lemma 1. In our scheme, the search algorithm re-

turns the correct output.

Proof. We show that if the search algorithms is run

with a correct ciphertext and a valid trapdoor, it out-

puts yes. Let us assume that the ciphertext be given

as J, and I. Here, J is a 1 × n array of all the en-

crypted keywords in the sentence, and I is the n × n

matrix of the ciphertext. Let us assume that the ci-

phertext is given by T , where T = (T

, T

). Fur-

ther, we assume that T

= (M

, N

), T

= (M

, N

= (r

, r

, . . . , r

), and N

= (h

, h

, . . . , h

), M

, s

, . . . , s

c−1

), and N

= (

, . . . ,

c−1

) for some

c ∈ [1, n]. If the trapdoor is valid, then by deﬁni-

tion, there must exist keywords w

, w

, . . . , w

∈ [1, n],

such that h

= Hash

(Enc

) ∗ r

);∀i ∈ [1, c], and

= Hash

||w

i+1

) ∗ s

);∀i ∈ [1, c − 1]. If the

phrase w

. . . w

exists in the ciphertext, then there

should be α

, α

, . . . , α

∈ [1, n], such that J[α

] =

Enc

);∀i ∈ [1, c], and I[α

][α

i+1

] = H

||w

i+1

Thus, h

= Hash

(J[α

] ∗ r

);∀i ∈ [1, c], and

Hash

(I[α

][α

i+1

] ∗ s

);∀i ∈ [1, c − 1]. Hence, the

search algorithm should return ‘yes’.

Now, we prove that if the search algorithm re-

turns ‘yes’ against some trapdoor T , the phrase that

T corresponds to, must be present in the ciphertext.

We parse T as (T

, T

), T

as (M

, N

), and T

, N

). Further, M

, N

, M

, and N

are parsed as

follows: M

= (r

, r

, . . . , r

), N

= (h

, h

, . . . , h

= (s

, s

, . . . , s

c−1

), and N

= (

, . . . ,

c−1

) for

some c ∈ [1, n]. Let w

. . . w

be the phrase that

corresponds to T . Thus, h

= Hash

(Enc

) ∗

) for all i ∈ [1, c], and

= Hash

||w

i+1

) ∗

) for i ∈ [1, c − 1]. If the search algorithm re-

turns ‘yes’, there must be α

, α

, . . . , α

∈ [1, n],

such that h

= Hash

(J[α

] ∗ r

);∀i ∈ [1, c], and

Hash

(I[α

][α

i+1

] ∗ s

);∀i ∈ [1, c − 1]. Now, if for

some j ∈ [1, c], J[α

] 6= Enc

), then we will have

a collision for the hash function Hash

for the pair

of inputs J[α

] ∗ r

, and Enc

) ∗ r

. The proba-

bility of this event is negligible. Again, if there is

some j ∈ [1, c − 1], such that w

j+1

does not occur

SECRYPT 2022 - 19th International Conference on Security and Cryptography

370

in the ciphertext, then we must have I[α

][α

i+1

]

←− Z

where Enc

) = J[α

], and Enc

j+1

) = J[α

i+1

for some i ∈ [1, c − 1]. Thus, the probability that

I[α

][α

i+1

] = H

||w

i+1

) is negligible. Hence, the

probability that

= Hash

(I[α

][α

i+1

] ∗ s

) will be

negligible too. Therefore, the probability that the

search returns ‘yes’ when the ciphertext does not

contain the phrase is negligible. This completes the

proof.

4 PERFORMANCE

In this section, we analyse the performance of our

symmetric searchable encryption scheme. First, we

calculate the amount of computation required to en-

crypt a sentence. Let n be the size of the sentence in

terms of the number of keywords. The ciphertext cor-

responding to the sentence is (J, I), where J is an array

of length n, and I is an n × n matrix. Thus, the size of

the ciphertext is n

+n. Computation of the ciphertext

requires n encryption operations, and n − 1 hash op-

erations. Thus, encrypting a sentence of length n re-

quires O(n) computations. The trapdoor correspond-

ing to a phrase of size c is of size 4c − 2. It requires

c encryption operations and 3c − 1 hash operations in

order to compute the trapdoor for a phrase having c

keywords. A search operation against a trapdoor for a

phrase of length c requires O(n∗c) hash operations, n

being the size of the sentence.

Comparison. Here we compare the performance of

our scheme with that of the schemes in (Uchide and

Kunihiro, 2016) and (Poon and Miri, 2019).

TSet based Approach of Phrase Search:

In (Uchide and Kunihiro, 2016), Uchide et al.

investigated TSet based approach for phrase search.

In the search phase of (Uchide and Kunihiro, 2016),

the most dominant cost is the |t| × (c–1) times

exponentiation, where |t| is the number of outputs

of TSet and c is the length of the query string.

We note that for query corresponding to a n-word

sentence, c = O(n), |t| = O(n

) and thus the number

of exponentions needed is O(n

) whereas, with our

algorithm, we need n ∗ c = O(n

) hash operations.

Bloom Filter based Approach of Phrase Search:

In (Poon and Miri, 2019), Poon et al. proposed phrase

search using bloom-ﬁlters. In (Poon and Miri, 2019),

for N number of documents, x number of distinct key-

words, c number of words in the query, b

number

of keyword pairs, b

keyword triplets and k num-

ber of bloom ﬁlter hash functions, the search com-

plexity is Mod(k(c − 2)N) + And(Nb

). Also to in-

sert x keywords in a m-bit bloom ﬁlter, the mini-

mum false positive probability p is achieved when

k =

ln(2) and m = −

x×ln(p)

ln(2)

. In our case the

probability of false positive is zero. Thus, at its

best, the search complexity of (Poon and Miri, 2019)

is Mod(k(q − 2)N) + And(Nb

) = Mod(

ln(2)(q −

2)N + And(Nb

). When N = 1, i.e., one document

with one n-word sentence such that all words are dis-

tinct, x = n. Also b

= O(n

) Thus search complexity

becomes Mod(−

ln(2)

(c − 2)) + And(b

). Thus they

need O(c) number of Mod operation and O(n

) num-

ber of And operation, whereas in our approach we

need number of hash operations which is quadratic

in n.

In Table 1, we provide a comparison between our

SSE scheme and some of the notable searchable en-

cryption schemes existing in the literature. It can be

seen in the table that among all the schemes that sup-

port phrase search, only our scheme does not have any

post-search leakage of any undue information.

5 CONCLUSION

In this paper, we propose a new symmetric search-

able encryption scheme that supports phrase search.

Our scheme encrypts a sentence of a document sepa-

rately. The encryption of a sentence yields a set of en-

crypted keywords and an adjacency matrix that stores

the ordering information about the keywords in the

sentence. To search in a ciphertext corresponding to

a sentence, a trapdoor is required. When the server

searches in a sentence using a trapdoor, the server

does not learn the physical position of the phrase in

the encrypted sentence. The proposed scheme avoids

the leakage associated with the searchable encryption

scheme by previous works. We have proved the se-

curity properties of our scheme. We have also imple-

mented the scheme using C and the OpenSSL library.

Our theoretical and experimental results show that our

scheme is suitable for deployment in real world sce-

narios.

A New Leakage Resilient Symmetric Searchable Encryption Scheme for Phrase Search

371

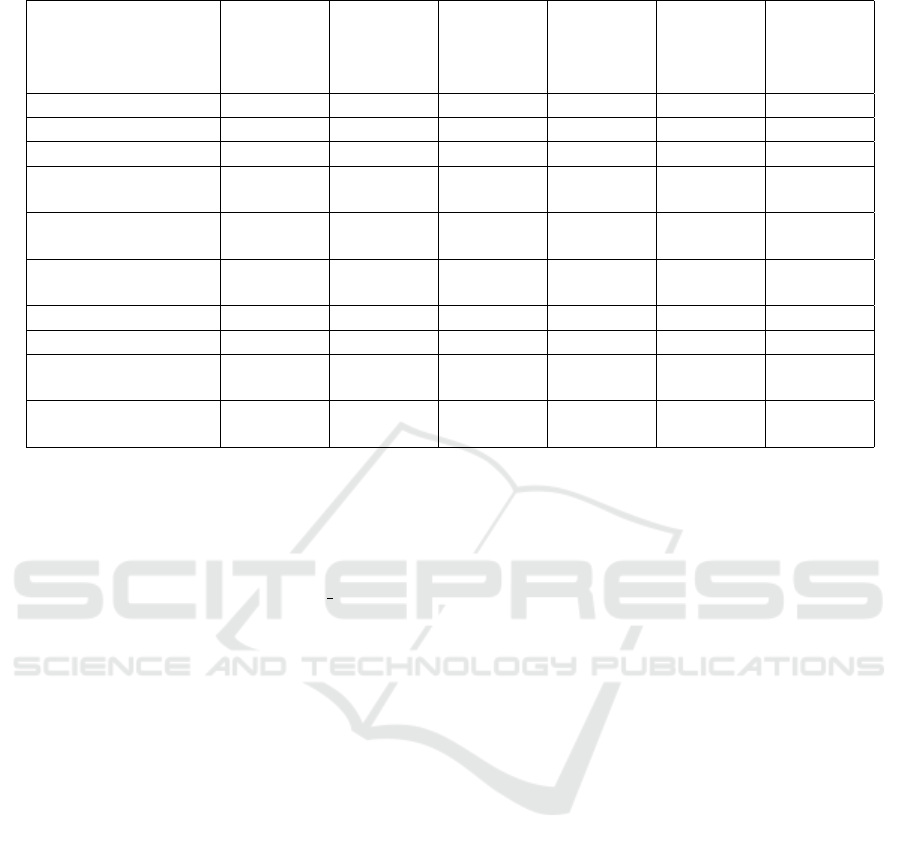
Table 1: properties and performances of different SSE schemes.

Property SSE (Curt-

mola

et al.,

2011)

PSS (Tang

et al.,

2012)

(Zit-

trower

and Zou,

2012)

LPSSE (Li

et al.,

2015b)

(Ghosh

Ray et al.,

2020)

This paper

String search

no yes yes yes yes yes

Non-adaptive security

yes yes no yes yes yes

Adaptive security

yes no no no no yes

Security against

active adversary

no no no no yes yes

Probabilistic

trapdoor

no no no no yes yes

Client storage

no dictionary

trusted

server

no no no

No. of rounds

1 2 2 1 1 1

Storage cost

O(N) O(N) O(N) O(N) O(N) O(N)

No. of encryptions

per keyword

O(N) O(N) O(N) O(N) 1 1

Leakage following a

– yes yes yes yes no

Properties and performances of different searchable encryption schemes. Search time is per keyword, where N is the number

of documents.

REFERENCES

(2007). http://www.fon.hum.uva.nl/david/ma ssp/2007

/timit/train/dr5/fsdc0/.

Boneh, D., Di Crescenzo, G., Ostrovsky, R., and Persiano,

G. (2004). Public Key Encryption With Keyword

Search. In International Conference on the Theory

and Applications of Cryptographic Techniques, pages

506–522. Springer.

Cao, N., Wang, C., Li, M., Ren, K., and Lou, W.

(2014). Privacy-Preserving Multi-Keyword Ranked

Search Over Encrypted Cloud Data. volume 25, pages

222–233. IEEE.

Cash, D., Jaeger, J., Jarecki, S., Jutla, C. S., Krawczyk, H.,

Rosu, M., and Steiner, M. (2014). Dynamic search-

able encryption in very-large databases: Data struc-

tures and implementation. In 21st Annual Network

and Distributed System Security Symposium, NDSS

2014, San Diego, California, USA, February 23-26,

2014. The Internet Society.

Cash, D., Jarecki, S., Jutla, C., Krawczyk, H., Ros¸u, M.-

C., and Steiner, M. (2013). Highly-Scalable Search-

able Symmetric Encryption With Support for Boolean

Queries. In Advances in Cryptology–CRYPTO 2013,

pages 353–373. Springer.

Chase, M. and Shen, E. (01 Jun. 2015). Substring-

searchable symmetric encryption. Proceedings on

Privacy Enhancing Technologies, 2015(2):263 – 281.

Curtmola, R., Garay, J., Kamara, S., and Ostrovsky, R.

(2006). Searchable symmetric encryption: Improved

deﬁnitions and efﬁcient constructions. In Proceed-

ings of the 13th ACM Conference on Computer and

Communications Security, CCS ’06, page 79–88, New

York, NY, USA. Association for Computing Machin-

ery.

Curtmola, R., Garay, J., Kamara, S., and Ostrovsky, R.

(2011). Searchable Symmetric Encryption: Improved

Deﬁnitions and Efﬁcient Constructions. volume 19,

pages 895–934. IOS Press.

Ghosh Ray, I., Rahulamathavan, Y., and Rajarajan, M.

(2020). A new lightweight symmetric searchable en-

cryption scheme for string identiﬁcation. IEEE Trans-

actions on Cloud Computing, 8(3):672–684.

Kamara, S., Papamanthou, C., and Roeder, T. (2012). Dy-

namic Searchable Symmetric Encryption. In Proceed-

ings of the 2012 ACM conference on Computer and

communications security, pages 965–976. ACM.

Kissel, Z. A. and Wang, J. (2013). Veriﬁable phrase search

over encrypted data secure against a semi-honest-but-

curious adversary. In 2013 IEEE 33rd International

Conference on Distributed Computing Systems Work-

shops, pages 126–131.

Li, M., Jia, W., Guo, C., Sun, W., and Tan, X. (2015a).

Lpsse: Lightweight phrase search with symmetric

searchable encryption in cloud storage. 2015 12th In-

ternational Conference on Information Technology -

New Generations, pages 174–178.

Li, M., Jia, W., Guo, C., Sun, W., and Tan, X. (2015b).

LPSSE: Lightweight Phrase Search With Symmetric

Searchable Encryption in Cloud Storage. In Informa-

tion Technology-New Generations (ITNG), 2015 12th

International Conference on, pages 174–178. IEEE.

Naveed, M., Prabhakaran, M., and Gunter, C. A. (2014).

Dynamic searchable encryption via blind storage. In

2014 IEEE Symposium on Security and Privacy, pages

639–654.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

372

Poon, H. T. and Miri, A. (2019). Fast phrase search for

encrypted cloud storage. IEEE Transactions on Cloud

Computing, 7(4):1002–1012.

Ray, I. G., Rahulamathavan, Y., and Rajarajan, M. (2020).

A new lightweight symmetric searchable encryption

scheme for string identiﬁcation. IEEE Trans. Cloud

Comput., 8(3):672–684.

Salam, M. I., Yau, W.-C., Chin, J.-J., Heng, S.-H., Ling,

H.-C., Phan, R. C., Poh, G. S., Tan, S.-Y., and Yap,

W.-S. (2015). Implementation of searchable symmet-

ric encryption for privacy-preserving keyword search

on cloud storage. Human-centric Computing and In-

formation Sciences, 5(1):1–16.

Song, D. X., Wagner, D., and Perrig, A. (2000). Practical

Techniques for Searches on Encrypted Data. In Secu-

rity and Privacy, 2000. S&P 2000. Proceedings. 2000

IEEE Symposium on, pages 44–55. IEEE.

Stefanov, E., Papamanthou, C., and Shi, E. (2014). Practical

Dynamic Searchable Encryption With Small Leakage.

In NDSS, volume 14, pages 23–26.

Sun, S.-F., Liu, J. K., Sakzad, A., Steinfeld, R., and Yuen,

T. H. (2016). An efﬁcient non-interactive multi-

client searchable encryption with support for boolean

queries. In Askoxylakis, I., Ioannidis, S., Katsikas, S.,

and Meadows, C., editors, Computer Security – ES-

ORICS 2016, pages 154–172, Cham. Springer Inter-

national Publishing.

Sun, W., Wang, B., Cao, N., Li, M., Lou, W., Hou, Y. T., and

Li, H. (2013). Privacy-preserving multi-keyword text

search in the cloud supporting similaritybased rank-

ing. In IN ASIACCS 2013.

Tang, Y., Gu, D., Ding, N., and Lu, H. (2012). Phrase

search over encrypted data with symmetric encryp-

tion scheme. In 2012 32nd International Conference

on Distributed Computing Systems Workshops, pages

471–480.

Tang, Y., Gu, D., Ding, N., and Lu, H. (2012). Phrase

Search Over Encrypted Data With Symmetric Encryp-

tion Scheme. In 2012 32nd International Conference

on Distributed Computing Systems Workshops, pages

471–480. IEEE.

Uchide, Y. and Kunihiro, N. (2016). Searchable symmetric

encryption capable of searching for an arbitrary string.

Security and Communication Networks, 9(12):1726–

1736.

Wang, B., Yu, S., Lou, W., and Hou, Y. T. (2014).

Privacy-preserving multi-keyword fuzzy search over

encrypted data in the cloud. In IEEE INFOCOM

2014 - IEEE Conference on Computer Communica-

tions, pages 2112–2120.

Zittrower, S. and Zou, C. C. (2012). Encrypted phrase

searching in the cloud. In 2012 IEEE Global Commu-

nications Conference (GLOBECOM), pages 764–770.

A New Leakage Resilient Symmetric Searchable Encryption Scheme for Phrase Search

373