Membership Inference Attacks on Aggregated Time Series with Linear

Programming

Antonin Voyez

1,3 a

, Tristan Allard

1 b

, Gildas Avoine

1,2 c

, Pierre Cauchois

Elisa Fromont

1,5,4 d

and Matthieu Simonin

Univ Rennes, CNRS, IRISA, France

INSA Rennes, CNRS, IRISA, France

ENEDIS, France

Inria, IRISA, France

IUF (Institut Universitaire de France), France

Keywords:

Privacy, Time Series, Membership Inference Attack, Subset Sum Problem, Gurobi.

Abstract:

Aggregating data is a widely used technique to protect privacy. Membership inference attacks on aggregated

data aim to infer whether a speciﬁc target belongs to a given aggregate. We propose to study how aggregated

time series data can be susceptible to simple membership inference privacy attacks in the presence of adver-

sarial background knowledge. We design a linear programming attack that strongly beneﬁts from the number

of data points published in the series and show on multiple public datasets how vulnerable the published data

can be if the size of the aggregated data is not carefully balanced with the published time series length. We

perform an extensive experimental evaluation of the attack on multiple publicly available datasets. We show

the vulnerability of aggregates made of thousands of time series when the aggregate length is not carefully

balanced with the published length of the time series.

1 INTRODUCTION

Private organizations and public bodies worldwide

are nowadays engaged in ambitious open data pro-

grams that aim at favoring the sharing and re-use

of data (The World Wide Web Foundation, 2017).

Opening data is rooted in century-old principles

and,

with today’s data collection capacities, is expected to

yield important and various beneﬁts (Deloitte, 2017;

The World Wide Web Foundation, 2017; The Euro-

pean Data Portal, 2015; OECD, 2020) (e.g., driving

public policies, strengthening citizens trust into gov-

ernments, fostering innovation, facilitating scientiﬁc

studies). Personal data are part of the open data move-

https://orcid.org/0000-0003-3248-1497

https://orcid.org/0000-0002-2777-0027

https://orcid.org/0000-0001-9743-1779

https://orcid.org/0000-0003-0133-3491

See, e.g., the XV

article of the Declaration of the

Rights of Man and of the Citizen (1789).

ment

and an ever-increasing quantity of information

about individiduals is made available online, often in

an aggregated form (e.g., averaged, summed up) in

order to comply with personal data protection laws

(e.g., the European GDPR

, the Californian CCPA

)

and (try to) avoid jeopardizing individual’s right to

privacy. In particular, datasets associating various

attributes, coming from the same data provider or

not, are especially valuable for understanding com-

plex correlations (e.g., gender, socio-economic data,

and mobility (Gauvin et al., 2020)).

Time series are considered as valuable data for

open data publication. They are unbounded se-

quences of measures performed over a given popula-

tion at a given sampling rate. For example, current

smart-meters enable the collection of ﬁne-grained

See, e.g., the GovLab Data Collaboratives effort (https:

//datacollaboratives.org/).

https://eur-lex.europa.eu/legal-content/EN/TXT/

HTML/?uri=CELEX:32016R0679

https://leginfo.legislature.ca.gov/faces/billTextClient.

xhtml?bill id=201720180SB1121

Voyez, A., Allard, T., Avoine, G., Cauchois, P., Fromont, E. and Simonin, M.

Membership Inference Attacks on Aggregated Time Series with Linear Programming.

DOI: 10.5220/0011276100003283

In Proceedings of the 19th International Conference on Security and Cr yptography (SECRYPT 2022), pages 193-204

ISBN: 978-989-758-590-6; ISSN: 2184-7711

193

electrical power consumption with one measure ev-

ery 30 minutes. Electrical consumption records are

then published under a variety of aggregated time

series

. Today, the publication of such datasets is

often encouraged by laws such as the EU directive

2019/1024

imposing to the states members to set up

open data programs for various information, includ-

ing energy consumption (Directive 2019/1024 Article

66).

The main protection measure, called threshold-

based aggregation in the following, consists in guar-

anteeing that the number of individuals per aggregate

is above a given threshold. The threshold is chosen

with the goal to preserve the subtle equilibrium be-

tween individual’s privacy and data utility (B

uscher

et al., 2017). Threshold-based aggregation may come

with additional protection measures (e.g., suppression

of outsiders, noise addition) but is often considered

as being sufﬁcient in real-life, even for sensitive data

(e.g., power consumption in France

), provided that

the threshold is high enough.

However, and despite its wide usage in real-life,

the lack of formal privacy guarantees of threshold-

based aggregation, together with the length of the

time series allowed to be published, does not allow to

formally claim that personal data is indeed protected.

In particular, powerful attackers may exist that hold

most of the raw data (if not all) and may use them for

performing membership inference attacks.

This new threat model is relevant in real-life situ-

ations, when the raw data are illegitimately accessed

after a (partial or total) disclosure, either acciden-

tally by careless employees or following an active at-

tack. Such threats must not be overlooked today as

witnessed by the ever-increasing list of major data

breaches. For example, the Ponemon Institute re-

ported in 2020 a strong rise in the number of insider-

caused cybersecurity incidents (+47% between 2018

and 2020)

. As another example, the 2021 Verizon

Data Breach Investigation Report shows the large

diversity of industries concerned (from ﬁnance and

healthcare to energy or transportation) and the distri-

bution of attack patterns having led to the breaches

Membership inference attacks form an important

part of the privacy attacks. They aim to infer whether

a speciﬁc target is present or absent from a dataset

See, e.g., the open data portal of the French national

electrical network manager (https://data.enedis.fr).

https://eur-lex.europa.eu/eli/dir/2019/1024/oj

https://www.legifrance.gouv.fr/codes/id/

LEGISCTA000034381202/2017-04-08

https://www.observeit.com/cost-of-insider-threats/

https://www.verizon.com/business/resources/reports/

dbir/2021/data-breach-statistics-by-industry/

using various methods such as statistical tests (Dwork

et al., 2017) and machine learning (Rigaki and Garcia,

2020). The presence of a target in a published aggre-

gate is a valuable knowledge for an attacker when the

aggregate is, or can be, publicly associated to other,

possibly sensitive, attributes.

Contributions. In this paper, we introduce (Sec-

tion 2) a new threat model where the attacker has ac-

cess to the published aggregates (e.g., averages, sums)

that are, or can be, associated to additional attributes,

and to the disclosed raw times series. He/she then

aims to determine whether (the time series of) a given

target is associated to the additional attribute(s). This

can actually be framed as a membership inference at-

tack. We then show (Section 3) that this member-

ship inference attack can be reduced to the subset sum

problem, which can be solved as a constraint pro-

gramming problem when data consist of time series.

Each time point serves as a constraint to efﬁciently

solve a subset sum problem. Based on this approach,

we perform (Section 4) experiments on real-life data

using the Gurobi solver, and show that our mem-

bership inference attack is successful in most cases.

Our ﬁndings demonstrate that breaking privacy when

aggregate-based techniques are used to publish time

series is much easier than expected. We analyse the

limit cases to eventually help publishers enforcing in-

dividuals’ privacy.

Table 1: Notations.

Notation Description

I Set of individuals

T Set of timestamps

S Full multiset of time series

Multiset of time series participating in

the aggregates

A Vector of aggregates published

θ Time budget of the attacker

p Pool size (number of solutions asked

to the solver)

P Set of solutions found by the attacker

G Adversarial guesses

| · | Cardinality

2 PROBLEM STATEMENT

2.1 Time Series

A time series is a timestamped sequence of data.

In the following, we consider ﬁxed-length univariate

integer-valued time series. We represent the full mul-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

194

tiset of time series as a |I |∗|T | matrix S (all notations

are deﬁned in Table 1) where the |I | rows represent

the time series of each individual and the |T | columns

represent the timestamps (i.e., a sequence of integers

from 1 to |T | for simplicity, see eq. 1). Each cell

i,t

∈ [d

min

, d

max

] thus represents the value of the i

individual at the t

timestamp. Without loss of gen-

erality, and unless explicitly stated, we consider in the

rest of the paper that d

min

= 0.

S =







1,1

··· S

1,|T |

|I |,1

··· S

|I |,|T |







(1)

2.2 The Publishing Environment

Publisher. As shown in Figure 1, the publishing en-

vironment considered consists of a publisher and an

attacker (described in Section 2.3). The publisher col-

lects from a set of individuals I a multiset of time se-

ries (where each individual produces a single ﬁxed-

length time series) associated to, possibly personal

and/or sensitive, additional attributes contextualizing

the time series (e.g., income, house surface, socio-

demographic information, electrical appliances).

Individuals

Collect

Get access

Publisher

Attacker

Publish aggregates

+ sensitive information

Who is in ?

(infer sensitive information)

Figure 1: The SUBSUM Attack.

Published Aggregates. The publisher selects a sub-

matrix S

of S and computes and publishes a vector

of aggregates A over S

. In this paper, we focus on

aggregates that are sums (we use the two terms in-

distinctly below). Note that all sum-based aggrega-

tion methods (e.g., average) can also be tackled by

our proposed attack with minor changes in the attack

constraints. Each aggregate is computed for a speciﬁc

timestamp t by summing the values of each individ-

ual in S

: A

∑

∀i

i,t

. The set of individuals se-

lected in S

represents the ground truth. We model

the ground truth as a vector of probability telling, for

each individual of S, which one is part of S

. The

probabilities of the i

individual is set to 1 if and only

if the i

individual is in S

, and to 0 otherwise. It is

worth noting that the sequences of aggregates A usu-

ally come along with the timestamps and the number

of time series aggregated.

Published Additional Attributes. To make the pub-

lished aggregates more valuable, they are usually as-

sociated with additional information that character-

izes the subpopulation in the aggregates. Such char-

acterizing attributes can be for example the average

surface of the households in the aggregates, the av-

erage age of the individuals, the incomes, the region,

etc. To illustrate this point, a practical case is the pub-

lication of the average daily electricity consumption

(time series) per region (attribute).

2.3 Threat Model

The usual threat model obviously considers an at-

tacker who aims to retrieve from the published aggre-

gates, protected through various privacy-preserving

measures, the identity (or associated valuable infor-

mation) of the people concerned by these data (Ja-

yaraman et al., 2021) (Bauer and Bindschaedler,

2020) (Pyrgelis et al., 2018). A step further consists

in considering a threat model where the attacker has

access both to the (published) aggregated time series

and to the (leaked) raw time series (while the addi-

tional attributes remain secret and the goal of the at-

tack remains unchanged). Two points should then be

discussed: the relevance of this scenario and the at-

tacker’s motivation to perform an attack in such a sce-

nario.

Due to legal requirements and widespread security

best practices, publishers usually store direct iden-

tiﬁers and raw time series in separate databases

applying for example traditional pseudonymization

schemes. Dedicated access control policies, archival

rules, or security measures can then be applied to each

database (e.g., retention period limited to a couple of

years for ﬁne-grained electric consumption time se-

ries). Isolating direct identiﬁers from time series in-

deed prevents direct re-identiﬁcations from malicious

employees or external attackers exploiting a leak

The same security principles might apply to the stor-

age of the additional, possibly sensitive, attributes.

Note that variants of the above context can be eas-

ily captured by our model. An example of a vari-

ant, common in real-life, is when the additional at-

tributes come from another data provider collaborat-

ing with the publisher for computing cross-database

We use the term database for simplicity without any

assumption on the underlying storage mechanisms.

The wealth of information contained in

pseudonymized time series still allows massive re-

identiﬁcations, but publishers seldom apply destructive

privacy-preserving schemes to the time series that they

store for preserving their utility.

Membership Inference Attacks on Aggregated Time Series with Linear Programming

195

statistics. Whatever the scenario, this results in a set

of databases, isolated one from the other, either for se-

curity reasons in order to mitigate the impacts of data

leaks, or simply because multiple data providers col-

laborate. Because data leaks are common, whether

they are due to insider attackers or to external ones,

we believe that considering that raw data may even-

tually leak is a conservative approach that deserves

to be explored. Obviously, if the identiﬁers, the time

series, and the additional attributes all leak together,

attacking the published aggregates is useless. How-

ever, in cases where only the raw times series leak, at-

tackers need to deploy membership inference attacks

for learning the association between a target individ-

ual (or more) and its attributes. In the following, we

consider this threat model. We show on a real-life ex-

ample that an attacker is able to efﬁciently retrieve the

attributes of a target using linear programming.

More formally, the adversarial background knowl-

edge consists of the full multiset of time series S.

Given his/her background knowledge S, the vector A

of timestamped aggregates, and the number of time

series aggregated, the attacker outputs a vector of

guesses G over the participation of each individual

to the vector of aggregates. The vector of guesses is

similar to the ground truth vector s.t. the i

value

of the vector of guesses represents the probability of

the participation of the i

individual to the aggregate.

The closer to the ground truth the guesses, the better

for the attacker.

3 THE SUBSUM ATTACK

The SUBSUM attack is based on solving the subset

sum problem (Kellerer et al., 2004) over the vector A

of aggregates given the set of time series S.

3.1 Constraint Programming and

Solvers

Constraint programming (CP) is a computation

paradigm that can be used to model mathematical op-

timization problems such as the subset sum problem.

The problem is modeled by a set of variables and for-

mulas, called constraints, that describe and bound the

problem, and an optimization objective. The objec-

tive can be to prove (or disprove) the feasibility of the

problem, or to ﬁnd real solutions matching the con-

straints, if any. Integer Programming (IP) focuses on

problems where all the variables are integers. An in-

teger programming set of constraints for solving the

subset sum problem has the following form:

∑

i≤n

(X[i] ·V [i]) == s (2)

where s is the sum to reach, V is a vector of integer

values and X a vector of Boolean values indicating

whether to add a speciﬁc weight to the bag (i.e., set to

1) or not (i.e., set to 0).

A wide variety of solvers are able to solve such

problem (e.g., Gurobi (Gurobi Optimization, 2020),

Choco (Charles Prud’homme et al., 2016), OR-

Tools (Laurent Perron, 2019)).

3.2 Attack Formulation

The SUBSUM attack solves a well known NP-hard

problem and would be highly inefﬁcient and not scale

in the general case. This is, in part, due to the fact that

for a given timestamp, an important set of individuals

may have similar values which may further increase

the combinatorics. By exploiting the different time

points (with different aggregate values but originating

from the same set of individuals), the solver is able

to prune the unsatisfactory solutions much faster and

converge, with enough constraints, to possibly unique

solutions if all individuals do not have identical values

as another individual in all time points.

Algorithm 1 thus combines multiple subset sum

problems, one for each aggregate (each timestamp),

into a single set of IP constraints. Let X be a vector

of |S | Boolean variables denoting the time series that

are (possibly in case of multiple solutions) part of the

aggregate. We deﬁne one constraint per aggregate in

A :

∑

i≤n

(X[i] · S

i,t

) == A

(3)

Once these constraints are deﬁned, we deﬁne one

ﬁnal constraint representing the attacker knowledge

of the number |S

| of individuals present in the ag-

gregates.

∑

i≤n

X[i] == |S

| (4)

Our objective is to ﬁnd less than p solutions (ide-

ally p = 2) to infer meaningful information about the

aggregate members within a reasonable time (the wall

time θ). The solver runs until one of the following

conditions is satisﬁed: (1) all the existing solutions

are found, (2) the maximum number of solutions, p,

is reached, (3) the time budget θ is exhausted. The

solver outputs a set P of up to p candidate solutions

together with a status code. Each solution is a vector

of probability, similarly to the ground truth vector, in-

dicating the individuals from S that, when summed up

together on the right timestamp(s), solve the given set

SECRYPT 2022 - 19th International Conference on Security and Cryptography

196

Algorithm 1: SUBSUM attack.

Input: The set of time series (S), the

aggregates (A), the time budget (θ),

the number of solutions to look for (p)

Output: The solutions found (P), the guesses

(G), the status code (status)

set time limit(θ)

set pool size( p)

for i ∈ |S| do

add variable(X

, {0, 1})

end

for t ∈ |A| do

add constraint(

∑

∀i∈S

i,t

== A

)

end

solve()

P = get solutions()

G = to probability vector(P )

status = get status()

return P , G, status

Functions used in the algorithm :

add variable(bounds): Deﬁne an integer

variable bounded to a given set of values.

add constraint(constraint): Deﬁne a

constraint binding the model.

set pool size(p): Deﬁne an upper bound p

on the number of solutions to search for.

set time limit(θ): Set the time budget θ of

the solver.

solve(): Solves the problem.

get status(): Get the status of the solver af-

ter its termination. We assume that at least the

two following statuses are available : OPTIMAL

(i.e., either p solutions are found or less than

p solutions are found but no more solutions

exist), TIMELIMIT (i.e., the time budget θ is

over) and INFEASIBLE (i.e., the model cannot

be solved).

get solutions(): Get the solutions found

by the solver (if any).

of constraints X. Finally, the attacker computes the

frequency of each individual in the set of solutions in

order to obtain his guesses G.

4 EXPERIMENTS

We perform an extensive experimental survey of the

attack using two open datasets: the CER ISSDA

dataset (CER, 2012) and the London Households En-

Table 2: Values of the parameters used in our experiments.

Parameter Value

S {ISSDA-30m, London-30m}

|S| {1000, 2000, 3000, 4000, 4500}

| {0%, 10%, . . . , 100%} × |S |

|A| {0%, 10%, . . . , 100%} × |S |

θ {1000, 2000, 4000, 8000, 86400}

p {2, 100}

ergy Consumption dataset. Our results show that

the SUBSUM attack is highly efﬁcient (e.g., absolute

success) when it’s requirements are met, i.e., when

the vector of aggregates published contains a sufﬁ-

cient number of aggregates (sufﬁcient number of con-

straints) and when the attacker has sufﬁcient comput-

ing power.

4.1 Settings

Experimental Environment. It consists of two soft-

ware modules

First, the driver module, written in Python, is in

charge of driving the complete set of experiments :

deploying the experiments, launching them, stopping

them, and ﬁnally fetching the experimental results.

Based on the driver, we deployed our experiments

on our own OAR2 (Linux)

computing cluster, allo-

cating 2 cores (2.6 GHz) and 2 GB RAM at least to

each experiment. Each experiment is a SUBSUM at-

tack fully parameterized (e.g., full set of time series,

aggregates published). We describe it below.

The second software module is the solver in

charge of performing a SUBSUM attack given a set

of parameters. We use in our experiments the Gurobi

solver (Gurobi Optimization, 2020), a well-known

and efﬁcient IP solver, but any other solver can be

used provided that it implements an API similar to

the one used in Algorithm 1.

Datasets. We performed our experiments over the

real-life ISSDA CER public dataset (CER, 2012)

which contains power consumption time series of

6435 individuals for over 1.5 years at a 30 mins rate.

Removing the time series containing at least one miss-

ing value left us with 4622 time series. We changed

the unit from kWh to Wh obtaining thus only inte-

ger values (required by our solver). We refer to this

cleaned dataset as ISSDA-30m.

We replicate the experiments on the real-life Lon-

Available here: https://gitlab.inria.fr/avoyez1/subsum

https://oar.imag.fr/

https://www.ucd.ie/issda/data/

commissionforenergyregulationcer

Membership Inference Attacks on Aggregated Time Series with Linear Programming

197

don Households Energy Consumption dataset (UK

Power Networks, 2013) containing 5567 individuals

for over 2.5 years at a 30 mins rate. As this dataset

contains a lot of missing values (all individuals have

at least one missing value), we ﬁlled the missing

values using the consumption of the previous week.

Then, we removed the individuals that have missing

values along several weeks. This left us with 5446 in-

dividuals. We also changed the unit from kWh to Wh

in order to obtain only integer values. We refer to this

cleaned dataset as London-30m.

Experimental Protocol. We consider three main pa-

rameters impacting the SUBSUM attack: the size |S|

of the set of time series, the size |A| of the vector of

aggregates published (number of constraints), and the

number of values aggregated in each aggregate |S

Table 2 shows the parameter values we use in our ex-

periments. For each triple of parameters, we generate

20 experiments

where each experiment is a SUB-

SUM attack over (1) a set of time series, (2) a vector

A of aggregates published, and (3) a time budget θ.

At each experiment, the full population S, together

with the individuals S

that are part of the vector of

aggregates, are randomly selected. We log for each

experiment the ground truth (i.e., the exact set of in-

dividuals in S

), the candidate solution(s) found by

the solver, the status of the solver, and the wall-clock

time elapsed during the attack.

Success Deﬁnition. Our experimental validation con-

siders a ﬂexible success deﬁnition. An attack is con-

sidered to be a success if the solver ﬁnds strictly less

than p solutions in the allowed time θ

. Indeed, this

implies (1) that the solution is part of the pool of so-

lutions and (2) that the solver found all the solutions.

We will especially focus on a pool size equals to 2.

In this case, a success occurs when the solver outputs

a single solution: the membership inference is per-

fect. However, a pool size equals to 2 is not always

sufﬁcient. In these cases, we increase the pool size

and analyze the solutions more deeply found by the

solver, showing the distribution of the guess vector

on the individuals that are part of the ground truth.

Performing 20 times the SUBSUM attack on the same

set of parameters is sufﬁcient for obtaining a stable success

rate for the given set of parameters.

Note that this is a somewhat precautionary success

measurement since the attacker will draw conclusions only

when he/she is certain that all solutions have been found

by the solver. Other success metrics can be considered in

which the attacker gains information from incomplete sets

of solutions returned by the solver. However, when the

solver reaches the time budget or when the pool p is ﬁlled,

the solver fails to prove the non-existence of other solutions.

Inference on incomplete results might be refuted by new, yet

undiscovered solutions.

4.2 Experimental Results

Our experiments aim at providing clear insights on

the conditions leading to successful SUBSUM attacks.

First, we start in Section 4.2.1 by studying the SUB-

SUM success rate according to the total number of

time series in the full population (population size),

the number of time series aggregated in the published

vector of aggregates (aggregate size), and the length

of this vector (number of constraints). We set here the

time budget to a value sufﬁciently high for not inter-

fering with the attack. Through this study, we observe

a clear relationship between the population size and

the published vector of aggregates (size and length)

for a successful SUBSUM attack. This allows us to

express both the size of the published vector of ag-

gregates and its length relatively, as a fraction of the

population size. Then, we study in Section 4.2.2 the

impact of the time budget on the success rate, setting

the other parameters to ﬁxed values. Finally, we study

in Section 4.2.3 the efﬁciency of the SUBSUM attack

on the full population available in our datasets.

4.2.1 Relationship between the Number of

Individuals and the Success

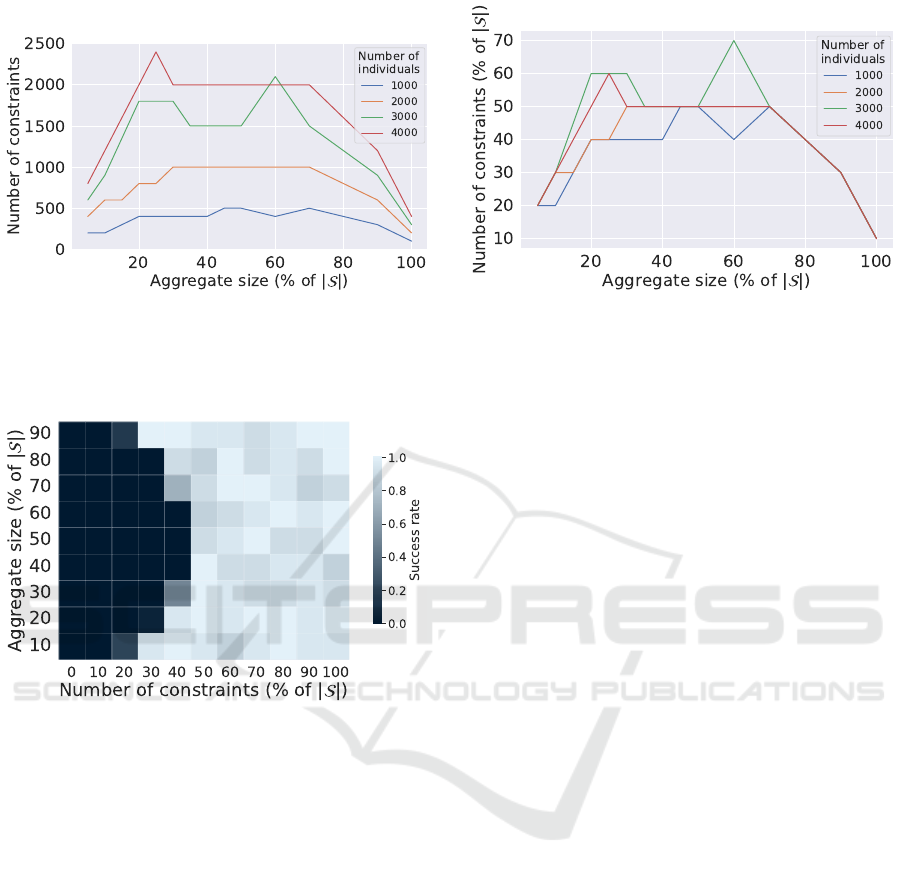
Figure 2 shows the minimal number of constraints re-

quired to have at least one success for several pop-

ulation sizes and for a time budget large enough for

not interfering (i.e., θ = 24h). We can see that, even

if the required number of constraints before getting a

success increases with the population size, it follows

a parabolic shape for all population sizes. Figure 3

shows the results of attacks with respect to the aggre-

gate size and the number of constraints for a small

dataset of 1000 individuals and a small time budget

of 1000s (approximately 15 minutes).

As already seen in Figure 2, Figure 3 shows that

the attacks fail in a parabolic area centered around ag-

gregates of half the population size. These failures

are due to the fact that the solver reaches the maxi-

mum allocated time. Outside this area of failure, the

attacks are mostly successful with the exception of a

few, randomly distributed, failed experiments which

depend on the original aggregate and population sam-

ples. In this ”light” area, the few failures are due to

the existence of several possible solutions (we provide

below in Section 4.2.3 an advanced analysis of the

cases where several solutions exist). After reaching

an aggregate size corresponding to 50% of the pop-

ulation, it is expected that the number of constraints

needed goes down again which comes from the fact

that knowing S, identifying |S

| individuals in S is at

least as difﬁcult as identifying |S| − |S

| individuals.

With a small aggregate size (lower than 50% of the

SECRYPT 2022 - 19th International Conference on Security and Cryptography

198

(a) Y axis: absolute number of constraints. (b) Y axis: number of constraints (% of the number of indi-

viduals).

Figure 2: Minimal number of constraints before getting at least one success. Parameters : Dataset = ISSDA-30m, |S | = {1000,

2000, 3000, 4000}, θ=24h, p=2, 20 repetitions.

Figure 3: Success rate (0 : all failed, 1 : all succeed). Pa-

rameters : Dataset = ISSDA-30m, |S| = 1000, θ=1000s,

p=2, 20 repetitions.

population size) the number of constraints needed is

often twice the size of the aggregate: in general the

number of constraints needed to successfully attack a

population of size |S| should be at least in the order of

the aggregate size |S

|. Conversely, if the number of

constraints is much lower than the aggregate size, the

dataset is deemed safe (relatively to the time budget θ

and to the pool size p) to the SUBSUM attack. Build-

ing on this result, in the following, both the aggregate

size |S

| and the length |A| of the vector of aggre-

gates (number of constraints) are expressed as a frac-

tion of the population size |S |. Note that the length

of the vector of aggregates might be larger than the

population size, resulting thus in fractions larger than

100% the population size.

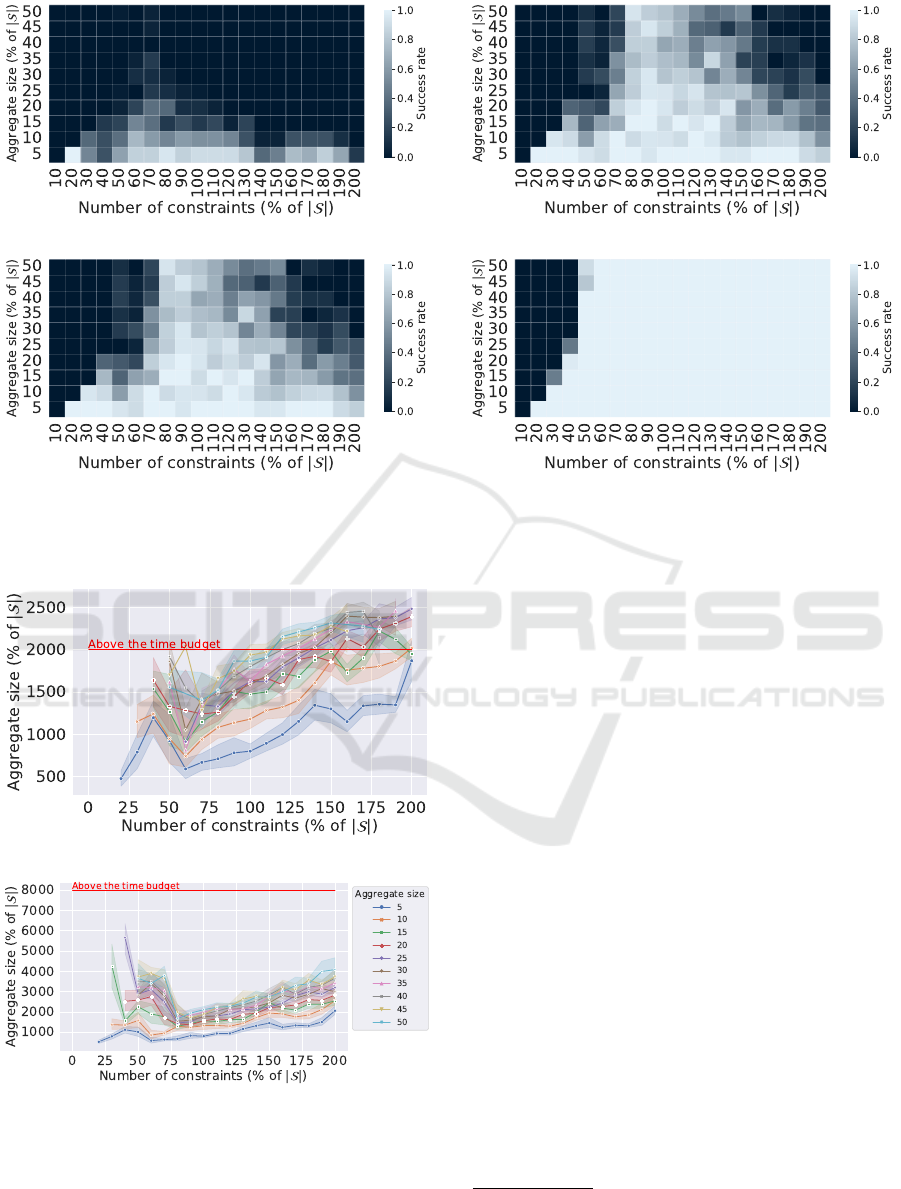
4.2.2 Impact of the Time Budget

For practical reasons, we evaluate the impact of the

time budget on a rather small dataset with |S| = 2000.

As can been seen in Figure 4, the time budget θ has an

impact on the attack success: the higher the time bud-

get, the higher the success rate. However, as shown

in Figure 4d, even with a high time budget, attacking

an aggregate with a small number of constraints (the

left dark sides of Figures 4b, 4c and 4d) will be un-

successful. Conversely, if the time budget is too low

and the number of constraints is too high (the right

black / grey area of the Figures 4a, 4b and 4c), the

solver does not have the time to solve the problem

with its given parameters. Figure 5 shows the experi-

ments time (in seconds). We note three areas of inter-

est: 1) an area with missing points (before reaching

25% of constraints) corresponding to the, previously

deﬁned, parabolic area of failures 2) the failures due

to reaching the allowed solver time and 3) when in-

creasing the number of constraints, the sudden drop

in execution time until a point where the attack is the

fastest for all aggregate sizes. After this point, the

execution time increases again linearly with the num-

ber of constraints up to the point where the execution

time reach the allowed time again (Figure 5b). There

is thus a clear compromise to make between the num-

ber of constraints used (that needs to be in the order of

the aggregate size) and the time budget. If the attacker

has a short time budget, he/she might prefer not using

all the available constraints at his/her disposal.

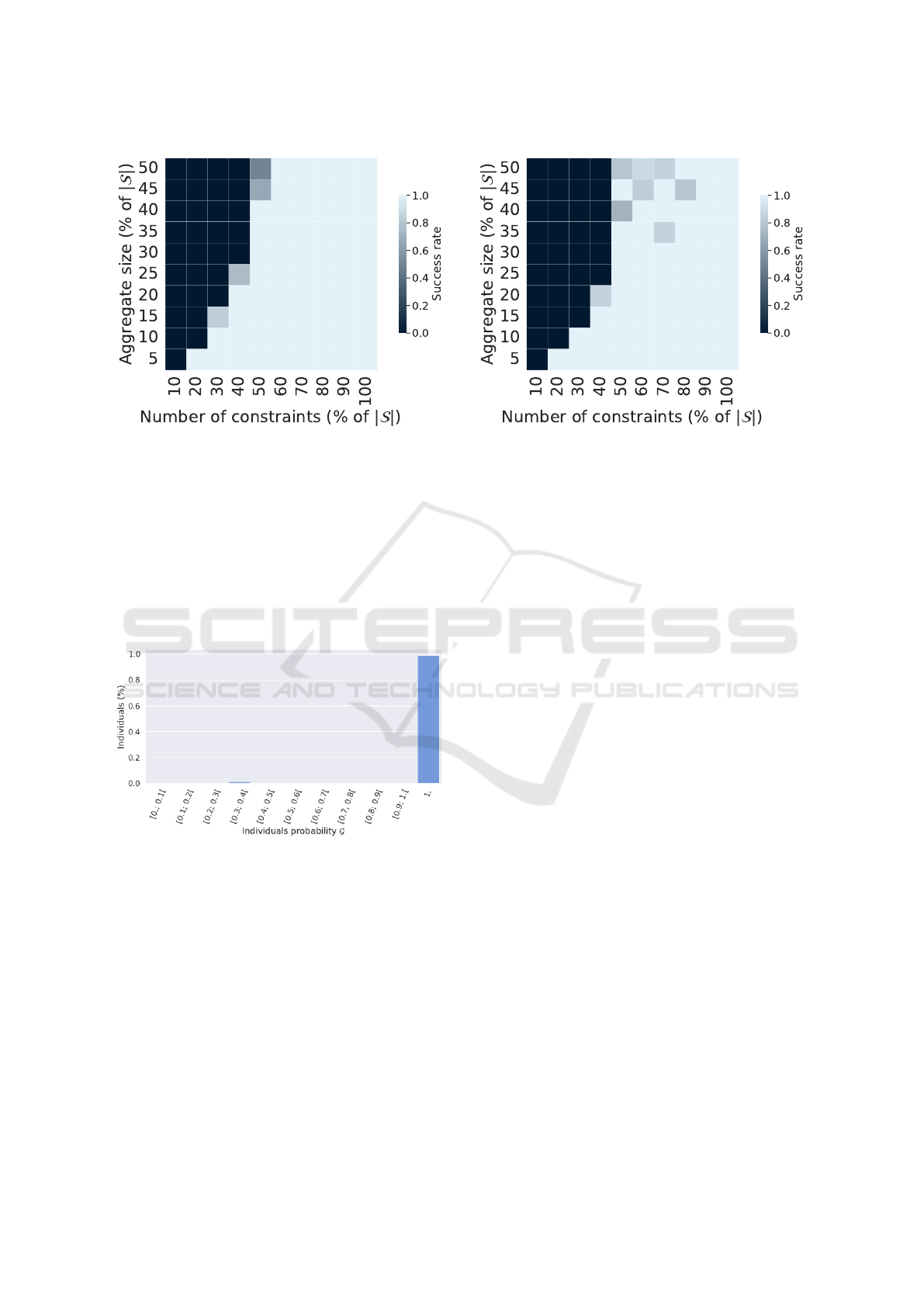
4.2.3 Attacking Large Populations

The attacks on our largest dataset provide results sim-

ilar to the ones previously described. However, since

the dataset is larger, we need to increase the time bud-

get to 24h to observe the same phenomena. As shown

in Figure 6, the relationship between the dataset size,

the aggregate size and the number of aggregates re-

Membership Inference Attacks on Aggregated Time Series with Linear Programming

199

(a) θ = 1000s. (b) θ = 2000s.

Figure 4: Evolution of the success (0 : all failed, 1 : all succeed) depending on the time budget. Parameters : dataset =

ISSDA-30m, |S | = 2000, θ = {1000s, 2000s, 4000s, 8000s}, p = 2, 20 repetitions.

(a) θ = 2000s.

(b) θ = 8000s.

Figure 5: Evolution of experiments time depending on the

time budget. Parameters : dataset = ISSDA-30m, |S| =

2000, θ = {2000s, 8000s}, p = 2, 20 repetitions.

quired for the attack to succeed is similar to what

we observed in the other experiments. In particular,

in this case, we need roughly twice more constraints

than the aggregate size until we reach an aggregate

size of 25% of |S|. After that, the number of con-

straints needed to reach a success remains stable at

50% of |S|.

It is worth to note that we set the pool size to

p = 100 in these experiments, meaning that the at-

tack is considered to be successful if the number of

solutions found is between 1 and 99. This allows us

to study the cases where several solutions are found,

which make G worth analyzing. We chose the experi-

ment in which the solver returned the highest number

of solutions and where the intersection of these solu-

tions is the smallest (in other words, where the num-

ber of individuals that are part of several solutions is

the highest). This case occurred in one of the 20 repe-

titions of the attack performed with the following pa-

rameters: dataset = ISSDA-30m, |S| = 4500, θ = 24h,

p = 100, |S

| = 225 (5%) and |A| = 900 (20%). It

resulted in a pool containing 3 solutions. We repre-

sent in Figure 7 the part of the guess vector limited to

the individuals found in the 3 solutions. Figure 7 is a

histogram showing the fraction of individuals (Y-axis)

associated to eleven possible ranges of guess in G

(X-axis). The ﬁgure shows that 224 (98.7%) individ-

uals appear in all the solutions: their membership can

Recall that the vector of guesses G contains for each

individual the probability that the individual participates to

SECRYPT 2022 - 19th International Conference on Security and Cryptography

200

(a) Dataset = London-30m. (b) Dataset = ISSDA-30m.

Figure 6: Attack success (0 : all fail, 1 : all succeed) for datasets of 4500 individuals. Parameters : dataset = {ISSDA-30m,

London-30m}, |S| = 4500, θ = 24h, p = 100, 20 repetitions.

thus be completely inferred with certainty while only

one individual differs in all three solutions: the mem-

bership probability of the corresponding individuals

is thus equal to 1/3. This shows that the SUBSUM at-

tack manages to gain signiﬁcant knowledge about the

aggregate members even when multiple solutions are

provided.

Figure 7: Focus on the experiment in which the solver re-

turned the highest number of solutions and where the inter-

section of these solutions is the smallest (3 solutions found

in this case). We show here the fraction of individuals as-

sociated to each possible adversarial guess value (organized

within eleven ranges). Parameters : dataset = ISSDA-30m,

|S| = 4500, θ = 24h, p = 100, |S

| = 225 (5%), |A| = 900

(20%).

5 RELATED WORKS

In the literature, attacks applicable against the

privacy-preserving publication of electrical consump-

tion data can be separated in three categories. First,

there is the Linear reconstruction attacks where the

attackers aim at ﬁnding back the original dataset from

a publication. Secondly, the Membership Inference

Attacks (MIA in short) looks if a speciﬁc individual

is part of a publication. Lastly, NonIntrusive Load

Monitoring (or NILM) tries to infers valuable infor-

mation (e.g., the devices used) from an electrical con-

sumption time series. We consider our attack as be-

ing a membership inference attack (we try to know

which individuals take part in a publication) by using

methodologies explored by the reconstruction attacks

(the usage of linear programming solvers).

5.1 Linear Reconstruction Attacks

Linear reconstruction attacks (Cohen and Nissim,

2020; Dinur and Nissim, 2003; Dwork et al., 2007;

Dwork and Yekhanin, 2008; Lacharit

e et al., 2018;

Quadrianto et al., 2008), illustrated by Cohen & al.

(Cohen and Nissim, 2020), are probably the closest

from our attack. In these attacks, an attacker is given

access to an interface allowing him to generate ag-

gregates from limited queries on the dataset. The at-

tacker sends a set of queries, each of them getting a

new aggregate from a randomly selected subset of the

dataset. Each query is then used to build a set of con-

straints that are then solved by a linear programming

solver. As for our attack, the goal is to extract private

information from a set of constraints. However, the

SUBSUM attack differs in several ways. First, the lin-

ear reconstruction attack aims to reconstruct a private

dataset (e.g., the values of the dataset elements) while

our attack aims to reconstruct private aggregates from

known data. The attack aims to infer the presence

or the absence of individuals in an aggregate and not

Membership Inference Attacks on Aggregated Time Series with Linear Programming

201

their values. Second, due to the different objective

of the attack, the attacker does not require the same

background knowledge. Our attack does not require

access to a query interface and can be performed on a

static set of aggregates as they are generally published

in open data programs. However, the large number of

queries required by the linear reconstruction attack is

somewhat balanced by the requirement of the individ-

uals’ values.

5.2 Membership Inference Attacks

Membership inference attacks are another family of

attacks where the attacker wishes to infer the pres-

ence or the absence of a target inside a dataset or

whether a target has played a part in the result of

a function (Dwork et al., 2017; Rigaki and Garcia,

2020). Datasets can broadly take the form of ag-

gregates (Bauer and Bindschaedler, 2020; B

uscher

et al., 2017; Jayaraman et al., 2021; Pyrgelis et al.,

2020a; Pyrgelis et al., 2018; Pyrgelis et al., 2020b;

Zhang et al., 2020), data used to train machine learn-

ing model (Long et al., 2020; Melis et al., 2019;

Salem et al., 2019; Shokri et al., 2017; Truex et al.,

2019; Yeom et al., 2018), genomics database (Homer

et al., 2008; Samani et al., 2015; Sankararaman

et al., 2009) or original data used to generate synthetic

ones (Stadler et al., 2020).

5.2.1 Membership Inference Attacks on

Aggregates

When membership inference attacks are applied to

aggregates (Bauer and Bindschaedler, 2020; B

uscher

et al., 2017; Jayaraman et al., 2021; Pyrgelis et al.,

2020a; Pyrgelis et al., 2018; Pyrgelis et al., 2020b;

Zhang et al., 2020), as in our approach, the aim is to

ﬁnd whether an individual is part of an aggregate or a

set of aggregates. In (Pyrgelis et al., 2018), an attacker

has access to a set of aggregates representing the num-

ber of people visiting a speciﬁc geographic point at a

particular time. Similarly to time series, each geo-

graphic point generates a new record at given periods.

Prior to the attack, the attacker has access to incom-

plete background knowledge about a target (a single

person) telling where it was at a given time. The target

can be present in the set of observed points or not. The

attacker will then train a machine learning classiﬁer

which will be able to infer whether or not the target

is present on at least one geographic point at a given

time outside his training range. Compared to our at-

tack, this attack required far less background knowl-

edge: only a few points where the target is present or

not. However its scale is limited: it is only able to

infer the presence or the absence of the target inside a

set of aggregates while our attack can reconstruct up

to every record present in the aggregate. Membership

inference can be applied to more generic data (Bauer

and Bindschaedler, 2020; Jayaraman et al., 2021). In

these cases a similar method is used: an attack model

is trained with similar data as the one attacked. This

model is then used to deduce the presence or the ab-

sence of a speciﬁc target in an aggregate.

5.2.2 Membership Inference Attack on ML

Models

These attacks (Long et al., 2020; Melis et al., 2019;

Salem et al., 2019; Shokri et al., 2017; Truex et al.,

2019; Yeom et al., 2018) aim to ﬁnd whether an in-

dividual is part of the dataset used to train a ma-

chine learning model. The attacker has access to un-

limited queries to a black box model and to records

sampled from the same distribution as the original

training data. Usually (Shokri et al., 2017; Truex

et al., 2019), the attacker will train an ML-based at-

tack model against multiple shadow models which

replicate the behavior of the attacked model and are

trained with some known datasets (with and without

the target individual). The attack model will then be

applied against the real model to attack. Membership

attacks on ML models requires knowledge of distri-

bution of the attacked records and large amount of

data to train the shadow models. However, they do

not need to get access to the real data used by the at-

tacked model. These attacks are, for now, limited to

attacking machine learning models and not aggregate

data.

5.3 Non Intrusive Load Monitoring

(NILM) introduced by Hart (Hart, 1992) in 1992 is

a ﬁeld of study aiming to extract information con-

tained in electric consumption time series such as the

occupancy of a household, the electric devices used

and even the TV program watched. NILM algorithms

can use a wide variety of methods to reach this goal

from ﬁnite state machines to knapsack-based algo-

rithms and machine learning classiﬁers. Despite not

being considered as privacy attacks, these algorithms

can be used as a tool to retrieve private information

contained in time series. To the best of our knowl-

edge, no attempt has been made to adapt NILM prin-

ciples to extract information contained in an aggrega-

tion of multiple electric load consumption time series.

NILM-based attacks may be used as a complement

of our attack either to ﬁlter a set of loads potentially

present in the aggregates or to train a NILM model

from the consumption values of the aggregates.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

202

6 CONCLUSION

Membership inference attacks aim to infer whether

a speciﬁc individual belongs to a given aggregate.

In this work, we introduced a new technique to per-

form inference attacks on (threshold-based) aggre-

gated time series. Given a publicly known dataset

of time series, and aggregated values (one value per

timestamp) calculated from a private subset of that

dataset, the adversary that we consider is able to re-

identify the individuals belonging to the private sub-

set. To do so, we modeled the membership inference

attack as a subset sum problem and we used Gurobi to

solve it. We completed experiments on two real-life

datasets containing power consumption time series,

from UK and Ireland, respectively. We showed that

if the number of available aggregated values is larger

than the aggregate size (i.e., the number of individ-

uals in the private subset), then the SUBSUM attack

is highly likely successful. Interesting future works

include relaxing the background knowledge required

by the SUBSUM attack (e.g., missing time series, ap-

proximate values) and coping with advanced privacy-

preserving approaches (e.g., differential privacy).

ACKNOWLEDGEMENTS

We would like to thank Charles Prud’homme (TASC,

IMT-Atlantique, LS2N-CNRS) for his help on the

choice of the solver. Some of the authors are sup-

ported by the TAILOR (”Foundations of Trustworthy

AI - Integrating Reasoning, Learning and Optimiza-

tion” - H2020-ICT-2018-20) project.

REFERENCES

Bauer, L. A. and Bindschaedler, V. (2020). Towards realistic

membership inferences: The case of survey data. In

ACSAC ’20: Annual Computer Security Applications

Conference, pages 116–128. ACM.

uscher, N., Boukoros, S., Bauregger, S., and Katzen-

beisser, S. (2017). Two is not enough: Privacy as-

sessment of aggregation schemes in smart metering.

Proc. Priv. Enhancing Technol., 2017(4):198–214.

CER (2012). CER Smart Metering Project - Electricity

Customer Behaviour Trial. Irish Social Science Data

Archive. (accessed may 11 2022). https://www.ucd.

ie/issda/data/commissionforenergyregulationcer.

Charles Prud’homme, Jean-Guillaume Fages, and Xavier

Lorca (2016). Choco solver documentation. http:

//www.choco-solver.org.

Cohen, A. and Nissim, K. (2020). Linear Program Recon-

struction in Practice. J. Priv. Conﬁdentiality, 10(1).

Deloitte (2017). Assessing the value of tﬂ’s open data and

digital partnerships.

Dinur, I. and Nissim, K. (2003). Revealing informa-

tion while preserving privacy. In Proceedings of

the Twenty-Second ACM SIGACT-SIGMOD-SIGART

Symposium on Principles of Database Systems, pages

202–210.

Dwork, C., McSherry, F., and Talwar, K. (2007). The price

of privacy and the limits of LP decoding. In Proceed-

ings of the 39th Annual ACM Symposium on Theory

of Computing, pages 85–94.

Dwork, C., Smith, A., Steinke, T., and Ullman, J. (2017).

Exposed! a survey of attacks on private data. Annual

Review of Statistics and Its Application, 4:61–84.

Dwork, C. and Yekhanin, S. (2008). New efﬁcient attacks

on statistical disclosure control mechanisms. In Ad-

vances in Cryptology - CRYPTO 2008, 28th Annual

International Cryptology Conferences, volume 5157

of Lecture Notes in Computer Science, pages 469–

480.

Gauvin, L., Tizzoni, M., Piaggesi, S., Young, A., Adler,

N., Verhulst, S., Ferres, L., and Cattuto, C. (2020).

Gender gaps in urban mobility. Humanities and Social

Sciences Communications, 7(1):1–13.

Gurobi Optimization, L. (2020). Gurobi optimizer. http:

//www.gurobi.com.

Hart, G. (1992). Nonintrusive appliance load monitoring.

Proceedings of the IEEE, 80(12):1870–1891.

Homer, N., Szelinger, S., Redman, M., Duggan, D., Tembe,

W., Muehling, J., Pearson, J. V., Stephan, D. A., Nel-

son, S. F., and Craig, D. W. (2008). Resolving in-

dividuals contributing trace amounts of dna to highly

complex mixtures using high-density snp genotyping

microarrays. PLoS Genet, 4(8):e1000167.

Jayaraman, B., Wang, L., Knipmeyer, K., Gu, Q., and

Evans, D. (2021). Revisiting membership inference

under realistic assumptions. Proc. Priv. Enhancing

Technol., 2021(2):348–368.

Kellerer, H., Pferschy, U., and Pisinger, D. (2004). The

subset sum problem. In Knapsack Problems, pages

73–115. Springer.

Lacharit

e, M., Minaud, B., and Paterson, K. G. (2018). Im-

proved reconstruction attacks on encrypted data using

range query leakage. In IEEE Symposium on Security

and Privacy, SP, pages 297–314.

Laurent Perron, Vincent Furnon, G. (2019). Or-tools. https:

//developers.google.com/optimization/.

Long, Y., Wang, L., Bu, D., Bindschaedler, V., Wang, X.,

Tang, H., Gunter, C. A., and Chen, K. (2020). A prag-

matic approach to membership inferences on machine

learning models. In IEEE European Symposium on

Security and Privacy, EuroS&P 2020, pages 521–534.

Melis, L., Song, C., Cristofaro, E. D., and Shmatikov, V.

(2019). Exploiting unintended feature leakage in col-

laborative learning. In 2019 IEEE Symposium on Se-

curity and Privacy, SP 2019, pages 691–706.

OECD (2020). Oecd open, useful and re-usable data (our-

data) index: 2019. https://www.oecd.org/gov/digital-

government/policy-paper-ourdata-index-2019.htm.

Membership Inference Attacks on Aggregated Time Series with Linear Programming

203

Pyrgelis, A., Troncoso, C., and Cristofaro, E. D. (2018).

Knock knock, who’s there? membership inference on

aggregate location data. In 25th Annual Network and

Distributed System Security Symposium, NDSS. The

Internet Society.

Pyrgelis, A., Troncoso, C., and Cristofaro, E. D. (2020a).

Measuring membership privacy on aggregate location

time-series. Proc. ACM Meas. Anal. Comput. Syst.,

4(2):36:1–36:28.

Pyrgelis, A., Troncoso, C., and Cristofaro, E. D. (2020b).

Measuring Membership Privacy on Aggregate Loca-

tion Time-Series. Proc. ACM Meas. Anal. Comput.

Syst., 4(2):36:1–36:28.

Quadrianto, N., Smola, A. J., Caetano, T. S., and Le, Q. V.

(2008). Estimating labels from label proportions. Pro-

ceedings of the Twenty-Fifth International Conference

on Machine Learning (ICML 2008), pages 776–783.

Rigaki, M. and Garcia, S. (2020). A survey of privacy at-

tacks in machine learning. CoRR, abs/2007.07646.

Salem, A., Zhang, Y., Humbert, M., Berrang, P., Fritz, M.,

and Backes, M. (2019). Ml-leaks: Model and data in-

dependent membership inference attacks and defenses

on machine learning models. In 26th Annual Network

and Distributed System Security Symposium, NDSS

2019.

Samani, S. S., Huang, Z., Ayday, E., Elliot, M., Fellay,

J., Hubaux, J., and Kutalik, Z. (2015). Quantifying

genomic privacy via inference attack with high-order

SNV correlations. In 2015 IEEE Symposium on Secu-

rity and Privacy Workshops, SPW 2015, pages 32–40.

Sankararaman, S., Obozinski, G., Jordan, M. I., and

Halperin, E. (2009). Genomic privacy and limits

of individual detection in a pool. Nature genetics,

41(9):965–967.

Shokri, R., Stronati, M., Song, C., and Shmatikov, V.

(2017). Membership Inference Attacks Against Ma-

chine Learning Models. In 2017 IEEE Symposium on

Security and Privacy, SP 2017, pages 3–18.

Stadler, T., Oprisanu, B., and Troncoso, C. (2020).

Synthetic data - A privacy mirage. CoRR,

abs/2011.07018.

The European Data Portal (2015). Creating value through

open data : Study on the impact of re-use of public

data resources. https://op.europa.eu/en/publication-

detail/-/publication/51ec011a-e13b-11e6-ad7c-

01aa75ed71a1.

The World Wide Web Foundation (2017). Open data barom-

eter - global report (4th ed.).

Truex, S., Liu, L., Gursoy, M. E., Wei, W., and Yu, L.

(2019). Effects of differential privacy and data skew-

ness on membership inference vulnerability. In First

IEEE International Conference on Trust, Privacy and

Security in Intelligent Systems and Applications, TPS-

ISA 2019, pages 82–91.

UK Power Networks (2013). SmartMeter Energy Con-

sumption Data in London Households (Accessed

May 11 2022). https://data.london.gov.uk/dataset/

smartmeter-energy-use-data-in-london-households.

Yeom, S., Giacomelli, I., Fredrikson, M., and Jha, S. (2018).

Privacy risk in machine learning: Analyzing the con-

nection to overﬁtting. In 31st IEEE Computer Security

Foundations Symposium, CSF 2018, pages 268–282.

Zhang, G., Zhang, A., and Zhao, P. (2020). Locmia: Mem-

bership inference attacks against aggregated location

data. IEEE Internet Things J., 7(12):11778–11788.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

204