
Graph Algorithms over Homomorphic Encryption for Data Cooperatives
Mark Dockendorf, Ram Dantu and John Long
Department of Computer Science and Engineering, University of North Texas
Keywords:
Homomorphic Encryption, Data Cooperatives, Graphs, Data Oblivious Algorithms, Shortest Path, Minimum
Spanning Tree, Harmonic Centrality, Betweenness Centrality, Random Walk.
Abstract:
“Big data” continues to grow in influence with few competitors able to challenge them. In order to slow the
growth of and eventually replace these “data silos”, we must enable competition from alternative sources that
respect users’ privacy, such as data cooperatives. In our previous work, we proposed an architecture for a
privacy-preserving data cooperative that relies on homomorphic encryption (HE) to ensure data privacy and
demonstrated ring-based BFS, degree centrality, and farness centrality over HE graph data. In this paper
we expand our suite of HE graph algorithms to include single-source shortest-path, all-pairs shortest-path,
minimum spanning tree, harmonic centrality, random walk, and betweenness centrality over HE graph data.
These graph analysis algorithms support the core service of a data cooperative: to provide data and insights
(or aggregates) to the service of the cooperative’s clients (researchers, companies, governments, etc.) while
maintaining the privacy of their users.
1 INTRODUCTION
Given the advantage that aggregated data gives the or-
ganizations that can afford it, the practice of amass-
ing large amounts of data will never go away entirely.
As long as organizations (companies, governments,
etc.) amass a net positive outcome from violating
their users’ privacy, they will continue to do so. Tar-
geted advertising’s success (from the advertisement
platform’s perspective) is a prime example: targeted
advertising tends to generate 4.5 times the clicks of
traditional advertising (Farahat, 2013). The primary
competition to these massive, privately-held data col-
lections (a.k.a “data silos”) are data cooperatives.
Data cooperatives, sometimes referred to as data
unions, function similarly to a credit union, except in-
stead of participants investing money, they invest their
data (Pentland and Hardjono, 2020). Participants do
not typically earn monetary interest from their invest-
ment; rather, participants in the data cooperative have
greater control over how their data is used and gain
other, non-monetary benefits. This does not mean that
it will not work for companies and governments, but
rather the data will be used in accordance with the will
of the participants: a mutualistic relationship rather
than a parasitic monopoly. The ability for your fa-
vorite coffee shop to know the best spot to add their
next location serves both the company’s bottom line
and your convenience. The ability for a government
to better route public transportation, better schedule
infrastructure maintenance, and more based on aggre-
gated data works for the benefit of both the govern-
ment officials and the people of the community. Data
cooperatives focus on serving both the privacy needs
of users and the data needs of companies, researchers,
governments, and more.
Data cooperatives can provide similar services to
those of their “data silo” counterparts. For exam-
ple, in a data cooperative-backed targeted advertising
service, participants would be able to control if the
service makes inferences from their history, past pur-
chases, demographic data, and/or their stated interests
as well as if the aforementioned data is uploaded to
the data cooperative. In the spirit of mutual benefit
for data use, participants could specify their interests
and block certain types of advertisements. This would
allow recovering addicts to block advertisements in-
volving their vice, and those that have had traumatic
experiences would be able to block subject matters
that remind them of said experience.
A real-world example of an existing data coop-
erative is HealthBank. HealthBank stores and ana-
lyzes personal health data, connecting patients, their
doctors, pharmaceutical companies, and researchers
in the common goal of improving health and well-
being for both the patients personally and humanity
Dockendorf, M., Dantu, R. and Long, J.
Graph Algorithms over Homomorphic Encryption for Data Cooperatives.
DOI: 10.5220/0011277000003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 205-214
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
205

as a whole.
Data cooperatives allow the sharing and use of ag-
gregated personal data, but have the same inherent
flaw as any other organization collecting data: users’
privacy is not inherently secured. The potential for
data misuse exists in a data cooperative just as it ex-
ists in “data silos”: a data cooperative may one day
decide to violate users’ privacy by allowing a myriad
of so-called “legitimate interests” to peek at the data.
To remove this possibility, your data needs to be en-
crypted.
Homomorphic encryption (HE) enables the shar-
ing of and computation over private data without dis-
closing the data itself to a third party. A toy example
would be a client using BFV to encrypt two integers,
x → E(x) and y → E(y), and offloading the product
operation to a 3rd party. The 3rd party would follow
the BFV procedure for multiplication and return E(z),
the encrypted product. Despite not knowing the clear-
text values for x and y, the third party will successfully
compute E(z), which will be decrypted by the client,
revealing z in cleartext. HE has already been applied
to cloud computing and relational databases.
With advancements in HE schemes BFV (Fan
and Vercauteren, 2012) (Iliashenko and Zucca, 2021),
TFHE (Chillotti et al., 2019), HEAAN (a.k.a.
CKKS) (Cheon et al., 2017), and more recently,
CHIMERA(Boura et al., 2020) and PEGASUS (jie
Lu et al., 2021), which enable conversion between
BFV, HEAAN, and TFHE, new possibilities in per-
formant fully homomorphic encryption (FHE) have
arisen. Where previously impossible, division of arbi-
trary ciphertexts is now a reality (via a CHIMERA or
PEGASUS scheme). By using homomorphic encryp-
tion within graph algorithms, a HE graph database can
be created that allows users to share their data in a way
that works for them through a data cooperative with a
greater level of security compared to a cleartext based
approach.
2 MOTIVATION
Graph analysis is core to solving many optimization
problems, and graph databases allow more flexibility
in both data types and data relationships than tradi-
tional relational databases. One goal of a data co-
operative is to rapidly adapt to changing data types,
so a database with a set schema is not ideal. Graph
databases are typically schema-less, and this flexibil-
ity allows them to adapt well to a wide variety of
data and changes in relationships between data. This
means that a graph database more easily adapts to the
types of data that are likely to be used in a data coop-
erative (Parra-Moyano et al., 2020). Graph databases
allow for well-established graph analysis algorithms,
such as page rank, label propagation, shortest path,
centralities, and others, to be used to gain insight on
their data. Thus, the graph structure lends itself to the
purposes of a data cooperative: (1) to allow partic-
ipants to contribute the data they want to invest–this
means different users will contribute different types,
amounts, and levels of detail in their data and (2) pro-
vide analytics over the data made available by par-
ticipants to meet the needs of researchers, companies,
governments, and more.
Homomorphic encryption can be used to share a
third parties’ computational power without leaking
any private data, or for use in multiparty computa-
tion in the case where a collection of parties want to
perform collaborative computations using their aggre-
gate data but not leak any raw data to their counter-
parts. These recent advancements in fully homomor-
phic encryption have lead to the possibility of more
performant arbitrary operations on encrypted data.
FHE enables the creation of data cooperatives
where privacy of participants is not a simple promise:
it is mathematically provable (Lyubashevsky et al.,
2012). Using multiparty HE (Mouchet et al., 2021)
or multi-key HE (L
´
opez-Alt et al., 2012) and work-
ing only on encrypted data, the chance of a successful
data breach can be greatly reduced.
2.1 Problem Definition
Data cooperatives are not inherently a panacea to
privately-held mass data collections. A textbook data
cooperative has the same two fundamental flaws as
privately-held data collections: (1) the holding entity
can peruse the personal data of users and (2) a sin-
gle data breach can expose the personal data of thou-
sands to millions of users as was the case when Face-
book was breached (Holmes, 2021). Both of these
fundamental flaws arise from the same problem: the
holding entity stores and operates on data in cleart-
ext. A solution to this problem is fully homomorphic
encryption.
To enable graph-based data cooperatives to work
under fully homomorphic encryption schemes, cur-
rent graph algorithms must be adapted to work with-
out control flow variance. Specifically, the control
flow of the algorithm must be blind to the data be-
ing operated on. This denies use of loops that are not
range-based and data-conditional branching in control
flow. However, conditional storage (ie. multiplexers)
or HE comparison (Cheon et al., 2019) can still be
used, as they do not alter control flow.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
206
2.2 Our Contributions
While some graph algorithms have been demon-
strated over homomorphic encryption (Anagreh et al.,
2021a) (Aly et al., 2013) (Meng et al., 2015) (Wang
et al., 2017) (Zhang et al., 2020) (Dockendorf et al.,
2021), ours tend to differ from the current solutions
in the artifacts that they yield. Minimum spanning
tree has been explored using oblivious parallel RAM
(Laud, 2014) and a homomorphic version of Prim’s
algorithm (Anagreh et al., 2021b). Our HE MST im-
plementation uses a Kruskal’s-style approach to min-
imum spanning tree, which yields significantly differ-
ent artifacts when the graph in question is not con-
nected: Prim’s yields a tree of the minimum for-
est that contains the starting vertex, while Kruskal’s
yields an entire minimum forest over all vertices.
Both our HE Bellman-Ford and HE Floyd-Warshall
enable re-constructable paths in addition to generat-
ing a distance vector or matrix respectively. In this
paper, we adapt Bellman-Ford, Floyd-Warshall, heap-
sort, Kruskal’s algorithm, harmonic centrality, ran-
dom walk, and betweenness centrality to work in a
HE scheme.
We have previously demonstrated ring-based
BFS, degree centrality, and farness centrality over HE
graph data (Dockendorf et al., 2021). In this paper,
we demonstrate:
Parallel HE Floyd-Warshall with Reconstructable
Paths. We offer a homomorphic Floyd-Warshall with
up to O(V
2
) parallelism (which may use individual ci-
phertexts or row-packed ciphertexts) that also creates
reconstrucable shortest paths, where (Anagreh et al.,
2021a) calculated only distance. Our Floyd-Warshall
is also trivially adaptable to packed HEAAN cipher-
texts and we provide pseudocode to do so.
HE Minimum Spanning Forest. We offer a homo-
morphic minimum spanning tree algorithm, homo-
morphic Kruskal’s algorithm, that has unique artifacts
compared to existing work (Anagreh et al., 2021b)
when the graph is disconnected. When G is discon-
nected, our HE Kruskal’s returns a minimum forest
over all connected components.
HE Harmonic Centrality. To our knowledge, we are
the first to demonstrate a harmonic centrality calcula-
tion over a HE graph.
HE Betweenness Centrality. To our knowledge, we
are the first to demonstrate homomorphic between-
ness centrality calculation over a HE graph.
HE Random Walk. We demonstrate homomorphic
random walk for HE graphs using a random 1-hot
vector encoding. This encoding produces one vertex
per vector in a matrix that is |V | by s, where s is the
number of steps in the random walk.
3 ARCHITECTURE
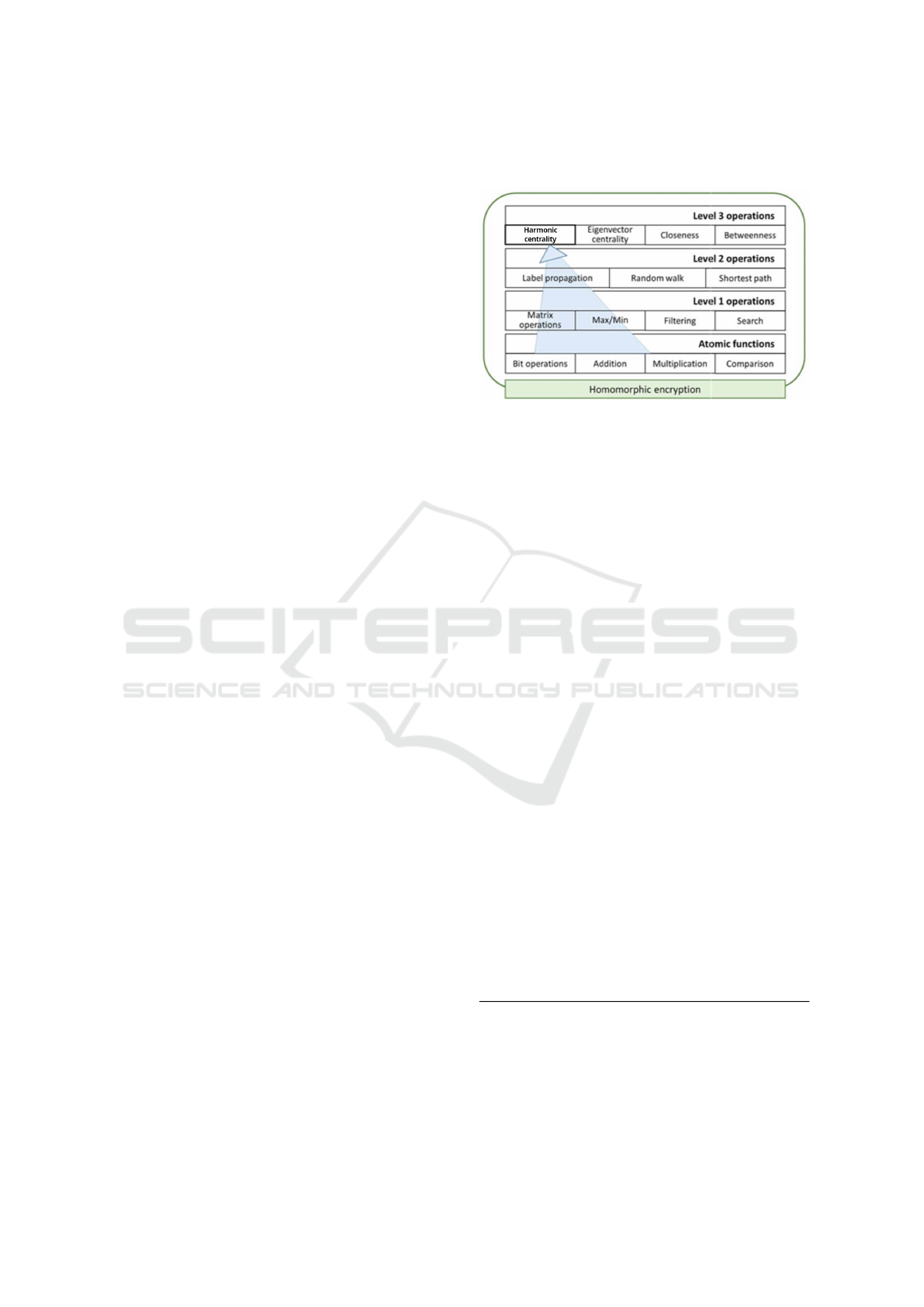
Figure 1: Our research focuses almost exclusively on level 2
and 3 operations. These upper-level operations focus on en-
abling graph algorithms over HE graph data. Parts or results
of level 2 operations are used for level 3 operations. For ex-
ample, betweenness uses parts of shortest path algorithms
and harmonic centrality uses the result of all-pairs-shortest-
path as its input. Atomic operations are assumed to be pro-
vided by the underlying homomorphic encryption schemes
(BFV, HEAAN, CHIMERA, PEGASUS, etc.), creating a
pseudo-API that we use to implement more complex func-
tionality. Some level 1 operations are also provided by cer-
tain HE data types. Where level 1 operations are not inher-
ent to the HE scheme, we create wrappers that implement
the functionality. This layered approach allows us to focus
on graph algorithms over HE graph data and leave the core
functionality and optimization of HE schemes to other re-
search teams.
The project follows a modular system, with arith-
metic operations being defined in HEfixed and HE-
double (TFHE (Chillotti et al., 2019) bit-based im-
plementations), graph algorithms that use generic op-
erators defined in HEgraph, and simple experiment
drivers as executable programs. HEgraph is a library
that contains homomorphic versions of BFS, degree
centrality, page rank, Bellman-Ford, Floyd-Warshall,
Kruskal’s (and its accompanying heapsort), random
walk, harmonic centrality, and betweenness centrality
as well as some trivial graph manipulations. An ex-
ample of one such trivial graph manipulation is con-
verting adjacency matrices to direct-distance matri-
ces: hollow matrices with all zeroes that are not on
the diagonal converted to “infinity”. Direct distance
is used by several of our algorithms; its pseudocode
follows.
Direct Distance
Input: G, the encrypted adjacency matrix
Output: M, the encrypted direct-distance matrix
let M be a matrix of dimension |V| by |V|
for all i := 0 to |V|-1:
for all j := 0 to |V|-1:
if (i = j):
Graph Algorithms over Homomorphic Encryption for Data Cooperatives
207
M[i,j] := E(0)
else:
M[i,j] := (G[i,j] != E(0)) ?
G[i,j] : E(inf)
While HEfixed uses procedural circuits (ie. flow
adder), HEdouble uses imported Bristol fashion cir-
cuits for IEEE-754 64-bit floating point values. We
implemented a circuit executor that used TFHE
boolean primitives and imported bristol fashion cir-
cuits to create an interface that provided all arithmetic
operations over IEEE-754 values.
Experiment drivers are trivial programs that:
1. import graphs or generate random graphs
2. invoke HEgraph’s encryption over the graph
3. time the duration of a chosen graph algorithm
4. decrypt the result
5. verify the result (using boost::graph where possi-
ble)
6. (optionally) display the result to the tester
Figure 2: Overall system architecture. The libhegraph con-
tains the primary contribution of this paper. Libhegraph
was written in a primitive-agnostic fashion, allowing the
numerical types library (HEfixed/HEdouble) to be swapped
for other implementations with minimal code modification.
Blocks in yellow were written by us, but do not contain sig-
nificant novelty and red blocks are works from other parties.
The interface between experiment drivers
and HEgraph is comprised of graph-level oper-
ations. The interface between HEgraph and the
HEfixed/HEdouble libraries is arithmetic operations,
which HEgraph uses to implement graph operations.
HEfixed/HEdouble interface with TFHE via boolean
logic to implement their arithmetic operations.
HEgraph can be configured to use HEAAN or BFV
schemes on algorithms that support it.
For the results presented in this paper, we used
exclusively HEfixed and HEdouble so that all results
would be inter-operable and could be used as part of
a query system for HE data. For example, the result
of homomorphic Kruskal’s could be packed back into
a graph structure, allowing all edges of a given vertex
that are part of the MST to be selected via binary ma-
trix multiply, a procedure described in our previous
paper (Dockendorf et al., 2021). This interoperability
of results is key to creating a query system for data
cooperatives using graph algorithms.
While the performance of the demonstrated
scheme is low, the bit-based FHE used can be eas-
ily replaced with a CHIMERA (Boura et al., 2020) or
PEGASUS (jie Lu et al., 2021) scheme for improved
performance. This modularity arises from HEgraph
using exclusively arithmetic as its interface to FHE
primitive libraries.
The overall flow of events is the same for all graph
algorithms tested. Since arithmetic operations are iso-
lated in a separate library from graph algorithms, our
TFHE-based arithmetic library can be exchanged for
any other arithmetic library that satisfies the needs of
the algorithm(s) in question.
Figure 3: Event flow between various components. While
the details of the algorithms vary, all follow the same over-
arching pattern. The experiment driver loads graph data,
invokes and times HEgraph’s operations, and compares re-
sults to known correct values. HEgraph contains all graph
algorithm logic and relies on external libraries for arith-
metic implementations. HEfixed/HEdouble provide arith-
metic operations over TFHE bits.
4 EXPERIMENTAL SETUP
Experiments were run using the following software
environment:
• Ubuntu 20.04.3 LTS operating system
• Compiler toolchain LLVM 10.0 (from Ubuntu
repository)
SECRYPT 2022 - 19th International Conference on Security and Cryptography
208

• TFHE version 1.1 (from Github repository)
(Chillotti et al., 2016)
• FFTW-3 version 3.3.8 for FFT implementation
(from Ubuntu repository)
• Linux kernel 5.4 (from Ubuntu repository)
As all data fit comfortably in memory, no pages
were swapped to disk, and timing did not include
reading data from disk or parsing; storage is not a
factor in the results. Experiments for Bellman-Ford,
Floyd-Warshall, heapsort, and Kruskal’s were run on
the following hardware environment:
• CPU: AMD 3960X (24C, 48T)
• Memory: 64 (16x4) GB ECC DDR4-3200
Experiments for harmonic centrality, random
walk, and betweenness centrality were run on the fol-
lowing hardware environment:
• CPU: AMD 3900X (12C, 24T)
• Memory: 32 (16x2) GB DDR4-3200
5 RESULTS
All experiments were performed with a bit-
constructed TFHE schemes; the complexities shown
in this paper are worst-case as no ciphertext packing
was used to allow SIMD. Homomorphic heapsort,
Bellman-Ford, Floyd-Warshall, and Kruskal’s were
performed using a fixed-point system. Random
walk, betweenness centrality, and harmonic centrality
were performed using a TFHE floating-point scheme
created by importing Bristol fashion circuits.
All algorithms explored here can be performed
on TFHE and CHIMERA/PEGASUS (Boura et al.,
2020)(jie Lu et al., 2021) schemes. Heapsort,
Bellman-Ford, Floyd-Warshall, and Kruskal’s are
also valid for BFV/BGV and HEAAN schemes due
to not needing division by ciphertext values.
Before exploring graph algorithms, a supporting
algorithm is needed: specifically, an efficient sorting
algorithm.
5.1 Homomorphic Heapsort
The primary disadvantage when sorting homomor-
phic values is that the best-case growth complexity
that can be obtained from a particular sort is the worst-
case complexity; that is, if the sort can even be con-
verted to an HE algorithm. This is due to all unstable
sorts having to be made data-oblivious: perform the
same operation regardless of the comparison results.
Heapsort has the advantages of being a Θ(nlog(n))
sort and using only swap/no-swap based on compar-
isons of homomorphic values. As a result, cleartext
heapsort does not significantly differ with its homo-
morphic counterpart and can be made stable using
min/max or a multiplexer.
For homomorphic heapsort to work, a comparison
and conditional swap is needed. This is possible on
BFV, BGV, HEAAN, and TFHE (bitwise) schemes.
While homomorphic quicksort, mergesort, and inser-
tion sort have been shown in previous work (Chat-
terjee and Sengupt, 2015), heapsort was not demon-
strated. This heapsort deomonstrated in 4 uses a Θ(b)
(where b is number of bits) compare-and-swap oper-
ator in a TFHE integer scheme.
Figure 4: Homomorphic heapsort growth complexity is lin-
earithmic with very small variance. This is expected as
cleartext heapsort is also linearithmic and the only modi-
fications required are a homomorphic comparison and con-
ditional swap operation. Besides this minor change, the al-
gorithm’s pseudocode is unchanged.
5.2 Homomorphic Bellman-Ford
Bellman-Ford is an alternative to Dijkstra’s algorithm
that uses a dynamic-programming approach. Since it
uses only storage based on conditionals does not al-
ter control flow based on the smallest value (as Dijk-
stra’s does), it is an ideal algorithm to transform to use
to solve the homomorphic single-source shortest-path
problem (SSSP).
Homomorphic Bellman-Ford’s pseudocode is
nearly identical to cleartext Bellman-Ford other than
2 major differences. The first major difference is
that the direct-distance matrix is computed, making M
from G, a hollow matrix with no zeroes other than on
the diagonal. This change will cause all ’0’ entries in
the adjacency matrix to become infinity; this step can
be skipped if such a matrix was pre-computed. The
second major difference comes from the use of an op-
eration that may take the form of a conditional store
or multiplexer that makes use of a homomorphic com-
parison operator (Cheon et al., 2019) (Iliashenko and
Zucca, 2021). Homomorphic Bellman-Ford requires
only addition and compare-and-swap operators: it is
Graph Algorithms over Homomorphic Encryption for Data Cooperatives
209

valid for BFV, BGV, HEAAN, and TFHE (assuming
an addition circuit is provided) schemes.
Unlike Floyd-Warshall, a multi-threaded imple-
mentation of Bellman-Ford would offer only O(V )
parallelism. Furthermore, Bellman-Ford offers short-
est paths for only a single vertex, while having the
same growth complexity as Floyd-Warshall. With
better alternative optimizations, multi-threaded ho-
momorphic Bellman-Ford was not implemented.
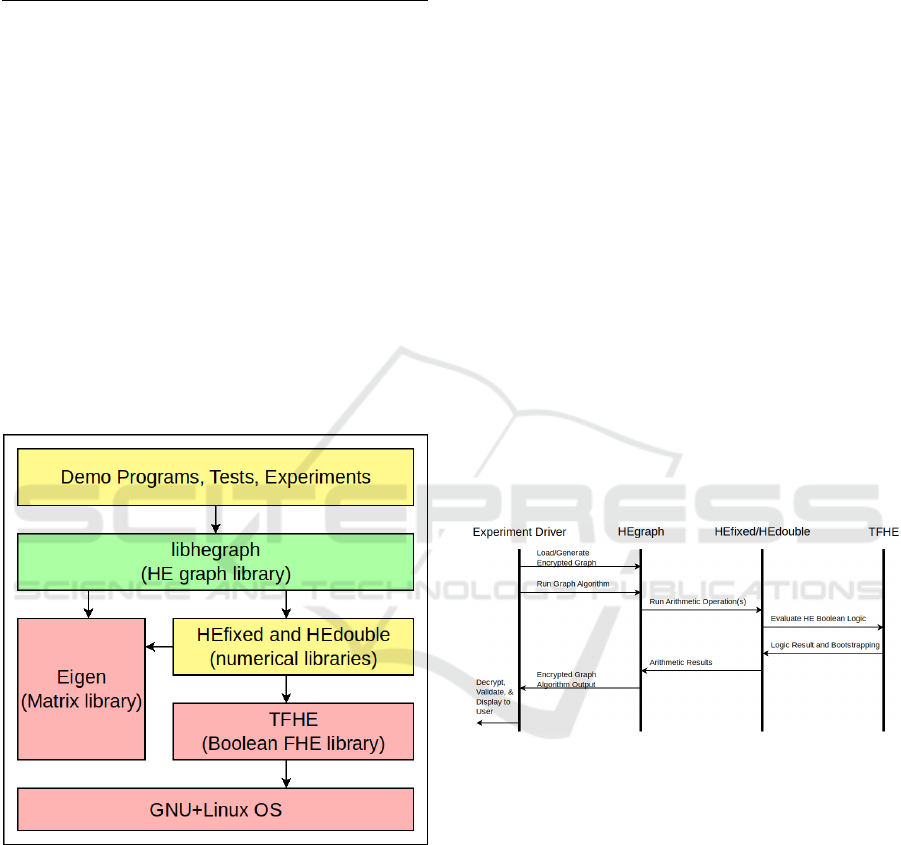
Figure 5: Bellman-Ford growth complexity is cubic with
very small variance. No additional complexity is added due
to HE. Parallelism is possible, but was not implemented due
to Floyd-Warshall having similar complexity while produc-
ing shortest paths for all pairs.
5.3 Homomorphic Floyd-Warshall
Floyd-Warshall is a dynamic programming solution
to the all-pairs shortest-path problem (APSP). The
time complexity of single-threaded Floyd-Warshall is
O(V
3
); this bound remains unchanged in the homo-
morphic implementation.
Multi-threaded Floyd-Warshall takes some addi-
tional setup time as it must first allocate a second dis-
tances matrix and predecessors matrix. Since, in the
worst case, Floyd-Warshall must reach the last ver-
tex every loop in order to get the new shortest path
for a vertex, the 2 inner loops can collapsed and run
completely in parallel assuming that the previous re-
sult is held constant. This provides O(V
2
) paral-
lelism. Swapping previous and current results every
outer loop continues until the outer loop of Floyd-
Warshall completes, at which time the distance and
predecessor matrix that were last written to are re-
turned. Homomorphic Floyd-Warshall can be shown
to be data-equivalent to its cleartext counterpart sim-
ply by replacing the ternaries with if-else statements
and performing unnecessary-statement eliminations.
Parallel Homomorphic Floyd-Warshall
Input: G, the encrypted adjacency matrix
Output: D, encrypted distance matrix, and N, the en-
crypted next-step matrix for reconstructing paths
D1, D2, N1, N2 are |V| by |V| matrices
for every possible edge in G[i,j]:
if i = j:
D1[i,j] := E(0)
N1[i,j] := E(j)
else:
D1[i,j] := (G[i,j] > E(0)) ? G[i,j] : E(inf)
N1[i,j] := (G[i,j] > E(0)) ? E(j) : E(null)
for k := 0 to |V|-1:
#parallel for collapse(2)
for i := 0 to |V|-1:
for j := 0 to |V|-1:
D2[i,j] := (D1[i,k] + D1[k,j] < D1[i,j]) ?
D1[i,k] + D1[k,j] : D1[i,j]
N2[i,j] := (D1[i,k] + D1[k,j] < D1[i,j]) ?
N1[i,k] : N1[i,j]
pointer swap D1 <-> D2
pointer swap N1 <-> N2
return D1, N1
Note that the matrices may use row-packed
BFV/HEAAN ciphertexts in conjunction with homo-
morphic comparison (Cheon et al., 2019) (Iliashenko
and Zucca, 2021) to parallelize the j loop. This al-
ternative would create O(V ) thread parallelism with
O(V ) SIMD parallelism through packed ciphertexts.
The adapted pseudocode for the main loop follows.
Parallel Packed HE Floyd-Warshall
Input: G, the encrypted adjacency matrix with row-
packed ciphertexts
Output: D, encrypted distance matrix, and N, the en-
crypted next-step matrix for reconstructing paths
D1, D2, N1, N2 are |V| by |V| matrices
// direct distance omitted
for k := 0 to |V|-1:
#parallel for
for i := 0 to |V|-1:
// vector with |V| instances of D1[i,k]
d := E(vector with 1-hot at index k)
n := d * N1[i]
d := d * D1[i]
d := d.sum_all_rotations()
n := n.sum_all_rotations()
D2[i] := (d + D1[k] < D1[i]) ?
d + D1[k] : D1[i]
N2[i] := (d + D1[k] < D1[i]) ?
n : N1[i]
pointer swap D1 <-> D2
pointer swap N1 <-> N2
return D1, N1
The above packed ciphertext version could yield
better growth complexity, assuming sum
a
ll
r
otations
or a similar operation that propagates the value from
a single slot into all slots can be performed in O(1)
or O(log(V )) bootstrappings. This is similar in
concept to the Floyd-Warshall found in (Anagreh
et al., 2021a), but does not offer interoperability with
SECRYPT 2022 - 19th International Conference on Security and Cryptography
210
TFHE-only results from other sections of this paper,
so it was not used in HEgraph. We plan to adopt
CHIMERA, PEGASUS, or a similar library as a com-
mon HE scheme for all algorithms presented in this
paper.
Figure 6: Floyd-Warshall growth complexity retains its
O(V
3
) cleartext growth complexity when performed over
HE data when not using packed ciphertexts.
Figure 7: Multi-threaded Floyd-Warshall without packed
ciphertexts is also O(V
3
), but scales well with hardware
parallelism: about 23x faster on a 24-core machine.
5.4 Homomorphic Kruskal
Kruskal’s algorithm builds a minimum spanning for-
est from a graph (a single tree if the graph is con-
nected). Kruskal’s uses a union-find data structure
with each vertex initially in its own set. Kruskal’s
then proceeds to add edges between vertices of differ-
ent sets from lowest weight to highest, merging sets
whenever an edge is added.
The major difference between other homomorphic
minimum spanning tree algorithms and ours occurs
when the graph is not connected. When the graph
in question is not connected, our algorithm returns a
minimum spanning forest of the graph: a set of trees
that are a MST for the vertices they span. The unique
artifact for this is that any edge added to the graph
that would link two trees of the returned forest will be
a part of the new minimum spanning forest regardless
of its weight.
The minimum spanning forest for any graph has
at most V − 1 edges. Since execution path cannot
change based on homomorphic data, V − 1 edges will
always be returned, but some may be marked as in-
valid (INT MAX) and will always be at the end of the
list. Homomorphic Kruskal assumes the input graph
is undirected and is valid for BFV, BGV, and TFHE
schemes.
Since we return the top |V | − 1 entries regardless
of whether the graph is connected or not, there may
be edges returned as such: ∞ → ∞ with ∞ cost. We
call ∞ (or −1) the false vertex because it will never
be indexed when the tree is loaded back into a graph
structure. Thus, these infinite weight self loops on the
false vertex will never affect a computational outcome
on the resultant graph.
Homomorphic Kruskal’s Algorithm
Input: G, the encrypted adjacency matrix
Output: edges, encrypted list of edges in tuple form
edges is a list of tuple (w,i,j)
edges := all G[i,j] where j > i,
w := (G[i,j]) ? G[i,j] : E(inf)
make_sets(0..V-1)
sort(edges by w)
foreach edge in edges:
s1 := find_set(edge.i)
s2 := find_set(edge.j)
sn := max(s1,s2)
union(edge.i,edge.j,sn)
edge := (s1 != s2) ?
edge : (E(inf),E(inf),E(inf))
sort(edges by w)
return edges[0..V-1)
Copy Graph’s Upper-right Values Copy the upper
right of the matrix (not including diagonal) and as-
semble tuples; note that V
1
(row) will always be less
than V
2
(column) due to this. If an edge does not ex-
ist in the adjacency matrix, the edge weight is set to
infinity.
Sort Copied Edges by Weight Running a sort on
the edges ensures that when iterating through them,
smaller edges are always encountered first.
Repeated Union-find Iterate through the sorted edges
performing find on each vertex in each edge. Union
the two vertices’ sets (this results in no change if the
vertices are already in the same set). If the vertices are
already part of the same set, set the weight and vertex
indices on the edge to infinity.
Sort Edges Again This causes all edges that were
not part of the minimum spanning forest (and sub-
sequently had their weights set to infinity) to fall to
lower positions. Performing union-find over all ver-
tices and sparing only edges that joined two disjoint
sets will spare a maximum of V − 1 edges. These
edges are part of the minimum spanning tree/forest.
Graph Algorithms over Homomorphic Encryption for Data Cooperatives
211
Return Top V − 1 Edges After the second sort, a max-
imum of V − 1 edges remain with valid values. Users
of this data need to understand that not all edges will
be valid if the graph was disconnected. When a graph
is disconnected, Kruskal’s returns a minimum span-
ning forest. All invalid edges will be at the end of the
list, so after the first invalid value is encountered, all
subsequent entries may be ignored.
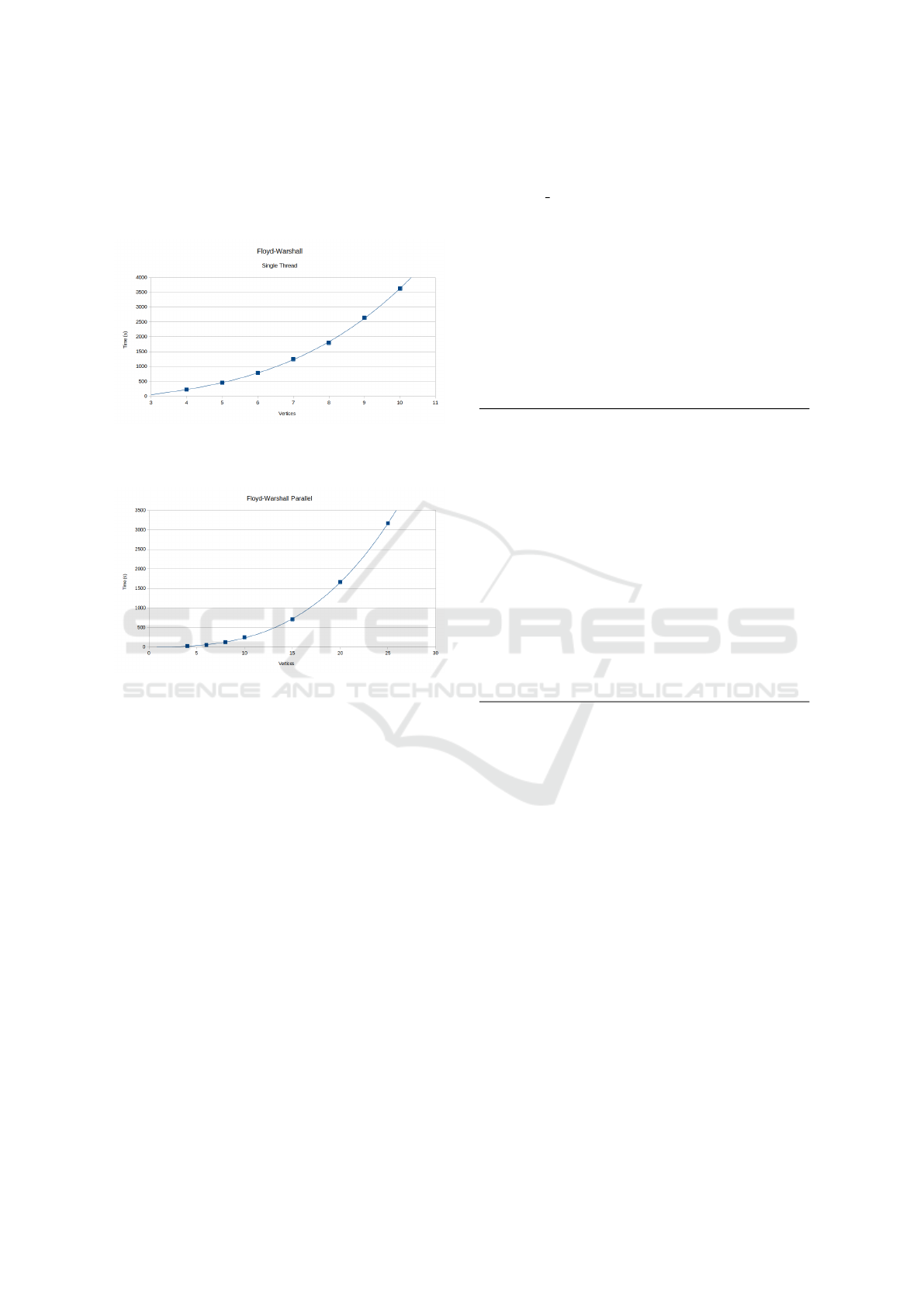
Figure 8: As the homomorphic algorithm uses a naive ap-
proach to performing Kruskal and TFHE-based ciphertexts,
complexity is O(V
3
). We are currently exploring a more
efficient implementation. Using CHIMERA or PEGASUS
will also improve performance.
5.5 Homomorphic Betweenness
Centrality
We measured the execution time of betweenness cen-
trality on different sized graphs and previously we de-
termined that the runtime complexity of data blind be-
tweenness centrality is O(N
5
). Figure 9 shows raw
execution time, which is on the order of hours for a
relatively small graph and figure 10 which shows the
5th root of the runtime vs the number of vertices. We
are currently exploring a more efficient implementa-
tion that uses dynamic programming to improve over
the naive approach.
Homomorphic betweenness centrality is valid
only on TFHE and CHIMERA/PEGASUS-style HE
schemes as division by HE ciphertexts is required.
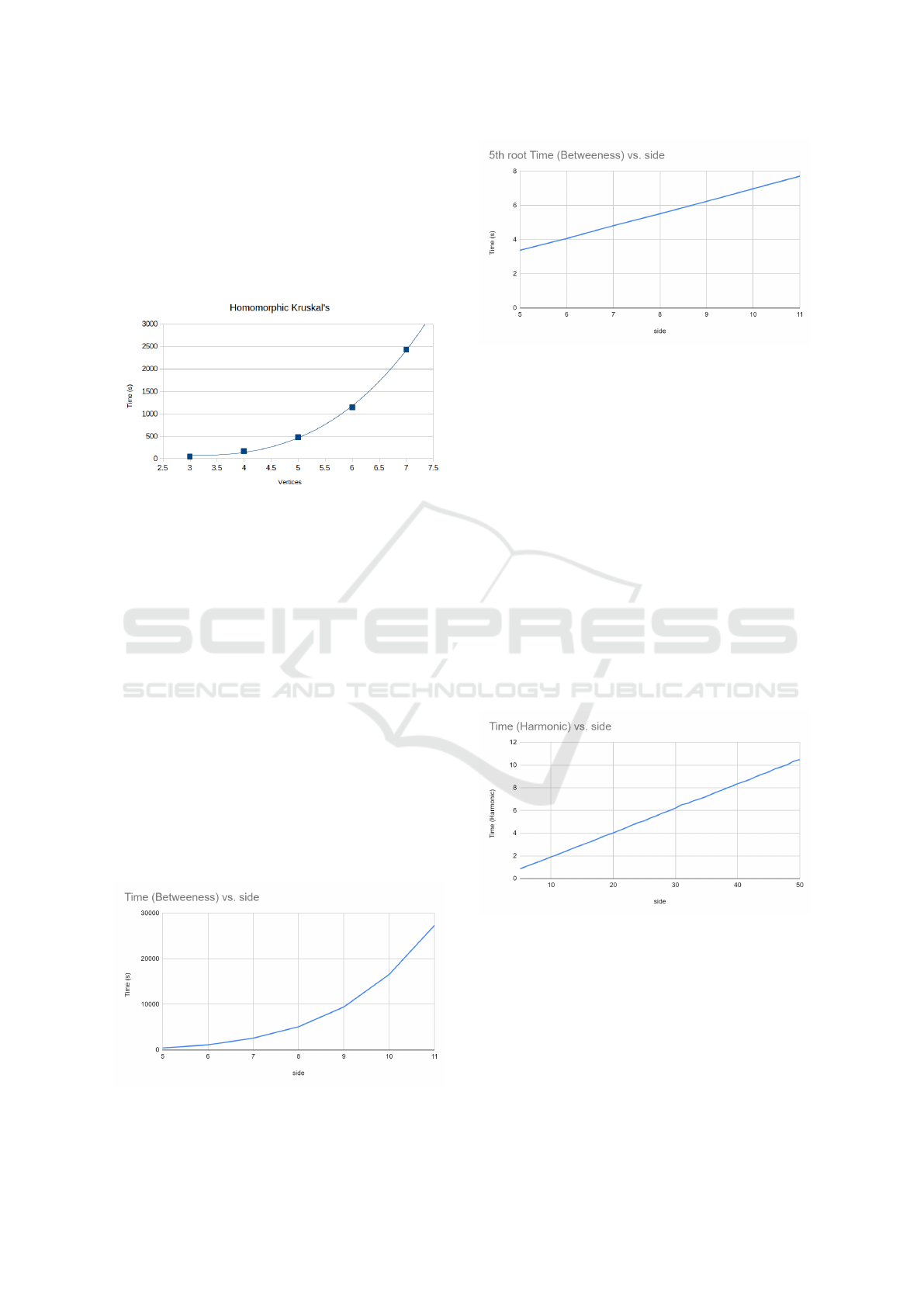
Figure 9: Naive homomorphic betweenness centrality (our
current algorithm) has a very long runtime: taking hours to
complete, even on small graphs.
Figure 10: Linearizing the runtime of betweenness central-
ity to the 5th root shows a strait line and validates our anal-
ysis of O(V
5
).
5.6 Homomorphic Harmonic Centrality
For harmonic centrality, we assume a pre-computed
distance matrix is present (from homomorphic Floyd-
Warshall, etc.). The resultant runtime is linear with
respect to the number of vertices in the graph. If
the distance matrix is not pre-computed, complexity
for the first harmonic centrality is O(V
4
) and all sub-
sequent calls are O(V ), assuming the graph has not
changed and the distance matrix is cached. Harmonic
centrality is faster than betweenness centrality as it
takes under 11 seconds to compute the harmonic cen-
trality for any given vertex in a graph of 50 vertices
using our TFHE-based HEdouble. Harmonic central-
ity requires inversion of ciphertexts, thus it is not valid
on standard BFV or HEAAN schemes, but is valid for
TFHE or CHIMERA/PEGASUS-based HE schemes.
Figure 11: With a pre-computed distance matrix (from ho-
momorphic Floyd-Warshall, etc.), harmonic centrality has
O(V ) growth complexity.
5.7 Homomorphic Random Walk
Random walk selects a random neighbor, adds it to
a list and moves onto that neighbor: this is repeated
s times to form a random path with s + 1 vertices.
Homomorphic random walk entails selecting a vec-
tor of all vertices and creating a random 1-hot encod-
ing from among the current vertex’s neighbors. Per-
SECRYPT 2022 - 19th International Conference on Security and Cryptography
212
forming a matrix-vector multiply with the transposed
weighted adjacency matrix results in the next vector
in the series.
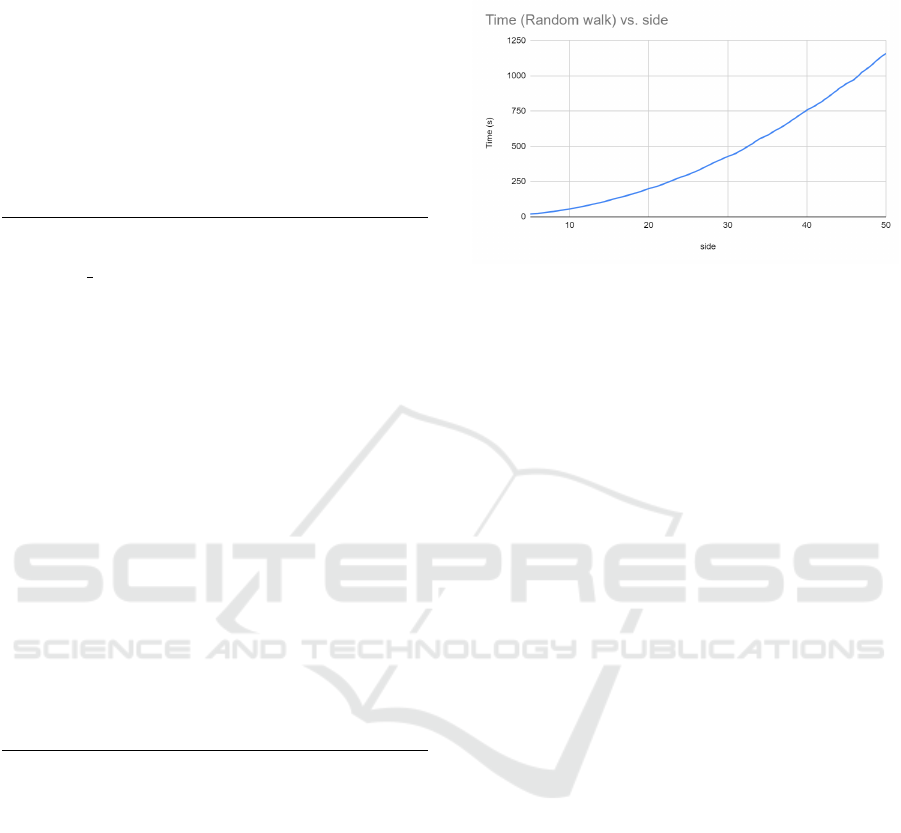
It takes on the order of 20 minutes to do a random
walk of two steps on a graph of size 50 using a float-
ing point TFHE-based scheme. In figure 12, we can
see a growth of O(V
2
∗ s). The slow growth is due to
parallelization that was done on the matrix multipli-
cation.
Select random is a supporting function for random
walk, so its pseudocode has been included as well.
Select Random
Input: v, an encrypted vector
Output: v out, encrypted 1-hot vector from among
non-zeros in v
r := E(random in range [0,1))
r := r * (sum of elements in v)
v_out := zero initialized vector with |V| elements
flag := !(sum > 0)
for i := 0 to |V|-1:
r := r - v[i]
v_out[i] := (r < E(0) && !flag) ? E(1) : E(0)
flag := r < E(0) | flag
return v_out
Homomorphic Random Walk
Input: G, the encrypted weighted adjacency matrix
Output: V, encrypted list vectors
V := empty list of vectors
vec := zero vector
vec[v] := 1
for i := 0 to s-1:
vec := G * vec
vec := select_random(vec)
V.append(vec)
return V
Homomorphic random walk generates a list of
1-hot encoded vectors that is a result of doing a
weighted random selection of outgoing edges and
traversing them s times starting from vertex v. The
edges of the supplied graph can have arbitrary
weights. This implementation does not prohibit “pac-
ing” (alternating between 2 vertices), but could be
modified to do so.
Clearly, since r ∗sum < sum when r ε [0, 1), r will
eventually go negative if the values that were added to
get sum are subtracted from r. When r goes negative,
f lag will be true for all subsequent loops. The f lag
prevents multiple values from being set to 1, so vec
o
ut
must be 1-hot from among nonzero values in vec.
Since P appends only 1-hot encoded vectors cho-
sen from among the outgoing edges of the previously
selected vertex, the hot elements of P form a path.
The randomness of this path depends on the RNG
used; therefore, this algorithm could be vulnerable to
malicious or lazy 3rd party random number selection.
Figure 12: Homomorphic random walk has a growth com-
plexity of O(V
2
∗ s), where s is the number of steps in the
walk. This experiment performed 2 steps (3 total vertices)
in a 50-vertex graph.
6 CONCLUSION
This collection of HE graph algorithms serves as a
core component of data cooperatives that decide to
use homomorphic encryption to protect their partic-
ipants’ data. We used a modular design that allows
a library providing basic HE arithmetic data types to
be swapped out as future advancements are made in
performant fully homomorphic encryption.
In this paper, we demonstrated numerous com-
mon graph algorithms adapted to work on HE graphs.
We demonstrated these algorithms on graphs with
individually packed ciphertexts in order to form di-
rect comparisons to the growth rates of their cleart-
ext counterparts. With packed ciphertexts, certain al-
gorithms, especially Bellman-Ford, Floyd-Warshall,
harmonic centrality, and random walk, will be much
faster as bootstrapping time tends to dominate calcu-
lation time in HE schemes.
Our homomorphic Floyd-Warshall goes beyond
shortest distance, creating re-constructable paths un-
der homomorphic encryption. Our homomorphic
Kruskal’s creates a minimum spanning forest when
the graph is not connected and can be further sped up
using parallel sorting.
We demonstrate betweenness centrality over HE
graphs, which requires division of ciphertexts in the
second to last step (immediately before the final sum-
mation). As all prior steps use operations supported
by BFV and HEAAN, faster calculation of between-
ness centrality will be made possible with dynamic
programming as well as using a HEAAN or BFV
to TFHE conversion immediately before the division
step instead of a purely-TFHE implementation; these
are left to future work.
Graph Algorithms over Homomorphic Encryption for Data Cooperatives
213

This work enables secured third-party analysis
of graph data from numerous sources and the cre-
ation and use of graph structures in HE data cooper-
atives. Applications for these HE graph algorithms
include privacy-preserving contact tracing, privacy-
preserving city planning, privacy-preserving cooper-
ative cyber-defense, and much more (Pentland and
Hardjono, 2020).
ACKNOWLEDGMENT
We thank National Security Agency for the partial
support through grants H98230-20-1-0329, H98230-
20-1-0403, H98230-20-1-0414, and H98230-21-1-
0262.
REFERENCES
Aly, A., Cuvelier, E., Mawet, S., Pereira, O., and Van Vyve,
M. (2013). Securely solving simple combinatorial
graph problems. volume 7859, pages 239–257.
Anagreh, M., Laud, P., and Vainikko, E. (2021a). Parallel
privacy-preserving shortest path algorithms. Cryptog-
raphy, 5(4).
Anagreh, M., Vainikko, E., and Laud, P. (2021b). Paral-
lel privacy-preserving computation of minimum span-
ning trees.
Boura, C., Gama, N., Georgieva, M., and Jetchev, D.
(2020). Chimera: Combining ring-lwe-based fully ho-
momorphic encryption schemes. Journal of Mathe-
matical Cryptology, 14(1):316–338.
Chatterjee, A. and Sengupt, I. (2015). Searching and sorting
of fully homomorphic encrypted data on cloud.
Cheon, A. H., Kim, D., and Ki, D. (2019). Efficient homo-
morphic comparison methods with optimal complex-
ity.
Cheon, J. H., Kim, A., Kim, M., and Song, Y. (2017). Ho-
momorphic encryption for arithmetic of approximate
numbers. In Takagi, T. and Peyrin, T., editors, Ad-
vances in Cryptology – ASIACRYPT 2017, pages 409–
437, Cham. Springer International Publishing.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(2019). Tfhe: Fast fully homomorphic encryption
over the torus. Journal of Cryptology, 33:34–91.
Chillotti, I., Gama, N., Georgieva, M., and Izabach
`
ene, M.
(August 2016). TFHE: Fast fully homomorphic en-
cryption library. https://tfhe.github.io/tfhe/.
Dockendorf, M., Dantu, R., Morozov, K., and Bhowmick,
S. (2021). Investing data with untrusted parties using
he. In SECRYPT.
Fan, J. and Vercauteren, F. (2012). Somewhat practical fully
homomorphic encryption. Cryptology ePrint Archive,
Report 2012/144. https://ia.cr/2012/144.
Farahat, A. (2013). How effective is targeted advertising?
In 2013 American Control Conference, pages 6014–
6021.
Holmes, A. (2021). 533 million facebook users’ phone
numbers and personal data have been leaked online.
Insider.
Iliashenko, I. and Zucca, V. (2021). Faster homomorphic
comparison operations for bgv and bfv. Proceedings
on Privacy Enhancing Technologies, pages 246–264.
jie Lu, W., Huang, Z., Hong, C., Ma, Y., and Qu, H.
(2021). Pegasus: Bridging polynomial and non-
polynomial evaluations in homomorphic encryption.
2021 IEEE Symposium on Security and Privacy (SP),
pages 1057–1073.
Laud, P. (2014). Privacy-preserving minimum spanning
trees through oblivious parallel ram for secure mul-
tiparty computation.
L
´
opez-Alt, A., Tromer, E., and Vaikuntanathan, V. (2012).
On-the-fly multiparty computation on the cloud via
multikey fully homomorphic encryption. Proceedings
of the Annual ACM Symposium on Theory of Comput-
ing.
Lyubashevsky, V., Peikert, C., and Regev, O. (2012). On
ideal lattices and learning with errors over rings.
Cryptology ePrint Archive, Report 2012/230. https:
//ia.cr/2012/230.
Meng, X., Kamara, S., Nissim, K., and Kollios, G. (2015).
Grecs: Graph encryption for approximate shortest dis-
tance queries. In CCS 2015 - Proceedings of the 22nd
ACM SIGSAC Conference on Computer and Com-
munications Security, Proceedings of the ACM Con-
ference on Computer and Communications Security,
pages 504–517. Association for Computing Machin-
ery.
Mouchet, C., Troncoso-Pastoriza, J. R., Bossuat, J.-P., and
Hubaux, J.-P. (2021). Multiparty homomorphic en-
cryption from ring-learning-with-errors. Proceedings
on Privacy Enhancing Technologies, 2021:291 – 311.
Parra-Moyano, J., Schmedders, K., and Pentland, A.
(2020). 3. shared data: Backbone of a new knowledge
economy. In Building the New Economy. 0 edition.
https://wip.mitpress.mit.edu/pub/yvy3qigg.
Pentland, A. and Hardjono, T. (2020). 2. data cooper-
atives. In Building the New Economy. 0 edition.
https://wip.mitpress.mit.edu/pub/pnxgvubq.
Wang, Q., Ren, K., Du, M., Li, Q., and Mohaisen, A.
(2017). Secgdb: Graph encryption for exact short-
est distance queries with efficient updates. In Kiayias,
A., editor, Financial Cryptography and Data Security,
pages 79–97, Cham. Springer International Publish-
ing.
Zhang, C., Zhu, L., Xu, C., Sharif, K., Zhang, C., and Liu,
X. (2020). Pgas: Privacy-preserving graph encryption
for accurate constrained shortest distance queries. In-
formation Sciences, 506:325–345.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
214
