Authentication Attacks on Projection-based Cancelable Biometric

Schemes

Axel Durbet

, Paul-Marie Grollemund

, Pascal Lafourcade

, Denis Migdal

and Kevin Thiry-Atighehchi

Universit

e Clermont-Auvergne, CNRS, Mines de Saint-

Etienne, LIMOS, France

Universit

e Clermont-Auvergne, CNRS, LMBP, France

Keywords:

Cancelable Biometrics, Local-sensitive Hash, Sobel Filter, Reversibility Attacks, Biohash.

Abstract:

Cancelable biometric schemes aim at generating secure biometric templates by combining user speciﬁc tokens,

such as password, stored secret or salt, along with biometric data. This type of transformation is constructed as

a composition of a biometric transformation with a feature extraction algorithm. The security requirements of

cancelable biometric schemes concern the irreversibility, unlinkability and revocability of templates, without

losing in accuracy of comparison. While several schemes were recently attacked regarding these requirements,

full reversibility of such a composition in order to produce colliding biometric characteristics, and speciﬁcally

presentation attacks, were never demonstrated to the best of our knowledge. In this paper, we formalize these

attacks for a traditional cancelable scheme with the help of integer linear programming (ILP) and quadratically

constrained quadratic programming (QCQP). Solving these optimization problems allows an adversary to

slightly alter its ﬁngerprint image in order to impersonate any individual. Moreover, in an even more severe

scenario, it is possible to simultaneously impersonate several individuals.

1 INTRODUCTION

Biometric authentication is seeing widespread use

due to the common integration of ﬁngerprint sensors

and cameras on many smart objects. Since biometrics

is more convenient and quicker to use, and biometric

characteristics cannot be lost or forgotten, biometric

authentication solutions are in general preferred over

their password or physical token counterparts. De-

spite their many advantages, biometric solutions are

not exempt from vulnerabilities. As biometric-based

technologies are deployed at a larger scale, central-

ized biometric databases and devices become natural

targets in cyberattacks. These cyberattacks have the

potential to be harmful on the long term if they lead

to the theft of biometric data. Therefore, a biomet-

ric data may actually be vulnerable to impersonation

attacks and privacy leakage.

Several criteria essential to biometric authenti-

cation systems have been identiﬁed in (ISO, 2011)

and (ISO, 2018): irreversibility, unlinkability, revo-

cability and performance preservation of templates.

Fulﬁlling this set of criteria is now necessary to com-

ply with the privacy principles of the GDPR.

Faced with the mentioned vulnerabilities and re-

quirements, the community has proposed primitives

dedicated to biometrics, so-called biometric template

protection (BTP) schemes. In this paper, we focus on

cancelable biometrics (CB) which is an example of

BTP scheme claimed to meet the four criterias. For

more details on BTP schemes, the reader is referred to

two surveys (Nandakumar and Jain, 2015) and (Nat-

gunanathan et al., 2016). In CB, a biometric template

is computed through a process where the inputs are

biometric data (e.g., biometric image) of a user and

a user speciﬁc token (e.g., a random key, seed, salt,

or password). A CB scheme generally consists of a

sequence of processes (an extraction of features fol-

lowed by a parameterized transformation) that pro-

duces the biometric templates, and a matcher to gen-

erate a matching score between the templates. With a

CB scheme, templates can be revoked, changed, and

renewed by changing user speciﬁc tokens. Cryptanal-

ysis of CB schemes with strong adversarial models

commonly assume that the attacker knows both the

biometric template and token of the user. This as-

sumption is plausible in practice because a user token

may have low entropy (e.g., a weak password), or it

may just have been compromised by an attacker. This

is the stolen-token scenario (Teoh et al., 2008).

In (Ratha et al., 2001), the ﬁrst CB scheme was

introduced in the case of face recognition. Since then,

several CB schemes have been proposed, including

the BioHash algorithm (Jin et al., 2004) applied on

568

Durbet, A., Grollemund, P., Lafourcade, P., Migdal, D. and Thiry-Atighehchi, K.

Authentication Attacks on Projection-based Cancelable Biometric Schemes.

DOI: 10.5220/0011277100003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 568-573

ISBN: 978-989-758-590-6; ISSN: 2184-7711

many modalities. CB schemes offer several advan-

tages such as efﬁcient implementation, high match-

ing accuracy, and revocability. However, several at-

tacks on a variety of CB schemes have been pro-

posed: attacks against privacy by approximating fea-

ture vectors or linking several templates of an individ-

ual, and authentication attacks by elevating the false

acceptance rate (FAR). We refer the reader to (Nagar

et al., 2010; Topcu et al., 2016) for attacks on Bio-

Hash type schemes, (Li and Hu, 2014) for attacks us-

ing the Attack via Record Multiplicity (ARM) tech-

nique, (Lacharme et al., 2013; Dong et al., 2019) for

attacks using genetic algorithms, as well as attacks us-

ing constrained programming on CB schemes (Gham-

mam et al., 2020; Topcu et al., 2016).

Contributions. In this paper, we propose re-

versibility attacks against some projection-based CB

schemes, such as the BioHash. The particularity of

our attacks, as opposed to previous works, is that we

reverse the complete sequence of treatments includ-

ing the feature extraction algorithm. This allows us to

construct impostor ﬁngerprint images, thus enabling

authentication (or presentation) attacks. In our au-

thentication attacks, an adversary, who already has

the knowledge of a user’s speciﬁc token and has at

least one ﬁngerprint template of the same user, tries

to alter her own ﬁngerprint image such that the ad-

versary can now use its own altered biometrics and

the stolen token to be falsely authenticated as a legiti-

mate user. The considered CB schemes are built upon

uniform random projection (URP) and a kernel based

feature extractor.To perform our attacks, we use In-

teger Linear Programming (ILP) as well as quadrat-

ically constrained quadratic programming (QCQP).

We state our results as follows:

1) Simple Authentication Attacks. A complete

reversal methodology of some projection-based CB

schemes, including the BioHash algorithm, is pro-

posed. The main ideas are to solve an integer lin-

ear program and a quadratically constrained quadratic

program to reverse both the projection and the feature

extraction. The solution provided by a solver is a ﬁn-

gerprint image of the attacker whose the amount of

changes is minimized. Practical resolutions are pro-

vided for tiny synthetic images.

2) One Fingerprint Image for Several Imperson-

ations. The ﬁrst attack is extended to produce a sin-

gle ﬁngerprint image that impersonates the identity

of several users. This ﬁngerprint image, when com-

bined with the distinct stolen tokens, produces tem-

plates that match exactly the stolen templates of the

respective users. To reach this objective, the attack

consists for the attacker to collect the pairs of (token,

template) of the target users to enlarge the set of con-

straints of a QCQP program.

Outline. Some background information and the ad-

versarial models are presented in Section 2. Section 3

provides our simple authentication attacks. Then, in

Section 4, it is shown how to impersonate several

users with different passwords. Finally, experimen-

tal evaluations and future works are discussed in Sec-

tion 5 and Section 5 respectively.

2 BACKGROUND

Cancelable biometric schemes generate secure bio-

metric templates by combining user speciﬁc tokens

such as password with a biometric data to create tem-

plates in respect of the four aforementioned criteria.

Biometric templates in CB schemes are constructed

in two steps: (i) Feature extraction: A feature vector

is derived from a biometric image; (ii) Transforma-

tion: A user speciﬁc token is used to transform the

user’s feature vector to a template.

In the following, we let (M

), (M

) and

) be three metric spaces, where M

, M

and

represent the ﬁngerprint image space, the feature

space and the template space, respectively; and D

and D

are the respective distance functions. Note

that D

and D

are instantiated with the Euclidean dis-

tance, while D

is instantiated with the Hamming dis-

tance.

2.1 Feature Extraction

Let U be the set of users of the biometric system. We

identify a user with its biometric characteristic, and

deﬁne a function BC(·) that takes a biometric charac-

teristic usr ∈ U as input, and outputs a digital repre-

sentation of biometric data I; for instance, the scan

image of a ﬁngerprint. Note that for two different

computations of I = BC(usr) and I

= BC (usr) (e.g.,

at different times, or different devices), we may have

I 6= I

due to the inherent noise in the measurement of

biometric data.

Deﬁnition 2.1. A biometric feature extraction scheme

is a pair of deterministic polynomial time algorithms

Π := (E,V ), where:

• E is the feature extractor that takes biometric

data I as input, and returns a feature vector

F ∈ M

• V is the veriﬁer that takes two feature vectors F =

E(I), F

= E(I

), and a threshold τ as input, and

returns True if D(F,F

) ≤ τ, and False otherwise.

Authentication Attacks on Projection-based Cancelable Biometric Schemes

569

An example of feature extraction is Sobel ﬁlter-

ing (Vincent and Folorunso, 2009). The resulting im-

age is obtained by computing two convolutions given

by the following matrices:





1 0 −1

2 0 −2

1 0 −1





and G





1 2 1

0 0 0

−1 −2 −1





Let ∗ denote the operator of convolution and I the

output matrix. Note that pixels at the edges of the

image are ignored and, their values are set to 0 in the

corresponding matrix I. The gradients, G

and G

are computed as follows G

= G

∗ I and G

= G

∗ I.

Then, the matrix of the output image S is computed as

+ G

where k·k

denotes the Euclidean norm.

However, the norm does not apply in the usual way.

In this case, it is applied coordinate by coordinate.

2.2 Generation of Templates with URP

Deﬁnition 2.2. Let K be the token (seed) space, rep-

resenting the set of tokens to be assigned to users. A

cancelable biometric scheme is a pair of deterministic

polynomial time algorithms Ξ := (T ,V ), where:

• T is the transformation that takes a feature vector

F ∈ M

and the token parameter P as input, and

returns a biometric template T = T (P,F) ∈ M

• V is the veriﬁer that takes two biometric tem-

plates T = T (P,F), T

= T (P

), and a thresh-

old τ

as input; and returns True if D

(T,T

) ≤

, and returns False otherwise.

The attacked CB instantiation, described in Al-

gorithm 1, is based on a uniform random projection

(URP). Such a projection serves as an embedding of a

high-dimensional space into a space of much lower

dimension while preserving approximately the dis-

tances between all pairs of points. Algorithm 1 as-

sumes the second factor, i.e., the token, is a password

and outputs a Biometric Compressed Vector (BCV).

Remark 2.2.1. BioHash instantiation is based on the

same type of projection, except that an additional step

of orthonormalization. This skipped step affects nei-

ther the accuracy nor the feasibility of the attacks.

2.3 Attack Models and Objectives

The objective of our attack is to impersonate one or

several users of a database. To perform this attack

some information are needed: the password of our tar-

get and the original BioHash of the target. We show

that anybody can perform a simple authentication at-

tack or a one ﬁngerprint image for several imperson-

ations attack by building a template preimage if he

knows the above information.

Algorithm 1: [URP-SOBEL].

Inputs : biometric data I; token parameter P

Output : BCV vector T = (t

,...,t

)

1: Apply Sobel ﬁlter on I to produce an n-sized fea-

ture vector: F = ( f

,..., f

2: Generate with the token P a family V of m pseu-

dorandom vectors V

,...,V

of size n according

to a uniform law U([−0.5,0.5]).

3: Arrange the family V as a matrix M of size n×m.

4: Compute T as the matrix-vector product F × M.

5: for t

in T do

6: if t

< 0 then t

= 0 else t

= 1

7: end for

8: return T

The informal deﬁnitions of (Ghammam et al.,

2020) are tailored for the rest of the paper. Let I ∈ M

be a ﬁngerprint image, and let T = Ξ.T (P,E(I)) ∈

be the template generated from I and the secret

parameter P. In our authentication attack, an adver-

sary is given T , P, and a threshold value τ

, and the

adversary tries to ﬁnd a ﬁngerprint image I

∗

∈ M

such that for T

∗

= Ξ.T (P,E(x

∗

)), T

∗

is exactly the

same as T , or T

∗

is close to T with respect to the dis-

tance function over M

and the threshold value τ

In this case, we say that I

∗

is a τ

-nearby-template

preimage of the template T .

A strategy for the adversary which have stolen the

secret parameter P is to alter her ﬁngerprint image I

such that P along with her extracted feature vector F

enable the generation of the exact template T . This

motivates the notion of template ﬁngerprint preimage

deﬁned below.

Deﬁnition 2.3 (Template Fingerprint Preimage).

Let I ∈ M

be a ﬁngerprint image, and T =

Ξ.T (P, Π.E(I)) ∈ M

a template for some secret

parameter P. A template preimage of T with re-

spect to P is a ﬁngerprint image I

∗

such that T =

Ξ.T (P, Π.E(I

∗

)).

Another authentication attack consists in gener-

ating a ﬁngerprint image that yields the exact tem-

plates of several distinct users with their correspond-

ing stolen tokens.

Deﬁnition 2.4 (n-template Fingerprint Preimage).

Let

,...,I

∈ M

be n ﬁngerprint images of distinct

users, and n templates T

= Ξ.T (P

,Π.E(I

)) ∈ M

for distinct secret parameters P

∀i ∈ {0,...,n}. A

n-template preimage of (I

,...,I

) with respect to

,...,P

) is a ﬁngerprint image I

∗

such that:

∀i ∈ {0,...,n},T

= Ξ.T (P

,Π.E(I

∗

)).

SECRYPT 2022 - 19th International Conference on Security and Cryptography

570

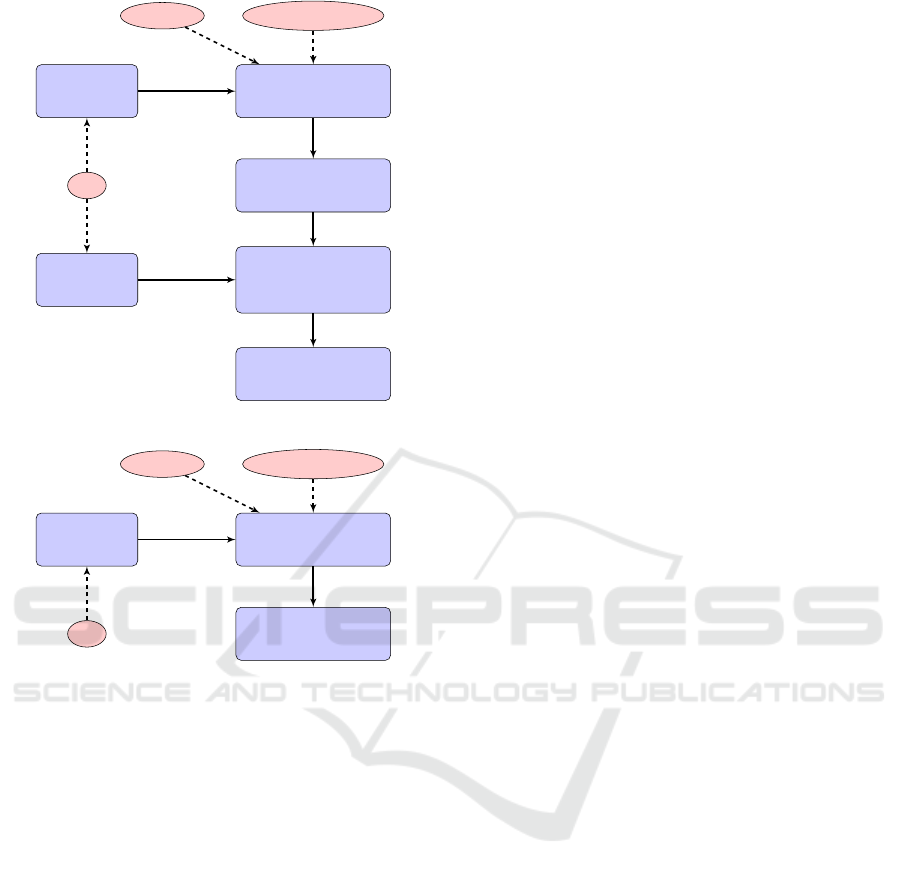
Target’s template

Password

Initialize the linear

system to obtain a good

output for the ﬁlter

Random attacker

ﬁltered image

Modiﬁed ﬁltered image

Initialize quadratic

system to ﬁnd a preim-

age of our modiﬁed

output of the ﬁlter

Return an image

for authentication

Random attacker

original image

Set objective

Solve

Set objective

Figure 1: Principle of the attack’s ﬁrst approach.

Target’s template

Password

Initialize the

quadratic system

Random

attacker image

Return an image

for authentication

Set objective

Solve

Figure 2: Principle of the attack’s second approach.

3 SIMPLE AUTHENTICATION

ATTACK

There are two ways of performing this attack. The

ﬁrst one includes two steps described in Section 3.1.

First, given an attacker feature vector, we seek the

slightest modiﬁcation of it such that its transforma-

tion by Ξ yields exactly the template of the victim.

Then, using the ﬁlter constraints of the convolution,

we seek the slightest variation of the attacker’s im-

age such that the ﬁltering of this variation produces

exactly the modiﬁed feature vector. The second ap-

proach described in Section 3.2 consists in generat-

ing all constraints at once and directly generating the

modiﬁed attacker’s image.

3.1 Two-phase Approach Formulation

The attack takes as input: the target’s password (P

the target’s template (T

) and the attacker’s image (I

This attack computes and uses these intermediate in-

formation: the attacker’s derivative features (F

) and

the modiﬁed attacker’s features (F

). The output is

a modiﬁed attacker’s image X whose complete trans-

formation using P

matches exactly T

First, the attacker (A) uses I

to compute the

derivative F

using the ﬁlter. Then, A computes her

modiﬁed image’s features F

whose derived template

using P

matches exactly the target template T

. As

described in Section 3.1.1, this is done by solving an

under-constrained linear system and seeking the near-

est modiﬁed features whose derived template using P

matches exactly T

. Next, using F

and I

, A com-

putes her modiﬁed image X whose image derivative

by Sobel ﬁlter matches exactly the modiﬁed features

. As described in Section 3.1.2, this is done by solv-

ing an under-constrained quadratic system and seek-

ing the nearest modiﬁed image X whose Sobel deriva-

tive matches exactly the features F

. Figure 1 gives an

overview of this ﬁrst method step by step, where in-

puts are in circles and different steps in boxes.

3.1.1 Getting a Correct Output for the Filter

For this part, we assume that we are after the ﬁlter. We

want to reverse target’s template by using the pass-

word. To do that, let X = (x

,...,x

), M the projec-

tion matrix derivated from target’s password and f the

quantization function which takes XM to create a bi-

nary template.

We know the projection matrix and the template

T . Thus, a pre-image of the projected vector can be

ﬁnd by solving a system under constraints. Notice

that the proposed attack works for many projections

system such as BioHash.

Let K

be all indices where T is equal to 0 and

all other indices. So, we seek a solution to the

following system:











< 0,∀i ∈ K

≥ 0,∀ j ∈ K

∈ R

,∀i ∈ (K

∪ K

)

With M

the i-th column of M. We seek to mini-

mize the distance between F and F

. By doing so, the

attacker can be authenticated by modifying the small-

est number of information of her own biometric fea-

ture vector.

This part of the attack solves the following prob-

lem. By taking F

= (o

,...,o

) the attacker’s bio-

metric features, M the projection matrix we have:

• Minimize: kX − F

• Under the following constraints:











< 0,∀i ∈ K

≥ 0,∀ j ∈ K

∈ R

,∀i ∈ (K

∪ K

)

With M

the i-th column of M.

Authentication Attacks on Projection-based Cancelable Biometric Schemes

571

3.1.2 Get a Preimage to Avoid Filter Effect

The ﬁlter leads to a loss of information. But we can

write a quadratic system to create a collision and get

a correct preimage. Let the image matrix be

I =







0,0

... o

0,width-1

length-1,0

... o

length-1,width-1







Applying the ﬁlter to that formal matrix yields a

new matrix D which has quadratic components. But,

we know that D must be equal to F

. Thus, we can

solve a quadratic system with (length × width) equa-

tions and (length × width) variables to ﬁnd a preim-

age.

Let I

= (o

i, j

) denote the attacker’s original im-

age, F

= (a

i, j

) its modiﬁed features, I

= (x

i, j

) the

modiﬁed original image and X = (x

i, j

) its augmented

form. We consider the augmented form as the original

matrix where zeroes are added all around the matrix

to compute the convolution without overﬂowing.

In the case of Sobel ﬁlter, we solve the following

problem:

• Minimize:

∑

i, j

− x

i, j

)

• Subject to the following constraints:











i, j

= x

(i−1, j−1)

+ 2x

(i, j−1)

+ x

(i+1, j−1)

− x

(i−1, j+1)

− 2x

(i, j+1)

− x

(i+1, j+1)

i, j

= x

(i−1, j−1)

+ 2x

(i−1, j)

+ x

(i−1, j+1)

− x

(i+1, j−1)

− 2x

(i+1, j)

− x

(i+1, j+1)

i, j

= α

i, j

+ β

i, j

,∀(i, j)

i, j

= 0 if i = 0 or i = length + 1

i, j

= 0 if j = 0 or j = width + 1

i, j

∈ J0,255K,∀(i, j)

3.2 Formulation as a Single Program

The attack takes as input the same parameters (P

and I

) and returns a modiﬁed attacker’s im-

age X whose complete transformation matches the

target template. The main idea is to merge both

steps described in Section 3.1. A unique constrained

quadratic system is solved to ﬁnd the nearest mod-

iﬁed image whose complete transformation matches

exactly the template (see Figure 2). Note that this sin-

gle program avoids some problems such as having an

intermediate feature vector which is not in the range

of the ﬁlter function.

Assume that I

= (o

i, j

)

n×m

is the attacker’s origi-

nal image, I

= (x

i, j

)

n×m

the modiﬁed original image

and X = (x

i, j

)

n×m

its augmented form. Let K

be all

indices where the template is equal to 0 and K

all

other indices. Let M = (a

i, j

)

(n∗m)×`

be the projection

matrix. Let Y

f lat

be the ﬂattened form of the matrix Y

where rows are concatenated in a single vector.

Thus, using the notations from the sections 3.1

and 3.2 we deﬁne the following problem for Sobel

ﬁlter:

• Minimize: kX − I

• Subject to the following constraints:













∗ X)

+ (G

∗ X)



f lat

< 0,∀i ∈ K

f lat

≥ 0,∀ j ∈ K

i, j

∈ J0,255K,∀(i, j)

Where the squaring stands for the coordinate by coor-

dinate squaring and M

the i-th column of M.

4 MULTIPLE COLLISIONS

ATTACK

In this attack, the attacker knows the templates and

passwords of the victims. Then, her goal is to use

all these information to generate one image that al-

lows her to impersonate all the victims using their

own password. The attack takes as input: the tar-

get’s templates (T

)

i∈µ

, the attacker’s image (I

) and

the target’s passwords (P)

i∈µ

. The output is a modi-

ﬁed attacker’s image X which matches all templates

for the corresponding password.

As in the single authentication attack, we deﬁne a

quadratic system with more constraints and a function

to minimize. Let M

be the projection matrix for the

i-th user. Assume that (K

)

is the list of all indices

where (T

)

is equal to 0 and (K

)

all other indices.

The other notations are the same as in Section 3.2.

The problem can be deﬁned as:

• Minimize: kX − I

• Under the following constraints where (M

)

is the

j-th column of M













∗ X)

+ (G

∗ X)



f lat

)

< 0,∀i ∈ µ, ∀ j ∈ (K

)

f lat

)

≥ 0,∀i ∈ µ, ∀k ∈ (K

)

i, j

∈ J0,255K,∀(i, j)

As matrices M

are fully random, the probability

of them forming an indexed family of linearly de-

pendent vectors is negligible, thus making the sys-

tem solvable. Assume that L(V

,...,V

) is the event

that (V

,...,V

) is an indexed family of linearly in-

dependent vectors, with n the size of vector and η

the number of precision bits for our numbers. It can

be shown that P(L(V

,...,V

)) = (

∏

i=2

η(n−i+1)

−

SECRYPT 2022 - 19th International Conference on Security and Cryptography

572

1)/(

∏

i=2

η(n−i+1)

). Since this probability is near 1,

the usurpation of

n/w

persons with w the size of the

template is a likely event.

5 EVALUATION AND

CONCLUSION

We evaluate our attack (Section 3.2) through our

Python implementation. Gurobi 9.1.2 is used to

solve the quadratic non-convex programs, on a com-

puter running on Debian 11, with an EPYC 7F72

dual processor (48 cores) and 256GB RAM. We have

launched resolutions of the programs 50 times, each

with a time limit of 150 seconds. Table 1 reports the

running times for the different settings along with the

amount of changes done in the attacker ﬁngerprint,

using Euclidian distance. With a 4×4-pixel image

and a 50-bit template, 150 seconds starts to be insuf-

ﬁcient to solve the system and optimize the criterion.

In 500 seconds, we solve the system with a 10×10-

pixel image for a better ratio amount of changes over

image size. Thus, the experiments are encouraging

for a NP-hard problem (Sahni, 1974).

Table 1: Summary of the experiments for a 50-bit template.

Image Size Template Size Mean Distance Mean Time (s)

2 × 2 99 0.14

2 × 3 117 32.76

3 × 3 50 133 150.0

4 × 3 144 146.67

4 × 4 177 150.0

In this paper, we present several authentication at-

tacks on a popular CB scheme consisting in a compo-

sition of a kernel-based ﬁlter with a projection-based

transformation, in the stolen token scenario. Their

particularity is to completely reverse a CB scheme to

impersonate any or several users. To the best of our

knowledge, this is the ﬁrst time that attacks are con-

ducted on a complete chain of treatments, including a

non-linear ﬁlter. The proposed methodology is to for-

malize the attacks as constrained optimization prob-

lems. As long as the attacker has access to one or

several templates with the corresponding passwords

or not, our attacks can be performed. Future work

will focus on ﬁnding optimizations and relaxations of

the systems to ensure the scaling of our attacks.

ACKNOWLEDGEMENT

The authors acknowledges the support of the French

Agence Nationale de la Recherche (ANR), under

grant ANR-20-CE39-0005 (project PRIVABIO).

REFERENCES

(2011). ISO/IEC24745:2011: Information technology – Se-

curity techniques – Biometric information protection.

Standard, International Organization for Standardiza-

tion.

(2018). ISO/IEC30136:2018(E): Information technology

– Performance testing of biometrictemplate protec-

tion scheme. Standard, International Organization for

Standardization.

Dong, X., Jin, Z., and Jin, A. T. B. (2019). A genetic algo-

rithm enabled similarity-based attack on cancellable

biometrics. In 2019 IEEE 10th International Confer-

ence on Biometrics Theory, Applications and Systems

(BTAS), pages 1–8.

Ghammam, L., Karabina, K., Lacharme, P., and Thiry-

Atighehchi, K. (2020). A cryptanalysis of two cance-

lable biometric schemes based on index-of-max hash-

ing. IEEE Transactions on Information Forensics and

Security, PP:1–12.

Jin, A. T. B., Ling, D. N. C., and Goh, A. (2004). Biohash-

ing: two factor authentication featuring ﬁngerprint

data and tokenised random number. Pattern Recog-

nition, 37(11):2245–2255.

Lacharme, P., Cherrier, E., and Rosenberger, C. (2013).

Preimage attack on biohashing. In 2013 Interna-

tional Conference on Security and Cryptography (SE-

CRYPT), pages 1–8.

Li, C. and Hu, J. (2014). Attacks via record multiplicity on

cancelable biometrics templates. Concurrency Com-

putation: Practice and Experience, pages 1593–1605.

Nagar, A., Nandakumar, K., and Jain, A. K. (2010). Bio-

metric template transformation: a security analysis. In

Memon, N. D., Dittmann, J., Alattar, A. M., and Delp,

E. J., editors, Media Forensics and Security, volume

7541 of SPIE Proceedings, page 75410O. SPIE.

Nandakumar, K. and Jain, A. K. (2015). Biometric tem-

plate protection: Bridging the performance gap be-

tween theory and practice. IEEE Signal Processing

Magazine, 32:88–100.

Natgunanathan, I., Mehmood, A., Xiang, Y., Beliakov, G.,

and Yearwood, J. (2016). Protection of privacy in bio-

metric data. IEEE Access, 4:880–892.

Ratha, N. K., Connell, J. H., and Bolle, R. M. (2001). En-

hancing security and privacy in biometrics-based au-

thentication system. IBM Systems J., 37(11):2245–

2255.

Sahni, S. (1974). Computationally related problems. SIAM

Journal on Computing, 3(4):262–279.

Teoh, A. B. J., Yip, W. K., and Lee, S. (2008). Can-

cellable biometrics and annotations on BioHash. Pat-

tern Recognition, 41(6):2034–2044.

Topcu, B., Karabat, C., Azadmanesh, M., and Erdo-

gan, H. (2016). Practical security and privacy at-

tacks against biometric hashing using sparse recovery.

EURASIP Journal on Advances in Signal Processing,

2016(1):100.

Vincent, O. and Folorunso, O. (2009). A descriptive algo-

rithm for sobel image edge detection.

Authentication Attacks on Projection-based Cancelable Biometric Schemes

573