
Weighted Attribute-based Encryption with Parallelized Decryption
Alexandru Ioni¸t
˘
a
1,2 a
1
Simion Stoilow Institute of Mathematics of the Romanian Academy, Bucharest, Romania
2
Department of Computer Science, Alexandru Ioan Cuza University of Ia¸si, Ia¸si, Romania
Keywords:
Attribute-based Encryption, Bilinear Maps, Public-key Encryption, Access Control, Key Policy.
Abstract:
Unlike conventional ABE systems, which support Boolean attributes (with only 2 states: 1 and 0, or "Present"
and "Absent"), Weighted Attribute-based Encryption schemes also support numerical values attached to at-
tributes, and each terminal node of the access structure contains a threshold for a minimum weight. We
propose a Weighted ABE system, with access policy of logarithmic expansion, by dividing each weighted
attribute in sub-attributes. On top of that, we show that the decryption can be parallelized, leading to a notable
improvement in running time, compared to the serial version.
1 INTRODUCTION
As interest in Cloud Computing and Internet of
Things grew significantly, so did the interest in more
expressive encryption and access control possibilities.
In this context, Attribute-based Encryption (ABE), in-
troduced in (Sahai and Waters, 2005) as an refine-
ment for Identity-based Encryption (Shamir, 1984),
witnessed great attention in the past decade.
Depending on how the access policy is linked to
the ABE systems, we have two main types:
• Key-policy ABE (KP-ABE), first introduced in
(Goyal et al., 2006) encrypts a message along-
side some attributes; the decryption keys have an
access structure (such as a Boolean formula) at-
tached. The decryption is possible if and only if
the key’s access structure is satisfied with the ci-
phertext’s attributes.
• Ciphertext-policy ABE (CP-ABE), in contrast
with KP-ABE, links the access structure to the
ciphertext, and attributes to the decryption keys.
First such system was proposed in (Bethencourt
et al., 2007).
Researchers are trying to find more and more flex-
ible access structures that can be used in ABE sys-
tems. Starting from well known ABE systems for
Boolean Access Trees (Goyal et al., 2006; Bethen-
court et al., 2007) and Linear Secret Sharing Schemes
(Waters, 2011), more complex ones are created for
Boolean Circuits ( ¸Tiplea and Dr
˘
agan, 2014; Hu and
a
https://orcid.org/0000-0002-9876-6121
Gao, 2017), non-monotonic access structures (Ostro-
vsky et al., 2007) or compartmented access structures
(Tiplea et al., 2020).
While conventional ABE supports only two
states for each attribute ("True"/"False" or
"Present"/"Absent"), a Weighted ABE system
extends the supported access structures to more
complex structure: Each attribute can have a value
associated to it. For example, in order to describe
a role in a software company, we could assign to
each position an integer, decreasing according to the
company’s hierarchy: "ROLE:4" could be a Junior
Developer, "ROLE:3" a Senior Developer, "ROLE:2"
- Manager, and "ROLE:1" - Director. Therefore,
different types of ABE were constructed in order to
meet these needs, such as ABE with Range Attributes
(Attrapadung et al., 2018), or Weighted ABE (Wang
et al., 2016; Li et al., 2021; Liu et al., 2014).
1.1 Related Work
The problem of weighted attributes and integer com-
parisons in the access structure has been a problem of
high interest, being addressed even from the first CP-
ABE system proposed by Bethencourt et al. (Bethen-
court et al., 2007) in 2007. They described a method
for realizing integer comparisons using access trees,
and by splitting every numerical attribute in 2log(N)
values, two for each bit of information.
One of the first Weighted ABE was proposed in
(Liu et al., 2014), a key-policy scheme which used
chained components in order to describe a weighted
attribute. Thus, their system is inefficient, the length
574
Ionit
,
˘
a, A.
Weighted Attribute-based Encryption with Parallelized Decryption.
DOI: 10.5220/0011278400003283
In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 574-579
ISBN: 978-989-758-590-6; ISSN: 2184-7711
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

of the chain being equal to the weight of the attribute,
resulting in linear number of components for each at-
tribute.
Wang et al. (Wang et al., 2016) proposed in 2016
a Weighted CP-ABE system which resolves the key
escrow problem for use in Cloud Systems. They sup-
port both weighted and binary attributes. However,
the size of the ciphertext and the encryption time grow
linear on the attribute weight, with each new weighted
attribute.
A more efficient solution for the ciphertext-policy
variant was proposed in (Xue et al., 2017) where
the authors achieved logarithmic expansion for each
weighted attribute, by using 0- and 1- Encodings of
the weights.
A very recent work (Li et al., 2021) presents an-
other Weighted CP-ABE approach using 0- and 1-
Encodings, which proves to be the most efficient in
practical performance tests among the existing CP-
ABE scheme with weighted attribute support. Their
system also support online and offline encryption, and
it is designed for the Internet of Health Things.
Another work in this area was proposed by At-
trapadung et al. (Attrapadung et al., 2018) in 2018,
which addresses the problem of range attributes. Un-
like weighted attributes, which have only a lower
bound on the attribute weight, a range attribute can
also have an upper bound for it’s value. Their sys-
tem is the first one with sub-linear complexity and no
restrictions upon the access tree policy.
1.2 Our Contribution
Using a similar idea to that described in (Bethencourt
et al., 2007) for integer comparisons (using sub-trees
in leaf nodes), we have constructed on top of (Goyal
et al., 2006) a Weighted KP-ABE system. However,
this approach works just as good for CP-ABE.
Compared to other Weighted ABE schemes, our
system uses a simpler mathematical construction,
while having similar performance in terms of algo-
rithms running time.
Our main goal is to show that this simple construc-
tion leads to an efficient and versatile Weighted ABE
system. When compared to existing schemes, our so-
lution will not be the most efficient, but it is not far off
either. The theoretical analysis (due to space limita-
tions, it was omitted in this short version of the paper)
of our schemes compared to the existing ones shows
that there not a big difference between them.
The main strength of our scheme is the simplic-
ity of the construction, which opens the possibility of
adding with ease new features to our scheme: access
revocation, encryption/decryption outsourcing or de-
centralization.
Furthermore, we have shown that our decryption
algorithm can be parallelized in order to make it
faster. We have compared the parallelized version
with the sequential one, in order to highlight the prac-
tical efficiency gain of this optimization.
2 PRELIMINARIES
Notations and Abbreviations.
Notation Meaning
W
A
weight of attribute A
attr(Γ) attribute corresponding to node Γ
ω
Γ
Minimum weight required for attr(Γ)
In
Γ
Set of input nodes for gate Γ
∆
i,S
(x) Lagrange coefficient:
∏
j∈S, j6=i
x− j
i− j
Bilinear Maps (Goyal et al., 2006). Given G
1
and
G
2
two multiplicative cyclic groups of prime order p,
a map e : G
1
×G
1
→ G
2
is called bilinear if it satisfies:
• e(x
a
,y
b
) = e(x, y)
ab
, for any x,y ∈ G
1
and a,b ∈
Z
p
;
• e(g,g) is a generator of G
2
, for any generator g of
G
1
.
G
1
is called a bilinear group if the operation in G
1
and e are both efficiently computable.
Access Structures (Beimel, 2011). Let p
1
,. .., p
n
be a set of parties. A collection A ⊆ 2
{p
1
,...,p
n
}
is
monotone if B ∈ A and B ⊆C imply that C ∈ A. An ac-
cess structure is a monotone collection A ⊆ 2
{p
1
,...,p
n
}
of non-empty subsets of {p
1
,. .., p
n
}. Sets in A are
called authorized, and sets not in A are called unau-
thorized.
Weighted Access Tree. A weighted access tree is a
tree access structure where
each internal node Γ represents a threshold gate: it
has an output wire (which leads to it’s parent node in
the tree), a number of input wires (σ
Γ
) and a threshold
value k
Γ
, 1 ≤ k
Γ
≤ σ
Γ
. A node of such type is consid-
ered to be satisfied if at least k
Γ
of it’s σ
Γ
children are
satisfied.
For every leaf node Γ, there exist a corresponding
attribute referred as attr(Γ). These gates can be of
two types:
• boolean - the node is satisfied if the corresponding
attribute is present, and it is unsatisfied (evaluated
with ⊥) if the attribute is missing.
Weighted Attribute-based Encryption with Parallelized Decryption
575

• weighted - the node has a minimum required
weight ω
Γ
attached to it. This gate receives as in-
put an attribute A = attr(Γ) with an integer weight
attached W
A
. The gate is satisfied if and only if
W
A
≥ ω
Γ
.
The weighted access tree is satisfied, if its root
node is satisfied.
KP-ABE Model. A Key-Policy Attribute-Based
Encryption scheme, as first described in (Goyal et al.,
2006), consists of four algorithms:
setup(λ). A randomized algorithm that takes as input
the implicit security parameter λ and return the
public and secret keys (MPK and MSK).
encrypt(m,A, MPK). A probabilistic algorithm that
encrypts a message m under a set of attributes A
with the public key MPK, and outputs the cipher-
text E.
keygen(C , MPK, MSK). This algorithm receives an
access structure, public and master keys, and out-
puts corresponding decryption keys DK.
decrypt(E,DK,MPK). Given the ciphertext E and
the decryption keys DK, the algorithm decrypts
the ciphertext and outputs the original message.
3 OUR CONSTRUCTION
We present a concrete KP-ABE construction for our
system. We make use of an alteration of the access
tree, similar to the one proposed in (Bethencourt et al.,
2007), in order to support integer comparisons. At
each leaf node we incorporate a sub-tree of logarith-
mic size which simulates the comparison between the
attribute weight and the required attribute threshold
weight in the access structure.
The construction from (Bethencourt et al., 2007)
presumes that for each attribute with values in
{0· ··N} we will have 2log
2
(N) sub-attribute, two for
each bit positions, covering the cases when each bit is
either 0, or 1. Our proposal is to have a sub-attribute
only for the bits that are set to 1. In this way, we
slightly reduce the number of attributes needed: In-
stead of giving exactly log(N) attributes in the de-
cryption key, one for each bit of information, we have
only Hw(N) sub-attributes, where Hw(x) is the Ham-
ming weight of x.
However, with this approach, we lose the possi-
bility of creating other type of comparisons except
"greater than" (">").
Since we want to check if the attribute’s value is
greater than the value ω
Γ
required in the leaf node Γ,
we process ω
Γ
’s bits b
`
.. .b
1
b
1
in order to create the
sub-tree. First, we eliminate the trailing (least sig-
nificant) zero’s from it’s binary representation to ob-
tain ω
0
Γ
= (b
`
.. .b
i+1
b
i
) such that b
i
= 1 and b
i−1
=
·· · = b
0
= 0 (These bits are irrelevant when checking
if some weight W
A
, with A = attr(Γ) is greater than
ω
Γ
). Then, for each bit b
j
from the binary representa-
tion of ω
0
Γ
, excluding the last bit i, add a new gate to
the system: if the bit is equal to 1, add an AND gate,
otherwise add an OR gate. This new gate will have as
parent the previous created gate (or will be connected
to the original tree, if this is the first gate created) and
two children:
• the leaf node for the sub-attribute A
j
(correspond-
ing to the j-th bit from the weight of attribute A)
• the next internal node (AND or OR gate) to be
created.
At the end, create a new leaf node for attribute A
i
,
corresponding to bit i, and set its parent to the last
created node.
Comparison Sub-tree Optimization. We observe
that our sub-tree for comparisons are formed out of
chained OR and AND gates. Therefore, we can com-
press this sub-tree, grouping together similar gates:
• each k consecutive OR gates can be compressed
in one "1 out of k + 1" threshold gate.
• each k consecutive AND gates can be compressed
in one "k + 1 out of k + 1" threshold gate.
3.1 Weighted KP-ABE Scheme
We describe further the construction of our Weighted
KP-ABE scheme. We consider our attribute universe
to be U = {1, 2 ·· · M}, each attribute being either
a Boolean or a numeric attribute. The numeric at-
tributes can have a maximum value of N. Denote with
` = log
2
(N) the number of bits required to describe
these values.
setup(λ) This algorithm receives a security parame-
ter λ, which is used to choose two multiplicative
groups G
1
and G
2
of prime order p, g a generator
of G
1
, and a bilinear map e : G
1
× G
1
→ G
2
.
For each attribute, we have two cases, depending
on the attribute type:
• If i it is a weighted attribute, then consider `
new sub-attributes: i.0,i.1, ··· i.`. For each sub-
attribute generate random t
i. j
, i ∈ U,1 ≤ j ≤ `
• If i is a Boolean attribute, choose randomly t
i
.
SECRYPT 2022 - 19th International Conference on Security and Cryptography
576

Algorithm 1: transform(T ).
1 `
N
← log
2
(N);
2 for every leaf node Γ in T corresponding to a
weighted attribute do
3 Let ω
Γ
= (b
`
·· ·b
1
b
0
)
2
the minimum
required weight ;
4 Find i such that b
i
= 1 and
b
i−1
= ·· · = b
0
= 0 ;
// Lest significant bit from ω
Γ
set to 1
5 Parent ← Γ ;
// This is a temporary variable
to store the last gate created
6 for every j in {`, ···i + 2,i + 1} do
7 Γ
j
← new leaf node ;
8 if b
j
= 1 then
9 if b
j
= b
j+1
then
10 k
Parent
← k
Parent
+ 1
11 else
12 T mp ← new (2/2)-gate
(simple AND gate). ;
13 parent(T mp) ← Parent ;
14 Parent ← T mp ;
15 else
16 if b
j
= b
j+1
then
17 continue ;
18 else
19 T mp ← new (1/2)-gate
(simple OR gate). ;
20 parent(T mp) ← Parent ;
21 Parent ← T mp ;
22 parent(Γ
j
) = Parent // Link the
leaf node to the last node
created
23 parent(Γ
i
) = Parent // Link the last
leaf, corresponding to bit i,
to the last node created
Next, choose random y ∈ Z
p
, and then set the pub-
lic key as:
MPK = hp,G
1
,G
2
,e,g,n,Y = e(g,g)
y
,T
α
= g
t
α
i
and the master key:
MSK = hy,(t
α
)i
Note that t
α
can be of type t
i
or t
i. j
depending on
the attribute type.
encrypt(m,A,MPK) The encryption algorithm re-
ceives a message m, and encrypts it under the
set of attributes A = {(A,W
A
) | A ∈ U, W
A
< N},
with the public key MPK. Normal (Boolean) at-
tributes, can be considered to have weight 0, or
1.
For each attribute A, it chooses the bits j set to
1 from it’s weight W
A
binary representation, and
computes for them the values T
s
i. j
= g
t
i. j
s
, where j
is the index of the respective bit, and i the index
of the attribute.
Then, generate a random element s, and compute
the ciphertext as:
E = hA, E
0
= mY
s
,T
s
i. j
= g
t
i. j
s
,g
s
i,i ∈ U, 1 ≤ j ≤ `
i
keygen(MPK,T ) We first need to modify the access
tree T such that we include at the leaf nodes the
sub-trees required to make the comparisons for
the weighted attributes, using the function defined
in Algorithm 1:
T
0
= transform(T )
First, it generates a random y, and shares it
through the tree, starting from the root node. For
each node Γ which has a threshold of k
Γ
, it gener-
ates a polynomial q
Γ
of degree k
Γ
− 1.
For the root node, it sets q
root
= y, and then
chooses k
root
− 1 more points randomly to com-
pletely define the polynomial. For every internal
node Γ, it sets q
Γ
(0) = q
parent
(index(Γ)) and then
chooses k
Γ
− 1 more points randomly. Finally,
every leaf node Γ should receive a value q
Γ
(0),
which is used to compute the key for the respec-
tive node:
D
Γ
= g
q
Γ
(0)/t
x
Note that x is of type i. j, it is a sub-attribute cor-
responding for bit j in attribute A = attr(Γ).
decrypt(E, DK) This algorithm receives a valid ci-
phertext and a decryption key, and returns the
original message. The simplest form of represen-
tation for the decryption algorithm is as an recur-
sive procedure. Let DecNode(E,D,Γ) be this al-
gorithm, applied to node Γ with ciphertext E, and
decryption key D. For every leaf node:
DecNode(E,D,Γ) =
e(D
Γ
,T
s
x
) = e(g,g)
q
Γ
(0)·s
,
if x = attr(Γ) ∈ A
⊥, otherwise
For the recursive case, we will consider an internal
node Γ with threshold k
x
. Consider the children z
of this node such that DecNode(E,D, z) 6=⊥. If
the number of such nodes is smaller than k
Γ
, then
Weighted Attribute-based Encryption with Parallelized Decryption
577
return ⊥, as there is insufficient data to recompute
the polynomial. Otherwise, compute the value:
DecNode(E,D,Γ) =
=
∏
z∈In
Γ
DecNode(E,D,z)
∆
i,In
0
Γ
(0)
where i = index(z), In
0
Γ
= {index(z)|z ∈ In
Γ
}
=
∏
z∈In
Γ
(e(g,g)
s·q
z
(0)
)
∆
i,In
0
Γ
(0)
=
∏
z∈In
Γ
(e(g,g)
s·q
parent(z)
(0)
)
∆
i,In
0
Γ
(0)
= e(g,g)
s·q
Γ
(0)
Calling the function on the root of the tree, we
obtain:
R = DecNode(E,D, root) = e(g,g)
s·q
root
(0)
= e(g,g)
ys
Finally, we can recover the message by comput-
ing:
m = E
0
/R = m · e(g,g)
ys
/e(g,g)
ys
3.2 Security & Extensions
Our system is, actually, an instance of Goyal’s KP-
ABE system (Goyal et al., 2006) with some attribute
relabeling. The only concrete change is in the struc-
ture of the access tree. Therefore, it inherits the lat-
ter’s security properties. If an attacker would have a
non-negligible advantage against our scheme, then an
attacker with non-negligible advantage against (Goyal
et al., 2006) would also exist. Any access tree
with comparison sub-trees in the leaf nodes is also a
valid input for Goyal’s KP-ABE system (Goyal et al.,
2006). (We can simply relabel the sub-attributes of
form i. j to a single integer α
i. j
).
Since Goyal’s KP-ABE system (Goyal et al.,
2006) is secure in the Selective Set Model for ABE,
under the decisional Bilinear Diffie-Hellman Prob-
lem, this also proves that our system is secure in the
Selective Set Model for ABE, under the same hard-
ness assumption.
Theorem 1. The Weighted KP-ABE system is secure
in the Key-Policy Attribute-based Selective-Set Model
under the bilinear Decisional Diffie-Hellman prob-
lem.
Proof. Due to space limitations, the formal proof is
omitted in this version of the paper.
Parallelized Decryption. During the decryption
phase, we can observe that the sub-trees referring to
attribute comparisons are independent one of each
other. This means that the decryption can be done
simultaneously on these parts of the access structure,
by creating a new thread for each sub-tree. When the
execution of the sub-threads is finished, the algorithm
may resume and compute the reconstruction of the se-
cret on the rest of the tree.
3.3 Other Extensions
The tree transformation method can be applied to
any CP-ABE or KP-ABE scheme that has an access
tree as policy. Therefore, many existing systems can
be extended to support weighted attributes alongside
other features, such as: encryption and decryption
outsourcing (Asim et al., 2014), multi-authority ABE
(Chase, 2007), revocation in a multi-authority system
(Qian et al., 2015).
Our proposed alteration for access trees can also
be made to Boolean circuits, in order to add support
for weighted attributes, one example of such scheme
being ( ¸Tiplea and Dr
˘
agan, 2014) or (Hu and Gao,
2017). The idea is the same as for access trees:
Replacing terminal nodes with small sub-circuits for
comparisons.
4 EXPERIMENTAL RESULTS
20 40
60
80 100
500
1,000
1,500
2,000
Number of Attributes
Time [ms]
Serial
Parallel
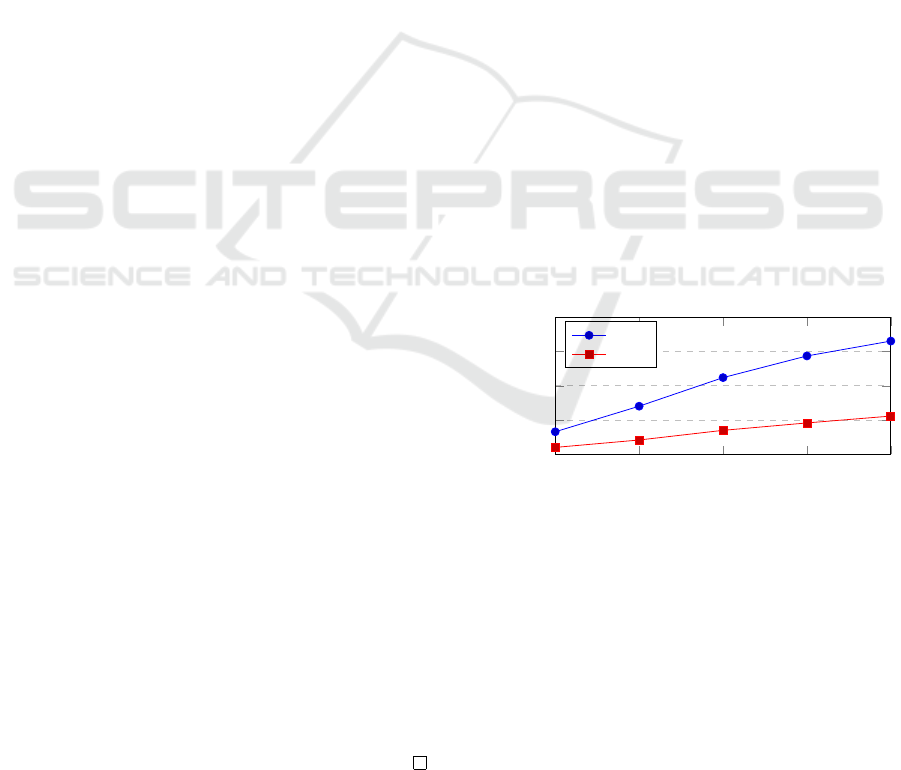
Figure 1: Performance tests.
Due to space limitations, we provide only a part of our
performance tests, limited to out Weighted KP-ABE
scheme with “Serial” and “Parallel” implementations
of the decryption algorithm.
We have tested our system against an access struc-
ture with variable number of weighted attribute, rang-
ing from 20 to 100. The access tree was formed
mostly by AND gates, and the threshold weight from
the leaf nodes was the maximum possible - it was
requiring 2
8
− 1 (and 2
16
− 1 for the 16 bit variant)
weight for each attribute. In the “parallel” imple-
mentation our program created a new thread for each
SECRYPT 2022 - 19th International Conference on Security and Cryptography
578

weighted attribute, which computed the result of the
sub-tree corresponding to that attribute. Our results
can be see in Figure 1.
5 CONCLUSIONS
While this approach is most likely not the most effi-
cient for Weighted ABE systems, it is not far away
from the best existing solution in terms of efficiency.
However, our variant provides a more simpler
and proven secure mathematical construction, which
lead to more versatility, inheriting all possible en-
hancements of the emblematic KP-ABE (Goyal et al.,
2006) and CP-ABE (Bethencourt et al., 2007) sys-
tems, such as: access revocation, outsourcing and
multi-authority.
On top of that, this Weighted ABE system proves
to be very suitable for parallelized decryption, in or-
der to make it more efficient: It is both easy to imple-
ment and offers great practical time benefit, without
any mathematical alteration of the system.
The performance tests show that this simple ap-
proach is suitable for practical use. While for the nor-
mal version we could use access policies up to 40-
50 attributes, for the parallel one, this number will
greatly increase to around 100.
REFERENCES
Asim, M., Petkovic, M., and Ignatenko, T. (2014).
Attribute-based encryption with encryption and de-
cryption outsourcing.
Attrapadung, N., Hanaoka, G., Ogawa, K., Ohtake, G.,
Watanabe, H., and Yamada, S. (2018). Attribute-
based encryption for range attributes. IEICE Trans-
actions on Fundamentals of Electronics, Communica-
tions and Computer Sciences, 101(9):1440–1455.
Beimel, A. (2011). Secret-sharing schemes: a survey. In
International conference on coding and cryptology,
pages 11–46. Springer.
Bethencourt, J., Sahai, A., and Waters, B. (2007).
Ciphertext-policy attribute-based encryption. In 2007
IEEE symposium on security and privacy (SP’07),
pages 321–334. IEEE.
Chase, M. (2007). Multi-authority attribute based encryp-
tion. In Theory of Cryptography Conference, pages
515–534. Springer.
Goyal, V., Pandey, O., Sahai, A., and Waters, B. (2006).
Attribute-based encryption for fine-grained access
control of encrypted data. In Proceedings of the 13th
ACM conference on Computer and communications
security, pages 89–98.
Hu, P. and Gao, H. (2017). Ciphertext-policy attribute-
based encryption for general circuits from bilinear
maps. Wuhan University Journal of Natural Sciences,
22(2):171–177.
Li, H., Yu, K., Liu, B., Feng, C., Qin, Z., and Srivastava,
G. (2021). An efficient ciphertext-policy weighted
attribute-based encryption for the internet of health
things. IEEE Journal of Biomedical and Health In-
formatics.
Liu, X., Zhu, H., Ma, J., Ma, J., and Ma, S. (2014).
Key-policy weighted attribute based encryption for
fine-grained access control. In 2014 IEEE Inter-
national Conference on Communications Workshops
(ICC), pages 694–699. IEEE.
Ostrovsky, R., Sahai, A., and Waters, B. (2007). Attribute-
based encryption with non-monotonic access struc-
tures. In Proceedings of the 14th ACM conference on
Computer and communications security, pages 195–
203.
Qian, H., Li, J., Zhang, Y., and Han, J. (2015).
Privacy-preserving personal health record using
multi-authority attribute-based encryption with revo-
cation. International Journal of Information Security,
14(6):487–497.
Sahai, A. and Waters, B. (2005). Fuzzy identity-based en-
cryption. In EuroCrypt, pages 457–473. Springer.
Shamir, A. (1984). Identity-based cryptosystems and sig-
nature schemes. In Workshop on the theory and ap-
plication of cryptographic techniques, pages 47–53.
Springer.
¸Tiplea, F. L. and Dr
˘
agan, C. C. (2014). Key-policy attribute-
based encryption for boolean circuits from bilinear
maps. In BalkanCryptSec, pages 175–193. Springer.
Tiplea, F. L., Ionita, A., and Nica, A.-M. (2020). Practi-
cally efficient attribute-based encryption for compart-
mented access structures. In ICETE (2), pages 201–
212.
Wang, S., Liang, K., Liu, J. K., Chen, J., Yu, J., and Xie, W.
(2016). Attribute-based data sharing scheme revisited
in cloud computing. IEEE Transactions on Informa-
tion Forensics and Security, 11(8):1661–1673.
Waters, B. (2011). Ciphertext-policy attribute-based en-
cryption: An expressive, efficient, and provably se-
cure realization. In International Workshop on Public
Key Cryptography, pages 53–70. Springer.
Xue, K., Hong, J., Xue, Y., Wei, D. S., Yu, N., and
Hong, P. (2017). Cabe: A new comparable attribute-
based encryption construction with 0-encoding and
1-encoding. IEEE Transactions on Computers,
66(9):1491–1503.
Weighted Attribute-based Encryption with Parallelized Decryption
579
