
Using Machine Learning Methods and the Influenza Simulation System
to Explore the Similarities of Taiwan’s Administrative Regions
Zong-Kai Lai
1
, Yi-Ting Chiang
1
, Tsan-sheng Hsu
2
and Hung-Jui Chang
1, ∗
1
Department of Applied Mathematics, Chung Yuan Christian University, Taoyuan, Taiwan, Republic of China
2
Institute of Information Science, Academia Sinica, Taipei, Taiwan, Republic of China
Keywords:
Simulation System, Clustering, Decision Tree, Data Utilization.
Abstract:
When designing public health policy to prevent the spread of disease, it is crucial to consider the difference in
each administrative region. Residents’ daily and inter-regions activities are essential when epidemic diseases
are spreading. Most of the statistical data in the traditional public health system cannot capture these behaviors.
The standard statistic data and the disease transmission behaviors are combined and equally considered in the
disease-transmission simulation system. According to the data from the simulation system, the administrative
regions in Taiwan are separated into one urban and three non-urban areas by the clustering algorithm. Then
we use decision tree algorithms to determine the main factors when deciding whether an area is rural or urban.
The experiment results show that the percentage of elders and the road infrastructure is the main feature for
determining the type of an area.
1 INTRODUCTION
From H1N1 (World Health Organization, 2010)
to COVID-19 (World Health Organization, 2022),
global epidemics have spread worldwide and caused
the deaths of millions of people and countless eco-
nomic losses (Lenzen et al., 2020). Those highly
spreading diseases have been one of the main threats
to all the governments during the past several years.
Understanding the administrative regions’ differences
becomes crucial to making public health policies
preciously and promptly (Bargain and Aminjonov,
2020).
The urban and rural areas are the most com-
mon categories for separating administrative re-
gions (Prothero, 1977). Researchers use the popu-
lation structure and economic data to decide the re-
gions’ type. However, those data cannot capture
the whole scope when facing disease transmission.
Therefore, disease transmission specified data are re-
quired to help the classification process. When dis-
cussing the disease spreading, the daily activities and
the interaction between connected regions are more
important (Balcan et al., 2009).
In this work, we have data from two different
data sources. The first part contains the Taiwan dis-
∗
Corresponding author.
ease transmission simulation system’s simulation re-
sult (simulation data) (Chang et al., 2014). The sec-
ond part contains the population structure data (geo-
data) from the census data and the open data set in
Taiwan (Opendata platform, 2022).
We use the simulation data as the input of the clus-
tering algorithm. Those regions in the same clustering
are similar in the view of disease transmission. The
results of the clustering process are combined with the
geodata as the input of the classification algorithm.
We use the classification algorithm to separate the ad-
ministrative regions in Taiwan into three categories:
the urban areas, the rural areas, and the in-between
areas. When using different data entries of the popu-
lation structure as the feature, the classification results
will slightly differ. We selected four feature sets from
the population structure data and generated four cor-
responding classification results. We combined the
classification results by a voting system to determine
the category of each region. Decision tree algorithms
help determine the most important features when de-
termining the region’s type under the disease trans-
mission. The experiment results show that the per-
centage of elders and young children and the road in-
frastructure is the main feature determining a region’s
type.
The remains of this paper are organized as fol-
lows. In Section 2, we describe the disease transmis-
416
Lai, Z., Chiang, Y., Hsu, T. and Chang, H.
Using Machine Learning Methods and the Influenza Simulation System to Explore the Similarities of Taiwan’s Administrative Regions.
DOI: 10.5220/0011279100003269
In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 416-422
ISBN: 978-989-758-583-8; ISSN: 2184-285X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Table 1: The number of agents in each age group.
Age group # agents Percentage
c
0
1,237,435 5.38%
c
1
3,656,485 15.89%
a
0
3,369,807 14.64%
a
1
12,115,050 52.64%
a
2
2,637,244 11.46%
Total number 23,016,021 100.00%
sion model and the corresponding output data. In Sec-
tion 3, we describe the data set used in this work. In
Section 4, we describe the region category decision
process. In Section 5, we show the experiment re-
sults. In Section 6, we discuss the experiment results.
Finally, in Section 7, we conclude this paper.
2 BACKGROUNDS
The Taiwan disease transmission simulation system
(TW system) (Chang et al., 2014) is an agent-based
heterogeneous stochastic model. Based on the census
data and other public government data, this system
simulated the disease transmission behavior in Tai-
wan.
In the TW system, agents are divided into five dif-
ferent age groups according to their ages. These five
groups are young children (c
0
, from 0 to 4 years old),
elder children (c
1
, from 5 to 18), young adults (a
0
,
from 19 to 29 years old), adults (a
1
, from 30 to 64
years old), and elders (a
2
, above 65 years old). In
the TW system, there are 23,016,021 agents within
368 administrative regions. In each region, the num-
ber of agents and the distribution of the age groups
are all different. The number of agents in each age
group in the TW model from c
0
to a
2
are 1,237,435,
3,656,485, 3,369,807, 12,115,050 and 2,637,244, re-
spectively. The population size is summarized in Ta-
ble 1.
According to the age group, agents have differ-
ent daily activities, and they may go to school, go
to work, go to the day-care center or stay at home.
When those agents go out in the daytime, they may
transfer to other region rather than their hometown for
working or educating. That is, they will cause inter-
region activities and enhance the disease’s spreading.
According to the census data, we can calculate the
probability that an agent will transfer to other region.
For example, WF
368x368
is the matrix of worker flow,
where W F
i, j
denotes the probability that a working
agent who lives in region i goes to work in region j.
The number of active agents in the daytime of a re-
gion includes two parts, those originally lived in that
region and stay in that region during the daytime, and
those transferred from other region during the day-
time. The agents will go back to their hometown dur-
ing the nighttime, causing the disease to spread lo-
cally.
The age distribution is one of the key factors
which infected disease’s spreading. Usually, only
those agents who belong to c
1
, a
0
, and a
1
will go
outside the regions. And those agents who belong to
c
0
and a
2
will stay in their hometowns. Moreover,
the younger children (c
0
) and the elders (a
2
) are more
easily infected. Therefore, the percentage of each age
group in one region becomes crucial.
3 DATASET
3.1 Simulation Dataset
In the simulation system, each place in the system has
its id. For example, each region has its region-id, each
school has its school-id, and each workplace has its
workplace-id. Moreover, in the simulation system, we
will record each agent’s person-id and its daily activ-
ities, that is, those places this agent will stay during
the daytime and the nighttime, and the corresponding
place-id of these places. Using the above data, we can
calculate the population size of each region during the
daytime and the nighttime.
For each agent, we also record the health state of
that agent, that is, whether it is infected or not. If an
agent has been infected, we will also record the source
of infection, the place-id, and the time whether the
transmission takes place and occurs.
During the simulation process, we use the above
data to calculate the number of infected agents in each
region and record their age group and daily activities.
Using the TW system, we can calculate the number of
infected agents in each age group in all regions. There
are five features from the simulation results, that is,
the incidence rate of each age group:
R
t,a,g
=
n
t,a,g
N
t,a,g
,
where n
t,a,g
and N
t,a,g
respectively represent the num-
ber of infected and infectiable people during time in-
terval t within age group a in region g. Because the
number of people in a specific region can be differ-
ent between weekday (t
w
) and holiday (t
h
), the final
incidence rate of each age group in each region is:
5
7
× R
t
w
,a,g
+
2
7
× R
t
h
,a,g
.
Using Machine Learning Methods and the Influenza Simulation System to Explore the Similarities of Taiwan’s Administrative Regions
417

Table 2: All data features and their usage.
Feature description # Clustering Classification
Infected ratio 5 Yes No
Adjusted ratio 5 Yes Yes
Population size 2 No Yes
Stay-in-town ratio 4 No Yes
3.2 Geodata Dataset
There are four features from the census data, which
denote the percentage of workers and students in dif-
ferent level who will not transfer to other regions dur-
ing the weekday. For example W F
i,i
is the stay-in-
town ratio of workers in region i. And we can calcu-
late these stay-in-town ratio for the elementary school
students, the middle school students, and the high
school students, respectively.
There are five features in the geodata features, the
adjusted ratio of the five age groups. For each age
group, we used the following formulae to compute the
“adjusted” age ratio (R
g
) of each region:
R
a,g
=
r
a,g
max
g∈G
r
a,g
,
where G is the set of all the 368 administrative regions
in Taiwan and r
a,g
is the age ratio of age group a in
region g.
3.3 Summary of Dataset
In total, we have 16 features for each region: five fea-
tures for the adjusted age ratio and five features for
the infected rate of each age group, the number of ac-
tives people on weekdays and holidays, and the stay-
in-town percentage of workers, elementary students,
middle school students, and high school students.
These are the input data of our experiments. Notice
that only 10 and 11 features are used in the clustering
and classification experiments, respectively. All the
features and usage are summarized in Table 2.
4 METHODOLOGY
The rural and urban areas may require different poli-
cies to deal with during the disease transmission. In
this work, we combined clustering and classification
methods to distinguish the rural and urban areas dur-
ing the outbreak of epidemic disease. Specifically,
we used the agglomerative clustering method to find
merge samples in districts and townships in Taiwan.
These samples are generated from the TW system.
Then we analyzed the results, recognizing the geopo-
litical characteristics of these clusters. These clusters
were assigned as rural or urban clusters and were used
as the labels (classes) to build decision trees. The re-
sults are models and important characteristics to dis-
tinguish the rural and urban areas from the perspective
of epidemic transmission.
In addition to the procedures mentioned above, we
tried to place more importance on some features in the
dataset. In the following sections, we describe of our
methodology. The detailed implementation, includ-
ing feature sets, parameter settings, and the toolkits
we used, is given in Section 5.
4.1 Data Clustering
We made use of agglomerative clustering in this work.
Agglomerative clustering is a hierarchical clustering
method that forms clusters in a bottom-up manner.
Specifically, each sample initially forms a cluster by
itself. Then the pairwise cluster distances are com-
puted, and the most “similar” pair of clusters are
merged into one new cluster. This step repeats un-
til there is one cluster. The agglomerative clustering
procedure generates a tree with each node as a clus-
ter, and the combination of children nodes becomes
their parent node. We can analyze the tree and find a
cutting point to decide how many clusters are in the
dataset.
4.2 Classification
We used a decision tree as the classification method.
The decision tree is a popular supervised machine
learning method that enjoys the merit of interpretabil-
ity. In a decision tree, each internal node corresponds
to a test of condition, or a decision, on a feature. And
the leaf nodes correspond to labels or classes of the
samples. Samples will be splits based on whether
they satisfy the condition or not. A decision tree
decides the sample’s label according to which leaf
node this sample reaches. For example, most decision
tree algorithms, ID3 (Quinlan, 1986) algorithm and
C4.5(Quinlan, 1993), construct the tree in a top-down
manner. The root node corresponds to the decision
(feature) that can best split the samples and be consid-
ered the most important one to separate the samples.
4.3 Repetitive Feature Utilization
The main procedure in our work consists of a pair of
clustering and classification procedures. Instead of
building one clustering and one classification model,
we built several pairs of models using different feature
sets, and these models vote to decide the label of sam-
ples. When building each model, we repetitively used
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
418

some features that are considered more important.
Heald-Sargent et al. examined 145 patients with
mild to moderate illness within one week of symptom
onset. They found that the children younger than five
years had significantly lower median cycle threshold
(CT) values (Heald-Sargent et al., 2020). This find-
ing indicates that young children may be important
drivers of COVID-19 spread. In addition, the el-
derly often have less obvious symptoms of infection,
whereas the morbidity and mortality of infectious dis-
eases increase with age. Policymakers should get
older people vaccinated against infectious diseases
more often (Bijkerk et al., ). Therefore, the features
we considered important are the ratio of the younger
and elder age groups in an area and the age groups’
incidence rate of infectious disease. We considered
these features more important than others for the au-
thority to set up anti-epidemic policies and used them
more times than other features.
5 EXPERIMENT
5.1 Setup
We conducted the experiments on a windows 10 PC
with Intel i7-9700k CPU with 32GB memory. We
used python scikit-learn package to implement both
clustering and classification procedures. For clus-
tering, we adopted Euclidean distance as the dis-
tance measurement and Ward’s minimum variance
method (Ward, 1963) to decide the clusters to be
merged.
We use the five age groups in our work as in the
TW system: the age group between 0 and 4 (c
0
), be-
tween 5 and 18 (c
1
), between 19 and 29 (a
0
), between
30 and 64 (a
1
), and age 65 and over (a
2
). We per-
formed data clustering and classification procedures
in four rounds. Each round uses only samples in some
age groups in the dataset. Therefore, the age groups
in the four rounds are
1. Age group c
0
, and a
2
2. Age group c
0
, c
1
, and a
2
3. Age group c
0
, c
1
, a
0
, and a
2
4. All age groups
We put more importance on the youngest and the
oldest age groups. The youngest and the oldest
age groups are anticipated in all the four clustering
and classification procedures. As a result, these age
groups can affect the result of the model more than
other age groups.
The geodata features in the four rounds were those
corresponding to the age group in that round. For ex-
ample, in the first round, there are four features (ad-
justed age ratio and the incidence rate of group c
0
and
a
2
.) We examined the clustering result and set the
number of clusters to four. The pseudocode of this
procedure is given in Algorithm 1.
Algorithm 1: The clustering procedure.
Require: D, the dataset
Ensure: D
c
, the set of four labeled datasets
G
s
← [c
0
, a
2
, c
1
, a
0
, a
1
] {Array of age groups}
FG← [ ]
for all g ∈ G
s
do
Use D to compute FG
g
{Compute geodata fea-
tures of samples in each age group}
Append FG
g
to the tail of array FG
end for
N
c
← 4 {Set the number of clusters to four}
S ← {c
0
}
D
c
← {}
for i = 1 to 4 do
S ← S ∪ FG
i
{Incrementally adding the geodata
of age group G
s
[i] to the dataset}
C
i
← cluster(S, N
c
) {Perform clustering}
D
c
← D
c
∪ Annotate(D,C
i
) {Set the label of
samples in D to urban or non-urban according
to C
i
}
end for
return D
c
The decision tree algorithm in scikit-learn is
CART (Breiman et al., 1984), which is similar to C4.5
but can perform both classification and regression.
The number of features in our classification procedure
was 11. These features included the adjusted age ra-
tios of all the age groups (five features) and the fea-
tures from the simulation system (’elementary ratio,’
’middle ratio,’ ’high ratio,’ ’work ratio,’ ’weekday,’
and ’holiday’). We used information gain (entropy) to
evaluate the impurity of data separation. Information
gain measures the uncertainty (entropy) of the distri-
bution of data’s labels before and after splitting the
data. The amount of entropy reduced is the informa-
tion gained by deciding to split to set. Therefore, after
splitting data samples, a decision that can reduce the
most uncertainty of the distribution of the labels was
considered the most effective one in our work. In ad-
dition, we set the maximum depth of the decision tree
to 3 to avoid overfitting. We randomly selected 90%
of the regions (331 samples) to train the model and
use the model to annotate all the regions. The pseu-
docode of this procedure is given in Algorithm 2.
Using Machine Learning Methods and the Influenza Simulation System to Explore the Similarities of Taiwan’s Administrative Regions
419

Algorithm 2: The classification procedure.
Require: D
c
, the set of four labeled datasets gener-
ated in the four rounds of clustering
Ensure: V, the final result
for all i = 1 to 368 do
V [i] ← 0
end for
Set the features of all the samples in D
c
to be the
simulation features and all adjusted age features.
for all D ∈ D
c
do
d ← 3 {Set the max depth of decision tree to 3}
Randomly select 90% of the regions from D to
construct a training dataset D
t
M ← Decision(D
t
, d) {Train a decision tree
model}
L ← Predict(M, D) {Annotate all the regions}
{Use the decision tree to vote all the regions}
for i = 1 to 368 do
if L[i] is urban then
V [i] ← V [i] +1
end if
end for
end for
{Set the final result by voting}
for all i = 1 to 368 do
if V [i] ≥ 3 then
V [i] ← urban
else
V [i] ← non-urban
end if
end for
return V
5.2 Experimental Results
Table 3 is the result of the four rounds of cluster-
ing. This table shows the number of administrative
regions in each cluster generated in each round. We
only used features about epidemic transmission con-
ditions when we performed clustering, samples in the
same cluster have similar epidemic transmission con-
ditions. We set the number of clusters to four and an-
alyzed these regions in these clusters. We found that
similar geopolitical characteristics can also be found
from the same cluster in these rounds in addition to
epidemic transmission conditions. Specifically, we
found one cluster consisting of the urban areas in spe-
cial municipalities in Taiwan. We assigned ID 1 to
this cluster. In addition, we can find another cluster
that corresponds to the areas in the Central Mountain
Range, which is the cluster with ID 2. Moreover, we
found the suburban areas around areas with ID 1 can
be found in one cluster. We assigned ID 3 to this clus-
ter. The last cluster, the cluster of ID 4, consists of
Table 3: The number of administrative regions in the clus-
ters in the four rounds, and the cluster IDs (1 to 4) and the
class (urban and non-urban) we assigned to these clusters.
Cluster ID
Round
1 2 3 4
urban non-urban
1 144 123 96 5
2 161 118 83 6
3 164 124 74 6
4 165 91 106 6
special uninhabited samples in our simulation dataset.
This result indicates that the condition of epidemic
transmission in an area is highly dependent on its de-
gree of urbanization. As a result, we assign the class
of samples in the first cluster to urban areas, and the
other clusters are non-urban areas.
After assigning classes to all samples, we built one
decision tree. We randomly selected 90 percent of
samples (331 samples) as the training dataset to train
the decision tree model in each round. We set the max
depth of the decision trees to two to identify the two
most effective features. The four decision trees are
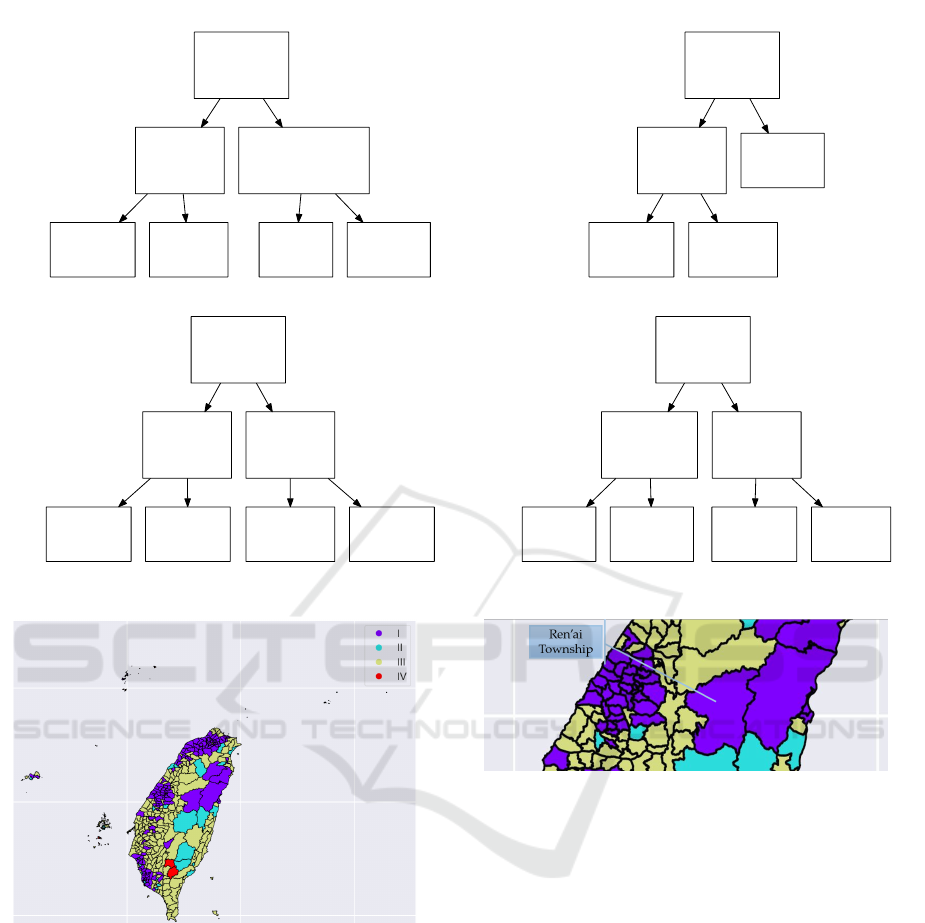
given in Figure 1.
From Figure 1, we can see that they all choose
the same feature in their root nodes. This feature is
the ratio of the elderly population in the area. The
next features in the decision tree in the four rounds are
respectively the ratio of infant and toddler population,
the ratio of the elder children (c
1
), and the ratio of the
young adult (a
0
) in the population.
We use the four decision trees to recognize all the
areas in Taiwan. Each decision uses the same set of
areas but with different age groups. As mentioned in
Section 4.3, this setting makes the younger and elder
age groups more important in our experiment. The
same area may be an urban or rural area by different
decision trees. An area may be classified as an urban
or rural area with one, two, three, or four times. We
use the four classification results to classify the areas
into three classes, the urban area, the suburban area,
and the rural area, by voting. Specifically, if an area
is classified as urban by three or four decision trees,
this area is assigned to an urban area. Similarly, if an
area is classified to non-urban by three or four deci-
sion trees, this area is assigned to a rural area. Finally,
an area classified as urban and non-urban for both two
times is assigned to a suburban area, and we ignored
the uninhabited areas in the dataset.
The map of divisions of Taiwan colored according
to our results is given in Figure 2. Type I, II, and III
are the urban, the suburban, and the rural area decided
by the voting results, respectively. Type IV are those
areas we ignored. These four classes represent areas
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
420
a_2 <= 0.139
entropy = 0.97
samples = 331
value = [199, 132]
class = y[0]
c_0 <= 0.099
entropy = 0.608
samples = 154
value = [23, 131]
class = y[1]
True
elementary_ratio <= 0.673
entropy = 0.05
samples = 177
value = [176, 1]
class = y[0]
False
entropy = 0.259
samples = 137
value = [6, 131]
class = y[1]
entropy = 0.0
samples = 17
value = [17, 0]
class = y[0]
entropy = 0.0
samples = 1
value = [0, 1]
class = y[1]
entropy = 0.0
samples = 176
value = [176, 0]
class = y[0]
a_2 <= 0.164
entropy = 0.988
samples = 331
value = [187, 144]
class = y[0]
c_1 <= 0.124
entropy = 0.835
samples = 196
value = [52, 144]
class = y[1]
True
entropy = 0.0
samples = 135
value = [135, 0]
class = y[0]
False
entropy = 0.169
samples = 40
value = [39, 1]
class = y[0]
entropy = 0.414
samples = 156
value = [13, 143]
class = y[1]
a_2 <= 0.136
entropy = 0.992
samples = 331
value = [183, 148]
class = y[0]
a_0 <= 0.115
entropy = 0.594
samples = 146
value = [21, 125]
class = y[1]
True
a_0 <= 0.155
entropy = 0.542
samples = 185
value = [162, 23]
class = y[0]
False
entropy = 0.998
samples = 36
value = [19, 17]
class = y[0]
entropy = 0.131
samples = 110
value = [2, 108]
class = y[1]
entropy = 0.344
samples = 171
value = [160, 11]
class = y[0]
entropy = 0.592
samples = 14
value = [2, 12]
class = y[1]
a_2 <= 0.133
entropy = 0.989
samples = 331
value = [186, 145]
class = y[0]
weekday <= 945.0
entropy = 0.474
samples = 138
value = [14, 124]
class = y[1]
True
a_0 <= 0.132
entropy = 0.496
samples = 193
value = [172, 21]
class = y[0]
False
entropy = 0.0
samples = 6
value = [6, 0]
class = y[0]
entropy = 0.33
samples = 132
value = [8, 124]
class = y[1]
entropy = 0.159
samples = 173
value = [169, 4]
class = y[0]
entropy = 0.61
samples = 20
value = [3, 17]
class = y[1]
Figure 1: Decision trees of all four clustering results.
Figure 2: Final results of administrative regions in Taiwan.
that have similar epidemic transmission conditions.
6 DISCUSSION
We examined the results given in Figure 2. We found
that some areas are considered non-urban areas or
suburban areas in Taiwan but are classified as subur-
ban areas or urban areas in our result. Two such ex-
amples, Ren’ai Township in Nantou and Xiulin Town-
ship in Hualien, are given in Figure 3. These two ar-
eas are usually considered non-urban areas. We found
that both townships are on the route of the Central
Figure 3: The regions affected by the Central Cross-Island
Highway.
Cross-Island Highway, one of the highways connect-
ing the west and the east areas of Taiwan. Road in-
frastructure may be why the condition of epidemic
transmission in the two townships is similar to that
in urban areas.
Figures 4 and 5 give some townships with similar
situation to what we mentioned above. In Figure 4,
Daxi District and Datong Township are not urban ar-
eas in Taiwan, but our model recognized them as ur-
ban areas. Similarly, Haiduan Township in Figure 5 is
a rural area in Taiwan, and this township is recognized
as a suburban area in our result. Provincial Highway 7
of Taiwan passes Daxi District and Datong Township,
and Provincial Highway 20 of Taiwan passes Haiduan
Township. Road infrastructure may play an important
role in epidemic transmission.
Using Machine Learning Methods and the Influenza Simulation System to Explore the Similarities of Taiwan’s Administrative Regions
421
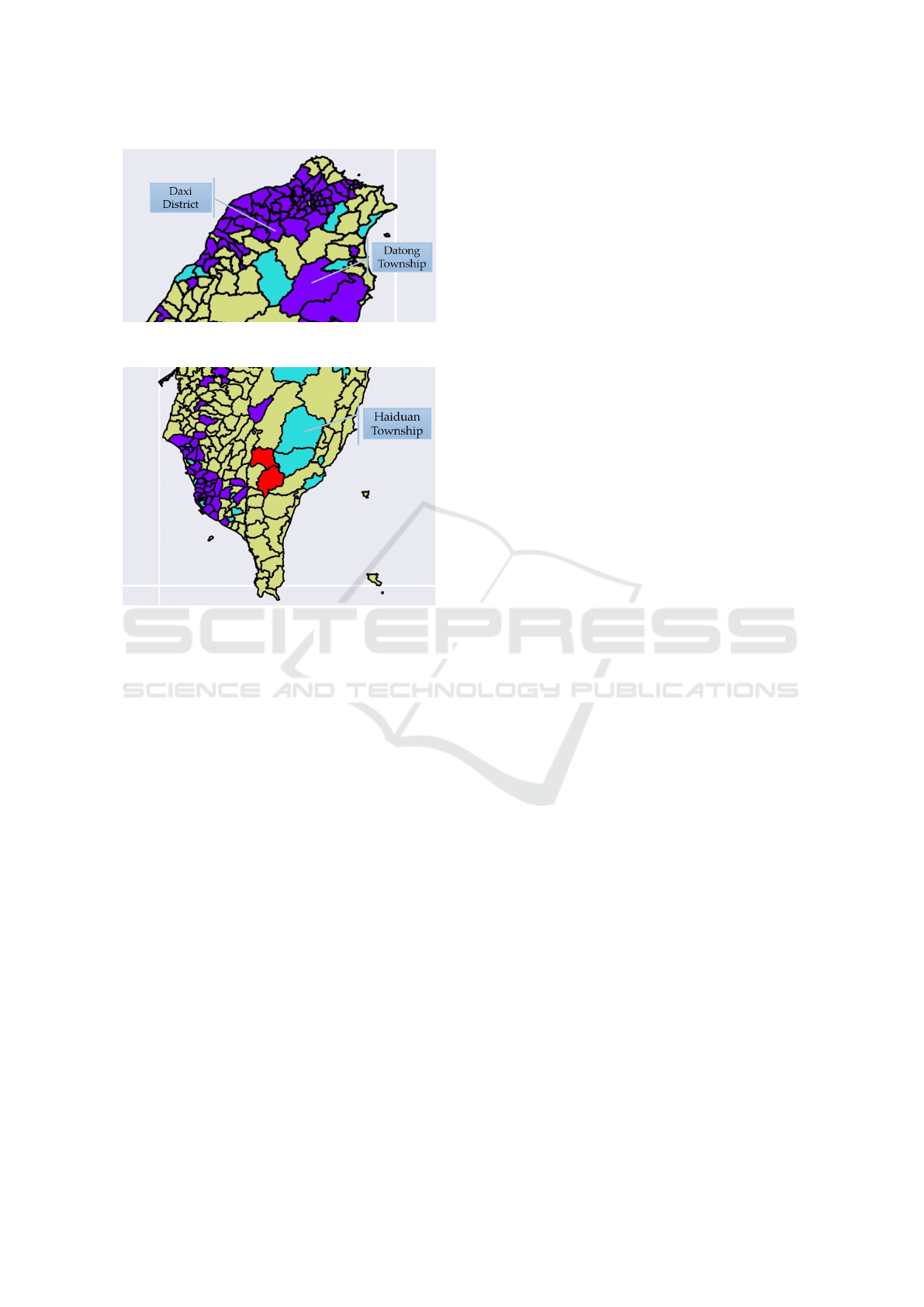
Figure 4: The regions affected by the North Link Highway.
Figure 5: The regions affected by the South Link Highway.
7 CONCLUSION
We used clustering methods to cluster the samples
generated by the simulation system of infectious dis-
eases to cluster administrative regions with similar
conditions of epidemic transmission. We also iden-
tified urban and non-urban areas by clustering meth-
ods. The result of clustering was then used to label
the samples to build decision trees. From the deci-
sion trees we built, we found age distributions are the
important features distinguishing the rural and urban
areas. In addition, by further analyzing the result, we
also found that road infrastructure may be important
to epidemic transmission.
ACKNOWLEDGMENT
This study was supported in part by MOST, Taiwan
by Grants 108-2221-E-001-011-MY3 and 110-2222-
E-033-005-.
REFERENCES
Balcan, D., Colizza, V., Gonc¸alves, B., Hu, H., Ramasco,
J. J., and Vespignani, A. (2009). Multiscale mobility
networks and the spatial spreading of infectious dis-
eases. Proceedings of the National Academy of Sci-
ences, 106(51):21484–21489.
Bargain, O. and Aminjonov, U. (2020). Trust and com-
pliance to public health policies in times of covid-19.
Journal of Public Economics, 192:104316.
Bijkerk, P., van Lier, E., van Vliet, J., and Kretzschmar,
M. Effecten van vergrijzing op infectieziekten. Ned
Tijdschr Geneeskd 2010;154:A1613.
Breiman, L., Friedman, J. H., Olshen, R. A., and Stone,
C. J. (1984). Classification and Regression Trees.
Wadsworth and Brooks, Monterey, CA.
Chang, H., Chuang, J., Chern, T., Stein, M., Coker, R.,
Wang, D., and Hsu, T. (2014). A comparison be-
tween a deterministic, compartmental model and an
individual based-stochastic model for simulating the
transmission dynamics of pandemic influenza. In 4th
International Conference On Simulation And Model-
ing Methodologies, Technologies And Applications,
SIMULTECH 2014, Vienna, Austria, August 28-30,
2014, pages 586–594. IEEE.
Heald-Sargent, T., Muller, W. J., Zheng, X., Rippe, J., Patel,
A. B., and Kociolek, L. K. (2020). Age-Related Dif-
ferences in Nasopharyngeal Severe Acute Respiratory
Syndrome Coronavirus 2 (SARS-CoV-2) Levels in
Patients With Mild to Moderate Coronavirus Disease
2019 (COVID-19). JAMA Pediatrics, 174(9):902–
903.
Lenzen, M., Li, M., Malik, A., Pomponi, F., Sun, Y.-
Y., Wiedmann, T., Faturay, F., Fry, J., Gallego, B.,
Geschke, A., et al. (2020). Global socio-economic
losses and environmental gains from the coronavirus
pandemic. PloS one, 15(7):e0235654.
Opendata platform (2022). Opendata platform. https://data.
gov.tw/en. Online; access 22 March, 2022.
Prothero, R. M. (1977). Disease and mobility: a neglected
factor in epidemiology. International journal of epi-
demiology, 6(3):259–267.
Quinlan, J. R. (1986). Induction of decision trees. Machine
Learning, 1:81–106.
Quinlan, J. R. (1993). C4.5: Programs for Machine Learn-
ing. Morgan Kaufmann Publishers Inc., San Fran-
cisco, CA, USA.
Ward, J. H. (1963). Hierarchical grouping to optimize an
objective function. Journal of the American Statistical
Association, 58(301):236–244.
World Health Organization (2010). Influenza a (h1n1)
pandemic 2009 - 2010. https://www.who.int/
emergencies/situations/influenza-a-(h1n1)-outbreak.
Online; access 22 March, 2022.
World Health Organization (2022). Coronavirus dis-
ease (covid-19) pandemic. https://www.who.int/
emergencies/diseases/novel-coronavirus-2019. On-
line; access 22 March, 2022.
DATA 2022 - 11th International Conference on Data Science, Technology and Applications
422
