
Maximum Correntropy Criterion-based UKF for Tightly Coupling
INS and UWB with non-Gaussian Uncertainty Noise
Seong Yun Cho
1a
, Jae Hong Lee
2b
and Chan Gook Park
2c
1
Division of Robotics and Mobility, Kyungil University, Gyeongsan, Republic of Korea
2
Department of Aerospace Engineering, Seoul National University, Seoul, Republic of Korea
Keywords: Maximum Correntropy Criterion, UKF, INS/UWB.
Abstract: In this paper, unscented Kalman filter (UKF) based on maximum correntropy criterion (MCC) instead of
minimum mean square error (MMSE) criterion, and it is applied to tightly coupled integration of inertial
navigation system (INS) and ultra wide-band (UWB). UWB can measure distance with an accuracy of less
than 30cm in line-of-sight environment, but provides distance measurement with various types of non-
Gaussian uncertainty noise in non-line-of-sight environment. In this case, if the INS/UWB system is
configured with the existing MMSE-based filter, a large error occurs. To solve this problem, in this paper,
UKF is designed based on MCC. Through simulation analysis, it is confirmed that the proposed filter has
robust characteristics against UWB uncertainty and enables stable INS/UWB integration.
1 INTRODUCTION
Consider a system integrating inertial navigation
system (INS) and ultra wide-band (UWB) for indoor
navigation. Although INS can accurately calculate 6-
degree of freedom motion, it has a problem of
accumulation of errors over time. UWB enables
accurate distance measurement and location
estimation in a line-of-sight (LoS) environment, but
in non-line-of-sight (NLoS) environment such as
indoors, accurate becomes impossible as various
types of uncertainty noise are included in distance
measurements (Cho, 2019). To integrate these two
systems, nonlinear filters such as extended Kalman
filter (EKF) (Brown and Hwang, 2012) and unscented
Kalman filter (UKF) (Julier et al., 2000) are generally
used in consideration of their nonlinear
characteristics. However, since these filters designed
based on minimum mean square error (MMSE) do
not properly respond to UWB uncertainty noise, a
large error may occur. In this paper, considering this
problem, maximum correntropy criterion (MCC)-
based UKF (MCUKF) is introduced.
The MCC-based filter is a filter that maximizes
the similarity between the measurements and the
a
https://orcid.org/0000-0002-4284-2156
b
https://orcid.org/0000-0002-8222-5435
c
https://orcid.org/0000-0002-7403-951X
estiamtes, and is designed based on the kernel
function reflecting the error characteristics of the
measurement. The kernel function is to indicate the
similarity of two random variables, and the total sum
of kernel function values including innovation and
residuals calculated in the measurement-update
process is determined as a cost function. Then, the
state variables are estimated so that this cost function
is maximized. In this process, when uncertainty noise
occurs in the UWB measurement, the MCC-based
filter adjusts the P matrix and R matrix, thereby
reducing the effect of the measurement uncertainity
noise on the system (Chen et al., 2017).
Recent research on MCC-based filters has
focused on kernel function design considering
various error probability distributions (Li et al., 2022,
Huang and Zhang, 2022). There are not many studies
to apply MCC to nonlinear systems. Ther purpose of
this study is to apply MCC to UKF so that is can be
used in nonlinear systems. And the designed MCUKF
is applied to tightly coupled INS/UWB integration
system.
The performane of the MCUKF-based INS/UWB
integrated navigation system is verified based on
simulation. Through simulation analysis, if non-
Cho, S., Lee, J. and Park, C.
Maximum Correntropy Criterion-based UKF for Tightly Coupling INS and UWB with non-Gaussian Uncertainty Noise.
DOI: 10.5220/0011286000003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 209-213
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
209

Gaussian uncertainty noise is included in the UWB
measurement, it is confirmed that MCUKF provides
a stable navigation solution by largely tuning the
value of the R matrix corresponding to the erroneous
measurement.
2 MCUKF-BASED INS/UWB
INTEGRATION
Considering the following discrete-time nonlinear
system model:
11
() , ~(0,)
() , ~ (0,)
kkk
kkk
x
fx w w N Q
yhx vvNR
−−
=+
=+
(1)
where subscript k is the discrete time,
N
k
x ∈ is the
state, and
M
k
y ∈ is the output.
k
w
and
k
v
are
uncorrelated zero-mean white Gaussian noise
processes, and the covariance matrices of the
processes are denoted by Q and R, respectively. The
state variables considering INS are set as
T
LL
xPosVelAtt
ε
=∇
(2)
where
L
Pos and
L
Vel are the position and velocity
in the local level coordinate system,
A
tt
is the
attitude expressed in Euler angles, and
∇
and
ε
are
the accelerometer bias and gyro bias, respectively.
In UKF, these state variables are converted into
sigma points. The number of sigma points is 2
N+1,
which is 31 because the system dimension
N is 15
(Julier et al., 2000).
The system function can be expressed as an INS
equations as follows (Farrell and Barth, 1999):
{
}
(
{
)
}
11
1,111
,1 ,1 1 1
11,11
,1 ,1 ,1
ˆ
()
(2 )
1
ˆ
2
()
LL L
kkk
LL Lb
kk bkkk
LL LL
ie k eL k k k
b
kk kibkk
bL L
Lk iek eLk
Pos Pos Vel dt
Vel Vel C f
Vel g dt
Qtn Qtn Qtn
Cdt
ωω
ωε
ωω
−−
−−−−
−−−−
−−−−
−− −
=+⋅
=+ −∇−
+×+⋅
=+ ∗ −
−+⋅
(3)
where
dt is the IMU output period, Qtn is the
quaternion,
b
f
and
b
ib
ω
are the accelerometer output
and gyro output, respectively,
ˆ
∇
and
ˆ
ε
are the
estimated accelerometer bias and gyro bias,
respectively,
L
ie
ω
is the Earth’s angular velocity
vector, and
L
eL
ω
is the rotational angular velocity
vector of the local level coordinate system caused by
the velocity.
In the time-propagation process, the sigma points
are propagated in synchronization with the IMU
output period based on (3).
When the distance measurement is obtained in
UWB, the measurement-update is processed. The
measurement function in (1) is as follows (Cho, 2019):
22
() ( () ) ( () ) ()
xy
kkkk
ri xi Pos yi Pos wi=− +− +
(4)
where
[() ()]
T
x
iyi is the location of the anchor
node i,
j
P
os is the j-axis location of the mobile node
in the local level coordinate system, and
()wi is the
noise contained in channel i. And
{1, 2, , }iM∈ .
In case of using calibrated UWB, w in (4) is
modelled as zero-mean noise in the LoS environment.
However, w may appear in the form of heavy-tailed
impulsive noise in the probability distribution in the
indoor environment. This error can be filtered out in
an MCC-based filter. In MCUKF, the cost function is
set as follows (Chen et al., 2017):
1
1
() (())
NM
i
J
xGei
NM
+
=
=
+
(5)
where G() is a kernel function, and the Gaussian
kernel function can be expressed as follows:
22
/2
()
e
Ge e
σ
−
=
(6)
where
σ
is the kernel bandwidth and is an important
design parameter in MCC.
The state variables are estimated to maximize the
cost function.
ˆ
arg max ( )
k
k
x
x
Jx= (7)
The convergence performance of the filter can be
improved by iteratively using one measurement based
on the fixed-point iteration algorithm in the
measurement-update process (Chen et al., 2017).
Using the innovation and residual calculated in this
process, the P matrix and R matrix are adjusted as
follows:
1
() ()
1
() ()
()
()
x
T
ka P ka P
yT
ka R ka R
P
BC B
RBCB
−−
−
=
=
(8)
where a is the iteration order,
T
P
Pk
BB P
−
= and
T
RR
BB R= .
k
P
−
should be calculated before the
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
210
measurement-update using the time-propagated
sigma points as follows:
1
1
1
ˆ
()
1
ˆˆ
(() )(() )
n
kk
i
n
T
kkkkk
i
xi
n
PixixQ
n
χ
χχ
−−
=
−−−−−
=
=
=−−+
(9)
where
21nN=+
, Q is the process noise covariance
matrix, and
()
k
i
χ
−
is the set of time-propagated i
th
sigma points.
In (8),
()
x
ka
C
and
()
y
ka
C
are calculated as follows:
()
()
()
()
()
()
()
()
()
()
(1) 0
0()
(1) 0
0()
x
ka
x
ka
x
ka
y
ka
y
ka
y
ka
Ge
C
Ge N
Ge
C
Ge M
=
=
(10)
where
1
() ( 1)
1
() ()
ˆ
ˆ
()
ˆ
()
x
ka P k ka
y
ka R k ka
eBxx
eByy
−− −
−
−−
=−
=−
(11)
Through this, the P matrix and R matrix are
adjusted based on the values calculated by inputting
the normalized innovation and the normalized
residual as input to the kernel function, respectively.
When the fixed-point iteration algorithm is
finished, the state variables and error covariance
matrix are updated as follows:
1
,() ,() ()
() ,() ,() ,()
ˆ
ˆˆ
()
k k xy k a yy k a k k a
TT
k ka xyk a yyka xyk a
xxP P yy
PP P P P
−− −
−−
=+ −
=−
(12)
where
,() () ( 1) ()
1
,() () () ()
1
1
ˆ
ˆˆ
()()
1
ˆˆ
()()
n
T
xyka ka ka k ka
i
n
T
yyka k ka k ka ka
i
Pxyy
n
PyyyyR
n
χ
−− −
−
=
−−
=
=−−
=−−+
(13)
In (12),
()
ˆ
ka
y
−
is constructed by calculating for
each channel based on (4).
3 SIMULATION RESULTS
To verify the performance of the proposed MCUKF-
based INS/UWB integrated navigation, a simulation
was carried out to apply this filter to navigation for
robots and pedestrians in an indoor environment. The
IMU used in the simulation is OEM-IMU-EG-320N,
and the specifications are as follows:
• gyro bias repeatability is 0.5 deg/sec
• angular random walk is 0.1 deg/√hr
• accelerometer bias repeatability is 15mg, and
• velocity random walk is 0.05 m/s/√hr.
The output frequency of the IMU was set to 50Hz,
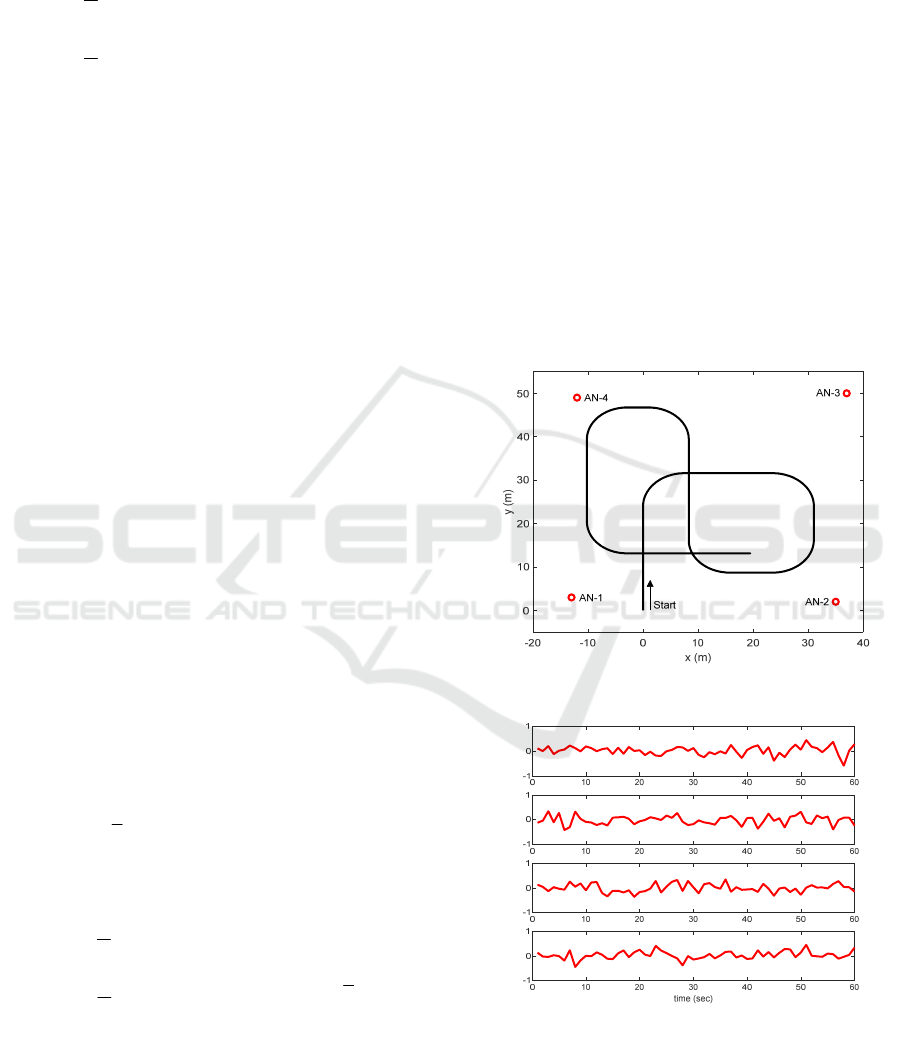
and that of the UWB was set to 1Hz. Four anchor
nodes are located as shown in Figure 1, and the
mobile node moves along the trajectory shown in this
figure for 60 seconds.
Figure 1: Simulation trajectory.
(a) measurement error
Figure 2: Simulation result in the first case.
Ch. 1 (m)Ch. 2 (m)Ch. 3 (m)Ch. 4 (m)
Maximum Correntropy Criterion-based UKF for Tightly Coupling INS and UWB with non-Gaussian Uncertainty Noise
211

(b) square root of adjusted R matrix
(c) position estimates
(d) positioning error
Figure 2: Simulation result in the first case (cont.).
In MCUKF, the kernel bandwidth was set to 1.3.
First, it is the case where w in (4) is white
Gaussian noise with zero-mean. The result is shown
in Figure 2. As can be seen in this figure, the
measurements have only Gaussian noise, and the R
matrix adjusted in MCUKF is similar to that set as the
initial value. And it can be confirmed that the
positioning performance of MCUKF is almost similar
to that of UKF in general case.
(a) measurement error
(b) square root of adjusted R matrix
(c) position estimates
(d) positioning error
Figure 3: Simulation result in the second case.
Ch. 1 (m)Ch. 2 (m)Ch. 3 (m)Ch. 4 (m)
y (m)
Ch. 1 (m)Ch. 2 (m)Ch. 3 (m)Ch. 4 (m)
Ch. 1 (m)Ch. 2 (m)Ch. 3 (m)Ch. 4 (m)
N (m)
e
r
r
o
r
(m)
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
212

Table 1: Summary of the simulation results.
positioning errors (first case)
filter mean standard deviation
UKF 0.16127 0.21896
MCUKF 0.16602 0.22280
positioning errors (second case)
filter mean standard deviation
UKF 0.51414 0.44778
MCUKF 0.26019 0.25141
In the second case, a total 10 impulse errors were
randomly generated in w, and the result of MCUKF
in this case is shown in Figure 3. It can be seen that
large and small impulse errors are randomly entered
into each channel of the distance measurements. And
it can be seen that the adjusted R in MCUKF increases
largely according to the impulse error generated for
each channel. Due to this, the channel with the
impulse error momentarily loses its function, and the
INS error is corrected using the measurements
obtained from the remaining channels. Therefore,
MUCKF is hardly affected by the impulse error.
It can be seen that the UKF positioning result is
greatly affected by the impulse error and the error
increases. The reason is that UKF is a filter designed
based on MMSE and cannot cope with non-Gaussian
noise. On the other hand, it is confirmed that the
positioning result of MCUKF is not affected by
impulse error. Therefore, MCUKF is evaluated to be
able to provide stable navigation information
regardless of positioning error.
The number of the estimated position information
for 60 seconds is 3000, and the mean and standard
deviation of the positioning errors are calculated for
each filter. And the result is summarized in Table 1.
Based on this table, the excellent performance of the
proposed MCUKF can be confirmed.
4 CONCLUSIONS
In this paper, MCUKF-based INS/UWB integrated
navigation system was introduced. To use MCC in
nonlinear system, MCUKF was designed by
combining MCC with UKF. And this filter was used
to integrated INS and UWB. UWB has non-Gaussian
uncertainty noise in an indoor environment. While
this causes a large estimation error in the existing
UKF, it is proven based on simulation that MCUKF
provides a stable navigation solution by tuning the R
matrix for each channel in which this error occurs.
Based on this paper, it is expected that stable
variables can be reliably estimated in a nonlinear
system including heavy-tailed non-Gaussian impulse
noise.
ACKNOWLEDGEMENTS
This work was supported by Institute of Information
& Communications Technology Planning &
Evaluation (IITP) grant funded by the Korea
government (NFA)
(No. 2019-0-01325, Development
of wireless communication tracking-based location
information system in disaster scene for fire-fighters
and person who requested rescue).
REFERENCES
Brown, R. G., Hwang, P. Y. C. (2012). Introduction to
random signals and applied Kalman filtering, John
Wiley & Sons, NJ.
Chen, B., Liu, X., Zhao, H., Principe, J. C. (2017).
Maximum correntropy Kalman filter, Automatica, vol.
76, pp. 70-77.
Cho, S. Y. (2019). Two-step calibration for UWB-based
indoor positioning system and positioning filter
considering channel common bias, Measurement
Science and Technology, vol. 30, pp. 025003.
Farrell, J. A., Barth, M. (1999). The global positioning
system & inertial navigation, McGraw-Hill, New York.
Huang, H., Zhang, H. (2022). Student’s t-kernel-based
maximum correntropy Kalman filter, Sensors, vol. 22,
pp. 1683.
Julier, S., Uhlmann, J., Durrant-Whyte, H. G. (2000). A
new method for the nonlinear transformation of means
and covariances, IEEE Trans. Automatic Control, vol.
45, pp. 477-482.
Li, X., Guo, Y., Meng, Q. (2022). Variational Bayesian-
based improved maximum mixture correntropy Kalman
filter for non-Gaussian noise, Entropy, vol. 24, pp. 117.
Maximum Correntropy Criterion-based UKF for Tightly Coupling INS and UWB with non-Gaussian Uncertainty Noise
213
