Data Partitioning Strategies for Simulating non-IID Data Distributions in

the DDM-PS-Eval Evaluation Platform

Mikołaj Markiewicz

and Jakub Koperwas

Institute of Computer Science, Warsaw University of Technology, Warsaw, Poland

Keywords:

Distributed Data Mining, Federated Learning, non-IID Data, Data Partitioning Strategies, Algorithm Evalua-

tion, Clustering, Classiﬁcation.

Abstract:

Nowadays, the size of the various datasets collected worldwide is growing rapidly. These data are stored in

different data centres or directly on IoT devices, and are thus located in different places. Data stored in different

locations may be uniformly distributed and convergent in terms of the information carried, and are then known

as independent and identically distributed (IID) data. In the real world, data collected in different geographic

regions tend to differ slightly or have completely different characteristics, and are then known as non-IID data.

Increasing numbers of new algorithms have been implemented to work with such distributed data without the

need to download all the data to one place. However, there is no standardised way of validating these, and

such algorithms are typically tested on IID data, which are uniformly distributed. The issue of non-IID data is

still an open problem for many algorithms, although the main categories of ”non-IID-ness” have been deﬁned.

The purpose of this paper is to introduce new data partitioning strategies and to demonstrate the impact of

non-IID data on the quality results of distributed processing. We propose multiple strategies for dividing a

single dataset into multiple partitions to simulate each of the major non-IID data category problems faced by

distributed algorithms. The proposed methods of data partitioning integrated with the DDM-PS-Eval platform

will enable the validation of future algorithms on datasets with different data distributions. A brief evaluation

of the proposed methods is presented using several distributed clustering and classiﬁcation algorithms.

1 INTRODUCTION

Various methods of data mining have been developed,

and in the last few years, there has been growing inter-

est in the study of federated learning (FL) techniques.

In this approach, a large amount of data is distributed

over a large number of devices that cooperate in the

learning process. It is worth noting that the concept

of FL represents a special case of general distributed

data mining (DDM) methods, which also deal with

distributed data but at different scales. For example,

the processing of megabytes of data stored in millions

of devices requires a different approach from the pro-

cessing of petabytes of data stored in a few data cen-

tres. A lack of knowledge about the characteristics

of the data distribution and the inability to download

all of the data locally are challenges for modern al-

gorithms operating in distributed environments. This

type of data, which are typically collected and stored

in different geographic regions, does not guarantee an

equal distribution of data samples for each location.

The data are then not independent and identically dis-

https://orcid.org/0000-0003-4229-8098

https://orcid.org/0000-0003-0693-5109

tributed (non-IID).

Research into non-IID data partitioning has be-

come very popular in the last few years, and re-

searchers have begun to pay more attention to the im-

pact of uneven data distributions on the results of dis-

tributed algorithms, as discussed in (Markiewicz and

Koperwas, 2019), (Sattler et al., 2019) or (Hsieh et al.,

2020). These studies have mainly analysed the skew

in data label distributions and training communica-

tion costs to improve efﬁciency, particularly for non-

IID data distribution. However, recent research has

focused on rigorous FL, which has been extensively

studied in terms of the algorithms used, FL systems

as a whole, and benchmarking tools for these systems.

The literature contains various approaches to valida-

tion (mainly tools or frameworks for benchmarking

FL algorithms), as summarised in a recent study of

such systems (Li et al., 2021b). Several publications

have documented new benchmark systems (Caldas

et al., 2018), (Luo et al., 2019) containing existing

non-IID partitioned datasets. Most of the latest tools

have focused on complete FL systems and the testing

of their components (Hu et al., 2020), (Bouraqqadi

et al., 2021), but have not placed particular emphasis

Markiewicz, M. and Koperwas, J.

Data Partitioning Strategies for Simulating non-IID Data Distributions in the DDM-PS-Eval Evaluation Platform.

DOI: 10.5220/0011290200003266

In Proceedings of the 17th International Conference on Software Technologies (ICSOFT 2022), pages 307-318

ISBN: 978-989-758-588-3; ISSN: 2184-2833

307

on a wide range of data partitioning strategies. Recent

work (Liu et al., 2020) and (Li et al., 2021a) have

demonstrated several approaches to generating non-

IID datasets, nevertheless for (Li et al., 2021a) data

generation only applies to provided datasets placed in

their benchmarking system. In (Liu et al., 2020), the

authors, among other things, simulate the problem of

skew in the feature distribution and distort the image

data by adding random noise, which is an interesting

but unrealistic approach, since it distorts the real data

attributes themselves. Many other tools are described

in (Li et al., 2021b), although there is as yet no gen-

eral consensus on how to properly evaluate distributed

algorithms and how to deﬁne metrics for the non-

IID-ness of data. Non-FL distributed processing tools

and algorithms have also been intensively developed

across the world. Like the FL benchmarking tools,

these tools were created for the purpose of validat-

ing other DDM methods, and can be found in (Lim

et al., 2019) and (Markiewicz and Koperwas, 2022).

The authors of the latter started preparations to en-

able the evaluation of the algorithms in the case of

non-uniform data distributions by allowing the use of

various user-deﬁned data partitioning strategies.

This paper represents a modest contribution to the

ongoing discussions of data partitioning methods for

simulating non-IID data distributions, with the aim of

facilitating better algorithm evaluations. Our current

research on data partitioning strategies focuses on the

horizontal partitioning of data. We consider the im-

pact and propose methods for simulating such data

distributions in order to face the open issues around

the use of distributed processing algorithms, as sum-

marised recently in (Kairouz et al., 2019). We deﬁne

various approaches to data partitioning that may be

appropriate for different research questions, as men-

tioned in a recent paper (Li et al., 2021b). Although

we cannot know the actual distribution for each dis-

tributed dataset in the real world, we can prepare the

implementation of the algorithm to be more resistant

to data distributions.

This paper is structured as follows. Section 2

refers to non-IID data partitioning and consists of two

substantial and related subsections. Subsection 2.1

provides an overview of an extended taxonomy of

non-IID data. The proposed data partitioning methods

are described in Subsection 2.2. Section 3 explains

the contribution and connection to the DDM-PS-Eval

platform. Section 4 reports the results of experiments

performed on the proposed data partitioning strate-

gies. Finally, Section 5 concludes with a summary

and plans for future work.

2 non-IID DATA PARTITIONING

In order to start designing partitioning strategies for

each non-IID data distribution, it is required to know

the origin of such distribution. The origin is directly

related to the data itself, and it would be beneﬁcial

to know where it formally belongs in the hierarchy of

data partitioning methods.

2.1 Extended Data Partitioning

Taxonomy

Data may be split in multiple ways in independent

data centres, or may simply be in separate physical

locations. A taxonomy of types of partitioning was

presented in (Kairouz et al., 2019) with regard to the

problem of FL. In this paper, we introduce new levels

to the ’Non-identical client distributions’ part of the

existing taxonomy. These new levels are related to

partitioning strategies and data properties. Extending

the existing taxonomy is required to create suitable

and non-overlapping partitioning strategies for data

distribution characteristics. This extension improves

the categorisation of the new and existing methods

within the taxonomy structure. It also helps to avoid

strategy duplication for already handled non-IID dis-

tributions. The focus of our attention is on numeri-

cal or nominal data rather than on text, as partitioning

such data is a different issue that needs to be investi-

gated separately. Another brief categorisation of non-

IID data related to images, which is partially beyond

the scope of this work, and time-series data, is pre-

sented in (Zhu et al., 2021).

We started our work by investigating the main cat-

egories of non-IID distributions in order to determine

which data properties are related to each category.

There are three properties that can be used to describe

a data distribution: the distribution of data attributes,

the distribution of labels (classes)

of the samples, or

the amount of data itself. These distributions can be

observed together, which naturally deﬁnes it as a tax-

onomy rather than a tree-structured hierarchy. The

listed properties form the parent level of the category

level. The second additional level introduced here de-

ﬁnes methods of realising the expected data partition-

ing for the purposes of quality evaluations of algo-

rithms. Having top levels in place, we can correctly

link partitioning strategies to the categories. The pro-

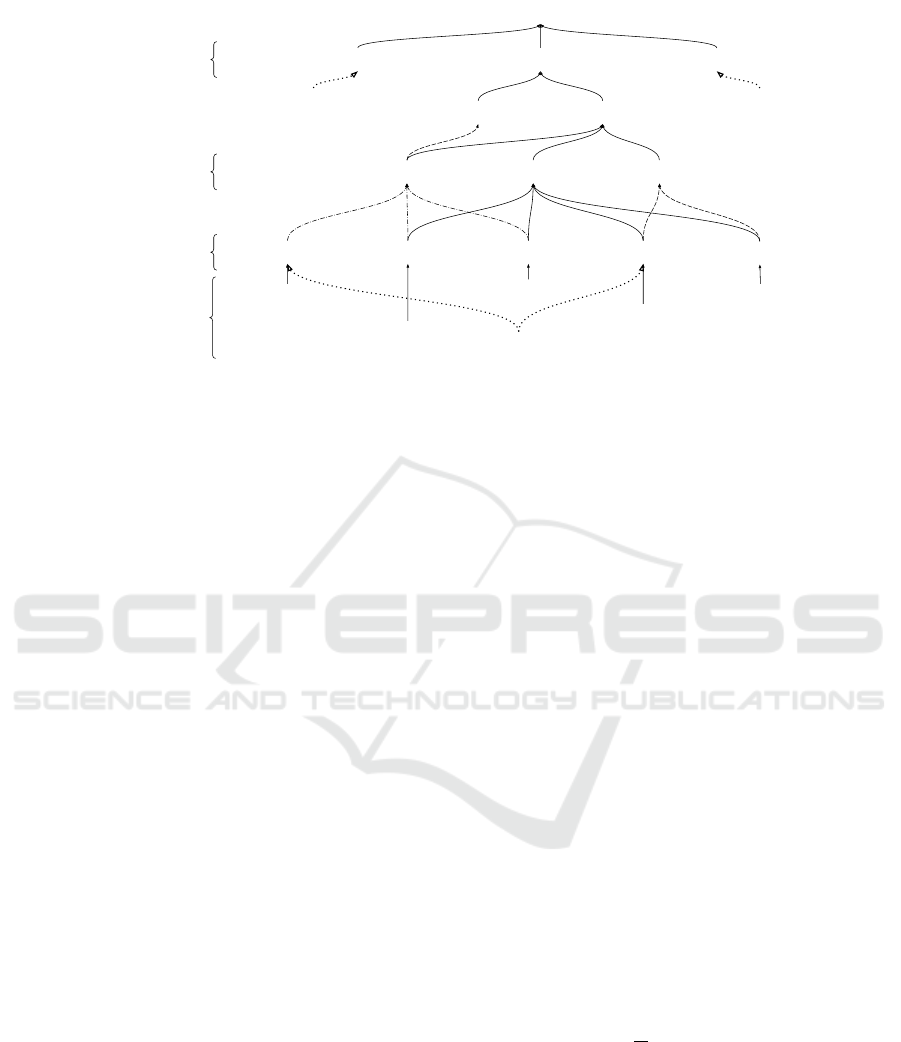
posed extended taxonomy, illustrated in Fig. 1, shows

data partitioning strategies associated with main cate-

gories and their relationship to data properties.

The terms ”class” and ”label” are used interchange-

ably in the text because their meaning is the same, but the

nomenclature depends on the context.

ICSOFT 2022 - 17th International Conference on Software Technologies

308

Vertical

Non-identical client distributions

Horizontal

Attribute related Label / class related Amount related

Covariate shift

Prior probability shift

Concept driftConcept shift

Unbalancedness

- “Dense and outliers”

- “Diff. statistical attr. distribution”

- …

- “Separated”

- “All but”

- “Missing some”

- “Most plus all”

- “Most plus some”

- …

- “Split by attribute”

- …

- “Change label”

- …

- “Unbalanced labels”

- …

Data property

Main category

Partitioning strategies

Dataset shiftViolations of independence

[...] […]

Source of dependence

Non-IID Data partitioning

[possible strategy mix]

Figure 1: Extended non-IID data partitioning taxonomy, including new levels in bold (the line style of the arrows is not

important, and is only used to indicate the groups).

The taxonomy presented in Fig. 1 gives us a more

detailed view of data distribution possibilities and

their origins. It also allows us to prepare a compre-

hensive test suite covering multiple non-IID data dis-

tributions to evaluate algorithms. Thanks to the taxon-

omy graph, we can quickly notice that both ’covariate

shift’, ’concept shift’, and ’concept drift’ categories

relate to data attributes. At the same time, they do

not consider the quantity amount of the data. On the

other hand, ’prior probability shift’ and ’unabalanced-

ness’ are closely related to the data quantity amount

unconcerned about data attributes. Based on this ob-

servation, we can state that a minimal test suite for

algorithm evaluation utilizing non-IID data requires

examining at least two of ﬁve partitioning categories.

Therefore, we cannot fulﬁl the correct but minimal

algorithm evaluation without using at least one par-

titioning strategy that belongs to each data property.

An example set of strategies that fulﬁl this condi-

tion would be the ’concept drift’ and ’unbalanced-

ness’ partitioning that covers each data property in-

troduced at the parent taxonomy level. A possible

strategy mix used as a single test suite covering multi-

ple data properties might be a different approximation

for algorithm evaluation; however, mixing strategies

is out of the scope for this work.

2.2 Data Partitioning Strategies

In the following sections, we provide details of the

proposed partitioning strategies with examples for

each main category. For each strategy, we assume that

the dataset and number of target partitions are pro-

vided as input along with the strategy parameters.

2.2.1 Covariate Shift (Feature Distribution

Skew)

One of the ﬁrst problems that arise is that data may be

placed in partitions with different distributions of at-

tributes. In other words, the combined histogram for

all ’split-separated’ data collected from each partition

would show relatively shifted attribute densities be-

tween the data in each partition. This is illustrated in

Fig. 2 and described in more detail below. Although

these partitions contain the same classes of data sam-

ple representatives, some of the attribute distributions

are slightly different. Examples include typical differ-

ences in handwriting characteristics, speed limit signs

that differ slightly between European countries (Grig-

orescu, 2018), or attributes describing the same plant

species based on their size, colour, etc., which vary

depending on the weather conditions and sunlight ex-

posure.

In this method, we want to perform partitioning

that will simulate this problem for a given dataset. It

is easy to get nearly separate and evenly spaced data

partitions based on a single attribute, by sorting the

data according to the value of the attribute and divid-

ing it into D equal parts. However, such parts have a

data shi f t equal to

, which is the relative distance

between the mean densities for these parts, as dis-

cussed below. Hence, to perform data splitting for dif-

ferent data shifts, we need to deﬁne an objective func-

tion for this problem. In our approach, we propose a

function that consists of two user-deﬁned parameters

and unknown variables deﬁned as mean data values

;n ∈ [1; splits]∧ n ∈ N for each data split. The ﬁrst

parameter (splits) is the number of partitions, and the

Data Partitioning Strategies for Simulating non-IID Data Distributions in the DDM-PS-Eval Evaluation Platform

309

second parameter (shi f t) is the distance between the

data distribution means of the splits, which is the tar-

get skew of the data. The objective function is de-

termined by mathematical induction. We deﬁne the

requirement for maintaining a certain ratio of the dis-

tances between the distribution centres of the splits in

Equation 1:

− min

max − min

−

− min

max − min

= shi f t

⇒

− M

max − min

= shi f t

∧

− M

max − min

= shi f t

∧ ... =⇒

− M

n−1

max − min

= shi f t

(1)

It follows from Equation 1 that an overall shift be-

tween ﬁrst and last is a multiple of the shi f t parame-

ter:

− M

max − min

− M

max − min

= 2 · shi f t

⇒

− M

max − min

= 2 · shi f t

=⇒

− M

max − min

= (n − 1) · shi f t

(2)

We can write the above expression as in Equation 3:

− M

max − min

splits

∑

n=2

− M

n−1

max − min

=⇒

splits

∑

n=2

− M

n−1

max − min

= (n − 1) · shi f t

(3)

Since n = splits, we obtain the ﬁnal restrictions for

the objective function as in Equation 4:











∑

splits

n=2

−M

n−1

max−min

= (splits − 1)· shi f t

∀n

−M

n−1

max−min

= shi f t

∧ splits > 1; shi f t ∈ (0,

splits

]

(4)

where min and max are the minimum and maximum

attribute values.

Solving this problem with these constraints is not

an easy task. Our goal is to minimise the difference

between the deﬁned target function and the selected

ratio. To achieve this, we need to search the space of

possible solutions, which grows with the amount of

data. We therefore approach this as a typical search

task that involves ﬁnding a solution that meets cer-

tain conditions. This can be done in many ways, in-

cluding brute force, random methods, or evolution-

ary algorithms. In our implementation, we choose the

simplest solution, which has two phases. We start by

sorting the data based on the selected attribute value,

to create an initial even split. We then iteratively move

a random sample from one split to another, rolling

back the operation if the objective function deterio-

rates. The stop condition is deﬁned in the standard

way, as a low epsilon value or a maximum number of

iterations. Several strategies for moving the data sam-

ples were tested, including random splits and moving

borderline data samples between partitions. However,

the most straightforward solution turned out to pro-

duce the best results. Fig. 2 gives an example of the

split obtained after applying the proposed method to a

single attribute. We can see how the distribution of at-

tribute values varies depending on the split numbers.

Using a higher value for the shi f t param, we obtain

far apart separated distributions with low overlapping

for each split. Each split represents a data distribu-

tion dedicated to an independent target partition. For

the low value of the shi ft param, attribute distribution

across splits is more mixed; however, the mean values

are notably disjoint.

0.0

0.5

1.0

1.5

Density

original, all data

data

splits=2, shift=0.5

split_1

split_2

4 6 8

0.0

0.5

1.0

1.5

Density

splits=3, shift=0.3

split_1

split_2

split_3

4 6 8

splits=3, shift=0.1

split_1

split_2

split_3

Iris dataset attribute split by 'sepal_length'

Figure 2: Example of attribute densities for the

’sepal length’ attribute of the Iris dataset, in the original

case and after applying the proposed splitting method.

Splitting a dataset using a covariate shift for mul-

tiple attributes at the same time is possible, and re-

quires that the function in Equation 4 is fulﬁlled

for each attribute independently. However, the task

then becomes more complex, and it may be impossi-

ble to achieve an acceptable function result for some

datasets. Nevertheless, experiments described in the

next section show that ”shifting” data based on even

one attribute affects the quality of the distributed al-

gorithms.

Another variation of the covariate shift ap-

proach that is worth mentioning is the use of the

’dense-and-outliers’ partitioning strategy mentioned

in (Markiewicz and Koperwas, 2022). The authors

suggested that separating anomalies and boundary

data from dense data clusters deﬁned by a data-

ICSOFT 2022 - 17th International Conference on Software Technologies

310

speciﬁc measure of similarity affects the quality of

distributed algorithms. Since the proposed method

operates on attribute values and their distribution, it

can be classiﬁed as a covariate shift partitioning strat-

egy.

2.2.2 Prior Probability Shift (Label Distribution

Skew)

Due to geographical or cultural differences, data sam-

ples from the same class may be stored on indepen-

dent nodes in different amounts. A typical example

of this would be the presence of kangaroos in various

regions around the world: this animal lives in the wild

only in Australia, although single individuals can be

found in a few zoos around the world. Another situa-

tion is represented by people from different countries

who emigrate and settle in groups that affect the dis-

tributions of the local communities. A third situation

is the use of English in books or conversations, which

is of course mainly found in the US or UK; however,

this particular language is also used all over the world.

On the basis of these examples, we can distinguish

many possibilities of separating data distributions into

independent data partitions. We therefore distinguish

the following partitioning strategies:

- ’separated [data]’, where it is assumed that data

samples with the same class are present only on

one partition.

- ’all [of the data] but [some]’, where speciﬁc la-

belled data samples are missing from some parti-

tions;

- ’most [of the data] plus some’, where the data are

partitioned according to labels and small subsets

of them are then scattered among several indepen-

dent partitions;

- ’most [of the data] plus all’, which is the same

as the previous strategy except that each subset is

also spread over each independent partition. This

scenario simulates the case where each partition

contains data for each label but with a different

distribution;

- ’with anomalies’, where most data are partitioned

evenly but contain anomalies - certain labels in

single quantities;

All of them are based on scattering data samples

across different partitions but with different and spe-

ciﬁc distributions for their cases. The ﬁrst three strate-

gies assume main concentrations of data samples with

certain classes and several classes missing within par-

titions. The last two strategies require representatives

of all data classes to be kept together on every parti-

tion but in different amounts. Based on analyses and

numerous experiments performed to receive distin-

guished distributions, we have concluded that a single

but parameterised method is sufﬁcient to address each

of the abovementioned strategies, rather than prepar-

ing separate, dedicated partitioning methods for each

of them.

The proposed method is divided into two stages,

related to labels and data quantities. First, we sep-

arate each class or group of classes depending on

the number of partitions. We then determine addi-

tional classes for partitions and classes for empty par-

titions

. When the number of partitions is greater than

the number of unique labels in the dataset, we need to

choose how to ﬁll the empty partitions, as there are

not enough unique labels available for each partition.

In our method, we have two options: to ﬁll empty

partitions evenly with samples of all labels, or select

the number of labels to be ﬁlled with data samples.

The most treacherous part is to avoid adding the same

label on every partition. We therefore use a cyclic it-

erator concept by adding classes in order which aligns

the distribution of label presence across partitions. As

a result of the ﬁrst stage, we create tuples with three

items: main labels of the partition, additional labels,

and labels to ﬁll empty partitions. An example of

the abovementioned partitioning methods is given in

Fig. 3. The ﬁgure shows the ﬁnal algorithm assign-

ment of different labels numbered from 0 to L to each

group of labels within D partitions.

d1=[0, 3] + [1, 2, 4] + []

d2=[1, 4] + [0, 2, 3] + []

d3=[2] + [4, 1, 3, 0] + []

Most plus all:

D=3

L=5

Add=all

d1=[0, 3] + [1, 2] + []

d2=[1, 4] + [3, 0] + []

d3=[2] + [1, 3, 4] + []

All but:

D=3

L=5

Add=-1

d1=[0, 3] + [1, 2] + []

d2=[1, 4] + [3, 0] + []

d3=[2] + [1, 3] + []

Separated:

D=3

L=5

Add=0

d1=[0, 3] + [1, 2] + []

d2=[1, 4] + [3, 0] + []

d3=[2] + [1, 3] + []

Most plus some:

D=3

L=5

Add=2

d1=[0] + [] + []

d2=[1] + [] + []

d3=[2] + [] + []

d4=[] + [] + [0, 1, 2]

d5=[] + [] + [0, 1, 2]

Separated:

D=5

L=3

Add=0

EmptyAdd=all

d1=[0] + [] + []

d2=[1] + [] + []

d3=[2] + [] + []

d4=[] + [] + [0, 1]

d5=[] + [] + [2, 0]

Separated:

D=5

L=3

Add=0

EmptyAdd=2

Legend:

1st [] - majority labels

2nd [] - additional labels

3rd [] - empty partition labels

L - labels >= D - partitions

EmptyAdd=0

L - labels < D - partitions

d1=[0] + [1] + []

d2=[1] + [2] + []

d3=[2] + [0] + []

d4=[] + [2] + [0, 1]

d5=[] + [1] + [2, 0]

All but:

D=5

L=3

Add=-1

EmptyAdd=2

Figure 3: Examples of different label partitioning strategies

depending on the parameters L (number of unique labels), D

(number of partitions), Add (additional number of labels),

and EmptyAdd (additional number of labels for empty par-

titions).

The second step uses simple mathematical pro-

portions based on the provided parameters and the

amounts of data to be transferred from the main sub-

sets. At the end of the process, the data samples are

randomised with a uniform distribution for each label

according to the deﬁned dependencies, and then split

An empty partition is one without a dedicated majority

of data samples for a speciﬁc label, which is possible when

the number of unique labels is lower than the number of

target partitions.

Data Partitioning Strategies for Simulating non-IID Data Distributions in the DDM-PS-Eval Evaluation Platform

311

between partitions. Both steps require several param-

eters related to the label separation itself and the quan-

tity of data samples to be distributed. The ﬁrst pair is

additionalClasses and emptyPartitionClasses, which

determine how many additional classes should exist

in the partition despite the initial number of labels

present in the partition, and how many labels add to

empty partitions. The second pair is emptyPercent

and additionalPercent, which describe the maximum

percentage of the data that should be used to ﬁll empty

partitions, and how much data should be used as ad-

ditional padding for other partitions. To keep the ma-

jority in the initial subsets, the ﬁrst should not be less

than 50%, and the second should be at most half the

value of the ﬁrst parameter. The same concept is de-

scribed in a recent paper by (Markiewicz and Koper-

was, 2019), with reference to different strategies for

preparing uneven data distributions.

There are many parameterisation possibilities,

which depend on the dataset used, the number of la-

bels, and the amount of data. By looking at the ﬁ-

nal result of this partitioning process, we can clearly

see that it is closely related to both the label and the

amount in terms of the data property. In itself, it does

not take attribute values into account; although this

is possible, it would involve mixing different non-IID

partitioning main categories rather than a single as-

pect of the data distribution.

2.2.3 Concept Drift (Same Label, Different

Features)

The term ’concept drift’ refers to a problem of dis-

tributed learning training phase in which a certain

set of data objects from the same class on each in-

dependent node is represented by samples with dis-

joint attribute values. It can refer to a fully disjoint set

of attribute values between nodes or simply a differ-

ent value distribution for some attributes in different

nodes. The most common example where this issue

occurs is a classiﬁcation task for pictures with houses,

where photos of houses are taken at different times of

the year or under different weather conditions. An-

other example is the features of people from differ-

ent regions of the world who differ in terms of their

height, weight, hair colour, etc., which has an impact

when exploring data on medical conditions. To simu-

late this type of data distribution, the dataset with the

selected label should be separated to obtain the most

separable data sample groups possible based on the

attribute values. A simple technique would be to ap-

ply a partitioning algorithm to a subset to ﬁnd a spe-

ciﬁc number of groups; however, this may be a non-

deterministic method. We took a different approach,

and our algorithm is deﬁned in Algorithm 1.

Algorithm 1: ’concept drift’ partitioning strategy.

Input Dataset Data, target label L, and partition

”drifts” D

Output Data partitioned into D partitions

1: Extract a data subset Data with label L;

2: [optional] Discretise the numerical attributes into

R ranges for further processing;

3: Group data into buckets consisting of samples

with the same attribute values, in order to sepa-

rate the individuals and groups of disjoint sets of

attribute values, where individuals are samples or

buckets of samples with the unique values of all

attributes. A disjoint set refers to a group of sam-

ples whose values for each attribute in every sam-

ple are disjoint to values for each attribute of every

sample from other sets. Fig. 4 gives an example

of this process. This example shows the result and

the second pass after processing step 5.2.;

4: [optional] For a dataset that contains only nom-

inal attributes, ﬁnd individuals - they are can-

didates for scattering anywhere because of com-

pletely different feature values than other sam-

ples; they can be treated as data anomalies;

5: Check whether it is possible to perform the se-

lected ”drift” from the groups found by checking

the conditions: |buckets \ individuals| ≥ D and

|bucket| >

|Data|

·r;∀bucket; where r - ratio with

default, but possibly parameterisable value 0.2, to

avoid highly unbalanced partitioning:

5.1: If the conditions are met, or all the attributes

have been checked, partitioning begins;

5.2: Otherwise, remove individuals from the Data

subset, exclude the single Data attribute with

the lowest entropy value, and repeat the steps,

starting with step 3;

6: Partitioning is done by dividing the found buckets

sorted by the value from the last examined at-

tribute into D partitions, where the number of

samples is divided between them as evenly as pos-

sible;

7: If any individuals are found, place them into par-

titions to ﬁll or equalise sample quantities be-

tween partitions;

7.1: [optional] For numerical data, the target par-

titions for individuals are those closest to the

centre in terms of the Euclidean distance (note

that without the discretisation performed in

Step 2, there is usually a large number of

individuals);

ICSOFT 2022 - 17th International Conference on Software Technologies

312

Id: a1, a2, a3

1 : a, b, c

2 : w, d, e

3 : x, y, z

4 : d, e, f

5 : w, b, b

6 : d, f, d

7 : c, c, f

8 : x, y, z

bucket 1:

ids=[1, 2, 5]

a1 =[a, w]

a2 =[b, d]

a3 =[c, e, b]

bucket 2:

ids=[3, 8]

a1 =[x]

a2 =[y]

a3 =[z]

bucket 3:

ids=[4, 6, 7]

a1 =[d, c]

a2 =[e, f, c]

a3 =[f, d]

individuals

Id: a2, a3

1 : b, c

2 : d, e

4 : e, f

5 : b, b

6 : f, d

7 : c, f

bucket 1:

ids=[1, 5]

a2 =[b]

a3 =[c, b]

bucket 2:

ids=[2]

a2 =[d]

a3 =[e]

bucket 3:

ids=[4, 7]

a2 =[e, c]

a3 =[f]

individuals

bucket 4:

ids=[6]

a2 =[f]

a3 =[d]

1st pass:

2nd pass:

3nd pass..

Figure 4: An example of found buckets with individuals for

the ﬁrst two passes of the ’concept drift’ strategy. Bolded

value with cyan background marks the attribute values re-

sponsible for grouping samples into the ﬁrst bucket. Sample

with id 5 affects the unrelated to each other samples with

ids 1 and 2, as they have a transitive similarity: 1 ∼ 5 ∧ 2 ∼

5 =⇒ 1 ∼ 2.

Although we assume here that drifting is per-

formed for one selected label, the same algorithm can

be applied to others. Examples of the partitioning re-

sults for the Iris dataset and the two-dimensional nu-

merical single ellipse Gaussian dataset are shown in

Fig. 5. With the use of colours and shapes, it is easy to

notice how data samples are divided separately from

each other. The dataset ﬁrmly separated represents

the same object class, e.g. the same genre of ﬂower

or cluster of points; however, divided as much as pos-

sible after attribute distribution examination. As a re-

sult, we obtain well-separated subclasses.

However, this approach may fail if the dataset can-

not be split in this way, in which case the method pro-

cessing comes down to splitting the data sorted by the

most diverse value of a single attribute. For images or

textual datasets, using the proposed approach should

additionally consider either a prior aggregation of at-

tributes or a reduction in the number of dimensions.

Without this preprocessing step, the algorithm would

try to carry out an analysis at too low a level of detail,

such as a single pixel value, which is irrelevant in the

overall scope.

2.2.4 Concept Shift (Same Features, Different

Label)

The concept of this issue relates to a divergent class

identiﬁcation of data objects described by the same

features in different regions, or simply a different un-

derstanding of what is represented by the characteris-

tics when marking the data used for training. This is

more related to the NLP process for sentiment anal-

ysis problems, where words can be tagged in differ-

ent ways in the training dataset depending on the un-

derstanding. An example of nominal data can be a

different understanding of a high or wealthy person

depending on the country. When classifying non-text

data, it is difﬁcult to avoid errors in processing. It is

(a) Iris dataset - ’Iris-setosa’ attribute.

(b) 2-dimensional single cluster dataset.

Figure 5: Scatter matrix plots for single label data parti-

tioned using the ’concept drift’ strategy.

almost impossible to evaluate the correct solution, as

training is based on previously known labels. When

the features of data objects are similar but labelled

differently, the only way to get a correct result is to

use fuzzy classiﬁcation, where the classiﬁed sample

can have multiple classes assigned to it. However, the

clustering task is not affected by this problem at all,

as it is an unsupervised learning method that does not

involve an analysis of the training data classes. Due to

the conditions mentioned above, the proposed method

of data partitioning consists of changing the label to

a new, unique one for a certain number of data sam-

ples. Our implementation of this partitioning strategy

allows us to change the label of training samples for

a subset of data with a selected class. This training

subset of size s ·

is then separated and the labels are

changed, where s is the number of parts of the data

subset to perform an independent label change, and N

is the number of partitions. Fig. 6 gives an example of

this type of partitioning. The exemplary dataset con-

sists of data samples of two different labels required

to be divided into three partitions and create two more

classes using ’concept shift’. As a result, we obtain

four classes distributed on three partitions where two

classes are artiﬁcially created from the chosen one.

Data Partitioning Strategies for Simulating non-IID Data Distributions in the DDM-PS-Eval Evaluation Platform

313

200 * C 200 * D

= 300 n

= 300

dataset size = 900

number of parts (s) = 2

worker nodes (N partitions) = 3

shift label = ‘B’

300 * ‘A’ 600 * ‘B’

100 * A

200 * B

Figure 6: ’concept shift’ partitioning strategy applied to

data samples labelled ’B’.

The overall purpose of using this method for val-

idation is to see how much such a divergent under-

standing of object class may affect the ﬁnal results.

This can be useful when the evaluated algorithm pro-

duces a fuzzy result or returns artefacts describing

samples rather than a simple classiﬁcation label.

2.2.5 Unbalancedness (Quantity Skew)

The last method of data partitioning described in this

paper is the preparation of unbalanced data in terms

of the number of samples. In this case, we assume

that some nodes have more data samples, and oth-

ers have signiﬁcantly fewer. The partitioning method

can be trivial by using random data partitioning along

with the probability weights of presence in each par-

tition. However, it would be difﬁcult to maintain the

ratio between sizes of those partitions with more data

samples and other partitions for various numbers of

target partitions. A simpliﬁed diagram illustrating pa-

rameterisation for this approach to obtain a ¼ ratio is

shown in Fig. 7.

However, our intention was to allow the user to

choose this ratio along with the number of nodes that

should contain more data samples. In order to make

this possible, a simple system of two equations has to

be solved, in which we have two unknown variables

and four known parameters. Equation 5 describes the

conditions to solve in order to ﬁnd unknown values L

and S, where L is the large amount of data and S is the

small amount of data; the known parameters from the

data description are C and W , where C is the dataset

size and W is the number of target partitions; and

the user-deﬁned parameters are node threshold T as

the number of target partitions that should have more

data, and ratio U which is the target unbalancedness.











T · L + (W − T ) · S = C

= U

=⇒











L =

U·(W −T )+T

S =

C−T ·L

W −T

(5)

Based on the previous example in Fig. 7, we can

obtain these numbers by using parameter values of

0.25 for the unbalancedness ratio and two nodes as

the threshold. In our implementation of this method,

it is also possible to select a proportional imbalance to

keep the same ratio for each class as a result of data

partitioning. 0 However, this behaviour is usually un-

desirable, as it tends towards the IID data distribution.

As a result of this partitioning strategy, the data sam-

ples are scattered among the partitions in the number

of the calculated partition sizes: L and S. Samples

are chosen from the original dataset by a uniformly

random function.

900 samples

= 400

100

dataset size = 900

worker nodes (N partitions) = 3

large partitions quantity = 2

target ratio = ¼ = 100 / 400

~44.5% ~44.5%

~11%

Figure 7: The trivial approach of ﬁnding the partition size

division.

It should also be noted that when the imbalance

factor is high, we do not consider ’unbalancedness’

alone, but in conjunction with the ’prior probability’

category, which in this case is related to the ’Label /

class related’ data property deﬁned in the taxonomy.

This is another indication that we are considering a

taxonomy rather than a hierarchy.

3 DDM-PS-EVAL PLATFORM

PARTITIONING COMPONENT

The DDM-PS-Eval platform created and described

by (Markiewicz and Koperwas, 2022) is a tool used

to perform comprehensive distributed data mining al-

gorithms evaluation. The most exciting element in

this platform referring to this work is the possibility of

running experiments on the same dataset but with dif-

ferent data distribution. This platform contains built-

in partitioning strategies and has been designed to be

easily extendable with new custom ones. It is possible

to write custom implementations following the given

interface rules and use them in the platform.

A crucial part of this work was to prepare working

implementations of partitioning strategies that expand

algorithms evaluation with different non-IID data dis-

tributions. Moreover, using the extended taxonomy

presented in section 2.1, already existing strategies

have been arranged into the main categories:

- ’uniform’, is treated as reference IID partitioning

and kept outside of non-IID data partitioning tax-

onomy;

- ’label-strategy’, during this work has become gen-

eralised and placed into the ’prior probability

shift’ category;

ICSOFT 2022 - 17th International Conference on Software Technologies

314

- ’dense-and-outliers’, aforementioned also in sec-

tion 2.2.1 and refers to the ’covariate shift’ cate-

gory.

We have prepared implementations of partitioning

strategies for the three missing categories in the plat-

form. These were ’concept drift’, ’covariate shift’,

and ’unbalancedness’. Adding them completes the

set of non-IID from the ’Non-identical client distri-

butions’ taxonomy branch.

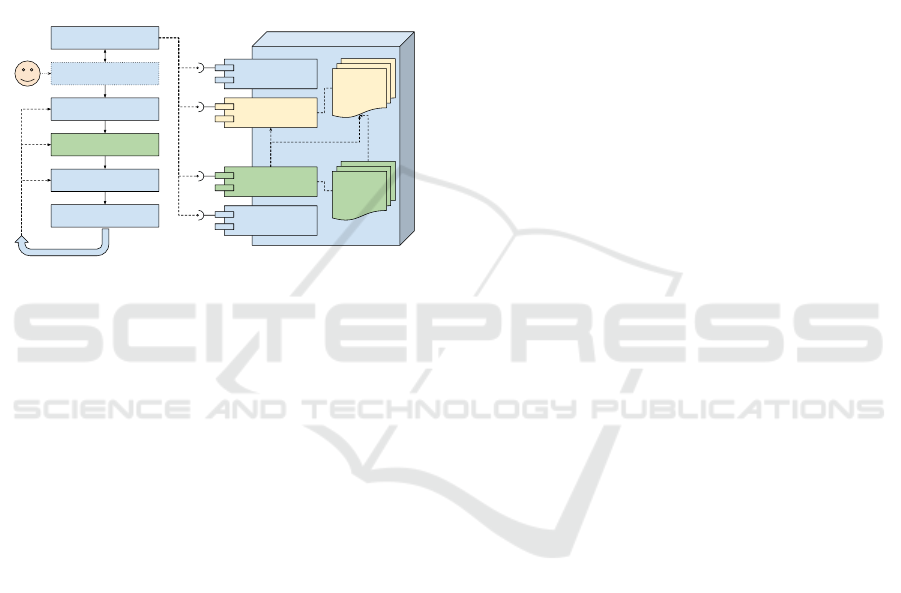
The overview of the most interesting and data-

related components of the platform is presented in

Fig. 8. The platform allows us to perform multiple

Load input essentials

Prepare test suite

DDM-PS-EVAL evaluation process

Scatter data

using partitioning strategy

Execute algorithm

Validate results

repeat

DDM-PS-EVAL

built-in

similarity

measures

built-in

partitioning

strategies

Data

loader

Similarity measure

loader

Partitioning strategy

loader

Slice of the DDM-PS-EVAL components

Algorithm

loader

Prepare environment

« use »

Figure 8: Fragment of the DDM-PS-Eval platform with es-

sential components related to data partitioning; a simpliﬁed

algorithm evaluation process on the left.

parameterised experiments using different built-in or

custom partitioning strategies. Partitioning strategy

components marked with a green background are re-

sponsible for this process.

3.1 Data Similarity Measures

Commonly, algorithms operating on numerical data

use Euclidean distance to compare data samples;

however, it is not a rule. Cosine distance works

better to compare a vector representation of text doc-

uments. On the other hand, specialised algorithms

can work with custom similarity metrics. Comparing

genomic data described by specialised structures is

an excellent example. The DDM-PS-Eval platform

is prepared to load and use custom data similarity

metrics for partitioning strategy alongside built-in

metrics. The already existing ’dense-and-outliers’

strategy uses this feature to calculate the distance

between data samples depending on data and the

provided similarity measure. Nevertheless, the

proposed in this work strategies do not require any

metric. They work directly on the data attributes,

labels or amounts related to labels. On the other

hand, to achieve a more sophisticated distribution

for ’prior probability shift’, moving more simi-

lar samples with the same class together between

partitions instead of random choice would be

beneﬁcial.

4 EXPERIMENTS

In order to verify the validity of the proposed parti-

tioning strategies, we carried out several experiments.

To illustrate the impact on the quality of the results,

we ran selected distributed algorithms for datasets

that were independently partitioned using multiple

strategies.

For the evaluation, we used four different dis-

tributed clustering algorithms and two simple dis-

tributed classiﬁers. The classiﬁers were a distributed

implementation of naive Bayes, which builds global

a priori probability statistics based on the collected

probabilities from local nodes, and the naive dis-

tributed SVM approach described in (Navia-V

azquez

et al., 2006), tentatively named DN-SVM. In the lat-

ter approach, the ﬁnal SVM model is trained on lo-

cally found support vectors sent from local nodes,

which are treated as global training data. The cluster-

ing algorithms were DK-means (Ji and Ling, 2007),

Opt-DKM (Markiewicz and Koperwas, 2019), a

lightweight clustering technique (Aouad et al., 2007)

tentatively named LCT, and a modiﬁed version of the

BIRCH algorithm (Zhang et al., 1997), which used

a partitioning approach for the ﬁnal clustering. This

modiﬁcation was made by combining the agglomer-

ative process in BIRCH with a partitioning method.

BIRCH clusters the data at the local nodes and sends

the cluster centroids to the global node, where the

same operation is performed by treating the centroids

as data samples to be clustered. Finally, global clus-

tering is done by assigning samples to the closest

global centroid.

The data used in the experiments included well-

known datasets from the UCI Machine Learning

Repository, such as the unbalanced Shuttle dataset

and the tiny MNIST dataset. We used the PCA algo-

rithm to preprocess and reduce MNIST data dimen-

sionality from 28x28 into 28 attributes to avoid ap-

plying partitioning strategies on raw pixel values. We

also used the noiseless ”Dataset 1”, which was in-

troduced with the CURE algorithm in (Guha et al.,

1998), and a dataset generated as two-dimensional

points arranged into Gaussian clusters with some

overlapping outliers to avoid perfect clustering re-

sults. The ﬁrst two of these are primarily used for the

task of classiﬁcation, whereas the last two are used for

clustering purposes. The full parameterisation of the

experiments is given in Table 1.

Data Partitioning Strategies for Simulating non-IID Data Distributions in the DDM-PS-Eval Evaluation Platform

315

Table 1: Summary of the test suite with experimental conﬁgurations.

Data (classes/groups, number of samples)

Shuttle (7, 58.000), MNIST (10, 70.000),

CURE (5, 2.000), Synthetic-Gaussians (7, 100.000)

Algorithms

Naive Bayes, DN-SVM,

DK-means, Opt-DKM, LCT, DP-BIRCH

Worker nodes / partitions

Three workers for the ﬁrst three literature datasets

Four workers for the synthetic dataset

Partitioning strategies

(parameterised separately for each dataset)

uniform, dense-outliers, covariate-shift,

separated, most-plus-some, most-plus-all, all-but,

concept-drift, concept-shift, unbalancedness

The results of the experiments on distributed clas-

siﬁcation are shown in Fig. 9, and those for distributed

clustering are shown in Fig. 10. In each chart, the ﬁrst

black bar on the left represents the results for uniform

data distribution, and the rest represents the other par-

titioning strategies. For the non-deterministic algo-

rithms, each bar shows the average result of 30 execu-

tions, with error bars representing the minimum and

maximum values of all executions. All experiments

were carried out on the DDM-PS-Eval platform pre-

sented in (Markiewicz and Koperwas, 2022) hence all

the methods proposed are ready to use, and have been

implemented in the way suggested by the authors

of (Markiewicz and Koperwas, 2022). This allowed

us to collect multiple forms of information, such as

the processing time, transfer load, and ﬁnal quality;

however, for clarity of presentation, only the quality

is presented in the charts. The quality measure used

for clustering is the adjusted Rand index, whereas for

classiﬁcation we use the F-score in response to the un-

balanced number of classes in the Shuttle dataset. The

number of partitions used is small, due to the small

number of classes and data samples, since the goal is

to show the impact of non-IID partitioning rather than

to add artiﬁcial complexity to the problem.

The primary goal of any algorithm design is to

obtain high-quality results regardless of data distri-

bution. However, in many implementations of dis-

tributed algorithms, the results are affected by differ-

ent data dispersion. Due to its nature, a distributed im-

plementation of the Naive Bayes algorithm produces

exactly the same results, regardless of the partition-

ing strategy used. The expected exception in experi-

mental results is poor accuracy obtained for the tested

classiﬁers using ’concept shift’ partitioning strategy,

as they are not fuzzy classiﬁers. The second clas-

siﬁer encountered problems with highly segregated

data, where the number of support vectors was small.

The clustering results showed how the mean and max-

imum possible values of the clustering quality might

Full results as raw data and an interactive

format are available at https://github.com/Kajo0/

icsoft-2022-experiments-results

vary depending on the data partitioning. It was found

that even using the k-means++ initialisation intro-

duced in (Arthur and Vassilvitskii, 2006) did not help

to avoid the impact of different data partitioning meth-

ods on the results. The effects of the different data

partitioning methods on the ﬁnal clustering are very

different, as shown in the results of the DK-Means

and Opt-DKM algorithms. It is also interesting that

in most cases, uniform data distribution made it difﬁ-

cult to obtain the best results, which was not expected

at the outset. However, this can be explained by the

density-based nature or non-deterministic initialisa-

tion of these algorithms.

An important implication of these ﬁndings is that

we can roughly summarise how each partitioning

strategy affects the algorithms examined here, as pre-

sented in Table 2. We cannot state that a particular

category of non-IID data affects calculations or results

for particular types of algorithms, for example par-

titioning or density-based methods. This is because

modern distributed algorithms are usually based on

an ensemble approach, and typically combine differ-

ent methods for better results. However, we can cer-

tainly determine the approximate level of the possible

impact of each main non-IID category on the algo-

rithm, as shown in Table 2. This approximation may

form a starting point for authors aiming to optimise

the implementation of their algorithm.

We also need to remember that the impact of non-

IID data partitioning on the quality of the algorithms

also depends on the characteristics of the data itself

without partitioning. This is illustrated in Figs. 9

and 10, where the distributions of the results for the

same algorithm differ between the datasets; this is

clearly visible for the DK-means algorithm, for in-

stance. Moreover, it is obvious that there are countless

test case parameterisations, including the selection of

dataset attributes, the size of the “drift” or “shift”,

and the number of target partitions. For this article,

we have selected more interesting results for the dif-

ferent partitioning strategies to emphasise the impact

of the data distribution. Depending on the behaviour

of the algorithm, the results may be better or worse,

ICSOFT 2022 - 17th International Conference on Software Technologies

316

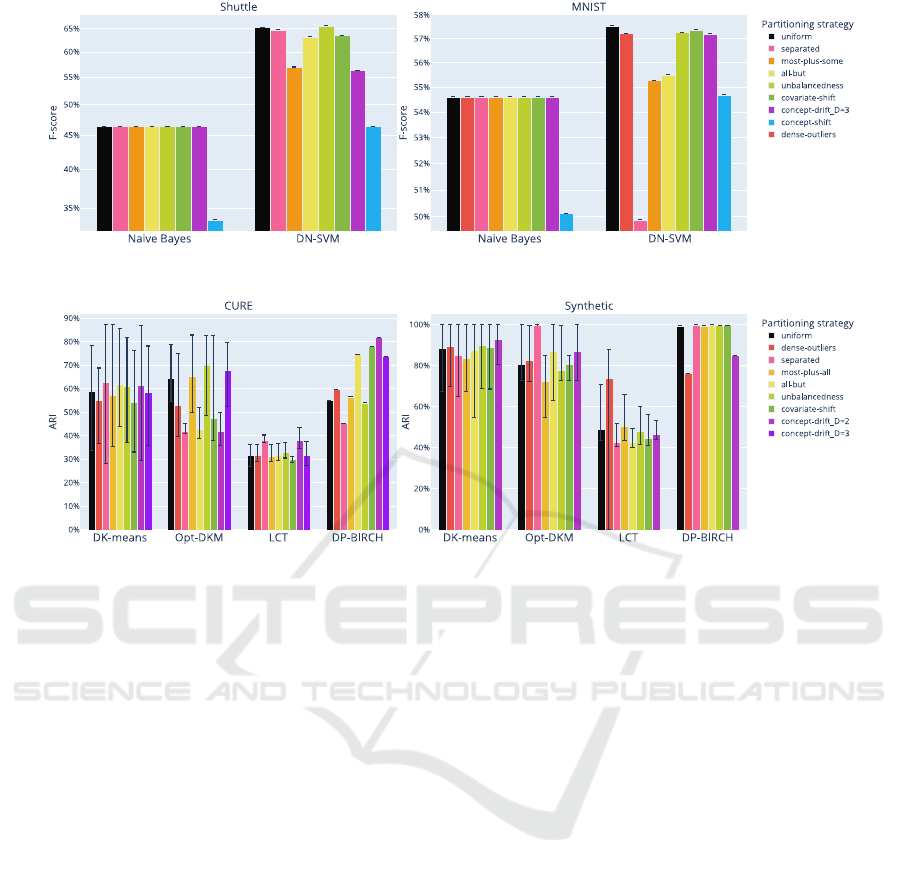
Figure 9: Comparison of results obtained for classiﬁcation using a logarithmic scale.

Figure 10: Comparison of average results obtained for clustering.

or may not change at all. For example, in the case

of distributed versions of density-based algorithms,

data separation is typically an obstacle in subsequent

phases of global aggregation. For this reason, it is

crucial to validate algorithms using multiple data par-

titioning strategies instead of a single uniform one.

All the methods proposed represent only a few

possibilities for the data distributions, and many more

are possible. At this point, it should be noted that

in terms of data partitioning, numerical data such as

images with large numbers of dimensions should be

treated differently from data collected from surveys,

which are used for classiﬁcation purposes. Moreover,

in some label-related strategies that perform dataset

separation based on the sample class, the number of

target partitions plays a role, which opens up another

discussion on how to deal with this.

5 CONCLUSIONS AND FUTURE

WORK

In this work, we extended the existing non-IID tax-

onomy by two levels. The ﬁrst is the data prop-

erty as the parent level of the main non-IID category.

Adding this level then allowed us to determine the re-

lation between data attribute and speciﬁc partitioning

strategies deﬁned as the new leaf-level of the taxon-

omy. We have presented multiple dataset partitioning

methods that simulate non-IID data dispersion for nu-

merical and nominal data, with detailed explanations

and examples for each category. The proposed meth-

ods have been evaluated for distributed clustering and

classiﬁcation algorithms using several datasets and

various algorithms. Results for different parameter-

isations have been presented and discussed. Each

described data partitioning strategy has been imple-

mented and is ready to work with the DDM-PS-Eval

platform. In conclusion, this study has shown that

there is a signiﬁcant impact of data partitioning on the

results provided by distributed algorithms. This work

paves the way for better validation of algorithms, in

order to allow for the design of algorithms that are

data distribution-agnostic.

Further research on different data partitioning

schemes, such as for textual datasets, is necessary to

extend our evaluation to other types of algorithms.

Future work will involve extending the proposed

methods to produce more realistic distributions of

non-IID data by mixing multiple partitioning strate-

gies based on attributes, labels, and quantity. Several

open issues need to be analysed and addressed, such

as the aforementioned mixture of strategies and deal-

ing with a large number of partitions for data with few

labels.

Data Partitioning Strategies for Simulating non-IID Data Distributions in the DDM-PS-Eval Evaluation Platform

317

Table 2: Summarised ranges of the negative impact of each partitioning strategy on the examined algorithms and datasets (L,

M, H indicate low (<5%), medium (<10%), high (≥10%) impact, respectively, and 0 indicates no noticeable impact or results

that are better than those obtained for uniform data distribution; for non-deterministic algorithms, separate differences were

taken into account for both mean and maximum values collected from multiple executions; bold cells indicate potentially high

impact).

Main non-IID category

of data partitioning strategy

Naive Bayes DN-SVM DK-means Opt-DKM LCT DP-BIRCH

Covariate shift 0 0 - L 0 - M 0 - H 0 - H 0 - H

Concept shift M-H H 0 0 - L 0 - H 0 - L

Concept drift 0 0 - M 0 - L 0 - H 0 - H L - H

Prior probability shift 0 0 - H 0 - L 0 - H 0 - H 0 - M

Unbalancedness 0 0 0 - L 0 - L 0 - H L - H

REFERENCES

Aouad, L. M., Le-Khac, N.-A., and Kechadi, T. M. (2007).

Lightweight clustering technique for distributed data

mining applications. In Industrial Conference on Data

Mining, pages 120–134. Springer.

Arthur, D. and Vassilvitskii, S. (2006). k-means++: The

advantages of careful seeding. Technical report, Stan-

ford.

Bouraqqadi, H., Berrag, A., Mhaouach, M., Bouhoute,

A., Fardousse, K., and Berrada, I. (2021).

Pyfed: extending PySyft with N-IID Feder-

ated Learning Benchmark. Proceedings of the

Canadian Conference on Artiﬁcial Intelligence.

https://caiac.pubpub.org/pub/7yr5bkck.

Caldas, S., Duddu, S. M. K., Wu, P., Li, T., Kone

J., McMahan, H. B., Smith, V., and Talwalkar, A.

(2018). Leaf: A benchmark for federated settings.

arXiv preprint arXiv:1812.01097.

Grigorescu, S. M. (2018). Generative one-shot learn-

ing (gol): A semi-parametric approach to one-shot

learning in autonomous vision. In 2018 IEEE In-

ternational Conference on Robotics and Automation

(ICRA), pages 7127–7134. IEEE.

Guha, S., Rastogi, R., and Shim, K. (1998). Cure: An ef-

ﬁcient clustering algorithm for large databases. ACM

Sigmod record, 27(2):73–84.

Hsieh, K., Phanishayee, A., Mutlu, O., and Gibbons, P.

(2020). The non-iid data quagmire of decentralized

machine learning. In International Conference on Ma-

chine Learning, pages 4387–4398. PMLR.

Hu, S., Li, Y., Liu, X., Li, Q., Wu, Z., and He, B.

(2020). The oarf benchmark suite: Characterization

and implications for federated learning systems. arXiv

preprint arXiv:2006.07856.

Ji, G. and Ling, X. (2007). Ensemble learning based dis-

tributed clustering. In Paciﬁc-Asia Conference on

Knowledge Discovery and Data Mining, pages 312–

321. Springer.

Kairouz, P., McMahan, H. B., Avent, B., Bellet, A., Bennis,

M., Bhagoji, A. N., Bonawitz, K., Charles, Z., Cor-

mode, G., Cummings, R., et al. (2019). Advances and

open problems in federated learning. arXiv preprint

arXiv:1912.04977.

Li, Q., Diao, Y., Chen, Q., and He, B. (2021a). Federated

learning on non-iid data silos: An experimental study.

arXiv preprint arXiv:2102.02079.

Li, Q., Wen, Z., Wu, Z., Hu, S., Wang, N., Li, Y., Liu,

X., and He, B. (2021b). A survey on federated learn-

ing systems: vision, hype and reality for data privacy

and protection. IEEE Transactions on Knowledge and

Data Engineering.

Lim

on, X., Guerra-Hern

andez, A., Cruz-Ram

ırez, N., and

Grimaldo, F. (2019). Modeling and implementing dis-

tributed data mining strategies in jaca-ddm. Knowl-

edge and Information Systems, 60(1):99–143.

Liu, L., Zhang, F., Xiao, J., and Wu, C. (2020). Evaluation

framework for large-scale federated learning. arXiv

preprint arXiv:2003.01575.

Luo, J., Wu, X., Luo, Y., Huang, A., Huang, Y., Liu, Y.,

and Yang, Q. (2019). Real-world image datasets for

federated learning. arXiv preprint arXiv:1910.11089.

Markiewicz, M. and Koperwas, J. (2019). Hybrid

partitioning-density algorithm for k-means cluster-

ing of distributed data utilizing optics. International

Journal of Data Warehousing and Mining (IJDWM),

15(4):1–20.

Markiewicz, M. and Koperwas, J. (2022). Evaluation

platform for ddm algorithms with the usage of non-

uniform data distribution strategies. International

Journal of Information Technologies and Systems Ap-

proach (IJITSA), 15(1):1–23.

Navia-V

azquez, A., Gutierrez-Gonzalez, D., Parrado-

Hern

andez, E., and Navarro-Abellan, J. (2006). Dis-

tributed support vector machines. IEEE Transactions

on Neural Networks, 17(4):1091.

Sattler, F., Wiedemann, S., M

uller, K.-R., and Samek, W.

(2019). Robust and communication-efﬁcient feder-

ated learning from non-iid data. IEEE transactions on

neural networks and learning systems, 31(9):3400–

3413.

Zhang, T., Ramakrishnan, R., and Livny, M. (1997). Birch:

A new data clustering algorithm and its applications.

Data Mining and Knowledge Discovery, 1(2):141–

182.

Zhu, H., Xu, J., Liu, S., and Jin, Y. (2021). Federated

learning on non-iid data: A survey. arXiv preprint

arXiv:2106.06843.

ICSOFT 2022 - 17th International Conference on Software Technologies

318