
Dynamic Decomposition of a Variety of Fungi
Yingzi Jiang
1,a,*
, Yuyan Zhang
1, b
, Yuchong Mao
2,c
and Tianhang Ji
1,d
1
Xuzhou Institute of mathematics and statistics, Xuzhou, Jiangsu, China
2
School of finance, Xuzhou Institute of Engineering, Xuzhou, Jiangsu, China
*Corresponding author:
a
fireyz@xzit.edu.cn
Keywords:
Multiple Regression Analysis Model, Biological Growth Kinetics, Lanchester Model, Fungi Community.
Abstract:
The carbon cycle describes the process of carbon exchange in the entire geochemical cycle and is an important
part of life on Earth. Part of the carbon cycle includes the decomposition of compounds so that carbon can be
updated and used in other forms. Based on the growth dynamics equation, this paper takes into account the
growth rate of fungi and the humidity resistance of fungi, establishes a multi-regression model and a
Lanchester model, analyzes the decomposition of various fungi on wood fibers, and expounds the role of
fungi in the ecosystem.
1 INTRODUCTION
1.1 Problem Background
Ground litter, also known as organic debris, refers
toall organic matter produced by biological
components in an ecosystem and eventually returned
to the surface of the land (LI 2016). It is the main
carrier of energy flow and material circulation above
and below ground (Wardle 2004). The carbon cycle
refers to a process in which carbon elements are
exchanged in four circles throughout the earth, as
shown in Figure 1:
Figure 1: Carbon cycle.
As the decomposers of organic matter in the
ecosystem, fungi play an essential and critical role in
the decomposition of ground litter.
2 MATERIALS AND METHOD
The growth and decomposition of microorganisms
such as fungi are also affected by temperature,
862
Jiang, Y., Zhang, Y., Mao, Y. and Ji, T.
Dynamic Decomposition of a Variety of Fungi.
DOI: 10.5220/0011298500003443
In Proceedings of the 4th International Conference on Biomedical Engineering and Bioinformatics (ICBEB 2022), pages 862-866
ISBN: 978-989-758-595-1
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
inoculation amount, electric field intensity and other
conditions (Kong 2001).
2.1 The Classification of Fungi
When studying the growth process on the interface of
fungi, logical models are often used to describe the
growth dynamic equation of fungi (Jin 1989).
1
n
X
m
dX X
X
dt X
β
=−
(1)
Where t is time, X is the biomass per unit area,
and Xm is the maximum biomass per unit area is the
growth rate constant.
2.1.1 Factors That Affect the Rate of Fungal
Decomposition
In order to rapidly degrade ground litter with fungi
that have different hyphae elongation and moisture
tolerance, it is necessary to ensure that temperature,
humidity, pH and other conditions are maintained
under appropriate conditions (Xue 1999).
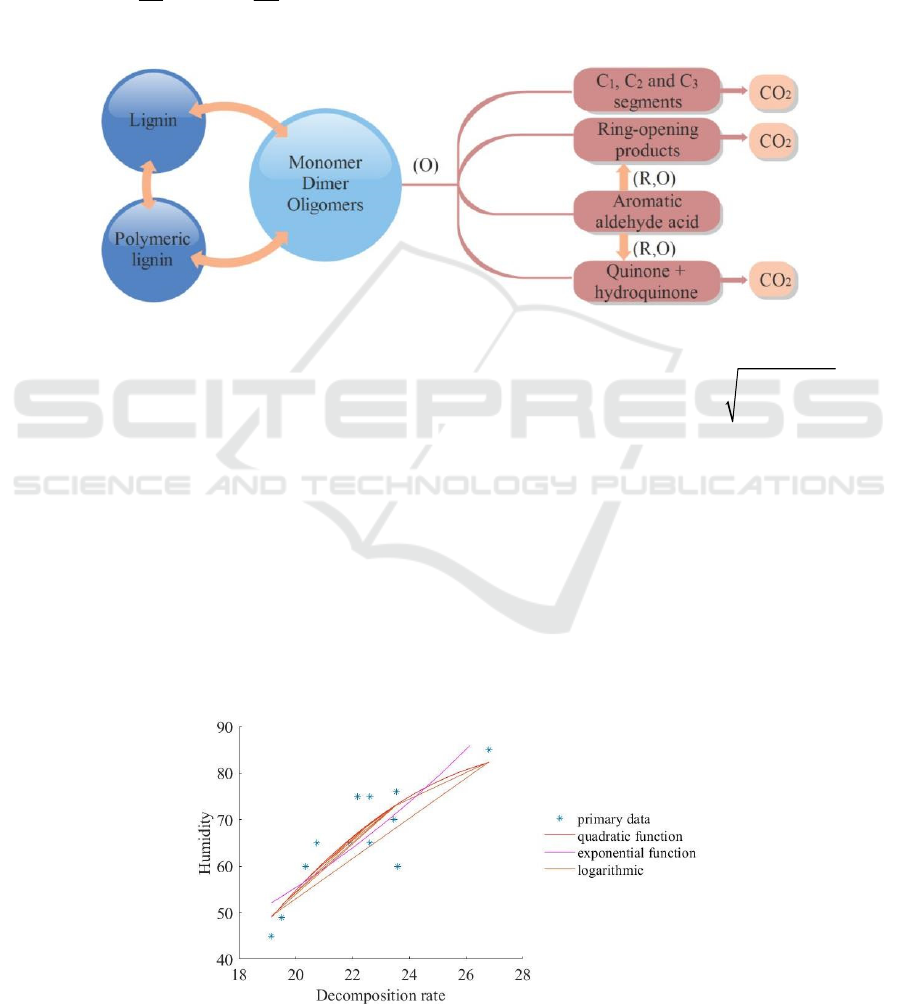
Figure 2: Lignin degradation diagram.
2.1.2 Establish Multivariate Nonlinear
Regression Model
Based on the fungal decomposition rate and
humidity, temperature and acidity as arguments, a
nonlinear regression model is established:
()
()
01 1 2 3
2
,, , ; , ,
0,
m
i
zfbb byyy
N
εσ
=
(2)
Where,
ε
is the random error term. In order to
minimize the square sum of the error between the
sample data of fungi decomposition rate and the
estimated fungi decomposition rate, the least square
method was used in parameter calculation in this
paper to minimize the error. That is:
()
()
2
01
1
min , , ,
n
mii
i
Rb b b z z
=
=−
(3)
Where,
()
01 1 2 3
=,,,;,,
imiii
zfbb byy y
is an
estimate of the rate of fungal decomposition.
Through data observation, it can be found that the
fungi decomposition rate has a non-linear
relationship with each index. Therefore, this paper
uses SPSS software to curve-fit each index and the
fungi decomposition rate, and uses quadratic,
logarithmic, and exponential functions for analysis.
Take the fitting figure 3 of the decomposition rate of
Armillaria as an example:
Figure 3: Relationship fitting grap.
Dynamic Decomposition of a Variety of Fungi
863
Therefore, the multivariate nonlinear regression
model of decomposition rate of Armillaria mellea and
environmental influencing factors can be obtained by
solving SPSS as follows:
222
1231 2 3
16.992 0.107 0.593 1.16 0.003 0.016 0.105yxxxxxx=+ − ++ + −
According to the above method analysis, it can be
found that different species and even different fungi
are affected by temperature, humidity, pH and other
environmental factors. Relatively speaking, the
higher the temperature, the faster the fungus breaks
down wood.
2.2 The Interaction of Fungi
The rate at which withpositor and wood fibers break
down depends not only on the type, characteristics
and environment of the fungus, but also on the
competition of the fungus's growth process
(Tadashi
2010).
2.2.1 Internal Competition for Fungi
According to the symmetrical fork model, the total
NA node for each active bud tube growing on the
interface is and the total number of growth segments
is determined by the number of active segments.
According to biological research, the proportion of
active organisms in total biomass is 33%. Available
based on growth dynamics equations:
3
TT
XA X
dX X
X
dt
ββ
==
(4)
For
T
X
, according to the definition of growth rate
and combined with the above equation, take the pair
to get (Lu 2016):
0
ln ln
3
X
T
X
Xt
β
=+
(5)
Based on the growth model of microorganisms in
the growth of several years, the growth state of the
fungus can be obtained during this period, so that the
performance of the fungus in the competitive process
can be studied.
When fungi are full on the interface, myceliums
collide with each other during growth, leading to
competition of substances and rendering some
mycelium inactive. The proportion of inventory will
decrease in a pair after the competition of mycelium:
()
0.33
kt t
v
FLe
α
−−
= . When
tt
α
=
,
TE
XX=
stop
growing, combined with the growth process of fungi,
can get the fungus internal competitive model:
()
0
ln 1
3
kt t
TX
E
XL
e
Xk
β
−−
=−
(6)
According to the establishment of the internal
competitive model of fungi, we can understand the
growth and development of fungi. when
environmental factors such as temperature and
humidity are in the optimal growth environment of
fungi.
Figure 4: Growth curve fitting of Armillaria.
We can see that in the process of separate growth
of Armillaria, the interaction of the fungi is in an
internal competition relationship. But competition
among fungi isn't just internal competition due to
growth interface constraints.
2.2.2 External Competition of Fungi
The Lanchester equation is mainly used to predict the
fighting situation of the two sides, this article
compares the competition of multiple fungi to multi-
army combat to obtain related models:
ICBEB 2022 - The International Conference on Biomedical Engineering and Bioinformatics
864

()
()
dx
cy x u t
dt
dy
dx y v t
dt
α
δ
=− − +
=− − +
(7)
Among them, and represent the attack power of
both sides of the competition,
α
and
δ
represent the
non-competitive damage factor of both sides of the
competition,
()
ut
and
()
vt
represent the number of
fungi regenerated by fungi.
The development of each fungus is in an
internalcompetition link because the interface has not
been overgrown in the early stage.
3 RESULTS & DISCUSSION
3.1 Fungi Are Affected by the
Environment
The fluctuation of the environment means that the
temperature and humidity that were originally
suitable for fungi growth will also change
accordingly, causing the growth and competition of
fungi to be affected to a certainextent, so this article
mainly considers the influence of environmental
fluctuations on the external competition of fungi.
1kk
F
F
dF
tT
+
−
=
(8)
Obtain the effect of the introduction of
environmental factors on the state equation:
*
1kk
F
AF C
+
=⋅+
. By adding the state equation
to the analysis of the fungus's external competition,
the following new Lanchester equation can be
obtained:
'
cA
F
EAF C=+
(9)
The growth and development of Armillaria
gallica, Armillaria tabescens and other fungi in arid
environments are much lower than the development
of tropical rain forest environments.
3.2 The Importance of the Diversity of
Fungal Communities
The rate at which fungi break down can be compared
to the amount of wood the fungus eats, creating
anOlsen model to break down fallen objects:
0
100% 100%
zt
t
P
RP e
P
−
=× = ×
(10)
Among them,
z is the decomposition rate of
garbage,
t
P
is the quality of falling material at the
moment, and
0
P
is the initial mass of falling material.
Among them, RP is the residual rate of withering
material.
A diagram of the amount of withering material
left over from the individual and co-action of chicken
honey ring bacteria, sequined honeycella and other
bacterial species was solved:
Table 1: Mass residual rate after decomposition.
Single
strain
Two
strains
Three
strains
Four
strains
0 1 1 1 1
1 0.95 0.94 0.94 0.93
2 0.89 0.87 0.83 0.85
3 0.83 0.81 0.79 0.69
4 0.77 0.74 0.73 0.53
5 0.71 0.67 0.68 0.47
6 0.65 0.61 0.55 0.32
7 0.59 0.54 0.47 0.27
8 0.53 0.47 0.39 0.19
9 0.47 0.41 0.23 0.13
10 0.41 0.34 0.13 0.08
Based on the above figure, it can be seen that
when Armillaria gallica, Armillaria tabescens and
other fungi act alone, the decomposition rate of
ground drop and wood fiber is slower than that of the
fungus group and the four fungi community. The
quality of the litter More residual rate. For this reason,
the diversity of fungi communities is beneficial to the
Dynamic Decomposition of a Variety of Fungi
865

decomposition of ground litter and wood fiber by
fungi.
4 CONCLUSIONS
As a decomposer in the ecosystem, fungi are also a
key component of the entire planet's carbon cycle.
There are many types and different shapes, and the
environments in which different fungi live are also
diverse. The growth mode of fungi is similar to that
of plants, and the way of nutrient intake is similar to
that of animals. It takes in the nutrients necessary for
life by decomposing organic matter into simple
substances that plants can absorb and use.
In fact, not only do fungi maintain plant
biodiversity in the soil, but plant diversity also acts on
fungi diversity. Studies have shown that fungi
diversity and plant diversity have a significant
positive correlation, and fungi diversity increases, the
fungi community can cooperate with each other to
help plants obtain more resources and nutrients, and
reduce nutrient competition(Wang 2020).
All in all, rich and diverse fungi are an
indispensable part of the earth. Fungi promote the
development of biodiversity in the ecosystem.
Biodiversity is also conducive to the development of
fungi diversity. The two develop in a balanced
manner to form a mutually beneficial and win-win
situation.
ACKNOWLEDGEMENTS
This paper is one of the phased achievements of the
general project of National Natural Science
Foundation of China, "Research on stability analysis
and stabilizing controller design of semi Markov
switched systems" (12071408).
REFERENCES
Jin Qirong, Zhang Jiming, Organic Acid Fermentation
Technology, Beijing: China Light Industry Press, 1989.
Kong Rixiang. Preliminary study on interface microbial
growth model and application.Tianjin University of
Science and Technology, 2001.
LI Yinong, Zhou Xiaomei, Zhang Naili, et al. Research
progress on litter decomposition in terrestrial
ecosystems [J]. Acta Ecologica Sinica, 2016, 36(16):
4977-4987.
Lu Xinping, Cai Yu'e. The role of AM fungi in
ecosystems[J]. Agriculture and Technology, 2016,
36(02): 18.
Tadashi Fukami,Ian A. Dickie,J. Paula Wilkie,Barbara C.
Paulus,Duckchul Park,Andrea Roberts,Peter K.
Buchanan,Robert B. Allen. Assembly history dictates
ecosystem functioning: evidence from wood
decomposer communities[J]. Ecology Letters, 2010,
13(6).
Wang Jianyu, Meng Zexin, Wang Rui, Tian Chen, Wang
Xinyu, Chen Kangli, Wang Zeyu, Hu Tianming, Chen
Wenqing. Regulation of soil fungi diversity on the
relationship between aboveground plant diversity and
productivity in alpine grassland at local scale[J].
Journal of Grassland ,2020,28(06):1498-1507.
Wardle DA. Ecological linkages between abovegroundand
belowground biota. Science,2004,304: 1629-1633.
Xue Dingyu.MATLAB Application Guide, Beijing:
Tsinghua University Press, 1999.
ICBEB 2022 - The International Conference on Biomedical Engineering and Bioinformatics
866
