Fixed-wing UAV Kinematics Model using Direction Restriction for

Formation Cooperative Flight

Yuxuan Fang, Yiping Yao, Feng Zhu* and Kai Chen

College of Systems Engineering, National University of Defense Technology, Changsha 410073, China

* Correspondence: zhufeng@nudt.edu.cn

Keywords: Trajectory Planning, Fixed-wing UAV, Kinematic Model, Formation Flight.

Abstract: Presently, existing fixed-wing UAV kinematics models typically require the planning algorithm to further

smooth the results to meet the trajectory requirements of the starting direction, while the commonly used

formation models often lead to track interference between formation members. In this paper, the formation

cooperative flight of fixed-wing UAVs was modeled. First, the linear velocities in the three-dimensional

direction of the traditional UAV model were changed to a linear velocity along the flight direction of the UAV,

and the turning angular velocities and linear acceleration were set to establish the kinematics model. Then,

based on the "Lead plane-Wingman" formation control structure, the order of friendly aircraft avoidance was

defined by setting the priority of the formation members, and the target point of the wingman was dynamically

calculated according to the target formation and real-time position of the leader plane. Finally, a UAV

formation cooperative flight model was obtained. Considering the formation of five UAVs as an example, a

simulation experiment was carried out, the results of which showed that the trajectory obtained based on the

above model could meet the kinematics and collision avoidance requirements in formation flight of the fixed-

wing UAVs.

1 INTRODUCTION

Presently, unmanned aerial vehicles (UAV) are widely

used in many fields, such as disaster detection, low-

altitude reconnaissance, atmospheric research,

communication relay, disaster area search, and rescue

missions (Qadir et al., 2021; Qu et al., 2014;

Sivakumar & TYJ, 2021). Some of the tasks involved

in these areas have security risks or require long

periods of continuous operation, making them

unsuitable for manned aircraft, contrast to UAVs

(Rajasree & Jisha, 2015). Compared with the rotor

UAV, the fixed-wing UAV has advantages of long

flight distance, long flight time, high speed, and higher

load capacity. It is suitable for missions with long

continuous working hours and high requirements for

airborne equipment (Y. et al., 2021). Currently, the

mission execution capability of a single UAV is

limited, and a UAV formation can improve the

efficiency at which missions are executed. A

reasonable formation can reduce task costs (i.e., by

saving fuel) (Qiannan et al., 2014) and improve

mission execution effectiveness (i.e., by increasing the

search scope) (Seiler et al., 2002). The planning of a

safe and feasible trajectory for each UAV according to

preset formation requirements is an important task in

the current fixed-wing UAV formation research (Gul

et al., 2021; Sharma et al., 2021). Reasonable UAV

kinematics and formation cooperative flight models

can provide appropriate constraints and planning

objectives for the trajectory planning of a UAV

formation (Aggarwal & Kumar, 2020), which makes

the planning results more feasible.

In the trajectory planning of UAVs, owing to

certain limitations of fixed-wing aircraft, including

flight direction and speed, there is a high demand for

flight-path feasibility. The common method is to

consider the UAV as a particle for trajectory planning

purposes and then smooth the results to get a

trajectory that meets the requirements (Huang et al.,

2016; Maini & Sujit, 2016; Sahingoz, 2014). By using

appropriate kinematic models to provide constraints,

the algorithm can consider the requirements of the

UAV in the track starting direction of the planning

process. However, in the scenario of multiple UAVs

flying together, coordination among the UAVs is the

main problem. Changing the UAV formation requires

changing the flight state of each UAV according to the

Fang, Y., Yao, Y., Zhu, F. and Chen, K.

Fixed-wing UAV Kinematics Model using Direction Restriction for Formation Cooperative Flight.

DOI: 10.5220/0011299200003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 92-101

ISBN: 978-989-758-578-4; ISSN: 2184-2841

mission requirements and environmental restrictions.

In this regard, the cooperation of all UAVs required.

That is, the flight trajectory of each UAV cannot be

planned independently. If the planning is based on a

simple formation model, interference of trajectories

can easily occur, which may make members of the

formation collide or result in difficulties maintaining

the target formation. Therefore, the path planning

algorithm must be based on reasonable UAV

kinematics and formation models to ensure feasibility

of the results (Tsourdos et al., 2011).

Based on the flight characteristics of fixed-wing

aircraft, a kinematics model for the fixed-wing UAV

can be established. According to the formation

structure of "Lead plane-Wingman" (Zhu et al., 2017),

the formation cooperation model of the UAV can be

established by designing formation flight rules for

both the lead plane and wingmen. Therefore, a fixed-

wing UAV kinematics model and a UAV formation

cooperative flight model are proposed in this paper.

The main contributions of this study are as follows:

1. A kinematics model for the fixed-wing UAV is

proposed. The linear and turning angular velocities

along the flight direction of the UAV are used to

replace the linear velocity in the three-dimensional

direction of the traditional UAV model, and the linear

acceleration is set, which meet the requirements of the

starting direction of the UAV in the planning results.

2. A UAV formation cooperative flight model is

proposed. Based on the formation structure of "Lead

plane-Wingman", the target points of the wingmen

are updated in real time according to the requirements

of the formation and position of the lead plane in the

process of formation flight. Priority is set for the

members of the formation to specify the order in

which UAVs avoid their teammates.

It should be noted that the situation addressed in

this study is the path planning level of the UAV, which

does not involve the design of the flight control

system at the bottom of the UAV (Y. et al., 2021).

This paper is organized as follows: Section 2

introduces current related research. Sections 3 and 4

introduce the models proposed in this paper. Section

5 presents the verification and experimental analyses.

Section 6 presents the conclusions and future work.

2 RELATED WORK

2.1 Kinematic Modeling of Fixed-wing

UAV

Establishing a kinematics model for the UAV is the

basis for trajectory planning. Feng et al. proposed a

hybrid algorithm that can effectively deal with the

influence of dynamic obstacles. However, due to the

lack of kinematic models for fixed-wing UAVs, its

planning result requires the UAV to avoid obstacles

by hovering first and then making a detour, which is

not a feasible flight trajectory (Feng et al., 2021).

Chen et al. modelled a UAV and used the artificial

potential field method to realize formation flight of

multiple UAVs, but the model does not consider the

flight characteristics of the fixed-wing UAV, which

leads to a large oscillation in the flight path; therefore,

this method is not ideal for the flight trajectory

planning of the fixed-wing UAV (Chen et al., 2015).

Phung and Ha combined many motion parameters of

the UAV as constraints and used a planning algorithm

to obtain the spherical vector-based particle swarm

optimization algorithm, thereby optimizing the track

point; however, this method does not consider the

starting flight direction of the UAV (Phung & Ha,

2021). Manathara and Ghose established a fixed-wing

UAV model to study the problem of multiple aircraft

reaching a destination simultaneously and solved the

constraint condition of the starting direction of the

UAV using Dubins curve (Manathara & Ghose, 2012).

However, the model only considers the direction

constraint of two-dimensional space and requires

UAVs to fly at a fixed speed; therefore, the planning

result based on this model has difficulties meeting the

requirements of UAVs in real scenarios.

2.2 Design of UAV Formation

Cooperative Flight Model

Establishing a UAV formation cooperation model is

important for UAV formation flight safety and

formation adjustment flexibility. Zhang et al.

modelled the formation of fixed-wing UAVs, but the

proposed planning method had few constraints on the

formation control model, resulting in poor

coordination among teammates and lack of flexibility

in formation adjustments (Zhang et al., 2018). Wei et

al. proposed a path planning model for multiple UAVs

based on the ant colony algorithm, but the model does

not study the formation coordination strategy;

therefore, the calculation results based on this model

show that the trajectories among UAVs are

independent and do not have the characteristics of

formation flight (Bai et al., 2021). Zhu et al.

established a multi-aircraft model for the formation

maintenance of multiple UAVs, but the model only

regulates the formation members in the formation

maintenance stage and cannot provide constraints and

planning objectives for the planning algorithm in the

formation assembly stage (Zhu et al., 2017).

Fixed-wing UAV Kinematics Model using Direction Restriction for Formation Cooperative Flight

In summary, regarding meeting the motion

performance constraints of the fixed-wing UAV, the

existing research models have some problems, that is,

the track is not smooth, the initial direction is not

considered, and the speed of the UAV is strictly

limited. In the research of formation flight, some of

the formation models focus on maintaining the

formation, while some prevent multi-aircraft

trajectory conflict by avoiding path crossover.

Therefore, these models have difficulties meeting the

coordination and cooperation requirements of UAVs

in formation flight.

3 KINEMATICS MODELING OF

FIXED-WING UAV USING

DIRECTION RESTRICTION

3.1 Position and Attitude Description of

UAV

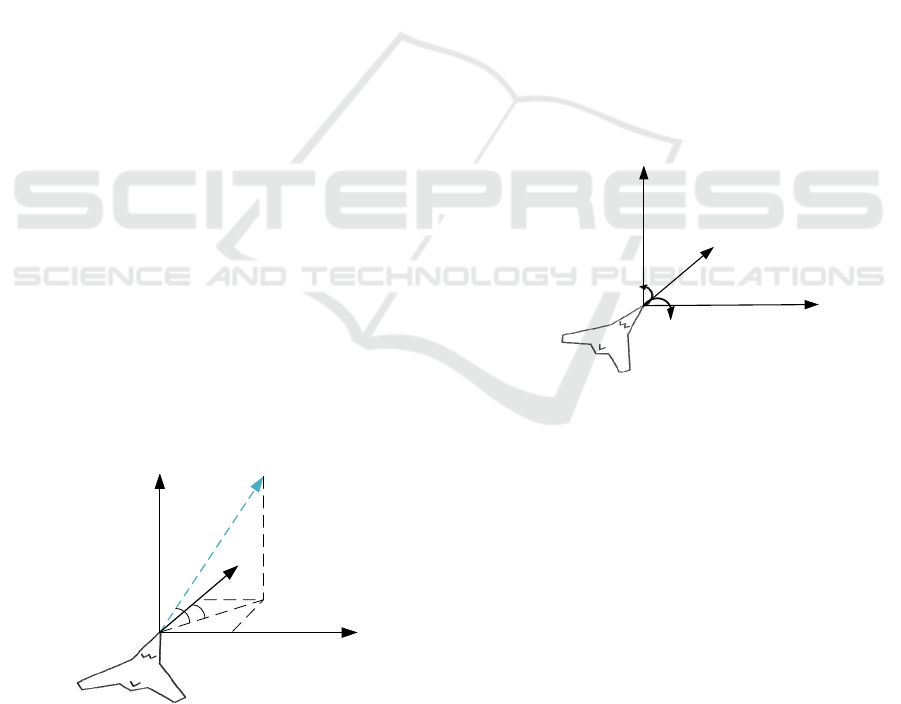
First, it is necessary to describe the position and

attitude of the UAV. A coordinate system that is

relatively stationary to the ground is defined, which is

called an inertial coordinate system (ICS) in this study,

and is marked as 𝑆



𝑜



𝑥



𝑦



𝑧



. As shown in Figure

1, where 𝑜



is a certain point on the ground, 𝑜



𝑥



points in a certain direction of the horizontal plane,

𝑜



𝑥



𝑦



is the horizontal plane, and 𝑜



𝑧



perpendicular to the ground and points to the sky. This

coordinate system conforms to the right-hand rule and

is used to represent the position and attitude of the

UAV in this study. This study focuses on the level of

route planning; therefore, the state matrix, P, of the

UAV in the inertial system is defined as follows:

𝑷=

𝑥𝑦𝑧𝜃𝜓



(1)

Figure 1: Inertial Coordinate System.

where x, y, and z are the coordinate positions of the

UAV in the ICS and 𝜃 and 𝜓 represent the attitude

information of the UAV. 𝜃 is the pitch angle (−𝜋/2≤

𝜃≤𝜋/2), and 𝜓 is the yaw angle (azimuth) (−𝜋≤

𝜓≤𝜋). This study runs at the planning level and does

not consider specific details of the UAV movement

process; therefore, it is not necessary to define the roll

angles of the UAV.

3.2 Motion State Modeling of UAV

based on Direction Restriction

A coordinate system that is relatively stationary to the

UAV is defined, which is called the vehicle coordinate

system (VCS) in this study, and is denoted by

𝑆



(

𝑜



𝑥



𝑦



𝑧



)

, w h e r e 𝑜



is a fixed position on the

UAV at some point in time, 𝑜



𝑥



points in the

direction of the head of the UAV and is in the same

direction during flight, 𝑜



𝑦



is parallel to the

horizontal plane and points to the right side of the

U AV, a n d 𝑜



𝑧



is vertically horizontal and points to

the top of the UAV. This coordinate system conforms

to the right-hand rule and is used to describe the

motion state of the UAV. The motion state matrix of

the UAV in the VCS is expressed as follows:



𝑣



𝑣



𝑣



𝑎



𝑎



𝑎







(2)

𝑣

𝜓

𝑣

Figure 2: Vehicle Coordinate System.

As shown in Figure 2, the linear, pitching angular

and yaw angular velocities of the UAV are denoted by

𝑣



, 𝑣



and 𝑣



, respectively. The linear, pitch angular

and yaw angular accelerations of the UAV are

denoted by 𝑎



, 𝑎



and 𝑎



, respectively.

The following assumptions are made about the

kinematic characteristics of the fixed-wing UAV:

1.The linear acceleration of the UAV is constant,

that is, 𝑎



is constant.

2.The UAV turns at a constant angular velocity.

3.The velocities of the UAV have an upper limit,

and the linear velocity has a lower limit, 𝑣





, which

is greater than 0.

The velocity matrix, 𝑽 , and the acceleration

matrix, 𝒂, are obtained as follows:

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications



𝑽=



𝑣



𝑣



𝑣







𝒂=



𝑎



𝑎



𝑎







(3)

According to the previous hypothesis, the

relationship between the velocity and acceleration is

as follows:

𝑽

(

𝑡



+∆𝑡

)

=

100

000

∙𝑽

(

𝑡



)

𝒇

(𝑡



)∙

∆𝑡00

010

001

∙𝒂

(4)

𝒇

=

𝑓



𝑓



𝑓



 (5)

where 𝑽

(

𝑡



)

is the velocity matrix of the UAV at time

𝑡



, ∆𝑡(s) is the step size of the time advance, and 𝒇 is

the velocity change trend matrix of the UAV. The

values of 𝑓



, 𝑓



,and 𝑓



are selected from 1, 0, and -1,

respectively, according to the requirements of the

planning algorithm at time 𝑡



. Consequently, the

relationship between the position and attitude of the

UAV as well as its velocity are obtained as follows:

⎩

⎪

⎨

⎪

⎧

𝑥=𝑣



cos𝜃 cos𝜓

𝑦=𝑣



cos𝜃 sin𝜓

𝑧=𝑣



sin𝜃

𝜃



=𝑣



𝜓



= 𝑣



(6)

4 PRIORITY AVOIDACE BASED

UAV FORMATION

COOPERATIVE FLIGHT

MODEL

4.1 Description of Formation Location

The formation in this study consists of a lead plane

and several wingmen. The role of the lead plane in the

formation is to lead the formation to fly to the target

area; therefore, the target point of the lead plane is set

in advance. The positions of the wingmen in the target

formation become their local target point, which

changes with the state of the lead aircraft. Therefore,

the target point of a wingman at a certain time must

be determined by the preset formation parameters and

current position and posture of the lead plane.

As shown in Figure 3, considering the V-shaped

formation as an example, the coordinate system

represented by the black solid line is the ICS. The

blue solid line represents a UAV as the lead plane, and

the blue dotted lines represents the local target points

of the wingmen. At this time, the lead plane is located

Wingmen

Lead plane

Figure 3: Method for Determining Wingmen Target Point.

at a certain point in the ICS. The coordinate system,

represented by the blue dotted line, represents the

VCS of the lead plane. If the lead plane is UAV 0, then

the equation for calculating the local target points of

the wingmen at a certain time is as follows:

𝑮



𝑨

𝒗𝒇

∙𝑩

𝒗𝒇

∙

𝑥





𝑦





𝑧











𝑥



𝑦



𝑧







(7)

𝑨

𝒗𝒇

=

cos𝜓



−sin𝜓



sin𝜓



cos𝜓



001

 (8)

𝑩

𝒗𝒇

=

cos𝜃



0sin𝜃



010

sin𝜃



0 cos𝜃



 (9)

where matrix 𝑮



=

𝑥





𝑦





𝑧









is the local target

point of jth wingman (j = 1, 2,…, n) in the ICS, 𝑨

𝒗𝒇

and 𝑩

𝒗𝒇

are matrices that transform coordinates from

the VCS to the ICS, 𝜓



and 𝜃



are the yaw and pitch

angles of the lead plane in the ICS, respectively,



𝑥





𝑦





𝑧









is the target point of a wingman

under the VCS of the lead plane,



𝑥



𝑦



𝑧







i s t h e

position of the lead plane under the ICS.

4.2 Coordination Rules for Formation

Members based on Avoidance

Priority

There may be a risk of collision between UAVs

during flight; therefore, it is necessary to formulate

obstacle avoidance rules for each UAV. The strategy

adopted in this study is to endow each UAV with the

characteristics of the obstacles, including their

position and size. When each UAV is flying towards

its target, the other UAVs are regarded as moving

obstacles.

Fixed-wing UAV Kinematics Model using Direction Restriction for Formation Cooperative Flight

In the UAV flight process, UAVs may avoid each

other in certain cases. Considering the case shown in

Figure 4 as an example, in a certain state, the target

point of Wingman 1, which is on the left, is on the

right, whereas the target point of Wingman 2, which

is on the right, is the opposite, and both wingmen fly

on the same horizontal plane. In this case, Wingman

1 must move in the positive direction of the 𝑜



𝑦



axis

to get close to the target point, whereas Wingman 2

must move in the opposite direction. During flight,

the distance between the two wingmen continuously

decreases. When the distance is sufficiently small, the

two wingmen perform an obstacle avoidance

operation. Because of the particularity of this scene,

the motion characteristics of the two wingmen are

geometrically symmetrical, so they repeatedly avoid

each other. As shown by the black dotted line track in

Figure 4, the wingmen eventually have difficulties

reaching the target points.

Wingman 1

Wingman 2

Target point

of Wingman 1

Target point

of Wingman 2

Lead plane

Figure 4: Mutual avoidance between wingmen.

To solve this problem, in this study, the avoidance

strategy of formation members is designed by setting

priority. In the initial setup, before the beginning of

the planning, the members of the formation are

numbered, and the order in which each UAV avoids

the others is defined according to the principle that

the priority decreases as the number increases.

According to this rule, in the case shown in Figure 4,

Wingman 1 only has to avoid the lead plane, whereas

Wingman 2 has to avoid the captain and Wingman 1.

Using this rule, the trajectories of the two wingmen

entering the avoidance phase can be obtained, as

shown by the blue dotted line in Figure 4.

5 SIMULATION RESULTS AND

ANALYSIS

The formation designed in this study consisted of five

fixed-wing UAVs, comprised of one lead plane and

four wingmen. This stipulates that all UAVs are

isomorphic (i.e., the performance is the same). The

performance parameters are listed in Table 1.

Table 1: Performance Parameter.

Parameter Type Value

UAVs'𝑅



(

𝑚

)

Initial 𝑣



(

𝑚𝑠

⁄)

100

𝑎



(𝑚/𝑠



)

10 (

𝑓



>0)

40 (

𝑓



<0)

𝑎



(

𝑟𝑎𝑑 𝑠

⁄)

𝜋/6

𝑎



(

𝑟𝑎𝑑 𝑠

⁄)

𝜋/6

Speed range

300≥𝑣



≥100

(

𝑚𝑠

⁄)

𝜋/6 ≥ 𝑣



≥−𝜋/6

(

𝑟𝑎𝑑 𝑠

⁄)

𝜋/6 ≥ 𝑣



≥−𝜋/6

(

𝑟𝑎𝑑 𝑠

⁄)

where 𝑅



is the collision radius of the UAV, that is,

the distance between the UAV and other obstacles

must not be less than 𝑅



; otherwise, it is considered

that the UAVs have collided.

5.1 Simulation Experiment of the

Kinematic Model of Fixed-wing

UAV

In this section, the simulation experiments based on

the fixed-wing UAV kinematics model proposed in

this paper, carried out to verify the rationality of the

trajectory planning results, are presented. In the

mission scene of the experiment, after dynamic

adjustment in the process of flying in the

predetermined direction, the five fixed-wing UAVs

fly to the new target area according to the newly

specified formation.

Based on the traditional UAV kinematics model

(Feng et al., 2021; Goerzen et al., 2010) and fixed-

wing UAV kinematics model proposed in this paper,

trajectory planning was carried out from the preset

starting point, and the trajectories near the starting

point of the UAV formation in three different initial

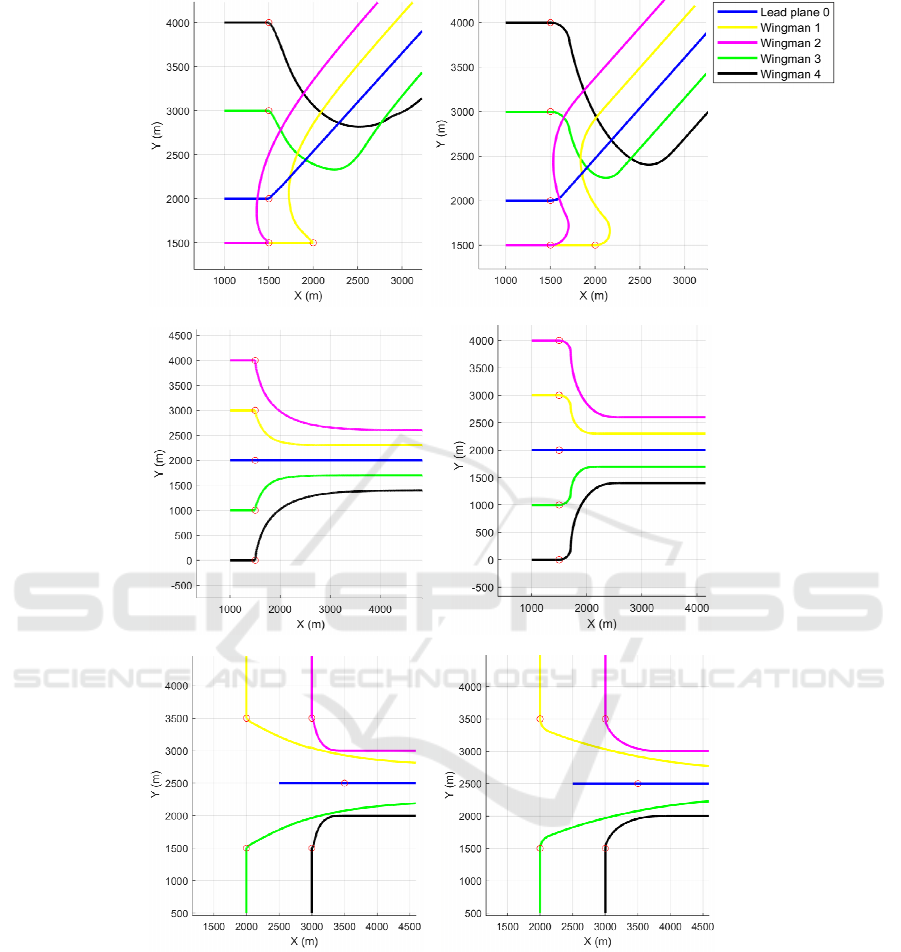
scenes were obtained, as shown in Figure 5. The red

circle in the picture is the starting point for the

formation of the UAVs. It can be deduced from the

figure that because the traditional UAV kinematics

model only considers the position of the UAV in the

constraints of the trajectory planning algorithm, the

resulting track requires the UAV to turn from a large

angle at the starting point of the planning.

Considering the pink and yellow tracks in Figure 5(a)

as an example, the initial direction of the planned

flight trajectory deviates greatly from the original

flight direction of the UAV, which is not in line with

the actual flight situation of the fixed-wing UAV.

However, the kinematics model proposed in this

paper considers not only the position constraints of

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

(a) (b)

(e) (f)

Figure 5: Trajectories generated based on the traditional model and the model proposed in this paper. (a, c, and e): traditional

model; (b, d, and f): model proposed in this paper).

the UAV, but also the direction adjustment restrictions

of the UAV; therefore, the resulting track is more

continuous and more in line with the actual flight

situation of the UAV

5.2 Simulation Experiment of the UAV

Formation Cooperative Flight

Model

This section presents the simulation experiments

carried out in several scenes to verify the feasibility

of the UAV formation cooperative flight model

Fixed-wing UAV Kinematics Model using Direction Restriction for Formation Cooperative Flight

(a)

(b)

(c)

(d)

Figure 6: Trajectory planning based on the UAV formation cooperative flight model.

proposed in this paper, including teammates collision

avoidance rules and formation flight ability.

Figure 6 shows the trajectory planning results of

each fixed-wing UAV, from the specified starting

point to the target point in four scenarios. Figures

6(a)–(c) show the trajectory planning results of the

formation members from different starting points and

directions. Figure 6(d) shows the flight trajectory

planning results of the UAV formation flight from the

original formation to their respective target points.

From the figure, we can observe that the tracks of

some formation members have crossed, which is a

relatively common situation in the actual environment

and requires the coordination of various UAVs to

prevent interference or conflict in trajectory planning.

The UAV formation cooperative flight model

proposed in this paper sets priority rules for formation

members to avoid conflict among them. Therefore,

when planning based on the model, if there is a

trajectory conflict, a flight path for avoiding the

teammate is planned according to the priority order.

As shown in Figure 6, the UAVs represented by

different color tracks have different priorities;

therefore, they avoid teammates that have proprieties

higher than their own and form a specified formation

or fly to their designated target area through a safe

flight trajectory. This verifies the feasibility of the

model proposed in this paper.

5.3 Comprehensive Simulation

Experiment

In this section, the artificial potential field method is

used to test the fixed-wing UAV kinematics model

and UAV formation cooperative flight model

proposed in this paper, thereby verifying that the

planning results based on these models are feasible

and can meet the collision avoidance requirements

among teammates.

According to the performance parameters

specified in Table 1, the flight trajectory planning

results of the formation flight and decentralization

process of five fixed-wing UAVs are shown in figure

7. Each UAV forms a target formation from the circle

in the figure and then flies in formation for a period

of time.

Figure 7: Formation flying and decentralization trajectory

planning of UAVs.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

Finally, the UAVs decentralize at the square box

in the figure and fly to their respective target areas

(triangle in the figure). As can be seen from the figure,

the algorithm is solved based on the kinematics model

for fixed-wing UAVs. Therefore, the generated

trajectory considers the initial flight direction of each

UAV, and the trajectory curve can better meet the

constraints of the trajectory tracking for fixed-wing

UAVs under actual conditions.

Figure 8 shows the distance between the wingmen

and the target points during the formation flight stage.

In this stage, the target point of each wingman is set

by the multi-UAV formation cooperative model

according to the position of the lead plane. As can be

seen from the figure, the wingmen fly from their

starting points to their respective target points.

Eventually, all the wingmen form a target formation

and continue to fly in formation with the lead plane.

Figure 9 shows the minimum distance among the

members of the formation and other UAVs during the

flight process. In the initial stage, the wingmen must

adjust their flight direction at a large angle to

assemble to the lead plane, so the distances among the

members of the formation changes abruptly.

Subsequently, the UAVs formed the designated

formation, and the distances among the members of

the formation remained stable. For approximately 25

s, as can be observed in the figure, the UAVs spread

out and flew to their respective target areas.

Figure 8: The situation of wingmen following the target points during the formation flight stage.

Figure 9: Minimum distance among formation members and teammates.

Fixed-wing UAV Kinematics Model using Direction Restriction for Formation Cooperative Flight

According to the setting in Table 1, the distances

among the UAVs should not less than 100 m. The

planning results show that the minimum distance

between each UAV and teammates is more than 100

m (red dotted line in the figure) during the entire flight,

and the UAVs can maintain a stable distance until the

formation is broken.

Thus, it can be observed that the fixed-wing UAV

kinematics model proposed in this paper can provide

constraints for the trajectory planning algorithm and

can meet the requirements of fixed-wing UAVs in a

real environment. Furthermore, it can effectively

provide the planning objectives and coordination

strategies of each UAV for the trajectory planning

algorithm, thereby improving formation flight and

meeting the requirements for collision avoidance

among teammates.

6 CONCLUSIONS

In this paper, considering the motion characteristics

of fixed-wing aircraft, a kinematic model suitable for

fixed-wing UAV was established. Subsequently,

based on the formation structure of "Lead plane-

Wingman", a UAV formation cooperative flight

model was established. Through a comparative

experiment with the traditional model, it was verified

that the fixed-wing UAV kinematics model can better

meet the motion constraints of the fixed-wing UAV.

Through simulation experiments using multiple

scenes, it was verified that the UAV formation

cooperative flight model can provide a processing

strategy for the cooperation and collision avoidance

among UAVs. Finally, through a complex mission

scene, it was verified that the planning results of a

multi-UAV flight based on the model proposed in this

paper can meet the flight trajectory feasibility and

collision avoidance requirements among teammates

during formation flight. The above experiments

showed that the model proposed in this paper can

provide the basis for the research on the formation

flight trajectory planning of the fixed-wing UAV.

However, the influences of the complexity of the

kinematics model and different collision avoidance

priority combinations on the planning algorithm and

planning results, respectively, were not investigated

in this study. In the future work, optimization of the

fixed-wing UAV formation model and a formation

emergency handling strategy will be investigated.

ACKNOWLEDGEMENTS

This research was funded by the National Natural

Science Foundation of China (no. 61903368).

REFERENCES

Aggarwal, S., Kumar, N. (2020). Path planning techniques

for unmanned aerial vehicles: A review, solutions, and

challenges. Computer communications, 149, 270–299.

Bai, X., Jiang, H., Cui, J., Lu, K., Chen, P., Zhang, M.

(2021). UAV path planning based on improved A∗ and

DWA algorithms. International journal of aerospace

engineering, 2021, 1–12. http://doi.org/10.1155/

2021/4511252

Chen, Y., Yu, J., Su, X., Luo, G. (2015). Path planning for

multi-UAV formation. Journal of intelligent & robotic

systems, 77(1), 229–246. http://doi.org/10.1007/

s10846-014-0077-y

Feng, J., Zhang, J., Zhang, G., Xie, S., Ding, Y., Liu, Z.

(2021). UAV dynamic path planning based on obstacle

position prediction in an unknown environment. IEEE

Access, 9, 154679–154691. http://doi.org/10.1109/

ACCESS.2021.3128295

Goerzen, C., Kong, Z., Mettler, B. (2010). A survey of

motion planning algorithms from the perspective of

autonomous UAV guidance. Journal of intelligent and

robotic systems, 57(1–4), 65–100. http://doi.org/

10.1007/s10846-009-9383-1

Gul, F., Mir, I., Abualigah, L., Sumari, P., Forestiero, A.

(2021). A consolidated review of path planning and

optimization techniques: Technical perspectives and

future directions. Electronics, 10(18), 2250.

http://doi.org/10.3390/electronics10182250

Huang, L., Qu, H., Ji, P., Liu, X., Fan, Z. (2016). A novel

coordinated path planning method using k-degree

smoothing for multi-UAVs. Applied soft computing, 48,

182–192. http://doi.org/10.1016/j.asoc.2016.06.046

Maini, P., Sujit, P. B. (2016). Path planning for a UAV with

kinematic constraints in the presence of polygonal

obstacles. 2016 International Conference on Unmanned

Aircraft Systems (ICUAS).

Manathara, J. G., Ghose, D. (2012). Rendezvous of multiple

UAVs with collision avoidance using consensus.

International journal of aerospace engineering

http://doi.org/10.1061/(ASCE)AS.1943

Phung, M. D., Ha, Q. P. (2021). Safety-enhanced UAV path

planning with spherical vector-based particle swarm

optimization. Applied soft computing, 107, 107376.

http://doi.org/10.1016/j.asoc.2021.107376

Qadir, Z., Ullah, F., Munawar, H. S., Al-Turjman, F. (2021).

Addressing disasters in smart cities through UAVs path

planning and 5G communications: A systematic review.

Computer communications, 168, 114–135.

http://doi.org/10.1016/j.comcom.2021.01.003

Qiannan, Z., Ziyang, Z., Chen, G., Ruyi, D. (2014). Path

planning of UAVs formation based on improved ant

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

100

colony optimization algorithm. Paper presented at the,

Yantai.

Qu, Y., Zhang, Y., Zhang, Y. (2014). Optimal flight path

planning for UAVs in 3-D threat environment. Paper

presented at the.

Rajasree, R., Jisha, V. R. (2015). Optimal formation control

of unmanned aerial vehicles with reconfiguration.

Paper presented at the 2015 International Conference

on Control, Communication & Computing, Trivandrum

India.

Sahingoz, O. K. (2014). Generation of bezier curve-based

flyable trajectories for multi-UAV systems with parallel

genetic algorithm. Journal of intelligent & robotic

systems, 74(1–2), 499–511. http://doi.org/10.1007/

s10846-013-9968-6

Seiler, P., Pant, A., Hedrick, K. (2002). Analysis of bird

formations. Paper presented at the.

Sharma, A., Shoval, S., Sharma, A., Pandey, J. K. (2021).

Path planning for multiple targets interception by the

swarm of UAVs based on swarm intelligence algorithms:

A review. Technical review - IETE, 1–23.

http://doi.org/10.1080/02564602.2021.1894250

Sivakumar, M., TYJ, N. M. (2021). A literature survey of

unmanned aerial vehicle usage for civil applications.

Journal of aerospace technology and management, 13

http://doi.org/10.1590/jatm.v13.1233

Tsourdos, A., White, B., Shanmugavel, M. (2011).

Cooperative Path Planning of Unmanned Aerial

Ve hi cl es . A John Wiley and Sons, Ltd., Publication.

Wang, Y., Yue, Y., Shan, M., He, L., Wang, D. (2021).

Formation reconstruction and trajectory replanning for

multi-UAV patrol. IEEE/ASME Transactions on

Mechatronics, 26(2), 719–729. http://doi.org/

10.1109/TMECH.2021.3056099

Zhang, J., Yan, J., Zhang, P. (2018). Fixed-wing UAV

formation control design with collision avoidance based

on an improved artificial potential field. IEEE Access,

6, 78342–78351. http://doi.org/10.1109/

ACCESS.2018.2885003

Zhu, X., Zhang, X., Yan, M., Qu, Y. (2017). Three-

dimensional formation keeping of multi-UAV based on

consensus. Journal of central south university, 24(6),

1387–1395. http://doi.org/10.1007/s11771-017-3543-4

Fixed-wing UAV Kinematics Model using Direction Restriction for Formation Cooperative Flight

101