
New Quantum Strategy for MIMO System Optimization
Mohammed R. Almasaoodi
1,2 a
, Abdulbasit M. A. Sabaawi
1,3 b
, Sara El Gaily
1c
and Sándor Imre
1d
1
Department of Networked Systems and Services, Budapest University of Technology and Economics,
Műegyetem rkp. 3., H-1111 Budapest, Hungary
2
Kerbala University, Kerbala, Iraq
3
College of Electronics Engineering, Ninevah University, Mosul, Iraq
Keywords: Quantum Computing, MIMO, Constrained Quantum Optimization Algorithm, Water Filling Algorithm,
Exhaustive Algorithm, Binary Searching Algorithm.
Abstract: Co-channel interference and noise power could affect the performance of the MIMO system and can be
evaluated with respect to the user’s signal to noise and interference ratio. As a result, the desired transmission
rate of the users could be satisfied by consuming more transmit power. Owing to this, a quantum optimization
strategy can be utilized in order to minimize the transmit power, as well as to achieve an optimum trade-off
within the throughput and the resulting interference and noise. In this study, a constrained quantum
optimization algorithm (CQOA) has been implemented in the MIMO-downlink system to reduce the transmit
power and computational complexity. An analytical study is conducted along with a comparison between the
water filling algorithm-based binary searching algorithm (WFA-BSA), exhaustive algorithm-based water
filling algorithm (EWFA), and the CQOA. Finally, simulation results show that the aforementioned methods
consume similar total transmit power, however, the computational complexity of the quantum strategy is
dramatically low compared to the other methods.
1 INTRODUCTION
The next 5G and 6G wireless communication
networks are expected to support the massive
exponential augmenting number of devices (Eid et al.,
2021; Dung et al., 2020). The multiple-input and
multiple-output (MIMO), a promising essential
method in 5G and 6G wireless communication,
boosts system throughput by increasing the number
of channels thanks to the adoption of multiple
transmit and receive antennas. The MIMO exploits
the power of multipath propagation to send and
receive simultaneously multiple data signals over the
same radio channel and space-time (Ahrens et al.,
2014; Marosits et al., 2021).
It is expected that the total number of 5G devices
will reach 13.1 million in 2025 (Report, 2021).
Merging 5G and MIMO technologies will lead to
a
https://orcid.org/0000-0003-1251-6314
b
https://orcid.org/0000-0002-9377-267X
c
https://orcid.org/0000-0001-7125-5236
d
https://orcid.org/0000-0002-2883-8919
deploying a massive number of base stations, which
will dramatically increase the power consumption by
1000 times (Johnson, 2018). For this sake,
information and communication technologies (ICTs)
working on leveraging this enormous energy usage.
Beside the high-power usage, MIMO systems suffer
from high computational complexity as the number of
antennas grows (Kyosti and Jamsa, 2007). To that
end, new cutting-edge technologies have emerged as
alternative solutions for increasing the transmission
rate of 5G and 6G wireless technologies, as well as
augmenting the signal-to-noise ratio, such as quantum
computing, quantum machine learning, etc.
The aim of these newly emerged technologies is
to lower the computational complexity and provide an
exponential speed over classical computers, as well
as increasing the accuracy of the obtained solutions.
Quantum computing proposes its capabilities as a
new futuristic alternative solution for MIMO systems
Almasaoodi, M., Sabaawi, A., El Gaily, S. and Imre, S.
New Quantum Strategy for MIMO System Optimization.
DOI: 10.5220/0011305100003286
In Proceedings of the 19th International Conference on Wireless Networks and Mobile Systems (WINSYS 2022), pages 61-68
ISBN: 978-989-758-592-0; ISSN: 2184-948X
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
61
in order to achieve high throughput and reduce both
the transmit power and the computational complexity.
In the present study, a constrained quantum
optimization algorithm (CQOA) for the downlink
MIMO system is implemented in order to minimize
the transmit power consumption with respect to the
target transmission rate of the user. To validate the
efficiency of the proposed quantum strategy, the
performance of the CQOA is compared with the
water filling algorithm-based binary searching
algorithm (WFA-BSA) and the exhaustive search-
based water filling algorithm (EWFA) in terms of
overall transmit power consumption and
computational complexity.
The remainder of the paper is organized as
follows: Section 2 describes the downlink MIMO
system where the flat fading channel is considered.
Section 3 introduces the implementation of the WFA-
BSA, EWFA, and CQOA. A computational
complexity analysis of the presented algorithms is
then conducted. Section 4 estimates the essential
stochastic parameter for running the binary searching
algorithm (BSA) embedded in the WFA-BSA and
CQOA. Section 5 demonstrates the efficiency of the
proposed quantum solution using simulation results.
Finally, a summary and future plans are included in
Section 6.
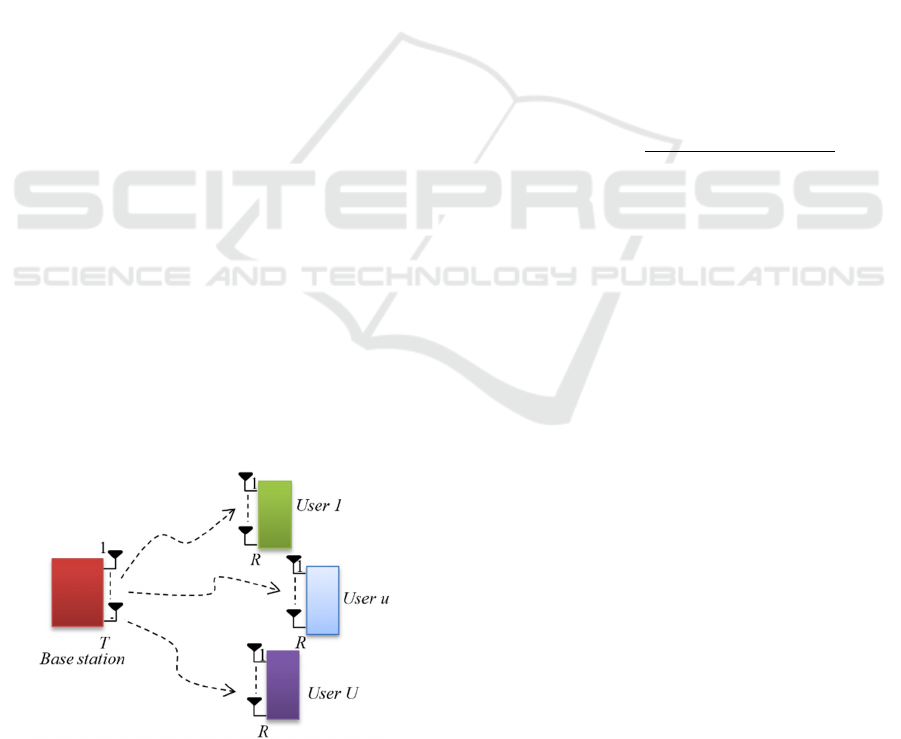
2 MIMO SYSTEM
A downlink MIMO system is considered, where a flat
fading is assumed. This model contains one base
station equipped with T antennas. Assuming that the
total number of users is U, each of them has R receive
antennas, as shown in Figure 1. Full knowledge about
the channel state information at both the receiver and
the transmitter sides is assumed.
Figure 1: A MIMO system has one base with T transmit
antennas and U users with an R receive antennas.
Let 𝒙
be the signal transmitted to the user 𝑢 such as,
𝒙
=
𝑥
,…,𝑥
(1)
The user u receives the signal 𝒚
()
,
𝒚
()
=𝑯
𝒙
+𝒏+𝛾𝑯
𝒙
(2)
where,
• 𝛾 is the scaling factor that describes the
interference ratio of the interferer users.
• 𝑯
refers to the channel state that is linked to
user u. Note that the channel pair is denoted by
subscripts (𝑟,𝑡) such that 𝑟 and 𝑡 refer to
receive and transmit antenna, respectively. The
coefficients of the matrix 𝐻
are represented
as
ℎ
,
()
.
• 𝒏 denotes the noise vector. All channels have
an identical power noise denoted 𝑛
.
•
∑
𝑯
𝒙
refers to the interference exercises
by the other remaining users.
The maximum transmission rate desired by user u is
given as,
𝐵
,
(
)
=𝐷∗𝑙𝑜𝑔
1 +
𝑔
,
()
𝑝
,
()
𝛾
∑
𝑔
,
()
𝑝
,
()
+ 𝑛
(3)
where the parameters D and 𝑔
,
()
refer to the
bandwidth and the channel gain, respectively, such
that
𝑔
,
()
=
ℎ
,
()
2
. The parameter
𝑝
,
(
)
denotes
the power usage of user u in the channel link (r,t).
One can easily verify that the total bit rate
associated with user u can be expressed as,
𝐵
()
=𝐵
,
()
.
(4)
Now we are in a position to express mathematically
the optimization problem. The aim is to select the best
optimum minimum overall transmit power with
respect to the bit rate target of the given user 𝐵
,
𝑚𝑖𝑛
𝑝
𝑟,𝑡
(
𝑢
)
𝑅
𝑟=1
𝑇
𝑡=1
𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 𝐵
(𝑢)
≥𝐵
𝑡𝑎𝑟𝑔𝑒𝑡
𝑢
∀𝑟,𝑡
𝑝
𝑟,𝑡
(
𝑢
)
≥0
(5)
3 ALGORITHMS
In the light of what has been discussed in Section 1.
One may conclude that among classical search and
WINSYS 2022 - 19th International Conference on Wireless Networks and Mobile Systems
62

optimization methods that have been extensively
extended and explored in improving the power
consumption of MIMO systems are: the water filling
algorithm (WFA), and the exhaustive algorithm (EA).
As commonly known, computational complexity
stands as a crucial pillar in selecting the best
optimization strategy for the given desired
optimization problem. This section introduces the
CQOA and compares the performance of the
aforementioned traditional algorithms with the
CQOA in terms of computational complexity.
In the sequel, each optimization strategy was
presented, followed by an implementation in the
proposed MIMO system.
3.1 WFA-BSA Implementation
The problem of reducing the total transmit power
usage subject to the desired transmission rate of a
certain user u can be solved by iterating over the
possible total power transmit using the binary
searching algorithm (BSA) (Knuth, 1998), and
applying the water filling algorithm with respect to
the candidate possible total transmit power selected
by the BSA, this new method called water filling
algorithm-based binary searching algorithm (WFA-
BSA). For this sake, deriving an appropriate solution
for (5) using the Karush–Kuhn–Tucker (KKT)
conditions is necessary. Reformulates the problem in
(5) yields,
𝑚𝑖𝑛𝑝
𝑟,𝑡
(
𝑢
)
𝑅
𝑟=1
𝑇
𝑡=1
𝑠𝑢𝑏𝑗𝑒𝑐𝑡 𝑡𝑜 −𝐵
(𝑢)
+𝐵
𝑡𝑎𝑟𝑔𝑒𝑡
𝑢
≤0
∀𝑟,𝑡 −𝑝
𝑟,𝑡
(
𝑢
)
≤0
(6)
The optimization problem stated in (6) is convex.
Thus, the KTT conditions can be implemented.
To solve the problem in (6), the Lagrangian
function for the optimization problem in (6) (denoted
by M) is constructed as,
𝑀= 𝑝
,
(
)
+𝑎∗−𝐵
(
)
+𝐵
−𝛽
,
∗𝑝
,
(
)
(7)
where𝑎 and
𝛽
,
refer to the Lagrangian multipliers.
Assuming that𝑝
,
(
)
≥0, the optimal solution can be
expressed as,
𝜕𝑀
𝜕𝑝
,
(
)
=0 𝑖𝑓𝑝
,
(
)
>0
𝜕𝑀
𝜕𝑝
,
(
)
≤0 𝑖𝑓𝑝
,
(
)
=0
(8)
According to the complementary slackness
∀𝑟,𝑡
𝛽
𝑟,𝑡
∗ 𝑝
𝑟,𝑡
(
𝑢
)
=0, this states that either
𝑝
,
(
)
=0 or 𝛽
,
=0, which means that if 𝑝
,
(
)
>0,
then
𝛽
,
=0. This can be easily verified as,
𝑝
,
(
)
∗
=𝑎𝐷−
𝛾
∑
𝑔
,
()
𝑝
,
()
+ 𝑛
𝑔
,
()
(9)
Let’s assume that 𝐼
∑
𝑔
,
()
𝑝
,
()
,
, where
the parameter 𝐼
denotes the co-channel interference
resulting from the remaining users 𝑣. The parameter
𝑝
,
(
)
∗
denotes the power usage of user u of the
channel link (r,t). It is considered that all channels
have identical power noise called 𝑛
. Note that 𝑥
≔
𝑚𝑎𝑥
(
𝑥,0
)
.
The value of 𝑎∗𝐷 describes the water level. For
finding the optimal minimum power transmission
with respect to the transmission rate of the user, the
WFA-BSA can be applied, which is explicitly
presented as follows,
1. We start with 𝐿 = 0: 𝑃
=𝑃
, 𝑃
=
𝑃
, and ∆𝑃=𝑃
−𝑃
2. 𝐿 = 𝐿 + 1
3. 𝑃
= 𝑃
+
4. 𝑓𝑙𝑎𝑔=𝑊𝐹𝐴 𝑃
,
:
• if 𝑓𝑙𝑎𝑔=𝑌𝑒𝑠, then 𝑃
,
=𝑃
,
𝑃
,
=𝑃
,
• Else 𝑃
,
=𝑃
,
, 𝑃
=𝑃
.
5. If L < 𝑙𝑜𝑔
(𝐺), then go to 2, else stop, then
𝑦
= 𝑃
The function 𝑊𝐹𝐴 𝑃
,
returns an answer to
whether the actual selected candidate for the total
transmit power satisfies the target transmission rate of
the given user or not given that G denotes the
maximum number of steps required to run the BSA.
More details about the WFA function will be
discussed in Section 3.4.
New Quantum Strategy for MIMO System Optimization
63

3.2 EA Implementation
To sort out the antenna combination that gives back
the optimum minimum overall transmit power of the
MIMO system, the exhaustive search method
examines all possible solutions resulting from all
transmit and receive antenna combinations. The EA
gives back an exact and accurate optimum solution.
In contrast, the EA iterates over all possible total
transmit scenarios which are computationally hard.
A special question arises if one is interested in
implementing the EA in the MIMO system described
in Section 2. In this case, the EA will be unable to
perform an appropriate distribution of power among
channels because the optimal decisions are based on
the interference and noise resulting from channels. To
solve this problem, one may extend the capabilities of
the EA by merging the exhaustive search and the
WFA. This new algorithm is called the exhaustive
search-based water filling algorithm (EWFA). The
EWFA iterates over the possible candidate for the
total transmit power scenarios and apply the water
filling method, the optimum minimum transmit
power is selected once the desired transmission rate
𝐵
is met.
3.3 CQOA Implementation
The CQOA (El Gaily and Imre, 2021) seeks the best
extreme value of a constrained goal function (or an
unsorted database). Its efficiency stems from the
combination of two methods: The BSA and the
constrained quantum relation testing (CQRT), which
is an extended version of the quantum relation testing
function (Imre, 2005; Imre, 2007). The CQRT gives
a clear indication into whether there exist at least one
or more database entries with respect to the applied
optimization problem type (minimization or
maximization of the goal function) of the reference
value, and the constraint C in a certain region of the
database. More details are given in (El Gaily and
Imre, 2021). The detailed algorithm is explicitly
shown below,
1. We start with 𝑆 = 0 : 𝑃
=
𝑃
, 𝑃
=𝑃
, and ∆𝑃=𝑃
−
𝑃
2. 𝑆 = 𝑆 + 1
3. 𝑃
= 𝑃
+
4. 𝑓𝑙𝑎𝑔=𝐶𝑄𝑅𝑇
(
𝑃
,𝑅,𝐶
)
:
• if 𝑓𝑙𝑎𝑔=𝑌𝑒𝑠, then 𝑃
,
=𝑃
,
𝑃
,
=𝑃
,
•
• Else 𝑃
=𝑃
, 𝑃
=𝑃
5. If S < 𝑙𝑜𝑔
(𝐺), then go to 2, else stop and
𝑦
= 𝑃
where the CQRT function has the following inputs,
which are defined as follows,
• 𝑃
: The newly actual updated mean value
of the total transmit power selected by the
BSA.
• 𝑅 : The index relation defines the
optimization type whether it is unconstraint or
constraint optimization. More details about the
setup of the symbol R are described in (El
Gaily and Imre, 2021). As the optimization
problem presented in (5) describes a
minimization of the total transmit power of the
MIMO system, the index relation R will be
assigned the symbol “≤”.
• 𝐶 : The function's constraint parameter.
According to the problem defined in (5), 𝐶=
𝐵
𝑡𝑎𝑟𝑔𝑒𝑡
𝑢
.
The CQRT allows the BSA to be adapted to work
with an unsorted database while maintaining high
speed and accuracy, which is why the CQOA
outperforms its traditional optimization counterpart.
The quantum phase estimation approach (Imre, 2005;
Imre, 2007; Imre and Balázs, 2005) is used to derive
the CQRT's power.
3.4 Computation Complexity Analysis
In search and optimization problems, computational
complexity plays a crucial role in selecting the best
optimization strategy for the given desired problem.
Thus, this section is devoted to compare the
performance of the WFA, EWFA, and CQOA in
terms of computational complexity.
Let 𝑁 denote the total number of channels, where
𝑁=𝑅∗𝑇. The implementation methodology of the
WFA-BSA in the proposed optimization problem is
described as follows: First, preparing the search space
(database entries), which represents all the possible
total transmit power scenarios of the BSA, where the
size space refers to the maximum number of steps G
needed to run the BSA (The computational
complexity of the BSA is 𝑙𝑜𝑔
(
𝐺
)
steps). The WFA
function is then applied. Note that the WFA sorts the
channels in an ascending manner with respect to the
WINSYS 2022 - 19th International Conference on Wireless Networks and Mobile Systems
64

resulting noise and interference power (The
computational complexity of the best classical sorting
method is known to be 𝑂𝑁𝑙𝑜𝑔
(
𝑁
)
steps). The
WFA selects the best optimum power that satisfies
the desired transmission rate𝐵
. For this purpose,
it is worthwhile to repeatedly remove the channel
with the highest interference and noise power when
the 𝐵
is not met and re-apply the WFA function.
The computational complexity of this operation is
𝑂
(
𝑁
)
steps, whereas the computational complexity
of the WFA-BSA is 𝑂𝑁
𝑙𝑜𝑔
(
𝑁
)
𝑙𝑜𝑔
(
𝐺
)
steps.
The EWFA's working methodology is similar to
that of the WFA-BSA with the exception that the
BSA is replaced by an exhaustive search. One can
conclude that the EWFA's computational complexity
is 𝑂𝐺𝑁
𝑙𝑜𝑔
(
𝑁
)
steps.
The computational complexity of the CQOA is
𝑂
𝑙𝑜𝑔
(
𝐺
)
𝑙𝑜𝑔
√
𝑁
(El Gaily and Imre, 2021).
On the other hand, the computational complexities of
the aforementioned strategies are listed in Table 1.
Table 1: The computational complexities of the
aforementioned optimization algorithms.
Methods Computational complexity
EWFA 𝑂𝐺𝑁
𝑙𝑜𝑔
(
𝑁
)
WFA-BSA 𝑂𝑁
𝑙𝑜𝑔
(
𝑁
)
𝑙𝑜𝑔
(
𝐺
)
.
CQOA 𝑂
𝑙𝑜𝑔
(
𝐺
)
𝑙𝑜𝑔
√
𝑁
.
4 CONFIGURATION OF THE
BSA
In the previous section, it was demonstrated that
estimating the value of G is very important for
running the BSA (embedded in the WFA and CQOA)
and the EA. This study estimates the value of G where
the co-channel interference is neglected. The
stochastic parameter G is strongly connected to the
maximum transmission power 𝑃
that can be
consumed by the MIMO system, as well as the
minimum difference between two different possible
transmit power scenarios denoted
𝛼. One reads the
value of G as,
𝐺=
𝑃
− 𝑃
𝛼
(10)
where 𝑃
denotes the minimum transmit power
consumed by the MIMO system. The parameter 𝛼
can be expressed as,
𝛼=min
,
𝑃
−𝑃
,
(11)
where 𝑃
and 𝑃
refer respectively to the total transmit
power of the possible scenarios 𝑖 and 𝑗 . The
expression of 𝑃
can be given as,
𝑃
=
∑∑
𝜆
−
,
,
(12)
where
λ
is the water level of the possible transmit
power of the 𝑖
scenario, note that λ
=𝑎
∗𝐷,
where 𝑎
refers to the obtained Lagrangian
coefficient of the 𝑖
scenario. On reads the
expression of 𝛼 as,
𝛼=𝑚𝑖𝑛
,
∑∑
𝜆
−
,
−
∑∑
𝜆
−
,
,
(13)
It is important to note that the power noise
summarized in the coefficient
,
of the channels
are sorted, before applying the 𝑊𝐹𝐴 𝑃
,
function described in Section 3.1. Moreover, it is
worth mentioning that the selected channels for each
scenario depend tightly on the coefficient
,
.
Let 𝑆
and 𝑆
be the set of channels chosen
respectively in the 𝑖
and 𝑗
scenarios. We consider
𝑆
the complement of 𝑆, such as 𝑆=𝑆
∩𝑆
. One can
define 𝑃
− 𝑃
as,
𝑃
−𝑃
=𝜆
−𝜆
+
𝑛
𝑔
,
−
𝑛
𝑔
,
(14)
It is clearly noticed that the coefficient
∑∑
𝜆
describes the number of channels for the 𝑖
scenario
multiplied by
𝜆
. One then reads,
𝜆
=𝑛
𝜆
(15)
where
𝑛
refers to the total number of channels in the
case of the 𝑖
scenario. In addition, it can be noticed
that the expression given in (16) is connected to
constant coefficients such as 𝑛
, 𝑔
,
, and 𝑔
,
.
𝑛
𝑔
,
−
𝑛
𝑔
,
(16)
Eq. (16) can be reformulated as the sum of
coefficients
belonging to 𝑆
channels set. The
expression of 𝑃
− 𝑃
can be re-expressed as,
New Quantum Strategy for MIMO System Optimization
65

𝑃
− 𝑃
= 𝑛
𝜆
− 𝑛
𝜆
+
𝑛
𝑔
∈
(17)
where 𝑔
represents the 𝑘
channel belonging to 𝑆
set. To estimate the value of 𝛼, we utilized the lower
bound of 𝑃
− 𝑃
. One can check that the lower
bound of 𝑃
− 𝑃
can be expressed as,
𝑛( 𝜆
− 𝜆
) ≤ 𝑃
− 𝑃
(18)
where
𝑛=𝑛
=𝑛
. Note that if the value of 𝛼 is very
small, it will not affect the search process of the BSA,
i.e., the logarithmic operation allows a high reduction
in terms of the total number of database entries. A
new lower bound of 𝑃
− 𝑃
can be seen as,
( 𝜆
− 𝜆
) ≤ 𝑃
− 𝑃
(19)
Consequently, the expression of the parameter 𝛼 can
be written as,
𝛼=𝑚𝑖𝑛
,
𝜆
− 𝜆
(20)
According to (20), the value of 𝛼 is strongly
connected to
𝜆
and 𝜆
of the 𝑖
and 𝑗
scenarios.
5 SIMULATIONS
To demonstrate the efficiency of the proposed
CQOA, a simulation environment was built to
compare the performance of the proposed CQOA
with the WFA-BSA and the EWFA.
To this end, three simulation environments were
built, where each one of them considers a MIMO
system type: MIMO 2×2, MIMO 4×4, and MIMO
8×8. It is interesting to note that the simulation
experiments aim to evaluate and compare the
performance of the CQOA, EWFA, and WFA-BSA
in terms of overall transmit power consumption of the
MIMO system and computational complexity.
We considered in every MIMO system type the
following:
• The total number of users is 32, where we
assumed that the channels of the 31 users
interfere with the last reference user.
• The channel gain is random, it depends on
channel fading, path loss, and the distance
between users.
• Path loss equals 4 dB.
• The distance between every two users equals
1000 meters.
• The desired target transmission rate of the
reference user is
𝐵
= 60 Mbps.
• The target transmission rate of 16 users is
similar and equals 50 Mbps.
• The target transmission rate of the remaining
15 users is similar and equals 55 Mbps.
• The used bandwidth 𝐷=10
Hz and 𝛾=
0.001.
• The transmitted data is one signal.
• The power noise of all channels is identical.
• The interference between channels
belonging to the reference user is not
assumed (there is no self-interference of the
desired user).
As it is already discussed, the step size is a very
important parameter for running the algorithms. For
this sake, it is considered that
𝛼= 0.0002, and the
maximum transmit power that can be reached by a
MIMO system type is 𝑃
= 0.02 Watt.
We repeat every simulation for different channel
gains for the aforementioned optimization strategies
(EWFA, WFA-BSA, and CQOA).
For each MIMO system type (MIMO 2×2,
MIMO 4×4, and MIMO 8×8), the simulations
were repeated 100 times. the average of the overall
transmit power consumption was then calculated, as
well as the power gain of every MIMO type versus
another MIMO type for each strategy, i.e., the CQOA,
EWFA, and WFA-BSA. Moreover, to show the
influence of the interference power resulting from the
other 31 users on the optimum power usage of the
reference user, the simulation is repeated with and
without considering the interference of users.
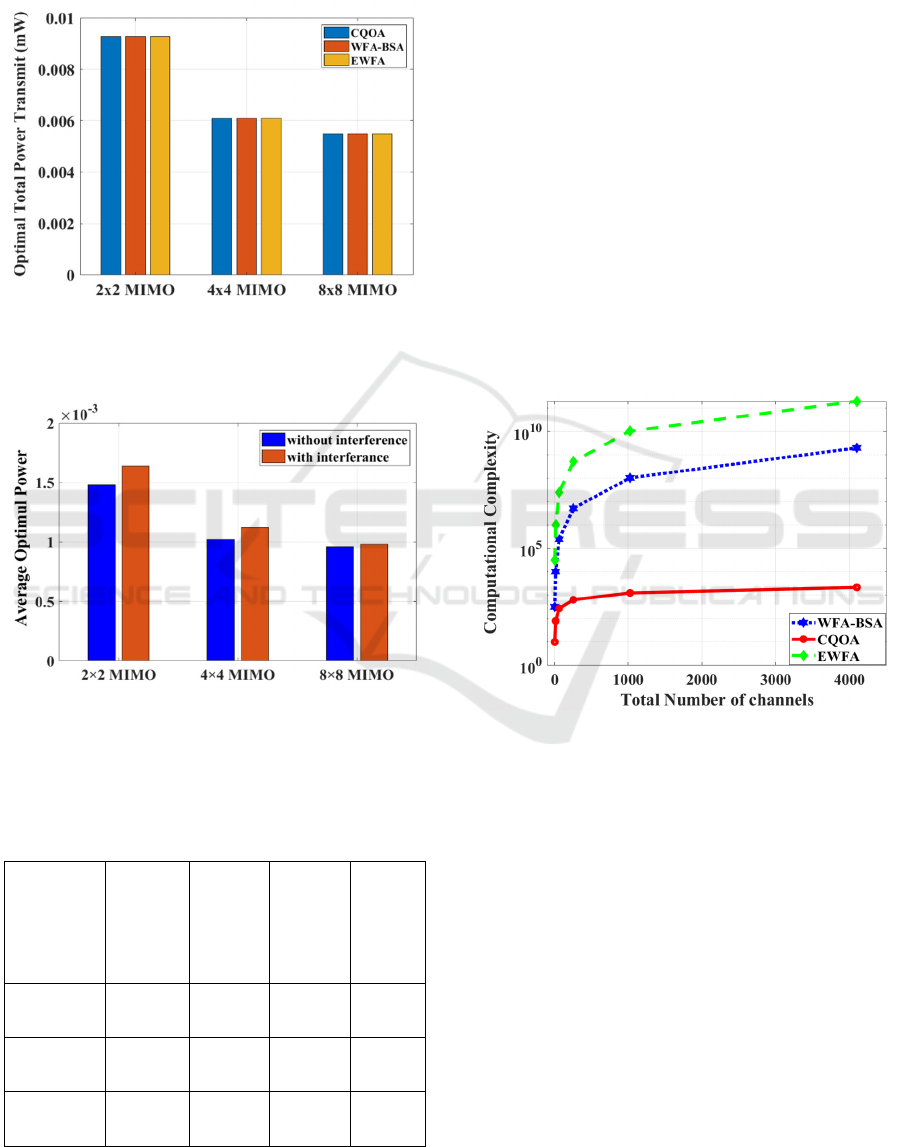
Figure 2 illustrates the total transmit power
consumption of the CQOA, EWFA, and WFA-BSA,
where the resulting interference power of users is
assumed. It is clearly noticeable that the three
optimization strategies consume the same optimum
minimum average total transmit power in each
MIMO system type. Also, one may observe that the
optimum total transmit power decreases when the
number of antennas of the MIMO system increases.
Figure 3 presents the influence of the interference
and noise power resulting from other 31 users on the
reference user. It is noticed that the optimum total
transmit power consumed before and after
considering interference of users is approximately
similar. This shows that the resulting interference
from the other 31 users has no significant effect on
the power usage of the reference user.
Table 2 shows the power gain of every MIMO
type versus another MIMO type. It is obvious that the
average optimum minimum power value decreases
WINSYS 2022 - 19th International Conference on Wireless Networks and Mobile Systems
66
with a higher number of antennas. For example, the
optimum power consumed in MIMO 8 x 8 compared
with MIMO 2 x 2 and MIMO 4 x 4 is much less by
41% and 10%, respectively.
Figure 2: The total transmit power consumed by the
WFA_BSA, EWFA, and CQOA, in the case of MIMO
2×2, MIMO 4×4, and MIMO 8 × 8.
Figure 3: The total transmit power consumed with and
without considering interference of users on the reference
user, in the case of MIMO 2×2, MIMO 4×4, and
MIMO 8 × 8.
Table 2: The power gain of each MIMO type versus another
MIMO type.
Average_
Power
Power
gain vs.
MIMO
2 x 2
Power
gain vs.
MIMO
4 x 4
Power
gain vs.
MIMO
8 x 8
MIMO 2 x 2
0.00928 * 34% 41%
MIMO 4 x 4
0.00610 -34% * 10%
MIMO 8 x 8
0.00548 -41% -10% *
To demonstrate the efficiency of the proposed
CQOA, another simulation experiment was
implemented to compare the performance in terms of
the computational complexity of the proposed CQOA
with other optimization algorithms. As it can be seen
from Figure 2, the CQOA, EWFA, and the WFA-
BSA require the same amount of transmit power in
each MIMO system type. However, from the
perspective of computational complexity (Figure 4),
it is clearly noticeable that the total number of steps
needed to identify the optimum transmit power
consumption of the CQOA is very low compared to
the other reference algorithms. For instance, the
WFA_BSA requires roughly 6.7x10
steps in MIMO
64 x 64, whereas the CQOA only requires 717 steps.
In addition, it is apparent that as the total number of
transmit antennas increases, the computational
complexity of the WFA_BSA and EWFA grows
exponentially, while the CQOA retains a low
computational complexity as the number of transmit
antennas grows.
Figure 4: The computational complexity of CQOA and
WTA_BSA.
6 CONCLUSIONS
This work investigated the reduction of the total
transmit power for different MIMO-downlink
systems by taking into consideration the transmission
bit rate target of the users. The implementation of the
WFA-BSA, EWFA, and CQOA is also studied. It is
proved by simulation environment for different
MIMO systems that the CQOA reduces the power
consumption with high exponential speed and
accuracy. While the WFA-BSA and EWFA consume
similar power as the CQOA with the price of high
computational complexity. In future work, the plan is
to expand the MIMO model by considering multiple
New Quantum Strategy for MIMO System Optimization
67

users and multiple base stations, as well as embedding
the orthogonal frequency-division multiplexing
(OFDM) technique in the MIMO system. In addition,
the maximum number of steps needed to run the BSA
with respect to the resulting interference and noise
power required to run the CQOA can be estimated.
ACKNOWLEDGMENTS
This research was supported by the Ministry of
Innovation and Technology and the National
Research, Development, and Innovation Office
within the Quantum Information National Laboratory
of Hungary.
REFERENCES
Ahrens, A., Cano-Broncano, F., & Benavente-Peces, C.
(2014). Resource Allocation in GMD and SVD-based
MIMO System.
Dang, S., Amin, O., Shihada, B., & Alouini, M. S. (2020).
What should 6G be? Nature Electronics, 3(1), 20–29.
https://doi.org/10.1038/s41928-019-0355-6
Knuth, D. (1998). Sorting and searching in the art of
computer programming (2nd ed., Vol. 3). Addison-
Wesley.
Eid, A., Hester, J. G. D., & Tentzeris, M. M. (2021). 5G as
a wireless power grid. Scientific Reports, 11(1).
https://doi.org/10.1038/s41598-020-79500-x
El Gaily, S., & Imre, S. (2021, March 17). Constrained
Quantum Optimization Algorithm. 2021 20th
International Symposium INFOTEH-JAHORINA,
INFOTEH 2021 - Proceedings. https://doi.org/10.1109/
INFOTEH51037.2021.9400679
Imre, S. (2005). Extreme Value Searching In Unsorted
Databases Based On Quantum Computing.
International Journal of Quantum Information, 03(01),
171–176. https://doi.org/10.1142/S0219749905000700
Imre, S. (2007). Quantum existence testing and its
application for finding extreme values in unsorted
databases. IEEE Transactions on Computers, 56(5),
706–710. https://doi.org/10.1109/TC.2007.1032
Johnson, D. (2018). The 5G Dilemma: More Base Stations,
More Antennas-Less Energy. IEEE Spectrum
Newsletter, 3.
Kyösti, P., & Jämsä, T. (2007). Complexity comparison of
MIMO channel modelling methods. Proceedings of 4th
IEEE International Symposium on Wireless
Communication Systems 2007, ISWCS, 219–
223.https://doi.org/10.1109/ISWCS.2007.4392334
Marosits, Á., Tabi, Z., Kallus, Z., Vaderna, P., Gódor, I., &
Zimborás, Z. (2021). Exploring embeddings for MIMO
channel decoding on quantum annealers.
Infocommunications Journal, 13(1), 11–16.
https://doi.org/10.36244/ICJ.2021.1.2
Imre S., & Balazs F. (2005). Quantum Computing and
Communications: An Engineering Approach. Wiley.
Zhu, Y., Li, J., Zhu, P., Wang, D., Ye, H., & You, X. (2022).
Load-Aware Dynamic Mode Selection for Network-
Assisted Full-Duplex Cell-Free Large-Scale Distributed
MIMO Systems. IEEE Access, 10, 22301–22310.
https://doi.org/10.1109/ACCESS.2022.31525 45
WINSYS 2022 - 19th International Conference on Wireless Networks and Mobile Systems
68
