
Analysis of Differential Algebraic Equation Systems for Connecting
Energy Storages of Generally Valid Functional Mock-up Units
Meik Ehlert
1a
, Christian Henke
1b
and Ansgar Trächtler
2c
1
Fraunhofer Institute for Mechatronic Systems Design IEM, Zukunftsmeile 1, Paderborn, Germany
2
Heinz-Nixdorf-Institute, University of Paderborn, Fürstenallee 11, Paderborn, Germany
Keywords: FMI, FMU, DAE, Energy Storage, Multi Body System, Model Coupling, Co-simulation.
Abstract: Functional Mock-up Units (FMU) refer to tool-independent models exported from their original simulation
tools. They enable component manufacturers and system integrators to exchange models across entire
production chains to validate solutions virtually. However, since system equations cannot be accessed or
modified in an FMU, numerical challenges can arise, especially when coupling similar energy storages. In
this paper, therefore, Differential Algebraic Systems of Equations are analyzed for their suitability for FMU
couplings. It is shown how such systems of equations can be described in a general way and how suitable
coupling constraints for FMUs are chosen. Subsequently, three solution approaches are presented and
analyzed for their feasibility with FMUs.
1 INTRODUCTION
Due to the increasing complexity in mechatronic
systems, a continuous simulation in the development
is indispensable (Michael et al., 2016). In this way,
partial solutions can already be virtually validated in
domain-specific development. This reduces the
construction of necessary prototypes and thus leads to
increased cost and time efficiency.
However, a particular challenge lies in the large
number of interacting domains. Specialized tools are
often used for different domains. System integrators
must therefore couple models from a heterogeneous
tool landscape with each other in order to represent
the overall system. The Functional Mock-up Interface
(FMI) has proven to be a widely used way of coupling
models in a tool-independent manner. Models are
exported from their original modeling tools as
compiled binary files. These are called Functional
Mock-up Units (FMU). The models can then be
interconnected via a standardized interface.
In addition to the tool-independent coupling of the
models, the FMI standard also allows industrial
know-how protection to be achieved. Since the model
behavior is represented by binary files, the internal
a
https://orcid.org/0000-0002-3905-4407
b
https://orcid.org/0000-0001-7611-7983
c
https://orcid.org/0000-0001-9987-1655
system equations can no longer be accessed or
changed. Thus the FMI standard can be used for a
modular model exchange over entire production
chains. Manufacturers of individual components, e.g.
from the electrical drive technology, have the
opportunity to pass on models to customers without
disclosing their know-how. This increases market
visibility and enlarges the customer base. On the other
hand, system integrators can test components from
different manufacturers virtually in their overall
solution.
The model boundaries of an FMU can be defined
as small as desired. For example, an FMU can
represent a physical component or an entire assembly.
However, a component can also be divided further, so
that an FMU can also be created at subcomponent
level. For example, an industrial converter can be
divided into a rectifier and an inverter. Similarly,
individual FMUs can be created from software
components, such as control algorithms. A large
number of FMUs in the overall system ensures
greater modularization. Individual submodels can be
exchanged and reused more easily. For example, the
user can assemble his own system model from a set
of prefabricated FMUs.
Ehlert, M., Henke, C. and Trächtler, A.
Analysis of Differential Algebraic Equation Systems for Connecting Energy Storages of Generally Valid Functional Mock-up Units.
DOI: 10.5220/0011305700003274
In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 311-318
ISBN: 978-989-758-578-4; ISSN: 2184-2841
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
311

However, the tighter the model boundaries are
chosen, the higher is the integration effort in the
overall system and numerical difficulties can occur.
This is especially the case when similar energy
storages are interconnected across model boundaries.
Energy storages are physical elements, such as
masses, springs, capacitances or inductances, whose
state is described by its stored energy. For example,
if two masses are rigidly coupled together, they have
the same state. However, if the two masses are
arranged in two different models, each model
calculates its own state for the masses, which are
independent of each other.
In this article, therefore, methods are analyzed
with which FMUs can be coupled to overall systems
in a generally valid way. Special attention is paid to
the representation of a total system as a differential
algebraic equation (DAE) system. The couplings
should be possible independently of the energy
storage distribution in the system, so that two similar
energy storages, which are arranged in different
FMUs, can be rigidly coupled. In this paper, masses
are considered as an example.
2 STATE OF THE ART
In the following, the required information about the
Functional Mock-up Interface is given. Subsequently,
methods for coupling two masses from conventional
modeling are presented. An evaluation is made
whether these methods can be implemented with the
FMI standard.
2.1 Functional Mock-up Interface
The Functional Mock-up Interface refers to a standard
agreed upon by various vendors of modeling and
simulation tools to export their models as binary files.
With this standard a Co-Simulation or a model
integration can be performed. The exported models
are called Functional Mock-up Units. The standard
was first published in 2011 and currently exists in
versions 1.0 and 2.0. In addition, a pre-release of
version 3.0 exists since 2021 (FMI Development
Group, 2014).
An FMU consists of two files, a DLL file and an
XML file. The DLL file is the binary file that
represents the model behavior. For this purpose, it
implements the system equations of a general
nonlinear system, as follows.
𝑥
𝑓
𝑥,𝑢,𝑡
(1)
𝑦𝑤
𝑥,𝑢,𝑡
(2)
With
𝑥: System State
𝑢: System Input
𝑦: System Output
𝑡: System Time
The DLL file offers functions to read and write
the variables. In addition, a single simulation step can
be executed. The equations 𝑓 and 𝑤, however, cannot
be accessed.
The XML file represents the model description,
which contains all the required model information. It
lists which variables the model contains. Value
references are specified for these variables, which can
be used for the model functions from the DLL file to
reference a variable. Other attributes that a variable
can have are variability and causality. Causality
specifies whether a variable is an input, output or
parameter. Variability specifies whether a variable
may be changed during the simulation. Possible
values here are fixed and tunable. For example, output
variables cannot be written by the user, but are only
calculated by the model (FMI Development Group,
2014).
In (Blochwitz et al., 2012) an approach was
presented to couple masses in different FMUs. For
this purpose, a function for calculating directional
derivatives is used, which was introduced in the FMI
2.0 version. This can be used to compute a Jacobian
matrix that can be used to solve algebraic loops
created by the coupling. However, for this approach,
the appropriate input and output variables for the
FMUs must be provided. In this approach, one mass
provides the position, velocity and acceleration as
output. The second mass uses these quantities as input
and calculates a counter torque as output. An example
is provided by the Standard Modelica Library in the
GenerationOfFMUs example. However, these
masses have different interfaces and are not
considered as generally valid in this article.
Furthermore, the determination of directional
derivatives refers only to the FMU inputs. Moreover,
this function is optional and is only implemented by
a few tools.
2.2 Coupling of Similar Energy
Storages
In this section, first the problems of coupling similar
energy storages are shown. Then, common
approaches for solving the problem are presented.
Table 1 summarizes the energy storages from the
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
312
mechanical and electrical domains and shows the
corresponding differential equations (Isermann,
2007). The input and output quantities given result
from the assumption that the equations are solved by
numerical integrations only.
Table 1: Equations of Energy Storages.
Energy
Storages
Equations Input Output
Inductor
𝚤
1
𝐿
∙𝑢
𝑢 𝑖
Capacitor
𝑢
1
𝐶
∙𝑖
𝑖 𝑢
Mass
𝑣
1
𝑚
∙𝐹
𝐹 𝑣
Spring
𝐹
𝑐∙𝑥
𝑐∙𝑣
𝑣 𝐹
The following system variables appear in the
equations from Table 1:
𝑢: voltage
𝑖: current
𝑣: velocity
𝐹: force
The parameters of the energy storages are given as:
𝐿: inductance
𝐶: capacity
𝑚: mass
𝑐: spring stiffness
In this paper masses are considered for coupling
similar energy storages. In order to couple two
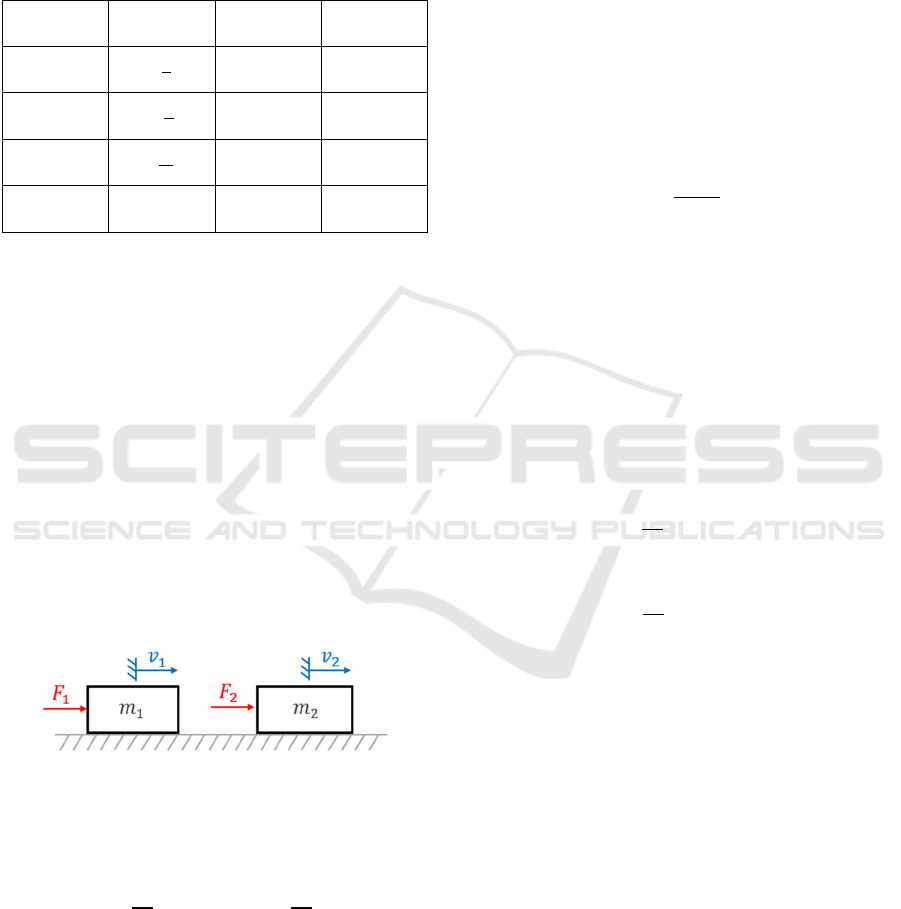
masses, they are first considered individually. Figure
1 shows a free cut of two masses 𝑚
and 𝑚
.
Figure 1: Free cut of two masses.
Each mass is driven by a force 𝐹, resulting in a
velocity 𝑣. The two masses are described by the
differential equations from table 1:
𝑣
𝐹
𝑣
𝐹
(3)
For each equation the input and output variables from
table 1 are given. Thus, each mass has the force 𝐹 as
input and the velocity 𝑣 as output. In this case the
problem with the coupling of two masses is obvious,
if they are located in different models. Both masses
expect a force as input. However, the first mass
provides a velocity as output, which cannot drive the
second mass. Thus, there is an interface
inconsistency. In (Ehlert et al., 2021) approaches
were presented with which energy storages can be
coupled, when all equations are known and
adjustable. These approaches are presented in the
following.
2.2.1 Substitute Variables
One of the most common methods for coupling
similar energy storages in conventional modeling is
the creation of substitute quantities. In this case, the
two masses are calculated to a total mass. This results
in a differential equation for both masses.
𝑣
𝐹 (4)
With this method, exact simulation results with a fast
computation time can be expected. However, the
system equations must be changed for this, which is
not possible with FMUs.
2.2.2 Fictitious Coupling Elements
Another possibility is the dynamic coupling via
fictitious coupling elements. In the case of two
masses, a fictitious spring is placed between the
masses. From this, the following differential
equations are derived:
𝑣
∙𝐹
𝐹
(5)
𝐹
𝑐∙𝑣
𝑣
(6)
𝑣
∙𝐹
𝐹
(7)
Each mass is only dependent on its own input force
and the fictitious spring force 𝐹
. Thus, the states of
the masses are decoupled from each other. The stiffer
the spring is chosen, the more a rigid coupling is
approximated.
However, this approach can lead to long
computation times if the spring is chosen to be very
stiff, since this results in small time constants in the
system. On the other hand, if the stiffness is too small,
the simulation results are distorted by fictitious
dynamics.
One possibility to solve the coupled system with
less computational effort is to perform an order
reduction before the simulation. Equations (5) to (7)
represent a third order differential equation system.
Since a rigid coupling is approximated here, the
difference of the independent states 𝑣
and 𝑣
will be
very small. Here, an order reduction can compute a
minimum order in which no independent states for the
Analysis of Differential Algebraic Equation Systems for Connecting Energy Storages of Generally Valid Functional Mock-up Units
313

velocities would be considered. In the field of
snapshot-based methods, there exist procedures for
model order reduction that can also be implemented
as a black box (Benner et al., 2021). It will be
separately analyzed if these methods can be applied
to FMUs.
2.2.3 Definition of Coupling Constraints
A third way of coupling similar energy storages is to
define constraints. Thereby, the ordinary differential
equations of the masses are arranged independently in
a state space model. This is completed by coupling
constraints to a Differential Algebraic System (DAE).
In (Najafi, 2018), an extension of the Functional
Mock-up Interface is presented to solve DAE systems
in FMUs. In this approach, however, the algebraic
constraints are part of the FMUs. In this paper, the
constraints are formed by the coupling. Thus, they are
located outside the FMUs and have to be solved by a
higher-level simulation algorithm considering the
available model information.
Since the ordinary differential equations from the
FMUs are considered independently, this approach
will be further analyzed.
3 MODEL COUPLING USING
DAE-SYSTEMS
For the model coupling using DAE systems, two
masses are considered again. Each mass is arranged
in its own FMU, as shown in Figure 2. Both FMUs
have at least one force input and one velocity output.
The coupling is realized via a constraint force 𝐹
,
which can be applied via the force inputs in the
FMUs. In addition, the first mass is actuated via a
driving force 𝐹
.
Figure 2: Coupled masses using coupling constraints.
For the example shown, a DAE system can now be
set up. DAE systems consist of a set of ordinary
differential equations (ODE) and a set of algebraic
constraints. The ordinary differential equations for
the system shown above are:
𝑣
𝐹
𝐹
𝑣
𝐹
(8)
Whereas an algebraic equation could limit the
velocities:
𝑣
𝑣
0
(9)
In general, DAE systems are defined as follows
(Janschek, 2010):
𝑥
𝑓
𝑥,𝑧,𝑢,𝑡
(10)
0𝑔
𝑥,𝑧,𝑡
(11)
Here, 𝑓 represents the set of ordinary differential
equations and 𝑔 the set of algebraic constraints. The
additional vector 𝑧
describes all algebraic variables
that do not occur differentially. It should be noted that
the DAE system represents the overall system and not
the individual FMUs. Therefore, the DAE system has
only the driving force 𝐹
as input and not the other
FMU inputs used for coupling. For the example
above, this results in the following assignments:
𝑥
𝑣
,𝑣
(12)
𝑧
𝐹
(13)
𝑢
𝐹
(14)
In order to be able to couple models using DAE
systems, possible coupling constraints are analyzed
first. Then, the index of a DAE system has to be
determined in order to be able to select a solution
approach based on it.
3.1 Choice of Coupling Constraints
Coupling constraints can be chosen differently for
different systems. An example is provided by the
Modelica modeling language (Elmquist et al., 1998).
Here, the user creates a topology of a system. The
modeling tool that implements the Modelica language
uses this topology to create coupling constraints for
the basic differential equations of the modeling
modules and thus generates a system of equations.
The coupling constraints are chosen in a way that the
potential quantities of two elements, that have been
connected with each other, are equal. The sum of all
flux quantities in this connection must result in zero.
In (Woernle, 2016) coupling conditions for
mechanical systems are classified. The constraints
can be divided into holonomic and non-holonomic
constraints. Holonomic constraints describe
constraints on the position level. Non-holonomic
constraints limit the velocities of the individual
models. A further classification takes place in
scleronome and rheonome constraints, whereby
scleronome constraints are time independent and
rheonome systems have a time dependence.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
314

In this paper, scleronomic bindings are chosen for
coupling different masses, since it is a rigid coupling
and no time dependence is necessary. Moreover, the
bindings are defined at velocity level to keep the
index of the DAE system small. Furthermore,
possible solution approaches for solving the DAE
system could be applied to other energy storages as
well. This assumes that the initial states of the masses
are equal. The resulting DAE system is classified as
nonholonomic scleronomic. The algebraic constraint
looks as follows:
𝑔𝑥
𝑥
𝑥
𝑣
𝑣
0 (15)
A detailed analysis of approaches for solving
holonomic DAE systems with FMUs can be given as
part of the future work.
3.2 Determination of the Index
The index of a DAE system is an indicator for the
degree of difficulty to solve the system. It describes
how often the algebraic constraints have to be
differentiated in time to transform the DAE system
into an ODE system. This procedure is also called
index reduction. If an ODE system could be formed,
it can be solved with ordinary numerical integration
methods.
To determine the index, the algebraic constraint is
first differentiated and checked whether it
subsequently represents another ODE. For this
purpose, the algebraic variables 𝑧
must occur in a
differentiated form.
𝑑
𝑑𝑡
𝑔𝑥
𝜕𝑔
𝜕𝑥
𝑥0
(16)
→
𝑑
𝑑𝑡
𝑔𝑥
𝜕𝑔
𝜕𝑥
𝑓
𝑥,𝑧,𝑢0
(17)
Since 𝑧
does not appear in equation (17), there is no
further ODE for the constraint. Therefore, it is not an
index 1 system and the constraint must be
differentiated further.
𝑑
𝑑𝑡
𝜕𝑔
𝜕𝑥
𝑓
𝑥,𝑧,𝑢
0 (18)
→
𝜕𝑔
𝜕𝑥
𝜕𝑓
𝜕𝑥
𝑥
𝜕𝑔
𝜕𝑥
𝜕𝑓
𝜕𝑢
𝑢
𝜕𝑔
𝜕𝑥
𝜕𝑓
𝜕
𝑧
𝑧0
(19)
To form another ODE, it must be possible to resolve
to 𝑧
. This leads to the following index 2 condition:
𝑑𝑒𝑡
𝜕𝑔
𝜕𝑥
𝜕𝑓
𝜕𝑧
0
(20)
𝑑𝑒𝑡
⎣
⎢
⎢
⎢
⎡
⎣
⎢
⎢
⎡
…
⋮⋱⋮
…
⎦
⎥
⎥
⎤
⎣
⎢
⎢
⎡
…
⋮⋱⋮
…
⎦
⎥
⎥
⎤
⎦
⎥
⎥
⎥
⎤
0 (21)
With the ODEs from equation (8), the assignment
from (12) - (14) and the constraint from (15) this
results in
𝑑𝑒𝑡
⎝
⎜
⎛
𝜕𝑔
𝜕𝑣
𝜕𝑔
𝜕𝑣
⎣
⎢
⎢
⎡
𝜕
𝑓
𝜕𝐹
𝜕
𝑓
𝜕𝐹
⎦
⎥
⎥
⎤
⎠
⎟
⎞
0 (22)
→𝑑𝑒𝑡
⎝
⎛
11
⎣
⎢
⎢
⎡
1
𝑚
1
𝑚
⎦
⎥
⎥
⎤
⎠
⎞
0
(23)
For 𝑚
𝑚
.
Thus, DAE systems for coupling different masses are
index 2 systems. In the following, it is explained how
these can be solved (Janschek, 2010).
3.3 Solving the DAE-system
The following section presents procedures that can be
used to solve the DAE systems described above.
However, in addition to the general conception, it
must also be evaluated whether these procedures can
be implemented with the information that are
provided by the FMUs.
DAE systems of index 2 can be solved directly
with implicit integration methods. Otherwise, index
reduction is necessary to reduce it further. With that
explicit integration methods can be used for
simulating an index 1 system or a full index reduction
to an ODE system is performed (Janschek, 2010). All
three possibilities are evaluated in the following.
3.3.1 Index Reduction
An index reduction has already been performed in the
determination of the index. Thereby, it can be seen in
equation (16) that a single differentiation of the
constraints is independent of the system equations in
the FMUs. However, since the coupling of the masses
are constraints of index 2, a second differentiation is
necessary. From equation (19) it can be seen that
partial derivatives of the FMU system equations are
necessary in this process. However, since these
equations are not known, the second differentiation
cannot be performed analytically with FMUs.
Analysis of Differential Algebraic Equation Systems for Connecting Energy Storages of Generally Valid Functional Mock-up Units
315

Therefor a numerical approach to calculate partial
derivatives is discussed in a later section.
At this point it should be mentioned that in the
FMI 2.0 standard there is the possibility to calculate
directional derivatives from FMUs. However, this
function is optional in the standard specification and
is only supported by a few tools. Furthermore, these
directional derivations refer to the input variables of
an FMU and not to general algebraic variables.
3.3.2 Explicit Integration Methods
Explicit integration methods perform a calculation of
a new state value based solely on past state values.
For DAE systems, this means that the ordinary
differential equations and the algebraic constraints
can be solved sequentially. This can be illustrated by
a simple Euler method applied to an index 1 system.
𝑥
𝑥
ℎ∙
𝑓
𝑥
,𝑧
→ 𝑥
(24)
0𝑔
𝑥
,𝑧
→ 𝑧
(25)
Here 𝑘 describes the previous number of integration
steps and ℎ the step size. For already known 𝑥
and
𝑧
, 𝑥
can be determined from the ordinary
differential equations. This 𝑥
can then be used to
calculate 𝑧
from the constraints. For the initial
values, 𝑥
is arbitrary. This implies that 𝑧
can be
derived directly from the constraint (Janschek, 2010).
However, explicit integration methods can only
be used for systems up to index 1. As mentioned in
section 3.3.1, the constraint can be differentiated
once, which obtains an index 1 system for an FMU
coupling. This results in a new constraint, which is
shown in equation (17). This constraint now depends
on the system equations 𝑓. If it is set equal to zero,
𝑧
can be determined. However, this is not directly
possible with the FMU system equations because the
output variables are not declared as tunable. Thus, the
FMU output cannot be written and the internal
parameters do not change.
One possibility to use this approach is to integrate
the constraint equation in a control loop, as shown in
Figure 3. In this case, only the input variables are
written in the FMU, whereby 𝑧
is adjusted by a P-
controller in such a way that the output is controlled
to zero. However, several iterations per time step may
be necessary until the output has reached its
stationary final value. To reduce the number of
iterations and the stationary error of the equation
output, the gain factor 𝐾 should be chosen very high.
Figure 3: Control loop for constraint equation.
3.3.3 Implicit Integration Methods
Implicit integration methods are used when a system
of equations cannot be solved sequentially. This is the
case for DAE systems of index 2, as will be shown
below using Euler's method.
𝑥
𝑥
ℎ∙
𝑓
𝑥
,𝑧
(26)
0𝑔
𝑥
(27)
Here, the constraint is independent of 𝑧
. Thus, the
algebraic variables cannot be determined for solving
the ordinary differential equations in the next
integration step. An implicit method must be chosen
here, in which equations (26) and (27) are formulated
into a root finding problem. The unknown quantities
𝑥
and 𝑧
can then be determined by a zero
search. An implicit Euler method looks as follows
(Janschek, 2010):
𝑥
𝑥
ℎ∙
𝑓
𝑥
,𝑧
(28)
0𝑔
𝑥
(29)
When formulating the root finding problem, a
substitution can be made for simplicity, introducing
the following new variables:
Φ
𝑃
≔
𝜑
,
𝜑
,
(30)
With
𝑃
≔𝑥
,𝑧
(31)
and
𝜑
,
𝑥
𝑥
𝑓
𝑥
,𝑧
(32)
𝜑
,
𝑔
𝑥
(33)
The root finding problem can thus be described in a
simple way.
Φ
𝑃
0 (34)
For the solution of this equation different iterative
methods for the root finding are possible. In the
following, the Newton-Raphson iteration from
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
316

(Schwarz et al., 2009) is considered. For this method
the following recursion rule results:
𝑃
,
𝑃
,
𝐽𝑃
,
Φ
𝑃
,
(35)
The variable 𝑖 denotes the number of previous
iterations of the Newton-Raphson method. Several
iterations are required per time step until 𝑃
,
is
close enough to 𝑃
,
. The Jacobian matrix 𝐽 is
defined as follows:
𝐽𝑃
⎣
⎢
⎢
⎢
⎡
𝜕𝜑
𝜕𝑥
𝜕𝜑
𝜕𝑧
𝜕𝜑
𝜕𝑥
𝜕𝜑
𝜕𝑥
⎦
⎥
⎥
⎥
⎤
(36)
Now it has to be evaluated whether this approach is
feasible with FMUs. Equation (36) shows that the
partial derivatives of the equations 𝜑
and 𝜑
are
needed to form the Jacobian matrix. However, these
equations depend on the FMU system equations 𝑓.
Since 𝑓 cannot be accessed from the FMUs, these
partial derivatives cannot be formed analytically.
Therefore, in the following section, a possibility of
numerical calculation of partial derivatives is
discussed.
3.4 Numerical Partial Differentiation
Both the index reduction and the implicit integration
methods depend on partial derivatives of the system
equations. Since these are not known, an analytical
solution is not possible. Here, a numerical solution
using difference quotients can be considered. A
numerical partial differentiation of the system
equation 𝑓 to 𝑥
looks as follows (Schwarz et al.,
2009):
𝜕𝑓
𝜕𝑥
𝑓
𝑥∆𝑥,𝑧,𝑢
𝑓
𝑥,𝑧,𝑢
∆𝑥
(37)
A differentiation according to 𝑧
results in
𝜕𝑓
𝜕𝑧
𝑓
𝑥,𝑧∆𝑧,𝑢
𝑓
𝑥,𝑧,𝑢
∆𝑧
(38)
With this approach, the system equations only have
to be evaluated and not changed. Thus, the difference
quotients offer an opportunity to couple and simulate
FMUs using DAE systems.
4 CONCLUSIONS
In this paper, methods for coupling masses from
different models were investigated. Thereby, the
couplings using DAE systems were dealt with in
more detail. It was shown how FMUs can be arranged
in such systems and how coupling constraints have to
be chosen. Subsequently, various possible solutions
were presented. A full index reduction or the direct
simulation via an implicit or explicit integration
method are suitable for solving the DAE system. For
index reduction and implicit solvers a numerical
partial differentiation is necessary. Explicit
integration methods could use a control algorithm to
solve the constraint equations of the DAE system. A
concrete implementation of a FMU coupling remains
to be validated afterwards. For this purpose one of the
presented solutions has to be chosen.
5 FUTURE WORK
As an outlook, the concrete implementation of an
FMU coupling via DAE systems can be given. For
this, first one of the presented solution methods must
be chosen. Thereby an index reduction up to an ODE
system or the solving with an implicit or explicit
integration method is suitable. The choice can
strongly depend on the application. For example, an
iterative method would not be suitable for real-time
applications.
Furthermore, the couplings of other energy
storages still need to be analyzed. These could lead to
changed coupling constraints. At the position level
further coupling constraints could be analyzed for
masses as well. Once coupling constraints are defined
for all relevant energy storages, the interaction with
the user of a simulation has to be defined. FMUs are
signal flow oriented models. However, the couplings
described here do not take place on the basis of
signals. An input must be found with which the user
determines the FMUs to be interconnected. From this
input, the coupling constraints have to be derived in
an automated way in order to build a DAE system.
Here, it is particularly important to analyze the
interfaces of the FMUs.
Besides the FMU coupling via DAE systems, the
dynamic coupling with fictious coupling elements
can be analyzed further. Here, a model order
reduction for black box models can be investigated to
reduce the computation time of the simulation.
REFERENCES
Benner, P.; Grivet-Talocia, S.; Quarteroni, A.; Rozza, G.;
Schilders, W.; Silveira, M. (2021). Model Order
Analysis of Differential Algebraic Equation Systems for Connecting Energy Storages of Generally Valid Functional Mock-up Units
317

Reduction – Volume 2: Snapshot-Based Methods and
Algorithms, De Gruyter GmbH.
Blochwitz, T.; Otter, M.; Akesson, J.; Arnold, M.; Clauß,
C.; Elmquist, H.; Friedrich, M.; Junghans, A.; Mauss,
J.; Neumerkel, D.; Olsson, H.; Viel, A. (2012).
Functional Mockup Interface 2.0: The Standard for
Tool independent Exchange of Simulation Models, 9th
International Modelica Conference.
Ehlert, M., Michael, J., Henke, C., Trächtler, A., Kalla, M.,
Bagaber, B., Ponick, B., Mertens, A. (2021).
Connecting Energy Storages from Tool Independent,
Signal-flow Oriented FMUs, International Conference
on Synthesis, Modeling, Analysis and
Simulation.Methods, and Applications to Circuit
Design (SMACD)
Elmqvist, H.; Mattson, S.; Otter, M. (1998). Modelica – The
new object-oriented Modeling Language, 12th
European Simulation Multiconference.
FMI Development Group (2014). Functional Mock-up
Interface for Model Exchange and Co-Simulation,
https://fmi-standard.org/
Isermann, R. (2007). Mechatronische Systeme, Springer
Berlin, 2007, ISBN 978-3-540-32336-5
Janschek, K. (2010). Systementwurf mechatronischer
Systeme, Springer-Verlag Berlin Heidelberg.
Michael, J.; Holtkötter, J.; Henke, C.; Trächtler, A. (2016).
Modellbildung und Simulation im Kontext des Systems
Engineering. In: ASIM-Treffen STS/GMMS 2016, S.
174-179
Najafi, M. (2018). Simulation of high-index DAEs and
ODEs with constraints in FMI, 2
nd
Japanese Modelica
Conference.
Schwarz, H., Köckler, N. (2009). Numerische Mathematik,
Vieweg + Teubner, Wiesbaden, 7th edition.
Woernle, C. (2016). Mehrkörpersysteme – Eine Einführung
in die Kinematik und Dynamik von Systemen starrer
Körper, Springer-Verlag Berlin Heidelberg, 2nd
edition.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
318
