
Nonlinear Set-based Model Predictive Control for Exploration:
Application to Environmental Missions
A. Anderson
1,2 a
, J. G. Martin
3 b
, N. Bouraqadi
1 c
, L. Etienne
1 d
, K. Langueh
1 e
,
L. Rajaoarisoa
1 f
, G. Lozenguez
1 g
, L. Fabresse
1 h
, J. M. Maestre
3 i
and E. Duviella
1 j
1
IMT Nord Europe, Institut Mines-T
´
el
´
ecom, Centre for Digital Systems, F-59000 Lille, France
2
Instituto de Desarrollo Tecnol
´
ogico para la Industria Qu
´
ımica (INTEC),
Consejo Nacional de Investigaciones Cient
´
ıficas y Tecnicas (CONICET), Santa Fe, Argentina
3
Departamento de Ingenier
´
ıa de Sistemas y Autom
´
atica, Universidad de Sevilla,
C/ Camino de los Descubrimientos, s/n., 41092 Sevilla, Spain
Keywords:
Nonlinear MPC, Unmanned Vehicles, Environmental Missions, Water Quality Assessment.
Abstract:
Acquiring vast and reliable data of physicochemical parameters is critical to environment monitoring. In the
context of water quality analysis, data collection solutions have to overcome challenges related to the scale of
environments to be explored. Sites to monitor can be large or remote. These challenges can be approached by
the use of Unmanned Vehicles (UVs). Robots provide both flexibility on intervention plans and technological
methods for real-time data acquisition. Being autonomous, UVs can explore areas difficult to access or far
from the shore. This paper presents a nonlinear Model Predictive Control (MPC) for UV-based exploration.
The strategy aims to improve the data collection of physicochemical parameters with the use of an Unmanned
Surface Vehicle (USV) targeting water quality analysis. We have performed simulations based on real field
experiments with a SPYBOAT® on the Heron Lake in Villeneuve d’Ascq, France. Numerical results suggest
that the proposed strategy outperforms the schedule of mission planning and exploration for large areas.
1 INTRODUCTION
The problem that we consider is that of explo-
ration missions, which implies both mission planning
and design of autonomous control strategies Nigam
(2014). Exploration requires offline and online mo-
tion planning, i.e., a sequence of connected linear
tracks covering the entire region to explore. In Go-
erzen et al. (2010) a complete overview of the existing
motion planning algorithms is provided. In case the
motion planning is solved offline, the parameterized
reference allows the USVs to navigate several desired
a
https://orcid.org/0000-0001-6626-500X
b
https://orcid.org/0000-0002-0362-5554
c
https://orcid.org/0000-0001-6459-4934
d
https://orcid.org/0000-0003-0931-843X
e
https://orcid.org/0000-0002-5984-2187
f
https://orcid.org/0000-0001-9624-5843
g
https://orcid.org/0000-0001-6875-7702
h
https://orcid.org/0000-0002-2223-7258
i
https://orcid.org/0000-0002-6343-5445
j
https://orcid.org/0000-0002-1622-0994
regions by an autonomous control strategy. A pop-
ular control technique of growing successes, particu-
larly in the field of MPC, is the path-following prob-
lem. A thorough review of Nonlinear MPC trajectory
tracking and path-following controllers with applica-
tion to nonholonomic robots can be found on Nasci-
mento and Saska (2019). On the other hand, for ex-
ploration missions performed by multitarget tracking,
there are several control designs adapted for specific
environments to provide an energy efficient and ro-
bust solution. For instance, Sarunic and Evans (2014)
provides a hierarchical MPC that enables an efficient
trajectory for the UAVs; a nonlinear MPC scheme for
navigation for constrained enviroment is proposed in
Lindqvist et al. (2020); Prodan et al. (2013) (the last
paper provide a path design via differential flatness);
Bertrand et al. (2014) presents a framework for the co-
operative guidance of a fleet of autonomous vehicles
with optimal trajectories obtained for an exploration
mission on a grid zone. A full discussion about the
general relation between different control objectives,
covering set-point stabilization, trajectory tracking,
path-following and their approaches within the non-
230
Anderson, A., Martin, J., Bouraqadi, N., Etienne, L., Langueh, K., Rajaoarisoa, L., Lozenguez, G., Fabresse, L., Maestre, J. and Duviella, E.
Nonlinear Set-based Model Predictive Control for Exploration: Application to Environmental Missions.
DOI: 10.5220/0011307300003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 230-237
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

linear MPC framework are included in Matschek et al.
(2019). Although interesting, the aforementioned
works and the most literature on MPC for exploration
are based on set-point stabilization and the benefits
of the set-based MPC (i.e., general invariant set sta-
bilization) on the exploration missions have not been
explore.
The stabilization of target sets instead of single
points is more suitable in cases where it is enough to
reach at least one state inside a target region. Such is
the case of water resource management, where the ex-
ploration mission usually aims to cover large surface
of water with an USV to visit regions where a mea-
surement needs to be acquired Anderson et al. (2022).
In this scenario, the properties of invariant sets are
useful to provide robustness, flexibility, extension of
the domain of attraction, between other benefits. The
set stabilization can be framed in the context of set-
based MPC Blanchini and Miani (2015); Anderson
et al. (2018) where a general invariant set is consid-
ered as a control objective.
In this context, the main contribution of this article
is to present a novel set-based MPC formulation for
nonlinear systems for exploration large areas with an
USV. The proposal is based on a set of meshing of the
region to be explored with a twofold aims, to config-
ure a simple motion planning offline for the problem
and to use the sets composing the meshing as target
sets for the controller. Several simulation results tar-
getting water quality assessment show the properties
of the proposed controller.
1.1 Notation
We denote with N the sets of integers, N
0
:= N ∪ {0}
and I
i
:= {0, 1,.. .,i}. The ceiling function is defined
by ceil(x) := min{n ∈ N : x ≤ n}. Consider two sets
U ⊂ R
n
and V ⊂ R
n
, containing the origin and a real
number λ. The Minkowski sum U ⊕ V ⊂ R
n
is de-
fined by U ⊕ V = {(u + v) : u ∈ U, v ∈ V }; the set
U \ V ⊂ R
n
is defined as U \ V = {u : u ∈ U ∧ u 6=
V }; and the set λU = {λu : u ∈ U} is a scaled set of
U. The close ball with center in x ∈ R
n
and radius
ε > 0 is given by B(x,ε) := {y ∈ R
n
: kx − yk ≤ ε}.
The point x is an interior point of U if the there exists
ε > 0 such that the open ball B(x,ε) ⊆ U. The inte-
rior of a set U is the set of all its interior points and it
is denoted by intU.
2 NONLINEAR SYSTEM AND
PRELIMINARY ANALYSIS
The dynamic process discussed in this work con-
sists in the class of discrete-time nonlinear system de-
scribed by the following equations
(
x(i + 1) = f (x(i),u(i)),
x(0) = x
0
,
(1)
where x(i) ∈ X ⊂ R
n
represents the measured states
of the system and u(i) ∈ U ⊂ R
m
the control input
at time i. The constraint sets X and U are compact
and convex with the origin inside, and the function
f : X × U → X is continuous with f (0, 0) = 0.
The following definition presents the concept of
invariance sets of control.
Definition 1 (Control Invariant Set - CIS). The set
Ω ⊂ X is a control invariant set (CIS) for system (1) if
for all x ∈ Ω there exists u ∈ U such that f (x, u) ∈ Ω.
The CIS has an associated corresponding input set
given by
Ψ(Ω) := {u ∈ U : ∃ x ∈ Ω such that f (x, u) ∈ Ω},
meaning that every input on Ψ(Ω) leaves at least one
state of Ω inside Ω.
A CIS is called a Contractive CIS if the condition
on Definition 1 is replaced by: for every x ∈ Ω there
is u ∈ U such that f (x,u) ∈ int Ω.
3 SET-BASED MPC
A generalization of the MPC controller for tracking
invariant sets is presented. The idea is to track and
reach sets that not only include stationary states, but
also transient states. We start with a quite general for-
mulation, that is particularized in the next subsections
to different applicable cases. Also consider the fol-
lowing definition.
Definition 2 (Generalized Distance Stage Cost Func-
tion). A generalized distance function d(x,Ω), from
x to the CIS Ω, is a function with the following prop-
erties: (1) d(x,Ω) is convex and continuous for all
x ∈ X, (2) d(x,Ω) = 0 for all x ∈ Ω, (3) d(x,Ω) > 0
for all x ∈ X \ Ω.
The proposed controller cost function will be
given by:
V
N
(x,Ω;u) =
N−1
∑
j=0
αd(x
j
,Ω) + βd(u
j
,Ψ(Ω)), (2)
Nonlinear Set-based Model Predictive Control for Exploration: Application to Environmental Missions
231

where α and β are positive real numbers, N is the
prediction horizon, the initial state x = x
0
, the pre-
dicted states x
j+1
= f (x
j
,u
j
) and the input sequence
u = {u
0
,· · · ,u
N−1
}.
Remark 3. The usual terminal cost associated with
the terminal predicted state x
N
can be omitted on Eq.
(2) if x
N
is force to belong to the set Ω, i.e., d(x
N
,Ω) =
0. As usual in MPC design, a local control action ¯u
that will act for predictions inside the terminal set Ω
will have also null cost since ¯u ∈ Ψ(U).
The general set-based MPC is given by the follow-
ing optimization problem solved at each sample time
k ∈ N.
min
u
V
N
(x,Ω;u) (3)
s.t. x
0
= x,
x
j+1
= f (x
j
,u
j
), j ∈ I
N−1
,
x
j
∈ X, u
j
∈ U, j ∈ I
N−1
,
x
N
∈ Ω
Taking into account the receding horizon policy,
the control law at time k is given by the first element
of the optimal sequence u
o
of the optimization prob-
lem given by (3) solved at time k.
Consider the next Lemma for the asymptotic sta-
bility of the closed-loop system.
Lemma 4. If Ω ⊂ X is a CIS for system (1) in the
cost function (2), then Ω is asymptotic stable for the
closed-loop system (1) controlled by the set-based
MPC given by (3).
Proof. The proof can be found on Blanchini and Mi-
ani (2015). It is stated that under the hypothesis of the
Lemma there is a Lyapunov function (given by the op-
timal cost V
0
N
(·)) that is a decreasing function on the
level sets of the generalized distance function used on
the function cost.
Next section presents an extension of the set-based
MPC to tracking multi-target sets.
3.1 Multi-target Tracking
Consider now that the closed-loop system has to reach
every element on the set
¯
Ω = {Ω
1
,Ω
2
,· · · ,Ω
K
} with
Ω
i
⊂ X for i = 1, ··· ,K, in the specified order. This
is, once the controlled system reaches the target set
Ω
j
∈
¯
Ω, the objective change to Ω
j+1
and so on un-
til the state of the system converge to Ω
K
. Clearly,
a condition must be establish in order to switch tar-
get every time the current target is reached. Here a
state-dependent MPC will be used to decide when a
target set is considered a reached set (according the
position of the current state). Consider the following
definition.
Definition 5 (Reached set). The first set on
¯
Ω, i.e.,
Ω
1
is considered a reached set if x(i) ∈ Ω
1
for some
i > 0. For k > 1, the target set Ω
k
∈
¯
Ω is considered
a reached set if x(i) ∈ Ω
k
for some i > 0 and the pre-
vious sets Ω
1
,. . .,Ω
k−1
are reached sets.
As it can be seen, the condition for a set on
¯
Ω to
be a reached set is defined inductively.
The current target set, Ω
x
, which it depends on the
position of the current state x = x(i) is given by the
definition.
Definition 6 (Current target set). Given the sates of
the closed-loop system x(i) ∈ X for i = 0,. ..,k, where
x = x(k) is the current state at time k. The current
target set, Ω
x
, is given by
Ω
x
:= {Ω
k+1
: k = max{i : Ω
i
is a reached set}}
(4)
In the case that there is not reached sets then Ω
x
:=
Ω
0
.
Ω
x
, for x = x(k), it defines the current objective on
time k.
The following MPC formulation to track sets is
based on the formulation presented on Limon et al.
(2005). The approach of this mentioned work was
to track sets with the aim of extends the domain of
attraction of the controller.
Considering the control law derived from solving
by the receding horizon strategy the following opti-
mization problem.
min
u
V (x,Ω
x
,u) (5)
s.t. x
0
= x,
x
j+1
= f (x
j
,u
j
), j ∈ I
N−1
,
x
j
∈ X, u
j
∈ U, j ∈ I
N−1
,
x
N
∈ Ω
x
,
For an asymptotic stability condition consider the
next Lemma.
Lemma 7. If Ω
j
∈
¯
Ω is a Contractive CIS for all j =
1,. . .,K, then every Ω
j
∈
¯
Ω is a reached set for the
closed-loop system controlled by the MPC given on
(5).
Proof. If the current target set Ω
x
= Ω
j
is a Contrac-
tive CIS for system (1), the results proposed on An-
derson et al. (2018) proves that the closed-loop sys-
tem will reach in finite-time the set Ω
x
. Therefore,
according the formulation, once the target set Ω
j
is
reached, the current state switch to Ω
x
= Ω
j+1
. The
proof is concluded by induction.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
232

The following section provides the main result of
the paper. The proposal is an extension of the above
MPC formulation that aims to improve the perfor-
mance of the controlled trajectory.
4 PROPOSED MPC
In this section, the MPC based on sets for tracking
multi-target set is extended to improve performance.
To this end a dual-MPC is formulated, where the goal
of the first mode is to reach only the current target
set Ω
x
= Ω
j
, by means of (5). The second mode is
activated when the current state x is close enough of
Ω
x
, this mode aims to give more importance to the
target set that became next, i.e., Ω
j+1
.
To trigger the second mode the current state must
be close enough of Ω
x
. This condition can be stated
by the inclusion of the current state on the fattening
set of Ω
x
.
Definition 8 (Fattening set). Let Ω
x
⊂ R
n
be the cur-
rent target set of control, and let ε > 0, we denote the
ε-fattening set of Ω
x
by
(Ω
x
)
ε
:= ∪{B(x,ε) : x ∈ Ω
x
}.
Remark 9. The term ’close enough’ of the current
target set is a parameter of the control design and can
be selected by chosen an appropriate ε.
The second mode is activated when the current
state is on (Ω
x
)
ε
, at this time the design of the con-
trol consider the next target set, i.e. if Ω
x
= Ω
j
then
the next target set is Ω
j+1
. The following properly
defines the second target set, Ω
+
x
:
Define Ω
x
as in Eq. (4), and the set Ω
+
x
as follows:
Ω
+
x
:=
Ω
j+1
, being Ω
j
= Ω
x
, x ∈ (Ω
x
)
ε
Ω
x
, otherwise
(6)
Note that, if the current state x /∈ (Ω
x
)
ε
, then it is
considered that Ω
+
x
= Ω
x
. This detail allows to for-
mulate the problem in a consistent way.
Consider now the function N
x
: X → I
N
that de-
fines the prediction horizon of the proposed con-
troller:
N
x
:=
ceil(
Nd(x,Ω
x
)
ε
), x ∈ (Ω
x
)
ε
N, otherwise
Note that for the first mode, i.e. when x /∈ (Ω
x
)
ε
,
the prediction horizon is N. For the second mode, i.e.
when x ∈ (Ω
x
)
ε
, the prediction horizon decreases with
the distance of the current state x to the current target
set. The ceil(·) function is considered for N
x
to be an
integer number.
Remark 10. Function N
x
is a decreasing function
with maximum value when x belongs to the bound-
ary of (Ω
x
)
ε
, given by N
x
= N; and a minimum value
when x ∈ Ω
x
, given by N
x
= 0.
The second mode computes N
x
predictions to min-
imize the distance of the states to Ω
x
, and N −N
x
pre-
dictions to minimize the distance of the states to Ω
+
x
.
The cost function is given by
J
N
(x;u) =
N
x
−1
∑
j=0
p`
Ω
x
(x
j
,u
j
) +
N−1
∑
j=N
x
q`
Ω
+
x
(x
j
,u
j
) (7)
where `
Ω
(x
j
,u
j
) := αd(x
j
,Ω) + βd(u
j
,Ψ(Ω)),
and p,q > 0 are weight values.
The nonlinear MPC is given by the following op-
timization problem solved at each sample time i ∈ N.
min
u
J
N
(x;u) (8)
s.t. x
0
= x,
x
j+1
= f (x
j
,u
j
), j ∈ I
N−1
,
x
j
∈ X, u
j
∈ U, j ∈ I
N−1
,
x
N
x
∈ Ω
x
,
x
N
∈ Ω
+
x
,
The solution of Problem (8) is the optimal con-
trol sequence u
0
= {u
0
0
,u
0
1
,· · · ,u
0
N−1
}. Taking into ac-
count the receding horizon policy, the control law at
time i is given by κ = u
0
0
(the first element of the op-
timal control sequence), which is applied to the real
plant at every time step i.
4.1 Some Quantitative Properties of the
Proposal
In what follows, some numerical results are shown to
clarify the nontrivial properties of the proposed con-
troller.
We consider the USV model represented by Eq.
(9). With abuse of notation let define the current state
of the vessel by
x(i) = (x,y, ψ,u,v, r),
for every time i ≥ 0. Where x, y, z represent position
sates, on the surface (x,y) and ψ is the ’direction po-
sition’ of the vehicle in the inertial frame. Meanwhile
u,v, r represent the velocities states, i.e., surge (for-
ward), sway (perpendicular) and yaw (angular), re-
spectively.
The first simulations attempts to show the an-
ticipatory behaviour of the proposed control. Con-
sider the paths given by
¯
Ω = {Ω
1
,· · · ,Ω
5
} and
¯
Ψ =
{Ψ
1
,· · · ,Ψ
5
} on the surface of the water (see Fig. 1).
This two paths are a reflection of each other.
Nonlinear Set-based Model Predictive Control for Exploration: Application to Environmental Missions
233
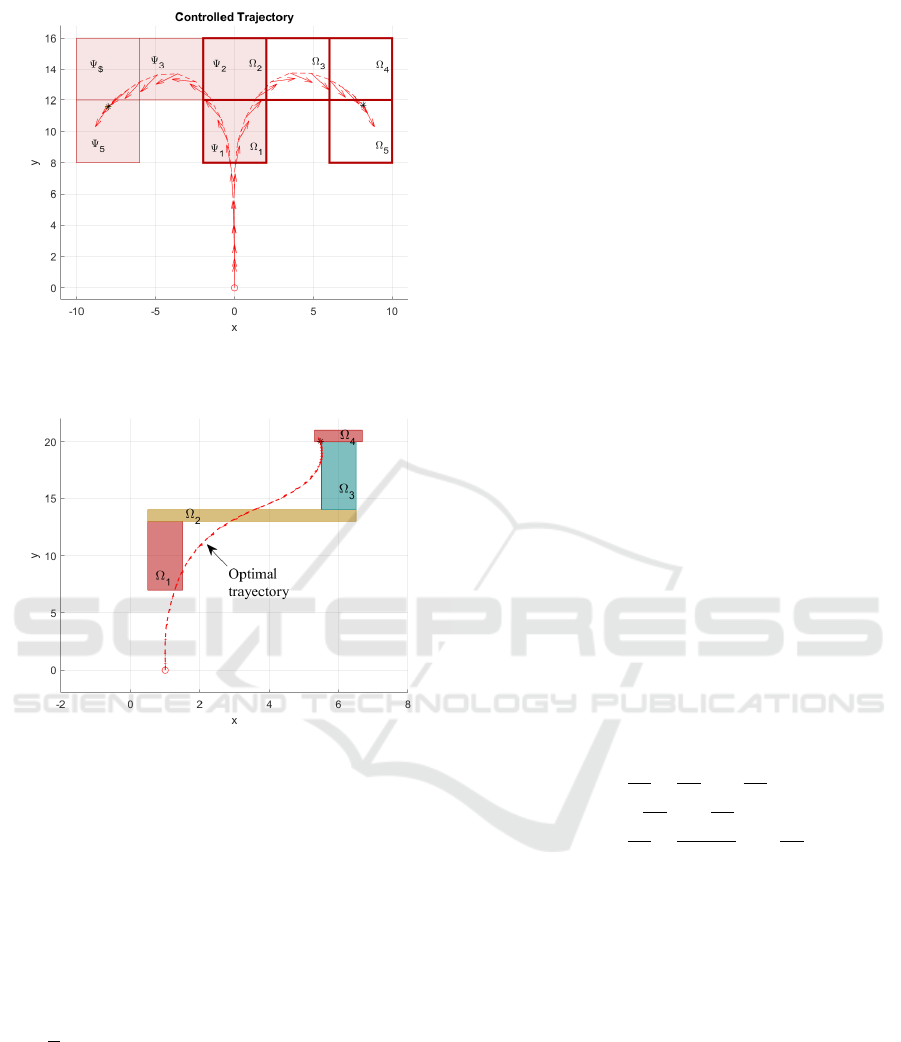
Figure 1: Two different controlled trajectories to follow
path
¯
Ω and path
¯
Ψ.
Figure 2: Optimal trajectory that pass over every target set
Ω
j
j = 1,. .., 4.
Note that both controlled trajectories of the vessel
are the same until the USV is ’close enough’ of the
first target set in order to activate the second mode of
the control. At this point, both trajectories take dif-
ferent directions according the orientation of the path
that is followed. This anticipatory behaviour remains
until the vessel reaches the last target set on every
path.
Consider now the scenario presented on Fig. 2.
The objective is to drive the initial state x(0) =
(0,0,
pi
2
,0, 0, 0) to Ω
1
, from there to Ω
2
then to Ω
3
and finally to Ω
4
. There are infinite trajectories and
countless strategies to fulfill this objective, however
the optimal trajectory - given by proposed strategy -
selects the optimal position to pass through Ω
j
con-
sidering that from there the system need to be driven
to Ω
j+1
, for j = 1,. .., 3. It is noteworthy that the opti-
mal trajectory reaches only the boundary of Ω
3
, since
it is enough to reach the last target set Ω
4
from there.
5 SPYBOAT®’S DESCRIPTION
In this section the description of the USV used on the
simulation results and the real experiment described
on Section 6 is presented.
The CT2MC company has designed a range of
vessels dedicated to answer the need of data monitor-
ing of freshwater resource. The SPYBOAT® technol-
ogy follows standard equipment configuration includ-
ing multiple sensors (localization system, compass,
sonar, camera) and is propelled by two independent
actuators. Thus the heading is controlled through a
differential thrust method.
The USV is equipped with a Hyperion optical sen-
sor from Valeport, for the measurement of the tur-
bidity. It is also equipped with Tripod sensors from
AquaLabo to measure the temperature, Dissolved
Oxygen, pH, and conductivity.
5.1 USV Nonlinear System
In Hervagault (2019) a kinematic model for the SPY-
BOAT® vessel was identified based following stan-
dard assumptions.
The marine craft moves on an horizontal plane and
only surge, sway and yaw are considered. The result-
ing is a nonlinear model given by the following equa-
tions.
˙x = u cos(ψ) − v sin(ψ),
˙y = u sin(ψ) + v cos(ψ),
˙
ψ = r,
˙u =
τ
u
m
11
+
m
22
m
11
vr +
X
u
m
11
u,
˙v = −
m
11
m
22
ur +
Y
v
m
22
v,
˙r =
τ
r
m
33
+
m
22
−m
11
m
33
uv +
N
r
m
33
r
(9)
The vector (x,y) is the position on the surface and
ψ the direction of the vessel, u, v,r are the surge, sway
and yaw velocities respectively. The inputs are given
by τ
u
= F
1
+ F
2
and τ
r
= b(F
1
− F
2
), where F
1
and F
2
are the port side and starboard side thrust forces, and
b represent 1/2 of the distance between thrusters. The
parameter X
u
, Y
v
and N
r
are the linear drag coefficient
in surge direction from surge, the linear drag coeffi-
cient in sway direction from yaw rate and the linear
drag moment coefficient from yaw rate, respectively.
The mass parameters m
ii
include added mass contri-
butions that represent hydraulic pressure forces and
torque due to forced harmonic motion of the vessel
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
234

which are proportional to acceleration:
m
11
=m + 0.05m,
m
22
=m + 0.5(ρπD
2
L),
m
33
=
m(L
2
+W
2
) + 0.5(0.1mB
2
+ ρπD
2
L
3
)
12
.
where m is the actual mass, L is the effective length
(hull’s length in the water), W is the width, D is the
mean submerged depth, B is the distance between pro-
pellers and ρ is the water density.
For more detail on the parameters of model (9) see
Hervagault (2019).
6 ENVIRONMENTAL MISSION
In this section some simulation results for exploration
mission targetting water quality map extraction are
presented. First, the problem statement and the gen-
eral objective of the mission are explained.
6.1 Problem Statement
In Anderson et al. (2022), a data collection of physic-
ochemical parameters (such as pH, turbidity, conduc-
tivity, temperature and dissolved oxygen) that indi-
cate the pollution index of water surface were studied
in a particular region of the Heron Lake in Villeneuve
d’Ascq, France (see region Ω on Fig. 3). In this ar-
tificial lake the water arrives from east and when the
level is too high water is pumped out to a nearby river
in the far western point. A natural remediation of the
water occurs in lake so a gradient of the parameters
can be expected between points on the entrance with
a high biodegradable inputs Ivanovsky et al. (2018).
Figure 3: Region Ω on the Heron lake, Villeneuve d’Ascq,
where the measurements need to be acquire.
Remark 11 (General Objective). In this context - as
was explain on Anderson et al. (2022) - the general
objective is to construct a limnological map of the re-
gion Ω, i.e., a map F : Ω → R
5
such that F assigns to
every point on Ω its approximation value of pH, tur-
bidity, conductivity, temperature and dissolved oxy-
gen (see Fig. 5 for dissolved oxygen).
The construction of map F on the region of inter-
est was discussed on Anderson et al. (2022), where an
approximation of F was proposed by geo-statistical
interpolation methods based on real measurements
provided by a hand-operated USV. The interpolation
method was necessary at this point in order to com-
plete uncovered points (unmeasured positions) due to
the irregularity of the hand-operated trajectory (see
Fig. 4).
Figure 4: Trajectory of the hand-operated vessel in region
Ω with decimal GPS coordinates.
To improve the data collection of the aforemen-
tioned physicochemical parameters, in what follows
the proposed control strategy is performed for a regu-
lar exploration of region Ω.
6.2 Motion Planning
The area of interest Ω was computed by the largest
convex set containing the entire data collection of Fig.
5. The design of the path to explore the complete re-
gion is based on a regular map meshing of Ω. The
map meshing consists in a collection of disjointed sets
{Ω
j
}
K
j=1
such that ∪Ω
j
contains the region Ω. The
size of every Ω
j
must be considered according the
size of the vessel, the accurate of the map F, the time
for the exploration mission, etc. On the other hand,
the shape of Ω
j
must be chosen according the best
performance of the controller. Figure 6 shows a mo-
tion planning for squares Ω
j
with a size of 100m
2
. A
discussion about the shapes and sizes of the meshing
is discussed on Anderson et al. (2022)
The controlled vessel reaches every set Ω
j
and
performes a direct in situ measurement of each pa-
rameters. The limnological map F is constructed by
this process.
Remark 12. The path
¯
Ω = {Ω
1
,· · · ,Ω
K
} is an or-
dered sequence that determines in which order the
target sets Ω
j
are reached. According to the mesh-
ing considered in this work, there are several possible
Nonlinear Set-based Model Predictive Control for Exploration: Application to Environmental Missions
235
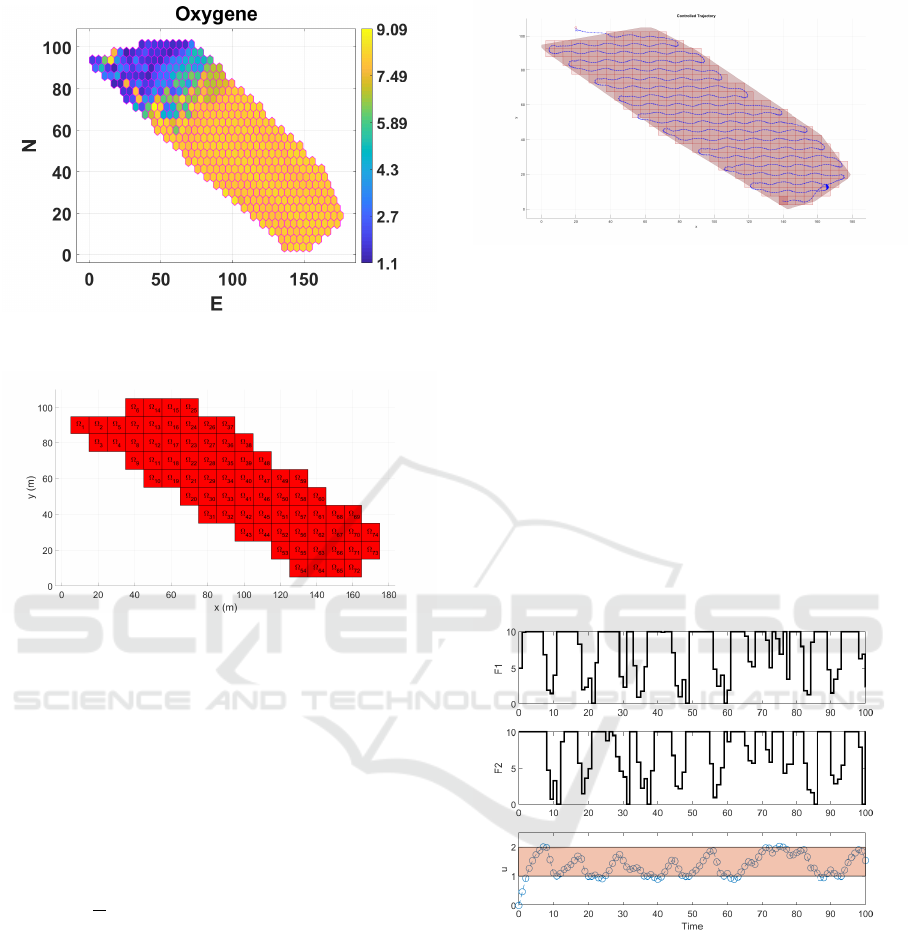
Figure 5: Limnological map F on Ω for the Dissolved Oxy-
gen (Anderson et al., 2022).
Figure 6: A motion planning to explore Ω.
regular paths for exploration; a proper motion path
would depend on the position of the initial state, wind,
water flow, etc.
6.3 Exploring Results
Fig. 7 shows the application of the proposed MPC
with a prediction horizon N = 15, a discretization
of the dynamical model (9) with discrete-time with
T = 1seg and initial state x(0) = (x, y,ψ,u,v, r) =
(20,105, −
pi
2
,0, 0, 0). To explore region Ω a regular
meshing of squares with a size of 25m
2
is used. Ev-
ery target set Ω
x
share an edge with the next target set
Ω
+
x
, so once the system enter into Ω, only the second
mode of the MPC (8) is used (the first mode is only
used at the beginning to reach Ω
1
). Fig. 7 shows the
controlled trajectory that reach every target set Ω
j
at
least one time.
In order to construct the map F by direct in situ
measurements of each parameters inside every target
set Ω
j
, the velocity u of the vessel must belongs to
certain range to allows the sensor to take every mea-
surement inside Ω
j
for all j = 1,. ..,K. This can be
approach by considering target sets of three dimen-
Figure 7: Controlled trajectory for exploring region Ω.
sions, i.e. if z = (x, y,ψ,u,v, r)
Ω
j
= {z ∈ R
6
: l
x
≤ x ≤ u
x
, l
y
≤ y ≤ u
y
,. . .
l
u
≤ u ≤ u
u
, ∞ ≤ ψ,v,r ≤ ∞}.
Note that there is no consideration to minimize states
ψ,v and r, which means that they are free. For the
simulations on Fig. 8 we consider that 1 ≤ u ≤ 2
for all Ω
j
, j = 1 .. . ,K, i.e., proj
u
Ω
j
= [1,2] for all
j. The figure shows the velocity state and inputs
for the time interval [0,100]. On the other hand, for
the simulations on Fig. 9 the target set for the ve-
locity is 0.5 ≤ u ≤ 1.5 for all Ω
j
, j = 1 . .., K, i.e.,
proj
u
Ω
j
= [0.5,1.5] for all j.
Figure 8: Inputs and velocity state for the target set
proj
u
Ω
j
= [1,2].
Remark 13. Simulation results suggest that the ex-
ploration of the region of interest Ω can be done with
a very simple motion planing and with an optimal tra-
jectory that reaches every point on the surface where
a measurement needs to be performed. Even more,
the velocity of the vessel can be selected for every tar-
get Ω
j
with j = 1. ..,K according the requirements
of the experiment. However, more simulation experi-
ments need to be done before the real implementation,
but they are out of the scope of this work.
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
236
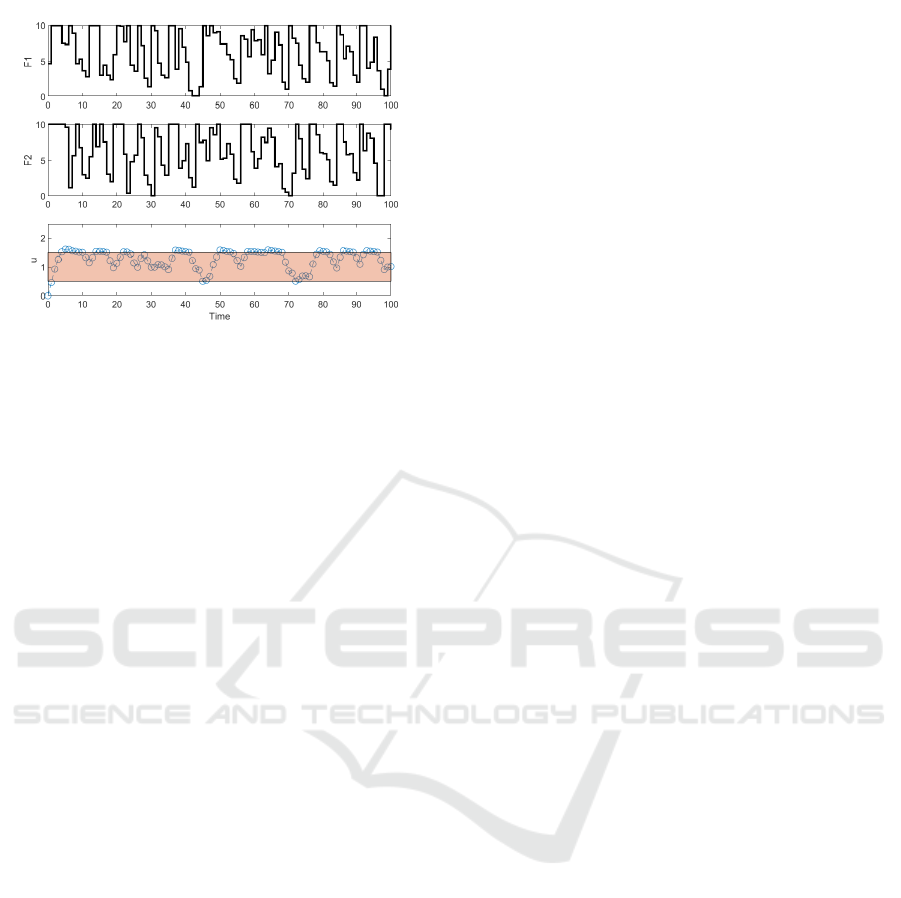
Figure 9: Inputs and velocity state u for the target set
proj
u
Ω
j
= [0.5,1.5].
7 CONCLUSION
Environmental missions were performed on Heron
Lake in Villeneuve d’Ascq, France. The main goal of
the experiment is to construct a temporal water qual-
ity profile of a region of the lake, where there is a sus-
picion of a source of pollution, so more experiments
are expected in the same region. To outperformed the
data collection results, in this paper a nonlinear MPC
for USV for exploration was presented. The strategy
shows that a simple schedule of mission planning can
be obtained, and the simulations proves that large wa-
ter surfaces can be tracked in an optimal and flexible
way. This results are expected to outperformed the
real exploration of large areas targeting data collec-
tion for water quality analysis.
ACKNOWLEDGEMENTS
Authors want to thanks the company https:
//www.bathydronesolutions.com/Bathy drone Solu-
tions (BDS) for its participation in the experiments,
and the Department of Economic Transformation,
Industry, Knowledge and Universities of the An-
dalusian Government (PAIDI 2020) [Ampliaci
´
on
Aquacollect, ref. P18-HO-4713].
REFERENCES
Anderson, A., Gonz
´
alez, A. H., Ferramosca, A., and Kof-
man, E. (2018). Finite-time convergence results in ro-
bust model predictive control. Optimal Control Appli-
cations and Methods, 39(5):1627–1637.
Anderson, A., Martin, J., Mougin, J., Bouraqadi, N., Du-
viella, E., Etienne, L., Fabresse, L., Langueh, K.,
Lozenguez, G., Alary, C., Billon, G., Superville, P.,
and Maestre, J. (2022). Water Quality Map Extraction
from Field Measurements Targetting Robotic Simula-
tions. working paper or preprint.
Bertrand, S., Marzat, J., Piet-Lahanier, H., Kahn, A., and
Rochefort, Y. (2014). MPC strategies for coopera-
tive guidance of autonomous vehicles. Aerospace Lab,
(8):1–18.
Blanchini, F. and Miani, S. (2015). Set-Theoretic Methods
in Control. Systems & Control: Foundations & Ap-
plications. Springer International Publishing.
Goerzen, C., Kong, Z., and Mettler, B. (2010). A survey of
motion planning algorithms from the perspective of
autonomous uav guidance. Journal of Intelligent and
Robotic Systems, 57(1):65–100.
Hervagault, Y. (2019). Design and Implementation of an Ef-
fective Communication and Coordination System for
Unmanned Surface Vehicles (USV). PhD thesis, Uni-
versit
´
e Grenoble Alpes.
Ivanovsky, A., Belles, A., Criquet, J., Dumoulin, D., Noble,
P., Alary, C., and Billon, G. (2018). Assessment of
the treatment efficiency of an urban stormwater pond
and its impact on the natural downstream watercourse.
Journal of Environmental Management, 226:120–130.
Limon, D., Alamo, T., and Camacho, E. F. (2005). Enlarg-
ing the domain of attraction of mpc controllers. Auto-
matica, 41(4):629–635.
Lindqvist, B., Mansouri, S. S., and Nikolakopoulos, G.
(2020). Non-linear mpc based navigation for micro
aerial vehicles in constrained environments. In 2020
European Control Conference (ECC), pages 837–842.
IEEE.
Matschek, J., B
¨
athge, T., Faulwasser, T., and Findeisen,
R. (2019). Nonlinear predictive control for trajectory
tracking and path following: An introduction and per-
spective. In Handbook of Model Predictive Control,
pages 169–198. Springer.
Nascimento, T. P. and Saska, M. (2019). Position and atti-
tude control of multi-rotor aerial vehicles: A survey.
Annual Reviews in Control, 48:129–146.
Nigam, N. (2014). The multiple unmanned air vehicle per-
sistent surveillance problem: A review. Machines,
2(1):13–72.
Prodan, I., Olaru, S., Bencatel, R., de Sousa, J. B.,
Stoica, C., and Niculescu, S.-I. (2013). Receding
horizon flight control for trajectory tracking of au-
tonomous aerial vehicles. Control Engineering Prac-
tice, 21(10):1334–1349.
Sarunic, P. and Evans, R. (2014). Hierarchical model
predictive control of uavs performing multitarget-
multisensor tracking. IEEE Transactions on
Aerospace and Electronic Systems, 50(3):2253–2268.
Nonlinear Set-based Model Predictive Control for Exploration: Application to Environmental Missions
237
