A2P: Attention-based Memory Access Prediction for

Graph Analytics

Pengmiao Zhang

1 a

, Rajgopal Kannan

2 b

, Anant V. Nori

and Viktor K. Prasanna

1 c

University of Southern California, U.S.A.

US Army Research Lab-West, U.S.A.

Processor Architecture Research Lab, Intel Labs, U.S.A.

Keywords:

Attention, Memory Access Prediction, Graph Analytics.

Abstract:

Graphs are widely used to represent real-life applications including social networks, web search engines, bioin-

formatics, etc. With the rise of Big Data, graph analytics offers signiﬁcant potential in exploring challenging

problems on relational data. Graph analytics is typically memory-bound. One way to hide the memory access

latency is through data prefetching, which relies on accurate memory access prediction. Traditional prefetch-

ers with pre-deﬁned rules cannot adapt to complex graph analytics memory patterns. Recently, Machine

Learning (ML) models, especially Long Short-Term Memory (LSTM), have shown improved performance for

memory access prediction. However, existing models have shortcomings including unstable LSTM models,

interleaved patterns in labels using consecutive deltas (difference between addresses), and large output dimen-

sions. We propose A2P, a novel attention-based memory access prediction model for graph analytics. We

apply multi-head attention to extract features, which are easier to be trained than LSTM. We design a novel

bitmap labeling method, which collects future deltas within a spatial range and makes the patterns easier to

be learned. By constraining the prediction range, bitmap labeling provides up to 5K× compression for model

output dimension. We further introduce a novel concept of super page, which allows the model prediction to

break the constraint of a physical page. For the widely used GAP benchmark, our results show that for the

top three predictions, A2P outperforms the widely used state-of-the-art LSTM-based model by 23.1% w.r.t.

Precision, 21.2% w.r.t. Recall, and 10.4% w.r.t. Coverage.

1 INTRODUCTION

Graphs are widely used structures that model net-

works consisting of nodes (or vertices, represent-

ing the entities in the system) and their inter-

connections called edges (representing relationships

between those entities). Graphs have been exploited

to describe social media, WWW, bioinformatics, and

transportation (Lakhotia et al., 2020). To generate,

process, and understand real-world graphs, the term

Graph Analytics was introduced that refers to the

study of data that can be represented as graphs. Par-

ticularly, with the rise of big data, graph analytics of-

fers high potential in studying how the entities relate

or could relate over traditional relational databases

because of its virtue in explicitly representing rela-

https://orcid.org/0000-0002-5411-3305

https://orcid.org/0000-0001-8736-3012

https://orcid.org/0000-0002-1609-8589

tions (Drosou et al., 2016).

Graph analytics are typically memory-

bound (Basak et al., 2019). Most frame-

works (Malewicz et al., 2010; Han and Daudjee,

2015; Low et al., 2012; Buluc¸ and Gilbert, 2011)

store the graph in a Compressed Sparse format (CSR

or CSC) (Siek et al., 2002) which allows efﬁcient

sequential access to the edges of a given vertex.

However, acquiring values of neighboring vertices

requires ﬁne-grained random accesses as neighbors

are scattered. For large graphs, such accesses

increase cache misses, becoming the bottleneck in

graph processing.

Data prefetching is a data access latency hiding

technique, which decouples and overlaps data trans-

fers and computation (Byna et al., 2008). In order

to reduce CPU stalls on a cache miss, data prefetch-

ing predicts future data accesses, initiates a data fetch,

and brings the data closer to the processor before it is

requested. A data prefetching strategy has to consider

Zhang, P., Kannan, R., Nori, A. and Prasanna, V.

A2P: Attention-based Memory Access Prediction for Graph Analytics.

DOI: 10.5220/0011309700003269

In Proceedings of the 11th International Conference on Data Science, Technology and Applications (DATA 2022), pages 135-145

ISBN: 978-989-758-583-8; ISSN: 2184-285X

135

various issues in order to mask the data access latency

efﬁciently.

The most essential step for prefetching is accurate

memory access prediction. The goal of memory ac-

cess prediction is to exploit the correlation between

history memory accesses to predict future one or more

memory access addresses.

Traditional hardware data prefetchers use pre-

deﬁned rules, based on spatial or temporal locality

of references (Kumar and Wilkerson, 1998), to pre-

dict future accesses. However, they are not powerful

enough to adapt to the increasingly complex memory

access patterns from graph analytics algorithms. For

prefetchers based on spatial locality (Michaud, 2016;

Shevgoor et al., 2015; Kim et al., 2016), the predic-

tion range is typically within a page, which limits

the diversity of prediction and shows low prediction

accuracy. For prefetchers based on temporal local-

ity (Wenisch et al., 2009; Jain and Lin, 2013), record

and replay are widely used, but the replaying mecha-

nism shows low generalizability of the prediction.

Machine Learning (ML) algorithms have shown

tremendous success in domains including sequence

prediction, which have provided insights into mem-

ory access prediction. The memory access stream

can be modeled as a time-series sequence. Pow-

erful sequence models such as LSTM (Long short-

term memory) (Greff et al., 2016) have been studied

to predict memory accesses. Due to the sparsity of

memory addresses for an application (Hashemi et al.,

2018a), prior works (Hashemi et al., 2018a; Srivas-

tava et al., 2019; Zhang et al., 2021; Srivastava et al.,

2020) takes the memory access deltas (a ”delta” is de-

ﬁned as the difference between consecutive access ad-

dresses) as input sequence and predicts the next delta

through classiﬁcation. LSTM-based delta prediction

has shown higher prediction performance than tradi-

tional prefetchers (Hashemi et al., 2018b; Srivastava

et al., 2019) due to its high accuracy and generaliz-

ability.

However, there are still shortcomings in existing

ML-based memory access prediction methods, espe-

cially when applying to complex memory patterns

in graph analytics. First, due to the large number

of parameters and the recurrent structure, training

an LSTM-based model is hard and its performance

is not stable (Zeyer et al., 2019). In comparison,

the Transformer (Vaswani et al., 2017), a sequence

model based on multi-head self-attention initially pro-

posed for machine translation, has achieved huge suc-

cess for sequence modeling tasks in many ﬁelds com-

pared to LSTM. Second, existing methods predict

only one next delta. Under ﬁne-grained memory ac-

cesses of neighboring nodes, the deltas between inter-

leaved patterns are labeled, which hinders the model

training. Also, in the prefetching context, one pre-

diction with a set of multiple predicted memory ac-

cesses regardless of the order is more practical (Van-

derwiel and Lilja, 2000; Zhang et al., 2022). Though

multiple predictions can be achieved by picking mul-

tiple outputs with top probabilities (Hashemi et al.,

2018b), the accuracy drops because the model is still

trained with one next delta as the label. Third, ex-

isting ML-based methods discard the locality of ref-

erences (Kumar and Wilkerson, 1998) used in tradi-

tional prefetchers. The model output delta is in the

entire address space, which causes an extremely large

output dimension for diverse memory access patterns

in graph analytics.

To address the shortcomings of existing methods,

we propose A2P , a novel Attention-based memory

Access Predictor for graph analytics. First, through

tokenization (Webster and Kit, 1992), we map the

memory access deltas to tokens, which are numeri-

cal values that can be processed directly by a neural

network. Second, we propose a novel bitmap labeling

method to collect deltas within a page to the current

address from future accesses. In this way, we model

memory access prediction as a multi-label classiﬁca-

tion problem. Then, we develop an attention-based

model to ﬁt the mapping between the delta tokens and

the bitmap labels to achieve a high prediction perfor-

mance. Furthermore, we introduce a novel concept

super page, which relaxes the spatial range from the

page size to larger ranges, aiming to detect delta pat-

terns beyond pages. Our contribution can be summa-

rized as follows:

• We develop A2P, a novel attention-based memory

access prediction model for graph analytics. We

use delta token sequences for model input and use

an attention-based network for feature extraction.

• We propose a novel bitmap labeling method to

collect multiple future deltas within a spatial

range as labels. Based on bitmap labeling, the

memory access prediction is reduced to a multi-

label classiﬁcation problem, which enables multi-

ple memory access predictions in each inference.

• We introduce a novel concept super page to relax

the range of spatial region from the typical one-

page size to several bits larger, which enables the

model to be trained by patterns beyond page range

while still taking advantage of spatial locality.

• We evaluate our method using widely used graph

analytics benchmark GAP (Beamer et al., 2015).

Results show that for the top three predictions,

A2P outperforms the widely used state-of-the-art

LSTM-based model predicting the next delta by

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

136

23.1% w.r.t. Precision, 21.2% w.r.t. Recall, and

10.4% w.r.t. Coverage.

2 GRAPH ANALYTICS

2.1 Background

Real world problems arising in web and social net-

works, transportation networks, biological systems

etc. are often modeled as graph computation prob-

lems. Applications in these domains generate huge

amounts of data that require efﬁcient large-scale

graph processing. However, with the rise of big data,

graph analytics is facing the challenge of high latency.

There are numerous studies in accelerating graph an-

alytics.

First, many distributed frameworks have been

proposed to process very large graphs on clus-

ters (Malewicz et al., 2010; Han and Daudjee, 2015).

However, because of the high communication over-

heads of distributed systems, even single threaded im-

plementations of graph algorithms have been shown

to outperform many such frameworks running on sev-

eral machines (McSherry et al., 2015).

Second, the growth in DDR capacity allows large

graphs to ﬁt in the main memory of a single server.

Consequently, many frameworks have been devel-

oped for high performance graph analytics on mul-

ticore platforms (Shun and Blelloch, 2013; Sundaram

et al., 2015; Nguyen et al., 2013). However, multi-

threaded graph algorithms may incur race conditions

and hence, require expensive synchronization (atom-

ics or locks) primitives that can signiﬁcantly decrease

performance and scalability. Furthermore, graph

computations are characterized by large communica-

tion volume and irregular access patterns that make it

challenging to efﬁciently utilize the resources even on

a single machine (Lumsdaine et al., 2007).

Third, recent advances in hardware technologies

offer potentially new avenues to accelerate graph an-

alytics, in particular, new memory technologies, such

as High Bandwidth Memory (HBM) and scratch-

pad caches. However, many graph analytics frame-

works are based on the conventional push-pull Vertex-

centric processing paradigm (Shun and Blelloch,

2013; Zhang et al., 2015; Grossman et al., 2018;

Besta et al., 2017), which allows every thread to

access and update data of arbitrary vertices in the

graph. Without signiﬁcant pre-processing, this leads

to unpredictable and ﬁne-grained random memory

accesses, thereby decreasing the utility of the wide

memory buses and deterministic caching features

offered by these new architectures. Some frame-

works and application speciﬁc programs (Roy et al.,

2013; Zhu et al., 2015; Zhou et al., 2017) have

adopted optimized edge-centric programming models

that improve access locality and reduce synchroniza-

tion overhead. However, these programming models

require touching all or a large fraction of the edges

of the graph in each iteration, and are not work op-

timal for algorithms with dynamic active vertex sets,

such as BFS, seeded random walk, etc. A work inefﬁ-

cient implementation can signiﬁcantly underperform

an efﬁcient serial algorithm if the useful work done

per iteration is very small.

In this work, we apply Machine Learning to de-

tect memory stream patterns in graph analytics appli-

cations and predict future memory accesses, which

is signiﬁcant for studying the memory patterns of

graph analytics algorithms, developing graph process-

ing frameworks, and designing prefetchers for graph

applications.

2.2 Graph Analytics Applications

In this work, we perform memory access prediction

and evaluate our model on ﬁve popular graph analyt-

ics applications:

Breadth-First Search (BFS) - Used for rooted graph

traversal or search. The BFS algorithm ﬁnds the par-

ent of every reachable node in the BFS tree rooted at

a given vertex. BFS is a fundamental algorithm and

often used within other graph applications.

Single Source Shortest Path (SSSP) - Finds the

shortest distance to all the nodes in a weighted graph

from a given source vertex. Using the same setting

as GAP (Beamer et al., 2015), we use non-negative

edges in this work. For unweighted graphs, BFS can

return the shortest path considering all the edges with

unit weight.

PageRank (PR) - A node ranking algorithm that de-

termines the “popularity” of nodes in a graph, orig-

inally used to sort web search results (Page et al.,

1999). PR is also an important benchmark for the

performance of Sparse Matrix-Vector (SpMV) mul-

tiplication, which is widely used in many scientiﬁc

and engineering applications (Asanovic et al., 2006;

Vuduc et al., 2005; Pingali et al., 2011).

Connected Components (CC) - Labels connected

components in a graph. A connected component

means a subgraph that all of its nodes are connected

to each other. Two nodes are connected if there is a

path between the two nodes. A connected component

is maximal, which means any nodes connected to the

component is part of the component.

Betweenness Centrality (BC) - Approximates the

betweenness centrality score for all the nodes in the

A2P: Attention-based Memory Access Prediction for Graph Analytics

137

graph by only computing the shortest paths from a

subset of the vertices. BC is a metric that attempts

to measure the importance of vertices within a graph.

BC can be computationally demanding as it requires

computing all of the shortest paths between all pairs

of vertices.

3 ML FOR MEMORY ACCESS

PREDICTION

3.1 Problem Formulation

The goal of memory access prediction is to exploit

the correlation between history memory accesses to

predict one or more future memory access addresses.

Due to the sparsity of memory address space for

an application, treating memory access prediction as

classiﬁcation problem instead of regression is a better

option (Hashemi et al., 2018a).

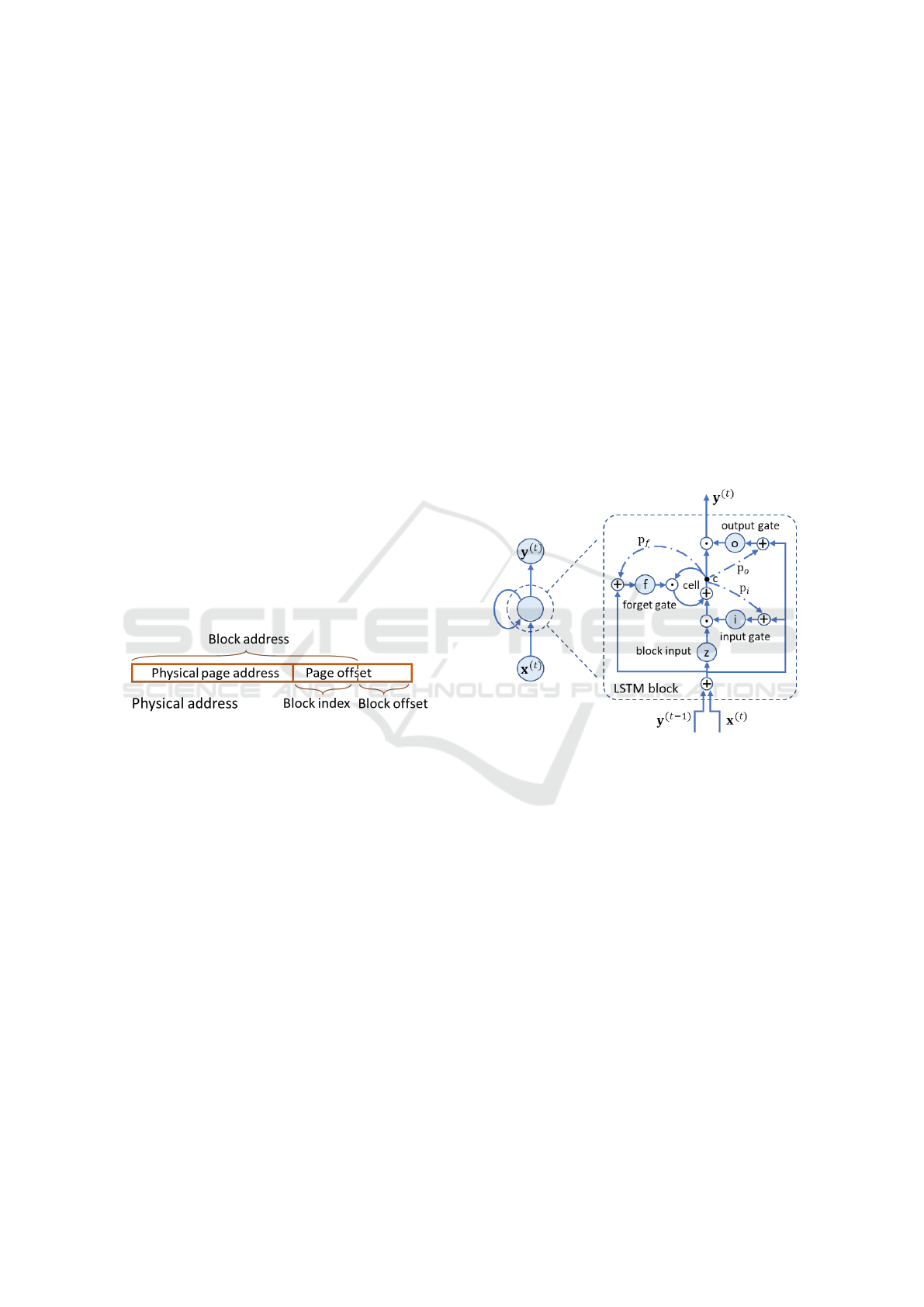
Figure 1 shows the ﬁelds in a physical memory

address. Data fetch operation is in the unit of a block

(cache line). Thus, memory access prediction consid-

ers only the block address space, ignoring the block

offset ﬁeld.

Figure 1: Fields in a physical address.

Let X

= {x

, x

, ..., x

} be the sequence of N his-

tory block addresses at time t. Let Y

= {y

, y

, ..., y

}

be a set of k outputs associated with future k block

addresses. Our goal is to approximates P(Y

), the

probability that the future addresses Y

will be ac-

cessed given the history events X

Because memory access prediction is modeled as

a classiﬁcation problem, the number of classes will be

extremely large when considering each unique block

address as a class. A commonly used technique to re-

duce the number of classes is to work on block deltas

instead of block addresses directly (Hashemi et al.,

2018b; Srivastava et al., 2019). A block delta is de-

ﬁned as the block address difference between con-

secutive memory accesses. We use delta for short in

later sections because we only work on block address

space.

A Machine Learning (ML) model can be devel-

oped and trained to learn the probability P(Y

). The

vector of history accesses X

is deﬁned as input fea-

ture, the actually accessed future addresses Y

is de-

ﬁned as output label. Using samples of input fea-

tures and output labels in a long memory trace, an ML

model can be trained to adapt to the data and construct

an approximation of the true probability.

3.2 Recurrent Neural Networks

Recurrent Neural Networks (RNNs) are widely used

for the task of memory access prediction (Hashemi

et al., 2018a; Srivastava et al., 2019; Zhang et al.,

2020; Zhang et al., 2021). RNNs exhibit temporal

dynamic behavior by storing sequential information

in their internal states. By assuming the dependence

between the current input and previous inputs, RNNs

perform better in sequence processing than basic neu-

ral networks that consider the time steps as dimen-

sions without time-series information.

Figure 2: The structure of LSTM.

LSTM (Long Short-Term Memory) (Greff et al.,

2016) is a variant of RNN that overcomes gradient

vanishing and exploding problems of basic RNNs. An

LSTM block (different from the address block in Sec-

tion 3.1) is composed of an input gate i

(t)

, a block in-

put gate z

(t)

, a forget gate f

(t)

, an output gate o

(t)

, an

memory cell c

(t)

and an output y

(t)

, as is shown in

Figure 2. The operation of each set of gates of the

layer is given by Equation 1.

(t)

= σ



(t)

+ R

(t−1)

+ p

c

(t−1)

+ b



(t)

= tanh



(t)

+ R

(t−1)

+ b



(t)

= σ



(t)

+ R

(t−1)

+ p

c

(t−1)

+ b



(t)

= σ



(t)

+ R

(t−1)

+ p

c

(t)

+ b



(t)

= i

(t)

z

(t)

+ f

(t)

c

(t−1)

(t)

= o

(t)

tanh



(t)



(1)

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

138

where x

(t)

is the input vector at time step t; y

(t−1)

is the output of the previous time step; c

(t−1)

is the

memory state of the previous time step; W

, W

are input weights for the input gate, block input

gate, forget gate and output gate, respectively; b

, b

are input bias for the four gates respectively;

, R

are recurrent bias for the four gates

respectively; p

, p

are peepholes that con-

nects directly from the memory cell to the gates; σ

and tanh are sigmoid and hyperbolic tangent functions

that serve as nonlinear activation functions.  is the

operation of Hadamard vector multiplication.

3.3 Attention Mechanism

Attention mechanism has shown powerful sequence

modeling capability without using recurrent struc-

tures. The Transformer (Vaswani et al., 2017), a se-

quence model based on multi-head self-attention ini-

tially proposed for machine translation, has achieved

huge success for sequence modeling tasks in many

ﬁelds compared to traditional recurrent models.

Figure 3: The structure of a Transformer layer.

The original Transformer uses an encoder-decoder

structure with a sinusoidal position encoding. A gen-

eral Transformer layer consists mainly of a multi-

head attention and a point-wise feed-forward, as is

shown in Figure 3.

Self-attention. Self-attention takes the embedding

of items as input, converts them to three matrices

through linear projection, then feeds them into a

scaled dot-product attention deﬁned as:

Attention(Q, K,V ) = softmax



√



V (2)

where Q represents the queries, K the keys, V the

values, d the dimension of layer input.

Multi-head Self-attention. One self-attention opera-

tion can be considered as one ”head”, we can apply

Multi-head Self-Attention (MSA) operation as fol-

lows:

MSA(Q, K,V ) = Concat (head

, . . . , head

head

= Attention



, KW

,VW



(3)

where the projection matrics W

∈

d×d

, H is the total number of heads, i is the index

of heads from 1 to H.

Point-wise Feed-forward. Point-wise Feed-Forward

Network (FFN) is deﬁned as follows:

FFN(x) = max (0, xW

+ b

(4)

4 MODEL

In this section we describe A2P, a novel attention-

based memory access prediction model for graph an-

alytics. The overall model structure is shown in Fig-

ure 4. A2P takes the deltas of block addresses as

input, tokenizes the deltas, and uses the delta to-

kens for neural network processing (see Section 4.1).

Then we collect future deltas within a spatial range

using bitmaps for model training labels (see Sec-

tion 4.2). We formulate the memory access prediction

task as a multi-label classiﬁcation problem and design

an attention-based neural network to ﬁt the mapping

from input delta tokens to bitmap labels (see Sec-

tion 4.3). During inference, the model predicts the

conﬁdence (probability) of deltas in a bitmap which

enables multiple delta predictions in one inference.

Furthermore, we introduce the notion of super page

that enables the the model learning patterns in a larger

spatial range (see Section 4.4).

Figure 4: Overall structure of A2P.

4.1 Delta Token Input

The memory access address is vast and

sparse (Hashemi et al., 2018b), so it is common

to use deltas (address difference between consecutive

A2P: Attention-based Memory Access Prediction for Graph Analytics

139

accesses) instead of the raw address for memory

access prediction. However, the deltas are still not

appropriate for model input because of the large

range. By considering the deltas as classes, we can

tokenize the deltas: mapping deltas into numerical

values for model processing.

Figure 5: Preprocessing for delta token input.

Figure 5 illustrates the preprocessing steps for

model input using an example access sequence. First,

the raw address is shifted by a block offset (6-bit in the

example). Then the deltas are computed from consec-

utive block addresses. The delta values are in a large

range, so we map the deltas to tokens, which can be

used for numerical calculation in a neural network.

4.2 Delta Bitmap Labeling

Unlike existing methods predicting the next one con-

secutive delta (Hashemi et al., 2018b; Srivastava

et al., 2019), we propose to predict multiple future

deltas within a spatial range. A heuristic spatial range

is one-page size, which is commonly used in state-of-

the-art spatial prefetchers (Michaud, 2016; Shevgoor

et al., 2015; Kim et al., 2016). We design a novel

bitmap labeling method to collect the labels for model

training.

Figure 6: Delta bitmap labeling process and the mapping

rules from delta to bitmap index.

Figure 6 illustrates the delta bitmap labeling

method. First, we scan a window of future memory

accesses to collect multiple future deltas to the cur-

rent block address. Then we deﬁne a bitmap with

the size as the range of deltas, which enables positive

and negative delta predictions. For example, given

the spatial range as a a-bit page offset with a b-bit

block offset, the delta range will be ±2

(a−b)

, leading

to the bitmap size as 2

(a−b)+1

. Figure 6 shows a sim-

ple example with delta range of ±4 and bitmap size at

8. By mapping both the positive and negative deltas

into the bitmap index, and setting the corresponding

locations as 1, we can construct a bitmap with multi-

ple labels for model training. Zero delta will not be

labeled or predicted because it means the same ad-

dress as the current request. Using bitmap labeling,

the model output dimension can be dramatically re-

duced from large delta range at entire address space

to a small page range, compared to predicting the next

consecutive delta.

4.3 Attention-based Network

With the above well-deﬁned input and output, we de-

velop an attention-based network to learn the map-

ping, as is shown in Figure 4. First the delta se-

quence is processed by a dense linear projection as

model input layer. Then, learnable 1D position em-

beddings (Dosovitskiy et al., 2020) are incorporated

to insert temporal information. With processed input

and position embeddings, multi-head attention-based

Transformer layers (Figure 3) are used to extract the

latent features. At last, using the features extracted

from the last Transformer layer, a multi-layer percep-

tron (MLP) is used for classiﬁcation output. Through

a sigmoid activation function for each bit in output

bitmap, the model predicts the probability for each

corresponding deltas, also referred to as delta conﬁ-

dence.

4.4 Super Page

In Section 4.2 we set the spatial range as a page size

following existing prefetching methods. Considering

the high learning capability of neural network models,

we propose to relax the spatial range so that the model

can learn and predict patterns beyond a page.

We deﬁne the relaxed range as super page, as

shown in Figure 7. With n-bit relaxation from page

offset, we can have a super page range. Then we col-

lect bitmap labels and predict deltas within the super

page instead of a physical page range. For exam-

ple, for a 12-bit physical page with 2-bit relaxation,

we can collect labels in a 14-bit super page. Differ-

ent graph analytics applications can beneﬁt variously

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

140

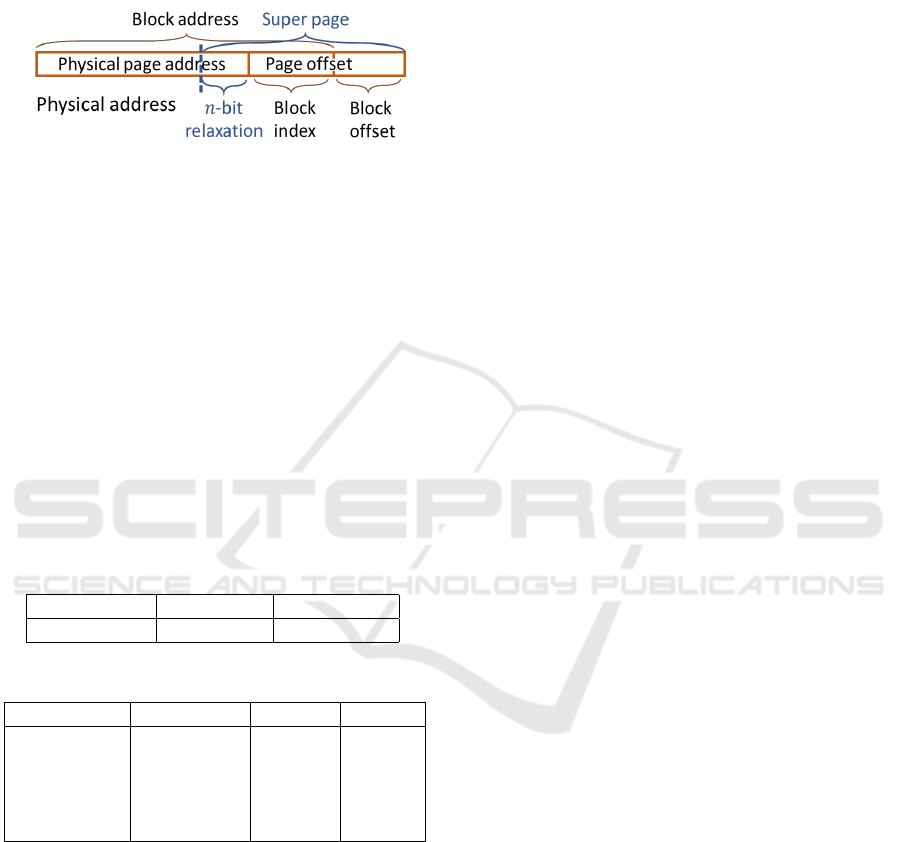
from the super page. Particularly, large graphs whose

nodes are stored beyond pages which are accessed in

a spatial pattern will beneﬁt signiﬁcantly from the su-

per page.

Figure 7: Super page with n-bit relaxation.

5 EVALUATION

5.1 Benchmark Suite

We evaluate A2P and the baselines using the applica-

tion traces generated from GAP (Beamer et al., 2015)

through simulator ChampSim (”ChampSim”, 2017).

The physical memory address conﬁguration is shown

in Table 1. After skipping the ﬁrst 1M instructions for

warm-up, we use the next 40M instructions for exper-

iments. We use the ﬁrst 20M instructions for model

training, the next 20M instructions for testing. The

statistics of the benchmark suite is shown in Table 2.

Table 1: Memory address conﬁguration.

Raw Address Page Offset Block Offset

64-bit 12-bit 6-bit

Table 2: Statistics of the benchmark suite.

Applications # Addresses # Deltas # Pages

BC 218K 202K 5.1K

BFS 316K 165K 15.7K

CC 158K 262K 2.5K

PR 311K 683K 4.9K

SSSP 179K 201K 4.1K

5.2 Implementation

To evaluate the effectiveness of our model, we imple-

ment four models as below. We denote bitmap label-

ing for a page range by ”-BP”, bitmap labeling for a

super page range by ”-BSP”. Speciﬁcally, ”-BSP-n”

denotes bitmap labeling for super page with n-bit re-

laxation.

• LSTM-Delta. This is a widely used state-of-the-

art model for memory access prediction (Srivas-

tava et al., 2019; Hashemi et al., 2018b). It takes

delta tokens as input and uses the next delta as la-

bel. An LSTM model is trained and outputs deltas

with top-k conﬁdence in prediction.

• LSTM-BP. An LSTM model takes delta tokens as

input and learns from delta bitmap labels within a

page. The output is deltas with top-k conﬁdence

in the bitmap.

• Attention-BP. An attention-based model takes

delta tokens as input and learns from delta bitmap

labels within a page. The output is deltas with

top-k conﬁdence in the bitmap.

• Attention-BSP (A2P). An attention-based model

takes delta tokens as input and learns from delta

bitmap within a super page. The output is deltas

with top-k conﬁdence in the bitmap. We explore

the super page size with relaxation bit n = 1, 2, 3,

and 4.

For LSTM-Delta, the output dimension will be the

number of deltas in Table 2, up to 683K. By using

bitmap labeling within a page, we reduce the abso-

lute value of deltas to a page range shifted by block

offset: 2

(12−6)

= 64, leading to the output dimension

to be 128 according to the mapping rules in Figure 6.

Bitmap labeling provides 5K× compression for out-

put dimension. For super page with n-bit relaxation,

the output dimension will be increased by 2

. For

n =1, 2, 3, and 4, the output dimensions are still sig-

niﬁcantly smaller than LSTM-Delta model.

5.3 Metrics

Since the models can give multiple predictions with

top k conﬁdence, we use Precision@k, Recall@k, and

Coverage@k to evaluate the prediction performance.

These metrics are widely used to evaluate recom-

mender systems (Chen and Liu, 2017; Silveira et al.,

2019) and have a good ﬁt for our problem.

• Precision@k: the proportion of correct predic-

tions in the top-k predictions. A correct prediction

refers to the case in which the predicted address is

requested in the following k accesses.

• Recall@k: the proportion of correct predictions

in the following k memory accesses. Repetitive

memory accesses or incorrect repetitive access

predictions can lead to a difference between Re-

call and Precision.

• Coverage@k: the cardinality of the set of all pre-

dictions over the entire set of addresses in testing.

It measures a model’s ability in covering the entire

range of memory accesses for an application.

A2P: Attention-based Memory Access Prediction for Graph Analytics

141

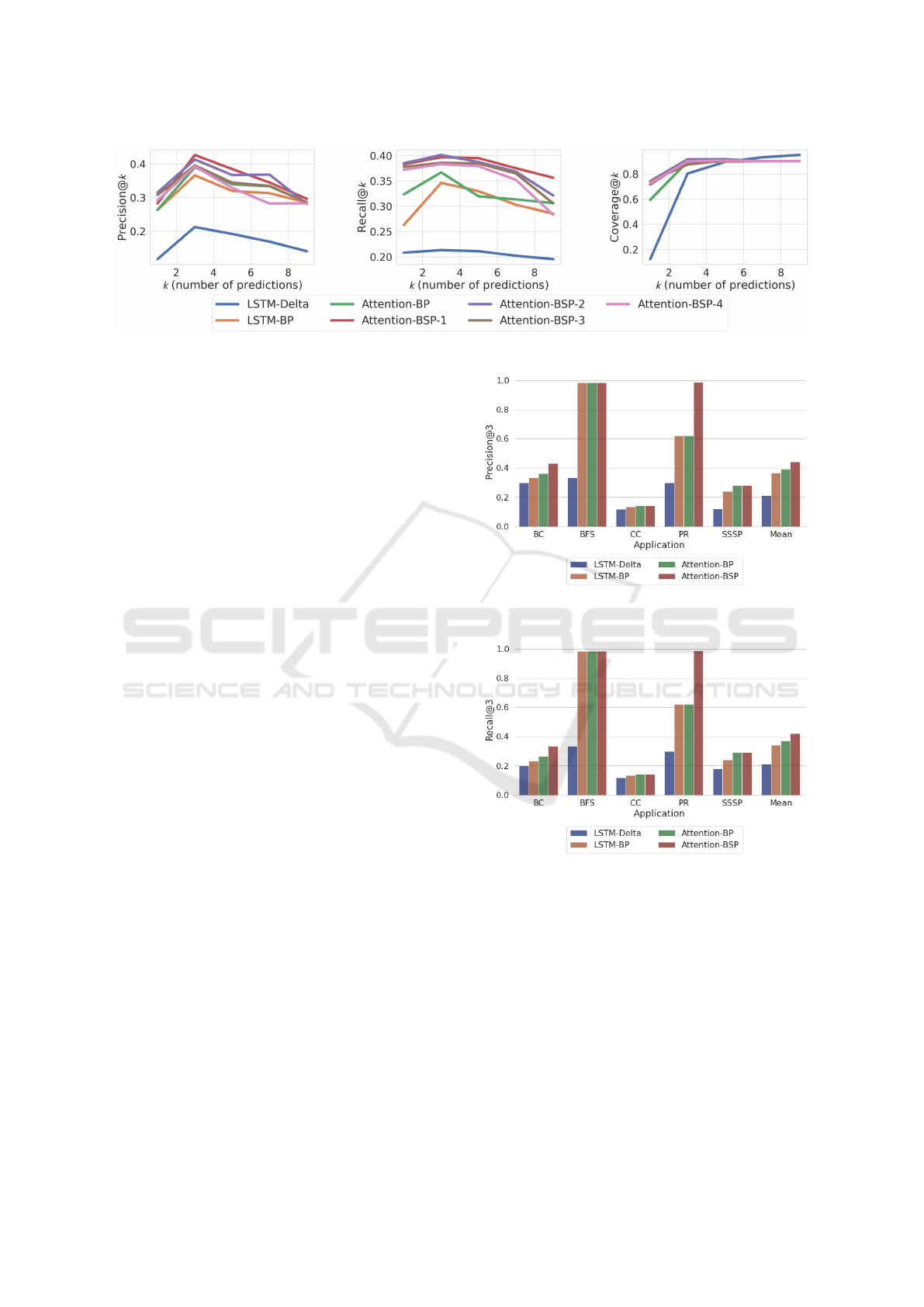
Figure 8: Precision, Recall, and Coverage at k top predictions for A2P and baselines.

5.4 Results

Figure 8 shows the Precision, Recall and Coverage

at k top predictions for all the implemented models.

We can make several observations. First, models us-

ing bitmap for labeling generally achieve higher Pre-

cision and Recall than LSTM-Delta which learns only

from the next delta. Even for k = 1, bitmap labeling

models that learns only within a spatial range outper-

form LSTM-Delta. This is because though LSTM-

Delta learns from the entire address space, the model

is hard to be trained and the interleaved patterns even

hamper the model learning on patterns within a spa-

tial range. Second, increasing k, the Precision and

Recall ﬁrst increase and then drop when k > 3. This

is because when k = 1, a correct prediction requires

exact match, when k increases to 3, more candidates

will be considered and there is higher probability to

match the prediction and future accesses. However,

more predictions with k > 3 will involve more predic-

tions with low conﬁdence, which leads to more incor-

rect predictions. Third, the relaxation for super page

range contributes to the model performance on Pre-

cision and Recall. 1-bit and 2-bit relaxation shows

notable performance improvement, while larger su-

per page shows little contribution, or even nega-

tively impacts the model performance. For example,

the Precision@7 for super page with 4-bit relaxation

(Attention-BSP-4) shows lower Precision than phys-

ical page range without relaxation (Attention-BP). In

addition, from the Coverage plot, we observe that the

Coverage of LSTM-Delta does not outperform other

models for k < 7 though it learns from the entire ad-

dress space. Only when low-conﬁdence predictions

are involved (k > 5), LSTM-Delta shows higher Cov-

erage.

Figure 9 and Figure 10 show the Precision@3

and Recall@3, respectively, for all the applications

in detail. We use the best-performing super page

size for each applications as the results in Attention-

BSP. Using geometric mean, LSTM-Delta, LSTM-

BP, Attention-BP, and Attention-BSP achieve Pre-

Figure 9: Precision@3 for A2P (Attention-BSP) and base-

lines.

Figure 10: Recall@3 for A2P (Attention-BSP) and base-

lines.

cision of 0.212, 0.366, 0.390, 0.443, respectively;

achieve Recall of 0.211, 0.340, 0.368, 0.423, respec-

tively. Attention-BSP model outperforms the baseline

LSTM-Delta by 23.1% w.r.t. Precision and 21.2%

w.r.t. Recall. We also observe that Attention-based

model achieves higher Precision and Recall than the

LSTM-based model when using the same labeling

method (BP). Particularly, PR beneﬁts the most from

the relaxation of page size. This is because the mem-

ory access of PR shows notable spatial patterns be-

yond pages. Super page successfully enables the

model to detect patterns in a larger range and con-

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

142

Figure 11: Coverage@3 for A2P (Attention-BSP) and base-

lines.

tributes to the prediction performance of PR.

Figure 11 shows the Coverage@3 of all the mod-

els and for all the applications. It shows that LSTM-

Delta, LSTM-BP, Attention-BP, and Attention-BSP

achieve average Coverage of 0.802, 0.897, 0.898,

0.907, respectively. We observe that learning within a

bitmap does not signiﬁcantly decrease the Coverage.

Though for applications BC, BFS, and CC, models

with bitmap labeling show slightly lower Coverage,

for PR and SSSP these models show even higher Cov-

erage than LSTM-Delta. Also super page contributes

to the Coverage of BC. Overall, A2P achieves 10.4%

higher Coverage than LSTM-Delta.

6 DISCUSSION

We discuss the beneﬁts of A2P to graph analytics

based on the model design and the evaluation results.

Sptaio-Temporal Locality. A2P reads the consec-

utive history accesses and learns the temporal pat-

terns, then predicts future accesses within a spatial

region. By making use of the spatio-temporal local-

ity, A2P achieves higher Precision and Recall com-

pared to the baselines.

Parallelizability. The multi-head attention mecha-

nism is embarrassingly parallelizable. In contrast,

LSTM, as a variant of the recurrent neural network,

requires recurrent steps and hard to be paralleled. The

parallelizability of A2P facilitates its hardware imple-

mentation, serving as a predictor for a hardware data

prefetcher.

Accelerating Graph Analytics. By accurately pre-

dicting memory access using A2P, data can be loaded

into a cache from the main memory before being

requested, i.e. data prefetching. Either being ap-

plied to software prefetching or hardware prefetching,

A2P can beneﬁt the acceleration of graph analytics.

7 CONCLUSION

In this paper, we presented A2P, a novel attention-

based memory access prediction model for graph an-

alytics, which addresses the problems of unstable

LSTM models, interleaved patterns in labels using

consecutive deltas, and large output dimensions in ex-

isting models. The key ideas of our model are us-

ing an attention-based neural network for prediction,

delta bitmaps for multi-label model learning, and spa-

tial range within a super page to constrain the output

dimension. Experimental results show that A2P out-

performs the state-of-the-art LSTM-based model by

23.1% w.r.t. Precision, 21.2% w.r.t. Recall, and

10.4% w.r.t. Coverage, at top 3 predictions. Graph

analytics can be accelerated by using our model to

predict and prefetch future memory accesses before

actual reference. In future work, we plan to explore

the incorporation of more context information to im-

prove the performance of memory access prediction.

ACKNOWLEDGEMENTS

This work has been supported by the U.S. Na-

tional Science Foundation under grant numbers CCF-

1912680 and PPoSS-2119816.

REFERENCES

Asanovic, K., Bodik, R., Catanzaro, B. C., Gebis, J. J.,

Husbands, P., Keutzer, K., Patterson, D. A., Plishker,

W. L., Shalf, J., Williams, S. W., et al. (2006). The

landscape of parallel computing research: A view

from berkeley. Technical report, Technical Report

UCB/EECS-2006-183, EECS Department, University

of California, Berkeley.

Basak, A., Li, S., Hu, X., Oh, S. M., Xie, X., Zhao, L.,

Jiang, X., and Xie, Y. (2019). Analysis and optimiza-

tion of the memory hierarchy for graph processing

workloads. In 2019 IEEE International Symposium on

High Performance Computer Architecture (HPCA),

pages 373–386. IEEE.

Beamer, S., Asanovi

c, K., and Patterson, D. (2015). The gap

benchmark suite. arXiv preprint arXiv:1508.03619.

Besta, M., Podstawski, M., Groner, L., Solomonik, E., and

Hoeﬂer, T. (2017). To push or to pull: On reducing

communication and synchronization in graph com-

putations. In Proceedings of the 26th International

Symposium on High-Performance Parallel and Dis-

tributed Computing, pages 93–104. ACM.

Buluc¸, A. and Gilbert, J. R. (2011). The combinatorial blas:

Design, implementation, and applications. The Inter-

national Journal of High Performance Computing Ap-

plications, 25(4):496–509.

A2P: Attention-based Memory Access Prediction for Graph Analytics

143

Byna, S., Chen, Y., and Sun, X.-H. (2008). A taxonomy of

data prefetching mechanisms. In 2008 International

Symposium on Parallel Architectures, Algorithms, and

Networks (i-span 2008), pages 19–24. IEEE.

”ChampSim” (2017). https://github.com/champsim/champsim.

Chen, M. and Liu, P. (2017). Performance evaluation of

recommender systems. International Journal of Per-

formability Engineering, 13(8):1246.

Dosovitskiy, A., Beyer, L., Kolesnikov, A., Weissenborn,

D., Zhai, X., Unterthiner, T., Dehghani, M., Minderer,

M., Heigold, G., Gelly, S., et al. (2020). An image is

worth 16x16 words: Transformers for image recogni-

tion at scale. arXiv preprint arXiv:2010.11929.

Drosou, A., Kalamaras, I., Papadopoulos, S., and Tzovaras,

D. (2016). An enhanced graph analytics platform

(gap) providing insight in big network data. Journal

of Innovation in Digital Ecosystems, 3(2):83–97.

Greff, K., Srivastava, R. K., Koutn

ık, J., Steunebrink, B. R.,

and Schmidhuber, J. (2016). Lstm: A search space

odyssey. IEEE transactions on neural networks and

learning systems, 28(10):2222–2232.

Grossman, S., Litz, H., and Kozyrakis, C. (2018). Making

pull-based graph processing performant. In Proceed-

ings of the 23rd ACM SIGPLAN Symposium on Prin-

ciples and Practice of Parallel Programming, pages

246–260. ACM.

Han, M. and Daudjee, K. (2015). Giraph unchained: bar-

rierless asynchronous parallel execution in pregel-like

graph processing systems. Proceedings of the VLDB

Endowment, 8(9):950–961.

Hashemi, M., Swersky, K., Smith, J. A., Ayers, G., Litz,

H., Chang, J., Kozyrakis, C., and Ranganathan, P.

(2018a). Learning memory access patterns. arXiv

preprint arXiv:1803.02329.

Hashemi, M., Swersky, K., Smith, J. A., Ayers, G., Litz,

H., Chang, J., Kozyrakis, C., and Ranganathan, P.

(2018b). Learning memory access patterns. CoRR,

abs/1803.02329.

Jain, A. and Lin, C. (2013). Linearizing irregular memory

accesses for improved correlated prefetching. In Pro-

ceedings of the 46th Annual IEEE/ACM International

Symposium on Microarchitecture, pages 247–259.

Kim, J., Pugsley, S. H., Gratz, P. V., Reddy, A. N., Wilk-

erson, C., and Chishti, Z. (2016). Path conﬁdence

based lookahead prefetching. In 2016 49th Annual

IEEE/ACM International Symposium on Microarchi-

tecture (MICRO), pages 1–12. IEEE.

Kumar, S. and Wilkerson, C. (1998). Exploiting spatial lo-

cality in data caches using spatial footprints. In Pro-

ceedings. 25th Annual International Symposium on

Computer Architecture (Cat. No. 98CB36235), pages

357–368. IEEE.

Lakhotia, K., Kannan, R., Pati, S., and Prasanna, V. (2020).

Gpop: A scalable cache-and memory-efﬁcient frame-

work for graph processing over parts. ACM Transac-

tions on Parallel Computing (TOPC), 7(1):1–24.

Low, Y., Bickson, D., Gonzalez, J., Guestrin, C., Kyrola, A.,

and Hellerstein, J. M. (2012). Distributed graphlab:

a framework for machine learning and data mining

in the cloud. Proceedings of the VLDB Endowment,

5(8):716–727.

Lumsdaine, A., Gregor, D., Hendrickson, B., and Berry, J.

(2007). Challenges in parallel graph processing. Par-

allel Processing Letters, 17(01):5–20.

Malewicz, G., Austern, M. H., Bik, A. J., Dehnert, J. C.,

Horn, I., Leiser, N., and Czajkowski, G. (2010).

Pregel: a system for large-scale graph processing. In

Proceedings of the 2010 ACM SIGMOD International

Conference on Management of data, pages 135–146.

ACM.

McSherry, F., Isard, M., and Murray, D. G. (2015). Scal-

ability! but at what cost? In Proceedings of the

15th USENIX Conference on Hot Topics in Operating

Systems, HOTOS’15, pages 14–14. USENIX Associ-

ation.

Michaud, P. (2016). Best-offset hardware prefetching. In

2016 IEEE International Symposium on High Perfor-

mance Computer Architecture (HPCA), pages 469–

480. IEEE.

Nguyen, D., Lenharth, A., and Pingali, K. (2013). A

lightweight infrastructure for graph analytics. In Pro-

ceedings of the Twenty-Fourth ACM Symposium on

Operating Systems Principles, pages 456–471. ACM.

Page, L., Brin, S., Motwani, R., and Winograd, T. (1999).

The pagerank citation ranking: Bringing order to the

web. Technical report, Stanford InfoLab.

Pingali, K., Nguyen, D., Kulkarni, M., Burtscher, M., Has-

saan, M. A., Kaleem, R., Lee, T.-H., Lenharth, A.,

Manevich, R., M

endez-Lojo, M., et al. (2011). The

tao of parallelism in algorithms. In ACM Sigplan No-

tices, volume 46, pages 12–25. ACM.

Roy, A., Mihailovic, I., and Zwaenepoel, W. (2013). X-

stream: Edge-centric graph processing using stream-

ing partitions. In Proceedings of the Twenty-Fourth

ACM Symposium on Operating Systems Principles,

pages 472–488. ACM.

Shevgoor, M., Koladiya, S., Balasubramonian, R., Wilker-

son, C., Pugsley, S. H., and Chishti, Z. (2015). Efﬁ-

ciently prefetching complex address patterns. In 2015

48th Annual IEEE/ACM International Symposium on

Microarchitecture (MICRO), pages 141–152. IEEE.

Shun, J. and Blelloch, G. E. (2013). Ligra: a lightweight

graph processing framework for shared memory. In

ACM Sigplan Notices, volume 48, pages 135–146.

ACM.

Siek, J., Lumsdaine, A., and Lee, L.-Q. (2002). The

boost graph library: user guide and reference man-

ual. Addison-Wesley.

Silveira, T., Zhang, M., Lin, X., Liu, Y., and Ma, S. (2019).

How good your recommender system is? a survey on

evaluations in recommendation. International Jour-

nal of Machine Learning and Cybernetics, 10(5):813–

831.

Srivastava, A., Lazaris, A., Brooks, B., Kannan, R., and

Prasanna, V. K. (2019). Predicting memory accesses:

the road to compact ml-driven prefetcher. In Proceed-

ings of the International Symposium on Memory Sys-

tems, pages 461–470.

DATA 2022 - 11th International Conference on Data Science, Technology and Applications

144

Srivastava, A., Wang, T.-Y., Zhang, P., De Rose, C. A. F.,

Kannan, R., and Prasanna, V. K. (2020). Memmap:

Compact and generalizable meta-lstm models for

memory access prediction. In Paciﬁc-Asia Conference

on Knowledge Discovery and Data Mining, pages 57–

68. Springer.

Sundaram, N., Satish, N., Patwary, M. M. A., Dulloor,

S. R., Anderson, M. J., Vadlamudi, S. G., Das, D.,

and Dubey, P. (2015). Graphmat: High performance

graph analytics made productive. Proceedings of the

VLDB Endowment, 8(11):1214–1225.

Vanderwiel, S. P. and Lilja, D. J. (2000). Data prefetch

mechanisms. ACM Computing Surveys (CSUR),

32(2):174–199.

Vaswani, A., Shazeer, N., Parmar, N., Uszkoreit, J., Jones,

L., Gomez, A. N., Kaiser, Ł., and Polosukhin, I.

(2017). Attention is all you need. In Advances in

neural information processing systems, pages 5998–

6008.

Vuduc, R., Demmel, J. W., and Yelick, K. A. (2005). Oski:

A library of automatically tuned sparse matrix kernels.

In Journal of Physics: Conference Series, page 521.

IOP Publishing.

Webster, J. J. and Kit, C. (1992). Tokenization as the initial

phase in nlp. In COLING 1992 Volume 4: The 14th

International Conference on Computational Linguis-

tics.

Wenisch, T. F., Ferdman, M., Ailamaki, A., Falsaﬁ, B., and

Moshovos, A. (2009). Practical off-chip meta-data for

temporal memory streaming. In 2009 IEEE 15th Inter-

national Symposium on High Performance Computer

Architecture, pages 79–90. IEEE.

Zeyer, A., Bahar, P., Irie, K., Schl

uter, R., and Ney, H.

(2019). A comparison of transformer and lstm en-

coder decoder models for asr. In 2019 IEEE Auto-

matic Speech Recognition and Understanding Work-

shop (ASRU), pages 8–15. IEEE.

Zhang, K., Chen, R., and Chen, H. (2015). Numa-aware

graph-structured analytics. ACM SIGPLAN Notices,

50(8):183–193.

Zhang, P., Srivastava, A., Brooks, B., Kannan, R., and

Prasanna, V. K. (2020). Raop: Recurrent neural

network augmented offset prefetcher. In The Inter-

national Symposium on Memory Systems (MEMSYS

2020).

Zhang, P., Srivastava, A., Nori, A. V., Kannan, R., and

Prasanna, V. K. (2022). Fine-grained address segmen-

tation for attention-based variable-degree prefetching.

In Proceedings of the 19th ACM International Confer-

ence on Computing Frontiers, pages 103–112.

Zhang, P., Srivastava, A., Wang, T.-Y., De Rose, C. A., Kan-

nan, R., and Prasanna, V. K. (2021). C-memmap:

clustering-driven compact, adaptable, and generaliz-

able meta-lstm models for memory access prediction.

International Journal of Data Science and Analytics,

pages 1–14.

Zhou, S., Lakhotia, K., Singapura, S. G., Zeng, H., Kannan,

R., Prasanna, V. K., Fox, J., Kim, E., Green, O., and

Bader, D. A. (2017). Design and implementation of

parallel pagerank on multicore platforms. In High Per-

formance Extreme Computing Conference (HPEC),

2017 IEEE, pages 1–6. IEEE.

Zhu, X., Han, W., and Chen, W. (2015). Gridgraph: Large-

scale graph processing on a single machine using 2-

level hierarchical partitioning. In 2015 USENIX An-

nual Technical Conference (USENIX ATC 15), pages

375–386. USENIX Association.

A2P: Attention-based Memory Access Prediction for Graph Analytics

145