Comparative Study between EKF, SVSF, Combined SVSF-EKF, and

ASVSF Approaches based Scale Estimation of Monocular SLAM

Elhaouari Kobzili

1 a

, Ahmed Allam

and Cherif Larbes

Electronic Department, National Polytechnic School, 10 Avenue des Fr

eres Oudek, ElHarrach, BP 182, Algiers, Algeria

Automatic Department, National Polytechnic School, 10 Avenue des Fr

eres Oudek, ElHarrach, BP 182, Algiers, Algeria

Keywords:

Monocular SLAM, Scale Estimation, Robust Filter, Multi-rate.

Abstract:

This paper presents a comparative study of scale recovering in monocular simultaneous localization and map-

ping (Mono-SLAM) by adopting and adapting four estimators into a multi-rate fusion mechanism and consid-

ering the scale as an element of the state vector. These estimators are: extended Kalman ﬁlter (EKF), smooth

variable structure ﬁlter (SVSF), combined SVSF-EKF, and particularly adaptive smooth variable structure ﬁl-

ter (ASVSF). The use of the ASVSF estimator represents the novelty of this paper because it provides a robust

estimation of the trajectory scale as well as the covariance matrix at each iteration. This later represents the

estimation incertitude. A second sensor is involved (inertial measurement unit (IMU)) as a reference to align

the up to scale trajectory provided by the Mono-SLAM box. The designed system allows ﬁnding the scale

factor with a rate not further than the IMU frequency and avoids complex synchronization. In order to outline

the limitation of each estimator used for scale recovering, a deep analysis of the proposed approaches in terms

of robustness, stability, accuracy, and real-time constraint was carried out.

1 INTRODUCTION

The autonomous navigation task of an unmanned

aerial vehicle (UAV) is an active ﬁeld. However the

localization of UAV in the environment of navigation

is crucial to realize its missions. To safely navigate the

robot, it must perceive and recognize its environment.

To deal with these requirements, the UAV must be

equipped with the simultaneous localization and map-

ping (SLAM) module. Recently, the world has seen a

sophisticated SLAM, based just on a monocular cam-

era (Mono-SLAM). The Mono-SLAM problems are

not completely solved, they are still under improve-

ment. The challenge of Mono-SLAM approaches is

to develop a solution of localization and mapping us-

ing just one camera with a compromise between price

and algorithmic complexity. In this context many

frameworks have been proposed in order to provide

a good estimated pose as parallel tracking and map-

ping (PTAM) (Klein and Murray, 2007) large scale

direct monocular simultaneous localization and map-

ping (LSD-SLAM) (Engel and Cremers, 2014), a ver-

satile and accurate Monocular SLAM System (ORB-

SLAM) (Mur-Artal et al., 2015), and Continuous Lo-

https://orcid.org/0000-0002-3112-9347

calization and Mapping in a Dynamic World (CD-

SLAM) (Pirker et al., 2011). With respect to the state-

of-the-art, all the previous Mono-SLAMs provide a

pose up to scale and suffer from the scale ambigu-

ity. In fact, this Mono-SLAM problem is due to the

physical limitation of depth measurement. The scale

error drifts by time, so it needs to be recovered at each

step. Recovering the scale means that a robot has

instantly a metric pose and a realistic interpretation

of the evolution area. Many approaches and meth-

ods have been proposed to solve the scale problem.

However, many authors have tackled the scale prob-

lem by designing sophisticated algorithms, based on

the same frames which are exploited by the Mono-

SLAM box. Other researchers recommended to con-

sider the Mono-SLAM as a box which provides a pose

up to scale, and involves other sensors as references.

This type of solution can be more suited to scale re-

covery. These sensors can ensure a continuous local-

ization separately from the Mono-SLAM box. With

a sensor of high rate, it is possible to ﬁnd the scale

factor long times before processing a new pose (up to

scale) provided by the Mono-SLAM box.

This paper is based on Gabriel Nutzi (Nutzi et al.,

2011) efforts, the inertial measurement unit (IMU)

data is considered as a reference to recover the ab-

668

Kobzili, E., Allam, A. and Larbes, C.

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM.

DOI: 10.5220/0011317100003271

In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 668-679

ISBN: 978-989-758-585-2; ISSN: 2184-2809

solute scale. We elaborate a multi-rate fusion mech-

anism which functions on irregular integration time.

To get a dynamic estimation of the scale, it is con-

sidered as an element of the state vector. Fortunately,

this situation is possible by enforcing the pose pro-

vided by the two boxes (Mono-SLAM and IMU) to

be in the same scale. This paper is an extension of our

works originally presented in (Kobzili et al., 2017a)

and (Kobzili et al., 2017b). The major difference is to

involve the ASVSF as an estimator to ﬁnd the metric

trajectory.

The main contributions of this paper per rapport

our previous works are:

• To involve exclusively, the ASVSF estimator to

determine the scale factor.

• To investigate the scale estimation using robust ﬁl-

ters, and developing those presented in (Kobzili

et al., 2017a; Kobzili et al., 2017b).

• To compare and analyze the performances of scale

estimation using EKF, SVSF, Combined SVSF-

EKF, and ASVSF.

• To perform the comparative study of the estima-

tors based scale recovering on real data.

This paper is organized as follows: Section. 2

gives the state-of-the-art of the different approaches

developed for scale recovering. Section. 3 sketches

the designed methodology of scale estimation and de-

tails the theories of the four estimators involving in

the scale estimation process. Section. 4 deals with

the presentation of the different results, by focusing

on performance analysis of the proposed estimators.

Section. 5 presents experiment results applied on a

well known dataset. In this part, the four estimators

are evaluated in terms of accuracy and real time con-

straint. Conclusion and further works are drawn in

Section. 6.

2 RELATED WORK

2.1 Global Context

In the last decade, the SLAM task has been treated

as an important ﬁeld of research. However, it has

been tackled primary as a ﬁltering problem. The most

popular solutions have been based on EKF-SLAM

(Smith et al., 1990), Fast-SLAM (Montemerlo, 2003),

and SLAM based state dependent Ricatti equation

(SDRE) (Nemra, 2011). Recently, the SLAM has

been solved by including vision sensors as the main

sources of information in order to deal with many real

life applications. In previous SLAM works, the scale

factor problem has not attracted so much attention

(the SLAM resolved based on stereo-vision), because

it is difﬁcult to get depths of features easily (based

on triangulation). Later, monocular SLAM became

more and more a popular research topic (Klein and

Murray, 2007; Engel and Cremers, 2014; Mur-Artal

et al., 2015; Pirker et al., 2011; Davison et al., 2007;

Civera et al., 2008; Eade and Drummond, 2006), by

emerging complex imaging algorithms.

2.2 Scale Recovering based on Vision

Some authors proposed to exploit camera frames by

extracting the adequate information needed for scale

calculation. These approaches took advantage of the

geometric nature of the environment by acquiring a

known objects from the real world to update the scale

value. We mention Davison et al (Davison et al.,

2007) method, which is based on a referenced points

existing in the navigating scene. In the same context,

there are other authors who suggested to use the road

map of the explored environment, by calculating the

correspondent homography to decrease scale ambigu-

ity (Simond and Rives, 2004; Dumortier et al., 2006;

Scaramuzza and Siegwart, 2008; Kitt et al., 2007). In

these previous solutions, the road was supposed ﬂat,

in order to keep the same distance between camera

and road. To reach the scale performances of stereo-

vision SLAMs, Shiyu Song (Song and Chandraker,

2014) includes a new cue combination framework for

ground plane estimation. The same steps were fol-

lowed by Johannes Grater (Grater et al., 2015). His

work was articulated on the vanishing points. Another

methodology of scale recovering based on extraction

of object classes from images of the explored region

(Botterill et al., 2013; Frost et al., 2016; Pillai and

Leonard, 2015). These objects are compared with the

real object’s dimensions to reduce the scale drift. Un-

fortunately, the majority of previous approaches suf-

fer from the level of images qualities, because they

are inﬂuenced by severe environment changes. The

utilization of a monocular camera only, can affect the

reliability of the designed system, so it is very im-

portant to involve other types of sensors to ﬁnd the

absolute scale.

2.3 Particular Techniques of Scale

Recovering

In a particular application of scale recovering, it is

possible to proﬁt from the non holonomic constraints

of cars during turns (Scaramuzza et al., 2009). This

approach has a restriction of regular turns in order to

deal with the real scale. A speciﬁc scheme of scale

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM

669

estimation was proposed in (Gutierrez-Gomez et al.,

2012), in which the author based on performing a

spectral analysis of vertical movement result of hu-

man walking by using empirical equations of human

motion. To avoid scale ambiguity, some authors sup-

posed to have partial information about the three di-

mensions of the environment geometry (Lothe, 2010).

2.4 Scale Recovering with an Additional

Sensor

Another framework is to use other sensor with Mono-

SLAM as adding another camera (Nister et al., 2006;

Lemaire et al., 2007), in which the 3D coordinates of

points are found based on the triangulation method,

but this solution is very heavy in terms of computa-

tion. All Mono-SLAMs need to close the loop in or-

der to eliminate drifts after realizing a considerable

trajectory, in this context, a sophisticated solution of

scale drift reducing is loop closing many times based

on collaborative SLAM (Forste et al., 2013). The ab-

solute position provided by the GPS is a good solu-

tion to recover the metric pose of the Mono-SLAM

box (Agrawal and Konolige, 2006; Ikeda et al., 2007).

Unfortunately, the GPS is not present all the time.

In the same context, it is possible to involve many

sensors into a mechanism scheme to limit the scale

drift as in (Zachariah and Jansson, 2011). In this

work, the author focused on airspeed and IMU sen-

sors. The previous work encourages us to proﬁt from

the multi rate scheme due to the high frequency of

scale recovery. Lv Qiang et al utilized Laser range in

an indoor situation to ﬁnd the scale of ORB-SLAM

by ﬁltering (Qiang et al., 2016). In this paper, the

IMU is used to recover the scale based on a fusion

mechanism. Recent efforts are given in (Strelow and

Singh, 2004; Hol et al., 2007; Weiss and Siegwart,

2011). They used very accurate inertial navigation

system (INS) with high rate, but this solution can’t

deal with our future works (realizing a low cost so-

lution for scale recovery). Our work, is based essen-

tially on Gabriel Nutzi’s work (Nutzi et al., 2011), in

which the author designed two solutions: the ﬁrst one

is about the spline ﬁtting task inspired and modiﬁed

from the paper of Jung and Taylor (Jung and Taylor,

2001). The designed system didn’t deal with the real

time constraint. In the second solution, the author

suggests to consider the scale factor as an element

of the state vector. In the last work, the author uti-

lizes a recent Mono-SLAM named PTAM (Klein and

Murray, 2007), this last was restricted to indoor ap-

plication. The author Gabriel Nutzi based his work

on EKF, which gives a good result in ordinary con-

ditions. These performances degraded in an outdoor

situation, especially in severe environmental changes,

and automatically inﬂuenced the scale value quality.

2.5 Scale Recovering and the

Robustness Involving

The method of scale factor recovery must provide the

scale value with a high robustness, but unfortunately

it is not the case for the EKF. To increase the ro-

bustness of scale estimation, we based our work on

a new robust ﬁlter named smooth variable structure

ﬁlter (SVSF) (Habibi, 2007). This ﬁlter is used into

a multi-rate mechanism by considering the Mono-

SLAM, and IMU data as measurements of the fu-

sion process. To improve the robustness of scale

estimation, a new solution is investigated, in which

the smooth variable structure ﬁlter (SVSF) (Habibi,

2007) is combined with the EKF (Combined SVSF-

EKF) (Habibi, 2008). This combination permits to

stay near performance of EKF. This solution allows

to beneﬁt from the advantage of SVSF and EKF. The

synergy created by the combination of the two ﬁlters

permit to exercise the SVSF force outside the smooth-

ing boundary layer, and to proﬁt from the accuracy of

EKF inside this layer. To go further in the comparison

of the approaches proposed, it is suggested to investi-

gate the improved version of SVSF named as adaptive

smooth variable structure ﬁlter (ASVSF) (Gadsden

and Habibi, 2010; Gadsden et al., 2011), in which,

it is based on an adaptive boundary layer. All esti-

mators suggested for scale estimation functioned into

a multi-rate mechanism (Armesto et al., 2004). This

paper is an extension of our previous works (Kobzili

et al., 2017a; Kobzili et al., 2017b). However, a deep

comparison between the scale approaches followed

by a performance analysis are detailed in our paper

sections.

3 METHODOLOGY

3.1 An Overview of the Designed

System

3.1.1 Parameters of the Designed System

We design a system able to provide a metric pose us-

ing Mono-SLAM data. This modular conception al-

lows us to change the Mono-SLAM box easily with-

out affecting the integrity of our system. All Mono-

SLAMs provide a pose up to scale. The camera pose

is deﬁned in six dimensions (6D), three for Cartesian

position X

SLAM,k



x y z



, and three for angu-

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

670

lar position φ

SLAM,k



ϕ θ ψ



. The camera’s

pose provides information about the trajectory, but it

is not a metric position due to depth ambiguity. The

rate of the Mono-SLAM suggested to be equal 20

Hz. In our simulation, the camera and the IMU are

assumed to have the same gravity center. The IMU

sensor provides accelerations, and angular rates with

a frequency of 200 Hz, deﬁned in the body frame

IMU



ax ay az



, ω

IMU



p q r



To be near the reality, the output of Mono-SLAM

is assumed to be affected by a zero mean Gaussian

noise of standard deviation σ

= 0.01m.

The standard deviation of noise affected acceler-

ations measurements of IMU is given by σ

= 2 ·

−3

m/s

, with a bias of σ

= 3 · 10

−3

m/s

. The

gyros of the considered IMU affected by noise with

a standard deviation value σ

= 1.6968 · 10

−4

rad/s,

and a bias σ

= 1.9393 · 10

−5

rad/s.

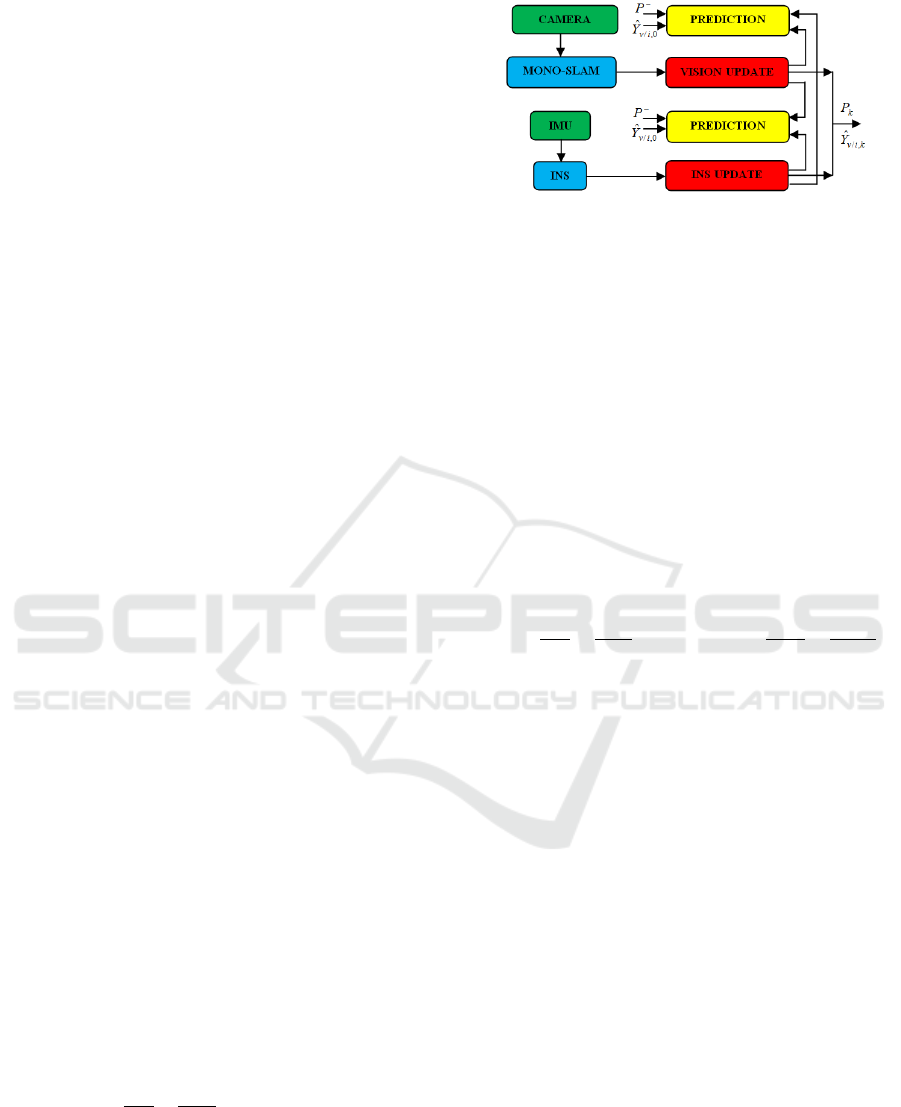
3.1.2 Synoptic Representation of the Designed

System

The system consists of two fusion processes with the

same prediction model based on a temporal motion.

The updating is realized by considering two measure-

ments coming from the Mono-SLAM and the IMU.

The transfer of state variation is alternated between

the two fusion processes into a multi rate mechnism

scheme.For more details about the designed system

see Fig. 1,

v/i,k

: represents the state vector of our

system. The notice v/i denotes vision and IMU. The

matrix P

is the covariance matrix, which is initialized

by P

3.2 Extended Kalman Filter Approach

The nonlinear prediction model proposed is given by:

(1). This model is detailed by the full expression

given by: (2). The scale factor is considered as an

element of the state vector which is injected in the

equations of position. For each step we get a new es-

timated scale based on the last measurement which is

used to correct the Mono-SLAM poses.

v/i,k

= f



k−1

,φ

k−1

,λ

k−1



+ q

(1)







T I

k−1

2λ

k−1

T I







k−1

(2)

Figure 1: An overview of the designed system.

The state vector elements are deﬁned in the navi-

gation frame, where x

∈ R

3×1

is the position vector

without scale, v

∈ R

3×1

and a

∈ R

3×1

represent the

velocity and acceleration vectors of the Camera-IMU

system. The Euler angles are φ

∈ R

3×1

, the vector

∈ R

3×1

is Euler angles velocities. The parameter

is the scale factor. The vector q

is a Gaussian

noise that affected our system. The index v/i deﬁnes

the prediction and the measurement in the case of vi-

sion or IMU. Where I

mean an identity and zero

matrixes of dimension 3 × 3, and 0

mean suc-

cessfully column and raw vectors of elements equal

to zero.

Our prediction model is a nonlinear system. Its

Jacobian matrix (F) is given by: (3).







T I

k−1

2λ

k−1

−

T v

k−1

−

k−1

2λ

k−1

T I







(3)

Its prior covariance matrix is given by: (4)

−

= FP

+ Q (4)

−

: represents the prior covariance matrix, and

Q is the noise covariance matrix. The matrix P

de-

ﬁnes the posterior covariance matrix which is initial-

ized by P

. To involve the multi-rate mechanism, it is

suggested to consider that there are two measurement

sources (Camera and IMU). When the Mono-SLAM

box provides a new measurement, our system calcu-

lates a prediction of the state vector using the last val-

ues and doing the updating by taking into considera-

tion the Mono-SLAM data. To deal with the appro-

priate time of prediction, we use the equation (5) to

calculate the time of integration.

T = t − T

(5)

t: is the time of calculation deﬁned by the loop of

execution (internal clock). The variable T

represents

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM

671

the time of the last estimated vector. In case of IMU

data, the estimation process has to recover the scale

many times due to its high frequency compared to the

Mono-SLAM observation.

The two measurement models used in our paper

for the Mono-SLAM and IMU boxes are given by

equations (6) and (9) which are cited afterwards. The

state vector observation of our system is goes through

two differents observation matrices depends on mea-

surments provided by the sensor used.

vm,k

= H

SLAM,k

(6)

The observation matrix of Mono-SLAM measure-

ments is given by (7).



3×1



(7)

The measurement vector provided by the Mono-

SLAM box is deﬁned by: (8).

SLAM,k



SLAM,k

1×6

SLAM,k

1×3



(8)

im,k

= H

IMU,k

(9)

The observation matrix of IMU measurements is

given as follows by: (10).



3×1



(10)

The measurement vector provided by the IMU box

is deﬁned by: (11).

IMU,k



1×6

IMU,k

1×3

IMU,k



(11)

The acceleration vector was calculated in the nav-

igation frame using IMU data which is given by: (12).

IMU,k

= C

(k − 1)a

IMU

+ g

(12)

The Euler angles velocities are deﬁned in the nav-

igation frame by the following equation (13).

IMU,k

= E

(k − 1)ω

(k) (13)

The matrixes C

(k − 1), and E

(k − 1) represent

the cosine direction, and the rotation rate conversion

from the body to the navigation frame. g

is the grav-

ity in the navigation frame.

The equations of the state vector correction us-

ing Mono-SLAM data are illustrated by the following

equations: (14), (15) and (16).

Kalman

v,k

= P

−



−

+ R



−1

(14)

v/i,k

v,k

+ K

Kalman

v,k



v,k

−Y

vm,k



(15)



− K

Kalman

v,k



−

(16)

The equations of state vector correction using

IMU data are illustrated by the following equations

(17), (18) and (19).

Kalman

i,k

= P

−



−

+ R



−1

(17)

v/i,k

i,k

+ K

Kalman

i,k



i,k

−Y

im,k



(18)



− K

Kalman

i,k



−

(19)

Where K

Kalman

v,k

, and K

Kalman

i,k

are deﬁned Kalman

gains for vision and IMU measurements.

The two matrixes R

, and R

are the noise covari-

ance associated with Mono-SLAM and IMU mea-

surements. The covariance matrix update is deﬁned

by P

3.3 Smooth Variable Structure Filter

Approach

The SVSF is a closed loop ﬁlter (predictor-corrector)

proposed by S. Habibi (Habibi, 2007), developed on

the base of variable structure theory and sliding mode

concepts, its structure based principally on a prior,

and posterior errors between prediction and observa-

tion of the state vector elements.

The advantages of SVSF estimator compared to

EKF are the robustness and stability. The lineariza-

tion of the system is not needed, and the noise model

is not necessary. The disadvantages of this estima-

tor are the non optimality as all nonlinear ﬁlters, the

chattering, and the choice of the superior limit of in-

certitude.

The previous prediction model (1) and (2) is uti-

lized. The state vector elements are initialized by

v/i,0

and the posterior error of estimation E

0/0

. The

update of our process is performed by using the two

considered measurements which are given by (6) and

(9). At a time, we use Mono-SLAM output, and at

another time the IMU. In this case, another observa-

tion matrixes are used H

= I

, and H

= I

, these

changes are due to the concept of SVSF mechanism.

The IMU vector measurements are given by the

following equation (20).

IMU,k



IMU



(20)

Where X

IMU,k

, V

IMU,k

, a

IMU,k

, φ

IMU,k

, and

IMU,k

are the position, the velocity, the acceleration, the Eu-

ler angles, and the angular rate vectors deﬁned in the

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

672

navigation frame. The acceleration and angular rate

vectors are synthesized using the INS mechanization

(12) and (13) based on temporal integration.

In the ﬁrst process update, we use Mono-SLAM

output based on the following equations (21), (22),

(23), and (24).

v,k/k−1

v,k

−Y

vm,k/k−1

(21)

SV SF

v,k

= H

diag

(



v,k/k−1



Abs

+ γ



k−1/k−1



Abs

)

◦

sat(

−1

v,k/k−1

)





diag(E

v,k/k−1

)



−1

(22)

The sign

◦

is the Schur operator (vector of element

by element multiply). Sat is the saturation function.

The notation Abs means absolute value.

v/i,k/k

= Y

v,k

+ K

SV SF

v,k

v,k/k−1

(23)

k/k

v,k

−Y

v/i,k/k

(24)

In the second, the IMU data are utilized to update

the state vector elements based on the following equa-

tions (25), (26), (27), and (28).

i,k/k−1

i,k

−Y

im,k/k−1

(25)

SV SF

i,k

= H

diag

(



i,k/k−1



Abs

+ γ



k−1/k−1



Abs

)

◦

sat(

−1

i,k/k−1

)



diag(E

i,k/k−1

)



−1

(26)

v/i,k/k

= Y

i,k

+ K

SV SF

i,k

i,k/k−1

(27)

k/k

i,k

−Y

v/i,k/k

(28)

Where



v,k/k−1

i,k/k−1



, E

k/k

deﬁne prior and

posterior errors, K

SV SF

v,k

, and K

SV SF

i,k

are the SVSF

gains calculated in case of vision and IMU obser-

vation H

, and H

are the pseudo inverses of the

two observation matrixes (Mono-SLAM and IMU)

for the vision and inertial measurements, the param-

eter γ ∈ R

16×16

(0 < γ ≤ 1) is a diagonal matrix, its

diagonal elements deﬁne the convergence rate of the

state vector elements. In our work, it is supposed the

following value γ = 0.5 × I

The diagonal matrix

−1

represents the inverse of

ψ. This last is a boundary constructed with respect to

the smoothing boundary layer vector.

−1







1/ψ

1,1

· · · 0

0 · · · 1/ψ

16,16







(29)

3.4 Combined SVSF-EKF Approach

The SVSF is a robust estimator compared to EKF.

The author S. Habibi suggests to combine SVSF

and EKF (Habibi, 2008) to improve estimator perfor-

mance. The author, based on the variable structure

ﬁlter (VSF) enforces the estimated elements to enter

into the smooth boundary layer. Inside the boundary

layer, the EKF is involved as a primary actor of esti-

mation. We use the same model of prediction given

by (1) and (2).

The two measurement vectors provided by Mono-

SLAM and IMU boxes are similar to (6) and (9). The

observation matrices are those utilized in Sect. 3.3.

The combined SVSF-EKF gains are represented

by the following equations (30) and (31).

v,k









v,k/k−1



+ γ



k−1/k−1





+ Π





◦

sat(K

Kalman

v,k

v,k/k−1

, 1)

(30)

i,k









i,k/k−1



+ γ



k−1/k−1





+ Π





◦

sat(K

Kalman

i,k

i,k/k−1

, 1)

(31)

The correction of the state vector elements are cal-

culated by the following manner (32) and (33); where

Kalman

v,k

, and K

Kalman

i,k

are the EKF gains with respect

to vision and IMU measurements calculated by (14)

and (17). The notation Ab means absolute value.

v/i,k/k

= Y

v,k

+ k

v,k

v,k/k−1

(32)

v/i,k/k

= Y

i,k

+ k

i,k

i,k/k−1

(33)

It is supposed Π = 0.9 × I

because, this matrix

of factors deﬁnes the magnitude of EKF dominating

inside the boundary layer. It must be higher than γ in

order to emphasize Kalman action within the bound-

ary layer.

3.5 Adaptive Smooth Variable

Structure Filter Approach

An adaptive estimator version can provide better scale

estimation in terms of robustness and accuracy. The

ASVSF (Gadsden and Habibi, 2010; Gadsden et al.,

2011)( adaptive smooth variable structure ﬁlter) uti-

lizes the covariance matrix in order to have an idea

about the probability of the estimated elements. The

new version of SVSF is deﬁned by the covariance ma-

trice derivative and an optimal boundary layer matrix

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM

673

opt

. The boundary layer matrix (29) being not diag-

onal, by including a full derivation of the covariance

matrix (Hol et al., 2007). The boundary layer

opt

obtained by: (34), which is given by: (35).

∂(trace[P])

∂

= 0 (34)

opt







1,1

· · · ψ

1,16

16,1

· · · ψ

16,16







(35)

In case of ASVSF we follow the same steps de-

ﬁned by Subsection. 3.3. The difference is in the

utilization of the covariance matrix to calculate the

boundary layer as given by (36) and (37). The correc-

tion part of the ASVSF ﬁlter needs the linearization

of the observation matrixes to calculate the optimal

boundary layer (35).

opt

v,k



+ R





−1

diag





v,k/k−1



Abs

+ γ



k−1/k−1



Abs

i

(36)

opt

i,k



+ R





−1

diag





i,k/k−1



Abs

+ γ



k−1/k−1



Abs

i

(37)

ASV SF

v,k

= H

diag

(



v,k/k−1



Abs

+ γ



k−1/k−1



Abs

)

◦

sat(



opt

v,k



−1

v,k/k−1

)





diag(E

v,k/k−1

)



−1

(38)

ASV SF

i,k

= H

diag

(



i,k/k−1



Abs

+ γ



k−1/k−1



Abs

)

◦

sat(



opt

i,k



−1

i,k/k−1

)





diag(E

i,k/k−1

)



−1

(39)

The previous gains are used in (38) and (39) to

provide the correction of state vector elements in (40)

and (41).

v/i,k/k

= Y

v,k

+ K

ASV SF

v,k

v,k/k−1

(40)

v/i,k/k

= Y

i,k

+ K

ASV SF

i,k

i,k/k−1

(41)

The update of the covariance matrices in the case

of vision and inertial measurement are given by: (42)

and (43).



− K

ASV SF

v,k



−



− K

ASV SF

v,k



ASV SF

v,k

ASV SF

v,k

(42)



− K

ASV SF

i,k



−



− K

ASV SF

i,k



ASV SF

i,k

ASV SF

i,k

(43)

4 SIMULATION RESULTS

4.1 Evaluation Scenarios

We suggest four scenarios of scale variation. At ﬁrst,

an arbitrary trajectory (on Matlab software) was sim-

ulated of the couple (Camera/IMU), and it is taken

into consideration the standard deviation noises sup-

posed in Sect. 3.1. In the ﬁrst scenario, the scale of

the Mono-SLAM is considered as the absolute scale

λ = 1, but we suggest a bad initialization λ

= 0.5

(the scale initialization is an important point of scale

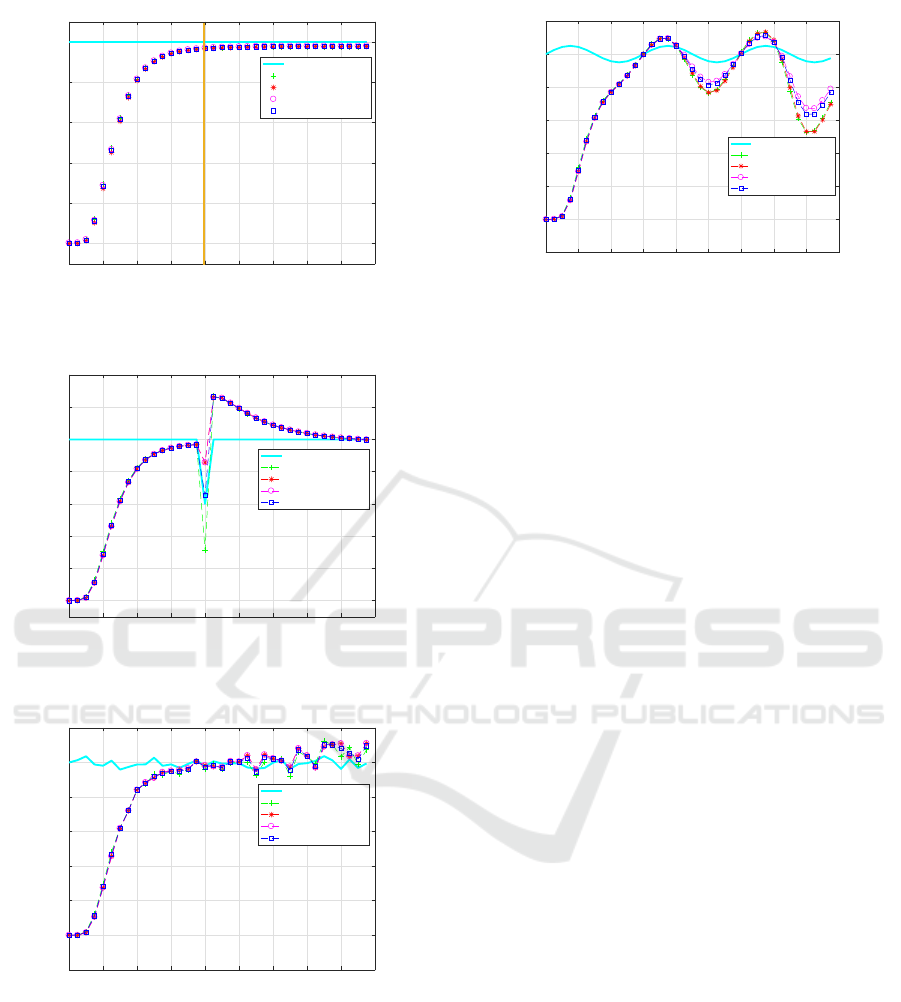
estimation). The output graph is given by Fig. 2. We

remark that the absolute scale estimation (by the four

estimators) is recovered after 8 seconds despite start-

ing with a worst case. ALL approaches stabilize in the

absolute scale after 8 seconds with an average error of

0.8% due to the noises affecting the other state vec-

tor elements. In terms of approaches comparison, the

different estimators retrieve the absolute scale by al-

most the same performance despite the bad initializa-

tion. In the second scenario, it is supposed the same

steps of the previous scenario, but after scale value

stabilization λ =∼ 1 ±0.8%, an atypical value was in-

cluded (λ = 0.8) of scale to compare the robustness of

the four estimators against outliers. In Fig. 3, we no-

tice that Combined SVSF-EKF approach is more ro-

bust than EKF, SVSF, and ASVSF in front of briskly

atypical scale value. In case of scale estimation, the

ASVSF solution does not provide a good result com-

pared to Combined SVSF-EKF. This result is due to

the scale noise nature at a time, and the concept of

variable structure combined with Kalman ﬁlter in an-

other time. For a deep comparison, the ASVSF found

the scale with a performance near Combined SVSF-

EKF estimator, and also it gives the scale incertitude

for each scale value estimated. In the third scenario,

we suppose just that the Mono-SLAM output is af-

fected by a scale factor λ = 1 + n with n is a noise of

standard deviation σ

= 10

−4

. The aim of this sce-

nario is to show the behavior and stability of the pro-

posed approaches in front of a scale with a noise. The

result is given by Fig. 4, we see that all estimators re-

sist against scale ﬂuctuation, and show a considerable

stability in case of scale with fulﬁllment to the small

standard deviation value of scale noise. To go further,

a comparison is performed later which will provide a

deep analysis about stability and robustness. It is con-

sidered in the fourth scenario, that the output of the

Mono-SLAM box is equal to the absolute scale plus

a sinusoidal variation λ = 1 + (1/40) · sin θ, with θ is

an angle of value 0 to 360 degrees. The purpose of

this scenario is to show the capability of scale track-

ing by the four estimators. The result is given by Fig.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

674

0 2 4 6 8 10 12 14 16 18

Time (s)

0.5

0.6

0.7

0.8

0.9

Scale

Absolute scale

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 2: The ﬁrst scenario of scale estimation using EKF,

SVSF, Combined SVSF-EKF, and ASVSF.

0 2 4 6 8 10 12 14 16 18

Time (s)

0.5

0.6

0.7

0.8

0.9

1.1

1.2

Scale

Absolute scale

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 3: The second scenario of scale estimation using

EKF, SVSF, Combined SVSF-EKF, and ASVSF.

0 2 4 6 8 10 12 14 16 18

Time (s)

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Scale

Absolute scale

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 4: The third scenario of scale estimation using EKF,

SVSF, Combined SVSF-EKF, and ASVSF.

5. It is remarkable that the Combined SVSF-EKF is

more accurate than the other estimators in terms of

scale tracking. By comparison of all proposed esti-

mators, we remark that, we have not a big difference

in terms of tracking, but this difference can be signif-

icantly larger in case of the long trajectory.

0 2 4 6 8 10 12 14 16 18

Time (s)

0.4

0.5

0.6

0.7

0.8

0.9

1.1

Scale

Absolute scale

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 5: The fourth scenario of scale estimation using

EKF, SVSF, Combined SVSF-EKF, and ASVSF.

4.2 Performances Analysis

We try to give an indepth analysis of the proposed es-

timators for scale estimation in terms of robustness,

stability, and accuracy based on the appropriate mea-

surement tools.

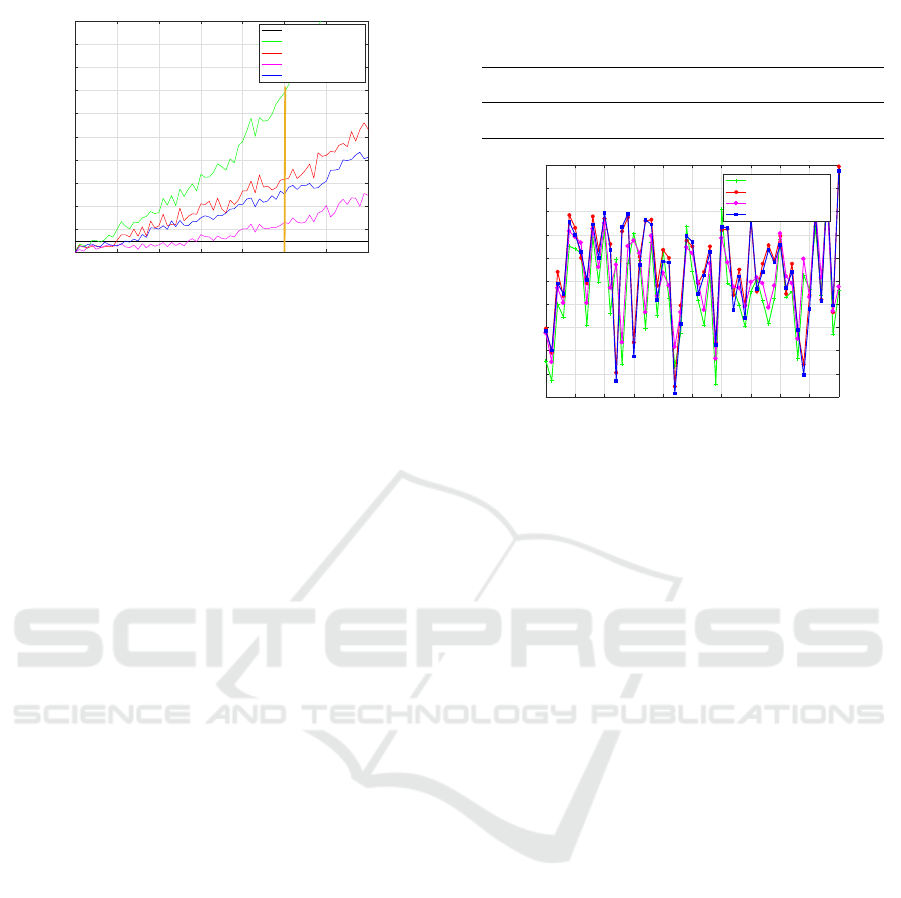
4.2.1 Robustness and Stability Analysis

To assess the robustness and stability measurement

(Maronna et al., 2006) of each estimator, the fol-

lowing manner is adopted; the Mono-SLAM scale is

supposed to be affected by noise of standard devia-

tion σ

= 10

−4

. A point is selected in the middle of

scale estimation process (this point has a typical scale

around the absolute scale), this last was changed by an

atypical scale. The value of this outlier is augmented

gradually until 100 percent of the scale contamina-

tion. The experience is repeated many times to get

signiﬁcant results. At the end, we measure the maxi-

mum bias of scale deviation compared to the absolute

scale for the four estimators using the formula (44).

Max

= max



− λ

Re f



(44)

Where λ

Re f

is the scale reference without contam-

ination, and λ

Max

signiﬁes the bias max of scale devi-

ation of a given contamination, the term λ

is the scale

value in the case of the same contamination measured

many times (i times). The results are given by the

graph in Fig. 6. It is remarkable that, all the estima-

tors involved in scale recovering lost their robustness

signiﬁcantly according to scale contamination until

instability of scale recovery process. The best estima-

tor in terms of robustness is the Combined SVSF-EKF

due to the synergy provided by the couple SVSF-

EKF. After, comes the ASVSF because it has the vari-

able structure force with an optimal gain ensured by

the variable boundary layer. The SVSF presents also

a signiﬁcant robustness under the ASVSF but better

than the classical solution (EKF). The maximum scale

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM

675

0 10 20 30 40 50 60 70

Scale contamination (Percents)

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

Bias Max of scale

Break Point level

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 6: The robustness and stability analysis of EKF,

SVSF, Combined SVSF-EKF, and ASVSF.

bias deviation allowed by scale recovery process de-

pends on the application. However, in our work, we

suggest that the bias max of scale tolerance is equal

to 0.1. It is remarkable that the Combined SVSF-

EKF has the best break point which is around 30%,

the ASVSF is about 15%, the SVSF is approximately

10%, and EKF is under 10%. Beyond these scale con-

taminations’ values, the robustness of the proposed

estimators are not guaranteed with respect to the max-

imum scale deviation supposed. In case of scale con-

tamination of 50 percent, the maximum deviation of

scale bias deviation does not exceed 0.3 for the Com-

bined SVSF-EKF approach. In case of ASVSF, the

deviation is approximately 0.5, for SVSF is about

0.6, and in the classical method the maximal devia-

tion of scale bias is 1.4 (this means instability of the

scale method). For the robust ﬁlter (SVSF, Combined

SVSF-EKF, and ASVSF) the stability of our system is

guaranteed compared to the EKF approach. But, it is

recommended to select the ASVSF estimator, because

it brings together many advantages as the robustness,

the accuracy, the uncertainty information, and the re-

spect of the real time constraint.

4.2.2 Accuracy Analysis

To analyze the accuracy and to give a quantiﬁcation of

the precision range of our methods, we try to measure

the accuracy of the suggested estimators by consider-

ing the following steps. The scale is affected by noise

of a standard deviation σ

= 10

−4

. Some points of

the scale estimation system are replaced by outliers

near scale tolerance (these scale values can be sup-

ported easily by our proposed system) of value equal

to 0.12 (in these points the scale becomes λ = 0.88).

The number of points touched by scale outliers is in-

creased gradually to 100 percent. For each contami-

nation, we calculate the corresponding average of the

root-mean-square error (RMSE). The graph of accu-

racy measurement is given by Fig. 7. It is remarkable

Table 1: The means RMSE of EKF, SVSF, Combined

SVSF-EKF, and ASVSF.

Est EKF SVSF Combined ASVSF

Mean 0.084 0.086 0.085 0.086

0 10 20 30 40 50 60 70 80 90 100

Percentage of Outliers (Percents)

0.074

0.076

0.078

0.08

0.082

0.084

0.086

0.088

0.09

0.092

0.094

RMSE

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 7: The accuracy analysis of EKF, SVSF, Combined

SVSF-EKF, and ASVSF.

that the Combined SVSF-EKF is near optimal perfor-

mance of the famous estimator EKF. There is not a

big difference between SVSF and ASVSF in terms of

accuracy, so it depends on the application in which it

is involved (in case of searching for high precision).

The graph of RMSE in case of ASVSF is near to the

Combined SVSF-EKF, so it is preferable to select the

ASVSF instead of the Combined SVSF-EKF despite

the superiority presented because, at least the ASVSF

provides an idea about the uncertainty of the scale

value. To understand better the Fig. 7, the Table 1 is

proposed which gives a summary of the means RMSE

for the four estimators proposed. The RMSE of all

the estimators is numerically close, but in case of the

scale value, the least difference is considerable.

5 EXPERIMENT RESULTS

5.1 The Environment of Experiment

The experiment results are realized by using a

dataset of a micro aerial vehicle (MAV) (an As-

cTec Fireﬂy hex-rotor helicopter). This MAV has

two monochrome front-down looking Cameras type

MT9V034 of a rate 20 Hz and an IMU type

ADIS16448 of MEMS technology with a rate of 200

Hz. The standard deviations of noises, biases, and the

frequencies of IMU are given in the Methodology sec-

tion. For more details about the system conﬁguration,

refer to (Burri et al., 2016).

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

676

-3 -2 -1 0 1 2 3 4 5 6

X (m)

-4

-2

Y (m)

Ground truth

Mono-SLAM trajectory

Figure 8: The top view of the trajectory obtained by the

Mono-SLAM and the ground truth in case of a real data

(MH 01 easy).

0 50 100 150 200 250 300 350

Time (s)

0.5

0.6

0.7

0.8

0.9

1.1

1.2

1.3

Scale

Scale of Mono-SLAM

EKF

SVSF

Combined SVSF-EKF

Figure 9: The scale estimation using EKF, SVSF, Combined

SVSF-EKF and ASVSF in case of a real data (MH 01 easy).

5.2 The Scale Recovering of a Real Data

To obtain the up to scale trajectory, we applied on

the image of the dataset a well known Mono-SLAM

named inverse depth parameterization for monocular

SLAM (Civera et al., 2008). This Mono-SLAM is

based essentially on the EKF. The brute force of this

solution is the representation of the depth by its in-

verse form. However, it allows to handle uncertainty

accurately during undelaying initialization and be-

yond. As all kinds of Mono-SLAM, it provides a tra-

jectory with an unknown scale as given by Fig. 8. We

applied the fourth proposed estimators to recover the

absolute scale on this up to scale trajectory as given by

Fig. 9. This ﬁgure shows the superiority of scale re-

covering of the robust ﬁlter against the classical solu-

tion (EKF). The Fig. 10 shows the 3D trajectory of the

MAV (ground truth) and the estimated trajectories re-

alized by the four estimators (EKF, SVSF, Combined

SVSF-EKF and ASVSF) in case of a real data (MH

01 easy). To provide a clear comparison between all

the estimators, we suggest to calculate the RMSE for

all these estimators as given by Fig. 11. The robust

ﬁlter provides a good result in term of scale tracking

in case of real data. This judgment stays valid for the

other scenarios choices from the dataset (MH 01 easy,

MH 03 medium, and MH 05 difﬁcult) as given by the

Table 2. The RMSE for the four estimators degraded

systematically by the quality of frames acquired from

the explored environment, this limitation is due to the

-1.5

-1

-0.5

Z (m)

0.5

Y (m)

X (m)

1.5

-2

-5

-4

Ground truth

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 10: The 3D trajectories of ground truth, EKF, SVSF,

Combined SVSF-EKF and ASVSF in case of a real data

(MH 01 easy).

0 1000 2000 3000 4000 5000 6000 7000

Iteration

0.05

0.1

0.15

0.2

0.25

Error (m)

EKF

SVSF

Combined SVSF-EKF

ASVSF

Figure 11: The RMSE of trajectories for EKF, SVSF, Com-

bined SVSF-EKF and ASVSF in case of a real data (MH 01

easy).

Table 2: The mean RMSE of scale estimation using EKF,

SVSF, Combined SVSF-EKF, and ASVSF in case of a real

data (MH 01 easy, MH 03 medium, and MH 05 difﬁcult)

MH 01 MH 03 MH 05

Length (m) 80.6 130.9 97.6

Duration (s) 182 132 111

Mean EKF 0.0857 0.0987 0.0997

Mean SVSF 0.0590 0.0773 0.0882

Mean Combined 0.0319 0.0468 0.0643

Mean ASVSF 0.0425 0.0564 0.0725

high perturbation of scale which is affected by the low

textured or darkness of frames acquired.

5.3 The Real Time Evaluation

The environment of development is Matlab, installed

into a computer of a characteristic; Intel(R) Core

(TM), processor i5 of frequency 2.40 GHz. In our

work, the scale is recovered into a multi-rate mecha-

nism. However, the Mono-SLAM utilized in our work

provides an up to scale trajectory in real time of fre-

quency 20 Hz. Our solutions permit to estimate the

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM

677

Table 3: The frequency of scale estimation for EKF, SVSF,

Combined SVSF-EKF, and ASVSF

Est EKF SVSF Combined ASVSF

Freq 93 Hz 105 Hz 88 Hz 97 Hz

scale many times between two poses, this mean that

it is possible to do another estimation stage in a pe-

riod of about 50 ms. From the Table 3, we note that

the scale value is improved within a frequency big-

ger than the vision part. But, this frequency, depends

essentially on the mathematical formulation for each

estimator. The frequency of estimation can not be

evaluated separately from the scale estimation quality.

Sure, that SVSF is the better in terms of frequency,

but, it is not the best in term of RMSE. The Com-

bined SVSF-EKF is a good estimator but also it is

not the fastest. The ASVSF can be considered as a

good estimator of scale because it allows to recover

the scale in real time with a rate of about 97 Hz and a

scale near Combined SVSF-EKF quality.

6 CONCLUSIONS

This paper focused on a timely problem which relies

to the Mono-SLAM ﬁeld. It treats the scale recov-

ering into a multi-rate fusion scheme. We have im-

plemented, and compared four approaches of scale

estimation: EKF, SVSF, Combined SVSF-EKF, and

ASVSF. The obtained results of this work, showed a

signiﬁcant performance of robust ﬁlters (SVSF, Com-

bined SVSF-EKF, and ASVSF) against the classical

solution (EKF) in terms of scale factor recovering

and real time constraint. The different results ob-

tained permit to focus on the Combined SVSF-EKF

method which provides a compromise between ro-

bustness and accuracy. But, in terms of real time

constraint, it is better to utilize the ASVSF estima-

tor. In addition, the ASVSF is near performance of

the Combined SVSF-EKF, and also it provides an as-

sesses about the incertitude of scale estimation as in

the case of the EKF. In this work, we showed that the

ﬁltering process into multi-rate mechanism allows the

determination of the scale factor with a rate superior

than the vision system 20 Hz especially for SVSF, and

ASVSF. As a future work, we plan to design from

scratch a new Mono-SLAM system with some new

ideas and to involve our solution to estimate the scale.

The complete system can be embedded easily onto a

MAV in order to navigate safely. In the same subject

studied in this paper, we propose to design another

system by many sensors and studying the fault toler-

ance of the developed system.

REFERENCES

Agrawal, M. and Konolige, K. (2006). Real-time localiza-

tion in outdoor environments using stereo vision and

inexpensive GPS. In International Conference on Pat-

tern Recognitionon, pages 1063–1068.

Armesto, L., Chroust, S., Vincze, M., and Tornero, J.

(2004). Multi-rate fusion with vision and iner-

tial sensors. In Robotics and Automation, Proceed-

ings. ICRA’04 International Conference on, volume 1,

pages 193–199. IEEE.

Botterill, T., Mills, S., and Green, R. (2013). Cor-

recting scale drift by object recognition in single-

camera SLAM. IEEE transactions on cybernetics,

43(6):1767–1780.

Burri, M., Nikolic, J., Gohl, P., and Schneider, T. (2016).

The euroc micro aerial vehicle datasets. The Inter-

national Journal of Robotics Research, 35(10):1157–

1163.

Civera, J., Davison, A., and Montiel, J. (2008). Inverse

depth parametrization for monocular SLAM. IEEE

transactions on robotics, 24(5):932–945.

Davison, A., Reid, I., and Molton, N. (2007). Mono SLAM:

Real-time single camera SLAM. IEEE Transactions on

Pattern Analysis & Machine Intelligence, (6):1052–

1067.

Dumortier, Y., Benenson, R., and Kais, M. (2006). Real-

time vehicle motion estimation using texture learning

and monocular vision. In International Conference on

Computer Vision and Graphics ICCVG.

Eade, E. and Drummond, T. (2006). Scalable monocu-

lar SLAM. In Computer Vision and Pattern Recog-

nition, 2006 IEEE Computer Society Conference on,

volume 1, pages 469–476. IEEE.

Engel, J. and Cremers, D. (2014). Lsd-SLAM: Large-scale

direct monocular SLAM. In European Conference on

Computer Vision, pages 834–849. Springer.

Forste, C., Lynen, S., Kneip, L., and Scaramuzza, D.

(2013). Collaborative monocular SLAM with multiple

micro aerial vehicles. In International Conference on

Intelligent Robots and Systems on, pages 3962–3970.

IEEE.

Frost, D., Kahler, O., and Murray, D. (2016). Object-

aware bundle adjustment for correcting monocular

scale drift. In Robotics and Automation (ICRA), In-

ternational Conference on, pages 4770–4776. IEEE.

Gadsden, S. and Habibi, S. (2010). A new form of

the smooth variable structure ﬁlter with a covariance

derivation. In Decision and Control (CDC), 49th Con-

ference on, pages 7389–7394. IEEE.

Gadsden, S., Sayed, M. E., and Habibi, S. (2011). Deriva-

tion of an optimal boundary layer width for the smooth

variable structure ﬁlter. In American Control Confer-

ence (ACC), pages 4922–4927. IEEE.

Grater, J., Schwarze, T., and Lauer, M. (2015). Robust scale

estimation for monocular visual odometry using struc-

ture from motion and vanishing points. In Intelligent

Vehicles Symposium (IV), 2015 IEEE, pages 475–480.

IEEE.

ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics

678

Gutierrez-Gomez, D., Puig, L., and Guerrero, J. (2012).

Full scaled 3d visual odometry from a single wear-

able omnidirectional camera. In Intelligent Robots

and Systems (IROS), RSJ International Conference

on, pages 4276–4281. IEEE.

Habibi, S. (2007). The smooth variable structure ﬁlter. Pro-

ceedings of the IEEE, 95(5):1026–1059.

Habibi, S. (2008). Combined variable structure and Kalman

ﬁltering approach. In American Control Conference,

2008, pages 1855–1862. IEEE.

Hol, J., Schon, T., Luinge, H., and Gustafsson, F. (2007).

Robust real-time tracking by fusing measurements

from inertial and vision sensors. Journal of Real Time

Image Processing, 02(02):149–160.

Ikeda, S., Sato, T., and Yamaguchi, K. (2007). Construction

of feature landmark database using omnidirectional

videos and GPS positions. In International Confer-

ence on Pattern Recognitionon, pages 249–256. IEEE.

Jung, S. and Taylor, C. (2001). Camera trajectory estimation

using inertial sensor measurements and structure from

motion results. In Proceedings of the IEEE Computer

Society Conference on Computer Vision and Pattern

Recognition, pages 732–737.

Kitt, B., Rehder, J., Chambers, A., and Schonbein, M.

(2007). Monocular visual odometry using a planar

road model to solve scale ambiguity. In Proc of Euro-

pean Conference on Mobile Robots.

Klein, G. and Murray, D. (2007). Parallel tracking and

mapping for small ar workspaces. In Mixed and Aug-

mented Reality, ISMAR, 6th IEEE and ACM Interna-

tional Symposium on, pages 225–234. IEEE.

Kobzili, E., Larbes, C., and Allam, A. (2017a). Multi-rate

robust scale estimation of monocular SLAM. In Sys-

tems and Control (ICSC), 6th International Confer-

ence on, pages 1–5. IEEE.

Kobzili, E., Larbes, C., and Allam, A. (2017b). Robust

absolute scale estimation of monocular SLAM using

a combined svsf-ekf strategy for mav navigation. In

1st Algerian Multi-Conference on Computer, Electri-

cal and Electronic Engineering. USTHB of Algiers.

Lemaire, T., Berger, C., Jung, I., and Lacroix, S.

(2007). Vision-based SLAM: Stereo and monocular

approaches. International Journal of Computer Vi-

sion, 74(3):343–364.

Lothe, P. (2010). Simultaneous localization and mapping

with monocular vision constraint with SIG. PhD the-

sis, University of Blase Pascal Clermont-Ferrand II,

France.

Maronna, R., Martin, R., and Yohai, V. (2006). Robust

statistics. Wiley Chichester.

Montemerlo, M. (2003). A factored solution to the simul-

taneous localization and mapping problem with un-

known data association. Ph. D. thesis, Carnegie Mel-

lon University, Pittsburgh.

Mur-Artal, R., Montiel, J., and Tardos, J. (2015). Orb-

SLAM: a versatile and accurate monocular SLAM sys-

tem. IEEE Transactions on Robotics, 31(5):1147–

1163.

Nemra, A. (2011). Robust airborne 3d visual simultane-

ous localisation and mapping. Ph. D. thesis, Cranﬁeld

University, England.

Nister, D., Naroditsky, O., and Bergen, J. (2006). Visual

odometry for ground vehicle applications. Journal of

Field Robotics, 23(1):3–20.

Nutzi, G., Weiss, S., Scaramuzza, D., and Siegwart, R.

(2011). Fusion of imu and vision for absolute scale

estimation in monocular SLAM. Journal of intelligent

& robotic systems, 61(1-4):287–299.

Pillai, S. and Leonard, J. (2015). Monocular SLAM sup-

ported object recognition. In Computer Vision and

Pattern Recognition.

Pirker, K., R

uther, M., and Bischof, H. (2011). Cd SLAM-

continuous localization and mapping in a dynamic

world. In Intelligent Robots and Systems (IROS), 2011

IEEE/RSJ International Conference on, pages 3990–

3997. IEEE.

Qiang, L., Jianye, M., Guosheng, W., and Huican, L.

(2016). Absolute scale estimation of orb-SLAM al-

gorithm based on laser ranging. In Robotics and Au-

tomation (ICRA), International Conference on, pages

10279–10283. IEEE.

Scaramuzza, D., Fraundorfer, F., Pollefeys, M., and Sieg-

wart, R. (2009). Absolute scale in structure from mo-

tion from a single vehicle mounted camera by exploit-

ing nonholonomic constraints. In Computer Vision,

12th International Conference on, pages 1413–1419.

IEEE.

Scaramuzza, D. and Siegwart, R. (2008). Appearance-

guided monocular omnidirectional visual odometry

for outdoor ground vehicles. IEEE transactions on

robotics, 24(5):1015–1026.

Simond, N. and Rives, P. (2004). Trajectography of an

uncalibrated stereo rig in urban environments. Intel-

ligent Robots and Systems, 2004.(IROS 2004). Pro-

ceedings. 2004 IEEE/RSJ International Conference

on, (4):3381–3386.

Smith, R., Self, M., and Cheeseman, P. (1990). Estimat-

ing uncertain spatial relationships in robotics. In Au-

tonomous robot vehicles, pages 167–193. Springer.

Song, S. and Chandraker, M. (2014). Robust scale estima-

tion in real-time monocular sfm for autonomous driv-

ing. In Proceedings of the IEEE Conference on Com-

puter Vision and Pattern Recognition, pages 1566–

1573.

Strelow, D. and Singh, S. (2004). Motion estimation from

image and inertial measurements. International Jour-

nal of Robotique Research, 23(12):1157–1195.

Weiss, S. and Siegwart, R. (2011). Real-time metric state

estimation for modular vision-inertial systems. In

International Conference on Robotics and Automa-

tion:(ICRA 2011), pages 4531–4537. IEEE.

Zachariah, D. and Jansson, M. (2011). Self-motion and

wind velocity estimation for small-scale uavs. In

Robotics and Automation (ICRA), International Con-

ference on, pages 1166–1171. IEEE.

Comparative Study between EKF, SVSF, Combined SVSF-EKF, and ASVSF Approaches based Scale Estimation of Monocular SLAM

679