
Generating a Multi-fidelity Simulation Model Estimating the Models’
Applicability with Machine Learning Algorithms
Christian Hürten
a
, Philipp Sieberg
b
and Dieter Schramm
c
Chair of Mechatronics, University of Duisburg-Essen, 47057 Duisburg, Germany
Keywords: Simulation, Model Fidelity, Multi-fidelity Model, Computational Effort, Machine Learning, Support Vector
Machine, Neural Network.
Abstract: Having access to large data sets recently gained increasing importance, especially in the context of automation
systems. Whether for the development of new systems or for testing purposes, a large amount of data is
required to satisfy the development goals and admission standards. This data is not only measured from
real-world tests, but with growing tendency generated from simulations, facing a trade-off between
computational effort and simulation model fidelity. This contribution proposes a method to assign individual
simulation runs the simulation model that has the lowest computation costs while still being capable of
producing the desired simulation output accuracy. The method is described and validated using support vector
machines and artificial neural networks as underlying vehicle simulation model classifiers in the development
of a lane change decision system.
1 INTRODUCTION
Over the last years, the availability of large data sets
has gained increasing importance in both research and
system development. Especially in the field of
automation, the demand for appropriate data is rising
as machine learning algorithms are receiving more
attention.
A popular application area for automation is the
automotive sector with its driver assistance systems
ranging from supportive systems like the lane
departure warning system to fully autonomous
driving vehicles. Even with classical controller
strategies and thus without the use of data-driven
algorithms, in the development process an exhaustive
amount of test cases has to be covered. Many of those
tests are nowadays performed in simulations.
(Paulweber, 2017)
On the one hand, the simulation-based testing
offers economic advantages. Depending on the
simulation environment, the test can be performed
faster than real-time, thus the development process
can be shortened. Furthermore, occurring system
failures do not harm testing personal nor real
a
https://orcid.org/0000-0002-6762-8877
b
https://orcid.org/0000-0002-4017-1352
c
https://orcid.org/0000-0002-7945-1853
hardware and can be eliminated before deployment in
expensive real-world prototypes. On the other hand,
tests in simulation environments come with practical
advantages. The tests can be carried out under
constant, deterministic environmental conditions,
which can be chosen independently of i.e. weather
impacts that real-world testing has to cope with.
(Sovani et al., 2017)
Other than providing an environment to test
developed systems, simulations can also be used in
the design process. Systems based on data-driven
machine learning algorithms need plenty of data to be
trained on. Whereas this data can be collected in the
real-world, using simulation data offers again a less
time and cost consuming alternative.
Using a simulation, the two important
characteristics are the underlying model’s fidelity and
the required computational resources. In general, the
more accurate the simulation model has to be, the
more computational power respective time is needed
for simulation.
While a complex simulation model may result in
highly accurate data for all regarded simulated events,
its complexity may not be necessary in each of these
Hürten, C., Sieberg, P. and Schramm, D.
Generating a Multi-fidelity Simulation Model Estimating the Models’ Applicability with Machine Learning Algorithms.
DOI: 10.5220/0011318100003274
In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 131-141
ISBN: 978-989-758-578-4; ISSN: 2184-2841
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
131

events. For some cases, a less complex model can be
sufficient in accuracy as well, whilst requiring less
computational resources.
As the trade-off between computational
requirements and model fidelity is not only subject to
automation system simulation but rather a general
problem in the field of simulations, many researchers
are investigating possible solutions, combining
multiple simulation models of varying fidelity to so-
called multi-fidelity models.
In (Fernandez-Godino et al., 2017), the authors
review different merging strategies for those multi-
fidelity models. E.g., the merging can be performed
by correcting the output of low fidelity models.
Therefore, the deviation from a high fidelity model is
analysed at given points, in the application this
deviation is estimated. (Biehler et al., 2015)
An alternative approach defines selection criteria
for each of the simulation models. This contribution
belongs to the latter strategy, the proposed method
uses a selection criterion per investigated model that
is learned from the models’ simulation data using
machine learning algorithms.
In the following, a short introduction into the
fundamentals of the used vehicle models and machine
learning algorithms is given. Afterwards, the
simulation framework is presented. Subsequently, the
proposed method is described before finally being
applied to the development of an automated lane
change decision system.
2 FUNDAMENTALS
This section presents an overview on the
fundamentals of the used vehicle models as well as
support vector machines and neural networks
2.1 Vehicle Dynamics
In this contribution, the simulations are performed
with four vehicle models. With increasing model
fidelity, those models are a point mass model, a linear
single-track model and two nonlinear single-track
models. Vehicle models with higher fidelity like a
dual-track model or a multi-body system are not
considered in this paper, since the focus of this work
is the presentation of the method determining the
required model fidelity. Furthermore, the performed
simulation does not include highly dynamical events
with high lateral accelerations and thus the single-
track models are sufficient to model the vehicles
dynamics accurately.
2.1.1 Point Mass Model
For the vehicle model with the lowest fidelity a point
mass model is used. The model uses the first order
Euler method to compute the vehicles position 𝒙 and
speed 𝒗 at discrete time intervals Δ𝑡 based on the
current acceleration 𝒂:
𝒙
𝑡Δ𝑡
𝒙
𝑡
𝒗
𝑡Δ𝑡
∙Δ𝑡
(1)
𝒗
𝑡Δ𝑡
𝒗
𝑡
𝒂
𝑡
∙Δ𝑡
(2)
In this model, neither rotational movement around
any axis nor tire characteristics are modelled.
(Alvarez Lopez et al., 2018)
2.1.2 Linear Single-Track Model
The linear single-track model is an often-used vehicle
simulation model describing the lateral behaviour of
a vehicle. For low lateral accelerations, this model is
very accurate but because of linearisation of the
equations, the model’s fidelity decreases with
increasing lateral accelerations.
The model does not include longitudinal forces,
thus only constant velocities can be simulated. The
only rotation allowed for this model is around the
vertical axis, the other rotations are restricted. Tire
modelling is done by a linear model depending on the
lateral slip angle and the cornering stiffness of the
tires. A detailed explanation of the model can be
found in many literature sources, e.g. in (Heißing &
Ersoy, 2011).
2.1.3 Nonlinear Single-Track Model
The highest fidelity models used in this work are
nonlinear single-track models. In general, this model
is modelling the movement in lateral and longitudinal
direction as well as the rotation around the vertical
axis. Considering the longitudinal component of the
model, an engine model is incorporated in
conjunction with resistance force modelling.
The vehicle-road contact point is modelled by the
empirical magic formula model, a nonlinear tire
model after (Pacejka, 2012). Since the equations of
this model are not linearized, the model does not
suffer from the accuracy loss for higher lateral
acceleration the linearized model has to deal with.
Optionally, this model can be complemented by a
roll and pitch model. Those models are linear models
of the rotational behaviour around the horizontal
axes. As those rotations are described by linear
models, they are only feasible for small rotational
movement. For further description of the nonlinear
single-track model and the roll model, please consider
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
132
(Schramm et al., 2018). The pitch model is described
in (Sieberg et al., 2019).
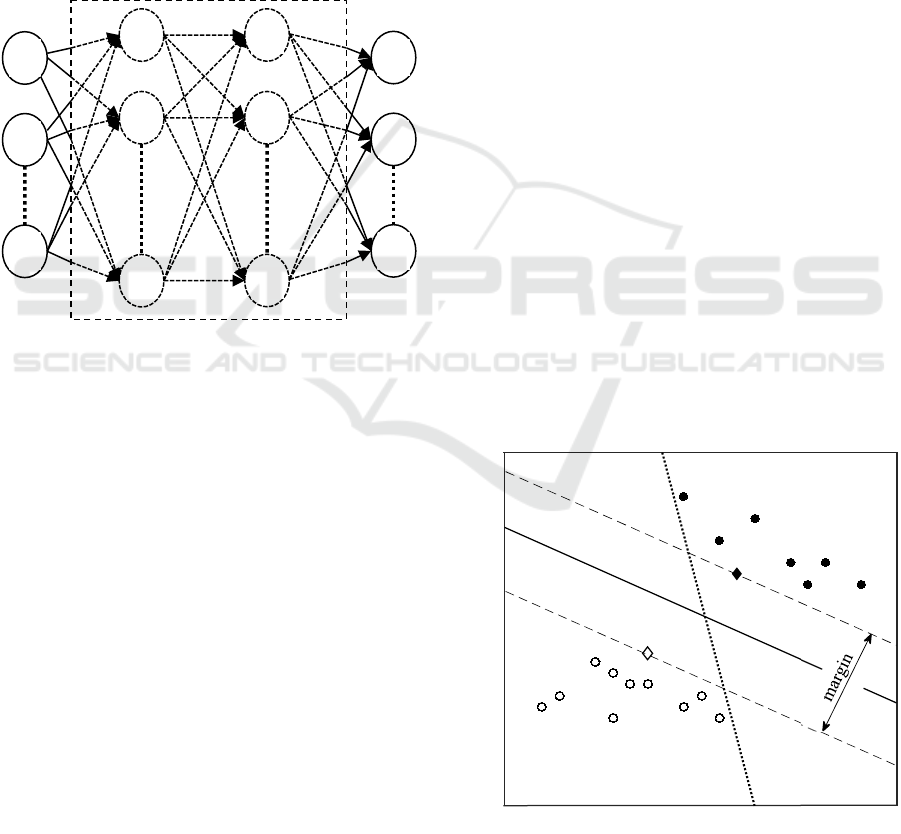
2.2 Artificial Neural Networks
The artificial neural networks (ANNs) considered in
this work are so-called fully-connected feedforward
neural networks. The signal flow in such ANNs is
always directed from the input-neurons through the
hidden neuron layers to the output neurons. Thereby,
every neuron of one layer – excluding the input layer
– is connected to all neurons of the preceding layer.
Figure 1 shows the structure of these ANNs,
exemplary with two hidden layers.
Figure 1: Fully-connected feedforward neural network with
two hidden layers.
In each neuron, its N inputs 𝒙∈ℝ
– hence the
outputs of the previous layer with N neurons inside –
are summed up with each input weighted by the
neuron’s weights 𝒘∈ℝ
. This sum is adjusted by
the neuron’s bias 𝑏∈ℝ to compensate for a possible
offset before the output of the neuron is calculated by
applying an activation function f
: ℝ→ℝ. Thus,
each neuron’s output 𝑦 can be described by:
𝑦f
𝒘
𝒙𝑏
(3)
Popular activation functions are the Tanh and
Sigmoid functions as well as the Exponential Linear
Unit (ELU) which is defined as follows:
f
x
x , x0
𝛼∙𝑒
1, x0
(4)
Thereby, the parameter 𝛼 describes the lower bound
of the function’s output. (Gron, 2017)
During the training of the ANN, the trainable
parameters weight and bias of the neurons are adapted
to fit the network to the given data. This is achieved
by the method of error backpropagation. Based on a
loss function, the difference between network output
and target output on the training data points is
computed. The error loss is then propagated
backwards through the ANN, from the output layer to
the input layer. During this backpropagation, the
gradients of the weights and biases are computed with
respect to the loss. These gradients are then used in
gradient descent algorithms to adjust the trainable
parameters with the goal of minimisation of the loss
function. As with all gradient based approaches,
finding the global minimum cannot be guaranteed and
the training algorithm may be stuck in a local
minimum. (Bishop, 2006).
2.3 Support Vector Machines
Support Vector Machines (SVMs) are maximum
margin binary classifier. Like many (binary)
classifiers, the algorithm tries to distinguish two
classes in data by placing a separating hyperplane in
the input space, defined by:
𝒘
𝒙𝑏0
(5
)
Hereby, 𝒙∈ℝ
describes the N-dimensional input
vector, also called the features of a data point 𝒙,𝑦
which also consists of the class membership 𝑦∈
1,1. The weights 𝒘∈ℝ
and the bias 𝑏∈ ℝ
compose the parameters that are adjusted when fitting
the SVM to a data set. Given two classes in the N-
dimensional input space that are linear separable, thus
separable by a (N-1)-dimensional hyperplane, often
many – if not infinite – hyperplanes can be fitted to
solve this task.
Figure 2: Classification hyperplane with maximized margin
(solid line) and arbitrary hyperplane (dotted line).
x
1
x
2
x
n
h
1,1
h
1,2
h
1,i
y
1
y
2
y
m
h
2,1
h
2,2
h
2,i
Input
layer
Hidden
layers
Output
layer
Variable 𝑥
Variable 𝑥
Generating a Multi-fidelity Simulation Model Estimating the Models’ Applicability with Machine Learning Algorithms
133

Being a maximum margin classifier, the SVM
chooses the hyperplane that is maximizing the
distance to the data points. Thus, the margin between
the two classes is maximized. This property of the
SVM gives an advantage over other classification
algorithms like neural networks choosing an arbitrary
separating hyperplane. The maximum margin
solution improves the generalisation ability of the
classifier if new data points lay outside the classes
data clusters the algorithm has been fitted on. In
Figure 2, a visualisation of a maximum margin and an
arbitrary hyperplane is given. (Bishop, 2006)
The underlying constrained optimisation problem
is defined by:
min
1
2
𝒘
𝒘
𝐶
𝑀
𝜉
(6)
The optimisation has to be performed under the
constraint for each data point 𝒙
,𝑦
to ideally be
located outside the margin:
𝑦
𝒘
𝒙
𝑏
1𝜉
(7)
Hereby, the first term of the objective function
focusses on maximizing the margin, the second on
minimizing the slack 𝜉0. The slack variable in
conjunction with the regularisation parameter 𝐶 is
used to allow margin violation. In general, no data
point may be located inside the margin, i.e.
∑
𝜉
0. This is only possible for strictly linear separable
classes. As most real-world problems do not satisfy
this condition, e.g. because of noise, small violations
are allowed to increase the overall performance of the
SVM algorithm.
The optimisation problem often is solved using
the method of Lagrange multipliers on the dual
optimisation problem.
As mentioned, the SVM can only be applied on
linear separable classes, with small deviations from
this norm being allowed. This limitation can be
bypassed by a transformation of the input space into
higher dimensionality, hence making it to a linear
classification problem in the transformed feature
space. This transformation leads to dot products in
high dimensional space required for the parameter
calculation, highly increasing the computational
costs. To avoid these extra computational costs, the
feature space transformation is not performed
explicitly. Using the kernel trick, the computational
costly dot products in high dimensions are replaced
with a kernel function, that produces the same result
but being more efficient to compute. (Schölkopf &
Smola, 2018)
3 SIMULATION
In this section, the scenario depicted in the simulation
is described. Afterwards, the used simulation
framework is presented. Finally, the procedure of data
generation is outlined.
3.1 Simulation Scenario
In this contribution, a scenario on a straight road with
two lanes is considered. In total, three different
vehicles are part of the situation: On one lane, there is
the ego vehicle that is approaching a slower car,
called front vehicle. On the neighbouring lane drives
a faster car, called back vehicle. The scenario is
illustrated in Figure 3.
Figure 3: Simulated traffic scenario.
The ego vehicle is equipped with an adaptive
cruise control (ACC). Monitoring the distance to the
ahead driving front vehicle, by default the ACC
secures a safe distance by applying the brake if
getting to close. In this work, a lane change shall be
performed instead. Therefore, the viability of a lane
change manoeuvre has to be checked, which is
constrained by the approaching back vehicle.
Using suitable sensors, the ego vehicle’s ACC has
knowledge of the velocity of each vehicle, 𝑣
, 𝑣
and 𝑣
, as well as of the distances 𝑑
and 𝑑
to
the other cars.
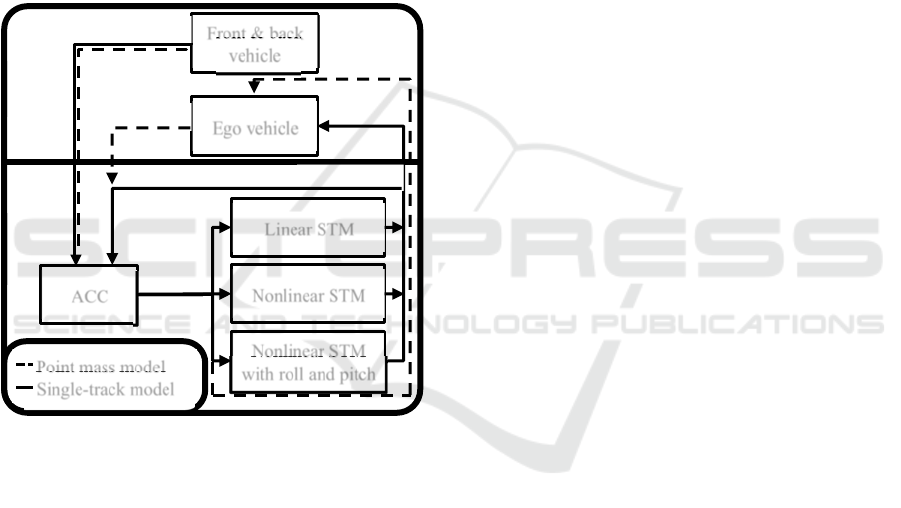
3.2 Simulation Framework
The simulation framework used in this contribution
consists of a co-simulation between
MATLAB/Simulink and the microscopic traffic
simulation software Eclipse SUMO (Alvarez Lopez
et al., 2018).
Internally, SUMO uses a point mass model to
simulate the vehicles behaviour. In this framework,
the front and back vehicle are modelled with this
simple vehicle model. Both vehicles are only driving
in longitudinal direction, hence the point mass model
is suitable for the simulation. While the front vehicle
is driving at constant speed, the back vehicle may
Ego vehicle Back vehicle Front vehicle
𝑑
𝑣
𝑣
𝑣
𝑑
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
134
brake to avoid a crash with the lane changing ego
vehicle. This braking reaction is modelled by
SUMO’s default driver model after (Krauß, 1998).
The ego vehicle is the subject of the vehicle model
investigation, as such it is modelled by the four
already introduced vehicle models, namely the point
mass model, the linear and the two nonlinear single-
track models. The computation of the point mass
model is also performed in SUMO. As the ego vehicle
has to carry out a lane change manoeuvre, the lateral
dynamics have to be considered as well. By default,
SUMO does not model lateral movement, instead the
cars jump from lane to lane in simulation. Activating
the Sublane Model, the lateral movement is modelled
by the point mass model as well. (Semrau &
Erdmann, 2016)
Figure 4: Structure of simulation framework with point
mass model and single-track models (STMs).
The other three advanced vehicle models are
implemented in MATLAB/Simulink. These models
require the input of the steering angle, the nonlinear
single-track models need the throttle and brake pedal
positions as well. The latter inputs are computed
using a PID controller, that controls the ego vehicle’s
velocity to be constant. For the two simpler vehicle
models, this assumption of constant velocity is
required.
The steering angle is computed using a lateral
guidance model after (Fiala, 2006). This model
assumes that the driver aligns the vehicle’s driving
direction to a targeted viewpoint, in case of a lane
change this viewpoint lays on the adjacent lane. Using
a PD controller computing the steering angle, the
vehicle’s direction is adjusted.
The ACC as well is modelled in Simulink,
monitoring the distance to the front vehicle and
giving the signal that a reaction, either a lane change
or a braking manoeuvre, is necessary.
The communication between both simulations is
built using TraCI, an interface integrated in SUMO.
Using TraCI4Matlab by (Wegener et al., 2008), the
interface can be accessed from MATLAB and, with
some adaptions, also from Simulink. The co-
simulation is managed by Simulink, controlling the
simulation steps inside SUMO and recording the
necessary data for later analysis. In Figure 4, the
framework is depicted.
3.3 Data Generation
The simulation parameters 𝒙 being changed are the
velocities of the vehicles as well as the distance of the
back vehicle when the ACC signal is invoked:
𝒙𝑣
,𝑣
,𝑣
,𝑑
(8)
When performing a lane change, the viability of
the manoeuvre is evaluated regarding dangerous
interferences with the other traffic participants.
Therefore, minimum distances between the cars have
to be maintained.
Further aspects being considered are the
deceleration of the back vehicle and the lateral
acceleration and jerk the ego vehicle is exposed to
during the lane change.
The limit for the deceleration of the back vehicle
is set to a maximum of 3 m/s² according to the
recommendation by the Institute of Transportation
Engineers (ITE Technical Committee, 1989). The
limitations to the lateral dynamics conform to the
requirements specified for partially automated lane
change systems in ISO 21202 (ISO, 2020).
4 MODEL BOUNDARIES
DETERMINATION
This section presents the proposed method to choose
the simulation model with the lowest required model
by estimating their application boundaries. Therefore,
the method is described using two different machine
learning algorithms, namely SVMs and ANNs.
Afterwards, the results are evaluated and compared.
Finally, a more precise adaption to the method is
presented.
Ego vehicle
Linear STM
SUMO
Simulink
Nonlinear STM
Nonlinear STM
with roll and pitch
ACC
position
lane
change
Front & back
vehicle
position
position
Point mass model
Single-track model
Generating a Multi-fidelity Simulation Model Estimating the Models’ Applicability with Machine Learning Algorithms
135

Table 1: Parameters varied in simulation.
Parameter
Minimum
value
Maximum
value
Step size
𝑣
30 km/h 70 km/h 5 km/h
𝑣
25 km/h 65 km/h 10 km/h
𝑣
40 km/h 140 km/h 10 km/h
𝑑
50 m 200 m 25 m
To demonstrate the method, a data set consisting
of 1,505 simulation parameter combinations is
generated. The different parameters chosen for those
runs are given in Table 1. Thereby, only reasonable
combinations are considered and disregarding, for
example, combinations where the front vehicle is
faster than the ego vehicle and thus no overtaking
takes place.
Each simulation run is computed with all four
vehicle models being applied once. The lane change
is performed in each simulation run and the feasibility
of the manoeuvre is evaluated afterwards. In total, per
vehicle model 𝑀1,505 labelled data points
𝒙
,𝑦
are available, where the label describes the
feasibility ( 𝑦
1 respectively the infeasibility
𝑦
0 of the lane change.
4.1 Data Preparation
Required is the definition of ground truth data, i.e. the
results the simulation models should produce. In
general, the best option is to choose real-world data.
As such data often is not available, like in this
contribution, the simulation model with the highest
fidelity and thus the closest real-world modelling
capability should be chosen to represent the ground
truth. Hence, in the following, the ground truth data
will be referencing the data produced with the
nonlinear single-track model with linear roll and pitch
modelling.
The next step is to evaluate the simulation models’
feasibility on given data points, i.e. the 1,505
simulation runs. By comparison of the simulation
results against the ground truth data, the models will be
determined to have sufficient fidelity if the simulation
result match the ground truth, else to be not suitable for
application. This comparison is performed for each
data point contained in the data set.
This way, a set of discrete points 𝒙
,𝑦
,
𝑚 1…1,505, is generated for each vehicle
model. These points consist of the simulation
parameters 𝒙
, at which the computed results are
compared against the ground truth, and the label 𝑦
defining the suitability of the model for this
simulation run.
Based on these discrete points, machine learning
algorithms are trained to estimate the simulation
models’ application boundaries, thus interpolating
between the given data. As a consequence, the given
data distribution should cover the simulation
parameter space sufficiently.
4.2 Classifier Training
In the following, ANNs and SVMs are trained using
the data points 𝒙
,𝑦
. As the SVM is only a
binary classifier, thus can only distinguish between
two classes, the ANNs are as well implemented as
binary classifiers for better comparison. Therefore,
for each vehicle model there will be a separate SVM
or ANN estimating if the model’s fidelity is sufficient
for a given data point. By cascading the binary
classifiers based on increasing simulation model
fidelity, the lowest fidelity model which is applicable
can be determined.
With both presented machine learning algorithms,
the data pre-processing is the same: The inputs 𝒙
are standardized to zero mean and unit variance.
Furthermore, the data set is split into two parts. 30 %
of the data is used as test data to verify the algorithms
after training. The remaining data is used for a grid
search hyperparameter optimisation in the training
process, performing a stratified 5-fold cross-
validation.
The evaluation of the trained algorithms is
performed using two metrics. Besides the standard
accuracy metric, the precision metric is used as well.
Table 2: SVMs hyperparameter variations.
Kernel Regularisation 𝐶
Kernel parameters
(Not feasible)-class
weighting
𝑟 𝛾 d
Linear 2
,2
,…,2
- - - 1,5,10,30,50
Polynomial 2
,2
,…,2
0,1,10 2
,2
,…,2
2,5 1,5,10,30,50
RBF 2
,2
,…,2
- 2
,2
,…,2
- 1,5,10,30,50
Sigmoid 2
,2
,…,2
0,1,10 2
,2
,…,2
- 1,5, 10,30,50
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
136

The precision is defined as follows, with 𝑡𝑝
standing for true positives and fp for false positives:
Precision
𝑡𝑝
𝑡𝑝
𝑓
𝑝
(9)
Hence, the precision is a measure for the correctness
of positive classifications. In this work, positive
classification means that the model is viable for the
given simulation parameters. Since it is desired to not
use a simulation model when its fidelity is not high
enough to produce the right results, no false positive
classifications should be made. Thus, the precision
should be 100 %. This is the constraint for all trained
classifiers to be satisfied, the accuracy metric is then
used to rank the classifiers with full precision.
4.2.1 Support Vector Machine
In the training of the SVMs, the hyperparameter
optimisation is done with respect to the kernel
functions and their respective parameters, the
regularisation and the class weighting. In terms of
kernel functions, linear, 2
nd
and 5
th
degree
polynomial, gaussian (radial basis function, RBF) and
sigmoid kernels are investigated. In total, 5,670
combinations were evaluated per vehicle model, the
hyperparameters evaluated are given in Table 2.
The class weighting is chosen as additional
hyperparameter, because depending on the used
vehicle model only a small part of the data set is
assigned the class “not feasible”. To counteract the
uneven class distribution, the weight of those samples
has to be increased.
The best found hyperparameters for the vehicle
models are shown in Table 3.
Table 3: Best found SVM hyperparameter combinations.
Vehicle
model
SVM parameters
Test
accuracy
Point mass
RBF kernel, 𝐶8,𝛾2
,
5-times weighting
0.8894
Linear
single-track
Polynomial kernel, d= 2, 𝐶
512, 𝛾2
,𝑟 1 50-times
weighting
0.6018
The nonlinear single-track model without roll and
pitch model is not included in the table. This is
because of the similarity to the ground truth, that is in
fact only the extension by the roll and pitch
behaviour. Since the dynamics in the manoeuvre are
not remarkably high, the impact of this extension is
almost negligible – only for one data point in the
whole data set the simulation outcome differed. With
only one data point in the data set being assigned the
“not feasible” class, training a data driven model is
pointless. Hence, the standard nonlinear single-track
model will be excluded in the further evaluations of
the machine learning algorithms. In application
phase, the single data point this model is not suitable
will be computed by the ground truth model.
The two given SVM hyperparameter
combinations for the point mass model and the linear
single-track model satisfy the 100 % precision
constraint in training and validation, and achieve the
overall highest validation accuracy in training phase.
Evaluating the fully trained SVMs on the so far
unseen test data yields a precision of 100 % as well
and the accuracy given in the table. Remarkable is the
much lower accuracy achieved for the linear single-
track model, which is presumably the cost for the
precision constraint, leading to a high required class
weighting and the tendency to underestimate the
viability of the vehicle model.
4.2.2 Artificial Neural Network
For the trained ANNs, the investigated
hyperparameters are given in Table 4 with a total of
2,304 combinations evaluated.
Table 4: Hyperparameters used in ANN training.
H
yp
er
p
aramete
r
Values
Hidden neurons
50
,
100
,
50,50
,
100,100
,
50,20,100,20
Activation function Sigmoid, Tanh, ELU
Dropout rate
0,0.2
L2-regularisation
0,0.01
Learning rate
10
,10
,10
,10
Learning rate deca
y
0, 0.3
(Not feasible)-class
wei
g
hts
1,5,10,50
Investigated are ANNs with one and two hidden
layers and varying neuron count per layer. For the
hidden layers, different activation functions are
evaluated. Furthermore, the influence of the learning
rate is considered by investigation of different start
learning rates and an optional learning rate decay of
30 % every 25 training epochs. Additionally, the
usage of regularisations methods, namely dropout and
L2-regularisation, is covered in the hyperparameter
optimisation.
The output layer of the ANNs consist of one
neuron with the Sigmoid activation function, thus the
ANNs are producing one single output ranging from
0 to 1 that can be interpreted as the “feasible” class
membership probability for the vehicle model. The
output layer is not subject to the hyperparameter
optimisation.
Generating a Multi-fidelity Simulation Model Estimating the Models’ Applicability with Machine Learning Algorithms
137
During this optimisation, the ANNs are trained
for a total of 100 training epochs. Based on precision
and accuracy in the cross-validation, the best found
models are given in Table 5.
Table 5: Best found ANN hyperparameter combinations.
Vehicle
model
Hyperparameters
Point mass
Hidden neurons: 100,20
Activation function: ELU
No dropout
L2-regularisation: 0.01
Learning rate: 0.01 and 30% decay rate
Class weight: 10
Linear
single-track
Hidden neurons: 50,50
Activation function: ELU
No dropout
L2-regularisation: 0.01
Learning rate: 0.001 without decay rate
Class weight: 50
In Table 6, the performance of the two trained
ANNs on the test data is given. Important to mention
is, that none of the investigated ANNs satisfy the full
precision constraint during the hyperparameter
optimisation regarding the linear single-track model.
Even using a 100-times weighting for the “not
feasible” class resulted in only one parameter
combination fulfilling the constraint while only
achieving an accuracy of 0.08. With this restriction in
mind, a hyperparameter combination was chosen that
produced one false positive classification in the
training phase.
Table 6: Test evaluation of trained ANNs.
Vehicle model Test precision Test accuracy
Point mass 1.0 0.8341
Linear single-
track
0.9972 0.8230
4.3 Classifier Validation
For validation purposes, a larger data set is generated
in simulation. Therefore, the vehicle model for each
simulation run is chosen by the trained ANNs
respectively SVMs. In total, the new data set consists
of 5,447 data points all located in the parameter
boundaries given in Table 1 but distributed with a
finer grid. For comparison against the ground truth,
the chosen simulation runs are performed with the
nonlinear single-track model with roll and pitch
model as well.
In the following, the accuracy of the data sets
generated with the model assignment by the machine
learning algorithms as well as the computing time
required for the simulation is discussed. In Figure 5,
the computations times are visualized, in Figure 6 the
number of wrongly assigned vehicle models. Therein,
the SVMs performance is labelled with “default
SVMs”.
4.3.1 Support Vector Machine
Using the trained SVMs to assign the vehicle model
for the simulation runs, 8 of the 5,447 simulation
results differ from the ground truth data. Hence, in
0.147 % of the simulations a vehicle model is chosen
whose model fidelity is not sufficient to compute the
manoeuvre.
Mentioned should be that one of the faulty vehicle
model assignments is not made by an SVM. Both
SVMs, the one for the point mass model as well as the
one for the linear single-track model, classified their
models to be not feasible for the given simulation
parametrisation. But as already stated, the difference
in the smaller first generated data set between the
nonlinear single-track models is vanishing and thus,
no algorithm could be trained for this vehicle model.
Rather, the only known simulation parameters the
default nonlinear single-track model is not feasible
are assigned to the ground truth model manually. In
the new larger data set, another simulation
parametrisation the ground truth model should be
used is contained resulting into one wrong
assignment.
Regarding the computation times needed for the
simulation runs, with the help of the SVMs a
reduction of about 72 % is achieved.
4.3.2 Artificial Neural Network
Considering the trained ANNs for the vehicle model
assignment, a total of 29 simulation runs result in a
differing simulation outcome compared to the ground
truth. This corresponds to a wrong model assignment
in 0.532 % of simulation runs. Again, one of the
wrong model assignments is made because of the
vanishing difference between both nonlinear single-
track models.
While achieving a reduced accuracy compared to
the SVMs, the computation time reduction is
enhanced, reducing the required time by 79 %.
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
138
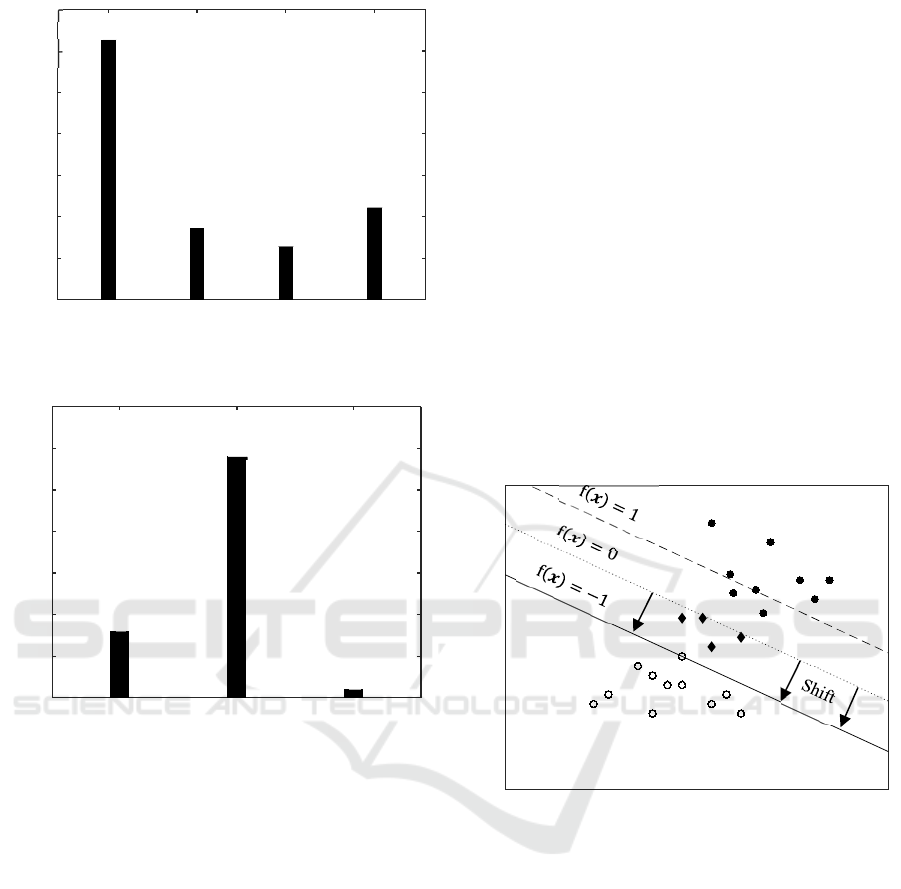
Figure 5: Computation times for data set generation.
Figure 6: Wrong model assignments in data set generation.
4.4 Shifted Classifier
As shown in the validation of the classifiers, for some
simulation runs the wrong vehicle model is chosen.
Thus, the wrong classifications are analysed
regarding the computed probabilities of class
membership.
In case of the ANNs, the output f
𝒙 ranges
from 0 to 1 and the decision boundary between both
classes is located in the middle, hence at f
𝒙
0.5. Investigating the wrong classifications, the
output was in average 0.4 away from the decision
boundary. Considering that the maximum distance is
0.5, those wrong classifications are made with a very
high probability.
For SVMs, the decision boundary is located at
f
𝒙
0 and the margin spans the area of
|
f
𝒙
|
1 in which preferably no classification is
placed. As stated in section 2.3, small violations of
the margin are allowed in the training controlled via
the regularisation parameter.
Taking a look at the SVMs’ outputs on the wrong
classified simulation runs, the average distance from
decision boundary is at 0.276 while no distance is
larger than 0.512 and thus every data point is located
in the middle of the margin. The approach of
maximizing the margin between the classes and
having it unpopulated by data points in training
improves the robustness of SVMs on new data points
which may lay outside the training data clusters.
By shifting the decision boundary from the middle
of the margin to its boundary, the precision of the
SVM can be improved. This way, for every data point
located inside the margin the simulation model is
classified to be not feasible. Hence, for every data
point the classifiers prediction is given with an
uncertainty, the simulation model is not chosen in
favour of the precision. In Figure 7, the decision
boundary shift is visualized
Figure 7: Shifted decision boundary.
To validate this proposed approach, a third full
data set is generated in the simulation using the SVMs
already trained but shifting their decision boundaries
accordingly. The results from comparison against the
ground truth data are also shown in Figure 5 and
Figure 6.
Using the shifted SVMs indeed improved the
precision of the classifier. Now in only 1 out of the
5,447 simulation runs a wrong vehicle model is
assigned, which again is the data point not classified
because of the vanishing difference between the
nonlinear single-track models. In fact, the two shifted
SVMs achieved a precision of 100 %.
The drawback of shifting the decision boundary is
the usage of more models with higher fidelity, thus
decreasing the achievable computation time
Ground
Truth
Default
SVMs
ANNs
0
20
40
60
100
80
Computation time [h]
Shifted
SVMs
125.1
34.3
25.8
44.5
120
140
Default
SVMs
ANNs
Shifted
SVMs
0
5
10
15
20
25
30
35
Wrong model assignments
8
29
1
Variable x
1
Variable x
2
Generating a Multi-fidelity Simulation Model Estimating the Models’ Applicability with Machine Learning Algorithms
139

reduction. With a reduction of about 64 %, the
required time still is highly reduced.
5 APPLICATION EXAMPLE
In this final section, the generated data sets are used
to train a lane change decision system (LCDS).
Therefore, the data set generated by the shifted SVMs
and the ground truth data set are considered. The
LCDS is implemented by an SVM for each data set,
comparing the suitability of those. The goal of the
LCDS is to classify the viability of a lane change at a
given situation.
The training of the SVM is made in accordance to
Section 4.2.1, i.e. the investigated hyperparameters,
given in Table 2, are evaluated with the help of a grid
search combined with a stratified 5-fold cross-
validation. The data preparation and splitting are done
accordingly too.
Since the application is a safety relevant feature, a
lane change should not be started in unfeasible
situations. To ensure this, again the precision of the
trained classifiers is constrained to be 100 %.
Table 7: Hyperparameters and performance of trained
LCDS.
Data
set
SVM parameters
Train
accuracy
Test
accuracy
Ground
Truth
RBF kernel, 𝐶0.5,𝛾1
10-times weighting
0.9465 0.9558
Shifted
SVMs
RBF kernel, 𝐶0.5,𝛾1
10-times weighting
0.9471 0.9558
In Table 7, the in the cross-validation best
performing hyperparameter combinations are given.
The precision of both trained LCDS satisfies the full
precision constraint on both training and test data and
therefore the system is making no false positive
classifications which could result in endangering
overtaking manoeuvres. While the hyperparameters
as well as the test accuracy do not show any
differences, the training accuracy has little deviations.
Since the high similarity between both data sets is
already known, the results are not surprising.
In general, most data driven algorithms perform
well even with some noise in the training data so that
small errors in data set generation may not affect the
application. Important to mention here is that the test
data should not contain errors, thus should be taken
from the ground truth. Else, the validation of the
trained algorithms loses its significance.
6 CONCLUSION
In this contribution, a method for assigning
simulation models with different model fidelity based
on their estimated validity is proposed. Therefore, the
models’ applicability boundaries are represented by
machine learning algorithms. The algorithms
investigated are support vector machines and
artificial neural networks.
For the algorithms to learn the models’
applicability, with each considered simulation model
a small data set is generated. Comparing the
simulation results against ground truth data, the
validity of the models can be determined at discrete
simulation parametrisations. Given this data,
classifiers can be fit to estimate the simulation
models’ feasibility.
Using these classifiers, larger data sets can be
generated only using a valid simulation model with
the lowest computational effort.
It is shown, that the proposed method can be used
to highly reduce the required computation time for
simulation data generation. Using ANNs or SVMs, a
computation time reduction of 79 % resp. 72 % is
achieved while generating a wrong simulation result
in only 0.53 % resp. 0.15 % of generated data.
Furthermore, it is proposed to shift the SVM’s
decision boundary to improve the accuracy of the
generated data set. This way, no loss in data set
accuracy was produced with the drawback of a lower
computation time reduction of 64 %.
Finally, a lane change decision system is
implemented using the generated data set. It is shown,
that the developed system achieves the same accuracy
as if it was trained on the highest fidelity model only.
Overall it can be stated, that the proposed method
can greatly reduce the required computation times
when generating large data sets by simulation.
Regarding the used machine learning algorithms, the
investigated SVMs overperform the ANNs in terms
of accuracy. In cases where the data set accuracy is
crucial, it is recommended to use the proposed shifted
SVMs for the classification.
A drawback of the method is the required
preparation of an initial data set for each investigated
simulation model. This data set should cover the
simulation parameter space in a sufficient manner to
provide enough information for the model
applicability estimation. Needing only small data
sets, the time required to generate the initial data sets
may exceed the later time savings.
It is also shown, that for models with high
similarity to the ground truth the method is not
applicable. In such case, only a vanishing part of the
SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications
140

data set contains information about the simulation
model’s applicability and the training of the machine
learning algorithms will fail.
Further research will investigate the possibility to
perform the initial estimator learning in an iterative
approach starting only with a small amount of initial
data points, thus being able to reduce the preparation
effort.
REFERENCES
Alvarez Lopez, P., Behrisch, M., Bieker-Walz, L.,
Erdmann, J., Flötteröd, Y.-P., Hilbrich, R., . . . Wießner,
E. (2018). Microscopic Traffic Simulation using
SUMO. Paper presented at the The 21st IEEE
International Conference on Intelligent Transportation
Systems, Maui, USA.
Biehler, J., Gee, M. W., & Wall, W. A. (2015). Towards
efficient uncertainty quantification in complex and
large-scale biomechanical problems based on a
Bayesian multi-fidelity scheme. Biomechanics and
Modeling in Mechanobiology, 14(3), 489-513.
doi:10.1007/s10237-014-0618-0
Bishop, C. M. (2006). Pattern recognition and machine
learning: New York : Springer.
Fernandez-Godino, M. G., Park, C., Kim, N., & Haftka, R.
(2017). Review of multi-fidelity models.
Fiala, E. (2006). Mensch und Fahrzeug: Fahrzeugführung
und sanfte Technik [Human and vehicle: Vehicle
guidance and smooth technology]. Wiesbaden: Vieweg.
Gron, A. (2017). Hands-On Machine Learning with Scikit-
Learn and TensorFlow: Concepts, Tools, and
Techniques to Build Intelligent Systems: O'Reilly
Media, Inc.
Heißing, B., & Ersoy, M. (2011). Chassis Handbook:
Fundamentals, Driving Dynamics, Components,
Mechatronics, Perspectives. Wiesbaden:
Vieweg+Teubner.
ISO. (2020). Intelligent transport systems - Partially
automated lane change systems (PALS) - Functional /
operational requirements and test procedures.
ITE Technical Committee. (1989). Determining Vehicle
Change Intervals: A Proposed Recommended Practice.
ITE Journal, 57, 27-32.
Krauß, S. (1998). Microscopic Modeling of Traffic Flow:
Investigation of Collision Free Vehicle Dynamics.
Retrieved from
Pacejka, H. B. (2012). Tire and Vehicle Dynamics (Third
Edition). Oxford: Butterworth-Heinemann.
Paulweber, M. (2017). Validation of Highly Automated
Safe and Secure Systems. In D. Watzenig & M. Horn
(Eds.), Automated Driving: Safer and More Efficient
Future Driving (pp. 437-450). Cham: Springer
International Publishing.
Schölkopf, B., & Smola, A. J. (2018). Learning with
Kernels: Support Vector Machines, Regularization,
Optimization, and Beyond: The MIT Press.
Schramm, D., Hiller, M., & Bardini, R. (2018). Vehicle
Dynamics - Modeling and Simulation: Springer-Verlag
Berlin Heidelberg.
Semrau, M., & Erdmann, J. (2016). Simulation framework
for testing ADAS in Chinese traffic situations. Paper
presented at the SUMO2016, Berlin.
Sieberg, P., Blume, S., Reicherts, S., & Schramm, D.
(2019). Nichtlineare modellbasierte pradiktive
Regelung der Fahrzeugdynamik in Bezug auf eine
aktive Wankstabilisierung und eine Nickreduzierung.
[Non-linear model-based predictive control of vehicle
dynamics in terms of active roll stabilization and pitch
reduction]. Forschung im Ingenieurwesen, 83(2), 119-
127. doi:10.1007/s10010-019-00337-6
Sovani, S., Johnson, L., & Duysens, J. (2017).
Incorporating high fidelity physics into ADAS and
autonomous vehicles simulation, Wiesbaden.
Wegener, A., Piórkowski, M., Raya, M., Hellbrück, H.,
Fischer, S., & Hubaux, J.-P. (2008).
TraCI: an interface
for coupling road traffic and network simulators. Paper
presented at the Proceedings of the 11th
communications and networking simulation
symposium, Ottawa, Canada.
Generating a Multi-fidelity Simulation Model Estimating the Models’ Applicability with Machine Learning Algorithms
141
