
Design of a Switched Control Lyapunov Function
for Mobile Robots Aggregation
Chrystian Edmundo Pool Yuca Huanca
1
, Gian Paolo Incremona
1 a
,
Roderich Groß
2 b
and Patrizio Colaneri
1 c
1
Dipartimento di Elettronica, Informazione e Bioingegneria, Politecnico di Milano, 20133 Milan, Italy
2
Department of Automatic Control and Systems Engineering, The University of Sheffield, Sheffield S1 3JD, U.K.
Keywords:
Swarm Robotics, Mobile Robots, Switched Systems, Control Lyapunov Functions, Collision Avoidance.
Abstract:
This paper proposes a novel aggregation strategy for a network of mobile wheeled robots with constrained
dynamics. The strategy assumes a centralized control architecture, which collects all the robot positions and
generates the control signals sent to the robots in the network. To do this a control Lyapunov function (CLF)
based approach is designed relying on a switched formulation of the robot models. Such a formulation is in fact
made possible by constraining the robot motion only to rotation and roto-translation in the plane. Moreover,
a collision avoidance objective is taken into account in the design of the CLF. The approach is analyzed, and
simulations as well as experiments with six robots show its effectiveness and practical applicability.
1 INTRODUCTION
Nowadays, distributed autonomous robotic systems
are increasingly applied in industrial and field oper-
ations, ranging from material delivery to precision
farming. In particular, advances and many researches
have been devoted to the so-called swarm robotics,
according to which a large number of mobile robots is
coordinated to achieve desired performance, e.g., av-
erage consensus and leader-follower tracking (Tzafes-
tas, 2012). The desired collective motion, which is
determined by the interaction of the robots among
each other or with the environment, is in fact appro-
priate to artificially emulate the behaviour of many
multi-agent systems present in nature.
1.1 Brief Literature Overview
In the context of distributed robotics, many control
methodologies have been developed in order to guar-
antee stability, taking into account the presence of
disturbances, communication constraints among the
agents, plug-and-play capabilities, and inaccuracies
due to sensors and actuators. Traditionally, the so-
called principle of locality has been exploited in dis-
a
https://orcid.org/0000-0003-1974-5646
b
https://orcid.org/0000-0003-1826-1375
c
https://orcid.org/0000-0002-6465-0737
tributed robotics, relying on the capability of the
robots to make use of information from their immedi-
ate surroundings (Parker et al., 2016; Brambilla et al.,
2013). Specifically, the robots viability property is
captured by a function designed to measure the per-
formance, and the goal becomes that of finding the
best approach to optimize such a cost. Among many
works in the literature, in (Beni, 1988; Bonabeau
et al., 1999), motivated by the collective behaviour in
social insect colonies and other animal communities,
a specific form of collective intelligence has been in-
troduced making the agents capable to self-organize
and produce predefined patterns.
Other applications of swarm robotics are devoted
to transportation of large objects, surveillance, for-
mation control in autonomous aircrafts or water ve-
hicles, see (Brambilla et al., 2013) for an overview
on this topic. Moreover, stability properties of these
systems have been formally investigated e.g., in (Gazi
and Passino, 2003; Gazi and Passino, 2004). Among
the used control approaches, in (Desai et al., 1998) for
instance a feedback linearization control technique is
proposed, making use only of local information to de-
rive a controller that exponentially stabilizes the rel-
ative distances between the robots of the system. In
(Egerstedt and Hu, 2001; Leonard and Fiorelli, 2001;
Ogren et al., 2001; Bachmayer and Leonard, 2002),
the concept of control Lyapunov functions (CLFs) is
492
Yuca Huanca, C., Incremona, G., Groß, R. and Colaneri, P.
Design of a Switched Control Lyapunov Function for Mobile Robots Aggregation.
DOI: 10.5220/0011319200003271
In Proceedings of the 19th International Conference on Informatics in Control, Automation and Robotics (ICINCO 2022), pages 492-499
ISBN: 978-989-758-585-2; ISSN: 2184-2809
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

introduced to formalize a constrained formation con-
trol problem. Moreover, in (Jin et al., 1994; Beni
and Liang, 1996), Lyapunov based methods are dis-
cussed for one and two dimensional swarm structures,
showing synchronous and asynchronous convergence
of the network to a predefined configuration. Other
works, as (Saska, 2016), rely instead on model pre-
dictive control strategies to achieve collision-free and
deadlock free navigation by multiple wheeled mobile
robots.
1.2 Contribution
Inspired by (Gauci et al., 2014), in this paper we
present an original formulation of a multi-robot sys-
tem recast in the framework of switched systems in
order to solve a rendezvous control problem. Specif-
ically, the main goal is to design a control approach
capable of making the robots in the network aggre-
gate, while guaranteeing collision avoidance. As in
(Gauci et al., 2014), a group of differential wheeled
robots aggregate by using only two modes of motion,
which represent rotation and roto-translation. Dif-
ferently from (Gauci et al., 2014), where each robot
chooses its mode based on the reading value of a
binary line-of-sight sensor, in the present paper, a
centralized approach is pursued where however the
amount of information sent to each robot is reduced to
only one bit. This latter approach offers superior per-
formance, and, by assuming idealised sensing, could
provide an upper bound for the performance of sys-
tems with concrete sensing implementations. In the
present paper, the constrained dynamics is recast into
a switched system with two modes. A centralized
control architecture is then proposed, so that all sys-
tem information are collected to generate the control
commands sent to each robot in the network. In par-
ticular, a CLF is designed proving stabilization of the
controlled multi-robot network, and also enabling a
collision avoidance property.
1.3 Outline of the Paper
The paper is organized as follows. In Section 2 the
model of the considered robot is defined and the con-
trol problem is formulated. In Section 3 the switched
version of the multi-robot system is derived, while
the proposed CLF based aggregation approach is in-
troduced and analyzed in Section 4. Simulation and
experimental results are illustrated in Section 5, and
some conclusions are finally drawn in Section 6.
2 MODELLING AND PROBLEM
FORMULATION
In this section the model of the considered wheeled
robots is described. Specifically, our proposal is based
on the kinematic unicycle-like model of the robot.
2.1 Robot Model
Consider a wheeled robot in the plane as illustrated in
Figure 1(a). It consists of two individually controlled
(a) wheeled robot
O
X
G
Y
G
p
x
p
p
y
XY
v
r
v
l
d
iw
r
θ
(b) robot planar view
p
ICR
v
t
v
l
v
r
R
w
(c) ICR point
p
i
p
j
d
i j
¯r
(d) robot aggregation
Figure 1: Wheeled robot (a), schematic rendering in the
plane (b) with instantaneous center of rotation (c), and ag-
gregation of two robots.
wheels, and a third passive castor wheel to provide
stabilization of the structure. Such a configuration al-
lows the robot to move in the plane indicated with
the global frame O − X
G
,Y
G
, while the robot frame is
given by p − X,Y (see Figure 1(b)). Note that, for
the sake of simplicity, a symmetric circular body with
center of mass and centroid coinciding with the robot
position p = [p
x
p
y
]
>
is considered. Moreover, let d
iw
be the inter-wheel distance, v
l
and v
r
be the left and
right wheel linear velocities, r the body radius and θ
the robot orientation. To reasonably reduce the com-
plexity of the model, the passive castor wheel is ig-
nored and the rolling motion of the main wheels is
instead constrained by the existence of the instanta-
neous center of rotation (ICR), that is the point lying
on the common lateral axis of the wheels (see Figure
1(c)). The angular speed is indicated as w, such that
v
r
:
= w
R +
d
iw
2
and v
l
:
= w
R −
d
iw
2
, with R being
the distance between the ICR and the centroid p.
Design of a Switched Control Lyapunov Function for Mobile Robots Aggregation
493

Now, consider the robot centroid p and its linear
velocity v
t
projected in the global frame as
v
t
= wR =
v
r
+ v
l
2
, (1a)
v
t
x
= v
t
cosθ, (1b)
v
t
y
= v
t
sinθ. (1c)
In order to write a state-space representation of the
system, we define the state vector as the robot pose
(i.e., position and orientation) x = [p
x
p
y
θ]
>
, while
the input vector is given by u = [v
r
v
l
]
>
. Therefore,
one can write (1) as the time-invariant nonlinear sys-
tem
˙x =
˙p
x
˙p
y
˙
θ
= f (x, u) =
v
r
+v
l
2
cosθ
v
r
+v
l
2
sinθ
1
d
iw
(v
r
− v
l
)
. (2)
Note that, the dependence of all the variables on time
is omitted when obvious for the sake of simplicity.
2.2 Problem Statement
Consider a network of N identical wheeled robots
with model as in (2). The problem to solve consists
of designing a control strategy constrained to dynam-
ics (2) with two modes, capable of making the robots
aggregate, and avoiding collisions among them (see
Figure 1(d), as an example where the aggregation of
two robots without collision is illustrated).
3 SWITCHED ROBOT SYSTEM
Now, by virtue of the robot dynamics constrained to
only two modes (rotation and roto-translation, in anal-
ogy with (Gauci et al., 2014)), model (2) can be recast
in the framework of switched systems and extended to
the case of a switched multi-robot system. In the fol-
lowing, let x
[i]
be the state of the ith robot in the net-
work, with i = 1, . . . , N. Consider the rotation around
the center of the robot and around its ICR determined
by the two pairs of velocities (v
r
0
, v
l
0
) and (v
r
1
, v
l
1
),
respectively. Then, let σ
[i]
(t) ∈ M , with M
:
= {0, 1},
be the so-called switching signal, so that the motion
mode is realized based on the following input vari-
ables,
u
[i]
= [v
[i]
r
v
[i]
l
]
>
:
=
(
[v
r
0
, v
l
0
]
>
, σ
[i]
= 0
[v
r
1
, v
l
1
]
>
, σ
[i]
= 1.
(3)
Therefore, letting f
[i]
σ
[i]
(u
[i]
)
(x
[i]
)
:
= f (x, u), the
switched nonlinear time-invariant system corre-
sponding to (2) is
˙x
[i]
= f
[i]
σ
[i]
(u
[i]
)
(x
[i]
), x
[i]
(0) = x
[i]
0
, (4)
where f
[i]
σ
[i]
(u
[i]
)
belongs to the set of vector fields
{ f
[i]
0
, f
[i]
1
}, with
f
[i]
0
:
=
0
0
1
d
iw
(v
r
0
− v
l
0
)
,
f
[i]
1
:
=
v
r
1
+v
l
1
2
cosθ
[i]
v
r
1
+v
l
1
2
sinθ
[i]
1
d
iw
(v
r
1
− v
l
1
)
,
indicating rotation and roto-translation, respectively.
Finally, the robot network model is obtained by re-
defining x = [x
[1]>
. . . x
[N]>
]
>
, v = [u
[1]>
. . . u
[N]>
]
>
,
and a switching string Σ(v) ∈ M
N
, with M
N
contain-
ing all the possible 2
N
switching signals configura-
tions, so that
˙x = f
Σ(v(t))
(x), x(0) = x
0
, (5)
where f
Σ(v(t))
belongs to the set { f
1
, . . . , f
2
N
}, with
f
1
:
=
f
[1]
0
.
.
.
f
[N]
0
, f
2
:
=
f
[1]
1
.
.
.
f
[N]
0
, . . . , f
2
N
:
=
f
[1]
1
.
.
.
f
[N]
1
.
4 THE PROPOSED STRATEGY
We are now in a position to introduce the proposed
control strategy to solve the problem stated in §2.
More precisely, our approach is based on the no-
tion of CLF (Sun and Zhao, 2001; Freeman and Koko-
tovic, 2008). In general, given a system of the form
˙x = f
σ
(x), with the vector field Lipschitz continuous
and σ ∈ M , a function V (x) is a CLF for the switched
system if V (x) is continuously differentiable, positive
definite and V (0) = 0, and for any x 6= 0, there always
exists σ such that
˙
V (x) = ∇V (x) f
σ
(x) < 0.
4.1 CLF Aggregation Strategy
In order to simplify the design of CLF, we take into
account only the robot positions without orientation,
hence the robots are considered as point masses. It is
worth mentioning that the embodied property of the
robots is a posteriori contemplated by the insertion of
a proper weighting matrix into the control law. More-
over, we consider a centralized architecture capable
of retrieving and sending all the needed information
to the robots.
Consider Figure 1(d), and let d
i j
(x
[i]
, x
[ j]
), ∀i, j =
1, . . . , N, i 6= j be the reciprocal distance function be-
tween the centers of two robots, defined as
d
i j
=
q
(p
[i]
x
− p
[ j]
x
)
2
+ (p
[i]
y
− p
[ j]
y
)
2
, (6)
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
494

whose derivatives are given by
˙
d
i j
=
1
d
i j
h
(p
[i]
x
− p
[ j]
x
)( ˙p
[i]
x
− ˙p
[ j]
x
)+
(p
[i]
y
− p
[ j]
y
)( ˙p
[i]
y
− ˙p
[ j]
y
)
i
. (7)
Now, collect all the distances and their derivatives in
the column vectors d and
˙
d, respectively, by omitting
the repeated values d
i j
= d
ji
. The candidate CLF is
then selected as
V (x)
:
=
1
2
d
>
d. (8)
In order to prove the stability property of the proposed
approach, compute the derivative of
˙
V
i j
, so that one
has
˙
V
i j
(x) =d
i j
˙
d
i j
=
h
(p
[i]
x
− p
[ j]
x
)( ˙p
[i]
x
− ˙p
[ j]
x
)
+(p
[i]
y
− p
[ j]
y
)( ˙p
[i]
y
− ˙p
[ j]
y
)
i
=σ
[i]
h
1
2
(v
r
[i]
1
+ v
l
[i]
1
)
(p
[i]
x
− p
[ j]
x
)cosθ
[i]
+
(p
[i]
y
− p
[ j]
y
)sinθ
[i]
i
−
σ
[ j]
h
1
2
(v
r
[i]
1
+ v
l
[i]
1
)
(p
[i]
x
− p
[ j]
x
)cosθ
[ j]
+
(p
[i]
y
− p
[ j]
y
)sinθ
[ j]
i
=σ
[i]
g
i j
(x) + σ
[ j]
g
ji
(x),
(9)
where
g
i j
(x)
:
=
h
1
2
(v
r
[i]
1
+ v
l
[i]
1
)
(p
[i]
x
− p
[ j]
x
)cosθ
[i]
+
(p
[i]
y
− p
[ j]
y
)sinθ
[i]
i
. (10)
The whole derivative of V can be therefore expressed
in a compact form as
˙
V (x) = d
>
˙
d =
σ
[1]
. . . σ
[N]
g
1
.
.
.
g
N
, (11)
with g
i
:
=
∑
N
k=1,k6=i
g
ik
.
The previous expression leads to a linear combi-
nation of state functions weighted by the switching
signals. Therefore, by a proper choice of the switch-
ing string such that
σ
[i]
=
(
1, g
i
< 0,
0, g
i
≥ 0.
, (12)
it can be guaranteed that
˙
V (x) is semi-negative defi-
nite, i.e.,
˙
V (x) =
N
∑
1
σ
i
g
i
(x) ≤ 0. (13)
The previous inequality means that when
˙
V = 0, then
the robots stop and start to rotate around their cen-
troid.
Remark 4.1 (Tracking control problem). Note that
tracking goal can be achieved by including in (8) an
additional term d
o
depending on the distance between
each robot and a target position p
o
= [p
o
x
p
o
y
]
>
, i.e.,
V (x)
:
=
1
2
d
>
o
d
o
+
1
2
d
>
d. (14)
Following the same previous reasoning, one obtains
˙
V (x) =
σ
[1]
. . . σ
[N]
h
1
(x) + g
1
(x)
.
.
.
h
N
(x) + g
N
(x)
=
N
∑
1
σ
[i]
[h
i
(x) + g
i
(x)] ≤ 0,
(15)
where
h
i
(x)
:
=
1
2
(v
r
[i]
1
+ v
l
[i]
1
)
(p
[i]
x
− p
o
x
)cosθ
[i]
+
(p
[i]
y
− p
o
y
)sinθ
[i]
i
, ∀i = 1, . . . , N. (16)
4.2 Collision Avoidance Property
Although the strategy previously presented allows to
achieve the desired robot aggregation, it does not take
into account possible collisions among the robots.
However, having in mind field implementation, it is
instrumental to consider the embodied property of the
robots and enable a collision avoidance strategy. This
property can be formalized as a constraint by impos-
ing that the distance between any two robots has to
be d
i j
> 2r. A way to introduce this constraint into
the control law consists in the manipulation of the se-
lected CLF (8).
Let
¯
d be a positive scalar parameter greater than
2r. The modified CLF V (x) becomes
V (x)
:
=
1
2
(d −
ˆ
d)
>
(d −
ˆ
d). (17)
where
ˆ
d is a column vector with all components equal
to
¯
d.
Additionally, let us introduce the desired mini-
mum distance between two robots d
min
, such that
2r ≤ d
min
<
¯
d. This allows us to define a state-
dependant weighting function
1
(d
i j
−d
min
)
2
(see Figure
2), aimed at penalizing the cost with increasing value
as d
i j
tends to 2r when d
i j
<
¯
d. Such a weighting
Design of a Switched Control Lyapunov Function for Mobile Robots Aggregation
495

O
d
W
d
min
¯
d
Figure 2: Weighting function W .
function is included in the CLF as a diagonal weight-
ing matrix given by
W
:
=
1
(d
12
−d
min
)
2
0 0
0
.
.
.
0
0 0
1
(d
N−1N
−d
min
)
2
, (18)
so that
V (x) =
(d
12
−
¯
d)
2
2(d
12
− d
min
)
2
+ ··· +
(d
N−1N
−
¯
d)
2
2(d
N−1N
− d
min
)
2
=
1
2
(d −
ˆ
d)
T
W (d −
ˆ
d).
(19)
Since for d
i j
≥
¯
d the modified CLF (19) accord-
ing to the designed weighting function W (see Figure
2) would make the robot move away from
¯
d, a state-
dependant parameter α
i j
(d
i j
) is introduced as domain
selector for each d
i j
in order to solve this issue, that is
α
i j
(d
i j
) =
(
(d
i j
− d
min
)
2
, d
i j
≥
¯
d
1, d
i j
<
¯
d
, (20)
with i 6= j and i, j = 1, . . . , N. Hence, the new weight-
ing matrix becomes
W
α
:
=
α
12
(d
12
−d
min
)
2
0 0
0
.
.
.
0
0 0
α
N−1N
(d
N−1N
−d
min
)
2
. (21)
Now, by computing the derivative of the generic
entry term
˙
V
i j
, two different cases need to be distin-
guished. More specifically, if d
i j
≥
¯
d, it yields
˙
V
i j
(x) =
˙
d
i j
(d
i j
−
¯
d)
=
1 −
¯
d
d
i j
h
(p
[i]
x
− p
[ j]
x
)( ˙p
[i]
x
− ˙p
[ j]
x
)
+(p
[i]
y
− p
[ j]
y
)( ˙p
[i]
y
− ˙p
[ j]
y
)
i
=
σ
[1]
. . . σ
[N]
˜g
1
(x)
.
.
.
˜g
N
(x)
,
(22)
with ˜g
i
:
=
∑
N
k=1,k6=i
1 −
¯
d
d
ik
g
ik
. Otherwise, if d
i j
<
¯
d, one has
˙
V
i j
(x) =
˙
d
i j
(d
i j
−
¯
d)
(
¯
d − d
min
)
(d
i j
− d
min
)
3
=
1 −
¯
d
d
i j
(
¯
d − d
min
)
(d
i j
− d
min
)
3
×
h
(p
[i]
x
− p
[ j]
x
)( ˙p
[i]
x
− ˙p
[ j]
x
)
+(p
[i]
y
− p
[ j]
y
)( ˙p
[i]
y
− ˙p
[ j]
y
)
i
=
σ
[1]
. . . σ
[N]
˜g
1
(x)
.
.
.
˜g
N
(x)
,
(23)
with this time ˜g
i
:
=
∑
N
k=1,k6=i
1 −
¯
d
d
ik
(
¯
d−d
min
)
(d
i j
−d
min
)
3
g
ik
.
In both cases, analogously to (13), the CLF deriva-
tive
˙
V (x) can be rewritten as a linear combination of
state functions weighted by the switching signals, and
as such it can be made semi-negative definite by a
proper choice of the switching signal. Moreover, as
mentioned in Remark 4.1, the tracking control prob-
lem can be addressed by defining V (x) as
V (x)
:
=
1
2
d
>
o
d
o
+
1
2
(d −
ˆ
d)
>
W
α
(d −
ˆ
d). (24)
Finally, the corresponding switching law is given by
Σ = arg min
Σ∈M
N
˙
V .
(25)
5 CASE STUDY
In this section simulation and experimental results
achieved by applying the proposed CLF based aggre-
gation strategy are illustrated.
5.1 Settings and Performance Metric
A network of N = 6 robots with random initial distri-
bution in the plane is considered. The main parame-
ters of the robots are listed in Table 1.
Moreover, in order to assess the behaviour of the
proposed approach, some performance metrics are
hereafter introduced. The first used index is given by
the ratio between the maximum number of robots ag-
gregated in a cluster, namely N
c
, and the total number
of robots in the network N, i.e.,
κ(t)
:
=
N
c
(t)
N
. (26)
Note that two robots are considered adjacent if the
distance between their centers is less than 4r. There-
fore, the robot network is fully aggregated when the
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
496
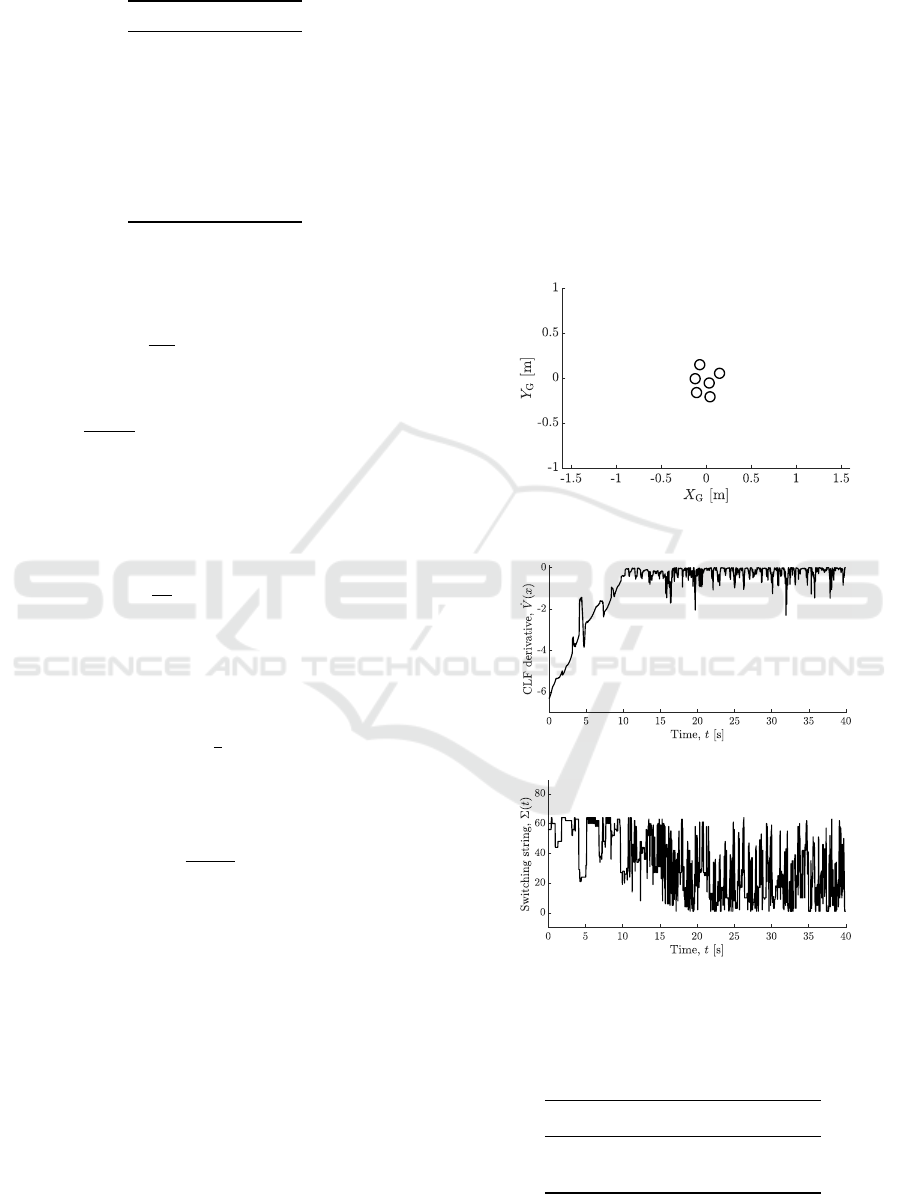
Table 1: Robot settings.
Parameter Value
r 0.055 m
d
iw
0.105 m
¯
d 2.9r
d
min
2.1r
R 0.2975 m
v
r
0
−0.2 m s
−1
v
l
0
0.2 m s
−1
v
r
1
−0.2 m s
−1
v
l
1
−0.14 m s
−1
number of robots in a cluster is N. The second in-
dex is the dispersion metric of the multi-robot system
given by
δ(t)
:
=
1
4r
2
N
∑
i=1
p
[i]
(t) − ¯p(t)
2
, (27)
with ¯p(t) being the centroid of the robots positions,
i.e., ¯p
:
=
∑
N
i=1
p
[i]
N
. Then, as term of comparison, we
consider the optimal dispersion for circular robots,
namely δ
?
, reported in (Graham and Sloane, 1990).
To fairly compare δ
?
with the actual dispersion of the
robots, we introduce the following modified disper-
sion metric
˜
δ(t)
:
=
1
¯
d
2
N
∑
i=1
p
[i]
(t) − ¯p(t)
2
. (28)
Note that
˜
δ is computed relying on
¯
d, and takes into
account the control objective of reaching a minimum
distance between two robots equal to
¯
d. To do this,
making reference to (Graham and Sloane, 1990) a fic-
titious radius equal to ¯r =
¯
d
2
is considered (see Figure
1(d)). Finally, the percentage error η
˜
δ
between the
dispersion
˜
δ and its lower bound given by δ
?
is com-
puted, i.e.,
η
˜
δ
=
˜
δ − δ
?
δ
?
100%. (29)
In order to assess the validity of the proposal, the av-
erage values of the performance metrics are computed
over 100 tests of 40 seconds. Simulations have been
executed relying on the kinematic model, using MAT-
LAB with sampling time T = 0.033 s, suitably chosen
such that the convergence properties of the proposed
control system are preserved.
5.2 Simulation Results
The outcome of the simulations is illustrated in the
following. Figure 3 shows the final configuration
of the robots which aggregate around their centroid
without colliding, as expected. In Figure 4, the deriva-
tive of the CLF, that is
˙
V , is illustrated, confirm-
ing the theoretical analysis reported in §4. In the
same figure, the corresponding switching string Σ(t)
is shown. Note that V is differentiable, and the deriva-
tive, i.e.,
˙
V , depends on the current operating mode of
the robots. As for the performance metrics, Figure 5
shows the dispersion metrics κ(t) in (26), δ(t) in (27)
and
˜
δ in (28), respectively, reporting the simulations
with maximum and minimum values (red lines), the
average value (blue line), the optimal dispersion δ
?
and maximum aggregation κ = 1 (green line), and the
50th test (black line).
Figure 3: Final aggregation of the robots in the plane.
(a) CLF derivative
(b) switching string
Figure 4: Time evolution of the CLF derivative
˙
V (x) (a),
and of the switching string Σ(t) (b) in simulations.
Table 2: Average metrics over 100 simulations.
Strategy δ
˜
δ η
˜
δ
SA 197.4 - -
CLF 12.2 5.8 20.08
Design of a Switched Control Lyapunov Function for Mobile Robots Aggregation
497

(a) cluster metric
(b) dispersion metric
(c) modified dispersion metric
Figure 5: Time evolution of the performance metrics κ
(a), δ (b), and
˜
δ (c) in simulations: average value over
100 tests (blue line), minimum and maximum metric values
(red lines), optimal dispersion δ
?
and maximum aggrega-
tion κ = 1 (green line), evolution of the performance metrics
for the 50th test (black line).
Finally, we compared our proposal with a self-
aggregation (SA) method reproducing the one in
(Gauci et al., 2014), under the same setting. However,
by construction, this method does not intrinsically
take into account collisions, but, if a possible colli-
sion is detected by the sensors, the robots stop and ro-
tate around their centroid, according to mode 0 in our
case. Taking into account the previous performance
indexes, the averaged results are reported in Table 2.
One can note that, as for the SA approach, the values
˜
δ and the corresponding η
˜
δ
are not computed since no
collision avoidance mechanism is taken into account.
However, it is evident that in terms of dispersion met-
ric δ, our approach performs better. If we consider the
optimal dispersion in (Graham and Sloane, 1990) for
6 robots, which is equal to δ
?
= 4.83, one can observe
that our proposal guarantees satisfactory results, with
a dispersion error equal to 20.08 %.
5.3 Experimental Results
In order to assess in practice the proposed control
approach, it has been implemented by using the re-
mote platform Robotarium (Wilson et al., 2020). The
same parameters adopted in simulation are consid-
ered, apart from the safety radius set equal to the
robot diameter. As for the performance indexes, their
average values are computed over 15 tests, and the
achieved average dispersion metric is δ = 11.59, that
is larger than the network theoretical lower bound,
while the average modified dispersion is
˜
δ = 5.51,
corresponding to a percentage error of the 14% with
respect to the optimal dispersion. These results con-
firm the validity of the model used in simulation and
the feasibility in practice of the proposed approach.
Figure 6 shows the dispersion metrics κ(t) in (26),
δ(t) in (27) and
˜
δ in (28), respectively, while a frame
of the experimental test is reported in Figure 7.
(a) cluster metric
(b) dispersion metric
(c) modified dispersion metric
Figure 6: Time evolution of the performance metrics κ (a),
δ (b), and
˜
δ (c) in the experimental tests: average value over
15 tests (blue line), minimum and maximum metric values
(red lines), optimal dispersion δ
?
and maximum aggrega-
tion κ = 1 (green line), evolution of the performance metrics
for the 7th test (black line).
ICINCO 2022 - 19th International Conference on Informatics in Control, Automation and Robotics
498

Figure 7: Experimental Robotarium platform with 6 robots.
6 CONCLUSIONS
This work has proposed a novel control strategy to
solve a rendezvous problem for a network of mobile
wheeled robots. The proposed approach is based on a
CLF suitably designed relying on a switched formula-
tion of the robot model with two modes. A centralized
control architecture allows to retrieve the robot loca-
tion in the environment, and to generate the best se-
quence of modes capable of making the robot aggre-
gate without colliding among each other. Simulation
and experimental results have shown the effectiveness
of the proposed approach. Future works could be de-
voted to the extension of the proposal to predictive
control and distributed control methods, and to the
case of more than two modes and more complex sce-
narios, for example, with communications delays.
ACKNOWLEDGEMENTS
This work has been partially supported by the Italian
Ministry for Research in the framework of the 2017
PRIN, Grant no. 2017YKXYXJ.
REFERENCES
Bachmayer, R. and Leonard, N. E. (2002). Vehicle networks
for gradient descent in a sampled environment. In 41st
IEEE Conference on Decision and Control, 2002.,
volume 1, pages 112–117, Las Vegas, NV, USA.
Beni, G. (1988). The concept of cellular robotic system. In
IEEE International Symposium on Intelligent Control,
pages 57–62, Arlington, VA, USA.
Beni, G. and Liang, P. (1996). Pattern reconfiguration in
swarms - convergence of a distributed asynchronous
and bounded iterative algorithm. IEEE Transactions
on Robotics and Automation, 12:485–490.
Bonabeau, E., Dorigo, M., and Theraulaz, G. (1999).
Swarm Intelligence : From Natural to Artificial Sys-
tems. Oxford University Press, Oxford, United King-
dom.
Brambilla, M., Ferrante, E., Birattari, M., and Dorigo, M.
(2013). Swarm robotics: a review from the swarm
engineering perspective. Swarm Intelligence, 7(-):1–
41.
Desai, J., Ostrowski, J., and Kumar, V. (1998). Control-
ling formations of multiple mobile robots. In IEEE In-
ternational Conference on Robotics and Automation,
volume 4, pages 2864–2869, Leuven, Belgium.
Egerstedt, M. and Hu, X. (2001). Formation constrained
multi-agent control. IEEE Transactions on Robotics
and Automation, 17(6):947–951.
Freeman, R. and Kokotovic, P. (2008). Robust Nonlin-
ear Control Design: State-Space and Lyapunov Tech-
niques. Birkh
¨
auser, Boston, MA, USA.
Gauci, M., Chen, J., Li, W., Dodd, T. J., and Roderich Groß,
R. (2014). Self-organized aggregation without com-
putation. The International Journal of Robotics Re-
search, 33(8):1145–1161.
Gazi, V. and Passino, K. M. (2003). Stability analysis of
swarms. IEEE Transactions on Automatic Control,
48(4):692–697.
Gazi, V. and Passino, K. M. (2004). Stability analysis of so-
cial foraging swarms. IEEE Transactions on Systems,
Man, and Cybernetics, Part B (Cybernetics), 34:539–
557.
Graham, R. L. and Sloane, N. J. A. (1990). Penny-packing
and two-dimensional codes. Discrete & Computa-
tional Geometry, 5(1):1–11.
Jin, K., Liang, P., and Beni, G. (1994). Stability of synchro-
nized distributed control of discrete swarm structures.
In IEEE International Conference on Robotics and
Automation, volume 2, pages 1033–1038, San Diego,
CA, USA.
Leonard, N. and Fiorelli, E. (2001). Virtual leaders, artifi-
cial potentials and coordinated control of groups. In
40th IEEE Conference on Decision and Control, vol-
ume 3, pages 2968–2973, Orlando, FL, USA.
Ogren, P., Egerstedt, M., and Hu, X. (2001). A control Lya-
punov function approach to multi-agent coordination.
In 40th IEEE Conference on Decision and Control,
volume 2, pages 1150–1155, Orlando, FL, USA.
Parker, L., Rus, D., and Sukhatme, G. (2016). Multiple Mo-
bile Robot Systems, pages 921–941. Intelligent Sys-
tems, Control and Automation: Science and Engineer-
ing. Springer, Cham, Germany.
Saska, M. (2016). Predictive control and stabilization of
nonholonomic formations with integrated spline-path
planning. Robotics and Autonomous Systems, 75:379–
397.
Sun, H. and Zhao, J. (2001). Control Lyapunov functions
for switched control systems. In American Control
Conference, volume 3, pages 1890–1891, Arlington,
VA, USA.
Tzafestas, S. (2012). Advances in Intelligent Autonomous
Systems. Intelligent Systems, Control and Automa-
tion: Science and Engineering. Springer, Dordrecht,
The Netherlands.
Wilson, S., Glotfelter, P., Wang, L., Mayya, S., Notomista,
G., Mote, M., and Egerstedt, M. (2020). The Robo-
tarium: Globally impactful opportunities, challenges,
and lessons learned in remote-access, distributed con-
trol of multirobot systems. IEEE Control Systems
Magazine, 40(1):26–44.
Design of a Switched Control Lyapunov Function for Mobile Robots Aggregation
499
