A Deep Learning Simulation Framework for Building Digital Twins of

Wind Farms: Concepts and Roadmap

Subodh M. Joshi

, Thivin Anandh

and Sashikumaar Ganesan

Department of Computational and Data Sciences, Indian Institute of Science, Bangalore, 560012, India

Keywords:

Digital Twins, Physics Informed Neural Networks, Dynamic Mode Decomposition, Wind Engineering,

Physics-AI Hybrid Modeling.

Abstract:

Simulation-based Digital Twins are often limited by the difﬁculties encountered in the real-time simulation

of continuous physical systems, for example, ﬂuid ﬂow simulations in complex domains. Classical methods

used to simulate such systems, such as the mesh-based methods, typically require state-of-the-art computing

infrastructure to get a rapid estimation of the trajectory of the system dynamics if the problem size is large.

We propose a simulation framework comprising of a Physics Informed Neural Network (PINN) and a model

order reduction strategy based on the Dynamic Mode Decomposition (DMD) technique for rapid simulation of

ﬂuid ﬂows, such as air, in complex domains. This framework is primarily targeted at realizing a Digital Twin

of a wind farm in terms of the aerodynamics aspects. However, the framework will be ﬂexible and capable

of creating simulation-based Digital Twins of other systems involving continuous physics. The reduced order

model aims to make this framework lightweight, such that a trained model will be able to run even on compact

edge devices. In this paper, we present the building blocks of this framework, a few key concepts, and a

roadmap for completing the framework. We illustrate our approach with the help of an example in transient

heat transfer.

1 INTRODUCTION

‘Digital Twins’ technology is set to transform main-

stream scientiﬁc computing thanks to a signiﬁcant rise

in computing power and the development of innova-

tive algorithms. Digital Twins are becoming ubiqui-

tous because they help in improved efﬁciency, safety,

and reliability of engineering systems. A Digital Twin

refers to a digital representation of any physical sys-

tem, such that it closely follows the physical system

and serves as its virtual counterpart. A Digital Twin

typically consists of a physical system, its virtual (dig-

ital) model, and a two-way ﬂow of data between the

two. Development of a Digital Twin in turn necessi-

tates the development of: (a) ‘faster than real-time’

simulation of the physical system on a computer (b) a

mechanism to incorporate real-time data from multi-

ple sensors into the simulation, and dynamically adapt

the simulation in response to these data, and (c) real-

time analytics predicting a future trajectory of the sys-

tem dynamics, which in turn helps in decision mak-

https://orcid.org/0000-0002-9239-8866

https://orcid.org/0000-0003-4969-3242

https://orcid.org/0000-0003-1858-3972

ing. Further, a Digital Twin necessarily involves a

two-way transfer of the information between the vir-

tual and the physical models, unlike a Digital Shadow,

which typically involves the ﬂow of information from

the physical system to its digital counterpart alone.

We refer to (Fuller et al., 2020) for a detailed discus-

sion on the engineering aspects of Digital Twins. Al-

though this technology has come a long way in the

last decade, it still needs to overcome a few hurdles to

fully mature. One such challenge faced by researchers

today is that of achieving a faster than real-time sim-

ulation of complex ﬂuid ﬂows encountered in many

physical systems (Molinaro et al., 2021).

In this paper, we propose a simulation framework

for real-time simulation of ﬂuid ﬂows, possibly in-

volving a domain with a complex shape. The key re-

quirement of such a framework would be to capture

all the essential aspects of the ﬂow physics while also

being computationally lightweight to achieve a near

real-time simulation. A few other desirable proper-

ties of the framework include:

1. Easy to use and easy to include new ﬂow physics.

2. Suitable for large and computationally challeng-

ing problems.

356

Joshi, S., Anandh, T. and Ganesan, S.

A Deep Learning Simulation Framework for Building Digital Twins of Wind Farms: Concepts and Roadmap.

DOI: 10.5220/0011319500003274

In Proceedings of the 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications (SIMULTECH 2022), pages 356-363

ISBN: 978-989-758-578-4; ISSN: 2184-2841

3. Amenable for parallelization for added accelera-

tion and lightweight to port even on edge devices

if required.

4. Flexible and easy to use with other libraries used

for data analysis, visualization, and computing.

The traditional methods for simulation of con-

tinuous physical systems, such as the mesh-based

methods, are often computationally expensive and

require state-of-the-art computing infrastructure for

simulations of large systems. In recent times, a

new class of numerical methods is gaining pop-

ularity for simulation of continuous physical sys-

tems, namely the Physics Informed Machine Learn-

ing methods (Karniadakis et al., 2021). Physics In-

formed Neural Networks (PINNs) is a revolutionary

method which solves constrained Partial Differential

Equations (PDEs) with the help of a Deep Learning

model (Raissi et al., 2019). This method has accrued

signiﬁcant attention since its inception thanks to its

strengths, viz. a) an elegant formulation b) compara-

ble accuracy to the classical methods at a marginal

computing cost c) availability of powerful libraries

for Machine / Deep Learning d) ability to exploit

Graphics Processing Units (GPUs) or hybrid com-

puting hardware platforms for parallel computing etc.

There have been several variations proposed inspired

from the original PINNs method. We present a short

literature review of Deep Learning-based simulation

methods in the next section. Due to the strengths of

the PINNs method, we choose it as the core physics

simulator for our framework. As a Proof-of-Concept

(PoC), we incorporate the original form of the PINNs

method into our framework. However, we subse-

quently plan to explore other improved techniques,

such as the variational PINNs (VPINNs).

The second essential component of our framework

includes a Reduced Order Model (ROM) based on

the Dynamic Mode Decomposition (DMD) strategy

(Schmid, 2010) on top of the PINNs model. DMD is

a technique for model order reduction where the sys-

tem dynamics is approximated to be linear in space-

time. DMD, also known as the Koopman mode anal-

ysis, gives a spectral decomposition of the spatio-

temporal data (Kutz et al., 2016). Depending on the

required level of the model ﬁdelity, only a few modes

of this spectral decomposition can be re-combined to

generate a reasonably accurate reconstruction of the

original spatio-temporal data. Unlike Proper Orthog-

onal Decomposition (POD), the DMD modes need

not be orthogonal and are accompanied by the time

dynamics. This is a very powerful technique to de-

rive a model-agnostic data-driven ROM of the phys-

ical/computational system. There exist a few vari-

ations of this method, suitable for different applica-

tions. We present further details of this technique and

a short literature survey in the next section. In the pro-

posed technique, the Koopman mode analysis is per-

formed to get the dynamic modes of the data-matrix

created from the output of the PINNs model. Only a

small number of dynamic modes, enough to capture

the maximum variance of the system is required to re-

construct the system-dynamics. The DMD ROM will

not only reduce the computing time for short-term

predictions, but also make our model lightweight in

order to port it even on an edge device. The trained

neural network or/and the DMD model can be de-

ployed on an edge device for short-term predictions,

which can then be re-trained periodically. The de-

tailed procedure to deploy a DMD ROM in synchro-

nization with the PINNs model is described in the

subsequent sections.

In this paper, we present the key concepts and

ideas behind the proposed framework, its building

blocks and the road-map for its implementation. The

rest of the paper is organized as follows: section

2 presents a detailed review of Physics Informed

Machine Learning and model order reduction using

DMD. Section 3 presents the proposed framework, its

building blocks, and the key concepts behind its op-

eration. We present one motivating example in tran-

sient heat transfer to demonstrate the working of our

framework in section 4. The road-map for its imple-

mentation is presented in section 5. Lastly, we present

the conclusions in section 6.

2 LITERATURE REVIEW

In the recent times, Machine Learning, and in par-

ticular Neural Networks are gaining popularity for

scientiﬁc computing (Aimone et al., 2017; Karni-

adakis et al., 2021) including ﬂuid dynamics simu-

lations (Brunton et al., 2020). A key strength of this

approach lies in the superior computational speedups

possible in contrast to the classical techniques for the

same level of numerical accuracy. In particular, the

Physics Informed Neural Networks (PINNs) intro-

duced by Raissi et al. (Raissi et al., 2019) have caught

the attention of the scientiﬁc community since intro-

duced in 2019. In PINNs, the loss function for the

neural network optimization includes the residual of

the governing PDEs in addition to the losses associ-

ated with the initial and the boundary conditions. The

derivatives of the conserved variables with respect to

the spatio-temporal variables required for constitut-

ing this loss function (i.e., inputs to the network) are

found through forward-mode Automatic Differentia-

tion (Raissi et al., 2019; G

une et al., 2018). PINNs

A Deep Learning Simulation Framework for Building Digital Twins of Wind Farms: Concepts and Roadmap

357

have been used in a wide range of applications, in-

cluding Navier-Stokes equations for modeling ﬂuid

ﬂows (Jin et al., 2021), earth system modeling (Ir-

rgang et al., 2021), high-speed ﬂows (Mao et al.,

2020), hyperbolic transport problems (Eduardo and

Florindo, 2021) etc. We refer to a recent pre-print

by Cuomo et. al. (Cuomo et al., 2022) for a de-

tailed survey of the PINNs method, a few of its vari-

ants and various applications are solved using it. As

a Proof-of-Concept (PoC), we have implemented the

original PINNs method of Raissi et al. in the current

(experimental) version of the framework. However,

we plan to incorporate the latest ML-based methods

in the proposed framework in the future.

The next important component of our framework

is the model order reduction scheme using Dynamic

Mode Decomposition (DMD). DMD was ﬁrst intro-

duced by Schmid for spectral analysis of the nu-

merical and experimental data for ﬂuid dynamics

(Schmid, 2010). Since its inception, several vari-

ants of this technique have been developed by various

researchers. (Schmid et al., 2011) presents a com-

prehensive review of applications of DMD in scien-

tiﬁc computing. In DMD, the spatio-temporal data is

decomposed in spectral modes (also called Dynamic

modes) and the associated time dynamics. The de-

tailed algorithm for DMD, its variations, a few ap-

plications and its connections with the Koopman-

mode analysis have been presented in (Kutz et al.,

2016). Additionally, we refer to the recent review of

the DMD method and its variants given in (Schmid,

2021). In our framework, we implement the DMD

ROM in PyDMD, an open-source Python library for

dynamic mode decomposition (Demo et al., 2018).

Further details regarding the implementation and the

working of our framework are presented in the next

section.

3 PINNs-DMD SIMULATION

FRAMEWORK FOR DIGITAL

TWINS

In this framework, we use a Physics Informed Neural

Network in its original (differential) form for carrying

out the ﬂuid ﬂow simulations. In the current version

of the software, we have implemented the original

PINN method from Raissi et. al. (Raissi et al., 2019).

However, we plan to explore other methods and de-

velop novel methods targeted for this application in

future. In the PoC version of our framework, we use

the Python-based library DeepXDE (Lu et al., 2021)

for the implementation of the PINN-based Navier-

Stokes equations solver. The output of the PINNs

model is used to create a spatio-temporal data ma-

trix which is in turn used for creating a reduced order

model (ROM). We use the classical DMD method for

the creation of this ROM. In the future, we plan to ex-

plore a more efﬁcient and accurate variant of DMD,

such as higher-order DMD or multi-resolution DMD

for this application. For the DMD implementation,

we use the open-source library PyDMD (Demo et al.,

2018). Since DeepXDE and PyDMD are both imple-

mented in Python, the integration of the two models

becomes easy. Further, Python offers a rich suite of

software libraries for analysis, computing and visu-

alization, which help in making the framework more

useful and versatile.

3.1 How the Proposed Framework

Works

The framework works as follows:

1. A Physics Informed Neural Network (PINN) acts

as a data-driven physics-aware solver. The PINN

model estimates the ﬂow conditions inside the do-

main, for example, a wind farm, respecting the

boundary conditions, the initial conditions, and

the ﬂow physics.

2. Once the boundary data become stable, the PINN

starts training a Dynamic Mode Decomposition

(DMD) reduced order model (ROM). This mainly

consists of creating the data-matrix containing the

spatio-temporal data corresponding to the ﬂow

variables such as velocity and pressure, followed

by spectral decomposition of this data to get Dy-

namic modes and the associated time dynamics.

3. The DMD ROM will be responsible for the real-

time prediction of ﬂow conditions on the domain.

We consider only a few prominent modes (cumu-

latively containing at least 90% energy) resulting

in reduced storage and processing power require-

ments. This in turn also allows us to run the ROM

model on a low-power computer such as an edge

device.

4. An analytics module keeps monitoring the time-

dependent boundary conditions. As soon as any

changes in the boundary conditions beyond a

threshold value are detected, the PINN model un-

dergoes an online training to accommodate the

changing boundary conditions.

5. When the changes stabilize, the PINN model re-

trains the DMD ROM to economically yield the

real-time ﬂow predictions.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

358

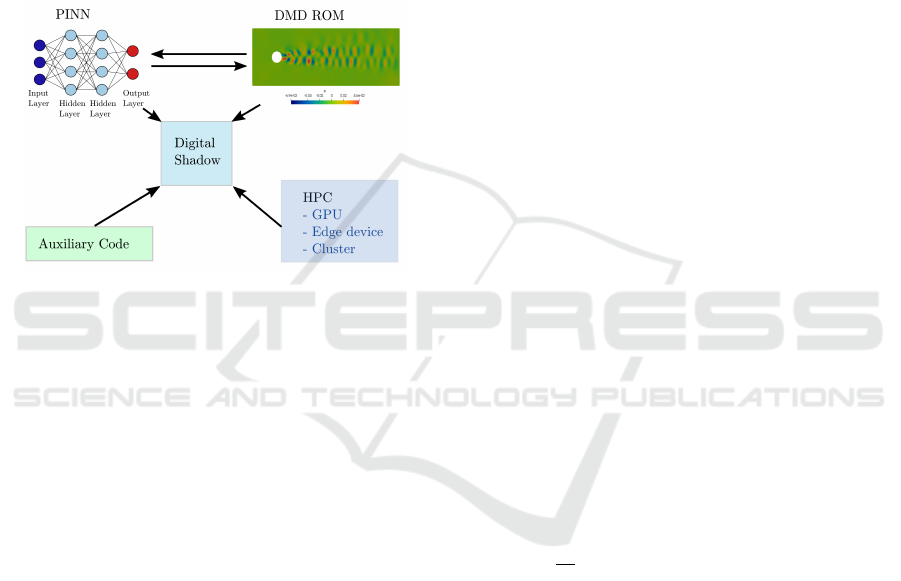
6. The PINN model will be trained on a high-

performance computing hardware such as a clus-

ter equipped with GPUs. However, once trained,

the model can be ported on an edge device such as

NVIDIA Jetson Nano. Alternately, the ROM can

be ported on the edge device, and the PINN can

be trained and deployed on a cluster computer.

7. The framework also contains some auxiliary code.

The auxiliary modules will be responsible for data

visualization, ﬁle handling and tools for analytics

such as anomaly detection, error monitoring, cre-

ating a meta-model, automated testing, etc.

Figure 1: A schematic illustrating the proposed framework.

Figure 1 shows a ‘Digital Shadow’ or the

simulation-based Digital Twin framework. In the cur-

rent work, we focus on the digital representation of

the physical system, and not on the feedback and the

control module. However, these components will be

considered for implementation in the future.

3.2 Strengths of This Approach

1. The use of PINNs as a physics solver offers three

main advantages:

(a) PINNs fundamentally perform a nonlinear re-

gression and are naturally suited for solving

coupled nonlinear PDEs. This makes the

framework versatile and allows the integration

of other physics to the framework as required

with relative ease.

(b) PINNs technology is based on Artiﬁcial Neu-

ral Networks (ANNs) and the backpropagation

algorithm. There are many powerful libraries

available for this purpose. Thus, the proposed

framework beneﬁts from these libraries.

methods for solving PDEs, the PINNs method

is relatively more amenable for parallel imple-

mentation using GPU devices. This imparts su-

perior speedups required for near real-time sim-

ulations.

2. The main advantage that this framework offers

compared to the traditional methods is that it fa-

cilitates continuous (online) training of the PINNs

model while the DMD ROM yields short-term

predictions.

3. The DMD based ROM makes the framework even

faster. DMD is a model-agnostic means to derive

a ROM model. Further, it is a very simple tech-

nique to implement. Once built, the deployment

of a DMD ROM requires very little computational

power and therefore is ideal for deployment on an

edge computing platform.

4. The entire framework is planned and developed

in Python, a general purpose programming lan-

guage. Many powerful libraries exist for Deep

Learning, data analysis, visualization, and ﬁle

handling in Python. The framework will greatly

beneﬁt from these libraries.

5. The framework is ﬂexible. The framework allows

the integration of different (and more powerful)

techniques for the physics simulation, as well as

the model order reduction. Thus, methods bet-

ter suited for different applications and hardware

platforms can be incorporated as required.

4 NUMERICAL EXAMPLE

4.1 Problem Description

We consider the 2D time-dependent diffusion equa-

tion (Ganesan and Tobiska, 2017) as follows,

∂u

∂t

− α∇

u = 0, in Ω = [0, 1]

(1)

α = 1

We consider a unit square as the computational do-

main. Initially, the entire domain has a uniform tem-

perature (u(t = 0) = u

) value of zero. The Bound-

ary conditions imposed on the problem are graphi-

cally illustrated in Figure 2. As the time advances,

the heat dissipates in the domain, affecting the tem-

perature (u(t)) at every point on the domain.

4.2 Numerical Solution

We simulate this system till time t = 0.15s. Fig-

ure 3 shows the temperature variation at the location

(x, y) := (0.5, 0.625). We also indicate the solutions

obtained using a Finite Element Method (FEM) in

A Deep Learning Simulation Framework for Building Digital Twins of Wind Farms: Concepts and Roadmap

359

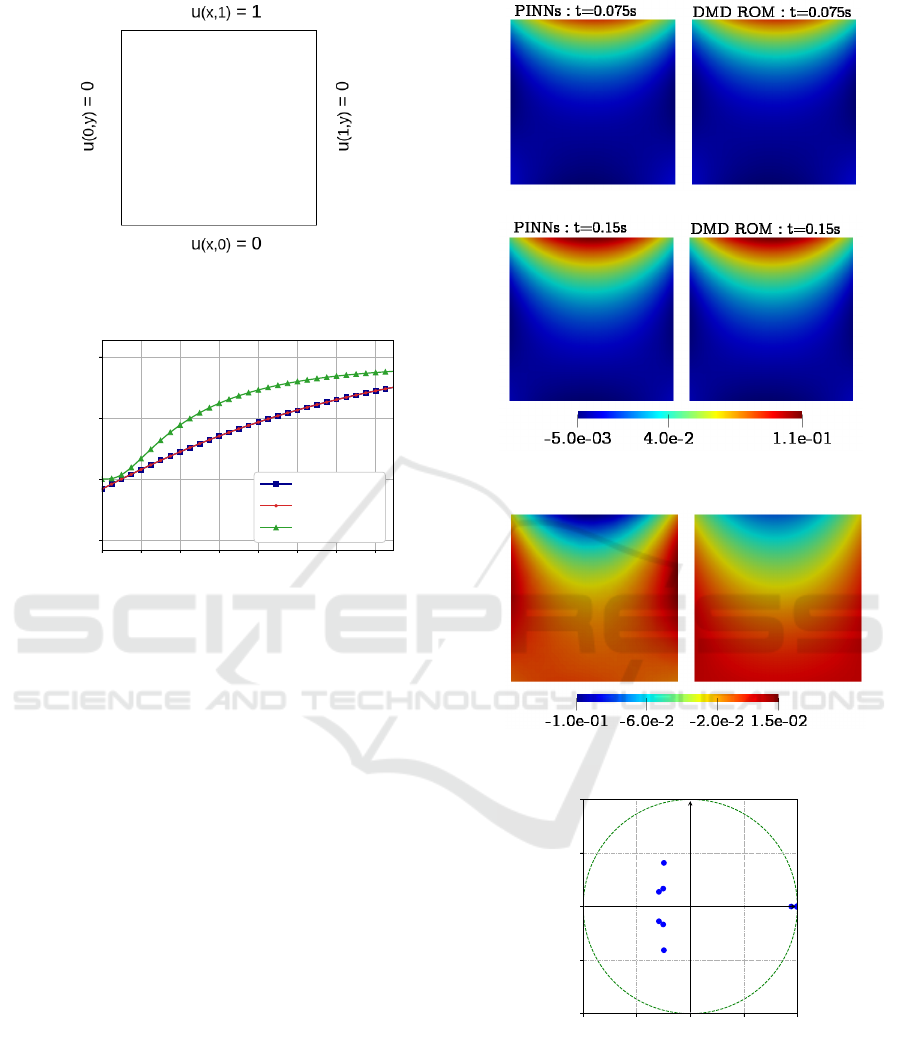
Figure 2: Computational domain (unit square) along with

the boundary conditions.

0.0 0.02 0.04 0.06 0.08 0.1 0.12 0.14

Time(s)

−0.02

0.00

0.02

0.04

u(t)

Solution at x = 0.5 y = 0.625

PINNs

DMD ROM

FEM

Figure 3: Time Series Solution at at y = 0.625.

the same ﬁgure. We refer to (Ganesan and Tobiska,

2017) for the theory and the implementation details

of FEM. It can be seen that the PINNs-based solution

follows a similar general trend of time evolution as

the FEM-based solution. The sparse sampling of data

used for training the PINNs model, which helps in

rapid training of the PINNs model, leads to the rel-

ative difference between the FEM solution and the

PINNs solution. However, the focus of this paper is

not on the comparison between the mesh-based meth-

ods (e.g., Finite Volume or Element methods) and the

PINNs method. Instead, we wish to emphasize on the

performance of the DMD ROM meta-model in com-

parison to the PINNs based physics solver, which is

the key idea behind this framework. It can be seen

from Figure 3 that the ROM solution obtained using

the DMD modes closely follows the PINNs solution.

These results show promise, and the proposed frame-

work can be developed further for more complex ap-

plications. In this PoC version of the framework, we

have deployed a rather crude PINNs model facilitates

rapid prototyping by reducing training time. There is

scope to improve the accuracy of the PINNs solver

with respect to the mesh-based numerical methods.

As listed in the roadmap of our framework in subse-

quent sections, we have accounted for these optimiza-

tions in our development plan.

Figure 4: Solution comparison - PINNs vs DMD ROM.

Figure 5: First Two DMD modes of the System.

−1.0 −0.5

0.0 0.5 1.0

Real p ar t

−1.0

−0.5

0.0

0.5

1.0

Imaginary par t

Figure 6: Eigenvalues in the complex plane.

Figure 4 shows the distribution of the solution

on the domain computed using the PINNs method

and the DMD ROM method derived from the PINNs

method. It can be seen that the reduced order model

produces an identical solution as the PINNs method.

Figure 5 shows the ﬁrst two eigenmodes obtained us-

ing the dynamic mode decomposition. These modes

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

360

show a visual representation of the spectral decompo-

sition using the DMD method. Figure 6 shows the

eigenvalues obtained during the dynamic mode de-

composition. It can be seen that all of the eigenval-

ues have the value of the real part less than 1, i.e.,

contained within the unit circle (also shown in the ﬁg-

ure). This shows that the DMD ROM model is sta-

ble in time and produces reliable results. Thus, the

PINNs model coupled with the DMD ROM produces

identical results as the PINNs model alone. The sig-

niﬁcance of this observation is that, once the bound-

ary data stabilizes, the DMD ROM alone can be used

for near-term predictions, and the cost associated with

the PINNs forward propagation is saved. Further,

the PINNs can undergo online training independently

to accommodate the changing boundary conditions

while the DMD ROM continues to produce the near-

term predictions. For large networks and complex

physical systems, this would result in considerable

savings in computing time.

5 ROADMAP FOR

IMPLEMENTATION

In this section, we discuss the roadmap for building

the proposed framework. The following points will

be considered during the development:

1. Core libraries for physics simulation:

We plan to implement the original PINN method

of Raissi et. al. (Raissi et al., 2019) to simulate

the wind ﬂow around the wind turbines in the ﬁrst

version of the framework. Once the proof of con-

cept (PoC) is built, the framework would be im-

proved by incorporating other state-of-the-art AI

solvers. In the PoC version, we plan to implement

the PINNs method using the DeepXDE library

(Lu et al., 2021). However, we will also explore

other, more powerful libraries such as NVIDIA

Modulus for large-scale problems in the future.

2. Reduced order model

In the current PoC framework, we have deployed

the classical DMD algorithm for model order re-

duction using the PyDMD library. In the fu-

ture, we plan to incorporate other advanced DMD-

based schemes (e.g. multi-resolution DMD,

Higher-order DMD etc.). Further, we plan to de-

ploy the DMD ROM on an edge device such as

NVIDIA Jetson Nano.

3. High performance computing

The challenge we foresee in developing a Digital

Twin of the entire wind farm, is the scaling of the

Deep Learning model on parallel hardware plat-

forms. We plan to develop a hardware-aware im-

plementation of the PINNs and the DMD models

to complete the online training rapidly.

4. Uncertainty quantiﬁcation

We plan to incorporate an inbuilt mechanism for

uncertainty quantiﬁcation, taking into account pa-

rameter uncertainties. Further, the initial and

boundary conditions can be considered as statis-

tical distributions rather than ﬁxed values, and ac-

cordingly, a statistical description of the ﬂow ﬁeld

can be sought (Yang and Perdikaris, 2019; Yang

et al., 2021).

5. Computing on edge devices

We plan to port the reduced order model on an

edge device. The purpose of this development is

twofold.

(a) It shows the capability of our approach to pre-

dict near-term physics, while being lightweight

in order to work even on an edge device.

(b) It serves the purpose of ﬂow prediction where

the HPC facilities are not readily available.

We will experiment with deploying the ROM as

well as the trained PINNs model on an edge de-

vice such as NVIDIA Jetson Nano.

6. Analytics

We can use the rich ecosystem of libraries and

softwares for data analytics, visualization, and ﬁle

handling that Python offers. The framework will

contain auxiliary code catering to data analysis

(for example, anomaly detection), visualization

of the physical data as well as time-series infor-

mation pertaining to the important ﬂow parame-

ters, displaying and monitoring error metrics etc.

Lastly, we plan to include code to export the raw

data in various ﬁle formats to facilitate scientiﬁc

visualization using third-party libraries.

7. Optimization

Finally, we plan to perform studies to derive the

best performing network architectures and hyper-

parameters for the PINNs model. This will en-

sure optimal performance from our PINNs and

DMD ROM models. Further, we plan to exper-

iment with the training process of PINNs itself.

In this regard, the important question to address

is whether we can train the PINNs on a range of

boundary values instead of a ﬁxed value in order

to minimize re-training of the PINNs, which can

be costly. We plan to validate our approach ﬁrst on

academic test cases (e.g., simple test cases in heat

transfer, incompressible ﬂuid dynamics, etc.) fol-

lowed by simulations of a single wind turbine, and

lastly, simulation of a wind farm. At each level of

A Deep Learning Simulation Framework for Building Digital Twins of Wind Farms: Concepts and Roadmap

361

testing, different aspects of the framework, such

as numerical accuracy, efﬁciency, hardware scal-

ing etc., will be tested, validated, and improved.

6 CONCLUSION

We propose a Python-based framework for

simulation-based Digital Twin of continuous

physical systems. The primary target application

for this framework is the simulation of a wind farm

from the aerodynamics point of view. However,

the framework can be easily adapted for use in

other ﬂuid ﬂow applications and other continuous

physical phenomena. We use PINNs as the main

physics simulator and a DMD-based ROM for further

accelerating the simulations. The novelty of this

approach lies in online training of the DMD ROM by

the PINNs model for rapid ﬂow prediction. Further,

the framework aims to provide an-inbuilt uncertainty

quantiﬁcation of the ﬂow variables and yield a

real-time simulation of the continuous systems via

online training. The training of the PINNs model

will take place in a cluster computer, whereas the

trained PINNs model, along with the DMD based

ROM, will be ported on an edge device. In this paper,

we have demonstrated our approach with the help of

an example in transient heat transfer. In the future,

we plan to develop this framework further to enable

real-time simulation of complex physical phenomena,

including aerodynamics simulations of a large wind

farm. Lastly, we also present a roadmap for the

implementation of the proposed framework, where

we identify a few challenges we may encounter and

steps for their mitigation.

ACKNOWLEDGEMENTS

The authors would like to thank Dr. Abhineet Gupta

and Dr. Suranjan Sarkar (Shell, Bangalore) for their

feedback and discussions. The authors would like to

thank the anonymous reviewers for their detailed re-

views.

REFERENCES

Aimone, J., Parekh, O., and Severa, W. (2017). Neural com-

puting for scientiﬁc computing applications. In ACM

International Conference Proceeding Series, volume

2017-July.

Brunton, S. L., Noack, B. R., and Koumoutsakos, P. (2020).

Machine Learning for Fluid Mechanics. Annual Re-

view of Fluid Mechanics, 52:477–508.

Cuomo, S., di Cola, V. S., Giampaolo, F., Rozza, G.,

Raissi, M., and Piccialli, F. (2022). Scientiﬁc Machine

Learning through Physics-Informed Neural Networks:

Where we are and What’s next. arXiv, 2201.05624.

Demo, N., Tezzele, M., and Rozza, G. (2018). PyDMD:

Python Dynamic Mode Decomposition. The Journal

of Open Source Software, 3(22):530.

Eduardo, A. and Florindo, J. B. (2021). A study on a

feedforward neural network to solve partial differen-

tial equations in hyperbolic-transport problems. In

Paszynski, M., Kranzlm

uller, D., Krzhizhanovskaya,

V. V., Dongarra, J. J., and Sloot, P. M. A., editors,

Computational Science – ICCS 2021, pages 398–411,

Cham. Springer International Publishing.

Fuller, A., Fan, Z., Day, C., and Barlow, C. (2020). Digital

Twin: Enabling Technologies, Challenges and Open

Research. IEEE Access.

Ganesan, S. and Tobiska, L. (2017). Finite elements: The-

ory and algorithms. Cambridge University Press.

une, A., Baydin, G., Pearlmutter, B. A., and Siskind, J. M.

(2018). Automatic Differentiation in Machine Learn-

ing: a Survey. Journal of Machine Learning Research,

18:1–43.

Irrgang, C., Boers, N., Sonnewald, M., Barnes, E. A.,

Kadow, C., Staneva, J., and Saynisch-Wagner, J.

(2021). Towards neural Earth system modelling by

integrating artiﬁcial intelligence in Earth system sci-

ence. Nature Machine Intelligence, 3:667–674.

Jin, X., Cai, S., Li, H., and Karniadakis, G. E. (2021).

NSFnets (Navier-Stokes ﬂow nets): Physics-informed

neural networks for the incompressible Navier-Stokes

equations. Journal of Computational Physics,

426:109951.

Karniadakis, G. E., Kevrekidis, I. G., Lu, L., Perdikaris,

P., Wang, S., and Yang, L. (2021). Physics-informed

machine learning. Nature Reviews Physics, 3(6):422–

440.

Kutz, J. N., Brunton, S. L., Brunton, B. W., and Proctor,

J. L. (2016). Dynamic Mode Decomposition: Data-

Driven Modeling of Complex Systems. SIAM-Society

for Industrial and Applied Mathematics, Philadelphia,

PA, USA.

Lu, L., Meng, X., Mao, Z., and Karniadakis, G. E. (2021).

DeepXDE: A deep learning library for solving differ-

ential equations. SIAM Review, 63(1):208–228.

Mao, Z., Jagtap, A. D., and Karniadakis, G. E. (2020).

Physics-informed neural networks for high-speed

ﬂows. Computer Methods in Applied Mechanics and

Engineering, 360:112789.

Molinaro, R., Singh, J., Catsoulis, S., Chidambaram, N.,

and Lakehal, D. (2021). Embedding data analytics

and CFD into the digital twin concept, volume 214.

Elsevier Ltd.

Raissi, M., Perdikaris, P., and Karniadakis, G. E. (2019).

Physics-informed neural networks: A deep learn-

ing framework for solving forward and inverse prob-

lems involving nonlinear partial differential equations.

Journal of Computational Physics, 378:686–707.

SIMULTECH 2022 - 12th International Conference on Simulation and Modeling Methodologies, Technologies and Applications

362

Schmid, P. J. (2010). Dynamic mode decomposition of nu-

merical and experimental data. Journal of Fluid Me-

chanics, 656(February 2015):5–28.

Schmid, P. J. (2021). Dynamic Mode Decomposition and Its

Variants. Annual Review of Fluid Mechanics, 54:225–

254.

Schmid, P. J., Li, L., Juniper, M. P., and Pust, O. (2011). Ap-

plications of the dynamic mode decomposition. The-

oretical and Computational Fluid Dynamics, 25(1-

4):249–259.

Yang, L., Meng, X., and Karniadakis, G. E. (2021). B-

pinns: Bayesian physics-informed neural networks for

forward and inverse pde problems with noisy data.

Journal of Computational Physics, 425:109913.

Yang, Y. and Perdikaris, P. (2019). Adversarial uncertainty

quantiﬁcation in physics-informed neural networks.

Journal of Computational Physics, 394:136–152.

A Deep Learning Simulation Framework for Building Digital Twins of Wind Farms: Concepts and Roadmap

363