zkBeacon: Proven Randomness Beacon based on Zero-knowledge

Veriﬁable Computation

Thomas Lavaur

1,2

and J

ome Lacan

ISAE-Supaero, Universit

e de Toulouse, France

Paul Sabatier, Universit

e de Toulouse, France

Keywords:

Randomness Beacon, Random Number Generation, zk-SNARK, zk-STARK, Veriﬁable Computation.

Abstract:

The generation of random numbers by a trusted third-party is essential to many cryptographic protocols.

Recently, the NIST proposed the standardization of randomness beacons, which are hash-based chains of

pulses. Each pulse contains a random number and is generated at regular time intervals. However, if the

owner of the beacon generator is untrusted, several attacks allow the manipulation of the provided random

numbers. In this paper, we ﬁrstly suggest protecting the ﬁrst hash functions of the NIST scheme by adding

a veriﬁable argument of knowledge. More precisely, we propose furnishing a zk-SNARK or a zk-STARK

with the hash to make the system more transparent and resistant to randomness manipulation. Secondly, we

propose a veriﬁable computation-based interactive protocol to allow a client, with the help of the beacon, to

generate proven randomness. Then, we show that connecting this system to a blockchain could have several

beneﬁts. We provide a security analysis with a model allowing a malicious beacon generator. We prove that

our ﬁrst application improves the resilience of the system against randomness manipulation attacks and that

the interactive protocol rules out timing attacks for the client and ensures the non-predictability of the random

numbers. Finally, we evaluated the computation cost with zk-SNARKs.

1 INTRODUCTION

The concept of the randomness beacon was intro-

duced in (Rabin, 1983). It can be viewed as a ser-

vice that generates a new beacon at regular time in-

tervals. This beacon is called a pulse and mainly

contains a fresh random number. While Rabin used

it to build speciﬁc cryptographic applications such

as contract signing, several other applications have

been proposed such as voting protocols (Moran and

Naor, 2010) or traceable signatures (Kiayias et al.,

). In order to make compatible potential concur-

rent randomness beacons, the US National Institute

of Standards and Technology (NIST) suggests a stan-

dard draft (Kelsey et al., 2019) enabling the emis-

sion of structured random numbers starting from raw

randomness. It has also proposed its own beacon

server (Nis, 2020), as well as some projects in Chile

(UChile, 2020) and Brazil (Bra, 2020). Basically, the

main issues that must be solved by these systems are

the quality of the randomness of the outputs, their

freshness and their immutability. These issues are de-

tailed in (Kelsey et al., 2019) and some countermea-

sures are proposed. However, the system is not ﬂaw-

less and attacks exist, especially conceivable from the

operator of the beacon.

The ﬁrst objective of our paper is to make the sys-

tem more transparent and resistant to various attacks

while maintaining its interesting structure and prop-

erties i.e., a chain of pulses using external raw en-

tropy. Secondly, we propose an interactive protocol

enabling the collaboration of the randomness beacon

and another party in order to generate a new proven

random number from their raw data. Both proposals

make use of veriﬁable computation (VC), which al-

lows proving that a given computation has been cor-

rectly performed with public or private inputs. Used

in the context of randomness beacons, they prove that

speciﬁc steps of the system were effectively done in

the process of the generation of the given outputs.

This paper is organized as follows. The next sec-

tion presents the state of the art concerning various as-

pects related to randomness beacons. In Section 3, we

describe the NIST scheme and its weaknesses. Then,

we detail our three main propositions: the addition

of a zero-knowledge VC scheme to prove the proper

generation of the pulses, an interactive protocol to en-

sure the freshness of the generated data, and the ad-

vantages of connecting the system to a blockchain. In

the fourth section, we present a security analysis for

406

Lavaur, T. and Lacan, J.

zkBeacon: Proven Randomness Beacon based on Zero-knowledge Veriﬁable Computation.

DOI: 10.5220/0011327500003283

In Proceedings of the 19th International Conference on Security and Cryptography (SECRYPT 2022), pages 406-414

ISBN: 978-989-758-590-6; ISSN: 2184-7711

our proposition. To this end, we analyze the poten-

tial attacks and examine how our systems respond to

them. In Section 5, we discuss the choice of certain

mechanisms (zk-SNARK or zk-STARK, hash func-

tion used, security level) and provide a performance

evaluation of an implementation of proof generation

for our systems. The last section concludes.

2 STATE OF THE ART

This section introduces the main concepts used in this

paper. First, we present the problem of reliable ran-

dom number generation and explain the principle of

the randomness beacon. The last part describes the

zero-knowledge VC schemes that will be used in this

paper to improve the trustworthiness of these random-

ness beacons.

2.1 Random Number Generation

Random numbers generated by a non-deterministic

generator are often consequently released by a trusted

third party due to the expensive equipment required.

Introduced by Micali, Rabin and Vadhan in 1999

(Micali et al., 1999), veriﬁable random functions

(VRF) aim to generate proven randomness. Based on

asymmetric cryptography, the inputs of this pseudo-

random function are a public value (the seed) and a

secret generation key. The output is composed of a

proof and the result. With a given public key and

the two parts of the output, anyone can verify the

proper execution of this function and thus of the ran-

dom number generation.

2.2 Public Randomness Beacons

When a system needs randomness generated by a

third-party, it is possible to use the services of a pub-

lic generator called a randomness beacon. For exam-

ple, this is the case for blockchains and some crypto-

graphic protocols. This concept of randomness bea-

cons was introduced in (Rabin, 1983) which describes

the generation of random numbers by a satellite or a

network node at regular time intervals. These regular

beacons are used to build security protocols such as

secure contract signing or conﬁdential disclosure.

Recently, the NIST has developed a standard de-

scribing an architecture that produces a chain of ran-

dom beacons. This standard explains how to con-

vert raw data from a source of entropy into a signed

and timestamped random number with the help of

hash functions. This proposition has already been

deployed and several organizations provide random

numbers based on it, such as the NIST itself (Nis,

2020) or public organizations from Chile (UChile,

2020) or Brazil (Bra, 2020). In addition to the de-

scription of the system, (Nis, 2020) provides a se-

curity analysis by identifying potential attacks and

proposing certain countermeasures. Efﬁcient ran-

domness beacons have been extensively studied in the

literature. For example, (Dharanikot et al., ) designed

a randomness beacon combining distributed random-

ness, by allowing users to join at any time, and cryp-

tographic delay functions.

2.3 Veriﬁable Computation and

Zero-knowledge Proofs

Introduced in (Goldwasser et al., 1989), a veriﬁable

computation is a cryptographic protocol allowing a

prover to provide a proof with the result of an NP

computation which attests to the validity of the com-

putation. Given the input, the output and the related

proof, the veriﬁer can validate the output of a compu-

tation as being the result of a public program without

needing to run it again. This proof can be interactive

or non-interactive.

There are a multitude of veriﬁable computation

protocols, but three main categories have emerged

and represent the vast majority of the systems used:

Succinct Non-interactive ARgument of Knowledge

(SNARK), Scalable and Transparent ARgument of

Knowledge (STARK) and universal SNARK. We will

not go into the history of the conception of these

proofs but we will detail the functioning, the advan-

tages and the disadvantages of these two families.

With the addition of zero-knowledge, some of the

inputs can be kept secret by hiding them and the in-

termediate steps of the computation (this secret part

is call the witness). This allows the prover to justify

the result of a computation without revealing speciﬁc

inputs. If the veriﬁer cannot retrieve the private in-

put from the output, they will not learn anything from

the proof except the result of that calculation and the

fact that the public program was computed correctly.

With this addition, the system is called zk-SNARK or

zk-STARK.

For SNARKs and STARKs the program needs to

be transformed into a polynomial representation. This

step is called arithmetization. In order to prove an

NP program, a SNARK program must be reduced to

a Rank 1 Constraint System (R1CS). A R1CS is com-

posed of polynomials extracted from multiplication

and addition gates; their number is denoted by n. For

STARKs, it must be reduces an Algebraic Intermedi-

ate Representation (AIR). An AIR is a set of polyno-

mials extracted from transition steps; their number is

zkBeacon: Proven Randomness Beacon based on Zero-knowledge Veriﬁable Computation

407

denoted by n. In both systems, n impacts prover com-

plexity.

SNARKs were introduced in practice in 2013

(Parno et al., 2013). The security of a zk-SNARK

protocol relies on a trusted setup. In order to limit vul-

nerabilities, we propose using the Powers of Tau cer-

emony (Bowe et al., 2017) to decentralize the trusted

setup. The Powers of Tau ceremony allows for the

decentralization of the ﬁrst step of the trusted setup

which is common to all speciﬁc zk-SNARK circuits.

At the end of this protocol, the only way to compro-

mise the system and forge a fake proof is if everyone

who participated in the protocol is corrupted or mali-

cious. By attracting many diverse and reputable par-

ticipants, it becomes unrealistic that all of them would

be compromised.

The trusted setup can either be circuit speciﬁc for

SNARKs or up to a certain amount of constraints for

universal SNARKs.

The two most used SNARK systems are Groth16

(Groth, 2016) and PLONK (Gabizon et al., 2019). In

the Groth16 system, the proof size does not depend

on the program’s complexity and is shorter than 200.

That is why Groth16 is often used. PLONK is a uni-

versal SNARK protocol with great performance.

STARKs are more recent, introduced in 2018

(Ben-Sasson et al., 2018). STARKs are based on hash

functions and when a quantum collision-resistant

hash function is used, STARKs are quantum resistant.

3 A TRUSTWORTHY BEACON

3.1 NIST Randomness Beacon

The NIST generation scheme aims to furnish ran-

dom numbers at regular time intervals (Kelsey et al.,

2019). These numbers are linked through a commit-

ment scheme and form a chain. Each number is sent

along with information about it and its construction,

all of this is structured and formatted into a pulse.

The pulse contains all the information needed for the

generation of the random number. Everything is con-

structed and calculated by the beacon app. We refer

the reader to (Kelsey et al., 2019) for their system. It

can also be view through our proposition by removing

our additions describes in 3.2 and Fig. 1.

All these steps and recommendations are ex-

plained in the NIST reference (Kelsey et al., 2019).

For our proposition, we will add cryptographic tools

to this scheme to increase transparency and secure

vulnerabilities, allowing users to be more conﬁdent in

it. Indeed, this scheme is vulnerable and users should

not be convinced that what they receive is fresh and

has not been altered.

Put simply, our ﬁrst idea was to apply VRFs to the

entropy seeds ρ

i,∗

. However, the veriﬁcation step of

the VRF needs the inputs and thus, would force the

system to reveal the values of the seeds, which sig-

niﬁcantly change the principle of the beacon genera-

tor. Moreover, different types of operations need to be

proved. These constraints led us to use more general

proofs, like VC arguments.

3.2 Zero-knowledge VC to Ensure the

Proper Generation of the Pulse

We propose proving the ﬁrst hash functions, which

transform the raw randomness of different random

number generators into a seed used to generate the ﬁ-

nal random number and a commitment, with the help

of VCs. In fact, the NIST model is already a bit trans-

parent in this regard but there is no guarantee about

the seed’s r

provenance. For a user, when they re-

ceive the pulse, they can already verify all the infor-

mation except for the r

value by redoing the whole

computation. However, several attacks can arise from

the user’s inability to check the origin of this value.

The hash function can be replaced in the protocol and

nobody would notice. With the addition of a VC ar-

gument, we aim to patch this vulnerability and make

the generation reliable by enabling the veriﬁcation of

while keeping the inputs secret. By doing this, we

ensure that C

is the output of a public program: two

hash functions.

For our scheme, we propose proving the two ﬁrst

hash functions: the public program is the hash func-

tions themselves. We propose furnishing the time T

of the pulse as a public input and ρ

i,1

, ρ

i,2

as the pri-

vate input.

Finally, we follow one of the NIST suggestions,

not present in the previous section, which consists of

adding a XOR between the output of the ﬁrst hash

and the freshly-generated random number R

to obtain

the new randLocal value: r

i+1

= Hash(ρ

i,1

||ρ

i,2

)⊕R

All these changes are presented in the left of Fig. 1.

For the security aspect, we decided to use a deter-

ministic signature instead of an HSM due to the fact

that its security is based entirely on the trustworthi-

ness of its creator. Information inside the message M

changes slightly from the original proposition so as to

adapt to our scheme. We removed the external value

which is not useful in our case and added the proof of

the commitment C

that resulted from a VC scheme.

The veriﬁcation only require redoing hash func-

tions, verifying a signature and an argument from a

VC protocol, which implies quick veriﬁcation on the

user-end.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

408

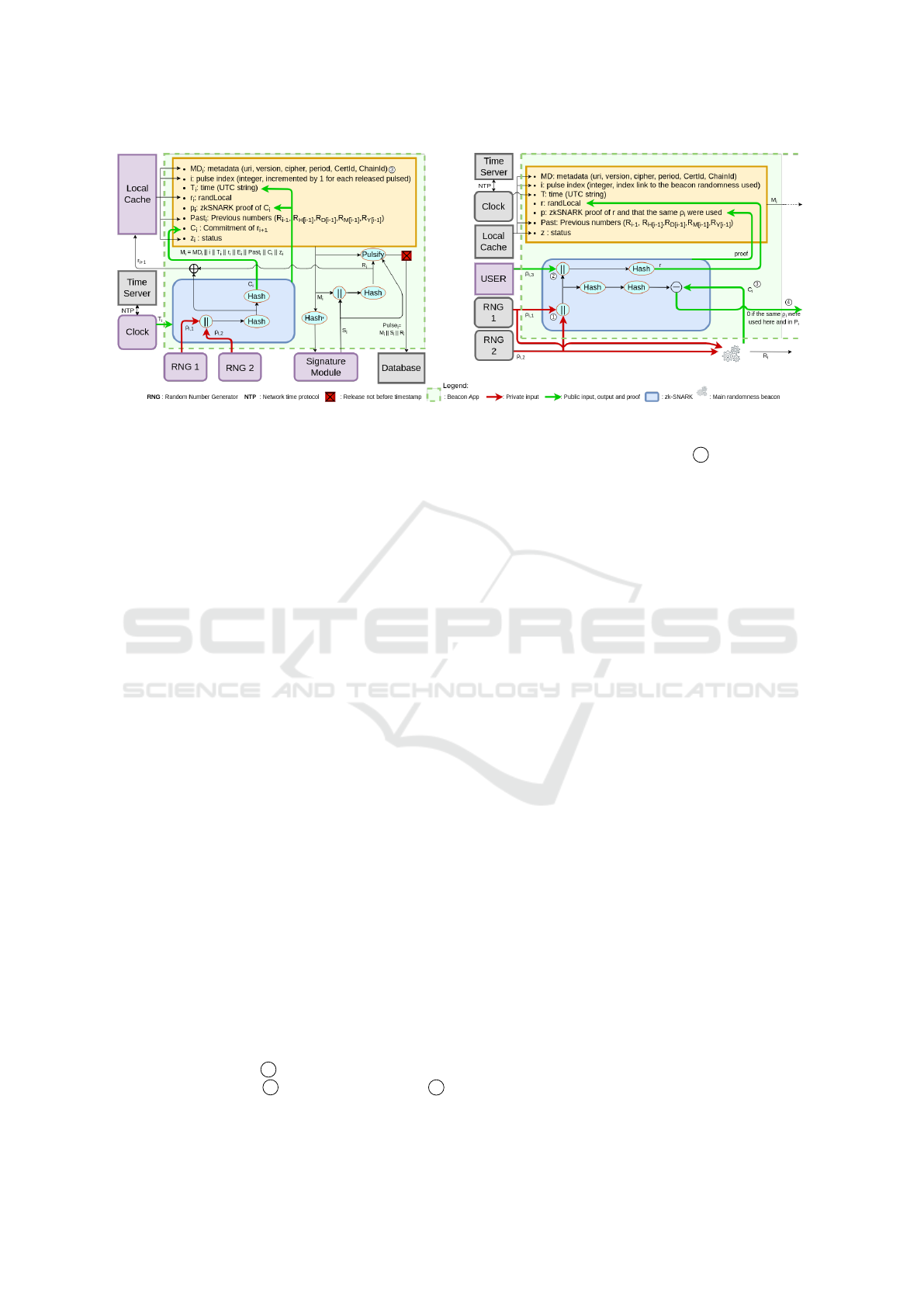
Figure 1: The zkBeacon random number generation model and the interactive protocol.

3.3 Interactive Protocol based on

Zero-knowledge VC to Ensure the

Freshness of the Pulses

Here, we exhibit our interactive protocol, allowing a

user to combine their entropy with that of the random-

ness beacon. This protocol is completely independent

of the beacon chain based on VC. Our second propo-

sition can even be applied to a classical beacon, such

as the one from the NIST.

When a client receives a new pulse from the ran-

domness beacon, even if all the computation was done

correctly, they cannot be sure that the entropy used

to generate the random number inside ρ

i,1

and ρ

i,2

sufﬁcient and unmanipulated. Moreover, the pulse is

supposed to be fresh but nothing guarantees that the

pulse was not created a long time ago.

In order to counter these possibilities, we propose

an interactive protocol where a user asks the beacon

to create an orphan pulse with three inputs: the same

i,1

and ρ

i,2

used in the last pulse and a new value ρ

i,3

that they provide. This enables multiple possibilities

to counter time attacks and bias on random numbers

from a malicious owner or adversary. This will be

discussed in Section 4.

In addition to classical ﬁelds (metadata, sta-

tus, index), an orphan pulse generated by the

beacon contains the randLocal r computed as

Hash(ρ

i,1

||ρ

i,2

||ρ

i,3

) and an argument of VC which

attests to the correct computation of r and that the

same ρ

i,1

and ρ

i,2

were used in the last pulse of the

main beacon chain. Here, the VC algorithm takes

i,1

and ρ

i,2

as private inputs so as not to disclose the

(main chain) randLocal value which will be used in

the (main chain) pulse 1 , ρ

i,3

as public input to in-

clude the user’s values 2 and C

as public input 3

in order to certify that ρ

i,1

and ρ

i,2

correspond to the

commitment sent in the last pulse 4 . All these steps

are summarized in the right of Fig. 1. If the beacon re-

sponds quickly (an order of seconds), the user is sure

to have fresh randomness if their input is random.

Depending on the context, the user can generate a

random number as described in (Kelsey et al., 2019)

(i.e., as the hash of the message and the signature) or,

if they want to avoid any potential beacon manipula-

tion, they can use the provided randLocal value di-

rectly (as a VRF). The interactive protocol has the ad-

vantage over a VRF to provide external entropy.

In the case of a frequently consulted beacon, to

ensure smooth scaling, it is possible to include sev-

eral random seeds from different users in the same

orphan pulse. Depending on the application and the

context, the beacon must choose between one orphan

pulse per user or regrouping several users for an or-

phan pulse at a regular time interval.

3.4 Connecting the Randomness Beacon

to a Blockchain

In this Section, we show that connecting a blockchain

to our randomness beacon has several beneﬁts for

both systems.

3.4.1 Beacon Chain Immutability

Even though the beacon chain provides a way to

link the pulse and thus, to avoid data modiﬁcations

a posteriori, we suggest decentralizing a part of the

database at the backend, storing the pulses or the ran-

dom numbers on a blockchain. This strategy should

improve the resilience of pulses against modiﬁca-

tion and remove vulnerabilities linked to a malicious

database thanks to blockchain immutability. This part

of the proposition is independent of the protocols pro-

posed above.

zkBeacon: Proven Randomness Beacon based on Zero-knowledge Veriﬁable Computation

409

3.4.2 Timestamped Random Number

A user can use the interactive protocol to certify the

freshness of the randomness by submitting an entropy

input ρ

i,3

deduced from a recent block of a blockchain

to the beacon. For example, assuming Ethereum takes

approximately 14 seconds to forge a new block, if

i,3

contains the nonce of the last block mined in the

blockchain, every third party using the random num-

ber published after the protocol will be convinced that

the number was not generated before the publication

of the block on the blockchain. Indeed, if a malicious

beacon is able to know the next nonce in advance, it

can reverse a hash function, which is supposed to be

impossible. This suggestion is dependent upon the

existence of an interactive protocol or the use of a

user input. It cannot be directly applied to the ofﬁ-

cial NIST beacon, or it requires a slight modiﬁcation

in order to take a user value into account.

3.4.3 Randomness for Blockchains

Blockchains often need a source of randomness for

many internal protocols. With our propositions, de-

tailed above, we can use the interactive protocol to au-

tomate the reception and use of random numbers. An

oracle can send a query to the beacon at regular time

intervals, asking it to furnish a random number with

entropy deduced using the last block as input. The

freshly generated randLocal value can be used as the

new random number inside the blockchain. Indeed,

we cannot store the whole pulse on a blockchain due

to the size of M

. However, we can use the randLocal

value as randomness on the blockchain by storing it

and its VC argument. By doing this, we ensure that

the randomness is not manipulated by the beacon, and

everything can be veriﬁed on the blockchain.

It should be noted that the oracle Chainlink pro-

vides a randomness service to smart contracts (Brei-

denbach et al., 2021). The principle consists of apply-

ing a Veriﬁable Random Function to a seed provided

by the smart contract. Like this solution, our proposal

is cryptographically veriﬁable, but it has the advan-

tage of using external entropy.

4 SECURITY ANALYSIS

In this section, we will follow the NIST draft (Kelsey

et al., 2019) and compare their analysis of possible at-

tacks on their system with our propositions. We will

reiterate any aspects necessary to the study of the se-

curity analysis.

4.1 Desired Properties

The main properties desired for a beacon are estab-

lished in three essential categories in (Kelsey et al.,

2019):

• relations that ensure the correct chaining process

between each pulse.

• availability of pulses with reduced human inter-

vention.

• random quality to ensure unpredictability and un-

biased, fresh randomness in each pulse; these

properties mainly come from the randLocal value.

The draft (Kelsey et al., 2019) asserts that the

properties above derive from the pulse design itself

when everything works as expected: without a breach,

with a full entropy input, with synchronous and ade-

quately fast communication and with a database that

is available and reliable.

To achieve all of these required qualities, we based

our model on cryptographic assumptions. Like in

(Kelsey et al., 2019), we will assume that the hash

functions used are one-way and collision resistant.

We will also consider that the output of the hash func-

tion used is indistinguishable from true randomness

when the input is unpredictable. Secondly, we will

assume that the signature scheme is unforgeable and

that its public key is certiﬁed correctly. For our model,

we will use a veriﬁable computation scheme, more

precisely, zk-SNARKs or zk-STARKs. These argu-

ments provide three additional cryptographic proper-

ties:

• completeness: if the prover (the number generator

in our case) is honest with a correct witness, they

must convince a veriﬁer.

• knowledge soundness: an honest veriﬁer will not

accept an invalid proof.

• zero-knowledge: the proof does not leak any in-

formation aside from the correct computation.

4.2 Adversary Model

In order to evaluate our system we need to describe

what kind of adversary can attempt an attack, what

their goal is and how they can reach it. We will con-

sider two different adversaries with different capabili-

ties. An adversary, or an attacker, can be semi-honest

or malicious. Our proposition is more general than

that of (Kelsey et al., 2019) regarding the security as-

sumptions by considering that the entire beacon can

be fully malicious and by removing the HSM which

was supposed safe.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

410

Adversaries’ goals are almost always the same but

the beneﬁts they could reap are plentiful. Firstly,

someone may want to discover the next random num-

ber or information about the next number in advance.

For example, if someone knows the parity of the next

random number ahead of the time indicated in its

timestamp, they are twice as likely to win if the num-

ber is used in a betting game. Secondly, an attacker

may also want to directly induce a change in the be-

havior of the protocol in order to alter the next random

number and once again be able to take advantage of

it. With the same goal, an adversary can modify the

database and change pasts numbers. Finally, the last

case we studied is the ability to shut down the system,

fork a chain or anything that can block users from

accessing the random beacon for a certain period of

time.

4.3 Attacks and Countermeasures

We will now present all of the attacks evoked in

(Kelsey et al., 2019), how they can occur, which parts

of the system have to be vulnerable and what is sug-

gested in order to avoid them. For each of them, we

will study the possibility of its occurrence and we re-

fer the reader to (Kelsey et al., 2019) for more detail

of their countermeasures. For each attack, we will

specify which proposal improves the security of our

overall model. Again, each proposal is independent

and can be applied or not. We consider the complete

system all three of our proposals.

4.3.1 Bias on RNG Outputs Due to a Malicious

Beacon App

In both the NIST scheme and ours, the ρ

which

are outputted from the RNGs, are never revealed to

the public and an attacker could choose values to re-

place them arbitrarily. They can even directly replace

= Hash(ρ

i,1

||ρ

i,2

) due to the one-way nature of the

hash function. Adding a XOR between r

and R

i−1

to produce the randLocal seed has been suggested.

With this adjustment, an attacker could not com-

pletely foresee the ﬁnal randLocal value which would

come from Hash(ρ

i,1

||ρ

i,2

) ⊕ R

i−1

and the commit-

ment value C

= Hash(Hash(ρ

i,1

||ρ

i,2

)). However, if

the adversary is able to control the beacon app for sev-

eral consecutive pulses, the fresh randomness prop-

erty is not conserved.

By adding our ﬁrst proposition, this attack is not

possible. Even if the ρ

are not revealed, the proof

provided by the VC protocol gives the ability to ver-

ify that the proposed r

is the result of a concatenation

followed by a given hash function. In our case, an at-

tacker who wants to alter the randomness of a pulse

will have to anticipate all of the information within

the pulse, i.e., two consecutive hashes, and a valid

proof. The proof itself is non-deterministic by the

zero-knowledge nature of VC and it changes for each

execution due to the different random numbers used

at each step in the protocol. Moreover, our scheme

includes the modiﬁcation suggested in (Kelsey et al.,

2019). This attack is completely avoided with our sys-

tem and renders the system more transparent thanks to

the guarantee of the correct r

computation.

4.3.2 Prediction and Exﬁltration Due to a

Malicious Beacon App

As in the previous Section, a malicious adversary can

alter the r

or ρ

values. By replacing these values

with a symmetric encryption scheme that has an ap-

propriate output length and outputs indistinguishable

from random, an attacker gains the ability to commu-

nicate with someone else who shares the secret key

without anyone knowing. This communication link

can be used to exﬁltrate internal information from the

beacon or from any program accessed by the attacker.

Another possible usage is the ability to completely

predict the next pulses by deterministically encrypt-

ing the index of the pulse. The draft (Kelsey et al.,

2019) does not provide any possible mitigation.

With the use of the proven beacon (ﬁrst proposi-

tion), such a change is, here too, not a possibility. The

proof will not be valid if a modiﬁcation has been made

on the public program and the random number will be

rejected by the users. This is a signiﬁcant improve-

ment compared to the previous proposition, even if

the generation of ρ

can still be manipulated.

4.3.3 Bias on the Freshly-generated Random

Number Due to a Malicious Beacon App

If an adversary can make multiple requests to an hon-

est HSM, they can ask for several signatures with dif-

ferent values of r

until they obtain a result with a

certain property enabling them to produce a ﬁnal R

with a desired attribute. They can also produce sev-

eral pulses in advance to give themselves more time

and be able to alter more bits of R

A mitigation proposed in (Kelsey et al., 2019) is

to use an HSM which imposes a delay between each

signature, or to partition the beacon app.

This mitigation does not solve the problem and

relies on an HSM. Moreover, the adversary may be

the operator of the system and the clients who receive

the pulses cannot verify if the system is partitioned or

not. This mitigation relies on the trustworthiness of

the owner and only avoids external attacks.

Thanks to the interactive protocol, the beacon

zkBeacon: Proven Randomness Beacon based on Zero-knowledge Veriﬁable Computation

411

server has a shorter time range to attempt this attack

because it cannot know the user’s input in advance.

We suggest introducing an X-second lag before the

beacon can answer, which drastically reduces the time

window for an adversary to generate multiple random

numbers.

4.3.4 Advanced Knowledge and Prediction.

It is clear that the construction of the pulse requiring

the knowledge of r

creates a vulnerability if the bea-

con is semi-honest. In fact, the beacon stores the rand-

Local value for the next pulse during the creation of a

new one. During this period of time, the beacon gains

the knowledge of the next randLocal, one pulse be-

fore users and thus has the information to produce R

For the same reasons, the beacon also knows R

before

users due to the time it needs to wait before transmit-

ting. If the beacon app is malicious, this leads to a

prediction of r

and R

. Another attack leading to ad-

vanced knowledge of R

relies on the internal clock. If

this clock, or time-server used by the internal clock to

synchronize itself, is malicious, it can give the beacon

app a fake time allowing for the premature creation

of a new pulse. If the beacon app remains honest, it

would release the pulse to the database. A malicious

database could then disclose the random numbers at

the right time, gaining the knowledge of every num-

ber generated in advance of other users.

The mitigations proposed by (Kelsey et al., 2019)

do not remove the above vulnerability, two of them

simply redirect trust to a timestamp service.

We followed one of the propositions and inserted

a XOR into the computation of randLocal, delaying

the knowledge of r

i+1

for the beacon. The interac-

tive protocol is not at all vulnerable to these attacks

due to the interactivity with the client. Even if the

beacon’s clock were malicious, the interactivity dras-

tically reduces the time during which the new random

number is known by the beacon, and a database is not

involved. Moreover, the client can check if the time

furnished by the beacon is in sync with their own local

clock. The beacon cannot compute the random num-

ber before it has access to the client’s input, delaying

the knowledge of the input for the beacon.

Secondly, with our third proposition, by using the

entropy from the last block of a blockchain as a part

of the public input, everyone will agree that the ran-

dom number is fresh and was not known until it was

released.

4.3.5 History Modiﬁcation Due to a Malicious

Database and Signature Key Access

When an adversary has access to the database and the

signature module key stored in the HSM, they have all

the tools needed to completely alter the information

stored in the database except the commitment link be-

tween two pulses. Consequently, they can compute

their own chain of random numbers and replace the

entire chain or the end of the existing one. The NIST

draft promotes the multiplication of external reposito-

ries.

Our system highly supports the decentralization of

the database and suggests using a blockchain to store,

at least, the proofs or the random numbers, and ex-

ploiting the immutability and distributed properties of

blockchains.

5 PERFORMANCE EVALUATION

This section describes what we used to evaluate our

system. We propose using of a new generation of

tools that enable drastically reducing the memory us-

age of the prover as well as the argument generation

time. After that, we discuss the performances ob-

tained, which demonstrate that deploying our system

is realistic on a standard computer.

5.1 Hash Functions Used

Today, programs are optimized to be evaluated as

quickly as possible. This often implies the use of

operations close to the CPU and therefore Boolean

operations. However, these operations are expensive

to prove. It is therefore important to ﬁnd programs

that are no longer just optimized for evaluation but

for evaluation and proving. Using arithmetic oper-

ations instead of boolean operations can increase the

evaluation time but greatly reduce the proof time, thus

improving overall complexity.

Even if VC protocols can have a succinct proof

size and veriﬁer constant time computation, like zk-

SNARKs, the complexity of the prover is at least lin-

ear in the number of constraints. With this in mind,

classical hash functions have a lot of constraints due

to the transformation of their logic construction into

arithmetic. In section 5.2, we show that SHA256 with

a 1024-bit input has around 90, 000 constraints in the

R1CS model. It is important to note that for SNARKs,

the size of the prover key is linear in regard to the

number of constraints.

However, several propositions of an alternative

SNARK-friendly (also STARK-friendly) hash func-

SECRYPT 2022 - 19th International Conference on Security and Cryptography

412

Table 1: Evaluation of the different circuits on 100 executions.

constraints witness prover key average proving time

SHA256 (1024 bits) 89,698 2.9 MB 59.9 MB 2.710 s

Rescue (1016 bits) 1,196 38.3 KB 727 KB 382 ms

zkBeacon (Section 3.2) 1,667 53.4 KB 961.5 KB 408 ms

interactive protocol (Section 3.3) 2,390 76.6 KB 1.5 MB 447 ms

tion, which is arithmetically oriented, have appeared

in the literature over the past few years. They aim to

be more efﬁcient regarding the number of constraints.

Following the lead of a recent survey (Ben-Sasson

et al., 2020) based on multiple security analyses, such

as (Beyne et al., 2020) and (Canteaut et al., 2020), we

will consider the usage of the Rescue hash function

(Aly et al., 2020). The Rescue function is based on

a sponge construction and can output different sizes

of data depending on the chosen parameters. In or-

der to compare the Rescue and SHA functions, we

implemented their R1CS circuits using Circom (cir,

2020) and generated their proofs and witnesses with

SnarkJS (sna, 2020). However, SnarkJS only relies on

the BN128 and BLS12 − 381 curves which are 128-bit

security curves. We decided to only evaluate 128-bit

security hash functions to remain consistent. We will

evaluate our proposition based on the SHA256 and

Rescue function. The Rescue hash function allows

faster computation and lighter memory usage. The

use of the Rescue function drastically reduces prover

and veriﬁer key sizes for SNARKs, as well as memory

consumption.

Even though Rescue is slower to evaluate than

SHA256 which is oriented for CPU use. It is impor-

tant to differentiate the proving time and the evalu-

ation time. At our scale, with only a thousand bits

in input, the Rescue hash functions take 7 times less

time to be evaluated and proved than SHA256 with

our implementation.

5.2 Implementation and Evaluation

For our implementation, we propose the use of the

Groth16 zk-SNARK scheme (Groth, 2016) which is

very efﬁcient in terms of communication (proof size)

and veriﬁer computation complexity, both in O(1). In

terms of computation and memory usage, this com-

plexity is O(nlog(n)). For the trusted setup phase,

we reuse the ceremony done in 2018 on the Zcash

blockchain (zca, 2018) in order to involve many fa-

mous participants without redoing all of the organiza-

tion.

We chose the Groth16 protocol because the proof

is tiny and this is important for our global sys-

tem. Groth16 proof size is less than 200 bytes while

STARK of two Rescue with weaker parameters than

ours is around 11 KB according to the evaluation

based on winterfell (win, 2021). The blockchain’s

block size is a key parameter. Most of existing

blockchains only support a small amount of infor-

mation per transaction, or the fees paid to include

the transaction increase with size. The second is be-

cause the blockchain veriﬁcation cost is feasible for

Groth16 and costly for STARKs (around 300k gas

on Ethereum for Groth16 and estimated at more than

2.5M for STARKs).

To evaluate our system, we used Circom to imple-

ment the Rescue and SHA256 circuits and evaluated

their proof generation using snarkJS. The SHA256

function has already been implemented by Circom in

the Circomlib available on github. We implemented

the Rescue function according to the Rescue-prime

speciﬁcation (Szepieniec et al., 2020). We used a

32 GB RAM computer with an Intel Core i7-10850H

CPU at 2.7 GHz on a 64-bit Ubuntu 20.04.3 LTS.

We implemented Rescue using parameters related

to elliptic curve choice. Having chosen the BN128

curve, we generated all other parameters based on a

capacity of 3 elements, a state width of 4 and a secu-

rity level of 128 bits with a 40% margin. To remain

coherent with our system, we evaluated Rescue with 4

elements of F

as input, which is approximately 1016

bits.

We evaluated the interactive protocol with the

same hash function. As private inputs, we took the

same length of 4 elements of F

and for the client’s

public input, we took 2 elements of F

, for a total of

1524 bits. In the end, the circuit is almost entirely 3

Rescue functions: one with 6 elements of input, one

with 4 and one with 1. Our results were obtained by

averaging over 100 executions and are summarized in

Table 1.

Thanks to this evaluation, we can state that our

proposition can be easily deployed on a standard com-

puter. Indeed, according to these results evaluated

on a standard personal computer, a zk-SNARK of a

pulse and a proof for the interactive protocol can be

both generated in less than 0.5 seconds. Moreover,

SnarkJS is not optimized and most of the measured

time is dedicated to loading the veriﬁer key and ini-

tializations.

zkBeacon: Proven Randomness Beacon based on Zero-knowledge Veriﬁable Computation

413

6 CONCLUSION

Our proposition aims to improve the randomness bea-

con concept standardized by the NIST.Our main ob-

jective is to keep the main interesting concepts of

randomness beacons, i.e., the use of external entropy

and the chaining of the pulses, but also to strengthen

user conﬁdence in the outputs. For that, we proposed

the addition of a veriﬁable computation argument on

the ﬁrst hash functions used in each pulse generation,

making our system more transparent.

The second part of our proposal is an interac-

tive protocol, limiting the possibility of timing at-

tacks and the lack of fresh randomness. We also sug-

gest connecting the database to a blockchain in order

to improve the immutability of the database, provide

timestamped random numbers and use the random-

ness beacon as a proven random number oracle for

the blockchain. We proved that our scheme supports a

security model with a malicious beacon generator. Fi-

nally, we benchmarked an implementation of our pro-

posal based on the Rescue hash function and Groth16

zk-SNARK and proved that the constraints in terms of

memory and CPU, are acceptable, even for a personal

computer.

ACKNOWLEDGEMENTS

The authors would like to thank Jonathan Detchart,

Thibault Gateau and Caroline Chanel for their help

on several aspects of this work.

REFERENCES

(2018). Zcash powers of taus ceremony attestation. Ac-

cessed: 24/03/2022.

(2020). CIRCOM: Circuit Compiler for Zero-Knowledge

Proofs. Accessed: 24/03/2022.

(2020). Inmetro Randomness Beacon. Accessed:

24/03/2022.

(2020). Nist Randomness Beacon. Accessed: 24/03/2022.

(2020). SNARKJS: JavaScript Implementation of zk-

SNARKs. Accessed: 24/03/2022.

(2021). Winterfell : A STARK prover and veriﬁer for arbi-

trary computations. Accessed: 28/04/2022.

Aly, A., Ashur, T., Ben-Sasson, E., Dhooghe, S., and Szepi-

eniec, A. (2020). Design of symmetric-key primitives

for advanced cryptographic protocols. IACR Transac-

tions on Symmetric Cryptology, pages 1–45.

Ben-Sasson, E., Bentov, I., Horesh, Y., and Riabzev, M.

(2018). Scalable, transparent, and post-quantum

secure computational integrity. Cryptology ePrint

Archive.

Ben-Sasson, E., Goldberg, L., and Levit, D. (2020). STARK

Friendly Hash-Survey and Recommendation. IACR

Cryptol. ePrint Arch., 2020:948.

Beyne, T., Canteaut, A., Leander, G., Naya-Plasencia, M.,

Perrin, L., and Wiemer, F. (2020). On the security of

the Rescue hash function. IACR Cryptol. ePrint Arch.,

2020:820.

Bowe, S., Gabizon, A., and Miers, I. (2017). Scalable

Multi-party Computation for zk-SNARK Parameters

in the Random Beacon Model. Cryptology ePrint

Archive, Report 2017/1050. https://ia.cr/2017/1050.

Breidenbach, L., Cachin, C., Chan, B., Coventry, A., Ellis,

S., Juels, A., Koushanfar, F., Miller, A., Magauran, B.,

Moroz, D., et al. (2021). Chainlink 2.0: Next Steps in

the Evolution of Decentralized Oracle Networks.

Canteaut, A., Beyne, T., Dinur, I., Eichlseder, M., Leander,

G., Leurent, G., Plasencia, M. N., Perrin, L., Sasaki,

Y., Todo, Y., et al. (2020). Report on the Security of

STARK-friendly Hash Functions (Version 2.0).

Dharanikot, S., Jensen, M., Kristensen, S., Michno, M.,

Pignolet, Y., Hansen, R., and Schmid, S. Breeding

Unicorns: Developing Trustworthy and Scalable Ran-

domness Beacons.

Gabizon, A., Williamson, Z. J., and Ciobotaru, O. (2019).

Plonk: Permutations over lagrange-bases for oe-

cumenical noninteractive arguments of knowledge.

Cryptology ePrint Archive.

Goldwasser, S., Micali, S., and Rackoff, C. (1989). The

knowledge complexity of interactive proof systems.

SIAM Journal on computing, 18(1):186–208.

Groth, J. (2016). On the size of pairing-based non-

interactive arguments. In Annual international confer-

ence on the theory and applications of cryptographic

techniques, pages 305–326. Springer.

Kelsey, J., Brandao, L., Peralta, R., and Booth, H. (2019).

Reference for Randomness Beacons, Format and Pro-

tocol Version 2, Draft NISTIR 8213. Technical report.

Accessed: 24/03/2022.

Kiayias, A., Tsiounis, Y., and Yung, M. Traceable Sig-

natures. In Advances in Cryptology - EUROCRYPT

2004.

Micali, S., Rabin, M., and Vadhan, S. (1999). Veriﬁable

random functions. In 40th annual symposium on foun-

dations of computer science (cat. No. 99CB37039),

pages 120–130. IEEE.

Moran, T. and Naor, M. (2010). Split-Ballot Voting: Ev-

erlasting Privacy with Distributed Trust. ACM Trans.

Inf. Syst. Secur., 13(2).

Parno, B., Howell, J., Gentry, C., and Raykova, M. (2013).

Pinocchio: Nearly practical veriﬁable computation. In

2013 IEEE Symposium on Security and Privacy, pages

238–252. IEEE.

Rabin, M. O. (1983). Transaction protection by beacons.

Journal of Computer and System Sciences, 27(2):256–

267.

Szepieniec, A., Ashur, T., and Dhooghe, S. (2020). Rescue-

Prime: a standard speciﬁcation (SoK). Cryptology

ePrint Archive.

UChile, R. (2020). Public, Transparent and Veriﬁable Ran-

domness. Accessed: 24/03/2022.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

414