Side-channel Analysis and Countermeasure for Implementation of

Lattice-based Signature

Kazuhide Fukushima

1 a

, Hiroki Okada

1 b

, Soﬁane Takarabt

, Amina Korchi

, Meziane Hamoud

Khaled Karray

, Youssef Souissy

and Sylvain Guilley

KDDI Research, Inc., 2-1-15 Ohara, Fujimino-shi, Saitama, 356–8502, Japan

Secure-IC, Z.A.C des Champs Blancs, 15 rue Claude Chappe, B

at. B, 35510, Cesson-S

evign

e, France

ﬁ

Keywords:

Post-quantum Cryptography, Lattice-based Cryptography, MLWRSign, Side-channel Analysis.

Abstract:

Lattice-based cryptography is believed to be a promising candidate for post-quantum cryptography (PQC).

The NIST announced that the third-round ﬁnalists in the standardization project of PQC (NIST-PQC) and

four out of seven ﬁnalists are lattice-based cryptography. An implementation is desired that is resistant to

side-channel analysis for the widespread use of lattice-based cryptography. This paper studies possible side-

channel analysis on the signature scheme MLWRSign, a lattice-based signature scheme. We apply differential

power analysis to the implementation of MLWRSign to specify all the sensitive parts. The experimental results

show that only Karatsuba and Toom-Cook multiplications can be vulnerable to DPA with the Hamming weight

power consumption model. Furthermore, we propose masking countermeasures for multiplication: inter-

functional and intra-functional masking. Our lightweight countermeasure is beneﬁcial to further enhance the

security of post-quantum cryptography, which is naturally resistant to side-channel attacks.

1 INTRODUCTION

Recently, there has been substantial research on quan-

tum computers that potentially provides the power

to break (Shor, 1994; Shor, 1997) current public-

key cryptography such as RSA and ECC in a feasi-

ble time. The NIST called for proposals to standard-

ize post-quantum cryptography (PQC) and public-key

cryptography registrant to quantum computers. There

are two categories in the NIST-PQC standardization

project: public-key encryption/KEMs and digital sig-

natures.

In addition to quantum computer threats, PQC

should protect against side-channel analysis. Cryp-

tographic algorithms are considered mathematically

robust; however, their implementation might leak sen-

sitive information through physical leakage. Physical

leakage is no more or less than an exhibited physical

property, such as power, electromagnetic emanation

(EM) (Huang et al., 2019), acoustic vibration, and

time computation.

Some attacks against PQC have already been pub-

https://orcid.org/0000-0003-2571-0116

https://orcid.org/0000-0002-5687-620X

lished; thus, designers should also consider these at-

tacks and implement countermeasures. Vulnerabili-

ties against timing attacks and differential power anal-

ysis (DPA) should be considered at an early stage

of conception by making the execution time constant

and the power consumption independent of secret

data. A masking scheme is the most studied coun-

termeasure in the state-of-the-art to defeat DPA. The

most important PQC algorithms families are lattice-

based, code-based, multivariate-based, hash-based,

and isogeny-based.

In this paper, we studied possible side-channel

analysis on the signature scheme MLWRSign, an

LWR variant of CRYSTALS-Dilithium that is one

of the ﬁnalists in the NIST-PQC competition. We

applied DPA to the implementation of MLWRSign

to specify all the sensitive parts. We found that

only Karatsuba and Toom-Cook multiplications can

be vulnerable to DPA with the Hamming weight

power consumption model. Furthermore, we pro-

posed masking countermeasures for multiplication:

inter-functional and intra-functional masking. Our

lightweight countermeasure is beneﬁcial to further

enhance the security of post-quantum cryptography,

which is naturally resistant to side-channel attacks.

Fukushima, K., Okada, H., Takarabt, S., Korchi, A., Hamoud, M., Karray, K., Souissy, Y. and Guilley, S.

Side-channel Analysis and Countermeasure for Implementation of Lattice-based Signature.

DOI: 10.5220/0011328400003283

In Proceedings of the 19th Inter national Conference on Security and Cryptography (SECRYPT 2022), pages 701-706

ISBN: 978-989-758-590-6; ISSN: 2184-7711

701

2 RELATED WORK

Cryptographic implementations can be vulnerable to

side-channel attacks. The different attacks studied

in the literature, such as DPA and template attacks,

can be transposed to the post-quantum implementa-

tions. Some publications have already addressed the

side-channel threats against post-quantum cryptogra-

phy. From a side-channel analysis viewpoint, the

critical parts are very similar since those algorithms

are based on the same speciﬁc problems (code-based

and lattice-based). The differences in algorithms do

not provide more resistance. A cautionary counter-

measure should be implemented to protect the criti-

cal parts of the algorithm. The private parts, includ-

ing key generation, signature, and decryption, should

implement countermeasures against side-channel at-

tacks.

Timing Attack. The ﬁrst timing attack, introduced

by Kocher, targets RSA implementations (Kocher,

1996). It takes advantage of the non-constant exe-

cution timing of modular multiplication. Other tim-

ing attacks (Dhem et al., 2000; Schindler, 2000;

Schindler, 2002) also take advantage of the non-

constant execution timing of the operations.

Cache-timing Attack. A cache is a small mem-

ory used to increase performance in modern pro-

cessors. Bernstein ﬁrst discovered cache attacks on

AES (Bernstein, 2005). Cache attacks are currently

an important research subject. Critical vulnerabilities

related to cache attacks and, more generally, microar-

chitectural attacks emerged, such as Spectre or Melt-

down (Kocher et al., 2019; Lipp et al., 2018) in 2017

and 2018. The latter is related to the operating system

and the CPU. Specter attacks exploit speculative exe-

cution, whereas meltdown exploits out-of-order exe-

cution. These attacks have several variants.

Simple Power Analysis. Simple power analysis

(SPA) is a visual inspection and analysis of the leak-

age trace. The timing duration and characteristic pat-

terns for each operation can be identiﬁed and mapped

to the algorithm.

Differential Power Analysis. The attacker makes

assumptions on intermediate variables during the exe-

cution of the algorithm in classical differential power

analysis (DPA). Several traces are acquired and cor-

related with the intermediate variables.

• Correlation Power Analysis (CPA) (Brier et al.,

2004): The CPA computes a leakage model and

correlates with traces vertically for each key hy-

pothesis. The highest peak corresponds to the best

key candidate.

• Linear Regression Analysis (LRA) (Lomn

e et al.,

2013): The LRA uses the least square method to

minimize the error (between the estimation and

the observation) and model the leakage trace with

the intermediate value.

• Collision Attack (Moradi et al., 2010): The colli-

sion attack builds the leakage model on the traces.

A more generic case of the collision attack is the

template attack (Rechberger and Oswald, 2005).

Fault Injection Attack. The differential fault at-

tack (DFA) exploits an introduced fault when com-

puting a sensitive operation. The fault can be per-

formed on data and instruction and achieved by laser

injection, EM injection, or glitches (on clock or volt-

age). When the signature is deterministic, the couple

(faulted result, correct result) can recover the whole

or partial private information.

3 LATTICE-BASED SIGNATURE:

MLWRSign

Okada et al. (Okada et al., 2020) proposed a

lattice-based digital signature scheme MLWRSign

that is a learning with rounding (LWR) variant in

CRYSTALS-Dilithium third-round ﬁnalists of the

standardization project of post-quantum cryptography

by NIST (NIST-PQC). The secret key in MLWR-

Sign is approximately 30% smaller than CRYSTALS-

Dilithium with the same security level due to the sim-

plicity of the LWR. The running time of MLWRSign

is comparable to that of CRYSTALS-Dilithium.

4 SIDE-CHANNEL ANALYSIS ON

MLWRSign

The target of evaluation (ToE) is an STM32 Nucleo-

64 [9] with 32 MHz max CPU frequency. The STM32

Nucleo-64 board provides an affordable and ﬂexible

method for users to try out new concepts and build

prototypes by choosing from various performance and

power consumption features provided by the STM32

microcontroller. The STM32 Nucleo-64 board does

not require any separate probe as it integrates the ST-

LINK debugger/programmer. The STM32 Nucleo-

64 board comes with the STM32 comprehensive free

SECRYPT 2022 - 19th International Conference on Security and Cryptography

702

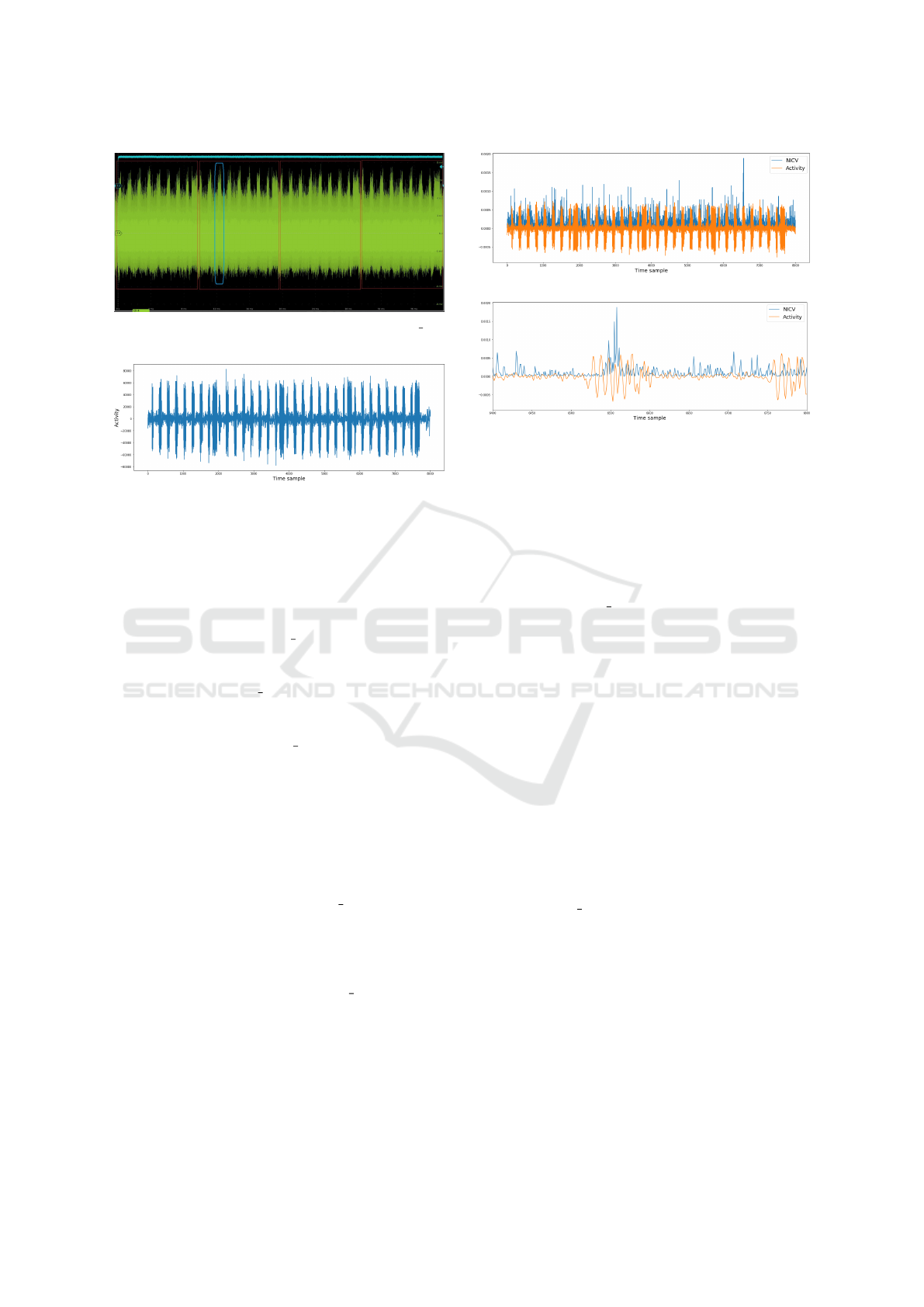
Figure 1: Acquisition of one execution of polyvecl mul

function.

Figure 2: Result of the bandpass ﬁlter.

software libraries and examples available with the

STM32Cube MCU Package.

4.1 Horizontal Analysis

Figure 1 shows one electromagnetic emanation (EM)

acquisition of the polyvecl

mul function (in green).

The blue curve shows the start and end of the exe-

cution. In particular, we have four large blocks that

correspond to the poly mul function (red rectangle).

In each block, we can distinguish seven patterns

related to the Karatsuba simple four functions (blue

rectangle) inside each poly mul function. We can

perform some processing of the traces to see these op-

erations more clearly. For this purpose, we ﬁrst per-

form an STFT to locate the interesting bound. The

scope is conﬁgured as follows:

• Sampling Rate: 31.25 MS/s,

• Filter: Low-pass at 20 MHz, and

• Impedance: 50.

The duration of each polyvec mul is approxi-

mately 40 ms. Figure 2 shows the result of the band-

pass ﬁlter 1–4 MHz applied to the short-time Fourier

transform (STFT) of the leakage traces in Fig. 1. The

Karatsuba multiplications are distinguishable inside

each polynomial multiplication (poly mul).

4.2 Vertical Analysis

The target of evaluation is run with different input

data. Each time, the power consumption or the elec-

tromagnetic radiation is acquired. Statistical analy-

sis is performed on the different traces to deduce the

(a) NICV result of polynomial multiplication

(b) Zoom on the leakage peak in Karatsuba multiplication

Figure 3: NICV result based on 10,000 ﬁltered traces.

manipulated values, hence the secret scalar. We can

cite the different methods as DPA, CPA, or LRA. The

real acquisitions are noisier than the simulated acqui-

sitions. As explained previously, many sensitive oper-

ations (that depend on s1) can be targeted. Hereafter

we perform our evaluation on the polynomial multi-

plication (polyvecl mul) function.

The key generation procedure and the signature

procedure have similar polynomial multiplications:

A ·

· s

and A

A ·

· y

y, respectively. The variable A is a

public parameter; thus, it is known by an attacker.

We acquired 10,000 traces with random s1 and ﬁxed

A to see how much this operation is leaking. Each

trace has 500,000 samples. We located the operations

that manipulate a subpart (nibble by nibble or byte

by byte) of this secret by performing NICV (Bhasin

et al., 2014) using the parameter s

. As the traces

were relatively noisy, we applied a bandpass fre-

quency ﬁlter (Fig. 2). We then compute the NICV

on the ﬁltered traces.

Figure 3a shows the raw trace (orange line)

and the NICV results (blue line) based on the

10,000 ﬁltered traces of the polynomical multiplica-

tion (polyvecl

mul function). A signiﬁcant leakage

can be seen at one Karatsuba multiplication. Fig-

ure 3b focuses on the peak that shows that the leakage

is in the Karatsuba multiplication. More signiﬁcant

leakage can be obtained with more traces.

Note that the traces are long, and the analysis can

be complex. The accuracy of the measurements is

also a compromise about the number of samples to

be acquired. We thus focused on smaller functions,

i.e., Karatsuba, to overcome these limits.

Side-channel Analysis and Countermeasure for Implementation of Lattice-based Signature

703

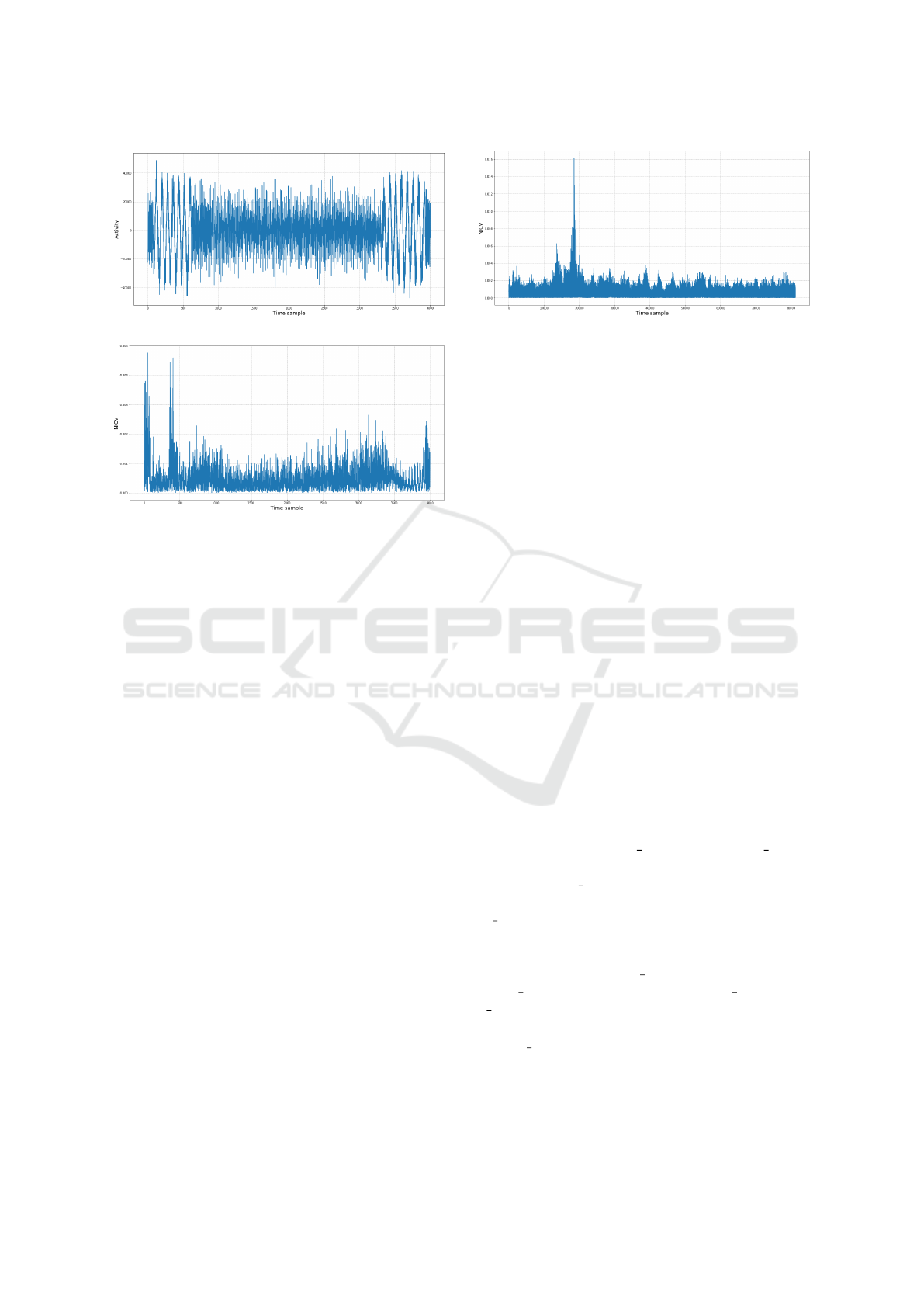
(a) Bandpass ﬁltered trace of Karatsuba multiplication

(b) NICV result of Karatsuba multiplication

Figure 4: Leakage trace of Karatsusba multiplication.

4.3 Analysis of Karatsuba

Multiplication

Most operations in the power traces are linked to

Karatsuba multiplication. We thus focused our anal-

ysis on this part of the algorithm. We select a sin-

gle Karatsuba multiplication to eliminate potential

sources of desynchronization.

The bandpass ﬁltered trace and NICV results of

Karatuba multiplication are shown in Fig. 4, and the

NICV result shows a signiﬁcant peak (Fig. 4b). How-

ever, this step is relative to the local copy of the inputs

and b

), and no leakage is identiﬁed in the com-

putation step.

The traces were not perfectly aligned; thus, we

added an operation to output a trigger signal to an in-

ternal loop in Karatusba multiplication to address the

desynchronization issue. Figure 5 shows that the leak-

age is signiﬁcant without any post-processing (ﬁlter-

ing) of the traces. We conﬁrmed that Karatsuba mul-

tiplication can be sensitive to side-channel analysis.

5 COUNTERMEASURE

We ﬁrst propose inter-functional masking as a pri-

mary countermeasure. The secret key generated in

the key generation algorithm is multiplied by random

values. The masked secret key used in the signing al-

gorithm changes randomly, making it challenging to

Figure 5: Leakage peak in NICV of internally syncronized

Karatsuba multiplication.

apply side-channel analysis.

We then proposed intra-functional masking as a

more sophisticated countermeasure. The intermedi-

ates values in the multiplication function are changed

by random masks and protect against side-channel

analyses.

5.1 Interfunctional Masking

We apply multiplicative masking to the secret key of

MLWRSign. The idea of multiplicative masking is to

write s as r

−1

×(r ×s). The masking value r is chosen

as a random number in Z

∗

or a random polynomial in

[x]. Our countermeasure uses an odd random inte-

ger r and q that is a power of 2 so that r is invertible in

. A brute force attack can be used to ﬁnd random

numbers, and template attacks are applicable to reveal

the secret parameter s. We can use a random polyno-

mial to increase the possible polynomial choices to

prevent template attacks.

The parameter s of the secret key is not stored as

the plain form at the end of the key generation af-

ter applying multiplicative masking. The secret pa-

rameter s is stored randomized as described in Al-

gorithm 1. A random mask r is selected uniformly

in Z

∗

The masked secret rs computed as rs = r × s.

The unmasking variable r inv is computed as r invr

−1

mod q. The secret parameter s is stored after the key

generation as (r inv, rs).

The multiplication c × s is performed as c × s =

(r inv × c) × rs. The total overhead is two multipli-

cations in Z

. Algorithm 2 describes multiplicative

masking for the sign algorithm.

The secret key (rs, r inv) can be refreshed to

(rs

′

, r

′

inv) with the property rs

′

× r

′

inv = rs ×

r inv = s. A new random integer r

′

is selected from

∗

and the new masked secret rs

′

is computed as

′

= (r inv × r

′

) × rs to maintain the property. r

inv

computed as the inverse of r

′

in Z

∗

. The refresh over-

head is two multiplications in Z

and an inversion in

∗

. Algorithm 3 describes refresh or multiplicative

masking.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

704

Algorithm 1: Multiplicative masking in key generation.

Input : s

Output: (rs, r inv)

1 repeat

2 r ←

∗

;

3 until r

′

is odd;

4 rs ← r × s mod q;

5 r inv ← r

−1

mod q;

6 return (rs, r inv);

Algorithm 2: Multiplication in sign.

Input : c, (rs, r inv)

Output: c × s

1 cs ← (r inv× c) × rs mod q;

2 return cs;

Algorithm 3: Refresh.

Input : (rs, r inv)

Output: (rs

′

, r

′

inv)

1 repeat

2 r

′

←

∗

;

3 until r

′

is odd;

4 rs

′

← (r inv × r

′

) × rs;

5 r

′

inv ← r

′−1

mod q;

6 return (rs

′

, r

′

inv);

5.2 Intrafunctional Masking

We can apply additive masking to immediate values

in the multiplication functions to achieve advanced

protection against side-channel analyses. MLWRSign

used Karatsuba and Toom-Cook multiplications. No

masking implementations for Toom-Cook multipli-

cation have been proposed, while masked Karatsuba

multiplication is available (Rebeiro and Mukhopad-

hyay, 2008). We thus propose additive masking for

Toom-Cook multiplication, where additive masking is

applied to points of polynomials, and pointwise mul-

tiplication is executed on masked values.

We show an example for the multiplication of

Q + a

and b

Q + b

where Q is modulo. The

polynomial expressions of the two integers are a(x) =

x + a

and b(x) = b

x + b

. The sample points can

be calculated as

a(−1) = −a

+ a

, a(0) = a

, a(1) = a

+ a

b(−1) = −b

+ b

, b(0) = b

, b(1) = b

+ b

for x = −1, 0, 1. We generate additive masks m

a(−1)

a(0)

, m

a(1)

, m

b(−1)

, m

b(0)

, m

b(1)

for six sample points

and obtain masked values a(−1) + m

a(−1)

, a(0) +

a(0)

, a(1)+m

a(1)

, b(−1)+m

b(−1)

, b(0)+m

b(0)

, and

b(1) + m

b(1)

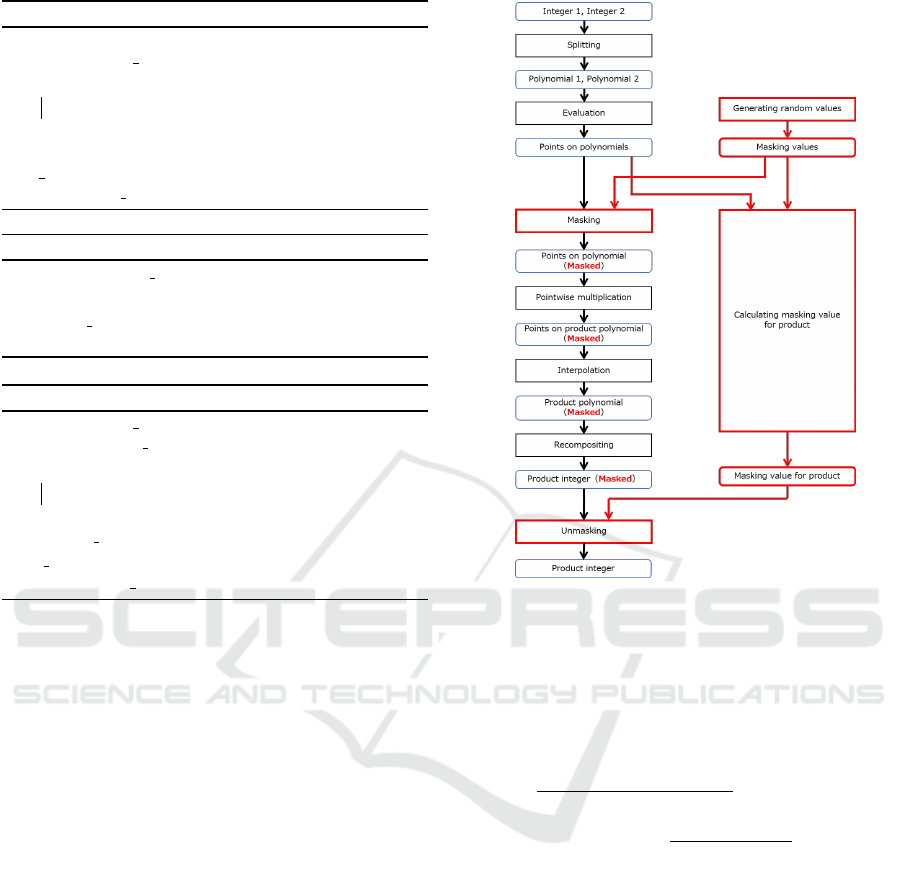
Figure 6: Masked Toom-Cook multiplication.

The masked product is computed from masked

sampled points based on the procedure of the orig-

inal Toom-Cook multiplication. The masking value

for the product is computed from the original sample

points, and masking values for sampling values are:

M =

M(−1) − 2M(0) + M(1)

M(1) − M(−1)

Q + M(0),

where M(x) = m

a(x)

b(x)

+ m

a(x)

b(x) + m

b(x)

a(x) for

x = −1, 0, 1.

We can recover the original product (a

Q + a

) ×

Q + b

) by subtracting the masking value for the

product M from the masked product that is the re-

sult of Toom-Cook multiplication. Figure 6 shows the

masked Toom-Cook multiplication where the newly

added data, procedure, and data ﬂow are highlighted

in red. The overhead of the intra-functional masking

is three multiplications and 13 additions in Z

6 CONCLUSION

This paper studied possible side-channel analysis on

signature scheme MLWRSign, an LWR variant of

Side-channel Analysis and Countermeasure for Implementation of Lattice-based Signature

705

CRYSTALS-Dilithium that is one of the ﬁnalists in

the NIST-PQC. We applied differential power anal-

ysis (DPA) to the implementation of MLWRSign to

specify all the sensitive parts. We have encountered

a desynchronization issue in the side-channel analy-

sis against post-quantum cryptography. One of the

causes is long leakage traces due to larger keys in

post-quantum cryptography. Another cause is the

complicated power consumption behavior of the mi-

croarchitecture of the target device. We insert an op-

eration that outputs synchronization triggers to candi-

date functions to avoid statistical synchronization to

address the difﬁculty. We found that only Karatsuba

and Toom-Cook multiplications can be vulnerable to

DPA with the Hamming weight power consumption

model. Nevertheless, we can distinguish only some

candidates from all possible keys. Furthermore, we

proposed masking countermeasures for multiplica-

tion: inter-functional and intra-functional masking.

Our lightweight countermeasure is beneﬁcial to en-

hance further the security of post-quantum cryptog-

raphy, which is naturally resistant to side-channel at-

tacks.

REFERENCES

Bernstein, D. (2005). Cache-timing attacks on

AES. https://cr.yp.to/antiforgery/cachetiming-

20050414.pdf.

Bhasin, S., Danger, J.-L., Guilley, S., and Najm, Z. (2014).

Nicv: normalized inter-class variance for detection of

side-channel leakage. In Electromagnetic Compatibil-

ity, Tokyo (EMC’14/Tokyo), 2014 International Sym-

posium on, pages 310–313. IEEE.

Brier, E., Clavier, C., and Olivier, F. (2004). Correlation

power analysis with a leakage model. In Joye, M.

and Quisquater, J.-J., editors, Cryptographic Hard-

ware and Embedded Systems - CHES 2004, pages 16–

29, Berlin, Heidelberg. Springer Berlin Heidelberg.

Dhem, J.-F., Koeune, F., Leroux, P.-A., Mestr

e, P.,

Quisquater, J.-J., and Willems, J.-L. (2000). A

practical implementation of the timing attack. In

Quisquater, J.-J. and Schneier, B., editors, Smart Card

Research and Applications, pages 167–182, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Huang, W.-L., Chen, J.-P., and Yang, B. (2019). Correlation

power analysis on ntru prime and related countermea-

sures. IACR Cryptol. ePrint Arch., 2019:100.

Kocher, P., Horn, J., Fogh, A., Genkin, D., Gruss, D., Haas,

W., Hamburg, M., Lipp, M., Mangard, S., Prescher,

T., Schwarz, M., and Yarom, Y. (2019). Spectre at-

tacks: Exploiting speculative execution. In 2019 IEEE

Symposium on Security and Privacy (SP), pages 1–19.

Kocher, P. C. (1996). Timing attacks on implementa-

tions of Difﬁe-Hellman, RSA, DSS, and other sys-

tems. In Koblitz, N., editor, Advances in Cryptology

— CRYPTO ’96, pages 104–113, Berlin, Heidelberg.

Springer Berlin Heidelberg.

Lipp, M., Schwarz, M., Gruss, D., Prescher, T., Haas, W.,

Fogh, A., Horn, J., Mangard, S., Kocher, P., Genkin,

D., Yarom, Y., and Hamburg, M. (2018). Meltdown:

Reading kernel memory from user space. In 27th

USENIX Security Symposium (USENIX Security 18),

pages 973–990, Baltimore, MD. USENIX Associa-

tion.

Lomn

e, V., Prouff, E., and Roche, T. (2013). Behind the

scene of side channel attacks. In Sako, K. and Sarkar,

P., editors, Advances in Cryptology - ASIACRYPT

2013, pages 506–525, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Moradi, A., Mischke, O., and Eisenbarth, T. (2010).

Correlation-enhanced power analysis collision attack.

In Mangard, S. and Standaert, F.-X., editors, Cryp-

tographic Hardware and Embedded Systems, CHES

2010, pages 125–139, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Okada, H., Takayasu, A., Fukushima, K., Kiyomoto, S.,

and Takagi, T. (2020). A compact digital signature

scheme based on the Module-LWRproblem. In Meng,

W., Gollmann, D., Jensen, C. D., and Zhou, J., editors,

Information and Communications Security, pages 73–

90, Cham. Springer International Publishing.

Rebeiro, C. and Mukhopadhyay, D. (2008). Power attack

resistant efﬁcient fpga architecture for karatsuba mul-

tiplier. In 21st International Conference on VLSI De-

sign (VLSID 2008), pages 706–711.

Rechberger, C. and Oswald, E. (2005). Practical template

attacks. In Lim, C. H. and Yung, M., editors, Infor-

mation Security Applications, pages 440–456, Berlin,

Heidelberg. Springer Berlin Heidelberg.

Schindler, W. (2000). A timing attack against RSA with the

Chinese remainder theorem. In Koc¸, C¸ . K. and Paar,

C., editors, Cryptographic Hardware and Embedded

Systems — CHES 2000, pages 109–124, Berlin, Hei-

delberg. Springer Berlin Heidelberg.

Schindler, W. (2002). A combined timing and power at-

tack. In Naccache, D. and Paillier, P., editors, Pub-

lic Key Cryptography, pages 263–279, Berlin, Heidel-

berg. Springer Berlin Heidelberg.

Shor, P. W. (1994). Algorithms for quantum computation:

discrete logarithms and factoring. In Proceedings 35th

Annual Symposium on Foundations of Computer Sci-

ence, pages 124–134.

Shor, P. W. (1997). Polynomial-time algorithms for

prime factorization and discrete logarithms on a

quantum computer. SIAM Journal on Computing,

26(5):1484–1509.

SECRYPT 2022 - 19th International Conference on Security and Cryptography

706