
Improving Car Detection from Aerial Footage with Elevation
Information and Markov Random Fields
Kevin Qiu
a
, Dimitri Bulatov
b
and Lukas Lucks
c
Fraunhofer IOSB Ettlingen, Gutleuthaus Str. 1, 76275 Ettlingen, Germany
Keywords:
DeepLab, Machine Learning, Remote Sensing, Markov Random Fields.
Abstract:
Convolutional neural networks are often trained on RGB images because it is standard practice to use transfer
learning using a pre-trained model. Satellite and aerial imagery, however, usually have additional bands, such
as infrared or elevation channels. Especially when it comes to detection of small objects, like cars, this addi-
tional information could provide a significant benefit. We developed a semantic segmentation model trained on
the combined optical and elevation data. Moreover, a post-processing routine using Markov Random Fields
was developed and compared to a sequence of pixel-wise and object-wise filtering steps. The models are
evaluated on the Potsdam dataset on the pixel and object-based level, whereby accuracies around 90% were
obtained.
1 INTRODUCTION
Vehicle detection in combined large-scale airborne
data has a wide range of applications. For improved
city planning, traffic flow estimation is essential. Also
for ecological sciences, it is helpful to know the av-
erage number of vehicles on the main roads, includ-
ing their velocities (Leitloff et al., 2014). In mili-
tary applications, vehicles may mean both targets and
threats (Gleason et al., 2011). Finally, for the applica-
tion of virtual tourism, situational awareness may be
increased if the so-called inpainting is applied to re-
fill the data from the temporary objects, like vehicles
(Leberl et al., 2007; Kottler et al., 2016). A success-
ful inpainting, which is our main motivation for this
paper, implies the necessity to detect every single ve-
hicle, including those partly occluded and away from
roads (Schilling et al., 2018b).
However, variations of scale, orientation, illumi-
nation, as well as the complexity of background repre-
sent the main challenges for vehicle detection. One of
the possibilities to reduce these effects is using mod-
ern Deep Learning architectures such as (Chen et al.,
2018), preferably trained with large data-bases, such
as ImageNet (Russakovsky et al., 2015), and relying
on sophisticated data augmentation modules, which
a
https://orcid.org/0000-0003-1512-4260
b
https://orcid.org/0000-0002-0560-2591
c
https://orcid.org/0000-0003-2961-3452
take into account to the problems mentioned above.
For single vehicle extraction, one can either use in-
stance segmentation networks, such as (Mo and Yan,
2020), but we omit them since they need even more
parameters to be determined, and thus, more train-
ing time is expected. Instead, we will concentrate
on post-processing routines using Markov Random
Fields. Their big advantage is that only a few pa-
rameters are needed to model, to a major part, quite
a broad spectrum of situations. From the pixel-wise
prediction we will impose soft non-local constraints
on pixel neighborhoods to improve detection results
on pixel and object level.
Another possibility to reduce at least the illumi-
nation variation is to use elevation data, which may
be acquired from optical images using the state-of-
the-art photogrammetric procedures (Snavely et al.,
2006). From dense point clouds, a digital surface
model can be created (Bulatov et al., 2014). There-
after, we can subtract from it the ground model and
obtain the relative elevation, in which cars appear as
standardized objects with respect to their elevation.
Thus, in this paper, we will assume the availability
of a high-quality relative elevation image in the same
coordinate system as the optical image. Still, several
questions will arise. First of all, what happens to the
moving vehicle, which are usually not modeled well
in photogrammetric point clouds. Second, how and
at which stage should the elevation data be consid-
ered to achieve the best results. If it is considered at
112
Qiu, K., Bulatov, D. and Lucks, L.
Improving Car Detection from Aerial Footage with Elevation Information and Markov Random Fields.
DOI: 10.5220/0011335900003289
In Proceedings of the 19th International Conference on Signal Processing and Multimedia Applications (SIGMAP 2022), pages 112-119
ISBN: 978-989-758-591-3; ISSN: 2184-9471
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

the beginning, then the problem of scarcity of training
data could become an obstacle. Otherwise, if used for
post-processing only, it is questionable whether insuf-
ficiencies committed at the beginning, such as missed
detections, can ever be corrected. Third, one could
argue that elevation, obtained from the optical data,
does not represent a new source of information, and
the benefit such elevation data can bring about is lim-
ited.
In order to be able to answer these questions, we
decided to develop a multi-branch architecture con-
sisting of a standard RGB branch and an improvised
second branch that contains elevation data and/or
some additional data typical for remote sensing. Us-
ing only one hyper-parameter for weighting, we can
compare predictions based on RGB data only with
those obtained by the improvised branch. As a second
contribution, we will apply the post-processing result
using MRFs. Their sophisticated priors ensure that
vehicles may or may not have a standardized height.
The fact that we are working on a two-class prob-
lem guarantees a fast convergence of a simple move-
making energy minimization method. To explore the
effect of MRFs, it is often helpful to perform train-
ing and prediction on rather low-quality data, such as
decay on resolution. The experiments are carried out
on the well-known Potsdam dataset because the avail-
able, though not always perfect ground truth provide
a solid basis for evaluations.
We organize this article into a summary of pre-
vious works in Section 2, followed by description of
our methodology in Section 3, results (Section 4) and
conclusions (Section 5).
2 PREVIOUS WORK
The methodology on vehicle detection in remote sens-
ing data can be subdivided into conventional and
deep-learning-based methods. In the first category,
detection can be carried out explicitly, leaving some
parts of the scene unconsidered (Zhao and Neva-
tia, 2003; Cao et al., 2019). Model-driven identi-
fication, sometimes denoted as segmentation (Bula-
tov and Schilling, 2016), has as its primary goal to
achieve the hightest possible recall value while the
precision is supposed to be improved after application
of the method of machine learning (Schilling et al.,
2018a; Madhogaria et al., 2015). For example, in
(Schilling et al., 2018a), stripes formed from almost
parallel line segments detected in the optical and el-
evation data were identified as the best tool to cre-
ate hypotheses. After this, a feature set over different
sensor data is used to perform classification and sin-
gle vehicle extraction. The next level of abstraction
is to use generic feature extractors such as histograms
of orientated gradients (HOG), scale-invariant feature
transform, or others for hypotheses generation, and
then to build a higher-level object description to sub-
ject these feature-rich instances to a classifier, like
AdaBoost or support vector machines (SVM) (Leit-
loff et al., 2014; Chen et al., 2015; Madhogaria et al.,
2015). The approach of (Yao et al., 2011) works in a
similar way, but it relies on 3D points.
We concentrate here more on deep-learning-based
methods because they became state of the art in many
tasks of object detection and semantic segmentation
due to their universality. Probably, the first approach
developed on vehicle detection from remote sensing
data using CNN techniques was that of (Chen et al.,
2014) who extracted multi-scale features and com-
bined it with a modified sliding window technique.
Furthermore, (Ammour et al., 2017) proposed extrac-
tion of deep features from segments and classifica-
tion of these features using SVM. The authors have
built on the progress in fully-convolutional networks
and residual learning to perform accurate segmenta-
tion of object borders. In their semantic boundary-
aware multitask learning network, detection and seg-
mentation of vehicle instances were trained simulta-
neously. Approximately at the same time, (Tayara
et al., 2017) accomplished detection of vehicles using
a pyramid-based network with convolutional down-
sampling as well as deconvolutional upsampling lay-
ers. As for the combined optical and elevation-based
features, (Schilling et al., 2018b) designed a two-
branch CNN model. The branches were built after a
pre-trained pseudo-Siamese network allowed to com-
pute features from RGB channels and elevation chan-
nels, which were successively merged. There was
also a module for single vehicle extraction and hav-
ing the heat-map as input. Overall, progress made
on fully-convolutional networks, equipped either with
encoder-decoder structures, with skip connections or
atrous convolutions (Chen et al., 2018), nowadays
helps to overcome pooling artifacts within the state-
of-the-art land cover classification pipelines, such as
(Volpi and Tuia, 2016; Liu et al., 2017). Therefrom,
obtaining the car class is a trivial operation, and a sin-
gle vehicle detection can be achieved by (Schilling
et al., 2018b), for instance. Two contributions (Tang
et al., 2017) and (Mo and Yan, 2020) rely on instance
segmentation. The hyper region proposal network
(Tang et al., 2017) aims at predicting all of the possi-
ble bounding boxes of vehicle-like objects with a high
recall rate. A cascade of boosted classifiers reduces
spurious detections by explicitly including them into
the loss function (hard negative example mining). In
Improving Car Detection from Aerial Footage with Elevation Information and Markov Random Fields
113

the work of (Chen et al., 2019), a modification of
DeepLabV3 (Chen et al., 2018), aimed at recognizing
fine-grained features, is proposed and the results are
post-processed using generalized Zero-shot learning.
Recognition of previously unseen vehicles takes place
using both latent attributes, obtained within a least
square minimization framework, and human-defined
attributes. One of the newest trends in Computer Vi-
sion is to use generative adversarial techniques. It is,
therefore, not surprising that the authors of (Ji et al.,
2019) applied a super-resolution convolutional neu-
ral network to train the detection of vehicles in an
end-to-end manner. This was done by integrating the
loss based on target detection directly into the super-
resolution network. The features at different scales
were combined to generate the finest feature map for
the subsequent detection.
Finally, we refer to literature aiming at car detec-
tion using MRFs and CRFs. A comprehensive op-
timization pipeline (Madhogaria et al., 2015) uses a
message-passing-like algorithm with features stem-
ming from color values of neighboring pixels. In the
segment-based method of (Liu et al., 2017) for gen-
eral semantic segmentation, a high-order CRF was
introduced, encouraging pixels of the same segment
to belong to the same class. The results for the car
class are quite high (F-score exceeding 94%); how-
ever, the accuracy depends strongly on the segmenta-
tion method.
3 METHODOLOGY
Throughout this paper, we use non-capital bold let-
ters x, y for pixels and pixelwise states s, and capital
italic letters for images J, relative elevation data Z,
and image-wise states S.
3.1 Combined DeepLabV3+ Model
Since the conventional DeeplabV3+ model, denoted
as Deeplab from now on, is described in (Chen et al.,
2018), we restrict ourselves to mentioning some im-
portant characteristics that make up difference to
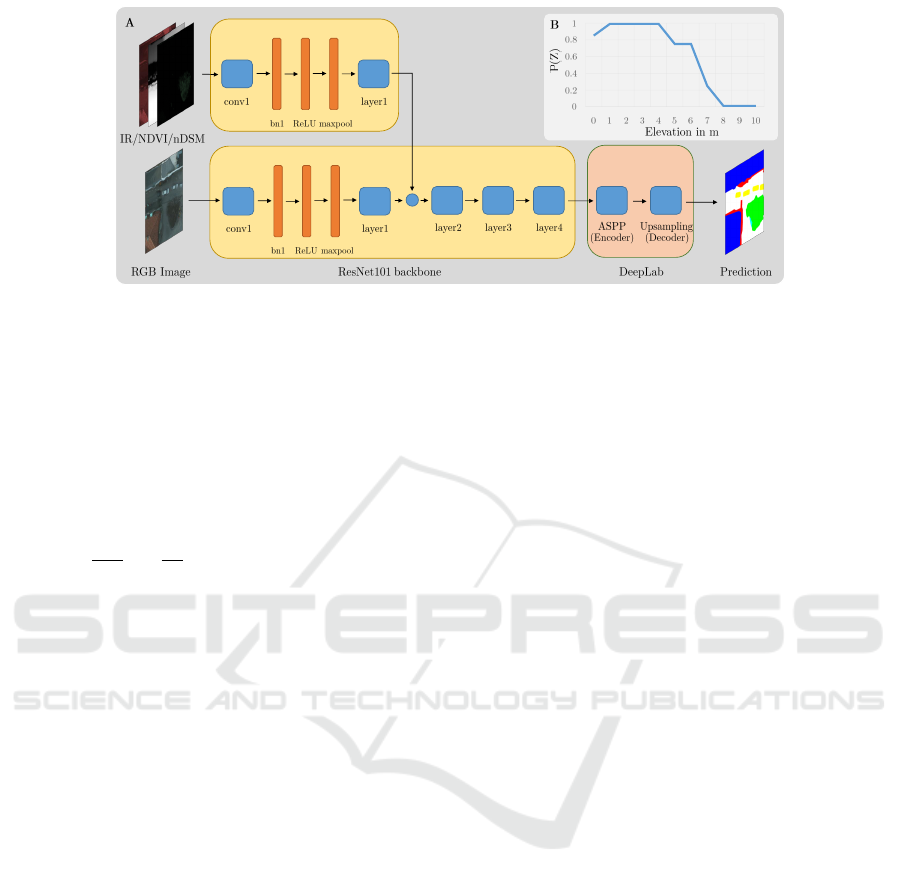
the proposed network, which is illustrated in Figure
1A. The backbone is ResNet101 (He et al., 2016).
The layers in Fig. 1A correspond to ResNet resid-
ual blocks. Similar to (Audebert et al., 2016), we
extended the architecture of Deeplab to accept six
input layers. Thus, the backbone is split into two
branches, where one branch processes the traditional
RGB image channels while the additional bands pro-
cess three more channels. For the dataset available
(see Section 4.1), these bands are the near-infrared
channel, the Normalized Differential Vegetation In-
dex (NDVI) channel, and the relative elevation. If
there are more than three additional bands, it is al-
ways possible to compute a PCA from these chan-
nels. The two branches are both initialized using the
pre-trained weights of ImageNet (Russakovsky et al.,
2015). Even though the pre-training was done on
RGB images, the earlier shallow levels of the net-
works are supposed to detect simple patterns, such as
edges and shapes, which was the reason to use pre-
trained weights for the additional branch, too. Also,
this fact motivated us to merge the features computed
for both as early as possible. At the first layer of
Deeplab, we applied a convex combination.
F = αF
J
+ (1 − α)F
H
, 0 ≤ α ≤ 1 (1)
which means that, for example, setting α = 1 is equiv-
alent to the conventional method, while a symmetric
weighting of features F
J,H
will be used in this work,
that is α = 0.5.
We perform the standard modules on data aug-
mentation during training to reduce overfitting effects.
Even though we focus on car detection in this paper,
we wish to preserve our network so general as possi-
ble bearing in mind the over-reaching goal of scene
representation using multi-modal input data. There-
fore all six available classes of the dataset are used for
training, and not two-class classification. The classes
include cas, tree, impervious surfaces, low vegetation,
clutter and building. The batch size is set to 8, the
output stride of Deeplab is set to 16, and Adamw opti-
mizer (Loshchilov and Hutter, 2017) was used to min-
imize the cross entropy as our loss function.
3.2 MRF
A Markov Random Field is a statistical model con-
sisting of an undirected graph that satisfies the lo-
cal Markov properties. The nodes of the graph are
random variables (x) whose state s is only depen-
dent on that of the neighbors. These neighbors, de-
noted by N, are represented by the graph edges. In
our case, the graph is a pixel grid, where the nodes
represent the pixels, and each pixel is connected to
its four direct neighbors. Each node x has only two
states: car (s
x
= 1) and non-car (s
x
= 0). We denote
by P(J) = P(J
x
|s
x
= 1) the value softmax probability
that x is a car pixel, which is the output of our neu-
ral network. Since the elevation channel incorporates
important information about absolute values typical
for cars, we also define the likelihood of a car having
a certain height as P(Z), shown in Fig. 1, B. Since
moving cars do not have salient relative elevations,
we set P(Z = 0) = 0.85. Elevation over 4 m is quite
SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications
114

unlikely for a car, and here is where the function P(Z)
experiences a steep decay.
Overall, the cost function is defined as:
E(s) =
∑
x
"
C
d
(s
x
) +
∑
x,y∈N
C
s
(s
x
, s
y
)
#
→ min (2)
The data C
d
(s
x
) and smoothness C
s
(s
x
, s
y
) term
across all graph nodes are summed up and minimized
to solve for the unknown S = {s
x
|x ∈ J}. The data
term includes the network-induced detection proba-
bility P
J
and the height probability P
Z
:
C
d
(s
x
= 1) = − log [βP
J∩Z
+ (1 − β)P
J∪Z
]. (3)
The term in square brackets in (3) is the combined
probability P
J∩Z
= P(J) · P(Z), since we can assume
P(J) and P(Z) to be statistically independent, and
P(J ∪Z) = P(J)+P(Z)−P(J)·P(Z). For most cases,
we want both probabilities to be high. However, in
some situations, we would be happy with a logical
“or”. For example, if a car is parked atop a roof, we
want to grant it an opportunity to be detected. Ac-
cording to fuzzy-logical concepts, we weight both ob-
servations with a scalar β, which usually lies between
0.5 and 1. We note that C
d
(s
x
= 0) is the negative
logarithm of the complementary to (3) probability.
The smoothing term in (2) is defined as:
C
s
=
0, if s
x
= s
y
λ · exp
−
∆
2
Z
σ
2
Z
−
∆
2
J
σ
2
J
, otherwise.
(4)
As usually, it penalizes neighbored pixels x and y if
they are labeled differently. The weight of penaliza-
tion depends inversely on how different the elevation
and color value of x and y. We denote by ∆Z the dif-
ference of elevations Z(x) − Z(y) and by ∆J the norm
of the difference in the CIELAB color space (Tomi-
naga, 1992). CIELAB is known to reflect human per-
ception of colors, which appear practically incorre-
lated in this representation. In order to balance the
data and smoothness terms, the parameter λ has to be
chosen carefully. We worked with the value 50 while
the choice σ
J
and σ
Z
was 1 and 5, respectively.
Minimization of (2) takes place using the Alpha-
expansion method of (Boykov et al., 2001). The fact
that we only have two labels for our MRF and also
due to the sub-modularity of our smoothness function
C
s
in (4) allows convergence to the global minimum
after only one iteration.
4 EXPERIMENTS
4.1 Potsdam Dataset
The Potsdam dataset (Rottensteiner et al., 2014) is
the ISPRS benchmark consisting of 14 patches with
6000 × 6000 pixels and a resolution of 5 cm. The
resulting area of approximately 1.26 km
2
contained
3820 vehicles. For all patches, there was image and
elevation data available. Besides, the dataset has a full
reference ground truth for the six land cover classes
and also a reference where the boundaries of the ob-
jects are eroded by a circular disc of three pixel ra-
dius. The full reference ground truth is used, and all
six classes are trained. The training data is kept at its
original resolution of 5cm and cropped into patches
of 512 × 512 pixels. To further explore the effect of
MRFs, we considered an older model allowing only to
differentiate between classes vehicle and background.
This model was trained with a standard DeepLab, us-
ing optical data only, but on the eroded reference data
and a reduced resolution of 10cm. There was also
no overlap between the 256 × 256 pixels data patches
during inference, resulting in worse detection accu-
racy.
In order to guarantee the fairness of the compar-
ison, we applied some post-processing steps to the
older model. For example, since the eroded labels
were used to train this model, the car detections are
systematically eroded as well, inspiring us to apply
morphological dilation. Since the elevation data was
not considered during CNN computation, we also per-
formed object-wise filtering. For every connected
component, the minimum median object height must
not exceed 10m while the minimum object size must
exceed 450 pixels, or 1.125m
2
. The minimum detec-
tion probability is set at 0.9.
4.2 Evaluation Strategy
Precision (p) and recall (r), as well as those unified
measures that can be formed from them, such Inter-
section over Union (IoU = (p
−1
+ r
−1
− 1)
−1
) and
F1-score, are the commonly used tools to assess the
accuracy of detection for small objects, like cars. We
decided to track these measures for both pixel-wise
and object-wise level because for many applications,
it would make a difference whether we correctly de-
tected half of the pixels of each car or 50% of the
cars completely and the other 50% not at all. Thus, to
decide whether a car has been detected on the object
level, we check whether there is a detection yielding
an IoU of at least 0.5. To do this, all cars and all con-
nected components formed by detections have been
Improving Car Detection from Aerial Footage with Elevation Information and Markov Random Fields
115
+
Figure 1: The architecture used in this article. bn and ASPP are abbreviations for Batch Normalization and Atrous Spatial
Pyramid Pooling, respectively (see (Chen et al., 2018)), while by layerX, we denote a residual block of ResNet. In the top
right image, the elevation-based likelihood P(Z) is depicted.
labeled, after which a 2D histogram has been com-
puted. From the entries of the 2D and two 1D his-
tograms, we compute the component-to-component
IoUs. Once we have found out which car has been
detected to a minimum threshold of IoU, which was
0.5, we can derive the object-based measures for pre-
cision, recall, IoU, and F1 score. Two latter ones are
denoted as IoU and F1 in Table 1.
4.3 Evaluation Results
4.3.1 Quantitative Assessment
As depicted in Table 1, the proposed network CNN
with only RGB data could obtain reasonably good re-
sults. We refrain from a more detailed comparison
with related approaches since, first of all, all of them
use different training/validation splits on the Potsdam
dataset. Secondly, only a few of them, like (Schilling
et al., 2018b) report object-wise scores. Finally, for
the reasons of space, we do not report results of a
comprehensive ablation study. We found out that
equal weighing both branches (α = 0.5 in the new
model) yielded the best performance. As expected,
using the near-infrared channel and relative elevation
(α = 0.5) with the new model yielded the best per-
formance. Since the detection was performed using
images at the finest-possible resolution, the pixelwise
results improve significantly neither after filtering nor
after the application of MRFs despite our extensive
trials on algorithm parameters β, σ
J
, and σ
H
. The ob-
jectwise F1-measure, however, increases from 0.879
to 0.918 after filtering.
Using RGB data only (α = 1.0), we obtain the
pixelwise F1-measure 0.890. After object-wise fil-
tering, the F1-measure increases by 0.1% while the
object-wise F1-measure increases by 4.8% to 0.901.
The comparability results obtained using image data
only confirms our apprehensions that the large param-
eter sets, obtained within a deep architecture from im-
ages only, already implicitly include the clues 3D data
may provide. However, one should take into account
some doubtful ground truth because, as the next sec-
tion 4.3.2 will show, the images were taken during
the winter, such that the cars are clearly visible un-
der the leafless trees but are not annotated into the
images. This fact actually shows the positive side of
our method, namely, its ability to generalize but con-
tribute to commission errors in Table 1.
Besides, Table 1, together with the images com-
ing next, show that both models are able to outper-
form the older model, which was derived from the
sub-optimal training data. The older model can be
significantly improved already using dilation and fil-
tering (pixelwise F1 increases from 0.771 to 0.857).
Besides correcting the eroded training data, dilation
can also merge separated segments classified as ve-
hicles and improve the objectwise results (F1 im-
proves from 0.754 to 0.865). For this model, we have
achieved a significant improvement using MRFs. It
is notable that a pixelwise improvement of MRFs is
bigger; however, the objectwise is lower, which has
to do with the fact that sometimes very narrow bor-
ders between very densely parked vehicles are added
to the car class, making the test on component-to-
component from Section 4.2 fail. This happens more
frequently in the case of dark cars upon similarly dark
soil where the color differences are lower. Occasion-
ally, false-positive detections, like trailers, containers,
or other rectangular-shaped objects, are falsely en-
larged by the MRF.
4.3.2 Qualitative Assessment
To gain an impression on differences in performance
of the considered methods, we refer to Figures 2 to 5.
SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications
116

Figure 2: Qualitative results on detection of vehicles. A:
RGB image, B: ground truth, where cars are colored in yel-
low. C: The combined network (left α = 1 and D: α = 0.5),
whereby true positives, true negatives, false positives and
false negatives are colored in white, black, red and dark-
green color, respectively. E: the older model without and F:
with MRF-based post-processing.
Table 1: Quantitative comparison of three different models.
All results are given percents. Underlined variables denote
object-wise values.
Method r p IoU F1 IoU F1
Comb. α = 0.5 86.9 91.7 80.5 89.2 78.5 87.9
. . . +filter 86.7 91.9 80.6 89.2 84.8 91.8
. . . +MRF+filter 91.5 86.2 79.8 88.8 79.7 88.7
Comb. α = 1.0 90.1 88.0 80.2 89.0 74.4 85.3
. . . +filter 89.0 88.3 80.4 89.1 82.0 90.1
. . . +MRF+filter 91.7 84.1 78.1 87.7 69.8 82.2
Older model 66.2 92.4 62.8 77.1 60.5 75.4
. . . + dilate + filter 86.7 84.7 74.9 85.6 78.5 88.0
. . . + MRF + filter 85.4 86.8 75.6 86.1 78.0 87.6
In Figure 2, we see that a dark car could be retrieved
using elevation information. This is possible either
using the MRF inference (image E), boosting up the
data term, or the combined Deeplab (C), which uses,
among others, the elevation channel. At the same
time, filtering does not produce new detections and
only suppresses the spurious ones. All other cars in
Figure 3: Another example on vehicle detection. See cap-
tion of Fig. 2 for further explanations. Note that the zoom
level differs from Fig. 2. The resolution remains at 5 cm.
the fragment have been detected, whereby we can see
that the images C and D resemble to their counterparts
on the right (E and F, respectively). Furthermore, Fig-
ure 3 shows an accumulation of market stands with
cars parked wildly among them, provoking a relative
confusion between the stands and the cars. Here we
see that the new model performs much better, since
it is also trained on the other classes of the Potsdam
dataset. However, one exception is a white car parked
too densely to the stands. Moreover, we see how the
MRFs, in general, improve the outlines in both bot-
tom images. In Figure 4, C, we can see how the
elevation information helps to detect confusion be-
tween the right-most car and the road lane while the
configuration with α = 1 produces two spikes on the
sides (B). Apart from this, in Figures 4 and 5, we
see the difference between the application of dilation
and MRFs. While the dilation sometimes overshoots
the label boundary and is quite fuzzy at the edges,
which happens due to the upscaling from the lower
resolution, using MRFs improves the border of de-
tections, making them closer to the actual labels. Fi-
nally, the ground truth image of Figure 5 shows how
Improving Car Detection from Aerial Footage with Elevation Information and Markov Random Fields
117

Figure 4: Example of a scene with moving cars. A: RGB
image as well as detections using the new pipeline (B:
α = 0 and C: α = 0). Bottom row: detections using the
old pipeline, result of dilation and filtering as well as result
of MRFs following by filtering. In images B-F, the color
choice is the same as in Figs. 2 and 3.
Figure 5: Exemplification of insufficiencies of the ground
truth data. From left to right: RGB image, ground truth, de-
tection result using the proposed network with α = 1, with-
out and with MRFs.
non-existent tree crowns in winter occlude cars and
slightly affect the result of MRFs. Since the new
DeepLab model is trained on all six classes, includ-
ing cars and trees, it is able to reproduce the occlu-
sion of cars by trees present in the ground truth. If
MRFs are then applied, the car detections tend to get
dilated to the entire car, even when that part is under-
neath a tree. This partialy explains why MRFs do not
improve in Table 1 for the newer DeepLab models.
This effect is not as pronounced on the older DeepLab
model, which was trained on just the car class. There,
even without MRFs, the model tends to detect the en-
tire car, even if underneath a tree because the model
generalized the car class.
5 CONCLUSION
We presented a method for vehicle detection from
high-resolution airborne data, whereby our innova-
tion to the DeepLabV3+ method (Chen et al., 2018)
is an additional branch relying on typical data for
remote sensing. Furthermore, an MRF-based work-
flow has been implemented. We applied our data
to the benchmark data test and obtained encourag-
ing results. The accuracies obtained are slightly be-
low those cited in related works (Chen et al., 2019;
Schilling et al., 2018b), where only pixelwise predic-
tion was reported. However, our workflow is general
enough to be applied to the problem of land cover
classification. For the most part, the false positives the
proposed method has produced were either different
moving objects, such as market stalls or trailers, or ar-
eas between densely parked cars with many shadows.
Fortunately, temporary objects of this kind are wel-
come to be removed during inpainting, which is our
main area of applications. We also experimented with
MRFs, which improved the results in the case of sub-
optimal training data. Here, MRFs are able to outper-
form simple object-wise filtering methods based on
the objects height and size. In the future, we plan to
test the workflow for datasets of a coarser resolution,
followed by the application of inpainting methods.
REFERENCES
Ammour, N., Alhichri, H., Bazi, Y., Benjdira, B., Alajlan,
N., and Zuair, M. (2017). Deep learning approach
for car detection in UAV imagery. Remote Sensing,
9(4/312):1–15.
Audebert, N., Le Saux, B., and Lef
`
evre, S. (2016). Seman-
tic segmentation of earth observation data using mul-
timodal and multi-scale deep networks. In Asian Con-
ference on Computer Vision, pages 180–196. Springer.
Boykov, Y., Veksler, O., and Zabih, R. (2001). Fast ap-
proximate energy minimization via graph cuts. IEEE
Transactions on Pattern Analysis and Machine Intel-
ligence, 23(11):1222–1239.
Bulatov, D., H
¨
aufel, G., Meidow, J., Pohl, M., Solbrig, P.,
and Wernerus, P. (2014). Context-based automatic
reconstruction and texturing of 3D urban terrain for
quick-response tasks. ISPRS Journal of Photogram-
metry and Remote Sensing, 93:157–170.
Bulatov, D. and Schilling, H. (2016). Segmentation meth-
ods for detection of stationary vehicles in combined
elevation and optical data. In IEEE International Con-
ference on Pattern Recognition, pages 603–608.
Cao, S., Yu, Y., Guan, H., Peng, D., and Yan, W. (2019).
Affine-function transformation-based object matching
for vehicle detection from unmanned aerial vehicle
imagery. Remote Sensing, 11(14):1708.
Chen, H., Luo, Y., Cao, L., Zhang, B., Guo, G., Wang, C.,
Li, J., and Ji, R. (2019). Generalized zero-shot vehicle
detection in remote sensing imagery via coarse-to-fine
framework. In International Joint Conference on Ar-
tificial Intelligence, pages 687–693.
Chen, L.-C., Zhu, Y., Papandreou, G., Schroff, F., and
Adam, H. (2018). Encoder-decoder with atrous sep-
arable convolution for semantic image segmentation.
SIGMAP 2022 - 19th International Conference on Signal Processing and Multimedia Applications
118

In European Conference on Computer Vision, pages
801–818.
Chen, X., Xiang, S., Liu, C.-L., and Pan, C.-H. (2014). Ve-
hicle detection in satellite images by hybrid deep con-
volutional neural networks. IEEE Geoscience and Re-
mote Sensing Letters, 11(10):1797–1801.
Chen, Z., Wang, C., Wen, C., Teng, X., Chen, Y., Guan, H.,
Luo, H., Cao, L., and Li, J. (2015). Vehicle detection
in high-resolution aerial images via sparse represen-
tation and superpixels. IEEE Transactions on Geo-
science and Remote Sensing, 54(1):103–116.
Gleason, J., Nefian, A. V., Bouyssounousse, X., Fong,
T., and Bebis, G. (2011). Vehicle detection from
aerial imagery. In IEEE International Conference on
Robotics and Automation, pages 2065–2070.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep
residual learning for image recognition. In IEEE con-
ference on computer vision and pattern recognition,
pages 770–778.
Ji, H., Gao, Z., Mei, T., and Ramesh, B. (2019). Vehicle
detection in remote sensing images leveraging on si-
multaneous super-resolution. IEEE Geoscience and
Remote Sensing Letters, 17(4):676–680.
Kottler, B., Bulatov, D., and Schilling, H. (2016). Improv-
ing semantic orthophotos by a fast method based on
harmonic inpainting. In IAPR Workshop on Pattern
Recognition in Remote Sensing (PRRS), pages 1–5.
IEEE.
Leberl, F., Bischof, H., Grabner, H., and Kluckner, S.
(2007). Recognizing cars in aerial imagery to improve
orthophotos. In ACM International Symposium on Ad-
vances in Geographic Information Systems, pages 1–
9.
Leitloff, J., Rosenbaum, D., Kurz, F., Meynberg, O., and
Reinartz, P. (2014). An operational system for es-
timating road traffic information from aerial images.
Remote Sensing, 6(11):11315–11341.
Liu, Y., Piramanayagam, S., Monteiro, S. T., and
Saber, E. (2017). Dense semantic labeling of
very-high-resolution aerial imagery and LiDAR with
fully-convolutional neural networks and higher-order
CRFs. In IEEE Conference on Computer Vision and
Pattern Recognition Workshops, pages 76–85.
Loshchilov, I. and Hutter, F. (2017). Fixing weight decay
regularization in adam. CoRR, abs/1711.05101.
Madhogaria, S., Baggenstoss, P. M., Schikora, M., Koch,
W., and Cremers, D. (2015). Car detection by fu-
sion of HOG and causal MRF. IEEE Transactions on
Aerospace and Electronic Systems, 51(1):575–590.
Mo, N. and Yan, L. (2020). Improved faster rcnn based on
feature amplification and oversampling data augmen-
tation for oriented vehicle detection in aerial images.
Remote Sensing, 12(16/2558):1–21.
Rottensteiner, F., Sohn, G., Gerke, M., Wegner, J. D., Bre-
itkopf, U., and Jung, J. (2014). Results of the ISPRS
benchmark on urban object detection and 3D build-
ing reconstruction. ISPRS Journal of Photogrammetry
and Remote Sensing, 93:256–271.
Russakovsky, O., Deng, J., Su, H., Krause, J., Satheesh, S.,
Ma, S., Huang, Z., Karpathy, A., Khosla, A., Bern-
stein, M., Berg, A. C., and Fei-Fei, L. (2015). Im-
ageNet large scale visual recognition challenge. In-
ternational Journal of Computer Vision, 115(3):211–
252.
Schilling, H., Bulatov, D., and Middelmann, H. (2018a).
Object-based detection of vehicles using combined
optical and elevation data. ISPRS Journal of Pho-
togrammetry and Remote Sensing, 136:85–105.
Schilling, H., Bulatov, D., Niessner, R., Middelmann,
W., and Soergel, U. (2018b). Detection of vehi-
cles in multisensor data via multibranch convolutional
neural networks. IEEE Journal of Selected Topics
in Applied Earth Observations and Remote Sensing,
11(11):4299–4316.
Snavely, N., Seitz, S. M., and Szeliski, R. (2006). Photo
tourism: exploring photo collections in 3D. In ACM
SIGGRAPH, pages 835–846.
Tang, T., Zhou, S., Deng, Z., Zou, H., and Lei, L. (2017).
Vehicle detection in aerial images based on region
convolutional neural networks and hard negative ex-
ample mining. Sensors, 17(2):336.
Tayara, H., Soo, K. G., and Chong, K. T. (2017). Vehicle de-
tection and counting in high-resolution aerial images
using convolutional regression neural network. IEEE
Access, 6:2220–2230.
Tominaga, S. (1992). Color classification of natural color
images. Color Research & Application, 17(4):230–
239.
Volpi, M. and Tuia, D. (2016). Dense semantic labeling
of subdecimeter resolution images with convolutional
neural networks. IEEE Transactions on Geoscience
and Remote Sensing, 55(2):881–893.
Yao, W., Hinz, S., and Stilla, U. (2011). Extraction and mo-
tion estimation of vehicles in single-pass airborne li-
dar data towards urban traffic analysis. ISPRS Journal
of Photogrammetry and Remote Sensing, 66(3):260–
271.
Zhao, T. and Nevatia, R. (2003). Car detection in low res-
olution aerial images. Image and Vision Computing,
21(8):693–703.
Improving Car Detection from Aerial Footage with Elevation Information and Markov Random Fields
119
