
cMinMax: A Fast Algorithm to Find the Corners of an N-dimensional
Convex Polytope
Dimitrios Chamzas
1,2 a
, Constantinos Chamzas
3 b
and Konstantinos Moustakas
1 c
1
Department of Electrical and Computer Engineering, University of Patras, Rio Campus, Patras 26504, Greece
2
McCormick School of Engineering, Northwestern University, 2145 Sheridan Road, Evanston, IL 60208, U.S.A.
3
Department of Computer Science, Rice University, Houston, TX 77251, U.S.A.
Keywords:
A
ugmen
t
ed Rea
lity
En
vir
onmen
t
s
, I
mage Reg
i
s
tr
a
ti
on
,
Con
v
e
x
Po
ly
gon Co
r
ne
r
D
e
t
ec
ti
on
A
l
go
rit
hm
,
N-dimensional Convex Polyhedrons.
Abstract:
D
u
ri
ng
t
he
l
as
t y
ea
r
s
, t
he eme
r
g
i
ng
fi
e
l
d o
f
A
ugmen
t
ed
& Virt
ua
l
Rea
lity (
A
R
-V
R
)
has seen
tr
emendous g
r
ow
t
h
.
A
t t
he same
ti
me
t
he
r
e
i
s a
tr
end
t
o de
v
e
l
op
l
ow cos
t
h
i
gh
-
qua
lity
A
R s
y
s
t
ems whe
r
e compu
ti
ng powe
r i
s
i
n demand
.
Fea
t
u
r
e po
i
n
t
s a
r
e e
xt
ens
iv
e
ly
used
i
n
t
hese
r
ea
l-ti
me
fr
ame
-r
a
t
e and 3
D
app
li
ca
ti
ons
, t
he
r
e
f
o
r
e
e
ffi
c
i
en
t
h
i
gh
-
speed
f
ea
t
u
r
e de
t
ec
t
o
r
s a
r
e necessa
ry.
Co
r
ne
r
s a
r
e such spec
i
a
l f
ea
t
u
r
es and o
ft
en a
r
e used as
t
he
fir
s
t
s
t
ep
i
n
t
he ma
r
ke
r
a
li
gnmen
t i
n
A
ugmen
t
ed Rea
lity (
A
R
).
Co
r
ne
r
s a
r
e a
l
so used
i
n
i
mage
r
eg
i
s
tr
a
ti
on and
r
ecogn
iti
on
, tr
ack
i
ng
,
S
L
A
M
, r
obo
t
pa
t
h
fi
nd
i
ng and 2
D
o
r
3
D
ob
j
ec
t
de
t
ec
ti
on and
r
e
tri
e
v
a
l. T
he
r
e
f
o
r
e
t
he
r
e
i
s
a
l
a
r
ge numbe
r
o
f
co
r
ne
r
de
t
ec
ti
on a
l
go
rit
hms bu
t
mos
t
o
f t
hem a
r
e
t
oo compu
t
a
ti
ona
lly i
n
t
ens
iv
e
f
o
r
use
i
n
r
ea
l-ti
me app
li
ca
ti
ons o
f
an
y
comp
l
e
xity.
Man
y ti
mes
t
he bo
r
de
r
o
f t
he
i
mage
i
s a con
v
e
x
po
ly
gon
.
Fo
r t
h
i
s
spec
i
a
l,
bu
t
qu
it
e common case
,
we ha
v
e de
v
e
l
oped a spec
ifi
c a
l
go
rit
hm
,
cM
i
nMa
x. T
he p
r
oposed a
l
go
rit
hm
i
s
f
as
t
e
r,
app
r
o
xi
ma
t
e
ly
b
y
a
f
ac
t
o
r
o
f 5
compa
r
ed
t
o
t
he w
i
de
ly
used Ha
rri
s Co
r
ne
r
D
e
t
ec
ti
on a
l
go
rit
hm
. I
n
add
iti
on
i
s h
i
gh
ly
pa
r
a
ll
e
li
zab
l
e
. T
he a
l
go
rit
hm
i
s su
it
ab
l
e
f
o
r t
he
f
as
t r
eg
i
s
tr
a
ti
on o
f
ma
r
ke
r
s
i
n augmen
t
ed
r
ea
lity
s
y
s
t
ems and
i
n app
li
ca
ti
ons whe
r
e a compu
t
a
ti
ona
lly
e
ffi
c
i
en
t r
ea
l ti
me
f
ea
t
u
r
e de
t
ec
t
o
r i
s necessa
ry. T
he
algorithm can also be extended to N-dimensional polyhedrons.
1 INTRODUCTION
A
ugmen
t
ed
& Virt
ua
l
Rea
lity (
A
R
-V
R
)
s
y
s
t
ems and
app
li
ca
ti
ons ha
v
e seen mass
iv
e de
v
e
l
opmen
t
and ha
v
e
been s
t
ud
i
ed e
xt
ens
iv
e
ly
o
v
e
r t
he
l
as
t f
ew decades
(
B
illi
nghu
r
s
t
e
t
a
l.,
2
015).
A
l
so w
it
h
t
he de
v
e
l
op
-
men
t
o
f t
h
r
ee
-
d
i
mens
i
ona
l
measu
ri
ng
t
echno
l
og
i
es
(
3
D
Scanne
r
s
) it i
s poss
i
b
l
e
t
o acqu
ir
e
t
h
r
ee
-
d
i
mens
i
ona
l
da
t
a us
i
ng
i
ne
x
pens
iv
e
t
h
r
ee d
i
mens
i
ona
l
scanne
r
s
r
a
i
s
-
i
ng
t
he e
x
pec
t
a
ti
on
t
ha
t t
h
r
ee
-
d
i
mens
i
ona
l
da
t
a and
i
n
t
e
rf
aces w
ill
be used
.
A
t t
he same
ti
me
t
he
r
e
i
s a
tr
end
t
o de
v
e
l
op
l
ow cos
t
h
i
gh
-
qua
lity
3
D A
R s
y
s
-
t
ems whe
r
e compu
ti
ng powe
r i
s
i
n demand
.
F
i
gu
r
e
1
shows such a
l
ow cos
t
3
D A
ugmen
t
ed Rea
lity
s
y
s
t
em
us
i
ng a
t
ang
i
b
l
e
i
n
t
e
rf
ace and cons
tr
uc
t
ed us
i
ng com
-
mod
ity
ha
r
dwa
r
e
(
Chamzas and Mous
t
akas
,
2
0
2
0). It
s
cen
tr
a
l
p
r
ocess
i
ng un
it i
s a Raspbe
rry
P
i 4
equ
i
pped
w
it
h a Raspbe
rry
came
r
a
.
Mo
r
eo
v
e
r
sma
rt
phones a
r
e
con
ti
nuous
ly
e
v
o
lvi
ng
,
add
i
ng mo
r
e compu
t
e
r
powe
r,
a
https://orcid.org/0000-0002-4375-5281
b
https://orcid.org/0000-0001-5830-5542
c
https://orcid.org/0000-0001-7617-227X
F
i
gu
r
e
1:
3
D A
ugmen
t
ed Rea
lity T
ang
i
b
l
e Use
r I
n
t
e
rf
ace
us
i
ng Commod
ity
Ha
r
dwa
r
e Us
i
ng cM
i
nMa
x t
o
r
eg
i
s
t
e
r
Rea
l
World to AR World.
mo
r
e senso
r
s
,
and h
i
gh
-
qua
lity
d
i
sp
l
a
y.
Mu
lti
came
r
as
and dep
t
h senso
r
s a
r
e some o
f t
he
ir r
ecen
t
add
iti
ons
.
T
he
r
e
f
o
r
e
,
we e
x
pec
t t
ha
t it
w
ill
be poss
i
b
l
e
t
o
i
m
-
p
l
emen
t
a
ll t
he
f
unc
ti
ona
liti
es o
f
an
A
R s
y
s
t
em
j
us
t
i
n a sma
rt
phone
. I
n
t
h
i
s cases
,
compu
ti
ng powe
r
w
ill
be
i
n demand and we w
ill
need
t
o de
v
e
l
op new
f
as
t
and e
ffi
c
i
en
t
a
l
go
rit
hms
.
O
ne o
f t
he ma
i
n p
r
ob
l
ems
Chamzas, D., Chamzas, C. and Moustakas, K.
cMinMax: A Fast Algorithm to Find the Corners of an N-dimensional Convex Polytope.
DOI: 10.5220/0010259002290236
In Proceedings of the 16th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2021) - Volume 1: GRAPP, pages
229-236
ISBN: 978-989-758-488-6
Copyright
c
2021 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
229

i
n
t
hese s
y
s
t
ems
i
s
t
he
r
eg
i
s
tr
a
ti
on o
f t
he Rea
l
and
Virt
ua
l
wo
rl
d
,
whe
r
e we need
t
o map
t
he
r
ea
l-
wo
rl
d
3
D
coo
r
d
i
na
t
es
(x
r
,y
r
,z
r
)
t
o
t
he d
i
g
it
a
l
wo
rl
d coo
r
d
i-
na
t
es
(x
v
,y
v
,z
v
)
.
O
ne common
ly
used
t
echn
i
que
i
s
t
he
i
mage ma
r
ke
r.
We p
l
ace an ob
j
ec
t, t
he ma
r
ke
r,
w
it
h
a known shape
i
n
t
he
r
ea
l
wo
rl
d and we wan
t t
o
fi
nd
a p
r
o
j
ec
tiv
e
tr
ans
f
o
r
ma
ti
on
t
ha
t
w
ill
map
t
h
i
s ob
j
ec
t
t
o
it
s
virt
ua
l
wo
rl
d coun
t
e
r
pa
rt. T
h
i
s
tr
ans
f
o
r
ma
ti
on
has
t
o be
r
eca
l
cu
l
a
t
ed e
v
e
ry ti
me
t
he came
r
a changes
pos
iti
on w
it
h
i
n
t
he
r
ea
l
wo
rl
d en
vir
onmen
t
and
f
o
r r
ea
l
ti
me s
y
s
t
ems
t
h
i
s
r
equ
ir
es a subs
t
an
ti
a
l
amoun
t
o
f t
he
s
y
s
t
ems compu
t
e
r r
esou
r
ces
. T
h
i
s becomes e
v
en wo
r
s
t
when we a
r
e dea
li
ng w
it
h ma
r
ke
rl
ess
A
R s
y
s
t
ems
.
A
common app
r
oach
t
o add
r
ess
t
h
i
s
r
eg
i
s
tr
a
ti
on p
r
ob
l
em
i
s
fi
nd
i
ng
f
ea
t
u
r
es on
t
he
r
ea
l
wo
rl
d ma
r
ke
r
and s
i
nce
we know
t
he
ir
pos
iti
on
i
n
t
he
Virt
ua
l
wo
rl
d
,
we can ca
l-
cu
l
a
t
e
t
he
r
equ
ir
ed p
r
o
j
ec
tiv
e
tr
ans
f
o
r
ma
ti
on
.
Co
r
ne
r
s
are such features.
D
e
t
ec
ti
ng Co
r
ne
r
s
i
s a
l
so
t
he
fir
s
t
s
t
ep
i
n man
y
Compu
t
e
r Vi
s
i
on and
O
b
j
ec
t i
den
tifi
ca
ti
on and
r
e
tri
e
v
a
l
t
asks
. It i
s a
l
so
i
mpo
rt
an
t t
o a
r
eas such as med
i
c
i
ne
,
eng
i
nee
ri
ng
,
en
t
e
rt
a
i
nmen
t
and so on
t
ha
t
a
r
e
i
nc
r
eas
-
i
ng
ly r
e
lyi
ng
i
n p
r
ocesses
t
ha
t r
equ
ir
e
t
h
i
s k
i
nd o
f
i
n
f
o
r
ma
ti
on
. I
n
t
h
i
s wo
r
k we p
r
esen
t
a s
i
mp
l
e and
f
as
t
a
l
go
rit
hm
t
ha
t
add
r
esses
t
he abo
v
e p
r
ob
l
em when
t
he
border of the image is a convex polygon.
2 PREVIOUS WORK
T
he p
r
ob
l
em
t
o
fi
nd
t
he co
r
ne
r
s
i
n an
i
mage was e
x
am
-
i
ned
i
n
t
he pas
t.
Mos
t
o
f t
he me
t
hods p
r
esen
t
ed we
r
e
based on
t
he o
ri
g
i
na
l
a
l
go
rit
hm p
r
oposed
i
n
(
Ha
rri
s
e
t
a
l., 1
988
),
whe
r
e
t
he
y
compu
t
e a co
r
ne
r
b
y
e
x
p
l
o
iti
ng
sudden changes
i
n
i
mage b
ri
gh
t
ness
.
SUS
A
N
(
Sm
it
h
and B
r
ad
y, 1
99
7) i
s ano
t
he
r
a
l
go
rit
hm w
i
de
ly
used
f
o
r
edge and co
r
ne
r
de
t
ec
ti
on
.
Us
i
ng mo
r
pho
l
og
i
ca
l
ope
r
a
t
o
r
s was ano
t
he
r
app
r
oach
(Li
n e
t
a
l., 1
998
)
used
t
o
fi
nd
t
he co
r
ne
r
s
i
n an
i
mage
.
A
d
iff
e
r
en
t
app
r
oach
us
i
ng mach
i
ne
l
ea
r
n
i
ng was a
l
so p
r
oposed
i
n
(
Ros
t
en
and Drummond, 2006).
W
it
h
t
he de
v
e
l
opmen
t
o
f t
h
r
ee
-
d
i
mens
i
ona
l t
echno
l-
og
y
and
t
he usage o
f V
R
&
A
R and Robo
ti
c s
y
s
t
ems
,
another field that is growing fast over the last years is
3
D
o
r
mu
lti
d
i
mens
i
ona
l
da
t
a
.
F
i
nd
i
ng po
i
n
t
s o
f i
n
t
e
r-
es
t i
n 3
D
c
l
ouds
(
Nous
i
as e
t
a
l.,
2
0
2
0
a
;
Nous
i
as e
t
a
l.,
2
0
2
0
b
)
o
r
decompos
i
ng mu
lti
d
i
mens
i
ona
l
wo
r
kspaces
i
n
t
o
l
oca
l
p
ri
m
itiv
es
(
Chamzas e
t
a
l.,
2
01
9
),
becomes
i
mpo
rt
an
t
and aga
i
n co
r
ne
r
s
(v
e
rti
ces
)
a
r
e one o
f t
hem
.
A
n e
xt
ens
i
on o
f
Ha
rri
s Co
r
ne
r
D
e
t
ec
ti
on a
l
go
rit
hm
t
o
3
D
was p
r
oposed
i
n
(
G
ł
omb
,
2
00
9
;
S
i
p
ir
an and Bus
-
t
os
,
2
011).
A
n e
x
amp
l
e o
f
e
xt
end
i
ng SUS
A
N
t
o 3
D
po
i
n
t
c
l
ouds
i
s desc
ri
bed
i
n
(
Wa
lt
e
r
e
t
a
l.,
2
00
9
)
wh
il
e
i
n
(
Ka
t
sou
l
as and Be
r
gen
,
2
001) t
he
r
e
i
s an
i
nd
ir
ec
t
me
t
hod
t
ha
t
e
xtr
ac
t
s edges
fr
om a 3
D
po
i
n
t
c
l
oud
,
and
t
hen
r
ega
r
ds
t
hese
i
n
t
e
r
sec
ti
on po
i
n
t
s as co
r
ne
r
s
. I
n
(
A
be e
t
a
l.,
2
017),
a
t
echn
i
que
i
s p
r
esen
t
ed
t
ha
t
es
-
ti
ma
t
es
t
he
v
e
rti
ces
i
n a 3
D
Po
i
n
t
C
l
oud on con
v
e
x
po
ly
hed
r
a su
rf
aces us
i
ng
D
e
l
auna
y T
e
tr
ahed
r
a
li
za
ti
on
.
Con
v
e
x
Hu
ll
a
l
go
rit
hms
(
Be
r
g e
t
a
l.,
2
01
3
; T
o
t
h e
t
a
l.,
2017) could also be used to determine the corners.
A
ll
o
f t
he abo
v
e a
l
go
rit
hms ha
v
e a cons
i
de
r
ab
l
e
p
r
ocess
i
ng cos
t
as compa
r
ed
t
o
t
he p
r
oposed
t
echn
i
que
,
wh
i
ch
i
s s
i
mp
l
e
, r
obus
t
and app
li
cab
l
e
t
o an
y
d
i
men
-
s
i
on
.
Mo
r
eo
v
e
r i
s h
i
gh
ly
pa
r
a
ll
e
li
zab
l
e
. T
he
i
npu
t i
n
t
he p
r
oposed me
t
hod
i
s a po
i
n
t
c
l
oud con
t
a
i
ned
i
n a
convex polytope acquired by an appropriate scanner.
3 THE ALGORITHM
I
n
i
mage
r
eg
i
s
tr
a
ti
on we o
ft
en need
t
o
fi
nd
t
he co
r
ne
r
s
o
f t
he
i
mage
.
Man
y ti
mes
t
he bo
r
de
r
o
f t
he
i
mage
i
s
a con
v
e
x
po
ly
gon
.
Fo
r t
h
i
s spec
i
a
l,
bu
t
qu
it
e common
case
,
we ha
v
e de
v
e
l
oped a spec
ifi
c a
l
go
rit
hm
, r
e
f
e
rr
ed
as cM
i
nMa
x. T
he a
l
go
rit
hm u
tili
zes
t
he
f
ac
t t
ha
t if
we
fi
nd
t
he
x-
coo
r
d
i
na
t
es o
f t
he p
ix
e
l
s
t
ha
t
be
l
ong
t
o
t
he
i
mage
, t
hen
t
he
ir
ma
xi
mum
,
x
max
, i
s a co
r
ne
r’
s coo
r
d
i-
na
t
e
.
S
i
m
il
a
rly f
o
r
x
min
,
y
min
and
y
max
. T
he p
r
oposed
a
l
go
rit
hm
i
s app
r
o
xi
ma
t
e
ly 5 ti
mes
f
as
t
e
r t
han
t
he Ha
r-
ri
s Co
r
ne
r
D
e
t
ec
ti
on
A
l
go
rit
hm
,
bu
t it
s app
li
cab
ility i
s
limited only to convex polygons.
3.1 The Algorithm Steps for 2D
The basic steps of the algorithm are
1.
P
r
epossess
i
ng
:
G
ene
r
a
t
e a b
i
na
ry v
e
r
s
i
on o
f t
he
image.
2.
If
φ
max
= 2ω
max
i
s
t
he e
x
pec
t
ed ma
xi
mum ang
l
e
of the polygon, choose M >
π
2(π−φ
max
)
,
3.
Fo
r
k = 0,1,..,M −1
, r
o
t
a
t
e
t
he
i
mage b
y
∆θ =
k ∗π/(2M) = k(π −φ
max
)
4.
P
r
o
j
ec
t t
he
i
mage on
t
he
v
e
rti
ca
l
and ho
ri
zon
t
a
l
a
xi
s and
fi
nd
t
he
(x
min
,x
max
,y
min
,y
max
)
. T
hese a
r
e
coo
r
d
i
na
t
es o
f f
ou
r
co
r
ne
r
s o
f t
he
r
o
t
a
t
ed con
v
e
x
polygon.
5.
Ro
t
a
t
e
t
he
i
mage backwa
r
ds b
y
−∆θ
t
o
t
he
i
n
i-
ti
a
l
pos
iti
on and
fi
nd
t
he coo
r
d
i
na
t
es o
f t
he
f
ou
r
corners.
6.
A
t t
he end
,
we ha
v
e
f
ound
4M
po
i
n
t
s wh
i
ch
i
s
g
r
ea
t
e
r t
han
t
he numbe
r
o
f
e
x
pec
t
ed po
ly
gon co
r-
ne
r
s
.
Hence
, t
he
r
e a
r
e mo
r
e
t
han one p
ix
e
l
s a
r
ound
each co
r
ne
r.
We e
v
a
l
ua
t
e now
t
he cen
tr
o
i
d
f
o
r
each
o
f t
hese bunches and
t
hese a
r
e
t
he es
ti
ma
t
ed co
r-
ners of the convex polygon.
GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications
230
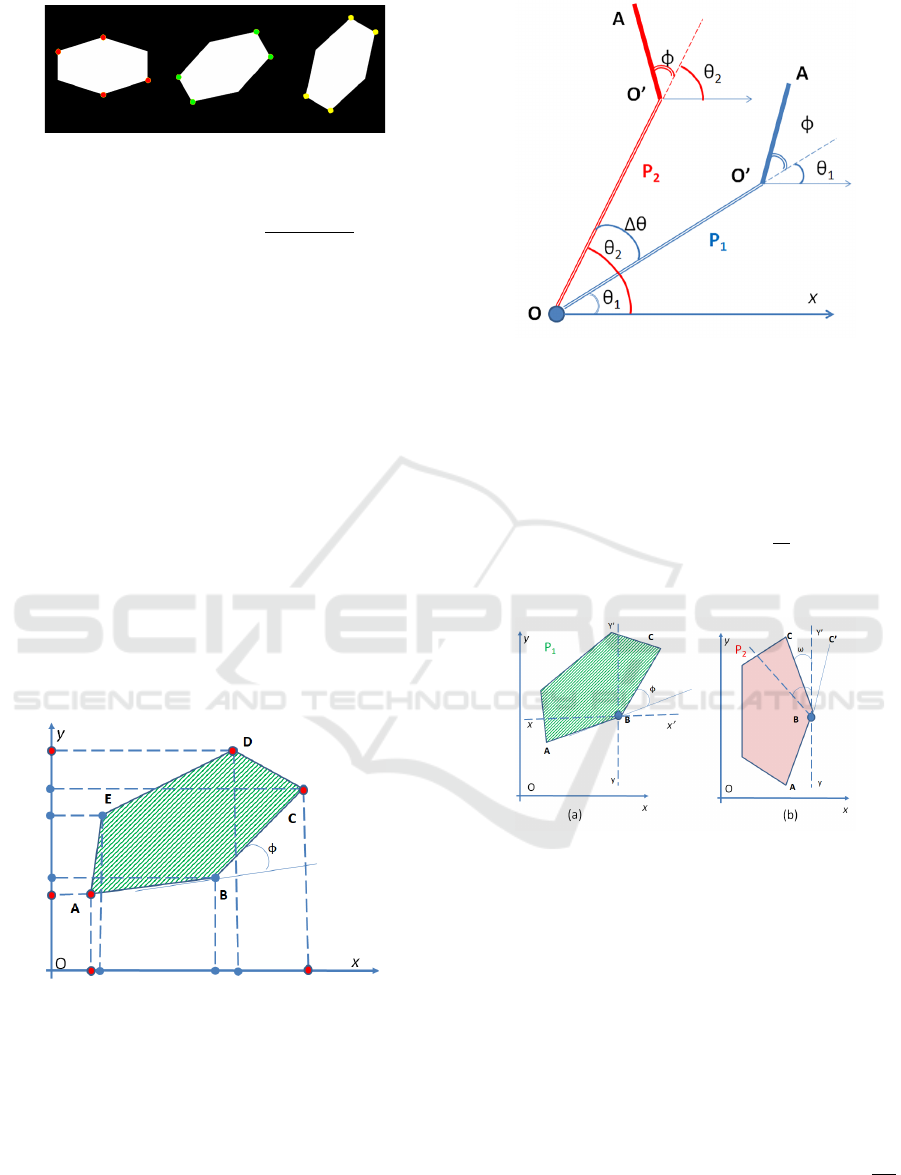
F
i
gu
r
e 2
:
D
e
t
ec
t
ed co
r
ne
r
s
i
n a he
x
agon
f
o
r
M
=
3
r
o
t
a
ti
ons
.
In each rotation we detect 4 corners.
I
n F
i
gu
r
e 2 we app
ly t
he a
l
go
rit
hm
i
n a he
x
agon
.
We have φ
max
= 150
◦
, thus M >
180
◦
2(180
◦
−150
◦
)
= 3
3.2 The Proof
I
n
t
h
i
s sec
ti
on we p
r
esen
t t
he
t
heo
r
e
ti
ca
l
backg
r
ound
for the algorithm.
The Problem: Find the N-corners in an image that
con
t
a
i
ns an ob
j
ec
t
w
it
h a bounda
ry t
ha
t i
s a con
v
e
x
polygon.
D
e
fi
n
iti
on
: L
e
t
us ha
v
e a con
v
e
x
po
ly
gon w
it
h N
-
co
r
ne
r
s w
it
h coo
r
d
i
na
t
es
I = (x
i
,y
i
)
i=1,N
.
O
ne co
r
ne
r
w
it
h coo
r
d
i
na
t
es
(x
k
,y
k
)
i
s ca
ll
ed d
i
sco
v
e
r
ab
l
e
, if
one
o
f it
s coo
r
d
i
na
t
es
i
s ma
xi
mum o
r
m
i
n
i
mum
i
n
t
he se
t
I, that is
x
k
= max or min o f (x
1
,x
2
,...,x
N
) or (1)
y
k
= max or min o f (y
1
,y
2
,...,y
N
)
E
x
amp
l
e
: I
n F
i
gu
r
e 3
, t
he co
r
ne
r
s
A,C,D
o
f t
he
pen
t
agon
(ABCDE)
a
r
e d
i
sco
v
e
r
ab
l
e
,
wh
il
e
B,E
a
r
e
not.
Figure 3: Discoverable Corners.
P
r
opos
iti
on
1:
We ha
v
e
t
wo connec
t
ed
li
nes
(OO
0
)
and
(O
0
A)
w
it
h
t
he ang
l
e
φ = ∠OO
0
A
t
o be cons
t
an
t
(
see F
i
gu
r
e
4). If
we
r
o
t
a
t
e
(OO
0
)
i
n
i
nc
r
emen
t
s o
f
∆θ
a
r
ound
O
, t
hen
(O
0
A)
w
ill r
o
t
a
t
e a
l
so
i
n
i
nc
r
emen
t
s o
f
∆θ around O
0
.
P
r
oo
f: L
e
t
us
r
o
t
a
t
e
(OO
0
)
b
y
∆θ = θ
2
−θ
1
, fr
om
pos
iti
on
P
1
t
o pos
iti
on
P
2
. T
he
li
ne segmen
t
(O
0
A)
r
o
t
a
t
es a
r
ound
O
0
fr
om
θ
1
+φ
t
o
θ
2
+φ
,
and
t
he change
i
s aga
i
n
∆θ = (θ
2
+φ) −(θ
1
+φ)
. T
he
r
e
f
o
r
e
if t
he
li
ne
Figure 4: Rotating Rigidly Connected Lines.
segmen
t
(OO
0
)
r
o
t
a
t
es a
r
ound
O
0
i
n
i
nc
r
emen
t
s o
f
∆θ
,
t
hen
,
neg
l
ec
ti
ng
tr
ans
l
a
ti
ons
, t
he
li
ne segmen
t
(O
0
A)
rotates also in increments of ∆θ around O
0
.
P
r
opos
iti
on 2
: I
n a con
v
e
x
po
ly
gon
,
B
i
s one o
f it
s
co
r
ne
r
s
,
∠B
i
s
it
s ang
l
e and
φ = 180
o
−∠B
it
s e
x
p
l
e
-
men
t
a
ry. If
we
r
o
t
a
t
e
t
he po
ly
gon a
r
ound
B
i
n
i
nc
r
e
-
men
t
s o
f
∆θ < φ
, t
hen
i
n a
t
mos
t
M ≥
2π
∆θ
r
o
t
a
ti
ons
, t
he
ad
j
acen
t
po
i
n
t
s
A
and
C
w
ill
be a
t l
eas
t
once
t
o
t
he
l
e
ft
side of vertical line yy
0
.
Figure 5: Invariant Rotation Center.
P
r
oo
f: L
e
t
us assume
t
ha
t
we
r
o
t
a
t
e
t
he po
ly
gon
coun
t
e
r
c
l
ockw
i
se a
r
ound B
, i
n
i
nc
r
emen
t
s o
f
∆θ
s
t
a
rt-
i
ng
fr
om pos
iti
on
P
1
(
F
i
g
. 5 (
a
)). I
n
M
s
t
eps
,
BC
w
ill
make a
f
u
ll r
o
t
a
ti
on a
r
ound
B
.
Now
l
e
t
us con
-
s
i
de
r
pos
iti
on
P
2
when
BC
mo
v
es
f
o
r t
he
fir
s
t ti
me
t
o
t
he
l
e
ft
o
f
yy
0
, (
F
i
g
. 5 (
b
)). T
hen
ω < φ
and
ω + ∠CBA < φ + ∠CBA = 180
o
. T
he
r
e
f
o
r
e po
i
n
t
A
i
s
t
o
t
he
l
e
ft
o
f
yy
0
.
S
i
nce
t
he po
ly
gon
i
s con
v
e
x,
a
ll
it
s co
r
ne
r
s a
r
e
t
o
t
he
l
e
ft
o
f
yy
0
, t
he
r
e
f
o
r
e
it
s coo
r
d
i-
na
t
e
x
B
,
w
ill
be a
t l
eas
t
once
t
he ma
xi
mum o
f
a
ll t
he
x-coordinates of the polygon angles.
Co
r
o
ll
a
ry 1:
Fo
r t
he co
r
ne
r
B
t
o be
discoverable
, it
i
s su
ffi
c
i
en
t t
o
r
o
t
a
t
e
t
he po
ly
gon a
r
ound
B
i
n
M ≥
pi
2∆θ
with ∆θ < φ (see Fig. 5).
P
r
oo
f: I
n o
r
de
r f
o
r
co
r
ne
r
B
t
o be d
i
sco
v
e
r
ab
l
e
, it
i
s enough
f
o
r it
s
t
wo ad
j
acen
t
edges
t
o be
t
o
t
he
l
e
ft
cMinMax: A Fast Algorithm to Find the Corners of an N-dimensional Convex Polytope
231

o
f
yy
0
,
o
r t
o
t
he
ri
gh
t
o
f
yy
0
,
o
r
abo
v
e
xx
0
o
r
be
l
ow
xx
0
.
Therefore we need only M ≥
pi
2∆θ
rotation steps.
T
heo
r
em
1:
We ha
v
e a con
v
e
x
po
ly
gon see F
i
g
. 5
(
a
)),
and
l
e
t
φ
be
t
he e
x
p
l
emen
t
a
ry
o
f it
s ma
xi
mum
ang
l
e
.
We se
l
ec
t
a po
i
n
t
O
and we
r
o
t
a
t
e
t
he po
ly
gon
a
r
ound
it i
n
i
nc
r
emen
t
s o
f
∆θ < φ
, t
hen
i
n a
t
mos
t
M ≥
π
2∆θ
,
a
ll it
s co
r
ne
r
s w
ill
be d
i
sco
v
e
r
ab
l
e a
t l
eas
t
once.
P
r
oo
f: L
e
t
B a co
r
ne
r
o
f t
he po
ly
gon
. T
he ang
l
e
be
t
ween
OB
and
it
s ad
j
acen
t
edges
i
s cons
t
an
t
du
ri
ng
t
he
r
o
t
a
ti
on a
r
ound
O
. T
hen because o
f
P
r
opos
iti
on
1,
as we
r
o
t
a
t
e
t
he po
ly
gon a
r
ound
O
i
n
i
nc
r
emen
t
s
o
f
∆θ
,
a
ll it
s edges a
r
e
r
o
t
a
ti
ng
i
n
i
nc
r
emen
t
s o
f
∆θ
a
r
ound
t
he
ir
ad
j
acen
t
co
r
ne
r
s
.
Consequen
tly
acco
r
d
i
ng
t
o Co
r
o
ll
a
ry 1 if
we
r
o
t
a
t
e
t
he con
v
e
x
po
ly
gon a
r
ound
a po
i
n
t
O
i
n
i
nc
r
emen
t
s o
f
∆θ < φ
, t
hen
i
n a
t
mos
t
M ≤
π
2∆θ
s
t
eps
,
a
ll it
s co
r
ne
r
s w
ill
be d
i
sco
v
e
r
ab
l
e a
t
least once.
3.3 Extension to N-dimensional Convex
Polyhedrons
T
he a
l
go
rit
hm can a
l
so be e
xt
ended
t
o N
-
d
i
mens
i
ona
l
polyhedrons.
D
e
fi
n
iti
on 2
:
A
se
t
C
i
s con
v
e
x if f
o
r
an
y
po
i
n
t
s
x,y ∈ C
t
he segmen
t
[x,y]
j
o
i
n
i
ng
t
hem be
l
ongs
t
o
C
.
A
con
v
e
x
po
ly
hed
r
on
i
s a po
ly
hed
r
on
t
ha
t,
as a
so
li
d
, f
o
r
ms a con
v
e
x
se
t.
A
no
t
he
r
de
fi
n
iti
on
i
s
:
A
con
v
e
x
po
ly
hed
r
on can a
l
so be de
fi
ned as a bounded
i
n
t
e
r
sec
ti
on o
f fi
n
it
e
ly
man
y
ha
lf-
spaces
(
G
r
unbaum
and Shephard, 1969; Gr
¨
unbaum, 2013).
D
e
fi
n
iti
on 3
: L
e
t
us ha
v
e a con
v
e
x
po
ly
hed
r
on w
it
h
N
-v
e
rti
ces w
it
h coo
r
d
i
na
t
es
I = (x
i
,y
i
,z
i
)
i=1,N
.
O
ne
v
e
rt
e
x
w
it
h coo
r
d
i
na
t
es
(x
k
,y
k
,z
k
)
i
s ca
ll
ed d
i
sco
v
e
r-
ab
l
e
, if
one o
f it
s coo
r
d
i
na
t
es
i
s ma
xi
mum o
r
m
i
n
i
mum
in the set I, that is
x
k
= max or min o f (x
1
,x
2
,...,x
N
) or
y
k
= max or min o f (y
1
,y
2
,...,y
N
) or (2)
z
k
= max or min o f (z
1
,z
2
,...,z
N
)
D
e
fi
n
iti
on
4: L
e
t
O
be a
v
e
rt
e
x
o
f t
he con
v
e
x
po
ly-
hed
r
on and
OA,OB,OC,OD,OE
it
s edges
(
F
i
gu
r
e 6
.
We de
fi
ne
O
1
OO
2
as
t
he M
i
n
i
mum Bound
i
ng Cone
f
o
r
t
he
v
e
rt
e
x
O
, t
he sma
ll
es
t
cone
t
ha
t it
s
t
op
i
s
t
he
v
e
rt
e
x
O
and
it
con
t
a
i
ns a
ll t
he edges o
f t
he
v
e
rt
e
x
O
. T
h
i
s
M
i
n
i
mum Bound
i
ng Cone w
ill
ha
v
e a
t l
eas
t t
wo o
f t
he
v
e
rt
e
x
edges on
it
s su
rf
ace and
t
he
r
es
t i
ns
i
de
. L
e
t
a
l
so
OK
be
it
s a
xi
s o
f
s
y
mme
try. T
h
i
s wa
y
we can assoc
i
a
t
e
w
it
h each
v
e
rt
e
x
o
f
a con
v
e
x
po
ly
hed
r
on an ang
l
e
, t
he
ang
l
e
∠O
1
OO
2
= 2ω
o
f t
he M
i
n
i
mum Bound
i
ng Cone
.
S
i
nce
t
he po
ly
hed
r
on
i
s con
v
e
x,
we ha
v
e
φ > 0
o
and
0
o
< ω = ∠KOO
2
< 90
o
.
P
r
opos
iti
on 3
: L
e
t
R
x
(θ),R
y
(θ),R
z
(θ)
be
t
he
r
o
-
t
a
ti
on ma
tri
ces b
y
θ
a
r
ound a
xi
s
x,y,z
r
espec
tiv
e
ly
Figure 6: Minimum Bounding Cone of a vertex.
and
N
θ
= d
2π
∆θ
e
and
N
φ
= d
2π
∆φ
e
,
whe
r
e
∆θ
and
∆φ
a
r
e
i
nc
r
emen
t
a
l r
o
t
a
ti
on angu
l
a
r
s
t
eps a
r
ound
t
he a
xi
s
z
and
z
.
We mu
lti
p
ly
a
v
ec
t
o
r
−→
OK
b
y t
he
r
o
t
a
ti
on ma
-
trix
R
zy
= R
y
(k∆φ)R
z
(m∆θ)
f
o
r
k = 0, 1, 2, ..., N
θ
−1
and
m = 0,1,2,...,N
φ
−1
. T
he
N
θ
N
φ
pos
iti
ons o
f t
he
r
o
t
a
t
ed
v
ec
t
o
r
a
r
e shown
i
n F
i
gu
r
e
7.
A
t l
eas
t f
o
r
one
o
f t
hem
, it
s d
i
s
t
ance
d
x
fr
om
t
he a
xi
s
x
i
s
l
ess
t
han
√
∆θ
2
+∆φ
2
2
. T
he same
i
s a
l
so
tr
ue
f
o
r
d
z
t
he d
i
s
t
ance o
f
a grid point from the axis z .
F
i
gu
r
e
7:
3
D G
ri
d o
f
a
v
ec
t
o
r
pos
iti
on
r
o
t
a
t
ed a
r
ound a
xi
s z
and axis y with ∆θ = ∆φ =
π
10
rads.
P
r
oo
f:
We
fir
s
t r
o
t
a
t
e a un
it v
ec
t
o
r
−→
OK
a
r
ound a
xi
s
z b
y
k∆θ
un
til it
goes
t
o
it
s nea
r
es
t
pos
iti
on
t
o p
l
ane
(x,
z
). T
h
i
s
i
s pos
iti
on
−−→
OK
1
i
n F
i
gu
r
e 8
. It
s d
i
s
t
ance
fr
om p
l
ane
(x
z
)
w
ill
be
l
ess
t
han
∆θ
2
. T
hen we
r
o
t
a
t
e
it
a
r
ound a
xi
s
y i
n s
t
eps o
f
∆φ
un
til it
goes
t
o
it
s nea
r
es
t
pos
iti
on
t
o p
l
ane
(x,y). T
h
i
s
i
s pos
iti
on
−−→
OK
f
i
n F
i
gu
r
e 8
.
It
s d
i
s
t
ance
fr
om p
l
ane
(xy)
w
ill
be
l
ess
t
han
∆φ
2
. T
hus
t
he
r
e
i
s a pa
ir
(k
x
,m
x
)
f
o
r
wh
i
ch
t
he
v
ec
t
o
r
−→
OK
goes
t
o
t
he g
ri
d pos
iti
on
−−→
OK
x
and
f
o
r t
h
i
s pos
iti
on
it
s d
i
s
t
ance
d
x
fr
om
t
he a
xi
s
x i
s
d
x
<
√
∆θ
2
+∆φ
2
2
.
S
i
m
il
a
rly f
o
r
ano
t
he
r
pa
ir
(k
z
,m
z
)
t
he
v
ec
t
o
r
−→
OK
goes
t
o
v
ec
t
o
r
−−→
OK
z
t
he c
l
oses
t
g
ri
d pos
iti
on
t
o a
xi
s z
.
Howe
v
e
r,
we can
ne
v
e
r
go c
l
ose
t
o second a
xi
s o
f r
o
t
a
ti
on
,
a
xi
s
y,
s
i
nce
for any position in the grid its angle to axis y remains
GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications
232
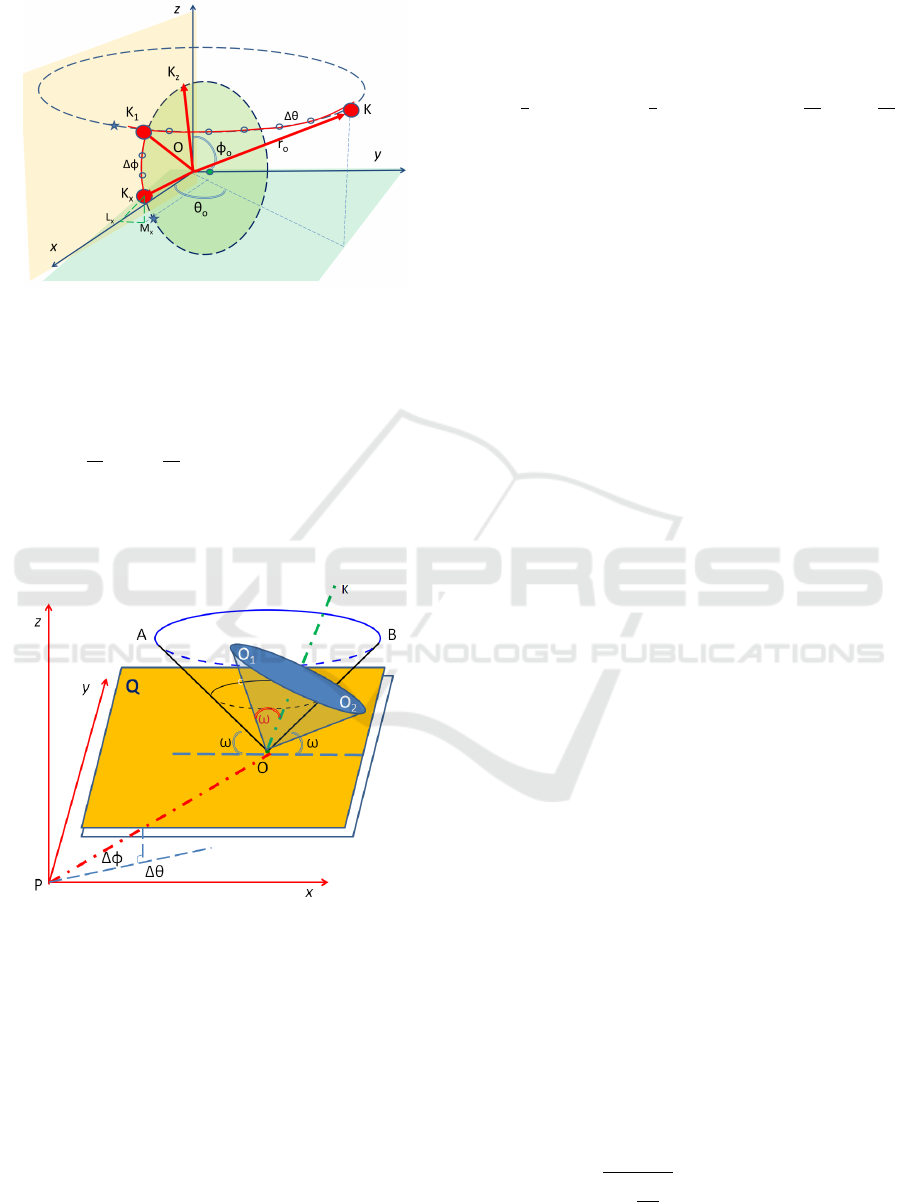
greater or equal to 90
o
−φ (see Figure 7) QED.
Figure 8: 3D Rotation of a vector around axis z and axis y.
P
r
opos
iti
on
4: I
n a con
v
e
x
po
ly
hed
r
on
, t
he ang
l
e
o
f t
he M
i
n
i
mum Bound
i
ng Cone o
f v
e
rt
e
x
O
i
s
2ω
.
If
we
r
o
t
a
t
e
t
he po
ly
hed
r
on
fir
s
t
a
r
ound a
xi
s z and
t
hen a
r
ound a
xi
s
y, i
n
i
nc
r
emen
t
s o
f
k∆θ
and
m∆φ
,
k =
0,...,N
θ
−1, m = 0,2,...,N
φ
−1
w
it
h
∆θ < ω,∆φ < ω
and
N
θ
≥
2π
∆θ
,N
φ
≥
2π
∆φ
, t
hen
t
he M
i
n
i
mum Bound
i
ng
Cone o
f v
e
rt
e
x
O
w
ill f
a
ll
a
t l
eas
t
once
i
n
t
he uppe
r
s
i
de o
f t
he p
l
ane
v
e
rti
ca
l t
o a
xi
s z
,
pass
i
ng
fr
om
O
(
see
F
i
gu
r
e
5).
A
l
so s
i
m
il
a
rly
w
ill
be once be
ll
ow and once
above the plane passing from O and vertical to axis x.
Figure 9: 3D Rotation of a Convex Polyhedron.
P
r
oo
f:
S
i
m
il
a
r t
o P
r
opos
iti
on 2
.
A
s we mu
lti
p
ly
t
he po
i
n
t
s o
f t
he po
ly
hed
r
on w
it
h
t
he
r
o
t
a
ti
on ma
trix
R
z
y
t
he d
ir
ec
ti
on o
f v
ec
t
o
r
−→
OK
w
ill
go
t
h
r
ough a
ll it
s
co
rr
espond
i
ng pos
iti
on
i
n
it
s 3
D
g
ri
d
.
A
s p
r
o
v
ed
i
n
P
r
opos
iti
on 3
,
a
t l
eas
t
one pos
iti
on o
f t
he 3
D
g
ri
d co
rr
e
-
spond
i
ng
t
o
t
he a
xi
s o
f
s
y
mme
try
OK
o
f t
he M
i
n
i
mum
Bound
i
ng Cone o
f v
e
rt
e
x
O
w
ill f
a
ll i
ns
i
de
t
he cone
(OAB). This cone is perpendicular to the plane Q and
the angle of its sides to Q is ω
T
heo
r
em 2
:
We ha
v
e a con
v
e
x
po
ly
hed
r
on
,
and
l
e
t
φ
max
= 2ω
max
be
t
he ma
xi
mum ang
l
e o
f
a
ll t
he M
i
n
-
i
mum Bound
i
ng Cones co
rr
espond
i
ng
t
o
it
s
v
e
rti
ces
.
We se
l
ec
t t
wo a
xi
s o
f t
he coo
r
d
i
na
t
e s
y
s
t
em
. i.
e
.
z
and
y
and b
y
mu
lti
p
lyi
ng a
ll t
he po
i
n
t
s w
it
h
t
he
r
o
t
a
-
ti
on ma
trix
R
z
y
,
we
r
o
t
a
t
e
t
he po
ly
gon a
r
ound
t
hem
w
it
h
k∆θ
and
m∆φ
whe
r
e
k = 1,...,N
θ
,m = 1,2,...,N
φ
,
∆θ <
π
2
−ω
max
,
∆φ <
π
2
−ω
max
and
N
θ
≥
2π
∆θ
,N
φ
≥
2π
∆φ
.
Then all its vertices will be discoverable at least once
in the axis x and axis z.
Proof: It follows from Proposition 4.
No
t
e
:
A
d
iff
e
r
en
t li
ne o
f
p
r
oo
f
cou
l
d be based on
t
he
f
ac
t t
ha
t t
he p
r
o
j
ec
ti
on o
f
con
v
e
x
po
ly
hed
r
on on a
p
l
ane
i
s a con
v
e
x
po
ly
gon
. T
hus we
r
o
t
a
t
e
t
he po
ly
he
-
d
r
on a
r
ound an a
xi
s
,
we p
r
o
j
ec
t it
on
t
he p
l
anes
t
ha
t
con
t
a
i
n
t
he a
xi
s and
t
hen we app
ly t
he 2
D
a
l
go
rit
hm
to the obtained convex polygons.
T
he e
xt
ens
i
on o
f t
he a
l
go
rit
hm
t
o N
-
d
i
mens
i
ona
l
Convex polytopes is straight forward.
4 IMPLEMENTATION
A
c
r
uc
i
a
l
pa
r
ame
t
e
r i
n
t
he abo
v
e a
l
go
rit
hm was
t
he
choice of M. With
φ
max
the expected maximum angle
o
f t
he po
ly
gon
, it
was shown
t
ha
t if
M ≥π/(π −φ
max
)
,
t
hen each co
r
ne
r
o
f t
he po
ly
gon w
ill
appea
r
a
t l
eas
t
once
i
n
t
he se
t
o
f t
he de
t
ec
t
ed co
r
ne
r
s
.
Fo
r
e
x
amp
l
e
,
f
o
r
an o
rt
hogona
l
pa
r
a
ll
e
l
og
r
am
,
φ
max
= 2π/4
,
M ≥ 2
and
if
we chose
M = 2
, t
he
r
o
t
a
ti
on s
t
ep
i
s
π/4
.
Fo
r
a
he
x
agon w
it
h equa
l
ang
l
es
,
φ
max
= 2π/3
,
M ≥ 3
and
if
we chose
M = 3
t
he
r
o
t
a
ti
on s
t
ep
i
s
π/6
.
Howe
v
e
r,
when an edge becomes nea
rly v
e
rti
ca
l t
o an a
xi
s
,
due
t
o
nume
ri
ca
l
accu
r
ac
y
and no
i
s
y
da
t
a
,
man
y ti
mes
t
he
r
e
a
r
e mo
r
e
t
han one
max
o
r
min
po
i
n
t
s
i
n
t
he p
r
o
j
ec
ti
on
on one a
xi
s
. I
n
t
h
i
s case we dec
i
ded
t
o neg
l
ec
t
a
ll
o
f
t
hem and go
t
he ne
xt r
o
t
a
ti
on s
t
ep
. T
hus
,
we mus
t
make mo
r
e
r
o
t
a
ti
on s
t
eps
t
han
t
he one p
r
ed
i
c
t
ed b
y t
he
t
heo
r
e
ti
ca
l
ana
ly
s
i
s
.
A
no
t
he
r
pa
r
ame
t
e
r i
s
t
he cen
t
e
r
of the image rotation.
A
gain, as it was shown, we can
choose an
y
po
i
n
t
as
t
he
i
mage
r
o
t
a
ti
on cen
t
e
r,
bu
t it i
s
e
x
pec
t
ed
t
ha
t if t
he
r
o
t
a
ti
on cen
t
e
r i
s
t
he cen
tr
o
i
d o
f
the convex polygon, the algorithm to be less sensitive
to numerical errors.
4.1 Examples
4.1.1 2D Case
Fo
r t
he 2
D
case
,
we used a 2
040x10
8
0
b
i
na
ry i
mage
o
f
a con
v
e
x
po
ly
gon w
it
h se
v
en co
r
ne
r
s F
i
gu
r
e
10
and
φ
max
≈ 158
◦
. T
he
r
equ
ir
ed numbe
r
o
f r
o
t
a
ti
ons mus
t
be a
t l
eas
t
M ≥
180
◦
180
◦
−158
◦
= 8.53
. T
hus we used N
=
9
rotations with ∆θ =
90
◦
9
= 10
◦
cMinMax: A Fast Algorithm to Find the Corners of an N-dimensional Convex Polytope
233
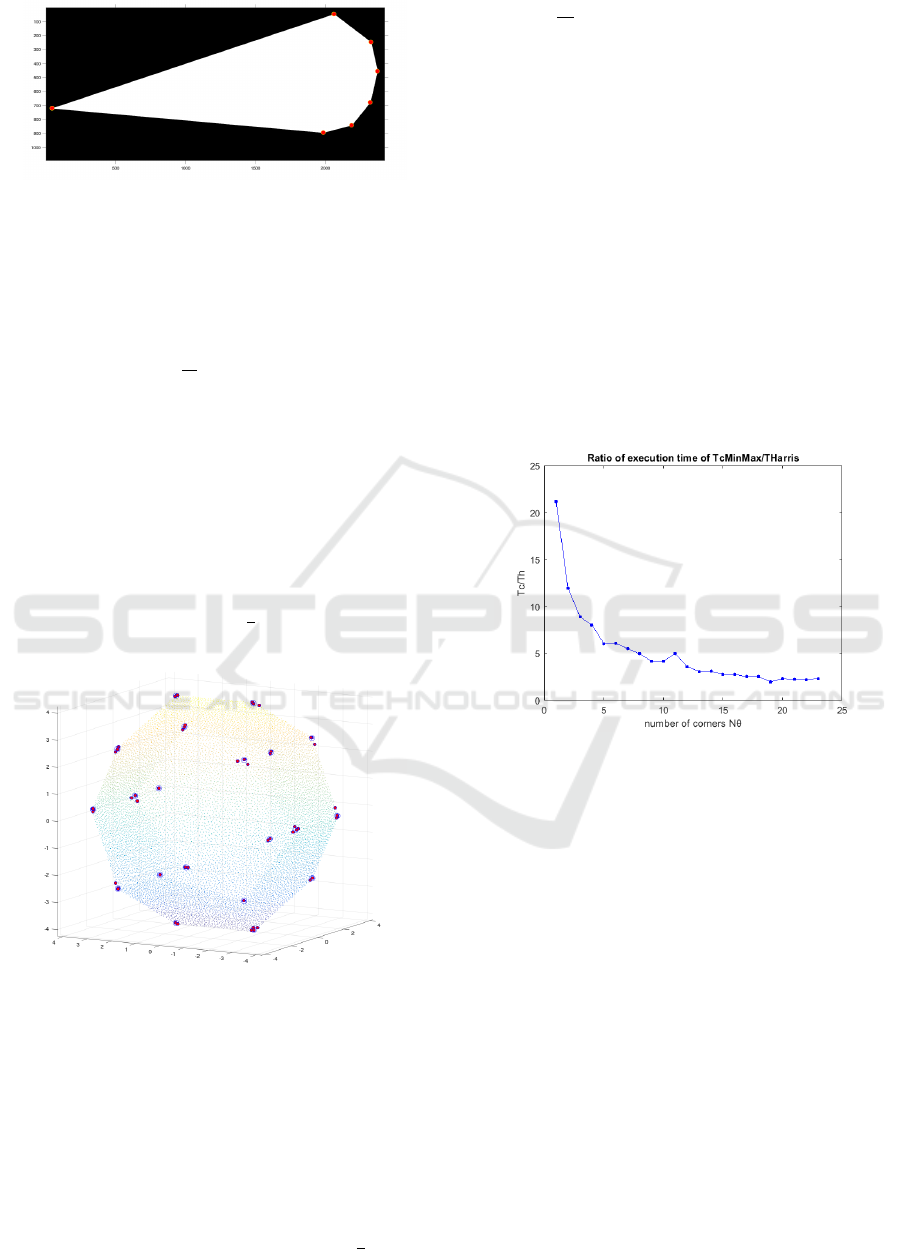
Figure 10: Estimated Corners in a heptagon (red dots).
4.1.2 3D Case
I
n
t
h
i
s e
x
amp
l
e we used a dodecahed
r
on po
i
n
t
c
l
oud
ob
t
a
i
ned
fr
om Mesh
L
ab
,
w
it
h
145
3
5
po
i
n
t
s
. T
he
l
eng
t
h
o
f it
s edge
i
s 3
.
236
1 . T
he
r
esu
lt
s
f
o
r t
h
i
s dodecahe
-
d
r
on w
it
h
∆θ = ∆φ =
π
20
a
r
e shown
i
n F
i
gu
r
e
11.
We
d
i
d 2
0x
2
0=400 r
o
t
a
ti
ons
, f
o
r
e
v
e
ry r
o
t
a
ti
on we
fi
nd
6 co
r
ne
r
s
,
2
i
n each a
xi
s
,
bu
t
on
ly
282 o
f t
hem we
r
e
accep
t
ed as
v
a
li
d and
t
he
y
we
r
e c
l
ass
ifi
ed as co
r
ne
r
s
.
Fo
r t
he o
t
he
r
cases
,
due
t
o nume
ri
ca
l
accu
r
ac
y
we had
mo
r
e
t
han one ma
x
o
r
m
i
n
i
n one a
xi
s and
t
he
y
we
r
e
r
e
j
ec
t
ed
. T
hese 282 po
i
n
t
s we
r
e c
l
us
t
e
r
ed
t
o 2
0
g
r
oups
,
and
t
he
ir
cen
tr
o
i
ds we
r
e
t
he es
ti
ma
t
ed co
r
ne
r
s
. T
he
a
v
e
r
age accu
r
ac
y
o
f t
he es
ti
ma
ti
on was app
r
o
xi
ma
t
e
2
%
o
f t
he edge
l
eng
t
h
. T
he ma
xi
mum ang
l
e o
f t
he
m
i
n
i
mum bound cone
i
s
ω
max
= 69.095
◦
,
and
t
heo
r
e
ti-
ca
lly
we cou
l
d use
∆θ = ∆φ =
π
9
,
bu
t
due
t
o nume
ri
ca
l
errors and noise we need less than half of it.
F
i
gu
r
e
11:
Es
ti
ma
t
ed Co
r
ne
r
s
i
n a dodecahed
r
on
(r
ed do
t
s
).
Circles indicate the weighted position of corners.
4.2 Evaluation: Computational
Complexity
L
e
t
us assume we ha
v
e a po
i
n
t
c
l
oud w
it
h
n
po
i
n
t
s
o
f
a N
-
d
i
mens
i
ona
l
po
lyt
ope and we know
t
ha
t t
he
φ
max
= 2ω
max
i
s
t
he e
x
pec
t
ed ma
xi
mum ang
l
e o
f
a
ll
t
he M
i
n
i
mum Bound
i
ng Cones co
rr
espond
i
ng
t
o
it
s
v
e
r-
ti
ces
. T
hen
, f
o
ll
ow
i
ng
T
heo
r
em 2
,
w
it
h
∆θ <
π
2
−ω
max
and
N
θ
≥
2π
∆θ
,
we ha
v
e
t
o pe
rf
o
r
m
(N −1)N
(N−1)
θ
r
o
-
t
a
ti
ons o
f
n
po
i
n
t
s
, i
n o
r
de
r
a
ll it
s
v
e
rti
ces
t
o be d
i
s
-
co
v
e
r
ab
l
e a
t l
eas
t
once
i
n one a
xi
s
. T
he
r
e
f
o
r
e
i
n e
v
e
ry
s
t
ep o
f t
he a
l
go
rit
hm we pe
rf
o
r
m one
r
o
t
a
ti
on and
t
hen
fi
nd
t
he
max
o
f t
he n po
i
n
t
s
x-
coo
r
d
i
na
t
es
.
Bo
t
h ope
r
a
-
ti
ons a
r
e o
f
comp
l
e
xity
O(n)
and we ha
v
e
t
o pe
rf
o
r
m
a
t l
eas
t
L = (N −1)N
(N−1)
θ
s
t
eps
, t
hus
t
he a
l
go
rit
hm
compu
t
a
ti
ona
l
comp
l
e
xity i
s
LO(n)
.
A
t t
h
i
s po
i
n
t
we
ha
v
e
t
o obse
rv
e
t
ha
t
each s
t
ep
i
s
i
ndependen
t fr
om
t
he
o
t
he
r
s
, t
he
r
e
f
o
r
e
t
he
y
can compu
t
ed
i
n pa
r
a
ll
e
l
and
t
he
p
r
oposed a
l
go
rit
hm
i
s h
i
gh
ly
pa
r
a
ll
e
li
zab
l
e
.
A
ssum
i
ng
t
ha
t t
he a
l
go
rit
hm
i
s
r
unn
i
ng
i
n a compu
t
e
r
w
it
h a
t l
eas
t
L
G
PUs
t
hen we can c
l
a
i
m
t
ha
t it
s comp
l
e
xity i
s
O(n)
.
Con
v
e
x
Hu
ll
and Ha
rri
s co
r
ne
r
D
e
t
ec
ti
on a
l
go
rit
hms
can a
l
so be used
t
o add
r
ess s
i
m
il
a
r
p
r
ob
l
ems
.
Con
v
e
x
Hu
ll
a
l
go
rit
hms a
r
e d
iffi
cu
lt t
o be pa
r
a
ll
e
li
zab
l
e and
t
he
ir
sequen
ti
a
l v
e
r
s
i
on
i
s o
f
O(nlog(n))
comp
l
e
xity
(
Be
r
g e
t
a
l.,
2
01
3
; T
o
t
h e
t
a
l.,
2
017). T
o compa
r
e
it
w
it
h
F
i
gu
r
e
1
2
:
Ra
ti
o o
f
e
x
ecu
ti
on
ti
me
f
o
r
cM
i
nMa
x
and Ha
rri
s
Co
r
ne
r
D
e
t
ec
ti
on a
l
go
rit
hm app
li
ed
t
o
r
egu
l
a
r
po
ly
gons w
it
h
3 to 25 corners.
t
he comp
l
e
xity
o
f
Ha
rri
s co
r
ne
r
de
t
ec
ti
on a
l
go
rit
hm
i
n 2
D
(
Chen e
t
a
l.,
2
00
9
),
we d
i
d
r
un bo
t
h o
f t
hem
i
n Ma
tL
ab
®
,
us
i
ng
t
he
detectHarrisFeatures()
com
-
mand
.
Fo
r
2
D
space we ha
v
e
N = 2
and
t
he comp
l
e
xity
o
f
cMinMax
i
s
N
θ
O(n)
.
Fo
r i
mages w
it
h 3
-1
2 co
r
ne
r
s
,
cM
i
n
i
Ma
x i
s on
t
he a
v
e
r
age
5 ti
mes
f
as
t
e
r t
han Ha
rri
s
Co
r
ne
r
de
t
ec
ti
on a
l
go
rit
hm
(
see F
i
gu
r
e
1
2
). I
n add
iti
on
t
he p
r
oposed a
l
go
rit
hm appea
r
s
t
o be
l
ess sens
itiv
e
t
o
sampling quantization errors.
5 RANDOM SAMPLING
Mos
t
o
f t
he
ti
mes
t
he numbe
r
o
f
unknown co
r
ne
r
s
i
s
no
t
g
iv
en and
i
n add
iti
on we do no
t
ha
v
e a good es
ti
ma
-
ti
on o
f
φ
max
. T
hus we canno
t
es
ti
ma
t
e a p
r
ope
r r
o
t
a
ti
on
s
t
ep
f
o
r t
he app
li
ca
ti
on o
f
cM
i
nMa
x.
O
ne app
r
oach
w
ill
be
t
o s
t
a
rt
w
it
h an
i
n
iti
a
l r
o
t
a
ti
on s
t
ep
.
Ne
xt
we
r
educe
it
and
try
aga
i
n
,
un
til t
he numbe
r
o
f
de
t
ec
t
ed
GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications
234

co
r
ne
r
s
r
ema
i
n cons
t
an
t.
A
n a
lt
e
r
na
tiv
e app
r
oach
i
s
t
o
r
o
t
a
t
e
t
he po
lyt
opes w
it
h ang
l
es se
l
ec
t
ed
r
andom
ly, I
n
t
h
i
s case
it i
s
i
mpo
rt
an
t t
o ha
v
e un
if
o
r
m
ly
d
i
s
tri
bu
t
ed
rotations. The 2D case is simple, but we have to to be
ca
r
e
f
u
l
when we dea
l
w
it
h ob
j
ec
t
s
i
n w
it
h d
i
mens
i
on
-
ality higher than two.
2-D
:
We se
l
ec
t
a
r
andom ang
l
e
∆θ
i
n
t
he c
l
osed
i
n
t
e
rv
a
l
[−π,π]
.
We
r
o
t
a
t
e
t
he con
v
e
x
po
ly
gon b
y
∆θ
and we
fi
nd
t
he e
xtr
emes o
f t
he coo
r
d
i
na
t
es
i
n
t
he
x-
a
xi
s and
y-
a
xi
s
.
We con
ti
nue un
til
no mo
r
e d
iff
e
r
en
t
co
r
ne
r
s a
r
e
detected.
F
i
gu
r
e
1
3
: (
a
)
Un
if
o
r
m
ly
d
i
s
tri
bu
t
ed po
i
n
t
s on a sphe
r
e
.
Red dots the 20 dodecahedron vertices. (b) A vector and its
r
o
t
a
t
ed pos
iti
ons
. (
c
)
H
i
s
t
og
r
am o
f (
a
)
a
r
ound
t
he 2
0 r
ed do
t
s
.
(d) Histogram of (b) around the 20 red dots.
3-D
:
We se
l
ec
t t
wo
r
andom ang
l
es
∆θ
and
∆φ
.
∆θ
i
s
un
if
o
r
m
ly
d
i
s
tri
bu
t
ed
i
n
t
he
i
n
t
e
rv
a
l
[−π/2,π/2]
.
∆φ
i
s
r
andom
ly
d
i
s
tri
bu
t
ed
i
n
t
he
i
n
t
e
rv
a
l
[−π,π]
w
it
h a den
-
s
ity
d
i
s
tri
bu
ti
on
f (φ) = sin(φ)/2
. T
h
i
s wa
y
we ha
v
e
mo
r
e po
i
n
t
s a
r
ound
t
he equa
t
o
r
φ = 0
,
gene
r
a
ti
ng
t
hus
un
if
o
r
m
ly
d
i
s
tri
bu
t
ed pa
ir
s
∆θ,∆φ
on a sphe
r
e
1
(
see
F
i
gu
r
e
1
3
(
a
)).
We
r
o
t
a
t
e now
t
he con
v
e
x
po
ly
hed
r
on
b
y
∆θ
and
∆φ
and we
fi
nd
t
he e
xtr
emes o
f t
he coo
r
d
i-
na
t
es
i
n
t
he
x-
a
xi
s
, y-
a
xi
s and z
-
a
xi
s
. T
o make
t
he
fi
na
l
pos
iti
on o
f t
he
r
o
t
a
t
ed po
i
n
t
s as
r
andom as poss
i
b
l
e
, i
n
e
v
e
ry
s
t
ep we peak
r
andom
ly
one o
f t
he poss
i
b
l
e s
ix
poss
i
b
l
e a
xi
s
r
o
t
a
ti
ons
. T
he
r
o
t
a
t
ed pos
iti
on o
f
a
v
ec
t
o
r
a
r
e shown
i
n F
i
gu
r
e
1
3
(
a
). I
n F
i
gu
r
e
1
3
(
c
)
and
(
d
)
we show
t
he h
i
s
t
og
r
ams
f
o
r (
a
)
and
(
b
).
Each o
f t
he 2
0
b
i
ns con
t
a
i
n
t
he po
i
n
t
s
t
ha
t
c
l
ose
t
o
t
he co
rr
espond
i
ng
vertex of dodecahedron (red dots in (a)).
T
o s
i
mp
lify
ou
r
ana
ly
s
i
s we w
ill
e
x
am
i
ne
t
he case
whe
r
e we
fi
nd
t
he ma
x
O
N
LY i
n
t
he
x-
a
xi
s
. It i
s c
l
ea
r
1
h
tt
p
://
co
ry
s
i
mon
.
g
it
hub
.i
o
/
a
rti
c
l
es
/
un
if
o
r
md
i
s
t
n
-
on
-
sphere/
t
ha
t i
n e
v
e
ry r
o
t
a
ti
on we de
t
ec
t
on
ly
O
NE co
r
ne
r. T
he
ques
ti
on we wan
t t
o answe
r i
s
,
how man
y ti
mes do we
ha
v
e
t
o
r
o
t
a
t
e a po
lyt
ope w
it
h N co
r
ne
r
s
, i
n o
r
de
r t
o
de
t
ec
t
a
ll it
s co
r
ne
r
s
. T
h
i
s p
r
ob
l
em
i
s equ
iv
a
l
en
t t
o
t
he
f
o
ll
ow
i
ng
D
i
e p
r
ob
l
em
(I
saac
, 1
996
), irr
espec
tiv
e o
f
t
he d
i
mens
i
ona
lity
o
f t
he po
lyt
ope space
, ”
Ro
ll
a d
i
e
w
it
h N
-f
aces
.
Wha
t i
s
t
he e
x
pec
t
ed numbe
r
o
f r
o
ll
s
t
o
get all its N faces?.
2
I
n F
i
gu
r
e
14,
we show
t
he
r
equ
ir
ed numbe
r
o
f r
o
t
a
-
ti
ons
f
o
r
2
D
and 3
D
canon
i
ca
l
po
lyt
opes w
it
h N
v
e
r-
tices. For the case of rotating in equal angle steps, for
t
he 2
D
canon
i
ca
l
po
ly
gons we ha
v
e
N
rot
=
2π
π−2ω
max
=
N
.
Fo
r
3
D
po
lyt
opes we ha
v
e
N
rot
=
2π
π−2ω
max
2
.
Fo
r
t
he p
l
a
t
on
i
c so
li
ds w
it
h
N = 4,6,8,12,20
,
we ha
v
e
t
ha
t
t
he
ir
ang
l
e
ω
max
o
f t
he
ir
M
i
n
i
mum Bound Cones a
r
e
35.26
◦
,45.00
◦
,54.74
◦
,58.28
◦
69.09
◦
r
espec
tiv
e
ly.
Fo
r
t
he
r
andom case
,
a canon
i
ca
l
po
lyt
ope
i
s equ
iv
a
l
en
t t
o
a
f
a
ir
d
i
e w
it
h N equ
i
p
r
obab
l
e
f
aces and
it i
s known
t
ha
t t
he e
x
pec
t
ed numbe
r
o
f r
o
ll
s
t
o ge
t
a
ll it
s N
f
aces
i
s
t
he ha
r
mon
i
c mean o
f
N
, i.
e
.
m
N
rot
= N
∑
N
n=1
1
n
.
F
r
om
F
i
gu
r
e
14
we conc
l
ude
t
ha
t f
o
r
2
D
it i
s p
r
e
f
e
r
ab
l
e
t
o
use
t
he
r
o
t
a
ti
on
i
n equa
l
s
t
eps
, f
o
r
3
D
, r
o
t
a
ti
on
i
n equa
l
s
t
eps and
r
andom
r
o
t
a
ti
on a
r
e equ
iv
a
l
en
t
bu
t f
o
r
h
i
ghe
r
d
i
mens
i
ons
t
he
r
andom
r
o
t
a
ti
on case
i
s e
x
pec
t
ed
t
o be
preferable.
F
i
gu
r
e
14:
Mean o
f r
equ
ir
ed Ro
t
a
ti
ons
f
o
r
a canon
i
ca
l
po
ly-
t
ope w
it
h N co
r
ne
r
s
(r
ed
li
ne
).
W
it
h b
l
ue dashed
li
ne and
w
it
h dash
-
do
t
b
l
ack
li
ne a
r
e
t
he
r
equ
ir
ed
r
o
t
a
ti
ons
f
o
r t
he
deterministic case for 2D polygon and 3D polyhedron.
6 CONCLUSIONS
A
new co
r
ne
r
es
ti
ma
ti
on
t
echn
i
que on N
-
d
i
mens
i
ona
l
po
i
n
t
c
l
ouds o
f
con
v
e
x
po
lyt
opes was p
r
oposed
i
n
t
h
i
s
con
tri
bu
ti
on
. T
he p
r
oposed a
l
go
rit
hm
i
s based on
t
he
f
ac
t t
ha
t t
he m
i
n and ma
x
o
f
p
r
o
j
ec
t
ed coo
r
d
i
na
t
es
i
n
an
y
a
x
es be
l
ong
t
o a co
r
ne
r.
Fo
r
2
D
we compa
r
ed
it
w
it
h
t
he Ha
rri
s co
r
ne
r
de
t
ec
ti
on a
l
go
rit
hm
(i
mp
l
emen
-
t
a
ti
on a
t
Ma
tl
ab
)
and
it
was app
r
o
xi
ma
t
e
ly 5 ti
mes
2
h
tt
p
://
www
.
c
i
s
.j
hu
.
edu
/
∼
xy
e
/
pape
r
s and pp
t
s
/
pp
t
s
/
SolutionsToFourProblemsOfRollingADie.pdf
cMinMax: A Fast Algorithm to Find the Corners of an N-dimensional Convex Polytope
235

f
as
t
e
r f
o
r
ob
j
ec
t
s w
it
h
l
ess
t
hen
10
co
r
ne
r
s
.
We de
-
fi
ned
t
he so
li
d ang
l
e o
f
a
v
e
rt
e
x
o
f
an N
-
d
i
mens
i
ona
l
con
v
e
x
po
ly
hed
r
on b
y i
n
tr
oduc
i
ng
t
he concep
t
o
f t
he
MinimumBoundingCone
and we p
r
o
v
ed
t
ha
t t
he a
l
go
-
rit
hm
t
e
r
m
i
na
t
es
i
n
fi
n
it
e s
t
eps and
t
he numbe
r
o
f
s
t
eps
depends on
t
he ma
xi
mum so
li
d ang
l
e o
f t
he con
v
e
x
po
lyt
ope
.
We s
t
ud
y
2 d
iff
e
r
en
t t
echn
i
ques
f
o
r r
o
t
a
ti
ng
t
he po
i
n
t
c
l
oud o
f t
he ob
j
ec
t,
e
it
he
r r
o
t
a
ti
ng b
y i
nc
r
e
-
men
t
a
l
ang
l
e s
t
eps
(
de
t
e
r
m
i
n
i
s
ti
c
)
o
r
b
y
choos
i
ng
t
he
ang
l
es o
f r
o
t
a
ti
on
r
andom
ly.
We conc
l
uded
t
ha
t f
o
r
2
D
if
p
r
e
f
e
r
ab
l
e
t
o use de
t
e
r
m
i
n
i
s
ti
c app
r
oach
, f
o
r
3
D
t
he
t
wo me
t
hods a
r
e equ
iv
a
l
en
t
bu
t f
o
r
h
i
ghe
r
d
i
mens
i
on
we e
x
pec
t t
he
r
andom
t
o be p
r
e
f
e
r
ab
l
e
.
A
no
t
he
r
ad
-
v
an
t
age o
f t
he a
l
go
rit
hm
i
s
t
ha
t it
can be
i
mp
l
emen
t
ed
us
i
ng pa
r
a
ll
e
l
p
r
ocess
i
ng s
i
nce a
ll t
he
r
o
t
a
ti
ons can be
e
x
ecu
t
ed s
i
mu
lt
aneous
ly.
A
li
m
it
a
ti
on o
f t
he p
r
oposed
a
l
go
rit
hm
i
s
t
ha
t it r
equ
ir
es a p
ri
o
r
es
ti
ma
ti
on o
f t
he
ma
xi
mum so
li
d ang
l
e o
f t
he con
v
e
x
po
lyt
ope and
i
n
f
u
t
u
r
e wo
r
k we w
ill try t
o add
r
ess
t
h
i
s p
r
ob
l
em
.
Usage
i
n
r
ea
l ti
me mu
lti
d
i
mens
i
ona
l
app
li
ca
ti
ons
i
s ano
t
he
r
one
,
so we p
l
an
t
o de
v
e
l
op a
f
as
t
e
r v
e
r
s
i
on o
f t
he a
l
go
-
rit
hm su
it
ab
l
e
f
o
r
g
r
aph
i
cs ca
r
ds us
i
ng mu
lti
p
l
e
G
PUs
b
y
e
x
p
l
o
iti
ng
it
s pa
r
a
ll
e
l i
mp
l
emen
t
a
ti
on
.
F
i
na
lly,
us
-
i
ng mo
r
pho
l
og
i
ca
l
ope
r
a
t
o
r
s we w
ill try t
o e
xt
end
it
s
applicability to non-convex objects,
ACKNOWLEDGMENTS
T
he au
t
ho
r
s w
i
sh
t
o
t
hank
t
he membe
r
s o
f t
he
Vi
sua
l-
i
za
ti
on
& Virt
ua
l
Rea
lity
G
r
oup o
f t
he Un
iv
e
r
s
ity
o
f
Pa
-
tr
as as we
ll
as
D
r.
A
.
Kou
t
soud
i
s and
D
r.
G
. I
oannak
i
s
fr
om
t
he Mu
lti
med
i
a Resea
r
ch
L
ab o
f t
he
X
an
t
h
i’
s
D
i-
vi
s
i
on o
f t
he
”
A
t
hena
”
Resea
r
ch and
I
nno
v
a
ti
on Cen
t
e
r,
f
o
r t
he
ir
use
f
u
l
commen
t
s and d
i
scuss
i
ons du
ri
ng
t
he
i
n
iti
a
l
p
r
epa
r
a
ti
on o
f t
h
i
s wo
r
k
.
Cons
t
an
ti
nos Chamzas
f
o
r t
h
i
s wo
r
k was suppo
rt
ed b
y
NSF
-
G
RFP
1
8
4
2
4
9
4
and Kons
t
an
ti
nos Mous
t
akas b
y t
he Eu
r
opean Un
i
on
’
s
Ho
ri
zon 2
0
2
0 r
esea
r
ch and
i
nno
v
a
ti
on p
r
og
r
amme un
-
der Grant Agreement No 871738 - CPSoSaware.
REFERENCES
A
be
,
S
.,
Mo
ri,
H
., T
o
y
ama
,
F
.,
and Sho
ji,
K
. (
2
017).
Co
r
ne
r
es
ti
ma
ti
on
f
o
r
3
D
po
i
n
t
c
l
oud on con
v
e
x
po
ly
hed
r
a
l
su
rf
aces us
i
ng de
l
auna
y t
e
tr
ahed
r
a
li
za
ti
on
. I
n P
r
oc
.
o
f
the Computer Graphics Inter. Conf., page 25. ACM.
Be
r
g
,
M
.,
Cheong
,
O
., v
an K
r
e
v
e
l
d
,
M
.,
and
O
v
e
r
ma
r
s
,
M
.
(
2
01
3
).
Compu
t
a
ti
ona
l
G
eome
try:
A
l
go
rit
hms and
Applications. Springer, 3nd edition.
B
illi
nghu
r
s
t,
M
.,
C
l
a
r
k
,
A
., L
ee
,
G
.,
e
t
a
l. (
2
015).
A
su
rv
e
y
o
f
augmen
t
ed
r
ea
lity.
Founda
ti
ons and
Tr
ends
®
i
n
Human–Computer Interaction, 8(2-3):73–272.
Chamzas
,
C
.,
Sh
riv
as
t
a
v
a
,
A
.,
and Ka
vr
ak
i, L.
E
. (
2
01
9
).
Us
-
i
ng
L
oca
l
E
x
pe
ri
ences
f
o
r
G
l
oba
l
Mo
ti
on P
l
ann
i
ng
. I
n
I
n
t
e
r
na
ti
ona
l
Con
f
e
r
ence on Robo
ti
cs and
A
u
t
oma
ti
on
(ICRA), pages 8606–8612.
Chamzas
,
D
.
and Mous
t
akas
,
K
. (
2
0
2
0).
3
D A
ugmen
t
ed Re
-
a
lity T
ang
i
b
l
e Use
r I
n
t
e
rf
ace us
i
ng Commod
ity
Ha
r
d
-
wa
r
e
. I
n
15t
h
I
n
t.
Con
f.
on Compu
t
e
r
G
r
aph
i
cs
T
heo
ry
and Applications (GRAPP), pages 384–391.
Chen
, J.,
Zou
, L.-
h
.,
Zhang
, J.,
and
D
ou
, L. (
2
00
9
). T
he
Compa
ri
son and
A
pp
li
ca
ti
on o
f
Co
r
ne
r
D
e
t
ec
ti
on
A
l-
gorithms. Journal of Multimedia, 4:435–441.
G
ł
omb
,
P
. (
2
00
9
).
D
e
t
ec
ti
on o
f i
n
t
e
r
es
t
po
i
n
t
s on 3
D
da
t
a
:
E
x-
t
end
i
ng
t
he ha
rri
s ope
r
a
t
o
r. I
n Compu
t
e
r
Recogn
iti
on
Systems 3, pages 103–111. Springer.
G
r
¨
unbaum
,
B
. (
2
01
3
).
Con
v
e
x
po
lyt
opes
, v
o
l
ume 22
1.
Springer Science & Business Media.
G
r
unbaum
,
B
.
and Shepha
r
d
,
G
.
C
. (1
969
).
Canon
i
ca
l
po
ly-
topes. Bulletin, London Math. Soc., 1(3):257–300.
Ha
rri
s
,
C
.
G
.,
S
t
ephens
,
M
.,
e
t
a
l. (1
988
).
A
comb
i
ned co
r
ne
r
and edge de
t
ec
t
o
r. I
n
A
lv
e
y vi
s
i
on con
f
e
r
ence
, v
o
l
ume
15.50, pages 10–5244. Citeseer.
I
saac
,
R
. (1
996
). T
he P
l
easu
r
es o
f
P
r
obab
ility (
8
.4
T
he coupon co
ll
ec
t
o
r’
s p
r
ob
l
em so
lv
ed
.
pp
.
8
0-
82
).
Springer-Verlag, New York, 2nd edition.
Ka
t
sou
l
as
,
D
.
and Be
r
gen
, L. (
2
001).
E
ffi
c
i
en
t
3
D
v
e
rt
e
x
de
t
ec
ti
on
i
n
r
ange
i
mages acqu
ir
ed w
it
h a
l
ase
r
senso
r.
I
n
J
o
i
n
t
Pa
tt
e
r
n Recogn
iti
on S
y
mpos
i
um
,
pages
11
6
–
123. Springer.
Li
n
,
R
.-
S
.,
Chu
,
C
.-
H
.,
and Hsueh
, Y.-
C
. (1
998
).
A
mod
ifi
ed
mo
r
pho
l
og
i
ca
l
co
r
ne
r
de
t
ec
t
o
r.
Pa
tt
e
r
n Recogn
iti
on
Letters, 19(3-4):279–286.
Nous
i
as
,
S
.,
A
rv
an
iti
s
,
G
., L
a
l
os
,
A
.
S
.,
Kou
l
amas
,
C
.,
Pa
vli
d
i
s
,
G
.,
Ka
l
oge
r
as
,
A
.,
and Mous
t
akas
,
K
. (
2
0
2
0
a
).
A
sa
li
enc
y
awa
r
e CNN
-
Based 3
D
Mode
l
s
i
mp
lifi
ca
ti
on
and comp
r
ess
i
on
fr
amewo
r
k
f
o
r r
emo
t
e
i
nspec
ti
on o
f
heritage sites. Access, 8:169982–170001.
Nous
i
as
,
S
.,
A
rv
an
iti
s
,
G
., L
a
l
os
,
A
.
S
.,
and Mous
t
akas
,
K
.
(
2
0
2
0
b
).
Mesh Sa
li
enc
y
D
e
t
ec
ti
on Us
i
ng Con
v
o
l
u
ti
ona
l
Neu
r
a
l
Ne
t
wo
r
ks
. I
n 2
0
2
0 I
n
t.
Con
f.
on Mu
lti
med
i
a
and Expo (ICME), pages 1–6. IEEE.
Ros
t
en
,
E
.
and
D
r
ummond
, T. (
2
00
6
).
Mach
i
ne
l
ea
r
n
i
ng
f
o
r
h
i
gh
-
speed co
r
ne
r
de
t
ec
ti
on
. I
n Eu
r
opean con
f
e
r
ence
on computer vision, pages 430–443. Springer.
S
i
p
ir
an
, I.
and Bus
t
os
,
B
. (
2
011).
Ha
rri
s 3d
:
a
r
obus
t
e
xt
en
-
s
i
on o
f t
he ha
rri
s ope
r
a
t
o
r f
o
r i
n
t
e
r
es
t
po
i
n
t
de
t
ec
ti
on
on 3d meshes. The Visual Computer, 27(11):963.
Sm
it
h
,
S
.
M
.
and B
r
ad
y, J.
M
. (1
99
7).
Susan
—
a new ap
-
p
r
oach
t
o
l
ow
l
e
v
e
l i
mage p
r
ocess
i
ng
. I
n
t
e
r
na
ti
ona
l
journal of computer vision, 23(1):45–78.
T
o
t
h
,
C
.
D
.,
O
’
Rou
r
ke
, J.,
and
G
oodman
, J.
E
. (
2
017).
Hand
-
book o
f
d
i
sc
r
e
t
e and compu
t
a
ti
ona
l
geome
try (
see
Chapter 26). CRC press.
Wa
lt
e
r,
N
.,
A
ub
r
e
t
on
,
O
.,
Fouge
r
o
ll
e
, Y.
D
.,
and
L
a
li
gan
t,
O
. (
2
00
9
).
Susan 3
D
ope
r
a
t
o
r,
p
ri
nc
i
pa
l
sa
li
enc
y
de
-
g
r
ees and d
ir
ec
ti
ons e
xtr
ac
ti
on and a b
ri
e
f
s
t
ud
y
on
t
he
r
obus
t
ness
t
o no
i
se
. I
n
1
6
t
h
I
n
t.
Con
f.
on
I
mage
Processing (ICIP), pages 3529–3532. IEEE.
GRAPP 2021 - 16th International Conference on Computer Graphics Theory and Applications
236
