
Salting as a Countermeasure against Attacks on Privacy Preserving
Record Linkage Techniques
Yanling Chen
1
, Rainer Schnell
1
, Frederik Armknecht
2
and Youzhe Heng
2
1
Methodology Research Unit, University of Duisburg-Essen, Duisburg, Germany
2
Practical Computer Science Unit, University of Mannheim, Mannheim, Germany
Keywords:
PPRL, Bloom Filter, Salting, Pattern Mining Attack, Graph-matching Attack.
Abstract:
Privacy-preserving record linkage (PPRL) is the research area dedicated to linking records from multiple
databases for the same patient without revealing identifying information during the linkage. A popular PPRL
approach is based on Bloom filters (BF). Recent research has shown that BF based PPRL could be vulnerable
to cryptanalysis attacks. Among several hardening techniques, salting was considered to be one of the most
suitable defences. A thorough evaluation of the amount of protection provided by salting is lacking from the
literature. In this paper, we empirically evaluate the effect of salting on privacy by demonstrating the resilience
of salted BF to the two most advanced attack methods: pattern mining and graph-matching. Experimental
results show that salting could improve resilience against both attacks, although more minor against graph-
matching attacks than pattern mining attacks.
1 INTRODUCTION
In medical research, especially in population covering
research, linking databases residing at different par-
ties such as hospitals, health insurance companies, or
population registries is often required. Records can be
easily linked if a common entity identifier across the
databases is available, otherwise, record linkage could
be already a challenge task since common attributes
must be used. In medical research, these common
attributes (often referred to as quasi-identifiers) are
typically names, dates of birth, addresses etc. They
are usually neither stable over time nor available for
all cases, and could be recorded with errors in many
cases. Finally, quasi-identifiers such as names are
widely considered as sensitive information, the leak-
age of which would violate data privacy regulations.
Over the last decade, many different PPRL meth-
ods have been suggested that are usually divided into
two categories: perturbation and secure multiparty
computation (SMC) based techniques (Vatsalan et al.,
2013). Perturbation-based techniques are generally
efficient; they provide adequate linkage quality and
are scalable to link large databases but lack privacy
protection proofs. SMC based techniques, although
provably secure and accurate, generally have high
computation and communication costs. Therefore,
the former is better suited for real-world applications.
One popular perturbation based technique is based
on Bloom filter (BF) encoding. In the context of
PPRL, (Schnell et al., 2009) initially suggested gen-
erating one BF per attribute, allowing multiple simi-
larities to be calculated if several attributes are used
to compare records. This approach is now usually
denoted as Attribute Bloom Filters (ABFs). Since
ABFs are susceptible to frequency-based privacy at-
tacks (Niedermeyer et al., 2014), encoding multiple
attribute values from a record into one single BF us-
ing an OR operation on separate BFs for each at-
tribute has been suggested under the label Crypto-
graphic Long term Key (CLK) (Schnell et al., 2011)
encoding. Record level Bloom filter (RBF) encoding
(Durham et al., 2014), as an alternative to CLK, also
encodes values from several attributes into one BF per
record. Different from CLK, RBF uses a weighted bit
sampling process to generate record level BFs.
1.1 Related Work
BF based PPRL is now being used in a variety of
real-world applications (Boyd et al., 2015; Antoni and
Schnell, 2019). However, research (Kuzu et al., 2011;
Niedermeyer et al., 2014; Christen et al., 2019; Chris-
ten et al., 2018; Vidanage et al., 2020) has shown that
BF based PPRL can be vulnerable to cryptanalysis at-
tacks aiming to re-identify some sensitive values in
Chen, Y., Schnell, R., Armknecht, F. and Heng, Y.
Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques.
DOI: 10.5220/0010787200003123
In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 5: HEALTHINF, pages 353-360
ISBN: 978-989-758-552-4; ISSN: 2184-4305
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
353

plaintext. Among the existing attacks, recently pro-
posed pattern mining attack (Christen et al., 2018)
and graph-matching attack (Vidanage et al., 2020) are
considered to be the most powerful since they could
provide more accurate re-identifications and they are
computationally efficient.
In response to earlier attacks, various BF harden-
ing techniques have been proposed, including balanc-
ing, salting, XOR-folding and so on (Christen et al.,
2020). In general, there is a trade-off between the
level of privacy and the linkage quality obtained when
using these techniques because hardened BFs likely
result in distorted similarities compared to plaintext
similarities (Christen et al., 2020; Franke et al., 2021).
As is remarked by (Christen et al., 2020), so far, for no
hardening technique, a proper proof of security exists.
Nevertheless, given the state of cryptanalysis attack
methods, salting seems to be one of the most promis-
ing. (Christen et al., 2020) recommended using salted
BF for PPRL if a stable salt could be extracted from
the available quasi-identifiers.
1.2 Our Contribution
In this paper, we evaluate the resilience of salted BF
against the two most advanced attack methods: pat-
tern mining and graph-matching. These attacks are
so far considered to be the most powerful attacks on
PPRL techniques. Therefore, investigating the limi-
tations of the attacks and their potential countermea-
sures are important for PPRL applications in practice.
To the best of our knowledge, this paper is the first
study on how different salt choices modify the fre-
quency distribution of the q-grams in the records and
the neighbourhood of the records in a dataset. Our re-
sults on investigating why salting is effective against
the pattern mining attack and how salting impacts the
performance of the graph matching attack is new. Fi-
nally, we provide additional evidence that the success
of both attacks depends critically on the data available
to the attacker.
2 PRELIMINARIES
2.1 Bloom Filter Encoding
BFs were developed to test whether an element is a
member of a certain set (Bloom, 1970). Formally, a
BF can be defined as follows.
Definition 1 (BF encoding). A Bloom filter bf con-
sists of an array of n bits, bf[0] to bf[n − 1], ini-
tially all set to 0. It uses k independent random hash
functions h
1
,··· , h
k
with range [0,··· ,n − 1]. Denote
H = {h
1
,··· , h
k
}. To store a set X = {x
1
,...,x
|X |
} in
the Bloom filter, for x ∈ X , the bits at positions h
j
(x)
in bf are set to 1, for 1 ≤ j ≤ k. Formally, we have
bf : X → {0, 1}
n
, where
bf[i] =
1, if ∃ x ∈ X ,h ∈ H s.t. h(x) = i;
0, else.
A Bloom filter based PPRL uses a BF to repre-
sent the set of q-grams generated from one or more
attribute values from each record that needs to be en-
coded. A q-gram is a sub-string of length q charac-
ters extracted from a string using a sliding window
approach. For instance, when using q = 2 (known as
bigrams), the string “bloom” is converted into the set
of bigrams: {bl,lo, oo, om}. Using BF encoding, each
bigram in the set {bl, lo,oo,om} is mapped to a set of
bit positions which are set to 1 in the resulting BF.
2.2 BF Encoding with Salting
In the PPRL literature, salting has been proposed as a
hardening technique in (Niedermeyer et al., 2014) to
incapacitate re-identification attacks on Bloom filters
by adding an extra string value to each q-gram be-
fore it is hashed. That is, instead of hashing q-grams,
salted q-grams are hashed.
As suggested in (Niedermeyer et al., 2014), for
PPRL, the salt values should be record-specific and
do not contain any errors (so preferably do not change
over time). In our application here we choose the fol-
lowing salts:
• the year of birth, or the full date of birth,
• the 2nd, 3rd letters of the first name, and if a first
name has less than 3 letters, pad it with ’2’,
• the 2nd, 3rd, 5th letters of the last name, and if the
last name has less than 5 letters, pad it with ’2’.
These salt choices are inspired by the Statistical
Linkage Key (often denoted as ’581’) used by the
Australian Institute of Health and Welfare (for de-
tails, see (Christen et al., 2020)). For simplicity,
we use ’salt-FN’, ’salt-LN’, ’salt-YOB’ to denote
the record-specific salt extracted from the first name
(FN), last name (LN) and year of birth (YOB) as de-
scribed above, respectively; and ’salt-FN+LN+YOB’
(or ”salt-All” for simplicity) be their concatenation.
2.3 Information and Statistical
Measures for a Distribution
As pointed out in (Christen et al., 2020), exploiting
frequency information is the main approach for many
HEALTHINF 2022 - 15th International Conference on Health Informatics
354

cryptanalysis attacks on PPRL based on BF encoding.
So a good hardening technique aims to reduce the fre-
quency information to the minimum. Ideally, the fre-
quency distribution of interest should be as close as
possible to be uniform, since this distribution gives
no specific information to an attacker. Here we re-
call some suitable measures of the deviation from the
uniform distribution.
2.3.1 Information Measures for a Distribution
Given a random variable W, we denote its probability
at W = w to be Pr{W = w}. Then the entropy H(W )
is defined by
H(W ) = −
∑
w
Pr{W = w}log
2
Pr{W = w}. (1)
The predictability of W is defined by max
w
Pr{W =
w} (i.e., the probability of the most likely case). Cor-
respondingly, the min-entropy H
∞
(W ) is
H
∞
(W ) = − log
2
(max
w
Pr{W = w}), (2)
that can be interpreted as the ”worst-case” entropy.
2.3.2 Distance Measures of Distributions
A method of measuring the distance between two
probability distributions is the Jensen-Shannon (JS)
divergence. In general, for two distributions P and Q,
their JS divergence D
JS
(P||Q) is defined by
D
JS
(P||Q) =
1
2
D
KL
(P||M) +
1
2
D
KL
(Q||M), (3)
where M = (P + Q)/2; and D
KL
(P||M) is the
Kullback-Leibler (KL) divergence:
D
KL
(P||M) =
∑
x
P(x)log
2
P(x)
M(x)
. (4)
2.3.3 Measures of Distributional Discrepancy
The inequality among values of a frequency distribu-
tion can be measured by its Gini coefficient. Let x
i
be
the frequency of label i, and there are n labels, then
the Gini coefficient G is given by:
G =
1
2n
2
¯x
n
∑
i=1
n
∑
j=1
|x
i
− x
j
|, (5)
where ¯x is the mean of the frequency distribution. A
Gini coefficient of 0 expresses perfect equality, while
a Gini coefficient of 1 expresses maximal inequality.
3 IMPACT OF SALTING ON THE
FREQUENCY DISTRIBUTION
Recall that in PPRL based on BF encoding, each
record string is first converted into a set of q-grams,
which is then mapped to a BF. If salting is applied, an
additional step prior to the BF encoding is to attach
the salt value to each q-gram before it is hashed. Let
X be the random variable (r.v.) of the q-gram; S be the
r.v. of the salt; X k S be the r.v. of the salted q-gram.
We have the following theorems, those proofs can
be obtained by applying basic inequalities in informa-
tion theory (Cover and Thomas, 2006).
Theorem 2. Sating increases the min-entropy, i.e.,
H
∞
(X) ≤ H
∞
(X kS).
Theorem 3. Sating increases the entropy, i.e.,
H(X) ≤ H(X k S) ≤ H(X) + H(S).
Theorem 2 and Theorem 3 show that salting in-
creases the min-entropy and the entropy of the ran-
dom variable applied; and the increase on the entropy
is upper bounded by the entropy of the salt. By def-
inition, min-entropy reflects the difficulty for a suc-
cessful guess of the random variable’s most probable
value, whilst entropy reflects the average difficulty for
a successful guess.
As an example, we consider X to be the random
variable of the q-gram in the attributes: FN, LN and
YOB, S be the random variable of ’salt-YOB’. As one
can see from Table 1, we have H(S) = 6.519. Ap-
plying ’salt-YOB’, we see from Table 2 that without
salting H
∞
(X) = 3.853 and H(X ) = 7.654; while with
salting H
∞
(X k S) = 9.366 and H(X k S) = 13.273.
Salting with ’salt-YOB’ leads to a min-entropy in-
crease by 5.513 and an entropy increase by 5.619 (up-
per bounded by the entropy of the salt, 6.519).
4 EXPERIMENTAL SETUP
4.1 Datasets
To evaluate the effectiveness of the salting technique
in enhancing the privacy against known attacks on
PPRL, we use for the experiments two public avail-
able synthetic training dataset (’census’, ’prd’) pro-
duced by the European Statistical Agency (Eurostat).
1
The datasets include about 25000 records containing
names, addresses, dates of birth, and gender etc.
1
Available at https://ec.europa.eu/eurostat/cros/content/
job-training en.
Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques
355

Table 1: Eurostat ’census’: Statistical summaries of salt-FN, salt-LN, salt-YOB and salt-ALL.
salt-FN salt-LN salt-YOB salt-All
Total number 261 427 104 24706
Entropy 6.626 6.862 6.519 14.578
Min-entropy 4.593 4.426 5.774 12.629
JS divergence 0.339 0.447 0.050 0.003
Gini coefficient 0.718 0.773 0.264 0.025
Table 2: Eurostat ’census’: (concatenated) FN, LN and YOB, their bigrams, and the four variants of salted bigrams.
FN,LN,YOB bigrams salt-FN salt-LN salt-YOB salt-All
Total number 25225 585 36333 38682 27999 299595
Entropy 14.620 7.654 13.137 12.990 13.273 18.182
Min-entropy 13.629 3.853 8.185 8.018 9.366 16.221
JS divergence 0.00057 0.339 0.349 0.366 0.278 0.0024
Gini coefficient 0.0046 0.720 0.733 0.741 0.666 0.019
4.2 Parameter Setup
The attributes under consideration for the generation
of salts include FN, LN and YOB. The resulting salts
are denoted as ’salt-FN’, ’salt-LN’, ’salt-YOB’ and
’salt-All’.
For BF encoding, we use the parameter settings:
q = 2,l = 1000, and k = 15, where q = 2 indicates that
bigrams are used in the BF encoding, l is the length of
the Bloom filter, and k is the number of hashing func-
tions. Note that BFs were encoded using the CLK
approach (Schnell et al., 2011) with random hashing
(Niedermeyer et al., 2014). These are parameters cur-
rently recommended or widely used in the literature
(Christen et al., 2020).
5 SALTING DIVERSIFIES THE
FREQUENCY DISTRIBUTION
The statistical summaries of different salt choices are
shown in Table 1. Among the single salt choices ’salt-
LN’ has the largest entropy; while ’salt-YOB’ has
the lowest JS divergence to the uniform distribution
and the smallest Gini coefficien, However, overall the
combination ’salt-ALL’ yields the smallest JS diver-
gence to the uniform distribution, the smallest Gini
coefficient and has the largest entropy. It is almost
unique for each record (24706 values of ’salt-All’ for
25343 entities).
Since a potential non-uniformity of the frequency
distribution of (salted) q-grams could be exploited by
an attacker (Christen et al., 2018), a comparison of
the frequency distributions of salted and unsalted q-
grams is of special interest here.
Using the three concatenated attributes FN, LN
and YOB as an example, the descriptive statistics of
the salted and unsalted bigram distributions are shown
in Table 2. Among the possible salt choices using a
single salt, the frequency distribution of the salted q-
grams using ’salt-YOB’ as salt is closest to the uni-
form distribution since its JS divergence and Gini co-
efficient are smallest, and its min-entropy is largest.
Nevertheless, the frequency distribution of the
salted q-grams with ’salt-ALL’ yields the best unifor-
mity among the considered salt variants, in terms of
both the JS divergence and Gini coefficient. In ad-
dition, its entropy and min-entropy increase are also
the largest. Consequently it would serve as the best
choice if it is stable for entities across datasets. How-
ever, in general, ’salt-ALL’ could be much less stable
since any error in ’salt-FN’, ’salt-LN’ or ’salt-YOB’
would remain in ’salt-ALL’, that might cause degra-
dation on the linkage quality.
6 SALTING AFFECTS LINKAGE
QUALITY
For the evaluation of linkage quality, we use samples
of n = 10000 records each of the Eurostat datasets
’census’ and ’prd’ with at least 90% of the records be-
ing true matches. In this section, ’salt-YOB’ is used
in the experiments. To assess linkage quality, we use
precision, recall, and the F-measure. To account for
the recent critique of the F-measure by (Hand and
Christen, 2017), we also use the mean of precision
and recall (MPR) as an alternative univariate measure
for the linkage quality.
The linkage quality (measured by MPR) as a func-
tion of a similarity threshold is shown in Fig. 1 (left).
Four different choices of the number of attributes and
the kind of salting are shown. We observe:
HEALTHINF 2022 - 15th International Conference on Health Informatics
356
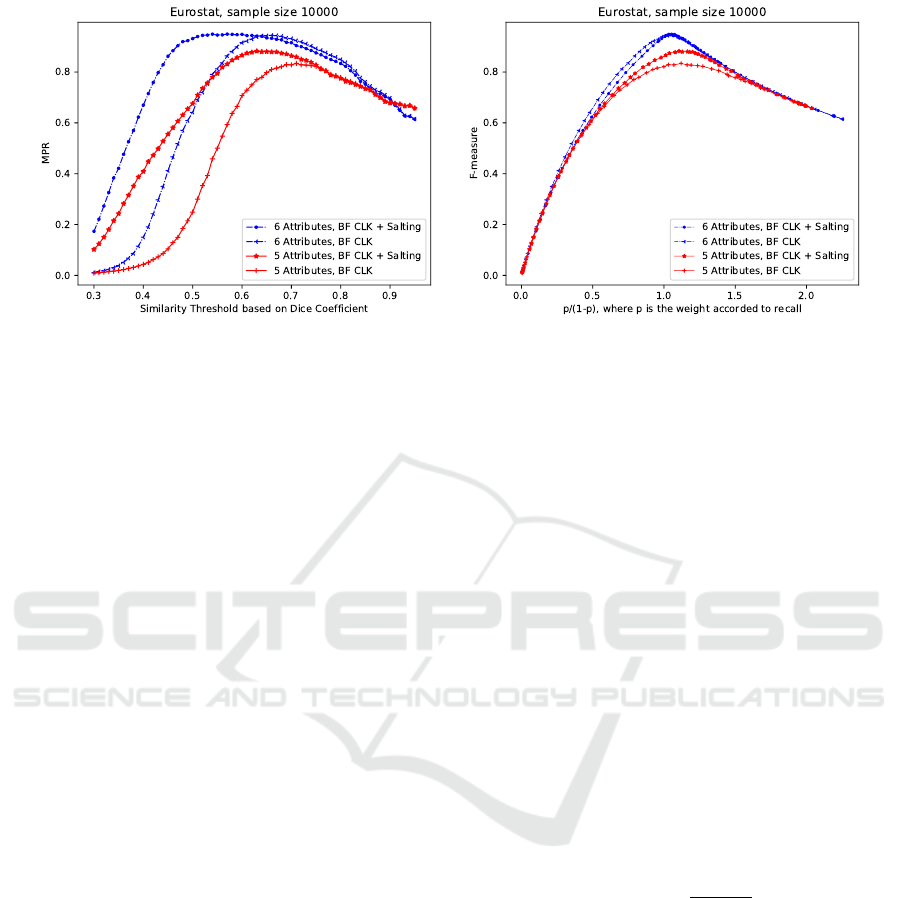
Figure 1: Linkage quality after different saltings (MPR left, F-measure right).
• For lower levels of similarity, salted BF might
yield higher MPR, indicating better linkage qual-
ity. This fact is caused by the propagation of dif-
ferences of salt values to other attribute values,
which could eliminate some false positives.
• Salting yields higher maximum MPR. Errors in
salt values may cause a slight decrease in linkage
quality at high thresholds, since some unwanted
false negatives may occur. However, this degra-
dation diminishes as the threshold increases until
the high threshold becomes the main cause of the
most false negatives.
The stability of the salt could be evaluated by
Pr{salt
a
= salt
b
|(record
a
,record
b
) is a match}. (6)
To obtain high linkage quality, a salt should be chosen
with high stability. For the sampled Eurostat datasets
in our experiments, the mean stability for salt-YOB
is 94.69% on average (with a standard derivation of
0.24%). The other salts show lower stabilities (salt-
FN: 84.68%, salt-LN: 84.86%, salt-ALL: 69.90%).
The plot in Fig. 1 (right) shows the effect of
salting on the F-measure of linkage quality. The x-
axis in the plot is the range of p/(1 − p), where p
and (1 − p) are the weights given to recall and pre-
cision, respectively, when interpreting F-measure as a
weighted arithmetic mean (Hand and Christen, 2017).
Salting results in higher F-values when a high weight
p is given to recall. Furthermore, the gain by salting
seems to be larger if fewer attributes are used.
7 SALTING IMPROVES PRIVACY
In this section, we assess the salting technique
with regard to the privacy protection it provides,
by demonstrating its resilience to the two most ad-
vanced attack methods: pattern mining (PM) and
graph matching (GM).
Before we proceed, we note that both attacks have
the following assumptions:
• The attacker has access to an encoded database E,
which contains sensitive data of people encoded
using a PPRL method such as BF encoding.
• The attacker has access to a plaintext database
P, which can be a publicly available population
database such as a telephone directory.
• The attacker does know or can guess the quasi-
identifying attributes that were encoded in E.
The goal of the attacker is to correctly re-identify as
many as possible the encoded records in plaintext.
Suppose that the encoded dataset E has n
E
en-
coded records, and the plaintext dataset P has n
P
records, where n
M
records are true matches between
them. Then the overlap rate between the plain and
encoded dataset can be defined by
r
overlap
=
2n
M
n
E
+ n
P
. (7)
Further, we assume that the attacker is aware of
whether salting is employed, and if yes, what kind of
salt value is applied.
7.1 Pattern Mining Attack
The pattern mining attack was proposed in (Chris-
ten et al., 2018). The codes using Python 2.7 in
Ubuntu 16.04 are made available by the authors at
https://dmm.anu.edu.au/pprlattack/.
The attack is based on the assumption that the dis-
tribution of the q-grams in the plaintext database P
provides a good approximation of the distribution of
Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques
357

Table 3: Results of PM Attack (Overlap 100%).
Attributes hardening
identified correct correctly identified # identical
q-grams bit-positions 1-to-1 record matches attributes values
FN
None 33/438 470/485 1822/1967
2169
salt-FN 5/4272 74/74 0
FN, LN
None 76/485 1093/1132 4609/4993
19026salt-FN 5/26189 72/73 0
salt-LN 3/27532 43/48 0
FN, LN, YOB
None 43/585 604/623 2906/3089
salt-FN 6/36333 87/87 0
salt-LN 5/38682 57/80 0 25225
salt-YOB 0/27999 0 0
salt-ALL 0/299595 0 0
Table 4: Results of PM Attack (Overlap 96%).
Attributes hardening
identified correct correctly identified # unique # identical
q-grams bit-positions 1-to-1 record matches attributes values attributes values
FN
None 8/432 102/103 294/294 2127(E)
1535
salt-FN 5/4212 74/74 0 2169(P)
FN, LN
None 73/483 985/1083 2089/2634 18629(E)
10701salt-FN 5/25900 72/72 0
salt-LN 3/27246 43/48 0 19026(P)
FN, LN, YOB
None 42/583 565/610 983/1625
12395
salt-FN 6/36021 86/88 0 24647(E)
salt-LN 5/38171 57/80 0
salt-YOB 0/27859 0 0 25225(P)
salt-ALL 0/293281 0 0
the q-grams in the corresponding plaintext of E. Espe-
cially, those frequent q-grams should have sufficiently
different frequencies so that they could be perfectly
aligned. Basically, the pattern mining technique ex-
ploits the non-uniformity and the inequality of the fre-
quencies in the frequency distribution of the q-grams.
For the evaluation of the attack performance, we
assess both the quality of re-identified q-grams and
the quality of re-identified records. In particular, we
consider the number of identified q-grams (over all
possible q-grams) and the accuracy of identified q-
grams for the former; and the number of identified 1-
to-1 record matches and how many were indeed true
matches for the latter.
As first example, we consider a case where an at-
tacker has access to a BF encoded database E and the
same dataset in plaintext P. Therefore, their overlap
rate is 100%. For the example, we use the ’census’
dataset. Table 3 shows the results for the pattern min-
ing attack, where different choices of attributes for a
record are considered. Using attribute FN as an ex-
ample, we observe:
• Without salting, the attacker could re-identify 33
out of 438 q-grams, which could lead to 1822 cor-
rect record matches out of 1967 identified 1-to-1
record matches. Since there are in total 2169 1-
to-1 true record matches, the accuracy of the re-
identification of the correspondence of the record
in plaintext and the encoded record is high.
• With salting (using ’salt-FN’), the total number of
q-grams is increased to 4272, out of which the
attacker could re-identify the bit positions for 5
salted q-grams. However, these are not sufficient
to identify any 1-to-1 record matches.
Moreover, as the number of attributes used for link-
age increases, the number of the salted q-grams be-
comes larger (salting increases the entropy). At the
same time, fewer (salted) q-grams will be identi-
fied than without salting (salting increases the min-
entropy). Therefore, salting is an effective counter-
measure against the pattern mining attack.
As a second example, we consider a high overlap
between the encoded dataset E and plaintext P. With
the example datasets ’prd’ as E and ’census’ as P we
observe an overlap of ≈ 96.2%. Table 4 shows the
results of the pattern mining attack. In this case, with-
out salting, the performance of the attack drops sub-
stantially compared to the previous case with com-
plete overlap between P and E. Furthermore, salt-
ing proves to be an effective countermeasure against
a pattern mining attack since it reduces the number of
identified q-grams considerably.
HEALTHINF 2022 - 15th International Conference on Health Informatics
358

Table 5: Eurostat: Results of GM Attack (Overlap 100%).
Sample size hardening
(# correct re-id, # wrong re-id)
max F-measure
max # correct re-id min # wrong re-id
1000
None (967, 6) (897, 0) 98.02%
Salt-FN (527, 147) (227, 33) 62.96%
Salt-LN (718, 78) (1, 0) 79.95%
Salt-YOB (299, 219) (22, 0) 39.39%
5000
None (4878, 0) (4878, 0) 98.76%
Salt-FN (4126, 235) (1036, 0) 88.18%
Salt-LN (4464, 123) (1, 0) 93.13%
Salt-YOB (3823, 502) (454, 0) 82.18%
Salt-ALL (5, 39) (2, 9) 0.20%
10000
None [9499, 2] [9494, 0] 97.42%
Salt-FN (8601, 290) (1, 0) 91.06%
Salt-LN (8874, 237) (1, 0) 93.17%
Salt-YOB (8737, 348) (639, 0) 91.56%
Salt-ALL (21, 130) (5, 2) 0.41%
Table 6: Eurostat: Results of GM Attack (Overlap > 80%).
Sample size hardening
(# correct re-id, # wrong re-id)
max F-measure
max # correct re-id min # wrong re-id
None (28, 729) (4, 35) 4.02%
1000 salt-FN (22, 406) (3, 31) 3.50%
r
overlap
= 83% salt-LN (14, 507) (4, 82) 2.07%
salt-YOB (14, 398) (3, 25) 2.25%
None (32, 1150) (6, 422) 2.44%
5000 salt-FN (88, 2656) (1, 0) 2.49%
r
overlap
= 86.66% salt-LN (97, 3159) (8, 378) 2.95%
salt-YOB (61, 3867) (1, 0) 1.55%
salt-ALL (2, 36) (2, 36) 0.09%
None (122, 7210) (15, 1846) 1.77%
10000 salt-FN (171, 5980) (10, 677) 2.34%
r
overlap
= 93.17% salt-LN (133, 5162) (63, 1856) 1.85%
salt-YOB (99, 6935) (12, 156) 1.21%
salt-ALL (7, 119) (1, 0) 0.15%
7.2 Graph Matching Attack
A very different type of attack from pattern mining is
graph-based, which was first discussed by Culnane et
al. (Culnane et al., 2017) on a PPRL method based on
a keyed-hash message authentication code (HMAC)
and similarity tables, and further extended by (Vidan-
age et al., 2020), who considered several PPRL en-
coding methods including BF encoding.
The basic idea behind the graph matching attack
is that given the two databases that are from the same
domain, their graph representations will contain sim-
ilar neighborhoods for nodes that represent the same
value (plaintext or encoded corresponding to one or
more entities) across the two databases. To evaluate
the performance of the attack, we consider the num-
ber of correct record re-identifications, the number of
wrong record re-identifications, and the F-measure of
the record re-identification. In the Tables 5 and 6 we
report the following statistics: 1) the maximum num-
ber of correct re-identifications followed by the least
number of wrong re-identifications, 2) the least num-
ber of wrong re-identifications followed by the maxi-
mum number of correct re-identifications, and 3) the
maximum F-measure of the record re-identification.
The graph similarity attack was initially imple-
mented on a large server (Xeon 2.1 GHz 16-Core
CPUs, 512 GBytes of memory) by (Vidanage et al.,
2020) using Python 2.7. Their code is available at
https://dmm.anu.edu.au/pprlattack/. For our simula-
tions, we randomly sampled records from the ’census’
dataset, resulting in samples of n = 1000,5000,10000
(to circumvent memory problems on a PC). As at-
tributes, we considered FN, LN and YOB.
Salting as a Countermeasure against Attacks on Privacy Preserving Record Linkage Techniques
359

First we consider the case where the attacker has
access to a BF encoded database E and the same
dataset in plaintext P. Clearly their overlap rate is
100%. Table 5 shows results for the graph matching
attack in this scenario. It is apparent that
• without salting, the attacker could re-identify
records with a maximum F-measure approaching
or exceeding 98%;
• With salting, the performance of the attacks drops,
regardless which measure is used for comparison.
Interestingly, this drop decreases with increasing
sample size.
However, a stable salt value, almost unique for each
record, could effectively thwart the graph-matching
attack. Salt-ALL reduced the maximum F-measure
of the re-identification from over 97% to below 0.5%.
Among the other salt variants, salt-YOB performs
best, especially for smaller samples.
As second example, we consider a case where
r
overlap
6= 100% but r
overlap
> 80%. Table 6 shows the
importance of the overlap rate for the success of the
graph matching attack. Given an overlap rate above
80%, both the maximum number of correct record
re-identifications and the maximum F-measure drops
strongly compared to the previous example given per-
fect overlap. For example, the maximum F-measure
drops from above 98% to about 1% ∼ 4%.
8 CONCLUSION
We studied the effect of salting on the resilience
against pattern mining and graph matching attacks in
PPRL. Salting was shown to be an effective counter-
measure against pattern mining attacks while less ef-
fective against graph matching attacks (unless a sta-
ble salt that is almost unique to each record value is
available). As an additional safeguard, salting is rec-
ommended for perturbation-based PPRL whenever a
stable salt is available.
REFERENCES
Antoni, M. and Schnell, R. (2019). The past, present
and future of the German Record Linkage Cen-
ter (GRLC). Jahrb
¨
ucher f
¨
ur National
¨
okonomie und
Statistik, 239(2):319 – 331.
Bloom, B. H. (1970). Space/time trade-offs in hash coding
with allowable errors. Communications of the ACM,
13:422–426.
Boyd, J., Randall, S., and Ferrante, A. (2015). Application
of privacy preserving techniques in operational record
linkage centres. In Medical Data Privacy Handbook,
pages 267–287. Springer, Netherlands.
Christen, P., Ranbaduge, T., and Schnell, R. (2020). Linking
Sensitive Data. Methods and Techniques for Practical
Privacy-Preserving Information Sharing. Springer,
Cham, Switzerland.
Christen, P., Ranbaduge, T., Vatsalan, D., and Schnell, R.
(2019). Precise and fast cryptanalysis for Bloom fil-
ter based privacy-preserving record linkage. IEEE
Transactions on Knowledge and Data Engineering,
31(11):2164–2177.
Christen, P., Vidanage, A., Ranbaduge, T., and Schnell, R.
(2018). Pattern-mining based cryptanalysis of Bloom
filters for privacy-preserving record linkage. In Ad-
vances in Knowledge Discovery and Data Mining,
pages 530–542, Cham. Springer Int. Publishing.
Cover, T. M. and Thomas, J. A. (2006). Elements of Infor-
mation Theory. Wiley-Interscience, USA.
Culnane, C., Rubinstein, B. I. P., and Teague, V. (2017).
Vulnerabilities in the use of similarity tables in com-
bination with pseudonymisation to preserve data pri-
vacy in the UK Office for National Statistics’ privacy-
preserving record linkage. CoRR, abs/1712.00871.
Durham, E. A., Kantarcioglu, M., Xue, Y., Toth, C., Kuzu,
M., and Malin, B. (2014). Composite Bloom filters for
secure record linkage. IEEE Transactions on Knowl-
edge and Data Engineering, 26(12):2956–2968.
Franke, M., Sehili, Z., Rohde, F., and Rahm, E. (2021).
Evaluation of hardening techniques for privacy-
preserving record linkage. In Proceedings of the
24th International Conference on Extending Database
Technology, EDBT 2021, Nicosia, Cyprus, March 23 -
26, 2021, pages 289–300. OpenProceedings.org.
Hand, D. and Christen, P. (2017). A note on using the
F-measure for evaluating record linkage algorithms.
Statistics and Computing, 28:539–547.
Kuzu, M., Kantarcioglu, M., Durham, E., and Malin, B.
(2011). A constraint satisfaction cryptanalysis of
Bloom filters in private record linkage. In Privacy En-
hancing Technologies 11th International Symposium,
PETS 2011 Waterloo, ON, Canada, July 27-29, 2011,
volume 6794, pages 226–245, Heidelberg. Springer.
Niedermeyer, F., Steinmetzer, S., Kroll, M., and Schnell, R.
(2014). Cryptanalysis of basic Bloom filters used for
privacy preserving record linkage. Journal of Privacy
and Confidentiality, 6(2):59–69.
Schnell, R., Bachteler, T., and Reiher, J. (2009). Privacy-
preserving Record Linkage Using Bloom filters. BMC
Medical Informatics & Decision Making, 9:41.
Schnell, R., Bachteler, T., and Reiher, J. (2011). A
novel error-tolerant anonymous linking code. Work-
ing Paper WP-GRLC-2011-02, German Record Link-
age Center, Duisburg.
Vatsalan, D., Christen, P., and Verykios, V. S. (2013). A
taxonomy of privacy-preserving record linkage tech-
niques. Information Systems, 38(6):946–969.
Vidanage, A., Christen, P., Ranbaduge, T., and Schnell,
R. (2020). A graph matching attack on privacy-
preserving record linkage. In CIKM ’20: The 29th
ACM International Conference on Information and
Knowledge Management, Virtual Event, Ireland, Oc-
tober 19-23, 2020, pages 1485–1494. ACM.
HEALTHINF 2022 - 15th International Conference on Health Informatics
360
