12-Lead ECG Reconstruction via Combinatoric Inclusion of Fewer

Standard ECG Leads with Implications for Lead Information and

Signiﬁcance

Utkars Jain

1 a

, Adam A. Butchy

1 b

, Michael T. Leasure

1 c

, Veronica A. Covalesky

2,3

Daniel Mccormick

2,3

and Gary S. Mintz

4 d

Heart Input Output Inc., 128 N. Craig Street, Suite 406, Pittsburgh, U.S.A.

Cardiology Consultants of Philadelphia, Philadelphia, Pennsylvania, U.S.A.

Jefferson University Hospital, Philadelphia, Pennsylvania, U.S.A.

The Cardiovascular Research Foundation, New York, U.S.A.

Keywords:

ECG, Limited Lead Systems, ECG Synthesis, ECG Reconstruction.

Abstract:

The electrocardiogram (ECG) is the most widely used, non-invasive, cardiovascular test. There exist many

lead variations including a one, three, six, and 12-lead device. In this work, we use ECGio, a validated

deep learning model for the assessment of coronary artery disease, to reconstruct ECG signals with various

combinations of leads, ranging from a single lead, to the full 12-leads. We are able to show 0.6536 R

, and

0.0747 mean absolute error (MAE) in the accurate reconstruction of a full 12-lead signal from just lead II.

We go one step further and look at which individual leads, and in what combinations, yield the most accurate

reconstructions as measured by R

and MAE. As you would expect, the larger the quantity of leads included,

the more accurate the reconstruction. Overall, the mean performance across all possible lead combinations

is 0.8335 R

, and 0.0538 MAE. This work opens the door for seeing if ECGio can handle systematic noise

injection and missing or misplaced leads.

1 INTRODUCTION

First introduced in the late 1800s, the electrocardio-

gram (ECG) is the most widely used, non-invasive,

cardiovascular test (AlGhatrif and Lindsay, 2012).

The ECG measures voltage generated in the heart as it

depolarizes and repolarizes by recording the potential

difference on the body’s surface. As it was adopted

clinically, ECG patterns were correlated with various

arrhythmias and cardiac conditions, often before the

underlying physiological mechanism was elucidated

(Yang et al., 2015). Currently, the ECG is an early-

stage diagnostic test, serving to identify and prelim-

inarily quantify myocardial infarctions (MI) (Mem-

bers et al., 2013), ischemia (Fihn et al., 2014), and

rhythm disorders such as atrial (January et al., 2014)

and ventricular tachycardias (Al-Khatib et al., 2018).

https://orcid.org/0000-0002-1800-0768

https://orcid.org/0000-0002-0096-0031

https://orcid.org/0000-0002-1488-712X

https://orcid.org/0000-0003-3296-8705

The most common ECG is a 12-lead although one,

three, and six lead devices are still in use. In the stan-

dard 12-lead ECG, there are ten different electrodes

(three limb and six chest leads and one electrode go-

ing to ground) that also generate three augmented

leads via linear combination of the limb and chest

leads. The names and are shown in Table 1. Besides

the number of leads, a multitude of lead placements

exist offering different trade-offs between lead place-

ment/number verse patient comfort and physicians’

ability to consistently and accurately place those ad-

ditional, nontraditional leads (Chou, 1986). The most

popular nontraditional lead placement conﬁgurations

include, but are not limited to, Frank’s Lead system

(Frank, 1956), and the four EASI electrode system

(Dower et al., 1988).

Additionally, devices such as the Holter Monitor,

Zio Patch

, AliveCor KardiaMoblie

, and Apple

iRhythm Technologies, Inc, San Francisco, Calif

AliveCor Inc, Mountain View, CA, USA

Jain, U., Butchy, A., Leasure, M., Covalesky, V., Mccormick, D. and Mintz, G.

12-Lead ECG Reconstruction via Combinatoric Inclusion of Fewer Standard ECG Leads with Implications for Lead Information and Signiﬁcance.

DOI: 10.5220/0010788600003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 4: BIOSIGNALS, pages 133-141

ISBN: 978-989-758-552-4; ISSN: 2184-4305

133

Table 1: The 12 leads, the location of the positive and nega-

tive electrodes, and which heart surface they are thought to

represent. “N” refers to neutral or electric ground.

Lead + Location - Location Surface

I Left Arm Right Arm Lateral

II Left Leg Right Arm Inferior

III Left Leg Left Arm Inferior

aVR Right Arm N None

aVL Left Arm N Lateral

aVF Left Leg N Inferior

Right side of sternum,

4th intercostal space

N Septum

Left side of sternum,

4th intercostal space

N Septum

V3 Between V2 & V4 N Anterior

Left midclavicular line,

5th intercostal place

N Anterior

V5 Left anterior axillary line N Lateral

V6 Left midaxillary line N Lateral

Watch

offer a varying number of leads and alterna-

tive lead placements, but still aim to capture signals

that are similar to the common 12-lead ECG.

Devices that employ fewer leads typically have

less chance of misplaced leads, but contain less infor-

mation. Thus, there are many methods and algorithms

to convert and/or reconstruct signals collected from

one device into another device (Finlay et al., 2007).

Until recently, the most common methods to re-

construct a 12-lead signal using fewer than the stan-

dard 12-leads was either linear regression (Trobec

and Toma

c, 2011) (Toma

c and Trobec, 2013a)

(Zhu et al., 2018) or through a principal component

analysis (Dawson et al., 2009) (Mann and Orglmeis-

ter, 2013). Within the last decade, there has been a

tremendous push in the ﬁeld of machine learning and

artiﬁcial intelligence to tackle this problem.

(Grande-Fidalgo et al., 2021) employed ANN to

reconstruct 12-lead ECG from a proprietary three-

lead device in 7 people. (Smith et al., 2021) created

a focus time-delay neural network (FTDNN) using 7

leads to derive the remaining 5 precordial leads (V1,

V3-V6). (Sohn et al., 2020a) created a long short-

term memory (LSTM) network to overcome the issue

of reduced horizontal components of the vector in the

electric signal obtained from the patch-type device at-

tached to the anterior chest.

For a more rigorous review of ECG reconstruc-

tion methods, please refer to (Trobec et al., 2018) and

(Toma

c and Trobec, 2013b). The assumption un-

derlying these attempts was that the information used

to make clinical decisions from a 12-lead ECG was

also present and extractable from a system with fewer

leads.

Heart Input Output, Inc. (DBA HEARTio) has

Apple Inc., Cupertino, CA, USA

developed a novel deep learning algorithm that re-

constructs a 12 lead ECG from missing leads. Our

algorithm, ECGio, was developed to screen patients

for coronary artery disease (CAD, the cause of most

rhythm disorders and acute events) and has been vali-

dated in 1,659 patients as veriﬁed by coronary angiog-

raphy (Leasure et al., 2021). This paper’s novel con-

tribution to lead reconstruction describes, ECGio’s

ability to take any number and/or combination of

leads and reconstruct an accurate representation of

the original 12-lead signal. For example, ECGio can

recreate a full 12-lead utilizing only Lead I and lead

aVR from a non-standard ECG recording device. In

addition, ECGio is not limited to only 12-lead recon-

struction, but can do a multitude of transformations

(i.e. 12 lead to 128 leads, etc.). As a deep learning

architecture, ECGio will continue to improve.

In this this paper. we demonstrate ECGio’s abil-

ity to accurately reconstruct a 12-lead ECG from a

single lead (any of the standard 12-leads). Next we

use combinations of leads to reconstruct the 12-lead

ECG. Finally, we look at ECGio’s ability to recon-

struct a 12-lead ECG and determine which leads were

most useful for faithful reconstruction

2 METHODS

2.1 Data Source

This is a study proof-of-concept study into the ability

of a deep learning model (ECGio) to reconstruct miss-

ing ECG information. There were 3 distinct experi-

ments done on 250 randomly selected patients from

PTB-XL, a large publicly available electrocardiogra-

phy dataset (Wagner et al., 2020). Only 250 patients

were used as a test set because of the high degree

of computation involved in the experiments although

other similar works have used fewer ECGs (Sohn

et al., 2020b). Overall, 1,023,750 different ECG in-

put combinations were constructed from the original

250 patients.

2.2 Data Standardization

We standardized the ECG signal in-put being sent

to the deep learning model. Each ECG signal was

clipped such that it represented one second of ECG

time and in the form N × M, where M was the number

of leads and N the number of samples. Since each sig-

nal was only one second in length, N was also equal

to the sampling rate. Using Fast Fourier Transform

(FFT), we resampled the signal to reduce the sam-

pling rate to 100Hz. To make sure only the infor-

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

134

mation within this band of frequencies was retained

while others were removed, we used a Bandpass But-

terworth ﬁlter with passband starting at 2Hz and ex-

tending to 40Hz.

The databased ECG signals were recorded in mil-

livolts (mV), with irregular maxima and minimum

values. To conform to best machine learning prac-

tices, we scaled each one second ECG segment to val-

ues between [-1. +1] using Equation 1 as is common

in deep learning to standardize input signals:

f (x) = 2

x − min(x)

max(x) − min(x)

− 1 (1)

where x represented an ECG array as recorded in

millivolts (mV), max(x) the maximum value along x,

and min(x) the minimum value along x. Any null val-

ues were converted to zeros. Eventually each signal

was detrended such that the isoelectric portions of the

ECG were equal to zero.

The 12-lead standardized data was the reference

when performance metrics were calculated. We did

not use raw voltage difference values as the reference

similar to Sohn et al., (Sohn et al., 2020b) to avoid

a large potential variance in the existence of muscle,

movement, or electric noise causing deviations from

signal to signal. Standardized signals would bring

a more fair comparison mathematically whereas a

straight comparison of performance metrics between

our results and others might not be prudent.

2.3 Experiments & Goals

There were three different experiments:

1. 1 Lead Reconstruction: Can ECGio use 1 lead

of ECG information to accurately and faithfully

reconstruct a 12 lead ECG? If so, which single

lead resulted in the highest performance?

2. Multi-lead Reconstruction: Can ECGio use dif-

ferent ECG lead combinations to accurately and

faithfully reconstruct a 12 lead ECG? If so, what

was the correlation between the number of leads

used as input and performance?

3. Lead Signiﬁcance: Did the inclusion or exclu-

sion of speciﬁc leads affect performance?

2.4 Performance Metrics

In all three experiments there were two key perfor-

mance metrics: mean absolute error (MAE) and the

Pearson correlation coefﬁcient (R

). For each of these

values, we calculated the mean (µ) and the standard

deviation (σ) similar to other studies. Furthermore,

these metrics were calculated easily and were easy to

interpret.

MAE was deﬁned as:

MAE(y, ˆy) =

∑

i=1

− ˆy

| (2)

where y is the ground truth and ˆy is the predicted

value. Each element of the 12-lead ECG array is used

for the purposes of this mean with no difference in

weighting among the leads.

is deﬁned as:

(y, ˆy) =

E[(y − µ

)( ˆy − µ

ˆy

)]

ˆy

(3)

where y is the ground truth and the ˆy is the predicted

value. Each element of the 12-lead ECG array is used

for the purposes of this mean with no difference in

weighting among the leads. E is used to indicate ex-

pectation, µ is the mean, and σ is the standard devia-

tion.

2.5 1 Lead Reconstruction

We used a previously-trained model of ECGio where

the input was an ECG in matrix format, and our out-

put of interest was an ECG in matrix format (Leasure

et al., 2021)). Although ECGio has many outputs, in

this paper only this reconstruction output was used.

As detailed in the methodology, the population of 250

ECGs from the PTB-XL database was standardized

before reconstruction. Each was inputted into ECGio

12 separate times, each time using a different single

lead of information while the remaining eleven leads

were masked to zero. Each time an ECG was inputted,

a unique lead index assured that each individual lead

was used once. After the input was propagated, the

reconstructed ECG was collected and stored.

2.6 Multi-lead Reconstruction

To determine the effect of lead number and signiﬁ-

cance, different leads were systematically included or

removed from the same 250 patient set. All possible

combinations of lead inclusion were explored for each

patient.

In this situation we let S = {1, 2, 3, ..., 11, 12}.

Let S

represent a set of all the combinations of S

with k length combinations. Then let A represent

the set that is the union of all the combinations, A =

, S

, ..., S

, S

}. Each set in A indicated

which leads in the input ECG should remain intact

and all others were masked to zero. Performance

statistics were averaged across each S

. In Table 2

combinations for each different S

and the total num-

ber of combinations done for the 250 ECG population

are shown.

12-Lead ECG Reconstruction via Combinatoric Inclusion of Fewer Standard ECG Leads with Implications for Lead Information and

Signiﬁcance

135

Table 2: All the possible lead combinations for just one pa-

tient’s ECG. The Total Combinations row results from mul-

tiplying the number of combinations for one ECG with the

total number of patients in the whole population (250).

# of Leads # of Combinations

1 12

2 66

3 220

4 495

5 792

6 924

7 792

8 495

9 220

10 66

11 12

12 1

Sum 4,095

Total Combinations 1,023,750

2.7 Lead Signiﬁcance

Based on the analyses performed above, we deter-

mined which leads, when included or excluded, lead

to a statistically signiﬁcant change in performance

by taking every combination c ∈ A and determining

which leads were included and which were excluded.

For example, if c

= {1, 2, 3}, then leads 1, 2, 3 were

included and the rest were excluded. When testing

the statistical signiﬁcance of lead 1, c

would be used

for the inclusion of lead 1, while any combination that

did not contain lead 1 would be excluded. It would be

the opposite scenario if it were leads 4-12.

This exercise was followed for every combination

in A until we had 24 subsets with each lead having

2 corresponding subsets indicating whether the lead

was or was not included. For each pair of subsets,

performance metrics were calculated and a p-value

calculated in order to determine if the difference be-

tween the distribution of the performance metrics was

statistically signiﬁcant.

3 RESULTS

3.1 1 Lead Reconstruction

The MAE and R

were calculated for each patient’s

ECG reconstruction using just one lead. These val-

ues were averaged across all 250 patients to obtain

Table 3: The MAE and R

mean and standard deviation

across the whole patient population of ECG reconstruction

from just one lead. The ﬁrst column includes which lead

was used for the reconstruction.

Lead MAE µ MAE σ R

µ R

I 0.0755 0.0238 0.6498 0.1914

II 0.0747 0.0274 0.6536 0.2172

III 0.0836 0.0280 0.6003 0.2215

aVR 0.0775 0.0280 0.6225 0.1986

aVL 0.0814 0.0279 0.6169 0.2105

aVF 0.0788 0.0270 0.6281 0.2020

V1 0.0834 0.0273 0.5734 0.2013

V2 0.0818 0.0258 0.5786 0.2117

V3 0.0792 0.0252 0.5952 0.1975

V4 0.0775 0.0248 0.6141 0.1971

V5 0.0757 0.0265 0.6317 0.2102

V6 0.0757 0.0261 0.6374 0.2026

Figure 1: The (A) MAE and (B) R

of all patients using a

particular lead. Outliers are shown as black diamonds.

the mean and standard deviations reported in Table 3.

To illustrate the spread in reconstruction ﬁdelity

within the population, Figure 1 shows two measures

of reconstruction ﬁdelity as box and whisker plots,

with outliers indicated as black diamonds.

We did not observe a huge deviation in reconstruc-

tion depending upon which lead was used. This points

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

136

to one lead including sufﬁcient information to recon-

struct a full 12-lead set. The mean best performance

was observed using lead II and the worst was with

lead III with a range of 0.0747 - 0.0836 for MAE,

and 0.6003 and 0.6536 for R

. Quite a few outliers

were observed and responsible for lowering the re-

construction ﬁdelity. The overall individual highest

performing ECG was with a MAE of 0.0321 and a R

of 0.964, with surprisingly only six leads selected for

input.

3.2 Multi-lead Reconstruction

In total, 1,023,750 different combinations were cre-

ated across all 250 patients. Reconstructions were

compared against the full, true patient 12-lead ECG

to calculate performance metrics. In Table 4, we re-

port the mean MAE and R

metrics of reconstruction

ﬁdelity, grouping the number of leads that went into

the reconstruction. To illustrate the spread in recon-

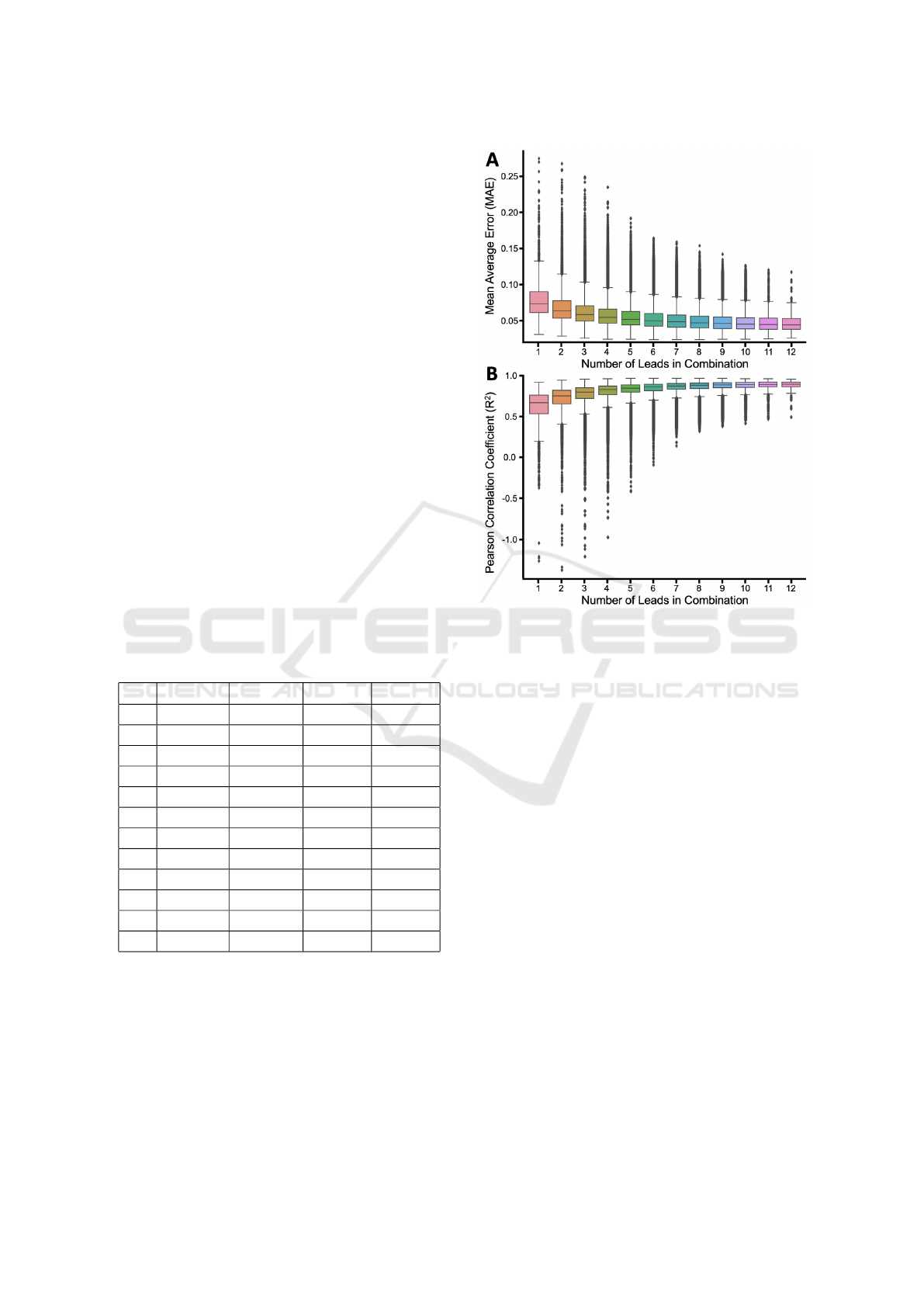
struction ﬁdelity based on the number of leads, Fig-

ure 2 shows two measures of reconstruction ﬁdelity

as box and whisker plots, with outliers indicated as

black diamonds.

Table 4: The MAE and R

mean and standard deviation

across the whole patient population for ECG reconstruc-

tions using different combinations of leads. For example,

in 2 leads, we report the performance of any reconstruction

that used any 2 lead combination for reconstruction.

# MAE µ MAE σ R

µ R

1 0.0787 0.0267 0.6168 0.2068

2 0.0684 0.0226 0.7127 0.1574

3 0.0623 0.0199 0.7662 0.1268

4 0.0582 0.0181 0.8005 0.1056

5 0.0552 0.0169 0.8243 0.0911

6 0.0529 0.0161 0.8415 0.0811

7 0.0512 0.0155 0.8539 0.0741

8 0.0499 0.0151 0.8629 0.0692

9 0.0490 0.0147 0.8694 0.0659

10 0.0483 0.0145 0.8743 0.0636

11 0.0477 0.0144 0.8779 0.0621

12 0.0474 0.0143 0.8806 0.0609

Overall and as expected, there was a consistent

increase in performance when more leads were in-

cluded. The best performing number of leads was

twelve and the worst performing was one with a range

of 0.0474 - 0.0787 for MAE, and 0.6168 - 0.8806 for

. There was also a decrease in the maximum nega-

tive range as more leads were inputted.

Figure 2: The (A) MAE and (B) R

of all patients using

a particular number of leads in combination. Outliers are

shown as black diamonds.

3.3 Lead Signiﬁcance

Finally, performance statistics were calculated for

various groups of leads depending on whether or not

the reconstruction used a speciﬁc lead or combina-

tion of leads. Table 5 reports the MAE and R

values

when speciﬁc leads were included and sent to EC-

Gio and when they were excluded. These groups in-

cluded reconstructions that used just one lead, up to

the full 12-leads, to identify which leads could sig-

niﬁcantly alter reconstruction ﬁdelity. P-values were

calculated by comparing the performance when the

lead was included against the performance of all re-

constructions when it was excluded. We calculated

p-values for both MAE and R

performance metrics,

and these values are reported in Table 6. Leads I, II,

III, aVL, aVF, V2, and V3 all had signiﬁcant differ-

ence (p-value <0.05) between reconstructions that in-

cluded these leads from those reconstructions that ex-

cluded these leads.

12-Lead ECG Reconstruction via Combinatoric Inclusion of Fewer Standard ECG Leads with Implications for Lead Information and

Signiﬁcance

137

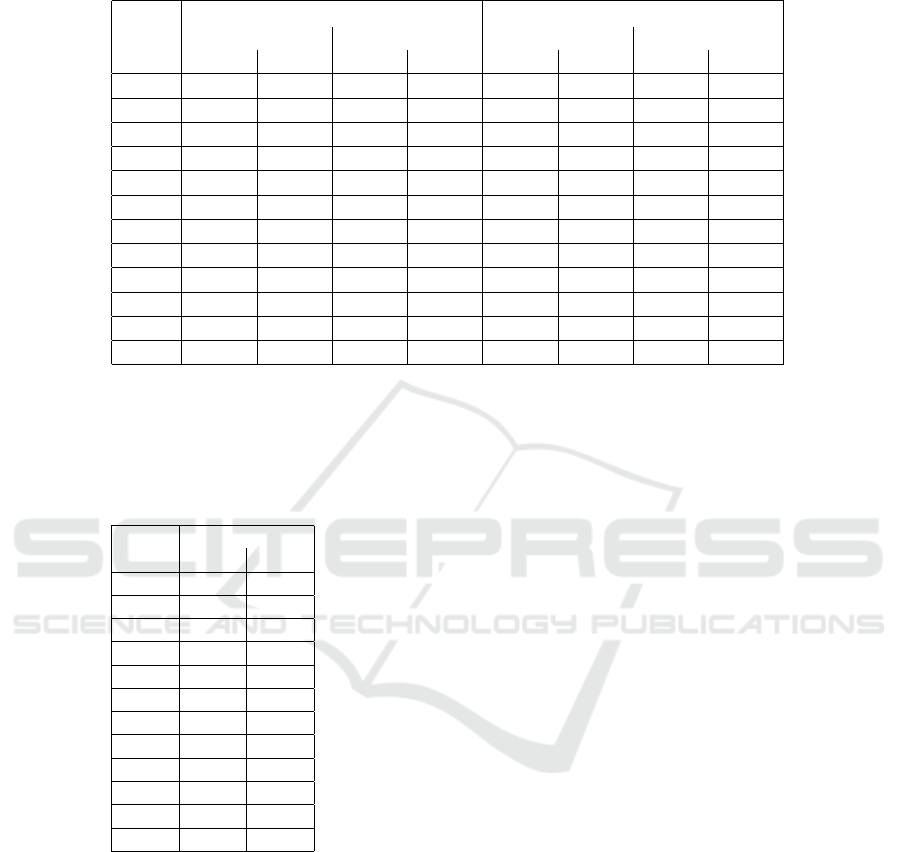
Table 5: The mean and standard deviations of performance statistics (MAE and R

) reported for all combinations of leads,

grouped based on which leads are included (with) and excluded (without). For example, the average MAE is reported for all

reconstructions that used Lead II in “With Lead” and all reconstructions that didn’t use Lead II in “Without Lead”.

Lead

MAE R

With Lead Without Lead With Lead Without Lead

µ σ µ σ µ σ µ σ

I 0.053 0.017 0.055 0.018 0.842 0.085 0.825 0.102

II 0.053 0.017 0.055 0.018 0.842 0.086 0.825 0.101

III 0.053 0.017 0.055 0.018 0.843 0.085 0.824 0.101

aVR 0.053 0.017 0.055 0.017 0.839 0.089 0.828 0.099

aVL 0.053 0.017 0.055 0.018 0.845 0.084 0.822 0.102

aVF 0.053 0.016 0.055 0.018 0.845 0.083 0.822 0.102

V1 0.053 0.017 0.055 0.018 0.841 0.086 0.826 0.100

V2 0.052 0.016 0.055 0.018 0.843 0.086 0.824 0.101

V3 0.052 0.016 0.055 0.018 0.844 0.086 0.823 0.100

V4 0.053 0.016 0.055 0.018 0.842 0.088 0.825 0.099

V5 0.053 0.016 0.055 0.018 0.840 0.089 0.827 0.099

V6 0.053 0.017 0.055 0.018 0.839 0.089 0.828 0.099

Table 6: Table reporting the p-values associated with the

level of signiﬁcance between the performance of the ECG

reconstructions that included (with) or excluded (without)

that particular lead. Both p-values are reported for MAE

and R

. Leads with R

p-values <0.05 are denoted with an

asterisk.

Lead

p-value

MAE R

I* 0.176 0.039

II* 0.157 0.049

III* 0.301 0.030

aVR 0.299 0.194

aVL* 0.159 0.008

aVF* 0.117 0.006

V1 0.136 0.062

V2* 0.050 0.018

V3* 0.041 0.009

V4 0.096 0.052

V5 0.163 0.111

V6 0.228 0.170

4 DISCUSSION

The purpose of this study was to determine whether

ECGio, a novel deep learning platform of HEARTio,

could reconstruct a full 12-lead ECG from one or

more leads. We used the mean absolute error (MAE)

and the Pearson correlation coefﬁcient (R

) which are

standard performance metrics to measure ECG recon-

struction ﬁdelity. Both measures were calculated by

comparing ECGio’s reconstruction to the normalized

ECG (as described in the methodology section). The

normalization process does remove the amplitude in-

formation from the signal, which can impact the phys-

iological importance of the ECG (i.e. certain condi-

tions where the deﬁnition is dependent on an ampli-

tude value). However, this doesn’t affect the many

pathologies where the qualitative features of the ECG

matter more than the amplitude.

An example of ECGio reconstruction is shown in

Figure 3, and demonstrates that complete correlation

may not be possible because some noise still exists

within the reference standard ECG and will not be

seen in the reconstruction. This can be illustrated

quantitatively, where despite there being a high visual

match between the original and reconstructed ECG,

the R

is not near 1. This noise is usually signal ar-

tifacts that result from issues with baseline recording

or our ﬁltering, and as signal noise in the middle of

the signal.

In the ﬁrst experiment we used only one lead of in-

formation to create a 12-lead ECG. This experiment

yielded moderate correlation between the reference

standard ECG and the reconstructed ECG. This level

of correlation might offer clinicians additional infor-

mation when dealing with limited technology (e.g. a

one-lead patch or even a one-lead smartwatch ECG).

Lead II performed best. A possible hypothesis was

that a limb lead was harder to recreate than a precor-

dial lead or that information from a limb lead can be

used to recreate precordial leads and not vise-versa.

It was also possible that this behavior was only extant

within this 250 ECG dataset and not in an extended

population.

In the second experiment, a higher level of recon-

struction was exhibited with more information pro-

vided within the input ECG. The correlation increased

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

138

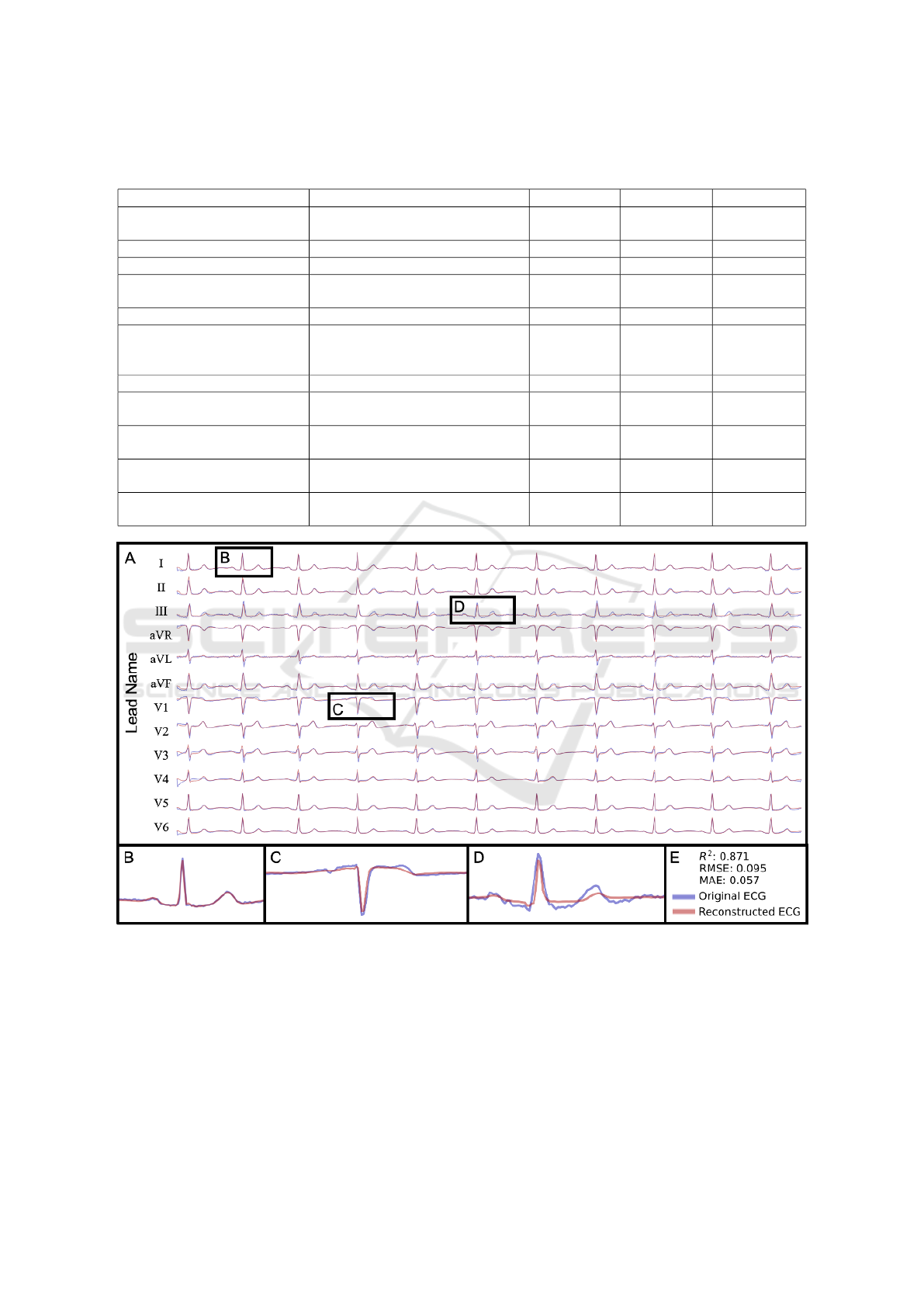
Table 7: This table showcases a sampling of other methods that are used in 12-lead ECG reconstruction. Note that the value

used for R

for this work is for the mean value for associated lead subset.

Ref Method Sample Size Lead Subset R

(Trobec and Toma

c, 2011) Linear Regression 65

2,3,4

lead subsets

0.954

(Zhu et al., 2018) Linear Regression 39 I, II, V2 0.947

(Dawson et al., 2009) Linear Afﬁne Transformation 448 3-lead VCG 0.819

(Mann and Orglmeister, 2013) Principal Component Analysis 24

6,9,11

lead subsets

0.950

(Grande-Fidalgo et al., 2021) Artiﬁcial Neural Network 7 3 leads 0.997

(Smith et al., 2021) Focus Time-Delay Neural Network 25

I, II, III

aVL, aVR

aVF, V2

0.861 - 0.968

(Sohn et al., 2020a) LSTM Network 60 3 lead patch 0.95

This Work

Multi-output Deep Learning Model

(ECGio)

250

Every

combination

0.835

This Work

Multi-output Deep Learning Model

(ECGio)

250 3 leads 0.762

This Work

Multi-output Deep Learning Model

(ECGio)

250 6 leads 0.842

This Work

Multi-output Deep Learning Model

(ECGio)

250 9 leads 0.869

Figure 3: (a) An ECG reconstructed by ECGio (in semi-transparent red) using only lead I and compared against the true,

original 12-lead ECG signal (in semi-transparent blue). (B) Enlarged lead I demonstrating that even though ECGio is given

lead 1, it performs corrections and approximations in an attempt to correct for noise in the input signal. (C) Enlarged lead V1

demonstrating ECGio’s reconstruction ability on an important precordial lead. (D) Enlarged lead III demonstrating ECGio’s

reconstruction ability on a noisy limb lead. This points to areas for improvement in future work. (E) Figure legend and

performance statistics (R

, Root Mean Square Error (RMSE) and MAE) for this particular one-lead reconstruction.

from moderate with 1 lead to high with 12-leads. This

type of behavior was expected especially for clini-

cians who would prefer a more authentic reconstruc-

tion.

In the ﬁnal experiment there were particular leads

that were more signiﬁcant in ECGio’s ability to re-

construct a full 12-lead ECG. Either ECGio weighed

information from some leads more highly than others,

12-Lead ECG Reconstruction via Combinatoric Inclusion of Fewer Standard ECG Leads with Implications for Lead Information and

Signiﬁcance

139

or some leads contained more information and were

therefore more signiﬁcant to understanding a full 12-

lead morphology. From the tests of signiﬁcance, leads

I,II, aVL, aVF, V2, and V3 – the majority of which

were limb leads – were statistically signiﬁcant. The

unipolar leads aVL and aVF were linear combina-

tions of limb leads and therefore their inclusion was

also signiﬁcant. V2 and V3 were also statistically sig-

niﬁcant and might be more important than other pre-

cordial leads. Again, this behavior might represent a

larger trend or might be limited to this dataset.

In Table 7, we compared our results against a sam-

pling of other methods with R

as the metric of com-

parison. At ﬁrst glance, our work contained a lower

R2 than others, but a few factors should be consid-

ered. (1) Our reference standard had the propensity to

ﬁltering artifacts as a result of standardization. (2)

This work was a generalized model that used any

combination of ECG leads and so that a decrease of

performance in favor of ﬂexibility was expected. (3)

We limited the length of time to 10 seconds and we ar-

tiﬁcially lowered the sampling rate to 100Hz, which

meant that there were less values in ﬂat areas, such as

isoelectric portions.

We also showed the potential of ECGio to be used

to reconstruct a full 12-lead ECG when leads were

either missing or unable to be collected. We also

showed that there were leads of an ECG that may con-

tain more information than others, namely the limb

leads. In future studies, ECGio’s scale, usability, and

clinical viability must be examined. We must deter-

mine if results scale and if they demonstrate a larger

trend in how ECG information is stored. The next step

must include a larger sample size with the potential to

capture the variance of ECGs. We need to show if the

information provided by this reconstruction matches-

up not only mathematically, but clinically. A future

study should compare the reference standard ECG to

the reconstruction in terms of clinical information de-

livered to physicians. In addition, the presence of ab-

normal beats and rhythms must be examined to deter-

mine if abnormal morphology affects ECGio’s recon-

struction capabilities.

REFERENCES

Al-Khatib, S. M., Stevenson, W. G., Ackerman, M. J.,

Bryant, W. J., Callans, D. J., Curtis, A. B., Deal,

B. J., Dickfeld, T., Field, M. E., Fonarow, G. C., et al.

(2018). 2017 aha/acc/hrs guideline for management

of patients with ventricular arrhythmias and the pre-

vention of sudden cardiac death: a report of the amer-

ican college of cardiology/american heart association

task force on clinical practice guidelines and the heart

rhythm society. Journal of the American College of

Cardiology, 72(14):e91–e220.

AlGhatrif, M. and Lindsay, J. (2012). A brief review: his-

tory to understand fundamentals of electrocardiogra-

phy. Journal of community hospital internal medicine

perspectives, 2(1):14383.

Dawson, D., Yang, H., Malshe, M., Bukkapatnam, S. T.,

Benjamin, B., and Komanduri, R. (2009). Lin-

ear afﬁne transformations between 3-lead (frank

xyz leads) vectorcardiogram and 12-lead electro-

cardiogram signals. Journal of electrocardiology,

42(6):622–630.

Dower, G. E., Yakush, A., Nazzal, S. B., Jutzy, R. V., and

Ruiz, C. E. (1988). Deriving the 12-lead electrocar-

diogram from four (easi) electrodes. Journal of elec-

trocardiology, 21:S182–S187.

Fihn, S. D., Blankenship, J. C., Alexander, K. P., Bittl, J. A.,

Byrne, J. G., Fletcher, B. J., Fonarow, G. C., Lange,

R. A., Levine, G. N., Maddox, T. M., et al. (2014).

2014 acc/aha/aats/pcna/scai/sts focused update of the

guideline for the diagnosis and management of pa-

tients with stable ischemic heart disease: a report of

the american college of cardiology/american heart as-

sociation task force on practice guidelines, and the

american association for thoracic surgery, preventive

cardiovascular nurses association, society for cardio-

vascular angiography and interventions, and society of

thoracic surgeons. Journal of the American College of

Cardiology, 64(18):1929–1949.

Finlay, D. D., Nugent, C. D., Kellett, J. G., Donnelly, M. P.,

McCullagh, P. J., and Black, N. D. (2007). Syn-

thesising the 12-lead electrocardiogram: Trends and

challenges. European journal of internal medicine,

18(8):566–570.

Frank, E. (1956). An accurate, clinically practical sys-

tem for spatial vectorcardiography. circulation,

13(5):737–749.

Grande-Fidalgo, A., Calpe, J., Red

on, M., Mill

an-Navarro,

C., and Soria-Olivas, E. (2021). Lead reconstruction

using artiﬁcial neural networks for ambulatory ecg ac-

quisition. Sensors, 21(16):5542.

January, C. T., Wann, L. S., Alpert, J. S., Calkins, H., Cigar-

roa, J. E., Cleveland, J. C., Conti, J. B., Ellinor, P. T.,

Ezekowitz, M. D., Field, M. E., et al. (2014). 2014

aha/acc/hrs guideline for the management of patients

with atrial ﬁbrillation: executive summary: a report

of the american college of cardiology/american heart

association task force on practice guidelines and the

heart rhythm society. Journal of the American Col-

lege of Cardiology, 64(21):2246–2280.

Leasure, M., Jain, U., Butchy, A., Otten, J., Covalesky,

V. A., McCormick, D., and Mintz, G. S. (2021).

Deep learning algorithm predicts angiographic coro-

nary artery disease in stable patients using only a stan-

dard 12-lead electrocardiogram. Canadian Journal of

Cardiology.

Mann, S. and Orglmeister, R. (2013). Pca-based

ecg lead reconstruction. Biomedical Engi-

neering/Biomedizinische Technik, 58(SI-1-Track-

G):000010151520134197.

BIOSIGNALS 2022 - 15th International Conference on Bio-inspired Systems and Signal Processing

140

Members, . W. C., Anderson, J. L., Adams, C. D., Antman,

E. M., Bridges, C. R., Califf, R. M., Casey Jr, D. E.,

Chavey, W. E., Fesmire, F. M., Hochman, J. S., et al.

(2013). 2012 accf/aha focused update incorporated

into the accf/aha 2007 guidelines for the management

of patients with unstable angina/non–st-elevation my-

ocardial infarction: a report of the american col-

lege of cardiology foundation/american heart associ-

ation task force on practice guidelines. Circulation,

127(23):e663–e828.

Smith, G. H., Van den Heever, D. J., and Swart, W. (2021).

The reconstruction of a 12-lead electrocardiogram

from a reduced lead set using a focus time-delay neu-

ral network. Acta Cardiologica Sinica, 37(1):47.

Sohn, J., Yang, S., Lee, J., Ku, Y., and Kim, H. C. (2020a).

Reconstruction of 12-lead electrocardiogram from a

three-lead patch-type device using a lstm network.

Sensors, 20(11):3278.

Sohn, J., Yang, S., Lee, J., Ku, Y., and Kim, H. C. (2020b).

Reconstruction of 12-lead electrocardiogram from a

three-lead patch-type device using a LSTM network.

Sensors, 20(11):3278.

Toma

c, I. and Trobec, R. (2013a). Electrocardiographic

systems with reduced numbers of leads—synthesis of

the 12-lead ecg. IEEE reviews in biomedical engineer-

ing, 7:126–142.

Toma

c, I. and Trobec, R. (2013b). Electrocardiographic

systems with reduced numbers of leads—synthesis of

the 12-lead ecg. IEEE reviews in biomedical engineer-

ing, 7:126–142.

Trobec, R., Toma

si, I., Rashkovska, A., and Avbelj, V.

(2018). Lead Theory of Differential Leads and Syn-

thesis of the Standard 12-Lead ECG, pages 77–100.

Springer International Publishing, Cham.

Trobec, R. and Toma

c, I. (2011). Synthesis of the 12-lead

electrocardiogram from differential leads. IEEE trans-

actions on information technology in biomedicine,

15(4):615–621.

Wagner, P., Strodthoff, N., Bousseljot, R.-D., Samek, W.,

and Schaeffter, T. (2020). Ptb-xl, a large publicly

available electrocardiography dataset.

Yang, X.-L., Liu, G.-Z., Tong, Y.-H., Yan, H., Xu, Z., Chen,

Q., Liu, X., Zhang, H.-H., Wang, H.-B., and Tan, S.-

H. (2015). The history, hotspots, and trends of elec-

trocardiogram. Journal of geriatric cardiology: JGC,

12(4):448.

Zhu, H., Pan, Y., Cheng, K.-T., and Huan, R. (2018).

A lightweight piecewise linear synthesis method for

standard 12-lead ecg signals based on adaptive region

segmentation. PloS one, 13(10):e0206170.

12-Lead ECG Reconstruction via Combinatoric Inclusion of Fewer Standard ECG Leads with Implications for Lead Information and

Signiﬁcance

141