
Iterative 3D Deformable Registration from Single-view RGB Images
using Differentiable Rendering
Arul Selvam Periyasamy
a
, Max Schwarz
b
and Sven Behnke
c
Autonomous Intelligent Systems, University of Bonn, Germany
Keywords:
Differentiable Rendering, Deformable Registration, Latent Shape-space Model.
Abstract:
For autonomous robotic systems, comprehensive 3D scene parsing is a prerequisite. Machine learning tech-
niques used for 3D scene parsing that incorporate knowledge about the process of 2D image generation from
3D scenes have a big potential. This has sparked an interest in differentiable renderers that provide approxi-
mate gradients of the rendered image with respect to scene and object parameters. An efficient differentiable
renderer facilitates approaching many 3D scene parsing problems using a render-and-compare framework,
where the object and scene parameters are optimized by minimizing the difference between rendered and ob-
served images. In this work, we introduce StilllebenDR, a light-weight scalable differentiable renderer built
as an extension to the Stillleben library and use it for 3D deformable registration from single-view RGB im-
ages. Our end-to-end differentiable pipeline achieves results comparable to state-of-the-art methods without
any training and outperforms the competing methods significantly in the presence of pose initialization errors.
1 INTRODUCTION
Image synthesis is the process of creating a 2D im-
age given a virtual camera, objects, and light sources.
Vision-as-inverse-graphics techniques aim to solve
computer vision problems by searching for camera,
object, and lighting parameters that generate the im-
age that best matches the observed image. Render-
and-compare serves as a powerful framework to real-
ize vision-as-inverse-graphics. The fundamental idea
of render-and-compare is to render the scene based on
the current parameter estimate and search for param-
eters that minimize the difference between rendered
and observed images. Employing a differentiable ren-
derer that not only generates an image based on the
given scene description but also provides gradients of
the rendered image with respect to object and scene
parameters enables the usage of efficient gradient-
based optimization methods for searching the best pa-
rameters. Although modern hardware allows generat-
ing high-quality physically realistic images, render-
ing is a trade-off between image quality and compute.
In particular, modeling secondary rendering effects is
compute intensive. However, in many robotics ap-
plications modeling secondary effects is not crucial.
a
https://orcid.org/0000-0002-9320-3928
b
https://orcid.org/0000-0002-9942-6604
c
https://orcid.org/0000-0002-5040-7525
Using image abstraction modules that are invariant
to secondary rendering effects allows for pixel-wise
comparison of rendered and observed images. This
facilitates the usage of render-and-compare in solv-
ing many real-world robotic perception tasks. In this
paper, we introduce StilllebenDR, an efficient, light-
weight differentiable renderer with PyTorch (Paszke
et al., 2019) integration. StilllebenDR is built on
top of Stillleben (Schwarz and Behnke (2020)). We
demonstrate its usage for solving the deformable reg-
istration task by combining it in a pipeline with a la-
tent shape-space model. Given a set of object meshes
belonging to instances of an object category and the
mesh of the canonical instance, deformable registra-
tion is the task of estimating the deformation from
the canonical mesh to other instances. Deformable
registration is crucial for robotic manipulation tasks
where robots have to transfer the grasping knowl-
edge from the canonical instance to other instances
of the same object category. Our proposed approach
for deformable registration does not need any depth
information and contrary to many state-of-the-model
methods for deformable registration, our approach
does not use any learning components to estimate the
deformation. Instead, our approach only needs seg-
mentation information. The proposed pipeline is end-
to-end differentiable and computes the deformation of
the canonical mesh to match the observed image us-
Periyasamy, A., Schwarz, M. and Behnke, S.
Iterative 3D Deformable Registration from Single-view RGB Images using Differentiable Rendering.
DOI: 10.5220/0010817100003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
107-116
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
107

ing the differentiable renderer. The flexibility of our
pipeline allows for joint pose optimization and de-
formable registration. This makes our pipeline less
susceptible to pose initialization errors. In short, our
contributions include:
1. StilllebenDR, a differentiable renderer with Py-
Torch integration,
2. an end-to-end differentiable pipeline for de-
formable object registration using a latent shape-
space model and differentiable rendering, and
3. a framework for joint object pose optimization
and deformable registration to make our pipeline
less susceptible to pose initialization errors.
StilllebenDR is made available as open-source
1
.
2 RELATED WORK
2.1 Differentiable Rendering
Deep learning methods have achieved impressive re-
sults in 3D scene parsing from 2D RGB images. Of
particular interest are methods for object pose esti-
mation (Bui et al., 2018; Hodan et al., 2020; Labbe
et al., 2020; Peng et al., 2019; Xiang et al., 2018)
and shape estimation (Gkioxari et al., 2019; Groueix
et al., 2018; Mescheder et al., 2019; Pan et al., 2019;
Wang et al., 2018). One remaining challenge in train-
ing 3D scene parsing models is the requirement of
high-quality labeled data. In contrast to 2D com-
puter vision tasks such as object detection or semantic
segmentation, collecting high-quality labeled datasets
for 3D scene parsing tasks like object pose estima-
tion or object shape estimation is a much more time-
consuming and error-prone process. One way to mit-
igate this issue is to use synthetic data (Hoda
ˇ
n et al.,
2020; Schwarz and Behnke, 2020). Another orthogo-
nal approach is to incorporate knowledge about 2D
image generation from a 3D scene as part of the
neural network architecture. This has sparked an
interest in approximate differentiable renderers with
methods such as OpenDR (Loper and Black, 2014),
PyTorch3D (Ravi et al., 2020), SoftRas (Liu et al.,
2019), and DIB-R (Chen et al., 2019). Kato et al.
(2020) compiled a detailed survey on differentiable
rendering formulations. All these differentiable ren-
derers implement rasterization in CUDA and provide
integration to PyTorch or other similar deep learning
frameworks. In contrast, StilllebenDR uses a classical
rasterization pipeline using OpenGL and implements
only backward functions for gradient computation in
1
https://ais-bonn.github.io/stillleben/stillleben.diff.html
PyTorch. StilllebenDR is built on the Stillleben li-
brary (Schwarz and Behnke, 2020), which is highly
optimized to create realistic scenes on the fly for train-
ing neural networks. StilllebenDR is designed as an
add-on to the forward renderer with only a minimal
overhead to the forward rendering process.
2.2 Render-and-Compare
Render-and-compare, i.e. iteratively improving a
scene model by synthesis and comparison with the
real world, has a long history in computer vision.
Zienkiewicz et al. (2016) used render-and-compare
to perform real-time height map fusion. Krull et al.
(2015) trained a CNN to output an energy score
that describes how well a rendered image and an
observed image match. The authors then used the
trained CNN to evaluate 6D pose hypotheses gener-
ated using Metropolis algorithm and search for the
hypothesis with the best energy score. Kundu et al.
(2018) used a render-and-compare loss function to
train a 3D R-CNN model (He et al., 2017) to per-
form 3D object detection and reconstruction. Moreno
et al. (2016) demonstrated the capabilities of differ-
entiable rendering and render-and-compare by esti-
mating pose, shape, light, and appearance parameters
jointly on a synthetic dataset. Pavlakos et al. (2018);
Xu et al. (2019) used render-and-compare to estimate
multi-human pose and shape from RGB images. Li
et al. (2018) formulated 6D object pose estimation as
iterative pose refinement process. Given an image of
an object rendered according to the current pose es-
timate and the observed image, the authors trained a
CNN to estimate a pose update that aligns the ren-
dered image with the observed image. This pose
refinement is done iteratively until the pose update
becomes negligible. Periyasamy et al. (2019) used
render-and-compare to refine 6D object poses for all
objects in a scene simultaneously. To enable compar-
ing rendered and observed images of complex scenes
with multiple objects, they used a learned dense de-
scriptor model as an abstraction module and com-
pared the images pixel-wise in the abstract descriptor
space instead of RGB space.
2.3 Deformable Registration
The deformable registration task differs from the
shape reconstruction task discussed in Section 2.1 in
the aspect that the objective is not shape reconstruc-
tion, but rather registering a given canonical model
with an observed instance which allows for transfer-
ring knowledge between the canonical and observed
instances. The canonical model needs to be de-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
108

formed to match the observed instance while main-
taining its geometric structure. Based on the formu-
lation for maintaining the geometric structure, many
RGB-D methods exist (Allen et al., 2003; Brown and
Rusinkiewicz, 2007; Kim et al., 2011; Myronenko
and Song, 2010; Rodriguez et al., 2018; Zeng et al.,
2010). For the sake of brevity, we focus on Deep-
CPD (Rodriguez et al., 2020), which our proposed
method is based upon. The authors model defor-
mation between instances of the same object cate-
gory with coherent point drift (CPD) and form a low-
dimensional shape-space of the deformation field us-
ing PCA. CPD and the latent shape-space are dis-
cussed in detail in Section Section 3.2. Given a single-
view RGB image, the authors trained a CNN to gener-
ate a deformation field for the vertices that are visible
in the image. The latent shape-space is updated based
on the deformation field. Finally, by regenerating the
deformation field from the latent space, deformation
vectors for all vertices—including the vertices not vis-
ible in the image—are generated. Our proposed ap-
proach, instead of learning to predict the deformation,
employs an end-to-end differentiable pipeline to opti-
mize the latent shape-space parameters during infer-
ence. This way, a separate training phase is not re-
quired anymore.
2.4 Image Comparison
Comparing two images in order to establish a measure
of similarity is a long-standing standing computer vi-
sion problem. Traditional methods like PSNR and
perceptual similarity methods like SSIM (Wang et al.,
2004), MSSIM (Wang et al., 2003), FSIM (Zhang
et al., 2011), HDR-VDP (Mantiuk et al., 2011) were
proposed to compare images. In an orthogonal di-
rection, intrinsic image decomposition methods were
proposed to decompose an image into intrinsic com-
ponents, such as shading, reflectance, and shape
to allow for comparison of images in a way that
is robust against secondary lighting effects (Barrow
et al., 1978; Finlayson et al., 2004; Tappen et al.,
2005). Lately, with the success of CNNs for com-
puter vision tasks, CNN features are used for com-
paring two images, even allowing comparing images
across two different modalities—rendered and real-
world (Appalaraju and Chaoji, 2017; Zagoruyko and
Komodakis, 2015; Zhang et al., 2018).
V
1
V
2
V
3
Faces
Renderer
RGB channels
Vertex indices &
Barycentric coordinates
Figure 1: Forward rendering. In addition to the RGB chan-
nels, we also render vertex indices and barycentric coor-
dinates per pixel as separate channels and store them for
backward computations.
3 METHOD
3.1 Stillleben Differentiable Renderer
State-of-the-art graphics engines use graphics APIs
such as OpenGL, DirectX, or Vulkan. These APIs
allow user-defined programs called shaders to run at
specified stages of the rendering pipeline. Break-
ing down the rendering process into shaders en-
ables highly parallel and flexible rendering processes.
We exploit the flexibility of the shaders to ren-
der additional information like vertex indices and
barycentric coordinates as separate channels in ad-
dition to the default RGB channels. Our differ-
entiable renderer StilllebenDR is built as an exten-
sion to Stillleben (Schwarz and Behnke, 2020). Stil-
lleben was developed to generate synthetic scenes
and ground truth annotations that serve as training
data for deep learning models online. To gener-
ate physically realistic scenes, Stillleben implements
sophisticated rendering techniques like Physically-
based Rendering (PBR) (Pharr et al., 2016), Image-
based Lighting (IBL) (Debevec, 2006), Ambient Oc-
clusion (SSAO) (Bavoil and Sainz, 2008), etc. Unlike
PyTorch3D (Ravi et al., 2020), SoftRas (Liu et al.,
2019), and DIB-R (Chen et al., 2019) that implement
rasterization on CUDA, we rely on OpenGL for for-
ward rendering. Implementing a rasterizer in CUDA
efficiently is not an easy task. In the OpenGL ras-
terization pipeline, parallelization is done over ver-
tices in the initial stages of the rendering pipeline
and over pixels in the later stages of the pipeline. A
myriad of optimizations employed by the common
OpenGL implementations greatly reduces the over-
all runtime complexity (Kuehne et al., 2005; Merry,
2012; Spitzer, 2003). StilllebenDR takes advantage
of the optimization done behind the scenes by the
OpenGL implementation and thus scales well for
complex scenes and high-definition meshes.
Iterative 3D Deformable Registration from Single-view RGB Images using Differentiable Rendering
109
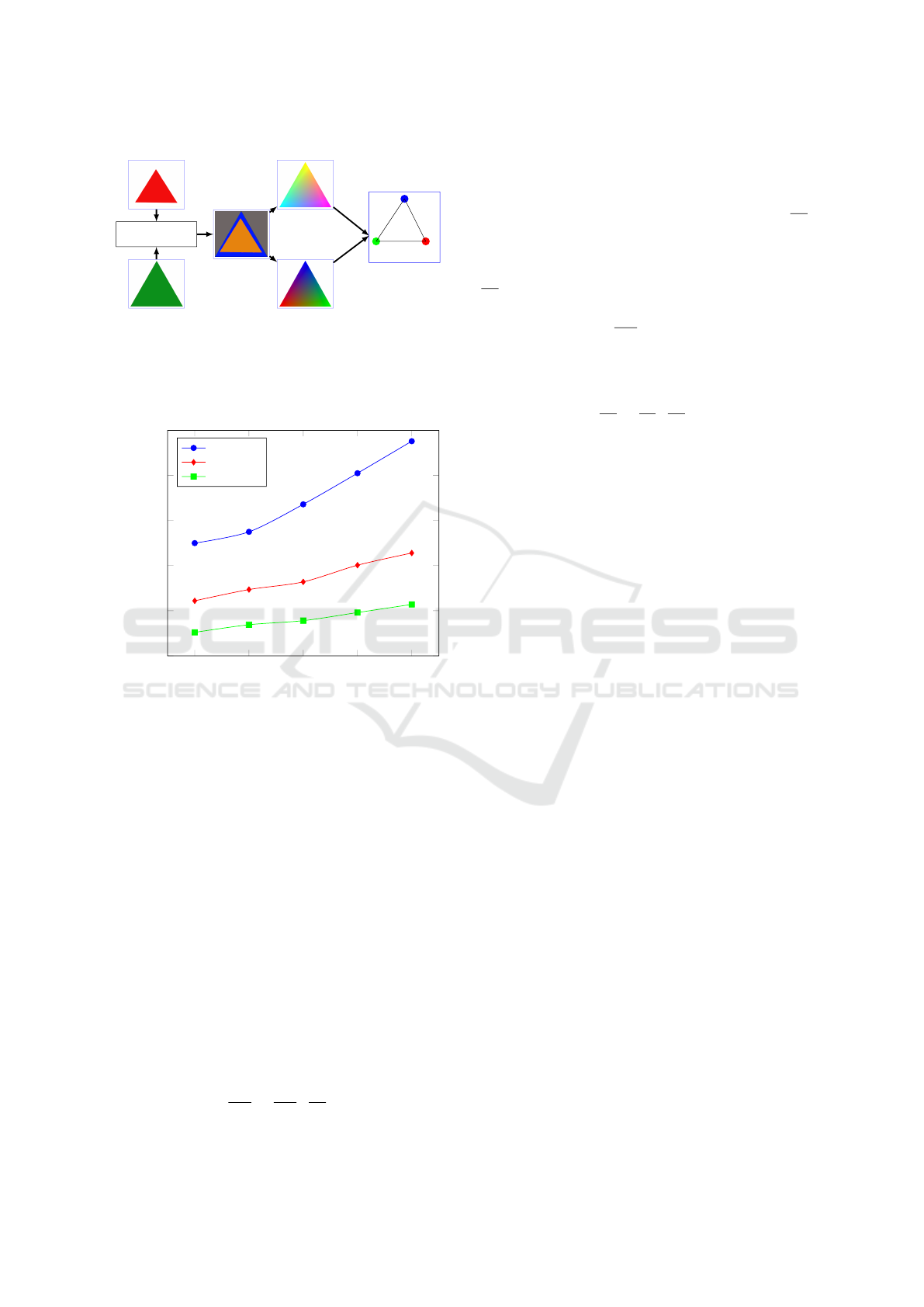
V
1
V
2
V
3
Observed
Rendered
Image comparison
loss
Vertex indices
Barycentric coordinates
Gradient of loss
w.r.t. rendered image
Faces
Figure 2: Backward rendering. The gradient of the image
comparison loss function is propagated to the vertices by
differentiating through the renderer using the vertex indices
and barycentric coordinates information stored during the
forward rendering step.
100 200 300 400 500
0
100
200
300
400
500
# Vertices [×10
3
]
Time[ms]
SoftRas
PyTorch3D
StilllebenDR
Figure 3: Runtime comparison between SoftRas (Liu et al.,
2019), PyTorch3D Ravi et al. (2020), and StilllebenDR
(ours). We report the average time taken by different differ-
entiable rendering approaches to perform forward rendering
(1024×1024 pixels) and backward gradient computations.
Given a face F constituting of vertices V with col-
ors C that is projected on a pixel I, the color of the
pixel I is computed as
I
rgb
=
∑
i
b
i
C
i
, (1)
where b
i
is the barycentric coordinates and
∑
i
b
i
= 1.
For brevity, we simply use the notation I instead of
I
rgb
.
While rendering an image as shown in Fig. 1, in
addition to the RGB channels, we render vertex in-
dices and barycentric coordinates as separate chan-
nels. We save these additional channels for backward
gradient computation.
The gradient of the loss function L with respect to
vertex V
i
is computed using chain rule as
∂L
∂V
i
=
∂I
∂V
i
·
∂L
∂I
, (2)
i.e., we break down the gradient of the loss function
with respect to a vertex as gradient of the loss func-
tion with respect to the rendered image and gradient
of the rendered image with respect to the vertex.
∂I
∂V
i
is computed automatically by PyTorch autograd. The
barycentric weights and the vertex indices stored dur-
ing the forward rendering step are used in computing
∂I
∂V
i
:
∂I
∂V
i
= C
i
. (3)
Similarly, we break down the gradient of the loss
function with respect to object pose P as follows:
∂L
∂P
=
∂I
∂P
·
∂L
∂I
. (4)
StilllebenDR takes advantage of the optimized
OpenGL library for forward rendering and the back-
ward gradient computations are implemented in Py-
Torch (Paszke et al., 2019). This enables Stil-
llebenDR to be more scalable than other differentiable
rendering libraries, such as SoftRas (Liu et al., 2019),
and PyTorch3D (Ravi et al., 2020). In Fig. 3, we the
show the scalability of our approach to differentiable
rendering by comparing the average time taken to ren-
der an image of size 1024×1024 with varying num-
ber of vertices and performing backward pass. We
performed the runtime comparison experiment on a
computer powered by Nvidia GTX Titan X GPU with
12 GBs of memory and Intel 4.0 GHz i7 CPU. Stil-
llebenDR is faster and more scalable than both Soft-
Ras, and PyTorch3D.
3.2 Deformable Registration
3.2.1 Coherent Point Drift
Given a template point set Y = (y
1
,...,y
M
)
T
, and a
reference point set X = (x
1
,...,x
N
)
T
(both being D-
dimensional), CPD considers Y as centroids of a
Gaussian Mixture Model (GMM) and fits Y towards
data points X by maximizing the likelihood of X
drawn from Y under the assumption of equal member-
ship probabilities for all GMM components and equal
isotropic covariances. In the context of deformable
registration, given a template point set and a reference
set, CPD is used to generate the deformed point set τ.
τ is formulated as displacement modeled by function
v on the initial set of template points Y
τ(Y,v) = Y + v(Y), (5)
where the displacement function v for any set of D-
dimensional points Z ∈ R
N×D
is defined as
v(Z) = G(Y,Z)W. (6)
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
110
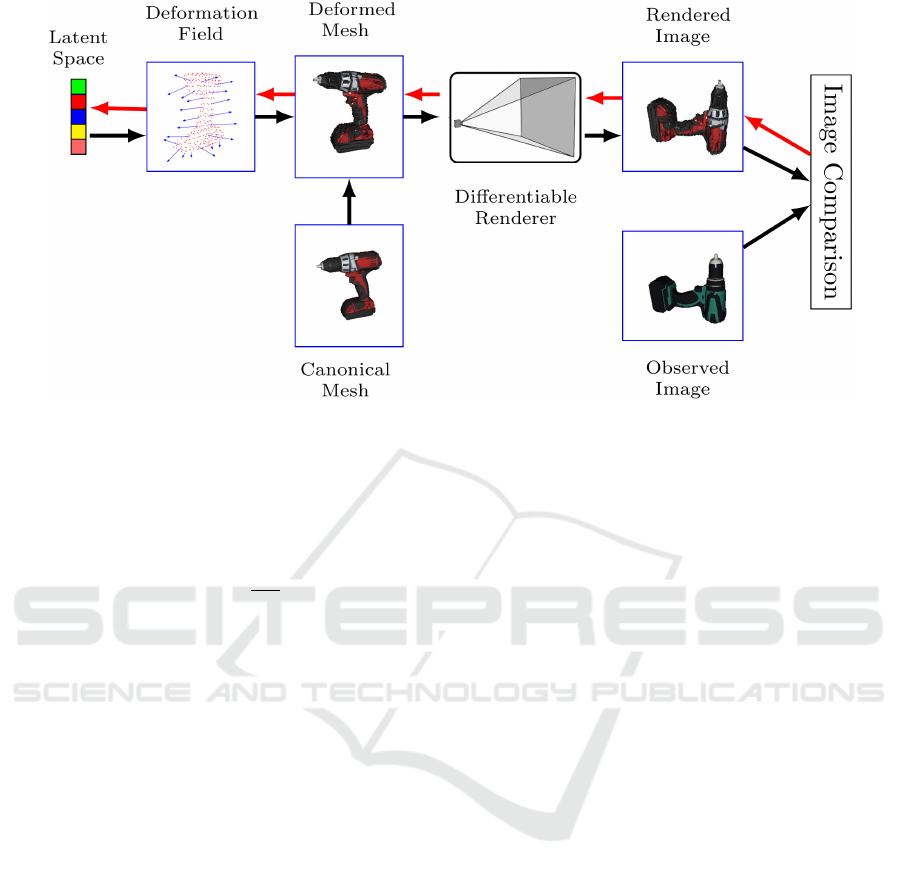
Figure 4: Proposed deformable registration pipeline. Latent shape-space parameters are optimized to minimize the difference
between rendered image of the deformed mesh and the observed mesh. Image comparison loss is minimized using gradients
obtained by differentiating through the rendering process. Black arrows indicate the forward rendering process and red arrows
indicate the backward gradient flow.
G(Y,Z) is the Gaussian kernel matrix. It is defined
element-wise as
G(y
i
,z
i
) = g
i j
= exp(−
1
2β
2
||y
i
− z
i
||
2
) (7)
and W is the matrix of kernel weights and can be in-
terpreted as a set of D-dimensional deformation vec-
tors for each point in the G. For a given reference
point set, W is estimated in the M-step of the EM al-
gorithm.
3.2.2 Latent Shape-space
Given an object category with multiple instances, we
create a low-dimensional latent shape-space that cap-
tures the deformations between the instances of that
category. We assume the instances of an object cate-
gory are aligned in a common coordinate frame. The
deformation of the canonical model C to an instance i
is modeled as
τ
i
(C
i
,W
i
) = C + G(C, C)W
i
. (8)
W
i
is the deformation field that deforms the canonical
instance C to any instance i. It has a constant shape
irrespective of i, i.e., shape of W
i
does not depend on
i, but rather it depends on the canonical instance C.
This allows us to construct a latent shape-space using
the principle components of W
i
. In our experiments,
we use latent shape-space of dimension five for all the
object categories. We refer the reader to Rodriguez
et al. (2020), and Rodriguez et al. (2018) for a detailed
explanation of the latent shape-space.
3.3 Deformable Registration Pipeline
Given the canonical instance, its corresponding latent
shape-space parameters S , and an observed image I
obs
of a novel object instance, our task is to find the la-
tent shape-space parameters S that register the canon-
ical mesh with the novel object instance. We formu-
late the task as gradient-based iterative optimization
using render-and-compare framework. Our proposed
pipeline is depicted in the Fig. 4. In the forward step,
we start with rendering the mesh generated using the
canonical latent shape-space parameters S . The ren-
dered image is denoted as I
rnd
. As discussed in Sec-
tion 3.1, in addition to RGB channels, we render the
vertex indices constituting the faces that are projected
onto each pixel and also the corresponding barycen-
tric weights. Finally, we compute the pixel-wise im-
age comparison loss. In the backward step, we prop-
agate the gradient of image comparison loss with re-
spect to the rendered image to the vertices through the
differentiable renderer and then further to the latent
space. We repeat this process until the image compar-
ison loss reaches a plateau.
3.3.1 Image Comparison
Comparing RGB images pixel-wise is not straightfor-
ward. In our case, instead of comparing the images in
the RGB space, we perform the comparison in a CNN
feature space as shown in Fig. 5. We use the features
of a U-Net model (Ronneberger et al., 2015) trained
for semantic segmentation on DeepCPD dataset. In-
Iterative 3D Deformable Registration from Single-view RGB Images using Differentiable Rendering
111
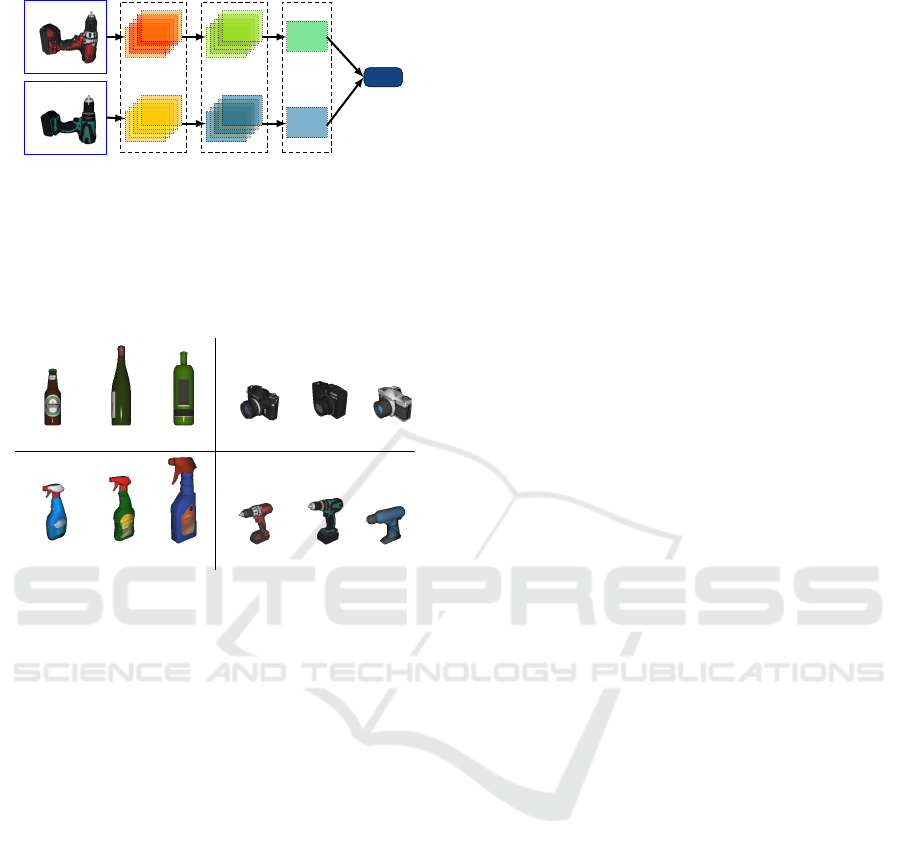
MSE
U-Net features
64×240×320
Canonical
64×240×320
Observed
Normalized
features
Aggregated
features
240×320
Figure 5: Image comparison operation. We compare the
rendered canonical and the observed image using U-Net
features. We normalize the extracted U-Net features and
normalize them between -1 and 1 and aggregate the fea-
tures along the channel dimension. Finally, we compute the
mean-squared error pixel-wise between the aggregated fea-
tures.
canonical test test canonical test test
canonical test test canonical test test
Figure 6: DeepCPD dataset with canonical instances and
exemplary test instances.
spired by the learned perceptual image patch similar-
ity metric (LPIPS) (Zhang et al., 2018), we formulate
the image comparison operation as follows. Given the
images I
rnd
and I
obs
, we extract the feature maps F
rnd
and F
obs
from the last layer before the final output
layer of the U-Net model respectively. F
rnd
and F
obs
∈ R
C×H×W
. We normalize F
rnd
and F
obs
between -1
and 1 and aggregate the features along the channel di-
mension and compute mean-squared error (MSE) on
the aggregated features.
4 EXPERIMENTS
4.1 Dataset
We use the DeepCPD dataset (Rodriguez et al., 2020)
to evaluate our approach for deformable registration.
The dataset consists of four object categories: bottles,
cameras, drills, and sprays (shown in Fig. 6). Each
category consists of a varying number of instances.
All the instances are aligned to have one common co-
ordinate frame, and one of the instances is selected
as the canonical model for each object category. All
except two instances are used for training and the ex-
empted two instances are used for testing. We com-
pare our approach with CLS (Myronenko and Song,
2010) and DeepCPD (Rodriguez et al., 2020). CLS
needs depth information though, while DeepCPD is
an RGB only method. Similar to the competing meth-
ods, we use the training instances to generate the
Gaussian Kernel matrix G described in Section 3.2.1.
But, in contrast to the DeepCPD, we do not use any
specialized learning-based modules to predict defor-
mation field. We only need semantic segmentation
information, which is a prerequisite for scene parsing.
we use the training dataset only for training the U-Net
semantic segmentation model. The segmentation in-
formation used to isolate target object pixels from the
background and the features of the U-Net segmenta-
tion model is used in image comparison module de-
scribed in Section 3.3.1.
4.2 Deformable Registration with
Known Poses
We perform deformable registration using our
proposed end-to-end differentiable pipeline using
stochastic gradient descent (SGD) with momentum
of 0.9. We also use exponential learning rate decay
with γ of 0.95. We run the optimization process until
the image comparison loss reaches a plateau, but limit
the maximum number of iterations to 30. Similarly to
our baseline methods, we assume that the canonical
mesh is initialized in the correct 6D pose and opti-
mize only the vertex positions. Meshes provided by
the DeepCPD dataset are not watertight. Tiny invis-
ible holes on the surface of the meshes develop into
larger visible holes during iterative deformable reg-
istration process. Large holes on the surface of the
meshes make comparing rendered and observed im-
ages harder. To alleviate this issue, we convert the
meshes provided by DeepCPD dataset into watertight
meshes using the ManifoldPlus algorithm (Huang
et al., 2020). Converting a non-watertight mesh into
watertight mesh retraining vertex color information is
non-trivial. Thus, most of the algorithms, including
ManifoldPlus, ignore the vertex color. Moreover, our
pipeline does not benefit from having vertex colors.
Thus, we use uniform red color for all the vertices in
the canonical mesh.
The quantitative comparison with other methods
is shown in Table 1. For each vertex in the test in-
stance, we compute `
2
error distance to the nearest
vertex in the deformed canonical mesh and report the
mean error of the vertices. The error is computed on
the subsampled set of points for test instances as pro-
vided by the DeepCPD dataset. Our method performs
only slightly worse than DeepCPD (Rodriguez et al.,
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
112

Known Pose With Pose Noise
Canonical Deformed Canonical Deformed Observed
Figure 7: Visualization of 3D deformation. The canonical mesh is deformed to fit the observed mesh iteratively using differ-
entiable rendering.
Table 1: Comparison of our approach with CLS (Myronenko and Song, 2010) and DeepCPD (Rodriguez et al., 2020). Mean
and (standard deviation) error values in µm.
Instance
Ground
Truth
Known Pose With Pose Noise
CLS DeepCPD Ours CLS DeepCPD Ours
(3D) (RGB) (RGB) (3D) (RGB) (RGB)
Camera T1 34.61 51.93 102.17 122.43 168.54 105.26 126.65
(1.97) (10.45) (47.89) (22.86) (357.8) (64.21) (28.31)
Camera T2 16.45 19.87 18.80 66.54 406.45 306.96 89.65
(1.61) (4.59) (5.11) (29.73) (492.03) (127.89) (33.54)
Bottle T1 23.25 25.92 45.21 52.63 297.79 227.90 75.41
(2.34) (5.18) (9.75) (19.45) (579.49) (146.0) (34.23)
Bottle T2 90.42 72.33 88.35 112.84 852.40 289.36 112.76
(28.54) (11.35) (18.39) (25.78) (1818) (147.68) (31.76)
Spray T1 29.84 30.78 47.87 77.74 1035 146.89 89.59
(1.42) (1.89) (12.99) (26.95) (406.69) (117.57) (33.75)
Spray T2 111.94 121.19 154.97 151.21 1488 255.69 178.42
(14.29) (19.16) (82.34) (79.76) (554.33) (167.32) (88.14)
Drill T1 21.18 28.86 52.71 71.54 232.35 92.96 84.34
(0.949) (1.42) (23.54) (34.56) (1325) (58.23) (43.56)
Drill T2 63.95 58.50 119.88 134.21 215.54 262.31 157.27
(5.23) (21.51) (107.43) (89.16) (565.48) (228.40) (96.36)
2020) but does not require any specialized learning
components for estimating deformation. The perfor-
mance across the different object categories is also
similar to DeepCPD, indicating that gradients of the
loss function with respect to the vertices computed us-
ing the differentiable renderer serves as a good surro-
gate for the learned CPD deformations. Additionally,
some qualitative visualizations are shown in Fig. 7.
Iterative 3D Deformable Registration from Single-view RGB Images using Differentiable Rendering
113

One can observe that the rendered deformed mesh
fits the observed mesh nicely. Our method not only
works for objects with simple geometry like bottles
but also for objects with complex geometry like drills
and sprays.
4.3 Joint Deformable Registration and
Pose Optimization
One of the major advantages of our approach com-
pared other methods is the ability to jointly optimize
for 6D object pose along with deformable registra-
tion. To demonstrate this feature, we randomly sam-
ple offsets in the range of [-0.05, 0.05] m for the x
and y translation components and [-15°and 15°] for
the rotation components. Although our method can
optimize z translation along with other pose param-
eters, optimizing both z translation and vertex posi-
tion jointly is an ill-posed problem. Thus, we include
offsets only for x and y translation components. Dur-
ing the joint pose optimization and deformable reg-
istration process, we update the shape parameters at
a higher frequency than the pose parameters, i.e. we
update the pose parameters once per three shape pa-
rameter updates. This is based on the observation that
the pose parameters require fewer updates to converge
than shape parameters. Quantitative results of joint
pose and shape optimization is presented in Table 1.
Our mean error only increases marginally when pose
noise is injected, indicating that our method is less
susceptible to pose initialization errors than compet-
ing methods.
5 CONCLUSION
We presented StilllebenDR, a lightweight differen-
tiable rendering library specifically designed for real-
time robotics applications and used it in an end-to-end
differentiable pipeline to solve deformable registra-
tion. Given a canonical object mesh and an observed
image of a novel instance of the same object cate-
gory, we optimize the latent shape-space of the canon-
ical mesh to minimize the error between rendered
canonical meshes and observed images. Our method
achieves results comparable to the state-of-the-art
methods for deformable registration from single-view
RGB images without any learning components. Fur-
thermore, our pipeline is easily extendable to include
object pose parameter optimization. We showed opti-
mizing object pose parameters along with deformable
registration makes our pipeline less susceptible to
pose initialization errors.
REFERENCES
Allen, B., Curless, B., and Popovi
´
c, Z. (2003). The space
of human body shapes: Reconstruction and parame-
terization from range scans. ACM Transactions On
Graphics (TOG), 22(3):587–594.
Appalaraju, S. and Chaoji, V. (2017). Image sim-
ilarity using deep CNN and curriculum learning.
arXiv:1709.08761.
Barrow, H., Tenenbaum, J., Hanson, A., and Riseman, E.
(1978). Recovering intrinsic scene characteristics.
The Journal of Computer and System Sciences, 2(3-
26):2.
Bavoil, L. and Sainz, M. (2008). Screen space am-
bient occlusion. NVIDIA developer information:
http://developers. nvidia. com, 6.
Brown, B. J. and Rusinkiewicz, S. (2007). Global non-rigid
alignment of 3D scans. In ACM SIGGRAPH.
Bui, M., Zakharov, S., Albarqouni, S., Ilic, S., and Navab,
N. (2018). When regression meets manifold learning
for object recognition and pose estimation. In IEEE
International Conference on Robotics and Automation
(ICRA).
Chen, W., Ling, H., Gao, J., Smith, E., Lehtinen, J., Jacob-
son, A., and Fidler, S. (2019). Learning to predict 3D
objects with an interpolation-based differentiable ren-
derer. In Advances in Neural Information Processing
Systems (NeurIPS), pages 9609–9619.
Debevec, P. (2006). Image-based lighting. ACM SIG-
GRAPH 2006 Courses.
Finlayson, G. D., Drew, M. S., and Lu, C. (2004). Intrinsic
images by entropy minimization. In European confer-
ence on computer vision (ECCV), pages 582–595.
Gkioxari, G., Malik, J., and Johnson, J. (2019). Mesh R-
CNN. In IEEE International Conference on Computer
Vision (ICCV), pages 9785–9795.
Groueix, T., Fisher, M., Kim, V. G., Russell, B. C., and
Aubry, M. (2018). A papier-m
ˆ
ach
´
e approach to learn-
ing 3D surface generation. In IEEE Conference on
Computer Vision and Pattern Recognition (CVPR).
He, K., Gkioxari, G., Doll
´
ar, P., and Girshick, R. (2017).
Mask R-CNN. In IEEE International conference on
Computer Vision (ICCV), pages 2961–2969.
Hodan, T., Barath, D., and Matas, J. (2020). EPOS: Esti-
mating 6D pose of objects with symmetries. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR).
Hoda
ˇ
n, T., Sundermeyer, M., Drost, B., Labb
´
e, Y., Brach-
mann, E., Michel, F., Rother, C., and Matas, J. (2020).
BOP challenge 2020 on 6D object localization. In
European Conference on Computer Vision (ECCV),
pages 577–594.
Huang, J., Zhou, Y., and Guibas, L. (2020). Mani-
foldPlus: A robust and scalable watertight mani-
fold surface generation method for triangle soups.
arXiv:2005.11621.
Kato, H., Beker, D., Morariu, M., Ando, T., Matsuoka, T.,
Kehl, W., and Gaidon, A. (2020). Differentiable ren-
dering: A survey. arXiv:2006.12057.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
114

Kim, V. G., Lipman, Y., and Funkhouser, T. (2011).
Blended intrinsic maps. ACM Transactions On
Graphics (TOG), 30(4):1–12.
Krull, A., Brachmann, E., Michel, F., Ying Yang, M.,
Gumhold, S., and Rother, C. (2015). Learning
analysis-by-synthesis for 6D pose estimation in RGB-
D images. In IEEE International Conference on Com-
puter Vision (ICCV), pages 954–962.
Kuehne, B., True, T., Commike, A., and Shreiner, D.
(2005). Performance OpenGL: Platform independent
techniques. In ACM SIGGRAPH 2005 Courses.
Kundu, A., Li, Y., and Rehg, J. M. (2018). 3D-RCNN:
Instance-level 3D object reconstruction via render-
and-compare. In IEEE Conference on Computer Vi-
sion and Pattern Recognition (CVPR), pages 3559–
3568.
Labbe, Y., Carpentier, J., Aubry, M., and Sivic, J. (2020).
CosyPose: Consistent multi-view multi-object 6D
pose estimation. In European Conference on Com-
puter Vision (ECCV).
Li, Y., Wang, G., Ji, X., Xiang, Y., and Fox, D. (2018).
DeepIM: Deep iterative matching for 6D pose esti-
mation. In European Conference on Computer Vision
(ECCV), pages 683–698.
Liu, S., Li, T., Chen, W., and Li, H. (2019). Soft Rasterizer:
A differentiable renderer for image-based 3D reason-
ing. In IEEE International Conference on Computer
Vision (ICCV), pages 7708–7717.
Loper, M. M. and Black, M. J. (2014). OpenDR: An ap-
proximate differentiable renderer. In European Con-
ference on Computer Vision (ECCV), pages 154–169.
Mantiuk, R., Kim, K. J., Rempel, A. G., and Heidrich, W.
(2011). HDR-VDP-2 : A calibrated visual metric
for visibility and quality predictions in all luminance
conditions. ACM Transactions on graphics (TOG),
30(4):1–14.
Merry, B. (2012). Performance tuning for tile-based archi-
tectures. OpenGL Insights, page 323.
Mescheder, L., Oechsle, M., Niemeyer, M., Nowozin, S.,
and Geiger, A. (2019). Occupancy networks: Learn-
ing 3D reconstruction in function space. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 4460–4470.
Moreno, P., Williams, C. K., Nash, C., and Kohli, P. (2016).
Overcoming occlusion with inverse graphics. In Euro-
pean Conference on Computer Vision (ECCV), pages
170–185.
Myronenko, A. and Song, X. (2010). Point set registra-
tion: Coherent point drift. IEEE Transactions on
Pattern Analysis and Machine Intelligence (TPAMI),
32(12):2262–2275.
Pan, J., Han, X., Chen, W., Tang, J., and Jia, K. (2019).
Deep mesh reconstruction from single RGB images
via topology modification networks. In IEEE Interna-
tional Conference on Computer Vision (ICCV), pages
9964–9973.
Paszke, A., Gross, S., Massa, F., Lerer, A., Bradbury, J.,
Chanan, G., Killeen, T., Lin, Z., Gimelshein, N.,
Antiga, L., Desmaison, A., Kopf, A., Yang, E., De-
Vito, Z., Raison, M., Tejani, A., Chilamkurthy, S.,
Steiner, B., Fang, L., Bai, J., and Chintala, S. (2019).
PyTorch: An imperative style, high-performance deep
learning library. In Advances in Neural Information
Processing Systems (NeurIPS), pages 8024–8035.
Pavlakos, G., Zhu, L., Zhou, X., and Daniilidis, K. (2018).
Learning to estimate 3D human pose and shape from a
single color image. In IEEE Conference on Computer
Vision and Pattern Recognition (CVPR), pages 459–
468.
Peng, S., Liu, Y., Huang, Q., Zhou, X., and Bao, H. (2019).
PVNet: Pixel-wise voting network for 6DOF pose es-
timation. In IEEE Conference on Computer Vision
and Pattern Recognition (CVPR), pages 4561–4570.
Periyasamy, A. S., Schwarz, M., and Behnke, S. (2019).
Refining 6D object pose predictions using abstract
render-and-compare. In IEEE-RAS 19th International
Conference on Humanoid Robots (Humanoids), pages
739–746.
Pharr, M., Jakob, W., and Humphreys, G. (2016). Phys-
ically based rendering: From theory to implementa-
tion. Morgan Kaufmann.
Ravi, N., Reizenstein, J., Novotny, D., Gordon, T., Lo, W.-
Y., Johnson, J., and Gkioxari, G. (2020). Accelerating
3D deep learning with PyTorch3D. In European Con-
ference on Computer Vision (ECCV).
Rodriguez, D., Cogswell, C., Koo, S., and Behnke, S.
(2018). Transferring grasping skills to novel instances
by latent space non-rigid registration. In IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 1–8.
Rodriguez, D., Huber, F., and Behnke, S. (2020). Category-
level 3D non-rigid registration from single-view RGB
images. IEEE/RSJ International Conference on Intel-
ligent Robots and Systems (IROS).
Ronneberger, O., Fischer, P., and Brox, T. (2015). U-
Net: Convolutional networks for biomedical image
segmentation. In International Conference on Medi-
cal image computing and computer-assisted interven-
tion (MICCAI), pages 234–241.
Schwarz, M. and Behnke, S. (2020). Stillleben: Realistic
scene synthesis for deep learning in robotics. IEEE
International Conference on Robotics and Automation
(ICRA).
Spitzer, J. (2003). OpenGL performance tuning. In NVIDIA
Corporation, GameDevelopers Conference.
Tappen, M. F., Freeman, W. T., and Adelson, E. H. (2005).
Recovering intrinsic images from a single image.
IEEE Transactions on Pattern Analysis and Machine
Intelligence (TPAMI), 27(9):1459–1472.
Wang, N., Zhang, Y., Li, Z., Fu, Y., Liu, W., and Jiang, Y.-
G. (2018). Pixel2Mesh: Generating 3D mesh models
from single RGB images. In European Conference on
Computer Vision (ECCV), pages 52–67.
Wang, Z., Bovik, A., Sheikh, H., and Simoncelli, E. (2004).
Image quality assessment: From error visibility to
structural similarity. IEEE Transactions on Image
Processing, 13(4):600–612.
Wang, Z., Simoncelli, E. P., and Bovik, A. C. (2003). Mul-
tiscale structural similarity for image quality assess-
Iterative 3D Deformable Registration from Single-view RGB Images using Differentiable Rendering
115

ment. In Asilomar Conference on Signals, Systems &
Computers (ACSSC), volume 2, pages 1398–1402.
Xiang, Y., Schmidt, T., Narayanan, V., and Fox, D. (2018).
PoseCNN: A convolutional neural network for 6D ob-
ject pose estimation in cluttered scenes. Robotics: Sci-
ence and Systems (RSS).
Xu, Y., Zhu, S.-C., and Tung, T. (2019). DenseRAC: Joint
3D pose and shape estimation by dense render-and-
compare. In IEEE International Conference on Com-
puter Vision (ICCV), pages 7760–7770.
Zagoruyko, S. and Komodakis, N. (2015). Learning to com-
pare image patches via convolutional neural networks.
In IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 4353–4361.
Zeng, Y., Wang, C., Wang, Y., Gu, X., Samaras, D., and
Paragios, N. (2010). Dense non-rigid surface registra-
tion using high-order graph matching. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 382–389.
Zhang, L., Zhang, L., Mou, X., and Zhang, D. (2011).
FSIM: A feature similarity index for image quality as-
sessment. IEEE Transactions on Image Processing,
20(8):2378–2386.
Zhang, R., Isola, P., Efros, A. A., Shechtman, E., and Wang,
O. (2018). The unreasonable effectiveness of deep
features as a perceptual metric. In IEEE Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 586–595.
Zienkiewicz, J., Davison, A., and Leutenegger, S. (2016).
Real-time height map fusion using differentiable ren-
dering. In IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS), pages 4280–
4287.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
116
