
Specularity, Shadow, and Occlusion Removal from Image Sequences
using Deep Residual Sets
Monika Kwiatkowski
a
and Olaf Hellwich
b
Computer Vision & Remote Sensing, Technische Universit
¨
at Berlin, Marchstr. 23, Berlin, Germany
Keywords:
Deep Sets, Deep Learning, Image Reconstruction, Background Reconstruction, Artifact Removal.
Abstract:
When taking images of planar objects, the images are often subject to unwanted artifacts such as speculari-
ties, shadows, and occlusions. While there are some methods that specialize in the removal of each type of
artifact individually, we offer a generalized solution. We implement an end-to-end deep learning approach
that removes artifacts from a series of images using a fully convolutional residual architecture and Deep Sets.
Our architecture can be used as general approach for many image restoration tasks and is robust to varying
sequence lengths and varying image resolutions. Furthermore, it enforces permutation invariance on the input
sequence. The architecture is optimized to process high resolution images. We also provide a simple online
algorithm that allows the processing of arbitrarily long image sequences without increasing the memory con-
sumption. We created a synthetic dataset as an initial proof-of-concept. Additionally, we created a smaller
dataset of real image sequences. In order to overcome the data scarcity of our real dataset, we use the syn-
thetic data for pre-training our model. Our evaluations show that our model outperforms many state of the art
methods that are used in related problems such as background subtraction and intrinsic image decomposition.
1 INTRODUCTION
When taking images of planar objects such as mag-
azines, paintings, posters, books, or facades, one is
confronted with many possible obstructions. Some of
these, such as specularities or shadows, may be due
to illumination, while others may be due to occlu-
sions. These effects can lead to information loss and
significantly reduce the image quality. It is often not
possible to capture a single flawless image, however
obstructions, such as specularities or occlusions, usu-
ally vary with the viewpoint of the camera or move
over time. Our proposed method aims to provide a
practical solution for reconstructing the content using
multiple partially-obstructed images.
We introduce a novel approach using deep learn-
ing that learns an end-to-end image transformation to
remove artifacts from a sequence of distorted images.
Due to the lack of an existing dataset, we generate
a synthetic dataset and a real dataset. Our synthetic
data creation process follows a realistic image forma-
tion model and creates complex artifacts containing
occlusions, specularities, shadows, and varying illu-
mination.
a
https://orcid.org/0000-0001-9808-1133
b
https://orcid.org/0000-0002-2871-9266
Training a deep neural network requires a large
amount of training data in order not to overfit. Our
real dataset is not large enough; however, we can
create an arbitrarily large amount of artificial data.
Therefore, we use a combined approach of pre-
training on artificial data (200,000 image sequences)
and only fine-tuning on the significantly smaller real
dataset (100 image sequences).
The proposed architecture uses the concept of
Deep Sets (Zaheer et al., 2017), making it robust to
varying lengths of input sequences and invariant to
permutation. We provide a memory-efficient algo-
rithm for processing arbitrarily long input sequences.
Furthermore, the architecture is fully-convolutional,
i.e. it can handle images of varying resolution. We
compare our deep learning method to unsupervised
methods that are commonly used for outlier removal,
background subtraction, and intrinsic image decom-
position.
2 RELATED WORK
Many methods deal with each problem individually,
typically modeling shadows as multiplicative distor-
tions of the original content, and specularities as ad-
118
Kwiatkowski, M. and Hellwich, O.
Specularity, Shadow, and Occlusion Removal from Image Sequences using Deep Residual Sets.
DOI: 10.5220/0010822300003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
118-125
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

ditive distortions. Some methods model the problem
as an intrinsic image decomposition, that is, an image
is decomposed into a reflectance image (albedo) and
a shading image. Reflectance describes the amount
of light an object reflects; it is an intrinsic value that
depends only on the object’s material. Shading is a
varying property that depends on the lighting condi-
tions and the position of objects relative to the light
sources. Background subtraction methods deal with
a similar problem. Given a series of images with a
dynamic foreground, the background has to be ex-
tracted, which is assumed to be constant.
One can differentiate between single-image and
multi-image approaches for artifact removal. Single-
image approaches use prior knowledge to identify
specularities (Artusi et al., 2011) and shadows (Fin-
layson et al., 2009), relying heavily on assumptions
about the appearance of said artifacts. Multi-image
approaches can use statistical properties (Weiss,
2001) or optimization (Yu, 2016) to combine infor-
mation from all images for reconstruction.
Deep learning approaches that do not rely on
rigid assumptions are used in many state-of-the-art
image processing tasks. Convolutional Neural Net-
works (CNNs) have been successfully used on sin-
gle images for shadow removal (Qu et al., 2017;
Hu et al., 2019) and specularity removal (Lin et al.,
2019). They have also been applied to intrinsic im-
age decomposition (Lettry et al., 2018). However,
none of these methods gives a general solution for
artifact removal. Moreover, there are few methods
that use multi-image approaches, even though addi-
tional images could provide more information for the
reconstruction. Furthermore, some objects, such as
paintings, photographs, or posters, can contain shad-
ows, specularities, and various objects as stylistic el-
ements. Single-image methods could distort parts of
the content by mistake. For example, without using
additional images, it can be impossible to differenti-
ate between a shadow that has been cast onto an book
cover and a shadow that is part of the book cover’s
content.
Our use case contains a combination of all previ-
ous problems: varying illumination, shadows, specu-
larities, and occlusions. This work proposes a univer-
sal approach, using deep learning that utilizes input
sequences in order to solve a more complex problem.
There are deep learning models that learn to trans-
form image sequences into single images (Chang and
Luo, 2019; Wang et al., 2018; Xingjian et al., 2015).
However, many methods that rely on RNNs, LSTMs,
transformers, or 3D convolutions do not enforce per-
mutation invariance or cannot handle dynamic se-
quence length. Moreover, many models are not very
memory efficient. They either require low resolution
images or they only process each image individually,
discarding a lot of information. Permutation invari-
ant CNNs have also been successfully used for image
deblurring (Aittala and Durand, 2018). However, the
proposed architecture can only handle low resolution
images.
Our work provides the following main contribu-
tions:
1. Our architecture removes shadows, occlusions,
and specularities simultaneously.
2. A synthetic dataset is created, using a 3D pipeline
to generate artificial image distortions. The
dataset can be used for pre-training machine
learning models.
3. A dataset with real distortions is created, using
commodity hardware.
4. We provide a general purpose deep learning archi-
tecture for image reconstruction from image se-
quences. The architecture is permutation invari-
ant, robust to varying sequence lengths, and ro-
bust to varying resolutions.
5. We show for our use case that one can overcome
data scarcity using pre-training on synthetic data.
6. The architecture was optimized to process images
sequences of at least 4K resolution. We provide a
simple online algorithm for processing arbitrarily
long image sequences using a constant memory
consumption.
3 DATASET
3.1 Synthetic Data
To the best of our knowledge, there is no la-
beled dataset containing aligned images with shad-
ows, specularities, and occlusions, together with
corresponding ground-truth. We therefore use a
dataset consisting of 207,572 images of book cov-
ers taken from Amazon (Iwana et al., 2016). We add
artificially-generated artifacts to these images and use
the original book cover as ground truth. The dataset
contains varying illuminations, occlusions and shad-
ows. Figure 1 shows how we create a 3D scene: we
position a plane such that it perfectly covers the im-
age plane when projected and apply one of our book
covers to this plane as a texture. We then generate
multiple point light sources of varying position, in-
tensity, and color. Afterwards, we position a random
object between the image plane and the book plane.
Specularity, Shadow, and Occlusion Removal from Image Sequences using Deep Residual Sets
119

Figure 1: Illustration of a random scene and the resulting
image. The white octahedron illustrates a point light source.
The pyramid shows the frustum of the perspective camera
and the image plane.
We create random reflectivity and roughness, which
affects the shininess of the texture and the brightness
of the book cover. These physical properties affect
the appearance of specularities and the effect of light-
ing on the underlying image. For occlusions, we use
a set of predefined geometries such as spheres, cones,
planes, etc. and we randomly sample a shape for each
scene, setting the orientation, size, texture, and posi-
tion of the object at random. Although we use a finite
number of shapes as occlusions, there are infinitely
many ways to position, scale and texturize them.
The dataset is not a perfect representation of a
realistic use-case, but it contains a broad variety of
image distortions, which makes it suitable for pre-
training our model. The pre-trained model can then
be fine-tuned on the real dataset.
3.2 Real Data
We create an additional dataset containing real image
sequences of planar objects, such as book covers and
movie covers. The dataset contains 100 image se-
quences, each containing 11 images. One image is
free of distortions, while the other 10 contain shad-
ows, specularities, and occlusions. The images were
taken indoors. The occlusions were created by plac-
ing various objects on top of the planar object. Specu-
larities were created with lamps and flashlights. Shad-
ows were cast onto the planar objects. The ground-
truth images were made by taking images of the pla-
nar objects under ambient illumination.
Each sequence was aligned using a feature based
method. We used a SIFT feature detector and
computed element-wise homographies between the
ground-truth image and all distorted images. In order
to further improve the alignment, we used a method
described by Schroeder et al. (2011) (Schroeder et al.,
2011). We then cropped the images so that they only
contain the content of the planar object.
4 DEEP LEARNING
4.1 Architecture
Our use-case requires the architecture to handle a dy-
namic number of input images. One possibility to im-
plement this would be to use models for sequential
data, such as recurrent neural networks or transform-
ers. However, RNNs and transformers are not permu-
tation invariant. Moreover, both architectures require
a lot of memory, limiting the maximal resolution of
the input images.
Therefore, we decided to use a Residual Network
for our architecture. Residual Networks (ResNets)
are used for many image restoration tasks; however,
they usually require a fixed number of input chan-
nels. To apply ResNets to dynamic input sequences,
we adapted the concept of Deep Sets by Zaheer et
al. (2017) (Zaheer et al., 2017). Deep Sets en-
force permutation invariance. Given a finite set X =
{x
1
, x
2
, ··· , x
N
}, a function f is permutation invariant,
if it can be decomposed as follows:
f (x
1
, x
2
, · ·· , x
N
) = ρ
N
∑
i=1
φ(x
i
)
!
(1)
ρ and φ describe deep learning models. Note that al-
though f takes an ordered sequence as input, the or-
der is irrelevant due to the commutative property of
the sum. Besides, neither ρ nor φ are dependent on N;
therefore, we can apply f to arbitrarily large image
sets.
We created an architecture that follows this de-
composition. The architecture consists of an encoder
φ and a decoder ρ, which both make use of resid-
ual blocks. However, we replace the summation by
a mean:
f (x
1
, x
2
, · ·· , x
N
) = ρ
1
N
N
∑
i=1
φ(x
i
)
!
(2)
The mean normalizes the embedding space and en-
forces a scale invariance. It has been shown that
ResNets are more robust to train than regular CNNs,
especially on data that is close to an identity mapping
(He et al., 2016). To increase the receptive field of
our architecture, we use dilation. Yu et al. (2017)
(Yu et al., 2017) showed that residual networks with
dilation have an increased receptive field and outper-
form most non-dilated models without increasing the
model complexity. Additionally, downsampling lay-
ers are used to reduce the dimensionality of the em-
bedding and to further increase the receptive field.
The downsampling layers are particularly necessary
to reduce memory consumption in order to apply the
architecture on high resolution image sequences.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
120

Figure 2 illustrates the encoder and decoder archi-
tecture and how they are combined. We use trans-
posed convolutions to upsample our feature maps.
Residual blocks decode the feature maps and generate
the resulting image. After every convolutional layer
in the encoder and decoder follows a ReLU-layer as
non-linearity. Our architecture is fully-convolutional
and can be applied on any image resolution.
Encoder
Image
Conv 2D
Strided
Conv 2D
Strided
Conv 2D
Residual
Block 1
Residual
Block 10
...
Embedding
Decoder
Residual
Block 1
Residual
Block 5
...
Embedding
Transposed
Conv 2D
Transposed
Conv 2D
Residual
Block 1
Residual
Block 6
...
Conv 2D Conv 2D
Restored
Image
Image n
Image 1
Image 2
...
Encoder
Encoder
Encoder
AVG Decoder
Restored
Image
Figure 2: The first two images illustrate the encoder and
decoder architecture. The third image shows how the en-
coder and decoder are used as building blocks in the overall
architecture.
4.2 Training
All our models are trained on a NVIDIA Geforce
RTX 2070 with 8GB memory. First, we train our
model on the synthetic data. We use 100,000 syn-
thetic image sequences for our training. The data
is split into 75% training data and 25% test data.
We use the Adam-optimizer with default parameters
β
1
= 0.9, β
2
= 0.999, ε = 10
−8
and a learning rate
λ = 0.0001. We use a decaying learning rate that is
reduced every 5 epochs by a factor of 10. The mean
squared error is used as optimization criterion. We
use varying sequence lengths of up to 9 images. We
use a batch size of 10 images sequences. All images
have a resolution of 256 × 256.
In order to apply our architecture to real images,
we fine-tune our previous model on real data. We split
the data into 60% training data and 40% test data. We
train the model using the same parameters as before.
The images have a resolution of 1024 × 1024. The
higher resolution increases memory consumption sig-
nificantly, such that the model is not able to process a
batch size of 10 images simultaneously. Instead, we
emulate the batch size by processing individual image
sequences and aggregating the gradients calculated by
backpropagation. After every 10th image sequence
we perform the optimization step.
4.3 Online Inference
The standard implementation of Deep Sets has a high
memory consumption, since an embedding φ(x
i
) has
to be computed and stored in memory for each input
image before summation. One can optimize this by
replacing the mean in (2) with an iterative computa-
tion:
e
0
:= 0 (3)
e
N
:=
1
N
N
∑
i=1
φ(x
i
) (4)
= e
N−1
+
φ(x
N
) − e
N−1
N
(5)
⇒ f (x
1
, · ·· , x
N
) = ρ(e
N
) (6)
A derivation for formula 5 can be seen in Finch
(2009)(Finch, 2009). e
N
is the accumulated average
of all results from the encoders up to the N-th input
image. e
N
can be computed iteratively using an on-
line algorithm (5). One can see that only the last ac-
cumulated result e
N−1
and the new encoding φ(x
N
)
have to be stored in memory instead of all embed-
dings φ(x
1
), · ·· φ(x
N
).
With this method, deep sets can be efficiently ap-
plied on arbitrarily long sequences. Formula (6) also
describes the applicability of online inference to real-
time data. Using this method, we are able to pro-
cess image sequences with 4K resolution on our GPU.
Note that the model requires much more memory dur-
ing training for gradient computations.
5 EVALUATION
5.1 Evaluation on Synthetic Data
We evaluate Residual Deep Set and several other
methods on our synthetic dataset using varying
lengths of input sequences n. From each image se-
quence, we randomly sample n images, which are
then used for reconstruction and evaluation; we repeat
this process 10 times for each image sequence. We
then compare the results of our architecture to those
of common approaches for outlier removal, back-
ground subtraction, and intrinsic image decomposi-
tion. Firstly, we use a pixel-wise median of the RGB
intensities for reference. Secondly, we use an intrin-
sic image decomposition method that uses a Maxi-
mum Likelihood Estimation (MLE) of the reflectance
Specularity, Shadow, and Occlusion Removal from Image Sequences using Deep Residual Sets
121

(Weiss, 2001). Thirdly, Robust PCA (RPCA) is being
used. RPCA uses optimization to decompose an im-
age into a low-rank image containing the content, and
a sparse image containing the artifacts(Bouwmans
et al., 2018). RPCA is a state-of-the-art method that
has been used both in background subtraction and in-
trinsic image decomposition (Yu, 2016). In addition,
the pixel-wise mean of the input sequence is used for
comparison as a worst-case solution that only attenu-
ates artifacts.
We use the mean squared error (MSE), the struc-
tural similarity index (SSIM), and the peak signal-to-
noise ratio (PSNR) as quality measures. 1,000 image
sequences, each containing 9 images from a valida-
tion set, are used for evaluation. Figures 3, 4 and
5 show the average error for each model on varying
lengths of input sequences.
Figure 3: MSE for each method applied on varying image
sequences of synthetic data.
Figure 4: SSIM for each method applied on varying image
sequences of synthetic data.
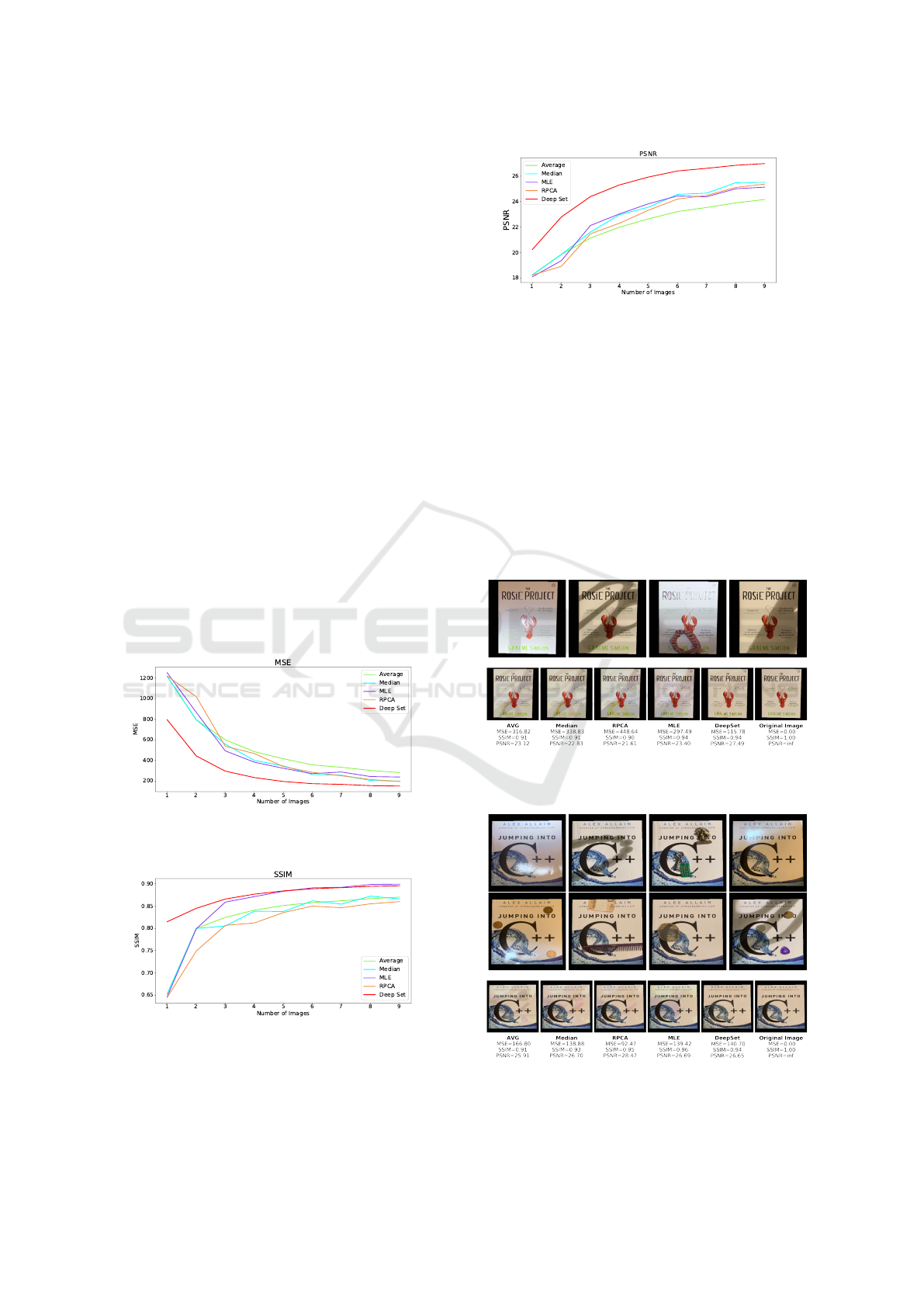
Figure 5: PSNR for each method applied on varying image
sequences of synthetic data.
Figure 6: Sequence of four distorted images from the syn-
thetic dataset with resulting reconstructions and error met-
rics.
Figure 7: Sequence of eight distorted images from the syn-
thetic dataset with resulting reconstructions and error met-
rics.
Our evaluation shows that the Deep Set architec-
ture has a consistently better performance compared
to all other unsupervised methods over all metrics.
As expected, the pixel-wise mean gives the worst re-
sults. Figures 6 and 7 illustrate the difficulty of the
reconstruction for classical outlier removal methods.
The artifacts overlap frequently and the underlying
content is rarely seen uncorrupted. The figures both
contain very complex illumination and specularities.
Even when parts of the image do not contain artifacts
such as shadows, occlusions, or specularities, the re-
construction is still ill-posed due to varying illumina-
tion. In figure 6, the statistical methods are unable to
remove the overlapping occlusions, while Deep Set is
able to extract the relevant content.
Since the encoder is applied on each image inde-
pendently, it is reasonable to assume that the averaged
embedding space of the encoders contains attenuated
features of artifacts, similar to the average in the RGB
color space. However, the result in figure 6 indicates
that the decoder is able to extract the real content from
the corrupted embedding. Moreover, the occlusions
are removed, despite their overlapping in three out of
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
122
four images. This implies that the architecture does
not solely rely on a pixel-wise consensus, but also
uses contextual information in each image.
Note that RPCA performs poorly on our synthetic
dataset. This is likely due to the fact, that RPCA as-
sumes sparse distortions. Since our image sequences
are relatively small compared to other background
subtraction tasks, many distortions are not considered
sparse by RPCA.
Figure 7 shows a sequence, where the illumina-
tion distorts the homogeneous color of the book. Al-
though it is impossible to extract the exact color, Deep
Set is the only method able to generate an image
with a homogeneous color. This requires a high-
level understanding of the image. We assume that the
large receptive field enables Deep Set to understand
the broader context of each image and makes it less
prone to errors inherent in methods, which are based
on pixel-wise statistics, e.g. mean, median or MLE
(Weiss, 2001).
5.2 Evaluation on Real Data
We use the 40 image sequences from our test set for
evaluation. All images have a resolution of 1024 ×
1024. We follow the same evaluation steps as for the
synthetic data. Figures 8, 9 and 10 show the results of
our evaluation.
Figure 8: MSE for each method applied on varying image
sequences of real data.
Figure 9: SSIM for each method applied on varying image
sequences of real data.
The evaluation on the real input images shows that
Deep Sets have the best performance with regards to
Figure 10: PSNR for each method applied on varying image
sequences of real data.
MSE and PSNR. MLE gives slightly better results
with regards to SSIM on longer input images. How-
ever, the examples in figure 11 and 12 show that no
metric fully captures the quality of the reconstruction.
In figure 11, the result of Deep Set has a much lower
MSE error than all of the other methods, but has the
same SSIM as MLE. In figure 12, RPCA has the re-
sult with the lowest MSE, although it contains more
ghosting artifacts than the results of MLE and Deep
Sets. Although the results of Deep Sets look promis-
ing, this suggests that MSE is not the most suitable
metric for optimizing our architecture. The exam-
Figure 11: Sequence of four distorted images from the real
dataset with resulting reconstructions, ground truth image,
and error metrics.
Figure 12: Sequence of eight distorted images from the real
dataset with reconstructed images, ground truth image, and
error metrics.
Specularity, Shadow, and Occlusion Removal from Image Sequences using Deep Residual Sets
123

ples also show that outlier removal methods such as
RPCA or median filtering, that are also used in back-
ground subtraction, can not remove varying illumina-
tion. The evaluation also confirms that one can com-
pensate for the lack of training data (with only 60 im-
age sequences available for training) using a synthetic
dataset.
6 ABLATION STUDY
In our ablation study, we tested various depths for
the encoder and decoder architecture. It is a trade-
off between reconstruction quality and memory-
consumption. The configuration shown in figure 2 is
best suited for our use case. Further increasing the
number of residual blocks for either component did
not significantly improve the quality of the resulting
model. However, the memory consumption increases
significantly with the depth of the encoder, because
the feature maps for each image in the sequence have
to be computed. Reducing the number of residual
blocks results in a worse reconstruction quality. Fur-
thermore, we evaluated the effect of dilation in our
residual blocks. Dilation significantly improves the
quality of the reconstruction, without changing the
number of parameters of the model, by increasing the
receptive field. Our Deep Residual Sets therefore an-
alyze a larger context of the images, which allows
them to better distinguish between a distorted image
patch and an undistorted one. Additionally, we tried
adding and removing downsampling layers (adjusting
upsampling layers accordingly). Increasing the num-
ber of downsampling layers reduces the quality of the
reconstruction due to information loss. However, not
using downsampling layers had no noticeable effect
on the reconstruction quality, it only increased the
memory consumption of the architecture. Memory
consumption is a limiting factor for our architecture.
It limits the batch size and maximum sequence length
of our model during training. Additionally, it limits
the maximum resolution our architecture can handle.
7 CONCLUSION AND FUTURE
WORK
In this paper, we introduced a deep learning architec-
ture, which can successfully learn to remove shadows,
specularities, and occlusions from image sequences.
The architecture uses residual blocks and the concept
of Deep Sets(Zaheer et al., 2017). The architecture
enforces permutation invariance and can be applied to
dynamic input sequences and high resolution images.
In section 4.3, we showed a memory-efficient method
for applying our architecture to arbitrarily long image
sequences, that is also suited for high resolutions, in-
cluding streaming data, without an increase in mem-
ory consumption.
We created a synthetic dataset containing complex
illumination, occlusions, shadows, and specularities
with corresponding ground truth data. The synthetic
dataset was initially created to establish a proof-of-
concept for our architecture and was later used for
pre-training the model. Our evaluation shows that
a supervised method can outperform unsupervised
methods for outlier removal, background subtraction,
and intrinsic image decomposition. Although the re-
construction is ambiguous and ill-posed, the model
was still able to generate images that were visually
consistent, see figure 7.
Furthermore, we evaluated our model on a real
dataset. Deep Set was able to compete with the ex-
isting methods. We showed that one can compensate
for the lack of a large dataset using synthetic data.
The model was pre-trained on synthetic data and fine-
tuned on the real data, resulting in a superior recon-
struction compared to unsupervised methods. This
method of pre-training on a large augmented dataset
combined with fine-tuning on a small real dataset is
especially helpful for use cases where it is hard or
impossible to obtain large datasets. We have shown
that Deep Sets are a simple and efficient method to
improve on existing deep learning models in image
restoration.
In future work, we are interested in applying Deep
Sets to other computer vision tasks utilizing multiple
images, such as super-resolution, background extrac-
tion, or panorama stitching. Introducing adversarial
loss could further enforce visually coherent results,
rather than exact reconstructions.
REFERENCES
Aittala, M. and Durand, F. (2018). Burst image deblurring
using permutation invariant convolutional neural net-
works. In Proceedings of the European Conference on
Computer Vision (ECCV), pages 731–747.
Artusi, A., Banterle, F., and Chetverikov, D. (2011). A
survey of specularity removal methods. In Computer
Graphics Forum, volume 30, pages 2208–2230. Wiley
Online Library.
Bouwmans, T., Javed, S., Zhang, H., Lin, Z., and Otazo,
R. (2018). On the applications of robust pca in im-
age and video processing. Proceedings of the IEEE,
106(8):1427–1457.
Chang, Y. and Luo, B. (2019). Bidirectional convolutional
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
124

lstm neural network for remote sensing image super-
resolution. Remote Sensing, 11(20):2333.
Finch, T. (2009). Incremental calculation of weighted mean
and variance.
Finlayson, G. D., Drew, M. S., and Lu, C. (2009). Entropy
minimization for shadow removal. International Jour-
nal of Computer Vision, 85(1):35–57.
He, K., Zhang, X., Ren, S., and Sun, J. (2016). Deep resid-
ual learning for image recognition. In Proceedings of
the IEEE conference on computer vision and pattern
recognition, pages 770–778.
Hu, X., Jiang, Y., Fu, C.-W., and Heng, P.-A. (2019). Mask-
shadowgan: Learning to remove shadows from un-
paired data. arXiv preprint arXiv:1903.10683.
Iwana, B. K., Rizvi, S. T. R., Ahmed, S., Dengel, A., and
Uchida, S. (2016). Judging a book by its cover. arXiv
preprint arXiv:1610.09204.
Lettry, L., Vanhoey, K., and Van Gool, L. (2018). Darn:
a deep adversarial residual network for intrinsic im-
age decomposition. In 2018 IEEE Winter Conference
on Applications of Computer Vision (WACV), pages
1359–1367. IEEE.
Lin, J., Seddik, M. E. A., Tamaazousti, M., Tamaazousti, Y.,
and Bartoli, A. (2019). Deep multi-class adversarial
specularity removal. In Scandinavian Conference on
Image Analysis, pages 3–15. Springer.
Qu, L., Tian, J., He, S., Tang, Y., and Lau, R. W. (2017). De-
shadownet: A multi-context embedding deep network
for shadow removal. In Proceedings of the IEEE Con-
ference on Computer Vision and Pattern Recognition,
pages 4067–4075.
Schroeder, P., Bartoli, A., Georgel, P., and Navab, N.
(2011). Closed-form solutions to multiple-view ho-
mography estimation. In 2011 IEEE Workshop on
Applications of Computer Vision (WACV), pages 650–
657.
Wang, W., Shen, J., Guo, F., Cheng, M.-M., and Borji,
A. (2018). Revisiting video saliency: A large-scale
benchmark and a new model. In Proceedings of the
IEEE Conference on Computer Vision and Pattern
Recognition, pages 4894–4903.
Weiss, Y. (2001). Deriving intrinsic images from image se-
quences. In Proceedings Eighth IEEE International
Conference on Computer Vision. ICCV 2001, vol-
ume 2, pages 68–75. IEEE.
Xingjian, S., Chen, Z., Wang, H., Yeung, D.-Y., Wong, W.-
K., and Woo, W.-c. (2015). Convolutional lstm net-
work: A machine learning approach for precipitation
nowcasting. In Advances in neural information pro-
cessing systems, pages 802–810.
Yu, F., Koltun, V., and Funkhouser, T. (2017). Dilated
residual networks. In Proceedings of the IEEE con-
ference on computer vision and pattern recognition,
pages 472–480.
Yu, J. (2016). Rank-constrained pca for intrinsic images de-
composition. In 2016 IEEE International Conference
on Image Processing (ICIP), pages 3578–3582. IEEE.
Zaheer, M., Kottur, S., Ravanbakhsh, S., Poczos, B.,
Salakhutdinov, R. R., and Smola, A. J. (2017). Deep
sets. In Advances in neural information processing
systems, pages 3391–3401.
Specularity, Shadow, and Occlusion Removal from Image Sequences using Deep Residual Sets
125
