
Viewpoint-independent Single-view 3D Object Reconstruction using
Reinforcement Learning
Seiya Ito
a
, Byeongjun Ju, Naoshi Kaneko
b
and Kazuhiko Sumi
c
Department of Integrated Information Technology, Aoyama Gakuin University, Fuchinobe, Sagamihara, Japan
Keywords:
3D Object Reconstruction, Reinforcement Learning.
Abstract:
This paper addresses the problem of reconstructing 3D object shapes from single-view images using rein-
forcement learning. Reinforcement learning allows us to interpret the reconstruction process of a 3D object
by visualizing sequentially selected actions. However, the conventional method used a single fixed viewpoint
and was not validated with an arbitrary viewpoint. To handle images from arbitrary viewpoints, we propose
a reinforcement learning framework that introduces an encoder to extract viewpoint-independent image fea-
tures. We train an encoder-decoder network to disentangle shape and viewpoint features from the image. The
parameters of the encoder part of the network are fixed, and the encoder is incorporated into the reinforcement
learning framework as an image feature extractor. Since the encoder learns to extract viewpoint-independent
features from images of arbitrary viewpoints, only images of a single viewpoint are needed for reinforcement
learning. The experimental results show that the proposed method can learn faster and achieves better accuracy
than the conventional method.
1 INTRODUCTION
Recovering the 3D shape of an object from im-
ages is one of the fundamental problems in com-
puter vision. It has a variety of applications such as
robotics, augmented reality, and human-computer in-
teraction. In recent years, 3D object reconstruction
has been greatly enhanced by deep learning. One
typical method is to train a neural network that out-
puts a 3D model directly from an image (Choy et al.,
2016; Girdhar et al., 2016; Hane et al., 2017; Fan
et al., 2017). Since this method only learns to out-
put plausible shapes from the data, it is difficult to
analyze how the method recovers the shape of the
object. Recently, several methods of approximating
the implicit function by neural networks have been
proposed (Mescheder et al., 2019; Park et al., 2019;
Chibane et al., 2020; Jiang et al., 2020; Ibing et al.,
2021). Since these methods learn the properties of
the 3D space, they are more interpretable than meth-
ods that estimate the shape directly from an image.
However, they do not provide a detailed step-by-step
reconstruction process.
a
https://orcid.org/0000-0002-7079-9116
b
https://orcid.org/0000-0002-5638-2509
c
https://orcid.org/0000-0002-9165-5912
While the reconstruction process is an essential
perspective in understanding how the model is recov-
ered during inference, it tends to be less noticeable.
One possible reason for this is that the 3D model is
generally more critical than the reconstruction pro-
cess since it is sufficient to obtain only the 3D model
for many applications. Nevertheless, making the re-
construction process interpretable has some potential.
For example, identifying the steps where inference
errors occur can feed into the development of better
methods. Moreover, analyzing the process of creat-
ing a good model may help us to elucidate effective
inference methods.
In order to make the reconstruction process inter-
pretable, a 3D object reconstruction method that mim-
ics human modeling using reinforcement learning has
been proposed (Lin et al., 2020). When humans use
modeling software to create a model, they divide it
into two stages: creating a coarse model and refin-
ing it. The reinforcement learning method learns an
agent for each of these stages. More specifically, start-
ing by placing multiple primitive shapes in 3D space,
it learns an agent that predicts a rough shape with
primitives and an agent that predicts a detailed shape
by deforming the mesh of primitives. As shown in
Fig. 1, this method provides an understandable recon-
struction process from a series of actions. However,
Ito, S., Ju, B., Kaneko, N. and Sumi, K.
Viewpoint-independent Single-view 3D Object Reconstruction using Reinforcement Learning.
DOI: 10.5220/0010825900003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
811-819
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
811

Figure 1: The reconstruction process. The method of (Lin et al., 2020) provides an understandable reconstruction process
using the action history. The top row shows the coarse shape reconstruction by deforming the primitives, and the bottom row
shows the detailed shape reconstruction by mesh deformation.
training and evaluation were performed using images
where all objects are rendered in the same pose and
from the same viewpoint. Therefore, the influence of
viewpoint changes is unexplored.
In this paper, we propose a 3D object reconstruc-
tion method based on reinforcement learning that can
handle image input from arbitrary viewpoints. The
proposed method is an extension of Lin et al.’s method
to handle arbitrary viewpoints. There are two chal-
lenges in learning using images from arbitrary view-
points: 1) how to handle arbitrary viewpoints, and 2)
how to train agents efficiently. For the first challenge,
we propose a viewpoint-independent image feature
extractor network trained on images from a few view-
points. For the second challenge, we propose a two-
stage learning strategy consisting of learning a feature
extractor and reinforcement learning. By pre-training
a viewpoint-independent image feature extractor net-
work, the proposed method can be trained on sin-
gle viewpoint images in reinforcement learning. In
our experiments, the proposed method achieves better
performance than the method of Lin et al. and shows
robustness to viewpoints.
2 RELATED WORK
This section reviews 3D object reconstruction from
images. We focus on the interpretability of the recon-
struction process.
Many methods have been proposed to recover
3D shapes in various representations such as vox-
els (Choy et al., 2016; Girdhar et al., 2016; Hane
et al., 2017; Riegler et al., 2017), point clouds (Fan
et al., 2017), and meshes (Wang et al., 2018; Wen
et al., 2019). Wang et al. proposed a method to
estimate the shape of an object in an input image
by transforming an elliptical mesh model as a refer-
ence (Wang et al., 2018). This method can interpret
the reconstruction process by tracking the model after
mesh deformation, but the process takes only a few
steps. Recently, approaches based on implicit func-
tions have shown promising results (Mescheder et al.,
2019; Park et al., 2019; Chibane et al., 2020; Jiang
et al., 2020; Ibing et al., 2021). Implicit functions
provide a compact representation of spaces such as
surfaces and occupancies. Unlike methods that di-
rectly output a model from an image, these methods
infer the properties of the space to recover the shape.
Therefore, it is possible to analyze how the final shape
is obtained. However, this is different from the pro-
cess of reconstruction from an image.
Another line of work is 3D object reconstruction
using a differentiable renderer (Kato et al., 2018; Liu
et al., 2019). Differentiable renderers can estimate 3D
shapes from images without 3D supervisory data. The
3D models estimated by the network during the learn-
ing process can be regarded as a shape reconstruction
process. However, it is difficult to obtain an accurate
3D model by inputting a single image only due to the
ambiguity of its shape.
Reinforcement learning is a method that allows
the interpretation of detailed reconstruction processes
even with a single image as input. Lin et al. pro-
posed a two-stage approach for reconstructing the 3D
shape of an object from a single image (Lin et al.,
2020). It defines the movement of vertices of multi-
ple cuboids as action and learns an agent that roughly
approximates the shape of the target object. Subse-
quently, additional vertices are added to the cuboids.
Another agent is then trained to refine the shape. Al-
though this approach is promising in terms of ex-
plainability, only images from the single fixed view-
point are used for training and evaluation. Through
preliminary experiments, we found that the accuracy
decreased when images from viewpoints unused for
training were given. Since reinforcement learning re-
quires a lot of time to obtain good rewards, it is in-
efficient to train with multiple views. Our method is
based on Lin et al.’s method, which is described in
detail in the next section.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
812

Prim-AgentMesh-Agent
𝑡
One-hot
encoding
・
・
・
16 32
1/5
1/3 1/3
64
Flatten
256
128 256
Concat
RGB Image
Step Number
Vertices of
Primitives
768 1024
675
・
・
・
Q-values
Action
Observation
FC + ReLU
Conv + BN + ReLU
FC
Max Pooling
𝑡
One-hot
encoding
・
・
・
16 32
64
Flatten
256
128 256
Concat
RGB Image
Step Number
Vertices of
Edge Loops
768 1024
360
・
・
・
Q-values
Action
Observation
Add Edge Loops
Feature Vectors
Feature Vectors
Reward
Reward
1/5 1/3 1/3
GT Model
3D Model
3D Model
Figure 2: Illustration of the overall framework for 3D object reconstruction based on reinforcement learning. We start by
placing multiple primitives in 3D space and learn a Prim-Agent that transforms the vertices of the primitives to roughly
approximate the target shape. Subsequently, we add edge loops to the resulting primitives and learn a Mesh-Agent that
deforms the mesh to recover the detailed shape. The numbers below the convolution and fully connected layers indicate the
output dimension. The numbers above the pooling layers represent the spatial resolution scale.
3 REVIEW OF
REINFORCEMENT LEARNING
FORMULATION
The proposed method is an extension of Lin et al.’s
method (Lin et al., 2020)
1
without viewpoint depen-
dency. This section reviews the formulation of their
reinforcement learning method. The overall frame-
work of Lin et al.’s method is illustrated in Fig. 2. In
this method, the shape of an object is recovered in two
stages in a coarse-to-fine manner. Specifically, it uses
the Prim-Agent to fit the 3D shape of the object in
the input image with multiple primitives, i.e., cuboids,
and the Mesh-Agent to obtain the detailed shape from
the model composed of the resulting cuboids. Sim-
ilar to their method, we also use these agents to re-
construct the 3D shape of an object. The proposed
method will be explained in Sec. 4, focusing on the
differences from their method.
1
While the original method takes a depth map as input,
it also takes an RGB image as input. The original code is
available at https://github.com/clinplayer/3DModelingRL
3.1 Primitive-based Shape Fitting
The goal at the first stage is to fit the rough shape
of the object in the input image with several primi-
tives. In this stage, the cuboid is used as a primitive
shape. Initially, m
3
cubes are placed evenly on the
3D grid. The shape of the cuboid is defined by the
coordinates of the two diagonal vertices. The Prim-
Agent manipulates the vertices of a cuboid based on
its current state. The environment rewards the Prim-
Agent for its actions, and the Prim-Agent is trained to
choose the optimal action. The detailed formulation
is described below.
State. Let a set of cuboids be P = {P
i
}
m
3
i=1
. The i-th
cuboid P
i
is defined by the two vertices V = (x, y, z)
and V
0
= (x
0
, y
0
, z
0
) on the diagonal. The state consists
of an input image, a set of cuboids, and a step number.
In this stage, m is set to 3.
Action. Moving the vertices of the i-th cuboid P
i
can be divided into three types: move V , move
V
0
, or delete P
i
. The movement range R = {r|r ∈
[−d, d], r 6= 0} is defined for each axis of each vertex.
The action space is a total of 2m
3
× 2d × 3 + m
3
with
two vertices of each cuboid, a move in each axis, and
Viewpoint-independent Single-view 3D Object Reconstruction using Reinforcement Learning
813

the removal of cuboids. In this stage, d = 2 is used,
and the total action space is 675.
Reward. In order for the Prim-Agent to choose the
appropriate action, the reward function based on the
intersection over union (IoU) is designed. The IoU
measures the overlap between the two shapes. Let T
denote the target shape. The IoU is defined as follows:
I
1
= IoU(
[
i
P
i
, T ), (1)
This term captures the global shape. In order for each
cuboid to cover much of the target shape, the local
IoU is computed:
I
2
=
1
|
¯
P |
∑
P
i
∈
¯
P
IoU(P
i
, T ), (2)
where
¯
P is the set of primitives that have not been
deleted. These two terms I
1
and I
2
are independent
of the number of primitives. To recover the shape of
the target with fewer primitives, the reward function
at the k-th step is defined as follows:
R
k
= α
1
(I
k
1
−I
k−1
1
)+α
2
(I
k
2
−I
k−1
2
)+α
3
(N
k
−N
k−1
),
(3)
where N
i
is the number of deleted primitives at the i-
th step and α
1
, α
2
, and α
3
are weighting coefficients.
Here, α
1
, α
2
, and α
3
are set to 1.0, 0.1, and 0.01,
respectively.
3.2 Mesh Deformation
The second stage aims to recover the detailed shape of
the object by deforming the resulting mesh of primi-
tives. Edge-based deformation is an effective method
to generate a natural shape with a small number of
vertices. Lin et al. assign edge loops to the cuboids
and train the Mesh-Agent to deform the mesh based
on the edge loops.
An edge loop is a series of connected edges on the
surface of an object. It circles the object and ends at
the starting point. The method of Lin et al. assigns n
edge loops to the cuboids obtained in the first stage.
For undeleted cuboids, edge loops are generated such
that the longest edge is perpendicular to an axis. The
number of edge loops assigned to a cuboid is propor-
tional to its volume, and the cuboids with larger vol-
umes are assigned more edge loops. Here, at least two
edge loops are assigned to a cuboid.
State. Let L = {L
i
}
n
i=1
be the set of edge loops. The
i-th edge loop L
i
is represented by two diagonal ver-
tices V
l
= (x
l
, y
l
, z
l
) and V
0
l
= (x
0
l
, y
0
l
, z
0
l
). The input
image, the set of edge loops, and the number of steps
are used for the state. In this stage, n is set to 10.
Action. Similar to Prim-Agent, Mesh-Agent de-
fines its action as the movement of two vertices that
make up an edge loop. For Mesh-Agent, d = 3 is
used, and the total action space is 360.
Reward. The role of the Mesh-Agent is to manip-
ulate the shape obtained by the Prim-Agent in more
detail to get closer to the target shape. Therefore, only
the IoU difference is used for the reward.
3.3 Imitation Learning
Imitation learning is a method of learning by using
actions that are optimal strategies. When the action
space is large, the probability of selecting the optimal
action by reinforcement learning alone is low, mak-
ing learning difficult. To solve this problem, Lin et al.
proposed a method to generate actions heuristically,
namely virtual experts. More specifically, the virtual
expert explores all potential actions and selects the ac-
tion that allows the agent to obtain the maximum re-
ward.
After imitation learning, reinforcement learning is
performed while retaining the generated action data.
However, if the number of viewpoints of images
used for reinforcement learning is increased, a large
amount of memory is required to maintain the data.
3.4 Reinforcement Learning
Lin et al. compared several algorithms (Ross et al.,
2011; van Hasselt et al., 2016; Hester et al., 2018) and
showed that DAgger with virtual experts using double
replay buffers based on Double DQN is effective. The
core idea is to reuse the experiences gained in imita-
tion learning for reinforcement learning to cope with
a large action space. The loss function is determined
by a sum of temporal difference update and the super-
vised loss such that the Q-value of the expert’s action
is at least marginally higher than the other actions:
L(θ) = L
T D
(θ) + L
S
(θ), (4)
L
S
(θ) = max
a∈A
(Q(s, a; θ) + l(s, a
E
, a)) − Q(s, a
E
;θ),
(5)
where A is a set of actions, Q(s, a, θ) is the Q-value of
an action a for the state s given the parameters of the
network θ, and l(s, a
E
, a) is a margin function that is
zero when the a is same as the expert’s action a
E
and
positive otherwise.
The reinforcement learning in the proposed
method follows the method of Lin et al. except that
the parameters of the image feature extraction net-
work are fixed. For more details, please refer to the
original paper (Lin et al., 2020).
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
814
RGB Image
Encoder
Viewpoint
Silhouette
𝑧
!"#$%
Classifier
16 32
1/5
1/3 1/3
64
Flatten
256 256
256
256
FC + ReLU
Conv + BN + ReLU
FC
Max Pooling
Deconv3D + BN + ReLU
Volume Projection
Deconv3D + Sigmoid
1128
64
32
2x
2x
2x
2x
256*
×4
!
Concat
Reshape
𝑧
&$
5
Decoder
Viewpoint-Independent
Image Feature Extractor
Feature
Volume
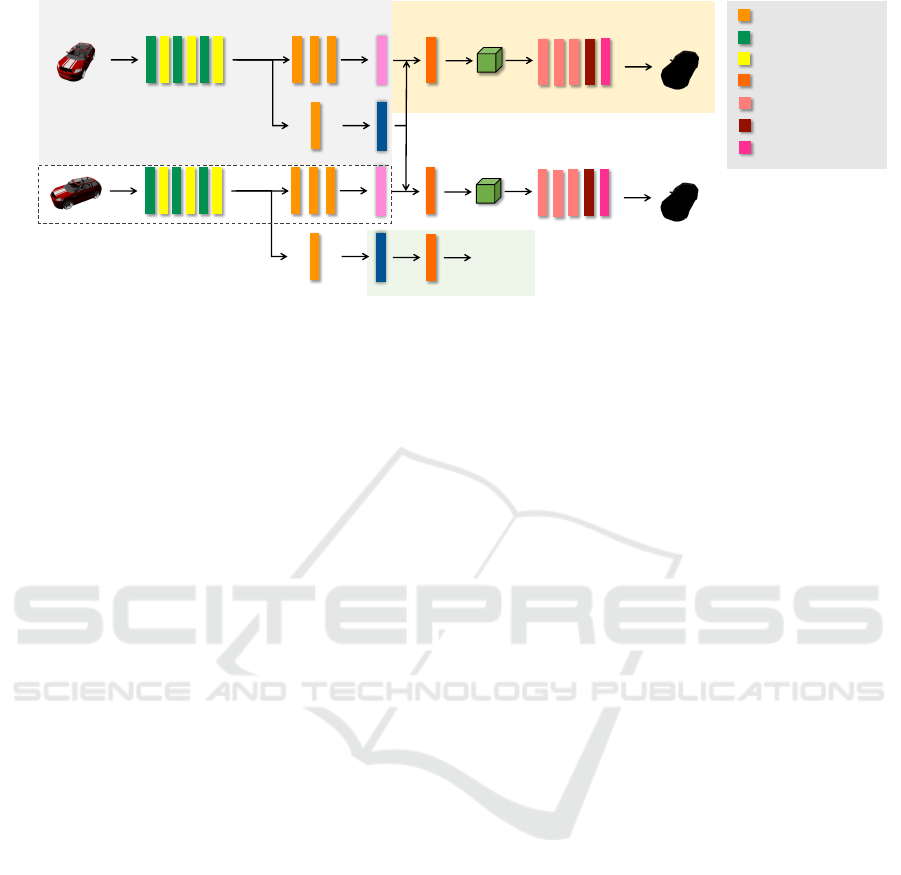
Figure 3: Illustration of the training pipeline for the encoder-decoder network. The encoder takes an RGB image as input
and extracts shape features and viewpoint features. The shape and viewpoint features are fed into the decoder network, which
outputs a silhouette of the input image corresponding to the viewpoint. By training the network with images from multiple
viewpoints and swapping the viewpoint features, the shape and viewpoint features are disentangled. The classification of
viewpoints encourages disentangling these features. The encoder-decoder network and the classier are shared between the
views. The network that extracts shape features from an image (surrounded by a dashed square) is used in reinforcement
learning. The numbers below the convolution and fully connected layers indicate the output dimension. The numbers above
the pooling and deconvolution layers represent the spatial resolution scale.
4 VIEWPOINT-INDEPENDENT
RECONSTRUCTION
The proposed method eliminates viewpoint depen-
dency by extracting viewpoint-independent features
from images. The overall architecture is the same
as (Lin et al., 2020), except for the image feature
extractor. As shown in Fig. 2, actions are inferred
from states, i.e., vertices of models, images, and steps.
We train an encoder-decoder network that decom-
poses image into features that encode object shape
and viewpoint. The shape features extracted by this
network are used as image features for reinforcement
learning.
4.1 Viewpoint-independent Image
Feature Extraction Network
The training pipeline for the encoder-decoder network
is illustrated in Fig. 3. The encoder network takes an
input image I
v
of the viewpoint v and outputs the im-
age features. These features are passed through two
separate fully connected layers to obtain the shape
features z
shape
and viewpoint features z
vp
. The de-
coder network D takes the shape features and the
viewpoint features z
vp
as inputs and produces a 3D
occupancy grid. The occupancy grid is then projected
onto the predefined viewpoint, yielding a silhouette
image I
s
. To encourage the learning of the encoder,
we use the viewpoint features z
vp
to classify the view-
points.
The proposed encoder network is a minor exten-
sion of the image feature extractor in the method of
Lin et al. The network consists of several convolu-
tional, batch normalization, and max-pooling layers
to generate 256-dimensional feature vectors from im-
ages. From these feature vectors, shape features are
generated through three fully connected layers with
the same number of dimensions (i.e., 256). In a sim-
ilar way, viewpoint features are generated through a
fully connected layer, and the resulting features are
fed into a classifier consisting of a fully connected
layer. The decoder network first constructs 256-
dimensional feature volumes of size 4
3
by passing
the shape features concatenated with viewpoint fea-
tures to a fully connected layer and then reshaping it.
Then, we upsample the feature volume through three
3D deconvolutional layers while reducing the number
of feature channels by half. Finally, we apply a 3D
deconvolution to obtain an occupancy map with size
64
3
.
Once the proposed network has been trained, the
image feature extractor of the proposed network is
incorporated into the reinforcement learning frame-
work. While adding the fully connected layers to
the original network increases the number of param-
eters, the image feature extractor does not need to be
trained by reinforcement learning. The losses to make
this image feature extractor viewpoint-independent
are explained in Sec. 4.3.
Viewpoint-independent Single-view 3D Object Reconstruction using Reinforcement Learning
815

(a) Input image. From left to right, the viewpoints are 0
◦
, 72
◦
, 144
◦
, 216
◦
, and 288
◦
.
(b) (Lin et al., 2020). From left to right, the IoU values are 0.616, 0.639, 0.657, 0.641, and 0.648.
(c) Ours. From left to right, the IoU values are 0.617, 0.702, 0.677, 0.709, and 0.783.
Figure 4: Qualitative comparison of the proposed method with the baseline method. In the baseline method, we trained agents
with five different perspectives. The proposed method trained the encoder with five views, but only one view was used for
reinforcement learning.
4.2 Volume Projection Layer
The decoder network generates a silhouette image
from the occupancy map corresponding to the pre-
defined viewpoint by a projection layer. The pro-
posed method first constructs the occupancy grid to
the viewpoint using shape and viewpoint features. For
each pixel x, the probability of a silhouette image I
s
(x)
is then calculated from the occupancies of the voxels
through which the ray passes {P
x
i
}
N
i=1
as follows:
I
s
(x) = max
k
P
x
k
(6)
This means that the maximum occupancy of the voxel
where the ray intersects is used as the silhouette value.
4.3 Loss Functions
To train the encoder-decoder network, we use images
from different viewpoints V . When each image is
passed through the encoder, shape features and view-
point features are obtained for each. To ensure that
the same object has the same shape features, we use
the difference in shape features as a loss:
L
shape
=
∑
v
0
∈
¯
V
|z
v
shape
− z
v
0
shape
|
1
(7)
where
¯
V represents all viewpoints except for v. To
enforce that the occupancy grid generated from the
shape features matches when projected to an arbitrary
viewpoint, we compute the silhouette loss:
L
silhouette
=
∑
v
0
∈V
|
ˆ
I
s
− D(z
v
0
shape
, z
v
vp
)|
1
(8)
where
ˆ
I
s
is the ground truth silhouette image. In addi-
tion, we introduce the viewpoint classification loss as
an auxiliary loss:
L
vp
= H(ˆv, v) (9)
where H is the cross entropy loss and ˆv is the ground
truth viewpoint. Finally, the overall loss function is
defined as follows:
L = λ
1
L
shape
+ λ
2
L
silhouette
+ λ
3
L
vp
(10)
where λ
1
, λ
2
, and λ
3
are weighting coefficients. Here,
λ
1
, λ
2
, and λ
3
are set to 1.0, 0.5, and 1.0, respectively.
5 EXPERIMENTS
5.1 Experimental Setup
In this work, we focus on the dependency of view-
points in 3D object reconstruction using reinforce-
ment learning. In this experiment, we basically follow
the experimental setup of Lin et al. (Lin et al., 2020)
and verify the effectiveness of the proposed method
for viewpoint dependency.
Dataset. We use the ShapeNet dataset (Chang et al.,
2015) for training and testing. Following Lin et al.,
we picked up three categories, i.e., cars, airplanes,
and guitars from ShapeNet. Each category contains
650 models, where 600 are used for training and the
remaining 50 for testing. For all models, we rendered
30 RGB images so that the camera rotated evenly
around the object.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
816

Table 1: Comparison of the proposed method with the baseline method. Note that this experiment uses RGB images as input.
While Lin et al. only report results using depth images as input, they provide models trained using RGB images. We used the
provided models to evaluate Lin et al.’s method that uses a single viewpoint for reinforcement learning.
Method
Viewpoints Car Airplane Guitar
Pre-training RL Evaluation Reward IoU Reward IoU Reward IoU
Lin et al. - 1 1 1.014 0.569 0.744 0.200 0.792 0.241
Lin et al. - 1 5 0.810 0.427 0.590 0.127 0.796 0.297
Lin et al. - 5 5 0.926 0.517 0.291 0.069 0.914 0.320
Ours 5 1 5 0.961 0.535 0.731 0.204 0.975 0.364
Ours 5 5 5 0.965 0.547 0.734 0.209 0.998 0.366
(a) Airplane
(b) Guitar
Figure 5: Comparison of the proposed method with the baseline method on the airplane and guitar classes. From top to
bottom, input images, results of the baseline method, and results of the proposed method are shown. From left to right, the
viewpoints are 0
◦
, 72
◦
, and 144
◦
.
Training. We first train the proposed encoder-
decoder network from scratch for 200 epochs.
The network was trained using the Adam opti-
mizer (Kingma and Ba, 2015) with a mini-batch
size of 32. The initial learning rate is set to 8e-4.
It takes about 2 hours to train the network on an
NVIDIA TITAN RTX GPU. Subsequently, the two
agents are trained in the same settings as the base-
line method (Lin et al., 2020), with 100 epochs each.
When training a single viewpoint, it takes about eight
days to train two agents. Five viewpoints require five
times as much learning time as one viewpoint. Since
the reinforcement learning of the proposed method
can learn from a single viewpoint, the five-viewpoint
setting of the proposed method is only two additional
hours to the time required for the one-view setting of
the baseline.
5.2 Comparison with the Baseline
Method
We compare the proposed method with the base-
line method (Lin et al., 2020) using images from
five viewpoints, i.e., 0
◦
, 72
◦
, 144
◦
, 216
◦
, and 288
◦
.
Here, the reinforcement learning setup in the pro-
posed method is the same as in Lin et al. For the
single-view training, we used images from 72
◦
.
Table 1 shows the quantitative evaluation of the
proposed method and the baseline method. We use
cumulative reward and IoU as evaluation metrics.
Since the baseline method trained with only one view-
point is less accurate than the method trained with five
viewpoints, it does not cope with unseen viewpoints.
Using multi-view images in the pre-training allows
the proposed method to learn with only one view-
point in the reinforcement learning stage and achieves
higher accuracy than the baseline. In addition, the ac-
curacy of the proposed method is further improved
when reinforcement learning is performed using im-
ages from five viewpoints. However, reinforcement
learning with five viewpoints requires a large amount
of memory, and the learning speed is slow. On the
other hand, the memory needed for pre-training in
the proposed method is smaller than reinforcement
learning. Moreover, the convergence time of the pre-
training and the reinforcement learning using a single
Viewpoint-independent Single-view 3D Object Reconstruction using Reinforcement Learning
817
(a) Car (b) Airplane (c) Guitar
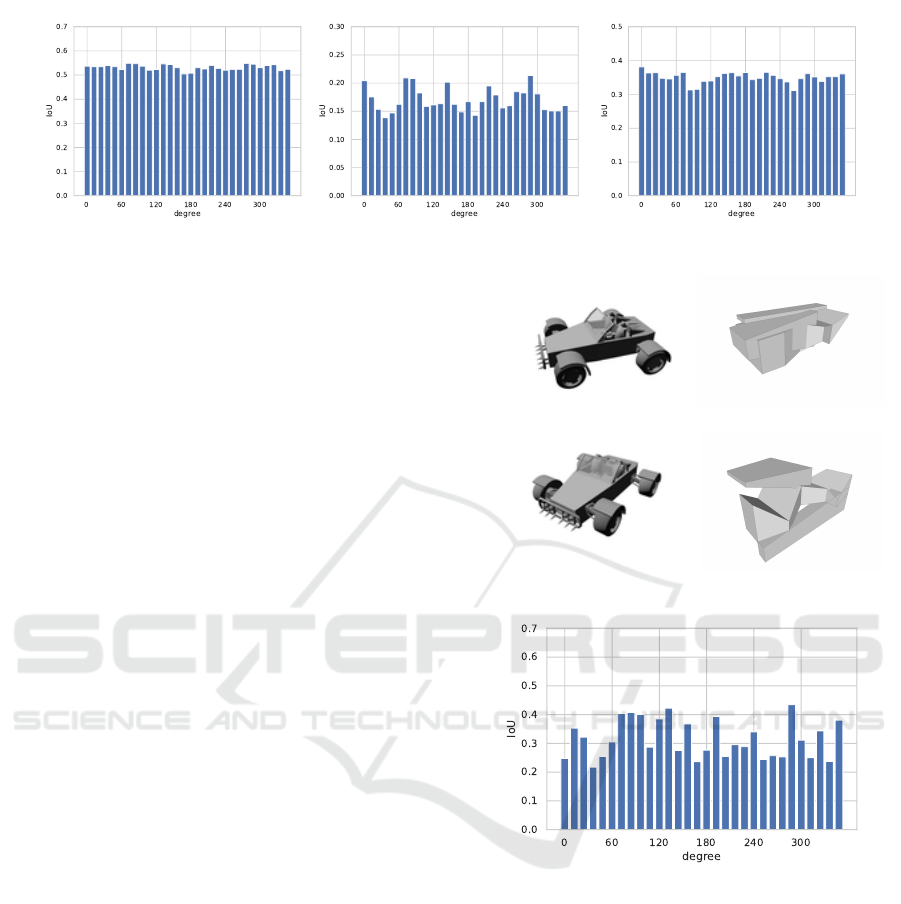
Figure 6: Performance of the proposed method with respect to viewpoints.
viewpoint image is shorter than that of the baseline
method with five viewpoints, suggesting that the pro-
posed method is more efficient.
The qualitative evaluation of the proposed method
and the baseline method is shown in Fig. 4. The pro-
posed method shows qualitatively less shape variation
between viewpoints than the baseline method. Fig. 5
shows the results of the proposed method for airplane
and guitar classes. As with the car class, similar mod-
els are reconstructed from different viewpoints.
5.3 Influence of Viewpoints
The goal of this study is to robustly recover the 3D
shape when the input image has a different viewpoint
from the training one. Fig. 6 shows mean IoU val-
ues of 30 viewpoints. Here, we used a model trained
with images from five viewpoints for pre-training and
one viewpoint for reinforcement learning. The model
trained by the proposed method is almost as accurate
as the one used for training, even when images from
viewpoints not used for training are input.
Although the proposed method is robust to the
viewpoint, the accuracy is low for some shapes as
well as the baseline method. Fig. 7 shows the fail-
ure example of the proposed method. The proposed
method is less accurate for any viewpoint when the
shape is complex. Fig. 7(c) shows that the accuracy
decreases for viewpoints far from the one used for
training, while it increases for viewpoints close to the
one used for training.
6 CONCLUSION
In this work, we proposed a 3D object reconstruc-
tion method using reinforcement learning that is ro-
bust to the viewpoint of the input image. The pro-
posed method first trains an encoder network to de-
compose image features into geometry and viewpoint
factors. Our method fixes the network parameters and
(a) Viewpoint used during training (72
◦
, IoU: 0.408)
(b) Unseen viewpoint (36
◦
, IoU: 0.218)
(c) IoU
Figure 7: Failure cases of the proposed method.
uses the network for reinforcement learning as an im-
age feature extractor. The proposed method achieved
more accurate estimation results than the baseline
method trained on images with multiple viewpoints.
In addition, we experimentally show that the proposed
method can estimate with the same accuracy even for
views that are not used for training.
ACKNOWLEDGEMENT
This work was supported by JSPS KAKENHI Grant
Number JP20J13300.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
818

REFERENCES
Chang, A. X., Funkhouser, T. A., Guibas, L. J., Hanra-
han, P., Huang, Q., Li, Z., Savarese, S., Savva, M.,
Song, S., Su, H., Xiao, J., Yi, L., and Yu, F. (2015).
ShapeNet: An Information-Rich 3D Model Reposi-
tory. CoRR, arXiv:1512.03012.
Chibane, J., Alldieck, T., and Pons-Moll, G. (2020). Im-
plicit Functions in Feature Space for 3D Shape Recon-
struction and Completion. In IEEE/CVF Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 6968–6979.
Choy, C. B., Xu, D., Gwak, J., Chen, K., and Savarese, S.
(2016). 3D-R2N2: A Unified Approach for Single and
Multi-view 3D Object Reconstruction. In European
Conference on Computer Vision (ECCV), pages 628–
644.
Fan, H., Su, H., and Guibas, L. J. (2017). A Point Set Gen-
eration Network for 3D Object Reconstruction from
a Single Image. In IEEE Conference on Computer
Vision and Pattern Recognition (CVPR), pages 2463–
2471.
Girdhar, R., Fouhey, D. F., Rodriguez, M., and Gupta, A.
(2016). Learning a Predictable and Generative Vector
Representation for Objects. In European Conference
on Computer Vision (ECCV), pages 484–499.
Hane, C., Tulsiani, S., and Malik, J. (2017). Hierarchical
Surface Prediction for 3D Object Reconstruction. In
International Conference on 3D Vision (3DV), pages
412–420.
Hester, T., Vecer
´
ık, M., Pietquin, O., Lanctot, M., Schaul,
T., Piot, B., Horgan, D., Quan, J., Sendonaris, A.,
Osband, I., Dulac-Arnold, G., Agapiou, J. P., Leibo,
J. Z., and Gruslys, A. (2018). Deep Q-learning From
Demonstrations. In Thirty-Second AAAI Conference
on Artificial Intelligence (AAAI), pages 3223–3230.
Ibing, M., Lim, I., and Kobbelt, L. (2021). 3D Shape Gen-
eration With Grid-Based Implicit Functions. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 13559–13568.
Jiang, C. M., Sud, A., Makadia, A., Huang, J., Nießner, M.,
and Funkhouser, T. A. (2020). Local Implicit Grid
Representations for 3D Scenes. In IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 6000–6009.
Kato, H., Ushiku, Y., and Harada, T. (2018). Neural 3D
Mesh Renderer. In IEEE Conference on Computer
Vision and Pattern Recognition (CVPR), pages 3907–
3916.
Kingma, D. P. and Ba, J. (2015). Adam: A Method for
Stochastic Optimization. In 3rd International Confer-
ence on Learning Representations (ICLR).
Lin, C., Fan, T., Wang, W., and Nießner, M. (2020). Model-
ing 3D Shapes by Reinforcement Learning. In Euro-
pean Conference on Computer Vision (ECCV), pages
545–561.
Liu, S., Chen, W., Li, T., and Li, H. (2019). Soft Raster-
izer: A Differentiable Renderer for Image-Based 3D
Reasoning. In IEEE/CVF International Conference
on Computer Vision (ICCV), pages 7707–7716.
Mescheder, L. M., Oechsle, M., Niemeyer, M., Nowozin,
S., and Geiger, A. (2019). Occupancy Networks:
Learning 3D Reconstruction in Function Space. In
IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 4460–4470.
Park, J. J., Florence, P., Straub, J., Newcombe, R. A., and
Lovegrove, S. (2019). DeepSDF: Learning Continu-
ous Signed Distance Functions for Shape Represen-
tation. In IEEE Conference on Computer Vision and
Pattern Recognition (CVPR), pages 165–174.
Riegler, G., Ulusoy, A. O., and Geiger, A. (2017). OctNet:
Learning Deep 3D Representations at High Resolu-
tions. In IEEE Conference on Computer Vision and
Pattern Recognition (CVPR), pages 6620–6629.
Ross, S., Gordon, G. J., and Bagnell, D. (2011). A Reduc-
tion of Imitation Learning and Structured Prediction
to No-Regret Online Learning. In Fourteenth Interna-
tional Conference on Artificial Intelligence and Statis-
tics (AISTATS), volume 15, pages 627–635.
van Hasselt, H., Guez, A., and Silver, D. (2016). Deep
Reinforcement Learning with Double Q-Learning. In
Thirtieth AAAI Conference on Artificial Intelligence
(AAAI), pages 2094–2100.
Wang, N., Zhang, Y., Li, Z., Fu, Y., Liu, W., and Jiang,
Y. (2018). Pixel2Mesh: Generating 3D Mesh Models
from Single RGB Images. In European Conference
on Computer Vision (ECCV), pages 55–71.
Wen, C., Zhang, Y., Li, Z., and Fu, Y. (2019).
Pixel2Mesh++: Multi-View 3D Mesh Generation via
Deformation. In IEEE/CVF International Conference
on Computer Vision (ICCV), pages 1042–1051.
Viewpoint-independent Single-view 3D Object Reconstruction using Reinforcement Learning
819
