
Ensemble Clustering for Histopathological Images Segmentation using
Convolutional Autoencoders
Ilias Rmouque
1
, Maxime Devanne
2 a
, Jonathan Weber
2 b
,
Germain Forestier
2 c
and C
´
edric Wemmert
1 d
1
ICube, University of Strasbourg, France
2
IRIMAS, University of Haute-Alsace, France
Keywords:
Digital Pathology, Deep Learning, Autoencoders, Histopathology, Ensemble Learning, Segmentation.
Abstract:
Unsupervised deep learning using autoencoders has shown excellent results in image analysis and computer
vision. However, only few studies have been presented in the field of digital pathology, where proper labelling
of the objects of interest is a particularly costly and difficult task. Thus, having a first fully unsupervised
segmentation could greatly help in the analysis process of such images. In this paper, many architectures of
convolutional autoencoders have been compared to study the influence of three main hyperparameters:
(1) number of convolutional layers, (2) number of convolutions in each layer and (3) size of the latent space.
Different clustering algorithms are also compared and we propose a new way to obtain more precise results
by applying ensemble clustering techniques which consists in combining multiple clustering results.
1 INTRODUCTION
Pathology is essential for the diagnosis evaluation
and understanding of many underlying biological and
physiological mechanisms. It is usually a visual eval-
uation by pathologists of a tissue sample using a mi-
croscope to identify its structural properties. Cur-
rently, the visual evaluation of microscopic specimens
is largely an unassisted process, and the pathologist’s
accuracy is established through extensive training,
comparative analysis, peer quality control and per-
sonal experience. However, this field has undergone
several technological revolutions in recent years with
the advent of virtual microscopy (conversion of glass
slides into high-resolution images called Whole Slide
Images - WSI), often referred to as ”digital pathol-
ogy”. Thus, major efforts have been made to design
image analysis tools, for example to identify basic
biological structures (stroma, immune cells, tumour,
etc.), in order to make it easier for doctors to (semi-
)automate the interpretation of slides. Meanwhile, au-
tomatic image analysis algorithms have recently made
extraordinary progress, particularly with the advent
a
https://orcid.org/0000-0002-1458-3855
b
https://orcid.org/0000-0002-3694-4703
c
https://orcid.org/0000-0002-4960-7554
d
https://orcid.org/0000-0002-4360-4918
of the deep learning methods introduced by Lecun et
al. (LeCun et al., 2015). Indeed, the performances of
these methods have exploded in recent years, allow-
ing the detection, classification and segmentation of
objects of interest in images and particularly in med-
ical images with high precision (Bukala et al., 2020;
Ando and Hotta, 2021). But most of these approaches
operate in supervised mode, i.e. they require many ex-
amples in order to provide an effective model. How-
ever, obtaining quality annotations on histopatholog-
ical images remains very costly. For example, in the
field of colorectal cancer WSI segmentation, Qaiser
et al. proposed a method based on persistent ho-
mology to classify tumour and non-tumour patches
from Hematoxylin & Eosin stained histology images
(Qaiser et al., 2016). To train their system, more than
18,000 annotated patches were needed. At the same
time, unsupervised approaches have shown their in-
terest in many applications for image analysis, such as
remote sensing (Liang et al., 2018; Mei et al., 2019).
Recently, they have also been applied to histopatho-
logical WSI analysis for cells segmentation (Junior
and Backes, 2021) or regions of interest classification
(Figueira et al., 2020). In particular for cancer, the au-
thors in (Yamamoto et al., 2019) describe an unsuper-
vised approach for extracting interesting information
from WSI that obtains better accuracy than human for
prognostic prediction of prostate cancer recurrence.
Rmouque, I., Devanne, M., Weber, J., Forestier, G. and Wemmert, C.
Ensemble Clustering for Histopathological Images Segmentation using Convolutional Autoencoders.
DOI: 10.5220/0010835300003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages
933-940
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved
933

In this paper, we are interested in automatic seg-
mentation in order to quickly extract regions of in-
terest (tumours for example) to make a more precise
analysis of these areas only. However, only few ap-
proaches on fully unsupervised segmentation of WSI
have been proposed. The first attempt to segment
regions of interest from WSI without any prior in-
formation or examples has been performed in (Khan
et al., 2013). The authors highlight tissue morphol-
ogy in breast cancer histology images by calculating
a set of Gabor filters to discriminate different regions.
In (Fouad et al., 2017), the authors use mathemati-
cal morphology to extract ‘virtual-cells’ (e.g. super-
pixels), for which morphological and colour features
are calculated to then apply a consensus clustering al-
gorithm to identify the different tissues in the image.
More recently, a similar approach has been presented
in (Landini et al., 2019), adding a semi-supervised
self-training classifier to the previous techniques that
enhances the results at the cost of partial supervision.
All these approaches propose to cluster the image
based on predefined features. However, deep learn-
ing approaches, particularly via autoencoding archi-
tectures, make it possible to avoid manual definition
of features by calculating a condensed representation
of the image in a latent space by applying convolu-
tional filters. Unfortunately, as stated in (Raza and
Singh, 2018), most applications of autoencoders in
digital pathology were developed to perform cell seg-
mentation or nuclei detection (Xu et al., 2015; Hou
et al., 2019), or stain normalisation (Janowczyk et al.,
2017). Therefore, we propose here to study the po-
tential of these approaches for WSI tissue segmenta-
tion. The aim is to try to automatically identify clus-
ters corresponding to each type of tissue in the WSI
that could then be labelled by pathologists.
In this paper, we present a study on how convolu-
tional autoencoders perform on WSI segmentation by
comparing different approaches. First, different au-
toencoders architectures are compared to quantify the
importance of hyperparameters of interest (number of
convolutional layers, number of convolutions by layer
and size of the latent space). Then, a multi-resolution
approach using an ensemble clustering framework is
evaluated, to see if such ensemble techniques could
provide more accurate results.
2 METHODS
2.1 Convolutional Autoencoders
In this section, we explore of the use of convolu-
tional autoencoders to cluster WSI histopathological
images. For this, we present several experiments to
evaluate the importance of each hyperparameter.
As shown in Figure 1, a Convolutional AutoEn-
coder (CAE) is a deep convolutional neural network
composed of two parts: an encoder and a decoder.
The main purpose of the CAE is to minimise a loss
function L, evaluating the difference between the in-
put and the output of the CAE (usually Mean Squared
Error). Once this function is minimised, we can as-
sume that the encoder part builds up a suitable sum-
mary of the input data, in the latent space, as the de-
coder part is capable of reconstructing an accurate
copy of it from this encoded representation.
The encoder is first constituted of the input layer
(having the size of the input image) which is con-
nected to N convolutional layers of diminishing size,
up to an information bottleneck of size Z, called the
latent space. The bottleneck is connected to a se-
ries of N convolutional layers of increasing size, un-
til reaching the size of the input. This second part
is called the decoder. Each convolution layer is com-
posed of C convolutions and is followed by three other
layers: a batch normalisation, an activation function
(ReLU) and a max pooling of size (2,2).
To perform the clustering, a trained CAE is used to
encode each patch of the whole image. Then, this en-
coded representation of the patch (in the latent space)
is given as the input of a clustering algorithm and a
cluster is assigned to the patch.
We decided to evaluate the influence of the three
hyperparameters N, Z and C. For each one, different
values were tested while fixing the two others (N =
2, Z = 250, C = 10). To evaluate the quality of the
results, the Adjusted Rand Index (ARI) is calculated
to compare the obtained clustering to the annotations
of the expert. The Rand Index computes a similarity
measure between two clusterings by considering all
pairs of samples and counting pairs that are assigned
in the same or different clusters in the predicted and
true clusterings. The score is then normalised into the
ARI score by:
ARI =
(RI − Expected RI)
(max(RI) − Expected RI)
(1)
Values of the ARI are close to 0 for random la-
belling independently of the number of clusters and
samples, and exactly 1 when the clusterings are iden-
tical (up to a permutation).
Each CAE was trained over a set of 10,000 differ-
ent patches randomly selected. As the result of both
the clustering and the training of the CAE are non-
deterministic, due to a high sensitivity to the initial
conditions, 10 autoencoders were trained and the re-
sults averaged for each hyperparameter value.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
934

Figure 1: Architecture of a CAE with N = 2, C = 10 and Z = 50.
We also investigated the performance of several
clustering algorithms, i.e Kmeans, Agglomerative
clustering (AggCl), Gaussian mixture (GM) and also
the not too deep clustering method (N2D) exposed in
(McConville et al., 2020). A clustering performed
directly with the Kmeans algorithm on the raw data
(without any data reduction by the CAE) has been cal-
culated as a baseline to evaluate the benefit of encod-
ing the data with the CAE.
2.2 Ensemble Clustering
As exposed in (Yamamoto et al., 2019), both micro-
structures and macro-structures give different infor-
mation. Pathologists also agree that identifying a sin-
gle cell is way more difficult without its surrounding
context and they always look at the WSI at lower
magnification (to better capture the context) before
zooming in at high magnification. Furthermore, in
(Alsubaie et al., 2018) an example of multi-resolution
lung cancer adenocarcinoma classification using deep
learning shows improvements in the overall accuracy.
Thus, we explored a way to improve the results by
using an ensemble of clustering methods, each focus-
ing on a different resolution. The objective is to merge
low level information (context) with high level infor-
mation (shape of the cells, etc.). For this, the con-
sensus method proposed in (Wemmert and Ganc¸arski,
2002) was used. This method is based on a the eval-
uation of the similarity between different clusterings
and the definition of corresponding clusters. Then, a
multi-view voting approach is computed to produce
a single result representing all clusterings. An exam-
ple of the architecture of the approach is depicted in
Figure 2.
We explored different configurations, but we only
present the two most representative which highlight
how the quality of the results can be improved by
using ensemble clustering. The first configuration,
E
multires
is composed of three clustering algorithms
(Kmeans) working on the latent space representation
of the image obtained by different CAE trained at dif-
ferent resolutions: 10× with 8 clusters, 5× with 6
clusters and 5× with 8 clusters. As the reconstructed
image from the autoencoder seems to focus more on
colour intensity than real structures, a second ensem-
ble configuration has been tested. To add diversity
and to force the final result to focus its attention more
on the structure of the objects, a clustering working on
a binary image (by thresholding the intensity of the
initial image) has been computed. Thus, the second
configuration (E
struct
) is composed of three clustering
algorithms (Kmeans) with the following parameters:
5× on the binary image with 6 clusters, 5× on the
binary image with 8 clusters and 10× on the initial
RGB image with 6 clusters.
3 EXPERIMENTS AND RESULTS
Our study was performed on 8 WSI of Haematoxylin
Eosin Saffron (HES) stained tissue extracted from
a cohort of patients built within the scope of the
AiCOLO project (INSERM/Plan Cancer) studying
colon cancer. The images have been provided by
Georges Franc¸ois Leclerc Centre (Dijon, France) and
acquired from two different centres. An example is
given in Figure 3a. HES stain distinguishes cell nuclei
in purple, from extracellular matrix and cytoplasm in
pink.
All images have been acquired at 20× magni-
fication (corresponding to 0.5 µm/pixel) but stored
at several resolutions in a pyramidal format. The
size of each image is around 90, 000 × 50, 000 pix-
els. To train autoencoders, 10, 000 patches of size
128× 128 pixels were randomly extracted at 10× res-
olution from all images (and 5× for the ensemble
approach), as this seems to be the minimal amount
Ensemble Clustering for Histopathological Images Segmentation using Convolutional Autoencoders
935
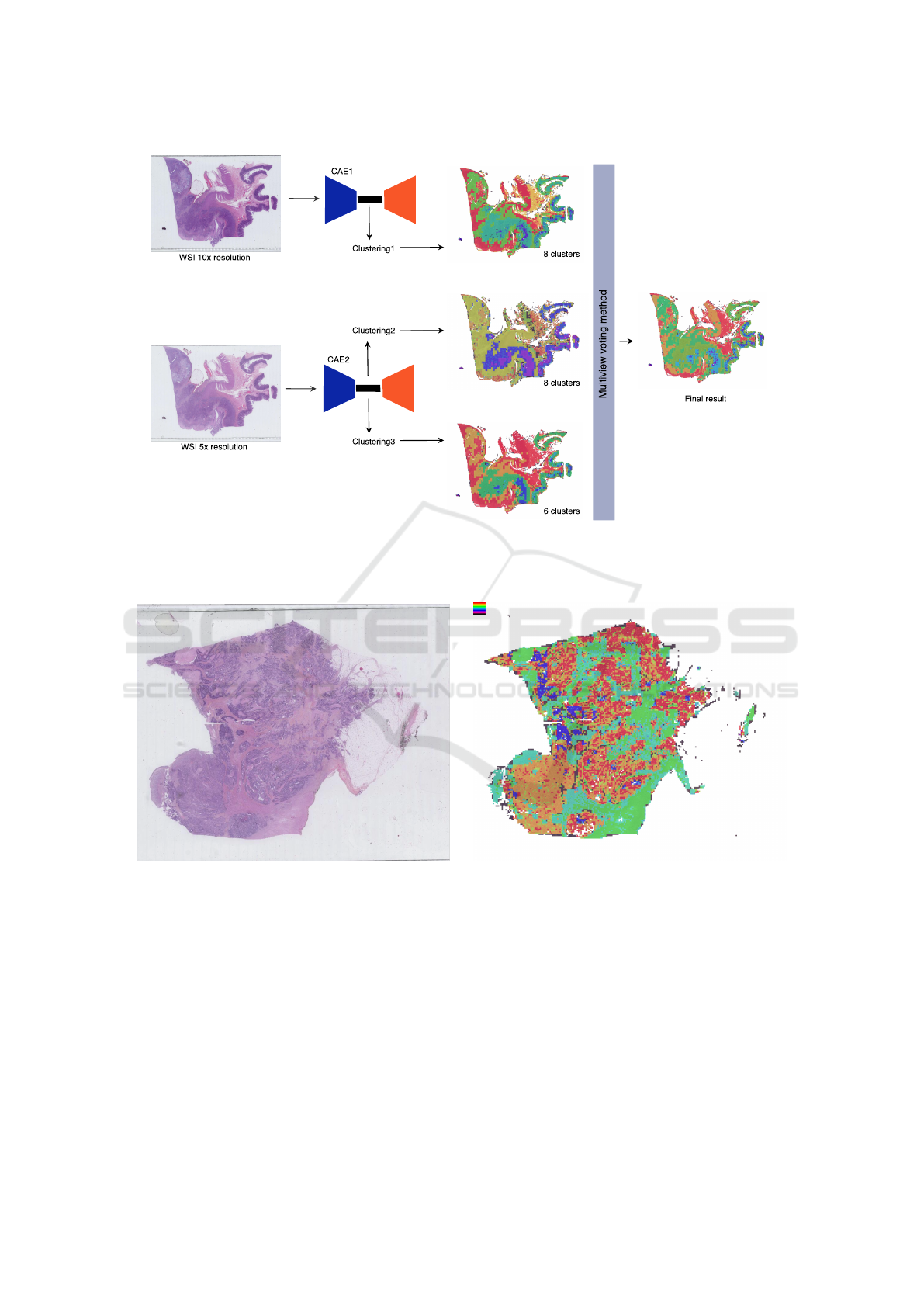
Figure 2: Architecture of the first ensemble configuration E
multires
: two CAE trained at different resolutions (10× and 5×)
produce different latent representations that are clustered. The three resulting clusterings are then merged through the multi-
view voting algorithm proposed in (Wemmert and Ganc¸arski, 2002).
(a) Example of a WSI of colon tissue stained with HES
(magnification: ×20, size: 97,920× 55,040 pixels)
(b) Example of clustering with 8 clusters (orange, red and
blue clusters corresponding to tumour)
Figure 3: Example of (a) a raw WSI and (b) a clustering result of this image.
of information required by human expert to classify
the tissue. Meanwhile, sparse manual annotations
of the five classes of tissue, tumour, stroma, outer
layer mucosa (crypts of Lieberkuhn and connective
tissue), immune cells, and necrosis, and two classes
for background and artefacts (ink marks, etc.) have
been performed by pathologists on the images (using
Cytomine(Mar
´
ee et al., 2016)), to be able to evaluate
the relevance of the clustering.
3.1 Evaluation of All Hyperparameters
of the CAE
First, results obtained without using the latent space
representation (see Table 1) are worse than all those
obtained when clustering the encoded data. This con-
firms the interest of using a CAE for WSI clustering.
As shown in Figure 4a, it appears that the number of
convolutions in each layer of convolutions (hyperpa-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
936
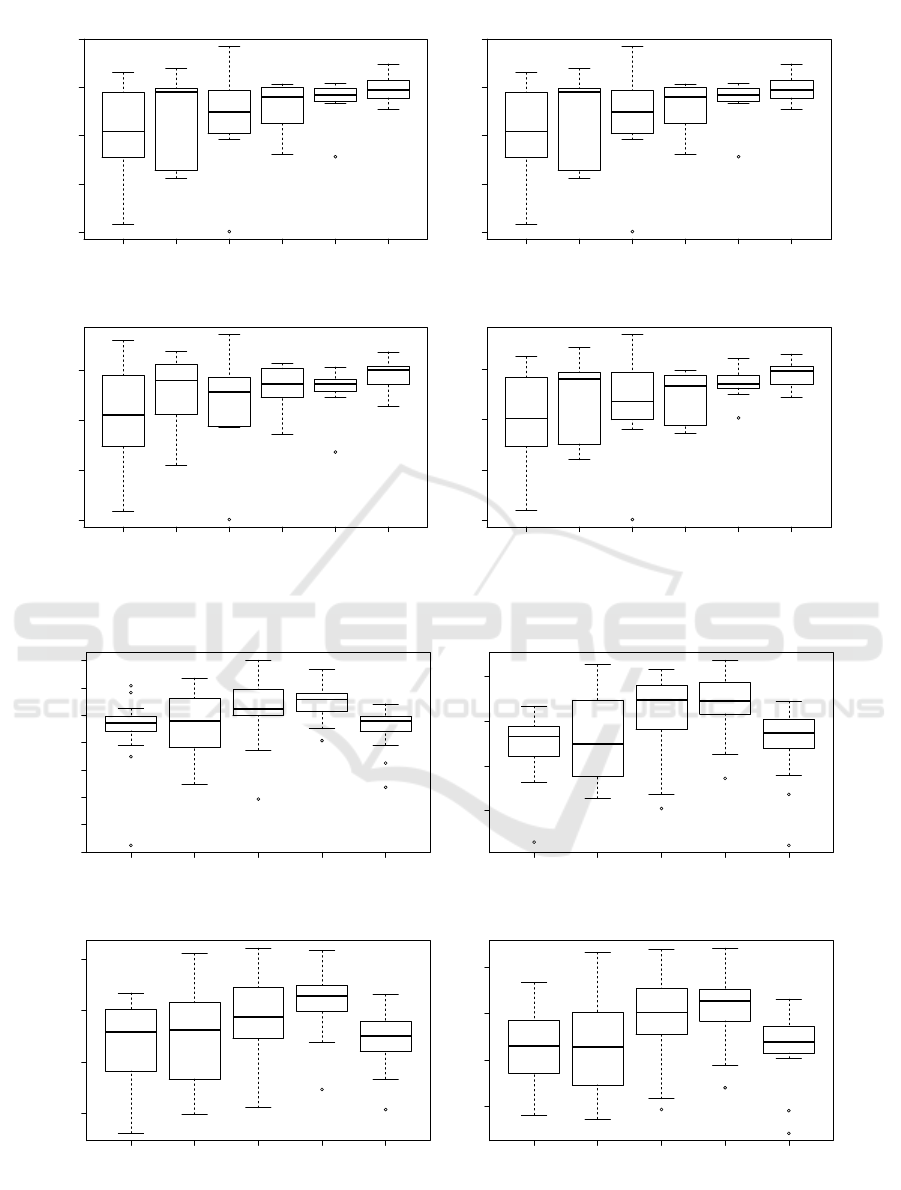
1 3 5 7 10 15
0.0 0.1 0.2 0.3 0.4
7 Clusters
C : Number of convolutions
ARI
1 3 5 7 10 15
0.0 0.1 0.2 0.3 0.4
8 Clusters
C : Number of convolutions
ARI
1 3 5 7 10 15
0.0 0.1 0.2 0.3
9 Clusters
C : Number of convolutions
ARI
1 3 5 7 10 15
0.0 0.1 0.2 0.3
10 Clusters
C : Number of convolutions
ARI
(a) Number of convolutions C in each layer of convolutions (N = 2, Z = 250)
1 2 3 4 5
0.15 0.20 0.25 0.30 0.35 0.40 0.45 0.50
7 Clusters
N : Number of layers
ARI
1 2 3 4 5
0.30 0.35 0.40 0.45
8 Clusters
N : Number of layers
ARI
1 2 3 4 5
0.30 0.35 0.40 0.45
9 Clusters
N : Number of layers
ARI
1 2 3 4 5
0.30 0.35 0.40 0.45
10 Clusters
N : Number of layers
ARI
(b) Number of layers of convolutions N (Z = 250, C = 10)
Figure 4: Evaluation of the ARI for the two main hyperparameters of the convolutions of the CAE comparing Kmeans
clustering on 7, 8, 9 and 10 clusters.
Ensemble Clustering for Histopathological Images Segmentation using Convolutional Autoencoders
937
10 25 50 100 250 500 1000
0.0 0.1 0.2 0.3 0.4
7 Clusters
Z : latent space size
ARI
10 25 50 100 250 500 1000
0.0 0.1 0.2 0.3 0.4
8 Clusters
Z : latent space size
ARI
10 25 50 100 250 500 1000
0.0 0.1 0.2 0.3 0.4
9 Clusters
Z : latent space size
ARI
10 25 50 100 250 500 1000
0.0 0.1 0.2 0.3 0.4
10 Clusters
Z : latent space size
ARI
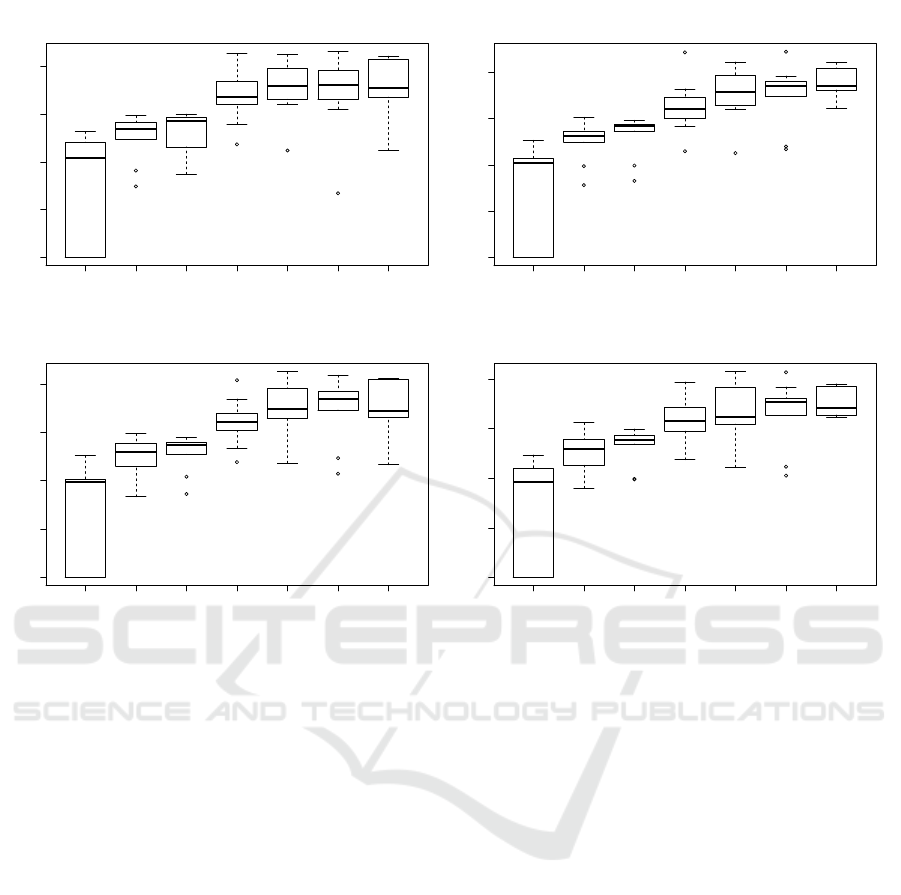
Figure 5: Evaluation of the ARI with different latent space sizes, comparing Kmeans clustering on 7, 8, 9 and 10 clusters.
rameter C) does not greatly affects the quality of the
autoencoder as only a apart from a slight narrowing of
the variability of the results. It’s quite easy to figure
out why: passed a certain number, additional convo-
lution brings to few complementary information. Fig-
ure 4b shows the evaluation of the ARI with different
number of convolution layers in the architecture. We
can notice an increase of the quality index up to 4 lay-
ers and then a brutal drop at 5. This indicates clearly
that too many convolutions (and poolings that down-
sample the information) reduce the information that
can further not be properly processed.
Nonetheless, as seen in Figure 5, the latent space
size Z, seems to greatly influence the pertinence of the
CAE. Indeed, the ARI clearly grows as there is more
space to encode the latent representation, as a more
precise information can be stored. Also, the more in-
formation is present in the latent representation, the
more classes can easily be differentiated. However,
it is also clear that a too large latent space will not
be able to summarise efficiently the information, and
thus, will not help the clustering algorithm to discrim-
inate the different tissues. Moreover, the larger the la-
tent space, the more memory and time are needed to
train the network.
3.2 Comparison of the CAE with the
Ensemble Approach
As seen in the previous experiment, the ARI tends to
give low scores because we only have very few an-
notations on each class of interest. So we decided to
compute a second evaluation criterion based on the
ability of the clustering to detect tumours areas in the
image, as it is the main class of interest in our project.
To associate the tumour class to a cluster, we calcu-
lated its tumour density (number of labelled tumour
pixels / number of total labelled pixels in the clus-
ter). All clusters having a density over 50% are kept
as ’tumour’, the others are labelled as ’not tumour’.
Thus, two evaluation criteria have been calculated on
the results and are presented in Table 1: the ARI as
in the previous experiment (see Eq.1) and the FScore
on the two-classes problem (tumour vs. not tumour)
(Van Rijsbergen, 1979).
3.3 Discussion
Classical methods applied on the latent space rep-
resentation of the CAE tend to show acceptable re-
sults. However, both ensemble clustering configura-
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
938

Table 1: Evaluation of the ARI and FScore of all clustering results obtained with the different methods.
Raw data Encoded data
Kmeans Kmeans AggCl GM N2D E
multires
E
struct
Image 1 0.39 0.89 0.48 0.96 0.38 0.94 0.27 0.73 0.43 0.97 0.47 0.96 0.42 0.88
Image 2 0.27 0.68 0.33 0.63 0.29 0.62 0.19 0.43 0.29 0.68 0.31 0.66 0.46 0.62
Image 3 0.25 0.76 0.39 0.87 0.35 0.85 0.22 0.76 0.31 0.88 0.37 0.87 0.45 0.91
Image 4 0.08 0.48 0.08 0.50 0.13 0.61 0.05 0.51 0.12 0.55 0.08 0.54 0.08 0.75
Image 5 0.11 0.65 0.11 0.64 0.10 0.60 0.10 0.62 0.11 0.65 0.12 0.65 0.17 0.72
Image 6 0.37 0.68 0.52 0.75 0.51 0.72 0.49 0.67 0.43 0.76 0.51 0.77 0.57 0.75
Image 7 0.28 0.68 0.35 0.73 0.33 0.75 0.14 0.61 0.37 0.74 0.41 0.76 0.36 0.84
Image 8 0.33 0.63 0.44 0.71 0.42 0.70 0.07 0.44 0.37 0.69 0.44 0.75 0.45 0.75
Mean 0.26 0.68 0.34 0.72 0.31 0.72 0.19 0.60 0.30 0.74 0.34 0.75 0.37 0.78
Stdv 0.11 0.12 0.16 0.14 0.14 0.12 0.14 0.13 0.13 0.13 0.16 0.13 0.16 0.09
tions seem to be more efficient in finding coherent
clusters corresponding to the classes of interest de-
fined by the pathologists.
Among all the exposed methods, E
struct
seems to
give the best results. It tends to confirm the impor-
tance of the shape of the objects on histopathological
images. Furthermore, it shows that even if convolu-
tional autoencoders aim at automatically finding the
best features to encode images, they can also take ad-
vantage of pre-computed features for some specific
tasks.
4 CONCLUSION
In this paper, we compared different configurations
of convolutional autoencoders in the field of unsuper-
vised learning for WSI histopathological image seg-
mentation. For this, different CAE architectures have
been compared to try to find the best configuration
and to study the influence of each hyperparameter.
Then, we proposed a new approach that uses ensem-
ble clustering technique to take advantage of multires-
olution information and structural features in the im-
age. This confirms the importance of having diversity
in an ensemble learning framework and that working
at different resolutions at the same time can really im-
prove the quality of the results.
ACKNOWLEDGEMENT
This work was supported by the AiCOLO project
funded by INSERM/Plan Cancer (MIC 2019).
REFERENCES
Alsubaie, N., Shaban, M., Snead, D., Khurram, A., and
Rajpoot, N. (2018). A multi-resolution deep learn-
ing framework for lung adenocarcinoma growth pat-
tern classification. In Annual Conference on Medi-
cal Image Understanding and Analysis, pages 3–11.
Springer.
Ando, T. and Hotta, K. (2021). Cell image segmentation by
feature random enhancement module. In Proceedings
of the 16th International Joint Conference on Com-
puter Vision, Imaging and Computer Graphics Theory
and Applications - Volume 4: VISAPP,, pages 520–
527. INSTICC, SciTePress.
Bukala, A., Cyganek, B., Koziarski, M., Kwolek, B., Ol-
borski, B., Antosz, Z., Swadzba, J., and Sitkowski,
P. (2020). Classification of histopathological images
using scale-invariant feature transform. In Farinella,
G. M., Radeva, P., and Braz, J., editors, Proceedings
of the 15th International Joint Conference on Com-
puter Vision, Imaging and Computer Graphics The-
ory and Applications, VISIGRAPP 2020, Volume 5:
VISAPP, Valletta, Malta, February 27-29, 2020, pages
506–512. SCITEPRESS.
Figueira, G., Wang, Y., Sun, L., Zhou, H., and Zhang,
Q. (2020). Adversarial-based domain adapta-
tion networks for unsupervised tumour detection in
histopathology. In 2020 IEEE 17th International Sym-
posium on Biomedical Imaging (ISBI), pages 1284–
1288. IEEE.
Fouad, S., Randell, D., Galton, A., Mehanna, H., and Lan-
dini, G. (2017). Unsupervised morphological segmen-
tation of tissue compartments in histopathological im-
ages. PloS one, 12(11):e0188717.
Hou, L., Nguyen, V., Kanevsky, A. B., Samaras, D., Kurc,
T. M., Zhao, T., Gupta, R. R., Gao, Y., Chen, W.,
Foran, D., et al. (2019). Sparse autoencoder for
unsupervised nucleus detection and representation in
histopathology images. Pattern recognition, 86:188–
200.
Janowczyk, A., Basavanhally, A., and Madabhushi, A.
(2017). Stain normalization using sparse autoencoders
Ensemble Clustering for Histopathological Images Segmentation using Convolutional Autoencoders
939

(stanosa): application to digital pathology. Computer-
ized Medical Imaging and Graphics, 57:50–61.
Junior, J. D. D. and Backes, A. R. (2021). Unsuper-
vised segmentation of leukocytes images using parti-
cle swarm. In VISIGRAPP (4: VISAPP), pages 439–
446.
Khan, A. M., El-Daly, H., Simmons, E., and Rajpoot, N. M.
(2013). Hymap: A hybrid magnitude-phase approach
to unsupervised segmentation of tumor areas in breast
cancer histology images. Journal of Pathology Infor-
matics, 4.
Landini, G., Fouad, S., Randell, D., and Mehanna, H.
(2019). Epithelium and stroma segmentation using
multiscale superpixel clustering. Journal of Pathology
Informatics, 10.
LeCun, Y., Bengio, Y., and Hinton, G. E. (2015). Deep
learning. Nature, 521(7553):436–444.
Liang, P., Shi, W., and Zhang, X. (2018). Remote sens-
ing image classification based on stacked denoising
autoencoder. Remote Sensing, 10(1):16.
Mar
´
ee, R., Rollus, L., St
´
evens, B., Hoyoux, R., Louppe,
G., Vandaele, R., Begon, J.-M., Kainz, P., Geurts, P.,
and Wehenkel, L. (2016). Collaborative analysis of
multi-gigapixel imaging data using Cytomine. Bioin-
formatics, 32(9):1395–1401.
McConville, R., Santos-Rodriguez, R., Piechocki, R. J., and
Craddock, I. (2020). N2d: (not too) deep clustering
via clustering the local manifold of an autoencoded
embedding.
Mei, S., Ji, J., Geng, Y., Zhang, Z., Li, X., and Du, Q.
(2019). Unsupervised spatial–spectral feature learn-
ing by 3d convolutional autoencoder for hyperspectral
classification. IEEE Transactions on Geoscience and
Remote Sensing, 57(9):6808–6820.
Qaiser, T., Sirinukunwattana, K., Nakane, K., Tsang, Y.-W.,
Epstein, D., and Rajpoot, N. (2016). Persistent homol-
ogy for fast tumor segmentation in whole slide his-
tology images. Procedia Computer Science, 90:119–
124.
Raza, K. and Singh, N. K. (2018). A tour of unsuper-
vised deep learning for medical image analysis. arXiv
preprint arXiv:1812.07715.
Van Rijsbergen, C. (1979). Information retrieval: the-
ory and practice. In Proceedings of the Joint
IBM/University of Newcastle upon Tyne Seminar on
Data Base Systems, pages 1–14.
Wemmert, C. and Ganc¸arski, P. (2002). A multi-view vot-
ing method to combine unsupervised classifications.
In Artificial Intelligence and Applications, pages 447–
452.
Xu, J., Xiang, L., Liu, Q., Gilmore, H., Wu, J., Tang,
J., and Madabhushi, A. (2015). Stacked sparse au-
toencoder (ssae) for nuclei detection on breast cancer
histopathology images. IEEE transactions on medical
imaging, 35(1):119–130.
Yamamoto, Y., Tsuzuki, T., Akatsuka, J., Ueki, M.,
Morikawa, H., Numata, Y., Takahara, T., Tsuyuki, T.,
Tsutsumi, K., Nakazawa, R., et al. (2019). Automated
acquisition of explainable knowledge from unanno-
tated histopathology images. Nature communications,
10(1):1–9.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
940
