
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and
Localization
Paul Bergmann
1,2 a
, Xin Jin
3 b
, David Sattlegger
1 c
and Carsten Steger
1 d
1
MVTec Software GmbH, Germany
2
Technical University of Munich, Germany
3
Karlsruhe Institute of Technology, Germany
Keywords:
Anomaly Detection, Dataset, Unsupervised Learning, Visual Inspection, 3D Computer Vision.
Abstract:
We introduce the first comprehensive 3D dataset for the task of unsupervised anomaly detection and localization.
It is inspired by real-world visual inspection scenarios in which a model has to detect various types of defects
on manufactured products, even if it is trained only on anomaly-free data. There are defects that manifest
themselves as anomalies in the geometric structure of an object. These cause significant deviations in a 3D
representation of the data. We employed a high-resolution industrial 3D sensor to acquire depth scans of 10
different object categories. For all object categories, we present a training and validation set, each of which
solely consists of scans of anomaly-free samples. The corresponding test sets contain samples showing various
defects such as scratches, dents, holes, contaminations, or deformations. Precise ground-truth annotations are
provided for every anomalous test sample. An initial benchmark of 3D anomaly detection methods on our
dataset indicates a considerable room for improvement.
1 INTRODUCTION
The increased availability and precision of modern 3D
sensors has led to significant advances in the field of
3D computer vision. The research community has used
these devices to create datasets for a wide variety of
real-world problems, such as point cloud registration
(Zeng et al., 2017), classification (Wu et al., 2015), 3D
semantic segmentation (Chang et al., 2015; Dai et al.,
2017), 3D object detection (Armeni et al., 2016), and
rigid pose estimation (Drost et al., 2017; Hoda
ˇ
n et al.,
2020). The development of new and improved algo-
rithms relies on the availability of such high quality
datasets.
A task of particular importance in many applica-
tions is to recognize anomalous data that deviates from
what a model has previously observed during training.
In manufacturing, for example, these kinds of methods
can be used to detect defects during inference, while
only being trained on anomaly-free samples. In au-
tonomous driving, it is safety critical that an intelligent
a
https://orcid.org/0000-0002-4458-3573
b
https://orcid.org/0000-0002-2078-8056
c
https://orcid.org/0000-0002-8336-4672
d
https://orcid.org/0000-0003-3426-1703
system can detect structures it has not seen during
training. This problem has attracted significant atten-
tion for color or grayscale images. Curiously, the field
of unsupervised anomaly detection is comparatively
unexplored in the 3D domain. We believe that a key
reason for this is the unavailability of suitable datasets.
To fill this gap and spark further interest in the de-
velopment of new methods, we introduce a real-world
dataset for the task of unsupervised 3D anomaly de-
tection and localization. Given a set of exclusively
anomaly-free 3D scans of an object, the task is to
detect and localize various types of anomalies. Our
dataset is inspired by industrial inspection scenarios.
This application has been identified as an important
use case for the task of unsupervised anomaly detec-
tion because the nature of all possible defects that may
occur in practice is often unknown. In addition, defec-
tive samples for training can be difficult to acquire and
precise labeling of defects is a laborious task. Figure 1
shows two prototypical samples of our new dataset.
Our main contributions are as follows:
•
We introduce the first comprehensive dataset for
unsupervised anomaly detection and localization
in three-dimensional data. It consists of 4147 high-
resolution 3D point cloud scans from 10 real-world
202
Bergmann, P., Jin, X., Sattlegger, D. and Steger, C.
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization.
DOI: 10.5220/0010865000003124
In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 5: VISAPP, pages
202-213
ISBN: 978-989-758-555-5; ISSN: 2184-4321
Copyright
c
2022 by SCITEPRESS – Science and Technology Publications, Lda. All rights reserved

Figure 1: Two samples representing the category potato of our new dataset. The sample on the left is anomaly-free while the
one on the right contains a nail stuck through the surface of the potato. We depict the point clouds overlaid with the associated
color values. For the anomalous sample, we additionally display the annotated ground truth.
object categories. While the training and validation
sets only contain anomaly-free data, the samples
in the test set contain various types of anomalies.
Precise ground truth annotations are provided for
each anomaly.
1
•
We evaluate current methods that were specifically
designed for unsupervised 3D anomaly localiza-
tion. Our initial benchmark reveals that existing
methods do not perform well on our dataset and
that there is considerable room for future improve-
ment.
2 RELATED WORK
Anomaly Detection in 2D.
For two-dimensional im-
age data, numerous synthetic and real-world bench-
mark datasets exist. They cover various domains,
e.g., autonomous driving (Blum et al., 2019), video
anomaly detection (Li et al., 2013; Lu et al., 2013;
Sultani et al., 2018), or industrial inspection scenarios.
Since we propose a new industrial inspection
dataset, we focus our summary on existing datasets
from this domain. The task is to detect and localize
defects on manufactured products when only a set of
anomaly-free training images is available. Huang et al.
(2018) present a surface inspection dataset of 1344
images of magnetic tiles. Test images contain various
types of anomalies, such as cracks or uneven areas.
Similar datasets exist that focus on the inspection of
a single repetitive two-dimensional texture (Carrera
et al., 2017; Song and Yan, 2013; Wieler and Hahn,
2007). Bergmann et al. (2019a, 2021) introduce a more
comprehensive dataset that contains a total of 5354 im-
ages showing instances of five texture and ten object
categories. The test set contains 73 distinct types of
anomalies, such as contaminations or scratches on the
manufactured products.
1
The dataset will be made publicly available at
https://www.mvtec.com/company/research/datasets.
The aforementioned datasets have led to the de-
velopment of numerous methods that are intended to
operate on 2D color images. A popular approach
(Bergmann et al., 2020; Cohen and Hoshen, 2021;
Salehi et al., 2021; Wang et al., 2021) is to model the
distribution of descriptors extracted from neural net-
works pretrained on large-scale datasets like ImageNet
(Krizhevsky et al., 2012). Networks that are pretrained
in such a way expect RGB images as input. The re-
sulting methods are therefore ill-suited to process 2D
representations of 3D data, such as depth images, and
cannot be easily transferred to 3D anomaly detection.
A different line of work uses generative models such as
convolutional autoencoders (AEs) (Masci et al., 2011)
or generative adversarial networks (GANs) (Goodfel-
low et al., 2014) to detect anomalies by evaluating a
pixelwise reconstruction error. Schlegl et al. (2019)
introduce f-AnoGAN, where a GAN is trained on the
anomaly-free training data. In a second step, an en-
coder network is trained to output latent samples that
reconstruct the respective input images when passed
to the generator of the GAN. Similarly, methods based
on autoencoders (Bergmann et al., 2019b; Park et al.,
2020) first encode input images with a low dimensional
latent sample, and then decode that sample to minimize
a pixelwise reconstruction error. For both approaches,
anomaly scores are computed by a pixelwise compar-
ison of an input image with its reconstruction. Since
these methods do not require a domain-specific pre-
training, they can be adapted to other two-dimensional
representations, such as depth images.
Anomaly Detection in 3D.
To date, there exists no
comprehensive 3D dataset designed explicitly for the
unsupervised detection and localization of anomalies.
Existing methods for this problem are evaluated on
two medical benchmarks that were originally intro-
duced for the supervised detection of diseases in brain
magnetic resonance (MR) scans. Menze et al. (2015),
Bakas et al. (2017), and Baid et al. (2021) present the
multimodal brain tumor image segmentation bench-
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization
203

Figure 2: Examples for all 10 dataset categories of the MVTec 3D-AD dataset. For each category, the left column shows an
anomaly-free point cloud with RGB values projected onto it. The second column shows a close-up view of an anomalous test
sample. Anomalous points are highlighted in the third column in red. Note that the background planes were removed for better
visibility.
mark (BRATS). It consists of 65 multi-contrast MR
scans from glioma patients. Each sample is provided
as a dense voxel grid and tumors were annotated by
radiologists in each image slice of the scan. Similarly,
Liew et al. (2018) provide the Anatomical Tracings of
Lesions After Stroke (ATLAS) dataset. It consists of
304 MR scans with corresponding ground truth anno-
tations of brain lesions. Both these datasets provide
3D information by stacking multiple grayscale images
to form a dense voxel grid. Hence, the nature of this
data is fundamentally different from the one in our
dataset that describes the geometric surface of objects.
Due to the lack of more diverse 3D datasets for
unsupervised anomaly detection, there exist only very
few methods designed for this task. Only recently,
Simarro Viana et al. (2021) introduced an extension
of f-AnoGAN to voxel data. As for the 2D case, a
GAN is trained to generate voxel grids that mimic the
training distribution using 3D convolutions. Subse-
quently, an encoder network is trained that maps input
samples to the corresponding latent samples of the gen-
erator. During inference, anomaly scores are derived
for each voxel element by comparing the input voxel
to the reconstructed one. Bengs et al. (2021) present
an autoencoder-based method that also operates on
voxel grids. A variational autoencoder is trained to
reconstruct voxel grids through a low-dimensional la-
tent variable. Anomaly scores are again derived by a
per-voxel comparison of the input to its reconstruction.
3 DESCRIPTION OF THE
DATASET
The MVTec 3D-AD dataset consists of 4147 scans
acquired by a high-resolution industrial 3D sensor. For
each of the 10 object categories, a set of anomaly-free
scans is provided for model training and validation.
The test set contains both, anomaly-free scans as well
as object samples that contain various types of anoma-
lies, such as scratches, dents, or contaminations. The
defects were devised and fabricated as they would
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
204

Table 1: Statistical overview of the MVTec 3D-AD dataset. For each category, we list the number of training, validation,
and test images. Test images are split into anomaly-free images and images containing anomalies. We report the number of
different defect types, the number of annotated regions, and the size of the (x, y, z) images for each category.
Category # Train
# Val
# Test
(good)
# Test
(anomalous)
# Defect
types
# Annotated
regions
Image size
(width × height)
bagel 244 22 22 88 4 112 800 × 800
cable gland 223 23 21 87 4 90 400 × 400
carrot 286 29 27 132 5 159 800 × 800
cookie 210 22 28 103 4 128 500 × 500
dowel 288 34 26 104 4 131 400 × 400
foam 236 27 20 80 4 115 900 × 900
peach 361 42 26 106 5 131 600 × 600
potato 300 33 22 92 4 115 800 × 800
rope 298 33 32 69 3 72 900 × 400
tire 210 29 25 87 4 95 600 × 800
total 2656 294 249 948 41 1148
occur in real-world inspection scenarios.
Five of the object categories in our dataset exhibit
considerable natural variations from sample to sam-
ple. These are bagel, carrot, cookie, peach, and potato.
Three more objects, foam, rope, and tire, have a stan-
dardized appearance but can be easily deformed. The
two remaining objects, cable gland and dowel, are
rigid. In principle, inspecting the last two could be
achieved by comparing an object’s geometry to a CAD
model. However, unsupervised methods should be
able to detect anomalies on all kinds of objects and
the creation of a CAD model might not always be
desirable or practical in a real application. An exam-
ple point cloud for each dataset category is shown in
Figure 2. The figure also displays some anomalies
together with the corresponding ground truth annota-
tions. The images of the bagel and the cookie show
cracks in the objects. The surfaces of the cable gland
and the dowel exhibit geometrical deformations. There
is a hole in the carrot and some contaminations on the
peach and the rope. Parts of the foam, the potato, and
the tire are cut off. These are prototypical examples of
the 41 types of anomalies present in our dataset. More
statistics on the dataset are listed in Table 1.
3.1 Data Acquisition and Preprocessing
All dataset scans were acquired with a Zivid One
+
Medium,
2
an industrial sensor that records high-
resolution 3D scans using structured light. The data
is provided by the sensor as a three-channel image
with a resolution of 1920
×
1200 pixels. The channels
represent the
x
,
y
, and
z
coordinates with respect to
the local camera coordinate frame. The
(x, y, z)
val-
ues of the image provide a one-to-one mapping to the
2
https://www.zivid.com/zivid-one-plus-medium-3d-
camera
corresponding point cloud. In addition, the sensor ac-
quires complementary RGB values for each
(x, y, z)
pixel. It was statically mounted to view all objects
of each individual category from the same angle. We
performed a calibration of the internal camera parame-
ters that allows to project 3D points into the respective
pixel coordinates (Steger et al., 2018). The scene was
illuminated by an indirect and diffuse light source.
For each dataset category, we specified a fixed rect-
angular domain and cropped the original
(x, y, z)
and
RGB images to reduce the amount of background pix-
els in the samples. The acquisition setup as well as the
preprocessing are very similar to real-world applica-
tions where an object is usually located in a defined
position and the illumination is chosen to best suit the
task. In addition, our setup enables and simplifies data
augmentation. All objects were recorded on a dark
background and the preprocessing leaves a sufficient
margin around the objects to allow for the applica-
tion of various data augmentation techniques, such
as crops, translations, or rotations. This enables the
use of our dataset for the training of data-hungry deep
learning methods, as demonstrated by our experiments
in Section 4.
Figure 3 shows the data provided for the anoma-
lous test sample of the peach displayed in Figure 2.
The image is of size 600
×
600 pixels, cropped from the
original sensor scan. The first three images visualize
the
x
,
y
, and
z
coordinates of the dataset sample, respec-
tively. White pixels mark areas where the sensor did
not return any 3D information due to, e.g., occlusions,
reflections, or sensor inaccuracies. The correspond-
ing RGB and ground truth annotation images are also
displayed.
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization
205
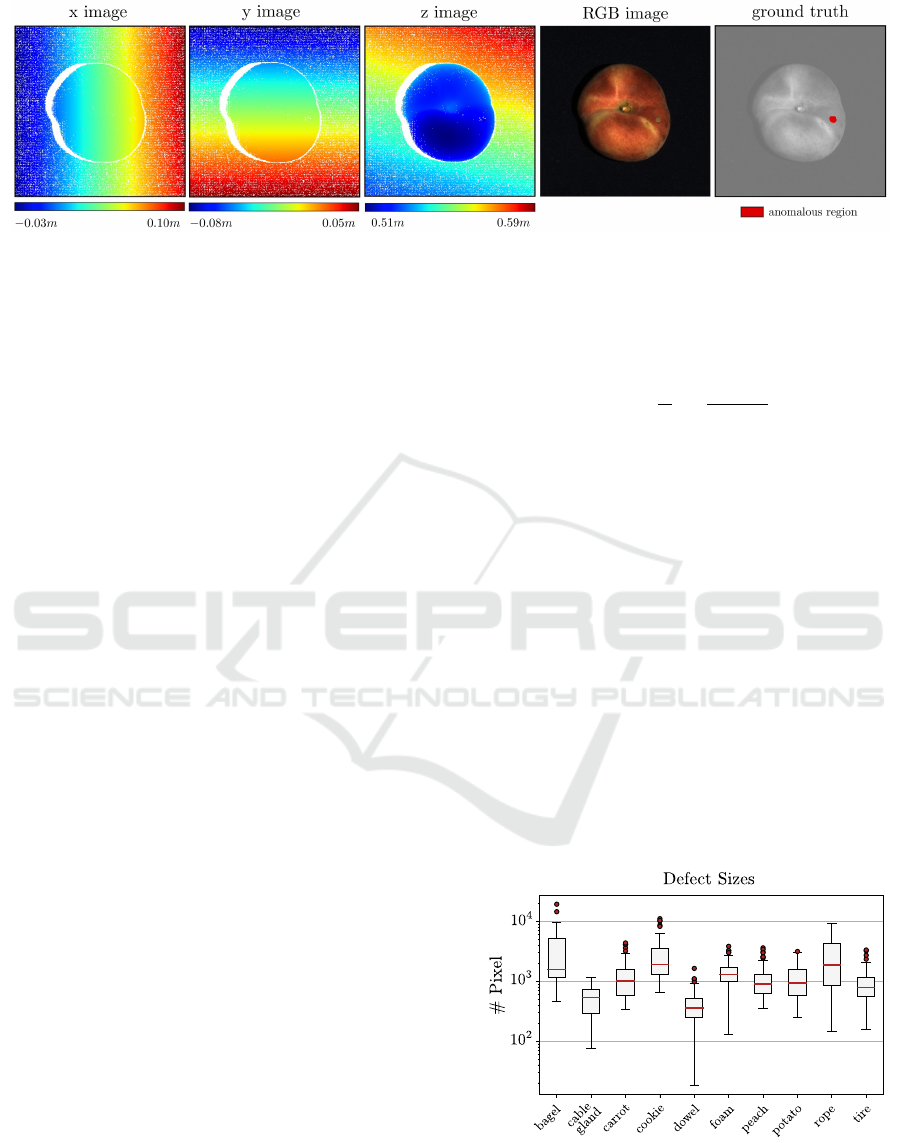
Figure 3: Visualization of the provided data for one anomalous test sample of the dataset category peach. In addition to three
images that encode the 3D coordinates of the object, RGB information as well as a pixel-precise ground-truth image are
provided.
3.2 Ground-truth Annotations
We provide precise ground-truth annotations for each
anomalous sample in the test set. Anomalies were
annotated in the 3D point clouds. Since there is a one-
to-one mapping of the 3D points to their respective
pixel locations in the
(x, y, z)
image, we make the an-
notations available as two-dimensional regions. This
procedure allows us to additionally label invalid sensor
pixels and thus annotate anomalies that manifest them-
selves through the absence of points. For example,
an anomaly might lead to a failure of 3D reconstruc-
tion and therefore yield invalid pixels in the 3D image.
Furthermore, if an anomaly is visible in the RGB im-
age and its corresponding color pixels are not already
included in the ground truth label, we append these
pixels to the annotation.
An example ground truth mask is shown in Fig-
ure 3, where a contamination is present on the peach.
In Figure 2, further annotations are visualized when
projected to the valid 3D points of a scene. The size
of the individual connected components of the anoma-
lies present in the test set varies greatly, from a few
hundred to several thousand pixels. Figure 4 visual-
izes their distribution as a box-and-whisker plot with
outliers on a logarithmic scale (Tukey, 1977).
3.3 Performance Evaluation
To assess the anomaly localization performance of a
method on our dataset, we require it to output a real-
valued anomaly score for each
(x, y, z)
pixel of the test
set. In contrast to only assigning anomaly scores to all
valid 3D points of the test samples, this allows the de-
tection of anomalies that manifest themselves through
invalid sensor pixels or missing 3D structures. These
anomaly scores are converted to binary predictions
using a threshold. We then compute the per-region
overlap (PRO) metric (Bergmann et al., 2021), which
is defined as the average relative overlap of the binary
prediction
P
with each connected component
C
k
of the
ground truth. The PRO value is computed as
PRO =
1
K
K
∑
k=1
|P ∩C
k
|
|C
k
|
, (1)
where
K
is the total number of ground truth compo-
nents. This process is repeated for multiple thresholds
and a curve is constructed by plotting the resulting
PRO values against the corresponding false positive
rates. The final performance measure is computed by
integrating this curve up to a limited false positive rate
and normalizing the resulting area to the interval
[0, 1]
.
This is a standard metric for the task of unsupervised
anomaly localization and is particularly useful when
anomalies vary significantly in size.
We want to stress that, when working with our
dataset, we strongly discourage to calculate the area
under the PRO curve up to high false positive rates.
We recommend to select the integration limit no larger
than 0.3. This is due to the fact that the anomalous
regions are very small compared to the size of the
images. At large false positive rates, the amount of
erroneously segmented pixels would be significantly
Figure 4: Size of anomalies for all objects in the dataset visu-
alized as a box-and-whisker plot. Defect areas are reported
as the total number of pixels within an annotated connected
component. Anomalies vary greatly in size for each dataset
category.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
206

larger than the number of actually anomalous pixels.
This would lead to segmentation results that are no
longer meaningful in practice.
Our dataset can also be used to assess the perfor-
mance of algorithms that make a binary decision for
each sample if it contains an anomaly or not. In this
case, we report the area under the ROC curve as a
standard classification metric.
3
4 INITIAL BENCHMARK
To examine how existing 3D anomaly localization
methods perform on our new dataset, we conducted an
initial benchmark. It is intended to serve as a baseline
for future methods. Very few methods have been pro-
posed explicitly for this task and all of them operate
on voxel data. This is mainly due to the fact that these
methods are originally intended to process MR or CT
scans that consist of several layers of intensity images.
As representatives from this class of methods, we in-
clude Voxel f-AnoGAN (Simarro Viana et al., 2021)
and our own implementation of a convolutional Voxel
AE (Bengs et al., 2021) in our benchmark. Predeces-
sors of these methods were developed for 2D image
data. The main difference between the 2D and 3D
methods is the use of 2D convolutions on images and
3D convolutions on voxel data, respectively. There-
fore, these methods are easily adapted to process depth
images and we include them in our benchmark as well.
In addition to these deep learning methods, we evalu-
ate the performance of variation models (Steger et al.,
2018) on voxel data and depth images. They detect
anomalies by calculating the pixel- or voxel-wise Ma-
halanobis distance to the training data distribution.
All evaluated methods can either operate solely on
the 3D data or can additionally process the color infor-
mation attached to each 3D point. We therefore also
compare the difference in performance when adding
color information to the models. Detailed information
on training parameters and model architectures can be
found in the Appendix.
4.1 Training and Evaluation Setup
Data Representation.
To represent dataset samples
as voxel grids, we first compute a global 3D bound-
ing box over the entire training set for each dataset
category. Then, a grid of
n × n × n
voxels is placed
at the center of the bounding box. The side length of
the grid is is chosen to be equal to the longest side
3
Evaluation scripts for the computation of all above
performance measures will be published together with the
dataset.
of the bounding box. If only 3D data is processed,
occupied and empty voxels are assigned the values
1
and
−1
, respectively. If RGB information is added,
empty voxels are assigned the vector
(−1, −1, −1)
.
Occupied voxels are assigned the average RGB value
of all points that fall inside the same grid cell.
For methods that process depth images, we com-
pute the euclidean distance to the camera center for
each valid pixel in the original
(x, y, z)
images. Invalid
pixels are assigned a distance of
0
. If color informa-
tion is included, the RGB channels are appended to
the single-channel depth image. For both, the voxel
grids and depth images, the RGB values are scaled to
the interval [0, 1].
Methods on Voxel Grids.
For all voxel-based meth-
ods, we use grids of size
64 × 64 × 64
voxels, as pro-
posed by Simarro Viana et al. (2021). To choose the
latent dimension of the compression-based methods,
we performed an ablation study, which is included in
the Appendix. Anomaly scores are computed by a
voxel-wise comparison of the input with its reconstruc-
tion.
The voxel grids of the samples of our dataset are
sparsely populated and the majority of voxels is empty.
We found that this leads to problems when training
the Voxel AE if each voxel is weighted equally in the
reconstruction loss. In this case, the model tends to
simply output an empty voxel grid to minimize the
reconstruction error. To address this imbalance, we
introduce a loss weight
w ∈ (0, 1)
that is computed as
the fraction of empty voxels in the training set. During
training, the loss at each voxel is then multiplied by
w
if the voxel is occupied and by (1 − w) otherwise.
For the Voxel Variation Model, we first compute
the mean and standard deviation of the training data
at each voxel. During inference, anomaly scores are
derived by computing the voxel-wise Mahalanobis
distance of each test sample to the training distribution.
Methods on Depth Images.
Our implementations
of Depth f-AnoGAN and the Depth AE both process
images at a resolution of
256 × 256
pixels. Input im-
ages are zoomed using nearest neighbor interpolation
for depth, and bilinear interpolation for color images.
Anomaly scores are derived by a per-pixel compari-
son of the input images and their reconstructions. The
Depth Variation Model processes images with their
original resolution and computes the mean and stan-
dard deviation over the entire training set at each image
pixel. Again, anomaly scores are derived by com-
puting the pixel-wise Mahalanobis distance from the
training distribution.
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization
207

Table 2: Anomaly localization results. The area under the PRO curve is reported for an integration limit of
0.3
for each
evaluated method and dataset category. The best performing methods are highlighted in boldface.
bagel
cable
gland
carrot cookie dowel foam peach potato rope tire mean
3D Only
Voxel
GAN 0.440 0.453 0.825 0.755 0.782 0.378 0.392 0.639 0.775 0.389 0.583
AE 0.260 0.341 0.581 0.351 0.502 0.234 0.351 0.658 0.015 0.185 0.348
VM 0.453 0.343 0.521 0.697 0.680 0.284 0.349 0.634 0.616 0.346 0.492
Depth
GAN 0.111 0.072 0.212 0.174 0.160 0.128 0.003 0.042 0.446 0.075 0.143
AE 0.147 0.069 0.293 0.217 0.207 0.181 0.164 0.066 0.545 0.142 0.203
VM 0.280 0.374 0.243 0.526 0.485 0.314 0.199 0.388 0.543 0.385 0.374
3D + RGB
Voxel
GAN 0.664 0.620 0.766 0.740 0.783 0.332 0.582 0.790 0.633 0.483 0.639
AE 0.467 0.750 0.808 0.550 0.765 0.473 0.721 0.918 0.019 0.170 0.564
VM 0.510 0.331 0.413 0.715 0.680 0.279 0.300 0.507 0.611 0.366 0.471
Depth
GAN 0.421 0.422 0.778 0.696 0.494 0.252 0.285 0.362 0.402 0.631 0.474
AE 0.432 0.158 0.808 0.491 0.841 0.406 0.262 0.216 0.716 0.478 0.481
VM 0.388 0.321 0.194 0.570 0.408 0.282 0.244 0.349 0.268 0.331 0.335
Dataset Augmentation.
Since the evaluated meth-
ods, except for the Variation Models, require large
amounts of training data, we use data augmentation to
increase the size of the training set. For each object
category, we first estimate the normal vector of the
background plane, which is constant across samples.
We then rotate each dataset sample around this nor-
mal vector by a certain angle and project the resulting
points and corresponding color values into the original
2D image grid using the internal camera parameters.
We augment each training sample 20 times by ran-
domly sampling angles from the interval [−5
◦
, 5
◦
].
Computation of Anomaly Maps.
All voxel-based
methods compute an anomaly score for each voxel
element. However, comparing their performance on
our dataset requires them to assign an anomaly score to
each pixel in the original
(x, y, z)
images. We therefore
project the anomaly scores to pixel coordinates using
the internal camera parameters of the 3D sensor. For
each voxel element, we project all 8 corner points
and compute the convex hull of the resulting projected
points. All image pixels within this region are assigned
the respective anomaly score of the voxel element. If
a pixel is assigned multiple anomaly scores, we select
their maximum.
Methods on depth images already assign a score to
each pixel. The anomaly maps of Depth f-AnoGAN
and the Depth AE are zoomed to the original image
size using bilinear interpolation.
4.2 Results
Table 2 lists quantitative results for each evaluated
method for the localization of anomalies. For each
dataset category, we report the normalized area un-
der the PRO curve with an upper integration limit of
0.3
. We further report the mean performance over all
categories. Here, we focus on the localization perfor-
mance of the evaluated methods. Results on sample
level anomaly classification can be found in the Ap-
pendix.
The first six rows in Table 2 show the performance
of each method when trained only on the 3D sensor
data without providing any color information. In this
case, the Voxel f-AnoGAN performs best on average
and on the majority of all dataset categories. It is fol-
lowed by the Voxel VM, which shows the best perfor-
mance on one of the objects. The Voxel AE performs
worse than the other two voxel-based methods. This
is because it tends to produce blurry and inaccurate
reconstructions. To get an impression of the recon-
struction quality of the evaluated methods, we show
some qualitative examples in the Appendix.
On average, each voxel-based method performs
better than its depth-based counterpart. Among all
depth-based methods, the Depth Variation Model per-
forms best. We found that the Depth AE and Depth f-
AnoGAN produce many false positives in the anomaly
maps around invalid pixels in the input data.
Figure 5 shows corresponding qualitative anomaly
localization results. For visualization purposes, the pre-
dicted anomaly scores were projected onto the input
point clouds. For each dataset sample, the correspond-
ing ground truth is visualized in red. While most of
the methods are able to localize some of the defects
in our dataset, they also yield a large number of false
positive predictions, either on the objects’ surfaces,
around the objects’ edges, or in the background. Due
to the reconstruction inaccuracies of the Voxel AE, it
can only detect the larger and more salient anomalies
in our dataset such as the one depicted in Figure 5.
In addition to evaluating each method on 3D data
only, we report the performance of the methods when
trained with RGB features at each 3D point. The
results are listed in the bottom six rows of Table 2.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
208
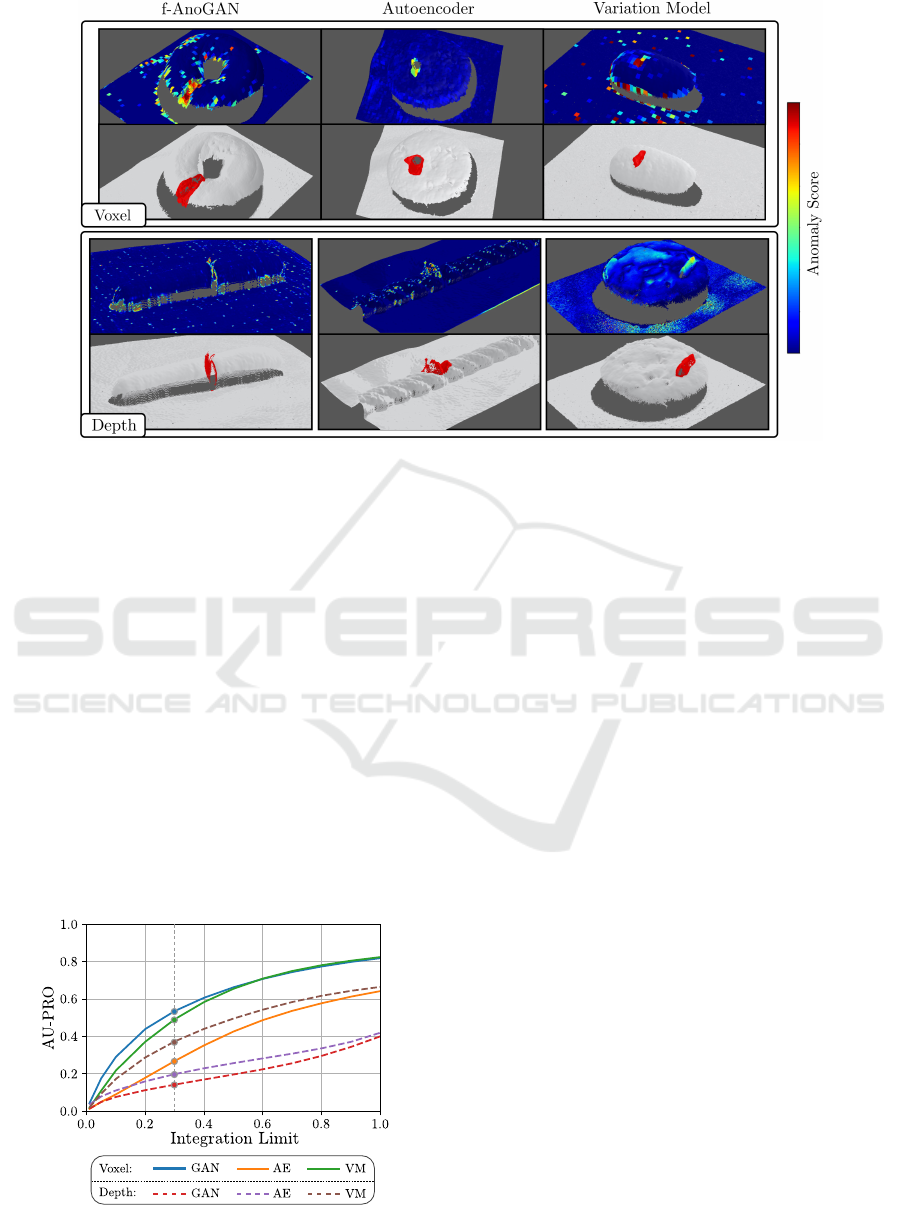
Figure 5: Qualitative anomaly localization results in which each individual method performed well. The top image visualizes
the anomaly scores as an overlay to the input point cloud. The bottom image shows the corresponding ground-truth annotation
in red. The displayed methods were only trained on the 3D data without adding color information.
Adding RGB information improves the performance
of all methods except for the Variation Models. Since
the RGB images do not contain invalid pixels, the
Depth AE and Depth f-AnoGAN benefit most from
the color information. Nevertheless, the voxel-based
methods still outperform their depth-based counter-
parts. Again, Voxel f-AnoGAN shows the best overall
performance. For some object categories, however, the
Voxel AE performs better than Voxel f-AnoGAN when
including color information.
As discussed in Section 3.3, it is important to se-
lect a suitable integration limit to compute the area
under the PRO curve. To illustrate this, Figure 6 shows
the dependence of the performance of each evaluated
method on the integration limit. All methods show a
monotonic increase in their AU-PRO. When integrat-
Figure 6: Dependence of AU-PRO on the integration limit.
The results of our benchmark are reported at a limit of 0.3.
ing to a false positive rate of
1
, the Voxel f-AnoGAN
and the Voxel VM surpass an AU-PRO of
0.8
, which
would suggest that these methods are close to solv-
ing the task. However, evaluating at large integration
limits include binary segmentation masks where the
number of false positive predictions is extremely high.
Since the area of the defects present in our dataset
is very small compared to the area of anomaly-free
pixels, such segmentation results are no longer mean-
ingful. We found that the performance of the evaluated
methods is insufficient for practical applications. We
therefore chose an integration limit of
0.3
to be able
to compare their relative performance. In the future,
we hope that our dataset sparks the development of
methods that achieve high AU-PRO scores at much
lower integration limits. In actual industrial inspec-
tion scenarios, a false positive rate of
0.3
is hardly
acceptable.
5 CONCLUSION
We presented a comprehensive 3D dataset for the task
of unsupervised detection and localization of anoma-
lies. The conceptualization and acquisition of the
dataset was inspired by real-world visual inspection
tasks. It consists of over 4000 point clouds depicting
instances of ten different object categories. The data
was acquired using a high-resolution structured light
3D sensor. About 1000 samples of the dataset con-
tain various types of anomalies and we provide precise
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization
209

ground truth annotations for all of them.
We performed an initial benchmark of the few ex-
isting methods showing that there is significant room
for improvement. In particular, the accuracy of the
evaluated methods is insufficient for them to be used
in real-world industrial applications. We are convinced
that suitable datasets are a key factor in the develop-
ment of new techniques and expect our dataset to spark
the design of better methods in the future.
REFERENCES
Armeni, I., Sener, O., Zamir, A. R., Jiang, H., Brilakis, I.,
Fischer, M., and Savarese, S. (2016). 3D Semantic
Parsing of Large-Scale Indoor Spaces. In IEEE Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 1534–1543.
Baid, U. et al. (2021). The RSNA-ASNR-MICCAI
BraTS 2021 Benchmark on Brain Tumor Segmen-
tation and Radiogenomic Classification. Preprint:
arXiv:2107.02314.
Bakas, S., Akbari, H., Sotiras, A., Bilello, M., Rozycki,
M., Kirby, J. S., et al. (2017). Advancing the cancer
genome atlas glioma MRI collections with expert seg-
mentation labels and radiomic features. Scientific Data,
4(1).
Bengs, M., Behrendt, F., Krüger, J., Opfer, R., and Schlaefer,
A. (2021). Three-dimensional deep learning with spa-
tial erasing for unsupervised anomaly segmentation in
brain MRI. International Journal of Computer Assisted
Radiology and Surgery, 16.
Bergmann, P., Batzner, K., Fauser, M., Sattlegger, D., and
Steger, C. (2021). The MVTec Anomaly Detection
Dataset: A Comprehensive Real-World Dataset for Un-
supervised Anomaly Detection. International Journal
of Computer Vision, 129(4):1038–1059.
Bergmann, P., Fauser, M., Sattlegger, D., and Steger, C.
(2019a). MVTec AD — A Comprehensive Real-World
Dataset for Unsupervised Anomaly Detection. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 9584–9592.
Bergmann, P., Fauser, M., Sattlegger, D., and Steger,
C. (2020). Uninformed Students: Student-Teacher
Anomaly Detection With Discriminative Latent Em-
beddings. In IEEE/CVF Conference on Computer Vi-
sion and Pattern Recognition (CVPR), pages 4182–
4191.
Bergmann, P., Löwe, S., Fauser, M., Sattlegger, D., and
Steger., C. (2019b). Improving Unsupervised Defect
Segmentation by Applying Structural Similarity to Au-
toencoders. In 14th International Joint Conference
on Computer Vision, Imaging and Computer Graphics
Theory and Applications - Volume 5: VISAPP, pages
372–380. INSTICC, SciTePress.
Blum, H., Sarlin, P.-E., Nieto, J., Siegwart, R., and Ca-
dena, C. (2019). Fishyscapes: A Benchmark for Safe
Semantic Segmentation in Autonomous Driving. In
IEEE/CVF International Conference on Computer Vi-
sion Workshops (ICCVW), pages 2403–2412.
Carrera, D., Manganini, F., Boracchi, G., and Lanzarone, E.
(2017). Defect Detection in SEM Images of Nanofi-
brous Materials. IEEE Transactions on Industrial In-
formatics, 13(2):551–561.
Chang, A. X., Funkhouser, T., Guibas, L., Hanrahan, P.,
Huang, Q., Li, Z., Savarese, S., Savva, M., Song, S.,
Su, H., Xiao, J., Yi, L., and Yu, F. (2015). ShapeNet:
An Information-Rich 3D Model Repository. Preprint:
arXiv:1512.03012.
Cohen, N. and Hoshen, Y. (2021). Sub-Image Anomaly De-
tection with Deep Pyramid Correspondences. Preprint:
arXiv:2005.02357.
Dai, A., Chang, A. X., Savva, M., Halber, M., Funkhouser,
T., and Nießner, M. (2017). ScanNet: Richly-
Annotated 3D Reconstructions of Indoor Scenes. In
IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 2432–2443.
Drost, B., Ulrich, M., Bergmann, P., Härtinger, P., and Steger,
C. (2017). Introducing MVTec ITODD — A Dataset
for 3D Object Recognition in Industry. In IEEE Inter-
national Conference on Computer Vision Workshops
(ICCVW), pages 2200–2208.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-
Farley, D., Ozair, S., Courville, A., and Bengio, Y.
(2014). Generative Adversarial Nets. In Advances in
Neural Information Processing Systems, pages 2672–
2680.
Hoda
ˇ
n, T., Sundermeyer, M., Drost, B., Labbé, Y., Brach-
mann, E., Michel, F., Rother, C., and Matas, J. (2020).
BOP Challenge 2020 on 6D Object Localization. Eu-
ropean Conference on Computer Vision Workshops
(ECCVW).
Huang, Y., Qiu, C., Guo, Y., Wang, X., and Yuan, K. (2018).
Surface Defect Saliency of Magnetic Tile. In 2018
IEEE 14th International Conference on Automation
Science and Engineering (CASE), pages 612–617.
Kingma, D. P. and Ba, J. (2015). Adam: A Method for
Stochastic Optimization. In 3rd International Confer-
ence on Learning Representations (ICLR).
Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2012). Ima-
geNet Classification with Deep Convolutional Neural
Networks. In 25th International Conference on Neu-
ral Information Processing Systems - Volume 1, pages
1097–1105.
Li, W.-X., Mahadevan, V., and Vasconcelos, N. (2013).
Anomaly Detection and Localization in Crowded
Scenes. IEEE Transactions on Pattern Analysis and
Machine Intelligence (TPAMI), 36(1):18–32.
Liew, S.-L., Anglin, J. M., Banks, N. W., et al. (2018). A
large, open source dataset of stroke anatomical brain
images and manual lesion segmentations. Scientific
data, 5:180011.
Lu, C., Shi, J., and Jia, J. (2013). Abnormal Event Detec-
tion at 150 FPS in MATLAB. In IEEE International
Conference on Computer Vision, pages 2720–2727.
Masci, J., Meier, U., Cire¸san, D., and Schmidhuber, J. (2011).
Stacked Convolutional Auto-Encoders for Hierarchi-
cal Feature Extraction. In Artificial Neural Networks
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
210

and Machine Learning – ICANN 2011, pages 52–59.
Springer Berlin Heidelberg.
Menze, B. H., Jakab, A., Bauer, S., Kalpathy-Cramer, J.,
Farahani, K., Kirby, J., et al. (2015). The Multi-
modal Brain Tumor Image Segmentation Benchmark
(BRATS). IEEE Transactions on Medical Imaging,
34(10):1993–2024.
Park, H., Noh, J., and Ham, B. (2020). Learning Memory-
Guided Normality for Anomaly Detection. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 14360–14369.
Salehi, M., Sadjadi, N., Baselizadeh, S., Rohban, M. H.,
and Rabiee, H. R. (2021). Multiresolution Knowledge
Distillation for Anomaly Detection. In IEEE/CVF Con-
ference on Computer Vision and Pattern Recognition
(CVPR), pages 14902–14912.
Schlegl, T., Seeböck, P., Waldstein, S., Langs, G., and
Schmidt-Erfurth, U. (2019). f-AnoGAN: Fast Unsuper-
vised Anomaly Detection with Generative Adversarial
Networks. Medical Image Analysis, 54.
Simarro Viana, J., de la Rosa, E., Vande Vyvere, T., Robben,
D., Sima, D. M., and Investigators, C.-T. P. a. (2021).
Unsupervised 3D Brain Anomaly Detection. In Brain-
lesion: Glioma, Multiple Sclerosis, Stroke and Trau-
matic Brain Injuries, pages 133–142. Springer Interna-
tional Publishing.
Song, K. and Yan, Y. (2013). A noise robust method based
on completed local binary patterns for hot-rolled steel
strip surface defects. Applied Surface Science, 285:858–
864.
Steger, C., Ulrich, M., and Wiedemann, C. (2018). Ma-
chine Vision Algorithms and Applications. Wiley-VCH,
Weinheim, 2nd edition.
Sultani, W., Chen, C., and Shah, M. (2018). Real-World
Anomaly Detection in Surveillance Videos. In IEEE
Conference on Computer Vision and Pattern Recogni-
tion (CVPR), pages 6479–6488.
Tukey, J. W. (1977). Exploratory Data Analysis. Addison-
Wesley Series in Behavioral Science. Addison-Wesley,
Reading, MA.
Ulyanov, D., Vedaldi, A., and Lempitsky, V. (2017). Im-
proved Texture Networks: Maximizing Quality and
Diversity in Feed-Forward Stylization and Texture Syn-
thesis. In IEEE Conference on Computer Vision and
Pattern Recognition (CVPR), pages 4105–4113.
Wang, S., Wu, L., Cui, L., and Shen, Y. (2021). Glancing
at the Patch: Anomaly Localization With Global and
Local Feature Comparison. In IEEE/CVF Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 254–263.
Wieler, M. and Hahn, T. (2007). Weakly Supervised Learn-
ing for Industrial Optical Inspection. 29th Annual
Symposium of the German Association for Pattern
Recognition.
Wu, Z., Song, S., Khosla, A., Yu, F., Zhang, L., Tang, X.,
and Xiao, J. (2015). 3D ShapeNets: A deep repre-
sentation for volumetric shapes. In IEEE Conference
on Computer Vision and Pattern Recognition (CVPR),
pages 1912–1920.
Zeng, A., Song, S., Nießner, M., Fisher, M., Xiao, J., and
Funkhouser, T. (2017). 3DMatch: Learning Local
Geometric Descriptors from RGB-D Reconstructions.
In IEEE Conference on Computer Vision and Pattern
Recognition (CVPR), pages 199–208.
APPENDIX
Details on Training Parameters
In this section, we provide details on training pa-
rameters as well as model architectures for the deep
learning-based methods.
Voxel f-AnoGAN.
For the implementation of Voxel
f-AnoGAN, we use the same network architecture as
proposed by Simarro Viana et al. (2021). The GAN
and the encoder network are both trained for
50
epochs
on the augmented version of our dataset with an initial
learning rate of
0.0002
and a batch size of
2
using the
Adam optimizer (Kingma and Ba, 2015). The weight
for the gradient penalty loss of the GAN is set to
10
and one generator training iteration is performed for
every
5
iterations of the discriminator training. During
the training of the encoder, the “izi” and “ziz” losses
are equally weighted by choosing a loss weight of 1.
Voxel Autoencoder.
The Voxel Autoencoder con-
sists of an encoder and a decoder network. Their archi-
tecture is the same as the one of the encoder and the
generator in Voxel f-AnoGAN, respectively. We train
for
50
epochs on the augmented version of our dataset
with a batch size of
2
using the Adam optimizer with
an initial learning rate of 0.0001.
Depth f-AnoGAN.
The Depth f-AnoGAN consists
of three sub-networks, i.e., an encoder, a discrimina-
tor, and a generator. The architecture of the encoder
is given in Table 3. It consists of a stack of
10
con-
volution blocks that compress an input image of size
256 × 256
pixels and
c
channels to a
d
-dimensional
latent vector. Each convolution block except the last
one is followed by an instance normalization layer
(Ulyanov et al., 2017) and a LeakyReLU with slope
0.05
. The architecture of the discriminator is identical
to the one of the encoder except that
d = 1
. The gen-
erator produces an image of size
256 × 256
pixels and
c
channels from a latent variable with
d
dimensions.
Its architecture is symmetric to the one in Table 3 in
the sense that convolutions are replaced by transposed
convolution layers. Both, the GAN and the encoder
network, are trained for
50
epochs using a batch size of
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization
211

4
and an initial learning rate of
0.0002
using the Adam
optimizer. During the training of the encoder, the “izi”
and “ziz” losses are equally weighted by choosing a
loss weight of 1.
Table 3: Encoder architecture of Depth f-AnoGAN and
Depth AE.
Layer Output Size Parameters
Kernel Size Stride Padding
Image 256 × 256 × c
conv1 128 × 128 × 32 4 2 1
conv2 64 × 64 × 32 4 2 1
conv3 32 × 32 × 32 4 2 1
conv4 32 × 32 × 32 3 1 1
conv5 16 × 16 × 64 4 2 1
conv6 16 × 16 × 64 3 1 1
conv7 8 × 8 × 128 4 2 1
conv8 8 × 8 × 64 3 1 1
conv9 8 × 8 × 32 3 1 1
conv10 1 × 1 × d 8 1 0
Depth Autoencoder.
For the encoder and decoder
of the Depth AE, we use the same architecture as
for the encoder and generator of Depth f-AnoGAN,
respectively. It is trained for
50
epochs using the Adam
optimizer at a batch size of
32
and an initial learning
rate of 0.0001.
Latent Dimensions of Compression-based
Methods
To select suitable latent dimensions for the evaluated
compression-based methods, we perform an ablation
study. Their mean performance over all object cat-
egories is given in Table 4. For the experiments in
Section 4, we use the respective latent dimension that
yielded the best mean performance in the ablation
study.
Table 4: Difference in performance when varying the latent
dimension of each compression-based method. We list the
area under the PRO curve up to an integration limit of
0.3
.
The best performing setting is highlighted in boldface.
Latent Dimension
128 512 2048
Voxel
GAN 0.536 0.583 0.555
AE 0.348 0.269 0.305
Depth
GAN 0.143 0.137 0.135
AE 0.199 0.203 0.199
Results for Anomaly Classification
In addition to the anomaly localization results in Ta-
ble 2, we provide results for the classification of dataset
samples as either anomalous or anomaly-free. Since
this requires a method to output a single anomaly score
for each dataset sample, we compute the maximum
anomaly score of each anomaly map. As performance
measure, we compute the area under the ROC curve.
Table 5 lists the results.
Quality of Reconstructions
For the methods based on AEs or GANs, the anomaly
detection performance significantly depends on the
quality of their reconstructions. To get an impression
of the reconstruction quality, Figure 7 shows two ex-
amples for each evaluated method.
To visualize the voxel-based methods, voxel grids
are converted to point clouds by applying a threshold to
each cell. A cell is classified as occupied if it contains a
value of 0.9 or higher. The Voxel AE tends to produce
blurry reconstructions around the objects’ surfaces.
The Voxel f-AnoGAN does not have this problem.
However, it sometimes fails to produce parts of the
input.
For the depth-based methods, inputs and recon-
structions are visualized as depth images. Darker
shades of blue indicate points that are further from
the camera center. White points indicate invalid pixels.
Both, the Depth f-AnoGAN and the Depth AE show
problems reconstructing noisy areas that exhibit many
invalid pixels.
VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications
212

Table 5: Anomaly classification results. We report the area under the ROC curve. The best-performing methods are highlighted
in boldface.
bagel
cable
gland
carrot cookie dowel foam peach potato rope tire mean
3D Only
Voxel
GAN 0.383 0.623 0.474 0.639 0.564 0.409 0.617 0.427 0.663 0.577 0.538
AE 0.693 0.425 0.515 0.790 0.494 0.558 0.537 0.484 0.639 0.583 0.572
VM 0.750 0.747 0.613 0.738 0.823 0.693 0.679 0.652 0.609 0.690 0.699
Depth
GAN 0.530 0.376 0.607 0.603 0.497 0.484 0.595 0.489 0.536 0.521 0.524
AE 0.468 0.731 0.497 0.673 0.534 0.417 0.485 0.549 0.564 0.546 0.546
VM 0.510 0.542 0.469 0.576 0.609 0.699 0.450 0.419 0.668 0.520 0.546
3D + RGB
Voxel
GAN 0.680 0.324 0.565 0.399 0.497 0.482 0.566 0.579 0.601 0.482 0.517
AE 0.510 0.540 0.384 0.693 0.446 0.632 0.550 0.494 0.721 0.413 0.538
VM 0.553 0.772 0.484 0.701 0.751 0.578 0.480 0.466 0.689 0.611 0.609
Depth
GAN 0.538 0.372 0.580 0.603 0.430 0.534 0.642 0.601 0.443 0.577 0.532
AE 0.648 0.502 0.650 0.488 0.805 0.522 0.712 0.529 0.540 0.552 0.595
VM 0.513 0.551 0.477 0.581 0.617 0.716 0.450 0.421 0.598 0.623 0.555
Figure 7: Examples of reconstructions for each compression-based method. For voxel-based methods, inputs and reconstructions
are visualized as point clouds. For depth-based methods, they are shown as depth images.
The MVTec 3D-AD Dataset for Unsupervised 3D Anomaly Detection and Localization
213
