Wavelet Transform for the Analysis of Convolutional Neural Networks in

Texture Recognition

Joao Batista Florindo

Institute of Mathematics, Statistics and Scientiﬁc Computing, University of Campinas,

Rua S

ergio Buarque de Holanda, 651, Cidade Universit

aria ”Zeferino Vaz”,

Distr. Barao Geraldo, CEP 13083-859, Campinas, SP, Brazil

Keywords:

Convolutional Neural Networks, Wavelet Transform, Multiscale Analysis, Fractal Theory, Texture

Recognition.

Abstract:

Convolutional neural networks have become omnipresent in applications of image recognition during the last

years. However, when it comes to texture analysis, classical techniques developed before the popularity of

deep learning has demonstrated potential to boost the performance of these networks, especially when they

are employed as feature extractor. Given this context, here we propose a novel method to analyze feature

maps of a convolutional network by wavelet transform. In the ﬁrst step, we compute the detail coefﬁcients

from the activation response on the penultimate layer. In the second one, a one-dimensional version of local

binary patterns are computed over the details to provide a local description of the frequency distribution.

The frequency analysis accomplished by wavelets has been reported to be related to the learning process of

the network. Wavelet details capture ﬁner features of the image without increasing the number of training

epochs, which is not possible, in feature extractor mode. This process also attenuates over-ﬁtting effect at the

same time that preserves the computational efﬁciency of feature extraction. Wavelet details are also directly

related to fractal dimension, an important feature of textures and that has also recently been found to be related

to generalization capabilities. The proposed methodology was evaluated on the classiﬁcation of benchmark

databases as well as in a real-world problem (identiﬁcation of plant species), outperforming the accuracy of

the original architecture and of several other state-of-the-art approaches.

1 INTRODUCTION

In the last years, convolutional neural networks

(CNN) have been successfully employed in a vari-

ety of tasks in computer vision, including image clas-

siﬁcation (Krizhevsky et al., 2017), object recogni-

tion (Ren et al., 2017), image segmentation (Chen

et al., 2018), video analysis (Ng et al., 2015), etc.

Among such tasks, an important topic that also has

beneﬁted from CNNs is texture recognition (Cim-

poi et al., 2016). Besides theoretical developments,

CNN-based algorithms have also been applied to sev-

eral real-world problems in which texture images play

fundamental role, such as in medicine (Shin et al.,

2016), remote sensing (Zhu et al., 2017), face recog-

nition (Taigman et al., 2014), and others.

Despite the great performance of classical CNN

architectures in texture recognition, it has been also

shown that other strategies can leverage the power of

https://orcid.org/0000-0002-0071-0227

those neural networks, either increasing the classiﬁ-

cation accuracy or reducing computational require-

ments for training of the learning model. In par-

ticular, traditional texture representations that have

been successful in the years before the populariza-

tion of deep learning have been recently rediscovered

and combined with CNNs in hybrid models that have

demonstrated interesting capabilities. A remarkable

example is deep ﬁlter banks (Cimpoi et al., 2016),

that use convolutional feature maps as local descrip-

tors and classical encodings like Fisher vectors and

“bag-of-visual-words”. In (Ji et al., 2020), the au-

thors obtain high classiﬁcation accuracy and perfor-

mance by introducing constraints and compression

techniques associated to local binary patterns (LBP)

(Ojala et al., 2002) to a convolutional/recurrent neu-

ral network. In (Anwer et al., 2018), LBP maps are

combined with the original image at different stages

of the CNN improving the recognition capacity. In T-

CNN (Andrearczyk and Whelan, 2016), CNN feature

502

Florindo, J.

Wavelet Transform for the Analysis of Convolutional Neural Networks in Texture Recognition.

DOI: 10.5220/0010866700003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

502-509

ISBN: 978-989-758-555-5; ISSN: 2184-4321

maps are also interpreted as ﬁlter banks and an energy

measure is established to provide feature vectors for

image representation. We should also mention here

the “handcrafted” CNN descriptors, that use CNN-

like architectures, but associated with pre-deﬁned ﬁl-

ter banks. Examples are NmzNet (Vu et al., 2017),

ScatNet (Bruna and Mallat, 2013), PCANet (Chan

et al., 2015), etc.

In this context, we propose the use of wavelet

transforms as a technique for the analysis of CNN

feature maps. Following ideas like those devel-

oped in (Cimpoi et al., 2016), we apply the wavelet

transform over the penultimate fully-connected layer

of the CNN. In the following, we calculated one-

dimensional binary patterns (Tirunagari et al., 2017)

of the detail signal to form the ﬁnal texture repre-

sentation. The frequency distribution of the neu-

ral response, here described by wavelet transform, is

known to be related to the learning evolution (Ra-

haman et al., 2019). Injecting such complementary

information to the image descriptors has potential to

be very beneﬁcial to a more robust representation.

Furthermore, using the different radii for binary pat-

terns ensures a second layer of multiscale analysis

over localized frequencies. Together, these transfor-

mations of the activation response are capable of ex-

pressing the localized frequency at multiple scale lev-

els, capturing a complete mapping of the CNN both

in frequency and spatial domain.

The proposed methodology was assessed on the

classiﬁcation of four benchmark data sets: KTHTIPS-

2b (Hayman et al., 2004), FMD (Sharan et al., 2009),

UIUC (Lazebnik et al., 2005), and UMD (Xu et al.,

2009). It was also applied to a practical problem, that

of identifying Brazilian plant species based on the leaf

surface texture (Casanova et al., 2009). The results

are competitive with the state-of-the-art on texture

recognition and suggest our proposal as a promising

approach for practical purposes, especially for smaller

datasets where the use of CNN as a feature extractor

is more appropriate.

2 PROPOSED METHOD

2.1 Motivation

An interesting result obtained by theoretical studies

on neural networks is that low frequencies (global

viewpoint) are learned before high frequencies (ﬁne

details) along the training epochs (Rahaman et al.,

2019). The reader can check, for example, Figure 2 in

(Ronen et al., 2019) for an intuition. Evidences sug-

gest that such “learning guided by frequency” phe-

nomena, conﬁrmed both theoretically for toy mod-

els and empirically on realistic deep neural networks,

does not occur by chance and that it could be ex-

plored further. In particular, if frequencies are im-

portant during the training, it makes sense to imagine

that they are relevant at the output of the network as

well. Given that the training usually stops after a ﬁxed

number of cycles, it is expected that the distribution of

frequencies in the output response of the network is

tightly related to the distribution on the input (image

in our case). On the other hand, it is also well known

in image processing and analysis that frequency anal-

ysis provides an alternative complementing viewpoint

of the original spatial representation. This same infor-

mation however has not been sufﬁciently explored on

the network response.

Fourier transform is the most well known tool for

frequency analysis and would be a natural candidate

for the same analysis on neural networks. Neverthe-

less, a simple observation of the response distribution

makes it clear how the information conveyed drasti-

cally varies depending on the observed region of the

signal. This is a consequence both of the random ini-

tialization and the complexity of the neural network

function. In this context, wavelet analysis is more

suitable as it supports the spatial localization together

with the frequency. We have in this way a more com-

plete description of the frequency distribution on the

network. Furthermore, the energy of wavelet details

is known to be directly related to the fractal dimen-

sion of the signal (Mallat, 2008). Besides being an

important feature in texture analysis (Xu et al., 2009),

recent studies have also established connections be-

tween such dimension and the generalization perfor-

mance of neural networks (Simsekli et al., 2020).

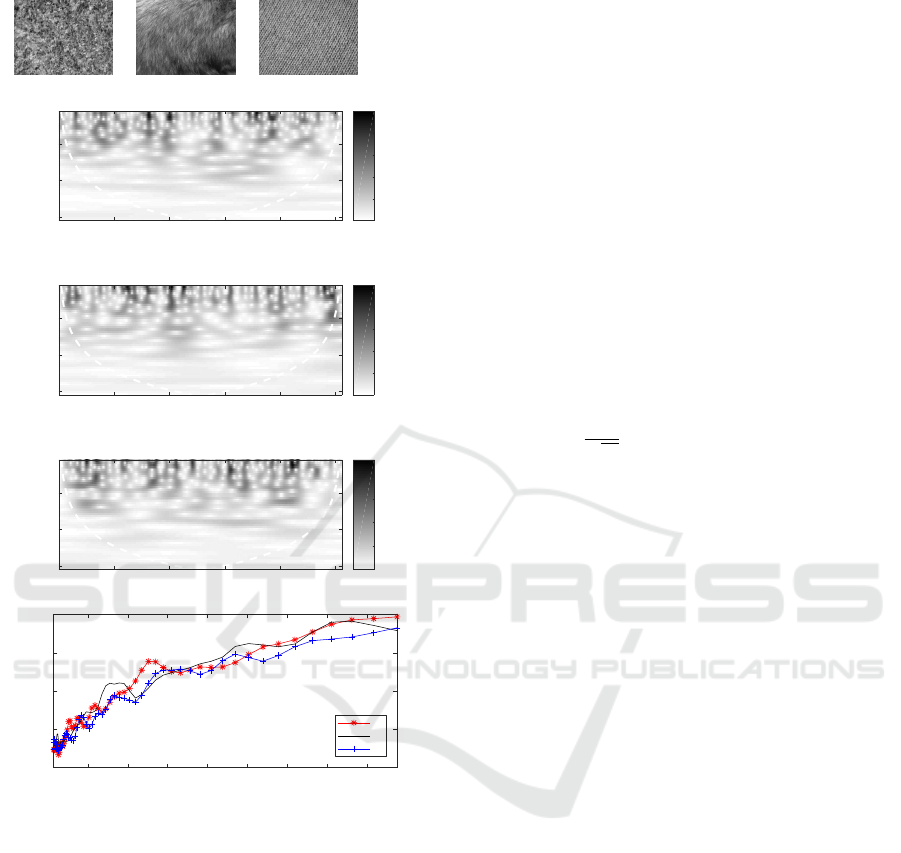
Figure 1 shows the wavelet scalograms and fre-

quency distribution at the penultimate layer of a CNN,

for three clearly different textures: an irregular pro-

ﬁle T1 (“pebbles”), a homogeneous texture T2 (“fur”)

and an artiﬁcial periodic material T3 (“corduroy”). At

the bottom we see the average energy contributed by

each frequency in each texture. T3 spectrum is more

balanced, not surpassing the magnitude of the other

samples with localized peaks. This corresponds to

moderate contribution of a larger band of frequencies

and is consequence of the multiscale regularity, corre-

sponding to multiple frequencies arising. For T1 and

T2, they alternate their inﬂuence in each frequency

region. T2 has two wide peaks around 0.1 and 0.25,

whilst T1 concentrates around 0.15 and 0.45. Such

shift to lower frequencies in T2, when compared with

T1, is a consequence of the regular patterns in T1,

even though we do not have the same homogeneity

presented by T3 now.

Wavelet Transform for the Analysis of Convolutional Neural Networks in Texture Recognition

503

T1 T2 T3

0 100 200 300 400 500

Time

0.008

0.031

0.125

Frequency

0.005

0.01

0.015

0.02

0.025

Magnitude

0 100 200 300 400 500

Time

0.008

0.031

0.125

Frequency

0.005

0.01

0.015

0.02

Magnitude

0 100 200 300 400 500

Time

0.008

0.031

0.125

Frequency

0.005

0.01

0.015

0.02

Magnitude

0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4

Frequency

Magnitude

Figure 1: Three types of textures: irregular (T1), natu-

ral regular (T2), and artiﬁcially periodic (T3). Below we

have the wavelet scalograms of each texture and the aver-

age magnitude on the frequency range.

Such remarkable behavior naturally points out

to the possibility of exploring wavelet decomposi-

tion of neural network responses. The combina-

tion of wavelets with neural networks has in fact

been explored in the literature (Zhang and Benveniste,

1992; Alexandridis and Zapranis, 2013; Fujieda et al.,

2017). These works, however, usually focus on intro-

ducing new trainable elements into the network archi-

tecture. Here we opt for a signiﬁcantly simpler strat-

egy of applying multi-resolution wavelets to the net-

work activation response, which besides having sim-

pler implementation, allows for more in-depth studies

in the future on how such responses are affected by

frequency response (a more elaborated version of the

analysis in Figure 1).

2.2 Implementation

Based on these assumptions, the proposed method

relies on the processing of the activation responses

of neurons at the penultimate fully-connected layer.

Here we use the VGGVD architecture as in (Cimpoi

et al., 2016). Each image is processed by the already

trained neural network outputting a vector of real val-

ues at that layer. Such vector is therefore processed

by a composite operator formed by a combination of

a discrete wavelet transform (Mallat, 2008) and local

binary patterns in their 1D version, as described in

(Tirunagari et al., 2017).

In the following we calculate the detail coefﬁ-

cients d

. In discrete domain they can be obtained

√

M−1

∑

n=0

(n), j ≥ j

, (1)

where j is the decomposition level, M is the length of

y and φ and ψ are the wavelet functions. These coefﬁ-

cients can be easily obtained in any modern scientiﬁc

programming language. Here we use symlet4 wavelet

functions (Mallat, 2008). Two levels of decomposi-

tion are employed here yielding the vectors d

1·

and

2·

In the next step, those detail vectors are linearly

combined with a predeﬁned weight α:



(1 −α)ds(y) + αd

1·

if 0 ≤ α ≤ 1,

(2 −α)ds(d

1·

) + (α −1)d

2·

if 1 ≤ α ≤ 2,

(2)

where ds is a downsampling function (here using a

lowpass Chebyshev Type I inﬁnite impulse response

ﬁlter of order 8). The downsampling operation is nec-

essary to make the combined vectors to have the same

length.

Finally, the descriptors are given by applying 1D

LBP with radius r over D

α,r

= LBP

). (3)

The proposed method essentially explores two

complementary fundamental viewpoints of the tex-

ture neural activation: the frequency and spatial dis-

tribution. At the same time it beneﬁts from all the

machinery of CNNs and their capacity of extracting

features in highly complex hierarchical organizations.

The efﬁcient local description provided by LBP over

the high frequency distribution captured by wavelet

details has the effect of providing a detailed map of

ﬁner details in the output CNN function. According to

studies like (Rahaman et al., 2019), this corresponds

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

504

precisely to characteristics learned in more advanced

stages of the CNN. On the other hand, frequency do-

main is not restrict to a well-localized point on the

loss surface, such that this type of analysis ends up

being less susceptible to over-ﬁtting than simply us-

ing a very large number of epochs in the CNN model.

3 EXPERIMENTS

We assess the performance of the proposed method

in texture recognition over four benchmark datasets

(KTHTIPS-2b (Hayman et al., 2004), FMD (Sharan

et al., 2009), UIUC (Lazebnik et al., 2005), and UMD

(Xu et al., 2009)) and an application to the identiﬁ-

cation of Brazilian plant species (database 1200Tex

(Casanova et al., 2009)).

KTH-TIPS2b database is composed by 4752 color

images of 11 different materials (classes). Unlike

classical texture databases, that are focused on visual

appearance, here each target group may contain sub-

stantially different images. This is particularly chal-

lenging mainly for classical local patch approaches

like LBP and bag-of-visual-words. Each material is

further divided into 4 samples, each sample corre-

sponding to particular settings of illumination, scale

and perspective. Here we adopt the most challeng-

ing protocol of training on 1 sample of each class and

testing on the remaining 3 samples.

FMD is also a material-based dataset. Comprises

10 classes with 100 color images per class and the

training/testing protocol is a random split with 50%

for training and 50% for testing, which is repeated 10

times to provide statistical measures.

UIUC and UMD, on the other hand, are typical

texture-based databases. Both comprise 25 classes

with 40 grayscale samples in each class. Both are also

collected under non-controlled conditions and share

variations in scale, illumination and viewpoint. The

most remarkable differnce is in resolution: whereas

UIUC has smaller images with size 640 ×480, UMD

images has resolution 1280 ×960.

1200Tex (Casanova et al., 2009) is a database of

color texture images acquired by scanning the leaf

surface of 60 species of Brazilian plants. The ob-

jective is to identify the respective species. A com-

mercial scanner is used and conditions of illumina-

tion, pose and scale are strictly controlled. For each

class (species) we have 60 image samples, each one

corresponding to a non-overlapping window with size

128 ×128. The training/testing split is the same one

used in UIUC and UMD, i.e., 50% for training and

50% for testing.

For the classiﬁcation we employed linear discrim-

inant analysis (Bishop, 2006), mainly for its ease of

interpretation and no need for tuning a large number

of hyper-parameters. Given the high number of fea-

tures, we also applied principal component analysis

(Bishop, 2006). The number of components was de-

ﬁned by cross-validation over the training set.

4 RESULTS

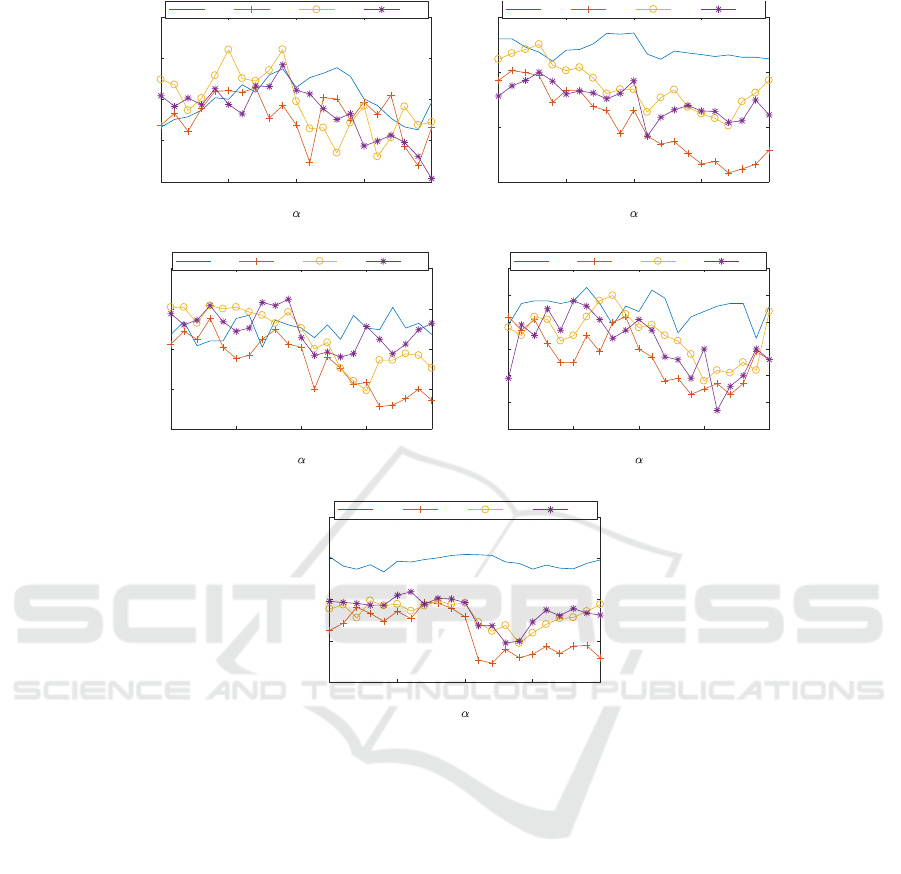
Figure 2 shows the classiﬁcation accuracies on the

compared databases when parameters r and α are var-

ied. In general, we observe that r = 0, i.e., the direct

use of wavelet transform is a good choice in most sce-

narios. Nevertheless, some signiﬁcant boost was ob-

tained in KTH and UIUC by using r = 2 and r = 3,

respectively. It can also be noticed that r = 2 and r = 3

are in general preferred over r = 1. Another interest-

ing point is that the best performance is achieved usu-

ally for α ≈ 1.0, which corresponds to the ﬁrst level

of detail coefﬁcients. Actually, we veriﬁed the accu-

racy for higher levels but no gain was obtained. Table

2 lists the best accuracies for each LBP radius, also

conﬁrming the effectiveness of using r = 0.

Tables 1 and 2 present the accuracies compared

to state-of-the art results published in the literatures

on the same databases and using the same protocol.

We separate KTH, FMD, UIUC, and UMD (bench-

mark data sets) from 1200Tex (application) due to

the comparatively reduced number of results for the

later in the literature. In both cases we notice the

proposed descriptors outperforming several state-of-

the-art methods, including advanced CNN-based so-

lutions. This is more evident in the most challenging

databases, i.e., KTH, FMD and 1200Tex. Even when

the proposed descriptors were surpassed in a few sit-

uations in UMD and UIUC databases, they achieved

higher accuracy in the other ones.

In summary, the presented results corroborate our

expectations of an improved performance of CNNs

when associated to the wavelet representation. The

details coefﬁcient were capable of extracting a ﬁne-

grained description of the image, but avoiding over-

ﬁtting due to the non-localized behavior of frequency

distribution. Altogether, this was the rationale behind

a more complete CNN representation for the texture

image, that was responsible for more robust descrip-

tors and, as a consequence, higher classiﬁcation accu-

racies in general.

Wavelet Transform for the Analysis of Convolutional Neural Networks in Texture Recognition

505

0 0.5 1 1.5 2

Accuracy (%)

r = 0 r = 1 r = 2 r = 3

0 0.5 1 1.5 2

Accuracy (%)

r = 0 r = 1 r = 2 r = 3

KTHTIPS-2b FMD

0 0.5 1 1.5 2

96.5

97.5

98.5

Accuracy (%)

r = 0 r = 1 r = 2 r = 3

0 0.5 1 1.5 2

98.0

98.2

98.4

98.6

98.8

99.0

99.2

Accuracy (%)

r = 0 r = 1 r = 2 r = 3

UIUC UMD

0 0.5 1 1.5 2

Accuracy (%)

r = 0 r = 1 r = 2 r = 3

1200Tex

Figure 2: Accuracies of the proposed method for different hyperparameters on the texture databases. Even though r = 0 works

ﬁne in most cases, LBP improved the accuracy in more complicated scenarios, e.g., in KTHTIPS-2b textures.

5 CONCLUSIONS

This work presented a new method for texture recog-

nition extracting wavelet details from the penultimate

layer of a CNN. Such coefﬁcients were also subjected

to LBP analysis to improve even further its ability of

capturing the complexity of a visual texture.

The performance of the proposal was evaluated

in terms of accuracy on the classiﬁcation of bench-

mark datasets and on a practical problem of identi-

fying plant species using the leaf surface texture. In

this tasks, the proposed method outperformed several

state-of-the-art approaches for texture recognition, at-

testing its potential as a powerful representation for

texture images.

The success of the proposed methodology can be

expected and explained in theoretical terms by a novel

perspective over the CNN offered by the localized fre-

quency analysis of wavelets. Detail coefﬁcients de-

scribe ﬁne-grained characteristics of the image at the

same time that frequency domain prevents over-ﬁtting

as the feature is not exactly localized in space.

ACKNOWLEDGEMENTS

J. B. Florindo gratefully acknowledges the ﬁnancial

support of S

ao Paulo Research Foundation (FAPESP)

(Grant #2020/01984-8) and from National Council

for Scientiﬁc and Technological Development, Brazil

(CNPq) (Grants #306030/2019-5 and #423292/2018-

8).

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

506

Table 1: Accuracies for different databases: KTHTIPS-2b, FMD, UIUC, and UMD. Several state-of-the-art approaches are

outperformed by the proposed method.

Method KTH2b FMD UIUC UMD

VZ-MR8 (Varma and Zisserman, 2005) 46.3 22.1 92.9 -

LBP (Ojala et al., 2002) 50.5 - 88.4 96.1

VZ-Joint (Varma and Zisserman, 2009) 53.3 23.8 78.4 -

BSIF (Kannala and Rahtu, 2012) 54.3 - 73.4 96.1

CLBP (Guo et al., 2010a) 57.3 43.6 95.7 98.6

LBP

riu2

/VAR (Ojala et al., 2002) 58.5 - 84.4 95.9

PCANet (NNC) (Chan et al., 2015) 59.4 - 57.7 90.5

RandNet (NNC) (Chan et al., 2015) 60.7 - 56.6 90.9

ScatNet (NNC) (Bruna and Mallat, 2013) 63.7 - 88.6 93.4

DeCAF (Cimpoi et al., 2014) 70.7 60.7 94.2 96.4

SIFT + BoVW (Cimpoi et al., 2014) 58.4 49.5 96.1 98.1

FC-CNN VGGM (Cimpoi et al., 2016) 71.0 70.3 94.5 97.2

FC-CNN AlexNet (Cimpoi et al., 2016) 71.5 64.8 91.1 95.9

FC-CNN VGGVD (Cimpoi et al., 2016) 75.4 77.4 97.0 97.7

RAMBP (Alkhatib and Haﬁane, 2019) 68.9 46.8 94.8 98.6

H2OEP (Song et al., 2021) 64.2 - - -

SWOBP (Song et al., 2020) 66.4 - - -

SLGP (Song et al., 2018b) 53.6 - - -

LBPC (Singh et al., 2018) 50.7 - - -

LETRIST (Song et al., 2018a) 65.3 - 97.7 98.8

BRINT

CPS

(Pan et al., 2019) - - 92.2 93.5

MRELBP

CPS

(Pan et al., 2019) - - 95.2 94.2

DSTNet (Florindo, 2020) 61.0 - 93.6 98.5

2D-LTP (Xiao et al., 2019) - 49.0 - -

Proposed 77.2 77.7 98.1 99.0

Table 2: State-of-the-art accuracies for 1200Tex. Outper-

forming computationally intensive methods like FV-CNN

is a remarkable achievement.

Method Accuracy (%)

LBPV (Guo et al., 2010b) 70.8

Network diffusion (Gonc¸alves et al., 2016) 75.8

FC-CNN VGGM (Cimpoi et al., 2016) 78.0

FV-CNN VGGM (Cimpoi et al., 2016) 83.1

Gabor (Casanova et al., 2009) 84.0

FC-CNN VGGVD (Cimpoi et al., 2016) 84.2

SIFT + BoVW (Cimpoi et al., 2014) 86.0

FV-CNN VGGVD (Cimpoi et al., 2016) 87.1

DSTNet (Florindo, 2020) 79.3

Proposed 88.2

REFERENCES

Alexandridis, A. K. and Zapranis, A. D. (2013). Wavelet

neural networks: A practical guide. Neural Networks,

42:1 – 27.

Alkhatib, M. and Haﬁane, A. (2019). Robust adaptive me-

dian binary pattern for noisy texture classiﬁcation and

retrieval. IEEE Transactions on Image Processing,

28(11):5407–5418.

Andrearczyk, V. and Whelan, P. F. (2016). Using ﬁlter

banks in convolutional neural networks for texture

classiﬁcation. Pattern Recognition Letters, 84:63 – 69.

Anwer, R. M., Khan, F. S., van de Weijer, J., Molinier, M.,

and Laaksonen, J. (2018). Binary patterns encoded

convolutional neural networks for texture recognition

and remote sensing scene classiﬁcation. ISPRS Jour-

nal of Photogrammetry and Remote Sensing, 138:74 –

85.

Bishop, C. M. (2006). Pattern Recognition and Ma-

chine Learning (Information Science and Statistics).

Springer-Verlag, Berlin, Heidelberg.

Bruna, J. and Mallat, S. (2013). Invariant scattering convo-

lution networks. IEEE Transactions on Pattern Anal-

ysis and Machine Intelligence, 35(8):1872–1886.

Casanova, D., de Mesquita S

a Junior, J. J., and Bruno, O. M.

(2009). Plant leaf identiﬁcation using gabor wavelets.

International Journal of Imaging Systems and Tech-

nology, 19(3):236–243.

Chan, T., Jia, K., Gao, S., Lu, J., Zeng, Z., and Ma, Y.

(2015). PCANet: A simple deep learning baseline for

image classiﬁcation? IEEE Transactions on Image

Processing, 24(12):5017–5032.

Chen, L.-C., Papandreou, G., Kokkinos, I., Murphy, K.,

and Yuille, A. L. (2018). DeepLab: Semantic Image

Segmentation with Deep Convolutional Nets, Atrous

Convolution, and Fully Connected CRFs. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 40(4):834–848.

Cimpoi, M., Maji, S., Kokkinos, I., Mohamed, S., and

Vedaldi, A. (2014). Describing textures in the wild.

Wavelet Transform for the Analysis of Convolutional Neural Networks in Texture Recognition

507

In Proceedings of the 2014 IEEE Conference on

Computer Vision and Pattern Recognition, CVPR

’14, pages 3606–3613, Washington, DC, USA. IEEE

Computer Society.

Cimpoi, M., Maji, S., Kokkinos, I., and Vedaldi, A. (2016).

Deep ﬁlter banks for texture recognition, description,

and segmentation. International Journal of Computer

Vision, 118(1):65–94.

Florindo, J. B. (2020). Dstnet: Successive applications of

the discrete schroedinger transform for texture recog-

nition. Information Sciences, 507:356–364.

Fujieda, S., Takayama, K., and Hachisuka, T. (2017).

Wavelet convolutional neural networks for texture

classiﬁcation.

Gonc¸alves, W. N., da Silva, N. R., da Fontoura Costa,

L., and Bruno, O. M. (2016). Texture recognition

based on diffusion in networks. Information Sciences,

364(C):51–71.

Guo, Z., Zhang, L., and Zhang, D. (2010a). A completed

modeling of local binary pattern operator for texture

classiﬁcation. Trans. Img. Proc., 19(6):1657–1663.

Guo, Z., Zhang, L., and Zhang, D. (2010b). Rota-

tion invariant texture classiﬁcation using lbp variance

(lbpv) with global matching. Pattern Recognition,

43(3):706–719.

Hayman, E., Caputo, B., Fritz, M., and Eklundh, J.-O.

(2004). On the signiﬁcance of real-world conditions

for material classiﬁcation. In Pajdla, T. and Matas, J.,

editors, Computer Vision - ECCV 2004, pages 253–

266, Berlin, Heidelberg. Springer Berlin Heidelberg.

Ji, L., Chang, M., Shen, Y., and Zhang, Q. (2020). Re-

current convolutions of binary-constraint cellular neu-

ral network for texture recognition. Neurocomputing,

387:161 – 171.

Kannala, J. and Rahtu, E. (2012). Bsif: Binarized statisti-

cal image features. In ICPR, pages 1363–1366. IEEE

Computer Society.

Krizhevsky, A., Sutskever, I., and Hinton, G. E. (2017). Im-

ageNet Classiﬁcation with Deep Convolutional Neu-

ral Networks. Communitions of the ACM, 60(6):84–

90.

Lazebnik, S., Schmid, C., and Ponce, J. (2005). A sparse

texture representation using local afﬁne regions. IEEE

Transactions on Pattern Analysis and Machine Intel-

ligence, 27(8):1265–1278.

Mallat, S. (2008). A Wavelet Tour of Signal Processing,

Third Edition: The Sparse Way. Academic Press, Inc.,

USA, 3rd edition.

Ng, J. Y.-H., Hausknecht, M., Vijayanarasimhan, S.,

Vinyals, O., Monga, R., and Toderici, G. (2015). Be-

yond Short Snippets: Deep Networks for Video Clas-

siﬁcation. In 2015 IEEE Conference on Computer

Vision and Pattern Recognition (CVPR), IEEE Con-

ference on Computer Vision and Pattern Recognition,

pages 4694–4702.

Ojala, T., Pietik

ainen, M., and M

aenp

a, T. (2002). Mul-

tiresolution gray-scale and rotation invariant texture

classiﬁcation with local binary patterns. IEEE Trans-

actions on Pattern Analysis and Machine Intelligence,

24(7):971–987.

Pan, Z., Wu, X., and Li, Z. (2019). Central pixel selec-

tion strategy based on local gray-value distribution

by using gradient information to enhance lbp for tex-

ture classiﬁcation. Expert Systems with Applications,

120:319–334.

Rahaman, N., Baratin, A., Arpit, D., Draxler, F., Lin, M.,

Hamprecht, F., Bengio, Y., and Courville, A. (2019).

On the spectral bias of neural networks. In Chaud-

huri, K. and Salakhutdinov, R., editors, Proceedings of

the 36th International Conference on Machine Learn-

ing, volume 97 of Proceedings of Machine Learning

Research, pages 5301–5310, Long Beach, California,

USA. PMLR.

Ren, S., He, K., Girshick, R., and Sun, J. (2017). Faster R-

CNN: Towards Real-Time Object Detection with Re-

gion Proposal Networks. IEEE Transactions on Pat-

tern Analysis and Machine Intelligence, 39(6):1137–

1149.

Ronen, B., Jacobs, D., Kasten, Y., and Kritchman, S.

(2019). The convergence rate of neural networks for

learned functions of different frequencies. In Wallach,

H., Larochelle, H., Beygelzimer, A., d'Alch

e-Buc, F.,

Fox, E., and Garnett, R., editors, Advances in Neural

Information Processing Systems, volume 32. Curran

Associates, Inc.

Sharan, L., Rosenholtz, R., and Adelson, E. H. (2009). Ma-

terial perceprion: What can you see in a brief glance?

Journal of Vision, 9(8):784.

Shin, H.-C., Roth, H. R., Gao, M., Lu, L., Xu, Z., Nogues,

I., Yao, J., Mollura, D., and Summers, R. M. (2016).

Deep Convolutional Neural Networks for Computer-

Aided Detection: CNN Architectures, Dataset Char-

acteristics and Transfer Learning. IEEE Transactions

on Medical Imaging, 35(5, SI):1285–1298.

Simsekli, U., Sener, O., Deligiannidis, G., and Erdogdu,

M. A. (2020). Hausdorff dimension, heavy tails, and

generalization in neural networks. In Advances in

Neural Information Processing Systems.

Singh, C., Walia, E., and Kaur, K. P. (2018). Color texture

description with novel local binary patterns for effec-

tive image retrieval. Pattern Recognition, 76:50–68.

Song, T., Feng, J., Wang, S., and Xie, Y. (2020). Spa-

tially weighted order binary pattern for color tex-

ture classiﬁcation. Expert Systems with Applications,

147:113167.

Song, T., Feng, J., Wang, Y., and Gao, C. (2021). Color

texture description based on holistic and hierarchi-

cal order-encoding patterns. In 2020 25th Inter-

national Conference on Pattern Recognition (ICPR),

pages 1306–1312.

Song, T., Li, H., Meng, F., Wu, Q., and Cai, J. (2018a).

Letrist: Locally encoded transform feature histogram

for rotation-invariant texture classiﬁcation. IEEE

Transactions on Circuits and Systems for Video Tech-

nology, 28(7):1565–1579.

Song, T., Xin, L., Gao, C., Zhang, G., and Zhang, T.

(2018b). Grayscale-inversion and rotation invariant

texture description using sorted local gradient pattern.

IEEE Signal Processing Letters, 25(5):625–629.

Taigman, Y., Yang, M., Ranzato, M., and Wolf, L. (2014).

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

508

DeepFace: Closing the Gap to Human-Level Perfor-

mance in Face Veriﬁcation. In 2014 IEEE Conference

on Computer Vision and Pattern Recognition (CVPR),

IEEE Conference on Computer Vision and Pattern

Recognition, pages 1701–1708.

Tirunagari, S., Kouchaki, S., Abasolo, D., and Poh, N.

(2017). One dimensional local binary patterns of elec-

troencephalogram signals for detecting alzheimer’s

disease. In 2017 22nd International Conference on

Digital Signal Processing (DSP), pages 1–5.

Varma, M. and Zisserman, A. (2005). A statistical approach

to texture classiﬁcation from single images. Interna-

tional Journal of Computer Vision, 62(1):61–81.

Varma, M. and Zisserman, A. (2009). A statistical ap-

proach to material classiﬁcation using image patch ex-

emplars. IEEE Transactions on Pattern Analysis and

Machine Intelligence, 31(11):2032–2047.

Vu, N., Nguyen, V., and Gosselin, P. (2017). A handcrafted

normalized-convolution network for texture classiﬁ-

cation. In 2017 IEEE International Conference on

Computer Vision Workshops (ICCVW), pages 1238–

1245.

Xiao, B., Wang, K., Bi, X., Li, W., and Han, J. (2019). 2d-

lbp: An enhanced local binary feature for texture im-

age classiﬁcation. IEEE Transactions on Circuits and

Systems for Video Technology, 29(9):2796–2808.

Xu, Y., Ji, H., and Ferm

uller, C. (2009). Viewpoint invari-

ant texture description using fractal analysis. Interna-

tional Journal of Computer Vision, 83(1):85–100.

Zhang, Q. and Benveniste, A. (1992). Wavelet networks.

IEEE Transactions on Neural Networks, 3(6):889–

898.

Zhu, X. X., Tuia, D., Mou, L., Xia, G.-S., Zhang, L., Xu,

F., and Fraundorfer, F. (2017). Deep Learning in Re-

mote Sensing. IEEE Geoscience and Remote Sensing

Magazine, 5(4):8–36.

Wavelet Transform for the Analysis of Convolutional Neural Networks in Texture Recognition

509