Improving the Efﬁciency of Autoencoders for Visual Defect Detection

with Orientation Normalization

Rich

ard R

adli and L

aszl

o Cz

uni

Faculty of Information Technology, University of Pannonia, Egyetem Street 10., Veszpr

em, Hungary

Keywords:

Autoencoder Neural Network, Convolutional Neural Network, Defect Detection, Unsupervised Anomaly

Detection, Spatial Transformer Network.

Abstract:

Autoencoders (AE) can have an important role in visual inspection since they are capable of unsupervised

learning of normal visual appearance and detection of visual defects as anomalies. Reducing the variability of

incoming structures can result in more efﬁcient representation in latent space and better reconstruction quality

for defect free inputs. In our paper we investigate the utilization of spatial transformer networks (STN) to

improve the efﬁciency of AEs in reconstruction and defect detection. We found that the simultaneous training

of the convolutional layers of the AEs and the weights of STNs doesn’t result in satisfactory reconstructions

by the decoder. Instead, the STN can be trained to normalize the orientation of the input images. We evaluate

the performance of the proposed mechanism, on three classes of input patterns, by reconstruction error and

standard anomaly detection metrics.

1 INTRODUCTION

The visual inspection of products is often inevitable

in many manufacturing processes. Since anomalous

items are often missing during the training process

unsupervised anomaly detection is the most suitable

approach to build a defect detection system. In our

paper we are to improve autoencoder (AE) neural

networks to reach better model generation at given

convolutional complexity and latent space size. As

a consequence we expect better accuracy to detect

anomalies. It is already shown that denoising AEs can

perform better than base AEs in anomaly detection

adli and Cz

uni, 2021), and that applying structural

similarity in the loss function during training can also

improve results (Bergmann et al., 2018). Now, our

idea is to apply geometric transformations to normal-

ize the rotation of the input images, thus AE can more

efﬁciently compress and reconstruct input patterns.

In Section 2 we introduce autoencoders, in Sec-

tion 3 we discuss the usage of AEs for anomaly de-

tection, while in Section 4 the operation of spatial

transformer networks (STNs) (Jaderberg et al., 2015)

is described. The combination of AEs with STNs is

discussed in Section 5. The proposed normalization

technique can be found in Section 6 and the dataset

used in experiments are introduced in 7. Results are

https://orcid.org/0000-0001-7667-9513

discussed in Section 8 and ﬁnally conclusions and fu-

ture work are given in 9.

2 DIFFERENT TYPES OF

AUTOENCODERS

AEs are deﬁned as feed-forward neural networks

containing three main sequential components:

the encoder network E : R

k×h×w

→ R

, the latent

space R

, and the decoder network D : R

→ R

k×h×w

x = D(E(x)) = D(z),

(1)

where x is the input data, z is the latent information,

and

x is the output of the network. Their similarity to

principal component analysis (PCA) is well known,

moreover, AEs could outperform linear or kernel

PCAs in many cases (Sakurada and Yairi, 2014) .

AEs can be categorized according to their loss

functions. The loss function (J), to learn a speciﬁc

task, can be generally formed this way:

J(x, ω) =

∑

kx −

xk + R(z),

(2)

where ω = (w

, b

, w

, b

) are the weights and

biases of the encoder and decoder networks and n is

Rádli, R. and Czúni, L.

Improving the Efﬁciency of Autoencoders for Visual Defect Detection with Orientation Normalization.

DOI: 10.5220/0010903600003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 4: VISAPP, pages

651-658

ISBN: 978-989-758-555-5; ISSN: 2184-4321

651

the number of elements in a batch. In sparse AEs R

is based on the Kullback-Leibler divergence or on the

L1 norm, the purpose is to make the most of the hid-

den unit’s activations close to zero. Contractive AEs

apply the Frobenius norm on the derivative of z as

a function of x to make the model resistant to small

perturbations; in an information theoretic-learning

autoencoder Renyi’s entropy is used; while feature

matching autoencoders (Dosovitskiy and Brox, 2016)

enforce the features of the input and its reconstruction

to be equal:

J(x,

x, ω) = w

∑

(x −

+ w

f t

∑

(F(x) − F(

x))

(3)

where F is a feature extractor which can be ﬁxed

or also trained. The SSIM-AE (Bergmann et al.,

2018) can be considered as a kind of feature matching

AEs (Eq. 3) where the loss function utilizes the struc-

tural similarity (Wang et al., 2004) of images repre-

senting, beside luminance, local variance and covari-

ance. The denoising autoencoder (DAE) is an exten-

sion of the basic autoencoder, which is trained to re-

construct corrupted input data. C denotes the corrupt-

ing function generating

x. Eq. 1 now becomes:

x = D(E(C(x))) = D(E(

x)) = D(z).

(4)

The applied loss can weight between untouched and

artiﬁcially corrupted areas. Variational AEs (VAEs)

impose constraints on the latent variables in a differ-

ent way, they estimate posteriori probability p(z|x)

with an assumption of a prior knowledge p(z) be-

ing a normal Gaussian distribution. Adversarial AEs

(AAEs) use generative adversarial networks (GANs)

to perform variational inference. VAEs and AAEs are

both generative models, and both are based on max-

imum likelihood. The difference between VAEs and

AAEs can be characterized that while VAEs apply ex-

plicit rules on z, AAEs control its distribution implic-

itly.

3 ANOMALY DETECTION WITH

AUTOENCODERS

AEs are among the candidates for unsupervised

anomaly detection in industrial applications, their re-

cent performance ranks them in the middle of the

state-of-the-art (Bergmann et al., 2021). Our purpose

is to ﬁnd ways to improve the detection accuracy of

baseline AEs. The detection of faults in images is

typically solved by computing the difference between

the input and the decoded signal. If it is above a given

threshold T , we set the detection map to 1:

m =

(

1, if ||x −

x|| > T,

0, otherwise.

(5)

The applied ||.|| can be various (e.g. L

, L

, SSIM

(Bergmann et al., 2018)).

In (Beggel et al., 2019) authors deal with the prob-

lem of training AEs when the training set is contami-

nated with some outliers. Their proposed adversarial

autoencoder imposes a prior distribution on the latent

representation, placing anomalies into low likelihood

regions, thus potential anomalies can be identiﬁed and

rejected already during training. (Tuluptceva et al.,

2020) proposes perceptual deep autoencoders where

relative-perceptual-L1 loss (Tuluptceva et al., 2020),

robust to low contrast and noise, is applied for train-

ing and also to predict the abnormality for new inputs.

In (Alaverdyan et al., 2020) an unsupervised siamese

autoencoder is proposed to detect anomalies in brain

MRI images by a one class SVM in latent space. The

role of the siamese network is to regularize the latent

space: R(z) (Eq. 2) is the cosine distance of two in-

dependent samples in the two siamese branches in the

latent space. In (R

adli and Cz

uni, 2021) blocks of

pixels were deleted as simulated noise in a denoising

SSIM-AE, and the SSIM-AE was forced to learn the

reconstruction of areas from neighboring territories;

this strategy resulted in better anomaly detection for

different classes of inputs when compared to the base

SSIM-AE.

The improvement of VAEs with STNs was pub-

lished in (Bidart and Wong, 2019) but there were

questions raised regarding the simultaneous learning

of VAE and STN weights, and its effect on anomaly

detection was not investigated at all. These are our

main questions in this article but we use AEs (instead

of VAEs) as the base, starting model.

For a deeper review on AEs and their application

we propose to check paper (Zhai et al., 2018).

3.1 The AE Framework in Our Study

Table 1 contains our autoencoder following the struc-

ture of (Bergmann et al., 2018) but applying squared

difference (L

) in the loss function instead of SSIM.

While the complexity of this structure could be im-

proved with success (such can be found in (R

adli and

uni, 2021)) but this convolutional AE can serve

as a good base model for our comparisons. The de-

coder part is simply building up the input image in a

symmetrical structure to the encoder using deconvo-

lutions.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

652

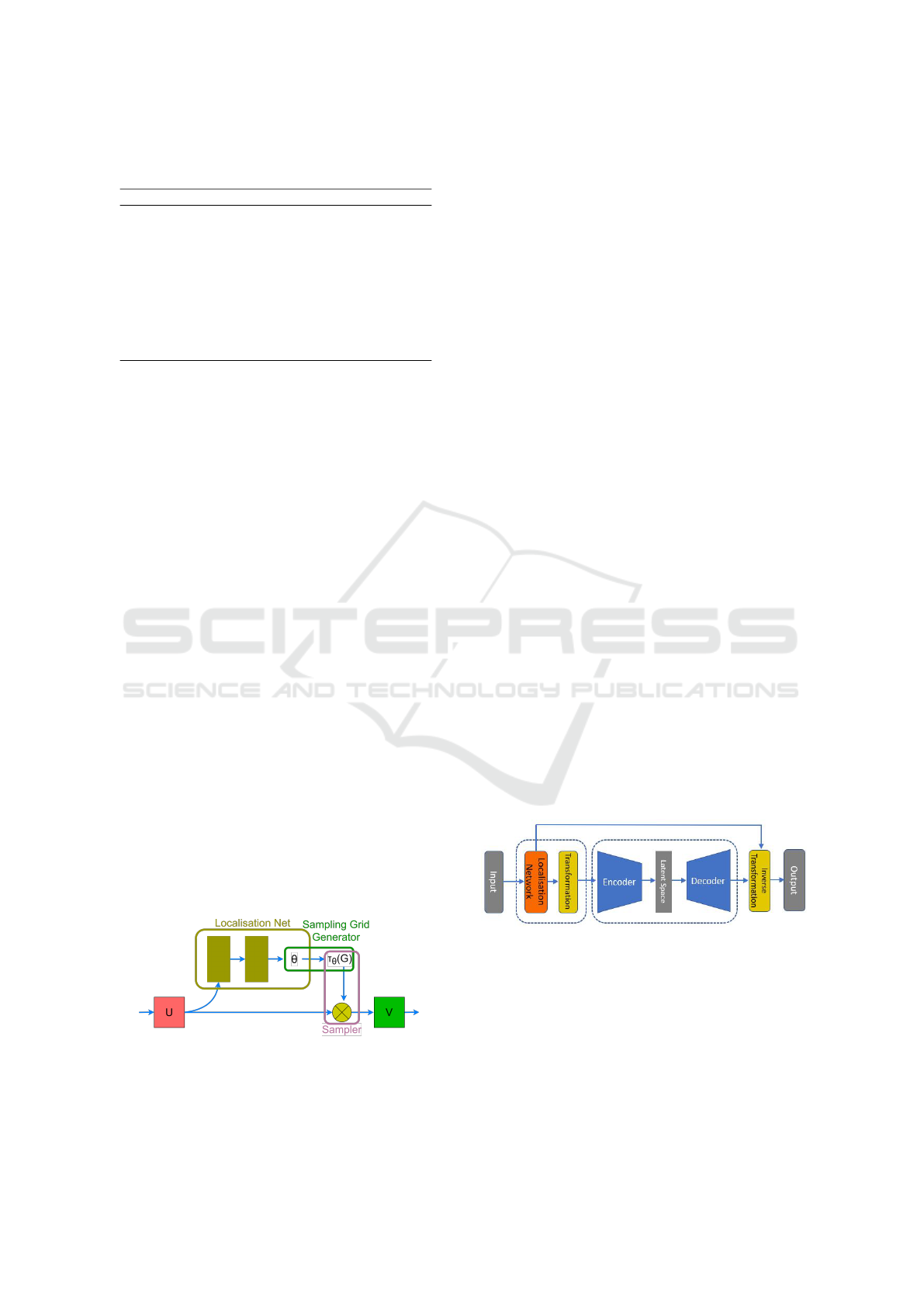
Table 1: Architecture of the applied encoder for input image

128 × 128 × 3. d = 100 for the texture and screw images.

Layer Output Size Kernel Stride Padding

Input 128x128x3

Conv1 64x64x32 4x4 2 1

Conv2 32x32x32 4x4 2 1

Conv3 32x32x32 3x3 1 1

Conv4 16x16x64 4x4 2 1

Conv5 16x16x64 3x3 1 1

Conv6 8x8x128 4x4 2 1

Conv7 8x8x64 3x3 1 1

Conv8 8x8x32 3x3 1 1

Conv9 1x1xd 8x8 1 0

4 SPATIAL TRANSFORMER

NETWORKS

Spatial transformer networks (STN) were proposed

by (Jaderberg et al., 2015), designed for the spatial

transformation of data within existing network archi-

tectures. It was shown that the use of the spatial trans-

formers results in models which learn invariance to

translation, scale, rotation and more generic warp-

ings, leading to state-of-the-art performance on sev-

eral benchmarks. STN consists of three main parts:

• Localisation subnetwork: its task is to ﬁgure out

the right transformation parameters θ. It can have

any form but should include a ﬁnal regression

layer to produce the transformation parameters.

(Typically afﬁne and perspective transformations

are in focus but in our study we focus only on ro-

tations as discussed later.)

• Sampling grid generator: to perform the geomet-

ric transformation of the input, each output value

should be computed by applying a sampling ker-

nel centered at a particular location in the input.

The sampling grid deﬁnes how to compute the lo-

cations of values on the input.

• Sampler: this part computes the result of transfor-

mation sampling the input according to the sam-

pling grid.

Figure 1: The base STN architecture, where U is the input

image or image features, and V is the transformed version

of them.

STNs are found to be useful in the improvement

of many classical image processing tasks. For ex-

ample in (Li et al., 2018) the recognition of jersey

numbers in soccer videos was improved by adding

STN to the front end of a classiﬁcation network. To

help the learning phase, a semi-supervised mecha-

nism was proposed, where the localisation error was

part of the loss function, beside softmax classiﬁca-

tion loss. In (Lee et al., 2019) the goal was to learn

a complex function that maps the appearance of input

image pairs to the parameters of the spatial transfor-

mation in order to register anatomical structures. To

guide the registration of the moving image to the ﬁxed

one, alternatives of the loss function contained pre-

pared structures-of-interest regions (segmentations or

landmarks) beside the pixel-wise registration error.

Discussing all applications are beyond our paper,

there are interesting ones, such as grasp detection

(Park and Chun, 2018), image retrieval (Ding et al.,

2020), or change detection (Chianucci and Savakis,

2016). The most similar paper to ours is (Bidart and

Wong, 2019), where VAE networks were extended

with STNs. Their ﬁndings are discussed in the next

section.

5 STNs WITH AUTOENCODERS

It seems straightforward that the insertion of an STN

at the front end of an AE and the inverse transfor-

mation after the decoder can result in better recon-

struction, since the STN might learn the best spatial

transformation warping images to similar scale, po-

sition, and orientation. This way the AE meets less

variability of input patterns, can more easily learn the

necessary convolutions, and ﬁnally can make a better

reconstruction. Figure 2 illustrates this conﬁguration.

Figure 2: STN inserted into an AE with the inverse spatial

transformation.

Unfortunately, to simultaneously ﬁnd the optimal

weights for either the localisation network and the AE

is not guaranteed. In (Bidart and Wong, 2019) the

same structure was used but instead of AE a VAE was

used. We quote the description of this problem from

(Bidart and Wong, 2019): ”We ﬁnd in practice there

are issues with the optimizer being caught in local

minima, so we use multiple random restarts, where

Improving the Efﬁciency of Autoencoders for Visual Defect Detection with Orientation Normalization

653

we ﬁrst try the loss at a set number of afﬁne param-

eters, and only perform gradient descent on the best

performing parameters.” Moreover, they investigated

only images from the MNIST database of handwrit-

ten digits, which are almost binary patterns from a

small size set of classes. Also, it is a question how

the combination of STNs and AEs perform in case of

more complicated structures (such as grayscale tex-

tures for example) and what effect does all these have

on anomaly detection. Since our AEs are fully con-

volutional and test images have the same scale, only

the orientation of input patterns should be compen-

sated by the STN, we can avoid the learning of trans-

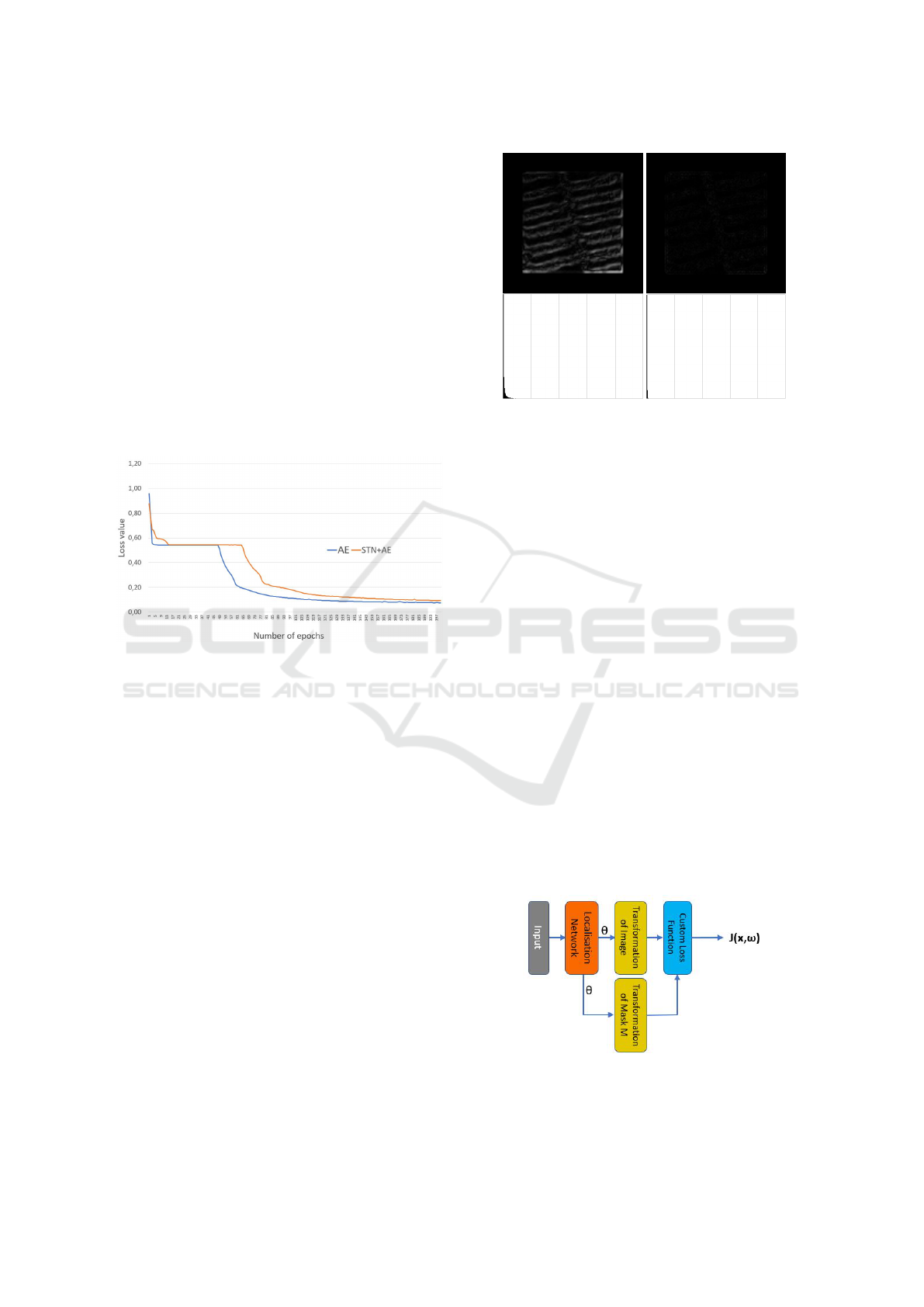
lation and scaling parameters. Fig. 3 illustrates typ-

ical learning curves for our pure AE (given in Sub-

section 3.1) and the one extended with the STN (as

illustrated by Fig. 2). Interestingly, in this example

Figure 3: Learning curves for AE and STN+AE for the class

Texture 1.

the inclusion of STN resulted in even higher loss val-

ues; the same happened with many other test images.

Thus the inclusion of STN did not improve the perfor-

mance of the AE. Looking for the reason of this per-

formance drop we found that the widely used Keras

implementation (STN, 2016) of the STN has low ac-

curacy. Fig. 4 illustrates the differences, when an

image was rotated by 45°and then back to its original

orientation. The error of interpolation computed with

code (STN, 2016) is very high (see Fig. 4 left). This

means that the inverse spatial transformation, after the

decoding step, will not accurately reproduce the same

orientation of the input and it will result in a larger

value in Eq. 5. To get rid of this transformation error

we replaced the grid generator and sampler of (STN,

2016) with the built in spatial transformation function

of TensorFlow (tfa.image.transform). As can be seen

on Fig. 4 right this implementation gives almost per-

fect inverse transformation.

To investigate the simultaneous optimization of AE

and STN weights we tested three strategies:

• We started both STN and AE with random

weights and the loss function used the square

Figure 4: Example for rotation and inverse rotation of a

Texture 1 image with 45°. Left: the difference image (be-

tween input and inverse rotated) shows inaccurate compu-

tations in the STN implementation (STN, 2016). Right:

the same difference image when rotations and their inverse

were performed by built in TensorFlow function, called

tfa.image.transform. In the second row the histograms are

given for better illustration.

function in Eq. 1 without any regularization

(R = 0).

• We separated the STN from the AE during train-

ing. STN was pre-trained to normalize the orien-

tation of input patterns as detailed in the following

section. During the training of the AE the locali-

sation network was frozen.

• The same as above but allowed the training to re-

ﬁne the weights of the STN.

In the next Section we discuss the case of pre-trained

STNs.

6 NORMALIZATION WITH STNs

The purpose of normalization STN is to rotate the in-

puts to the same orientation. To achieve this we built

an STN where the loss function is based on image

gradients.

Figure 5: STN with custom loss function as speciﬁed by Eq.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

654

Local image gradients were computed with a con-

volution kernel on the re-scaled variant (64 × 64) of

the image. To sub-press image noise and small de-

tails, Gaussian blur was applied before computing the

horizontal gradients by the vertical Sobel ﬁlter:





−1 0 +1

−2 0 +2

−1 0 +1





(6)

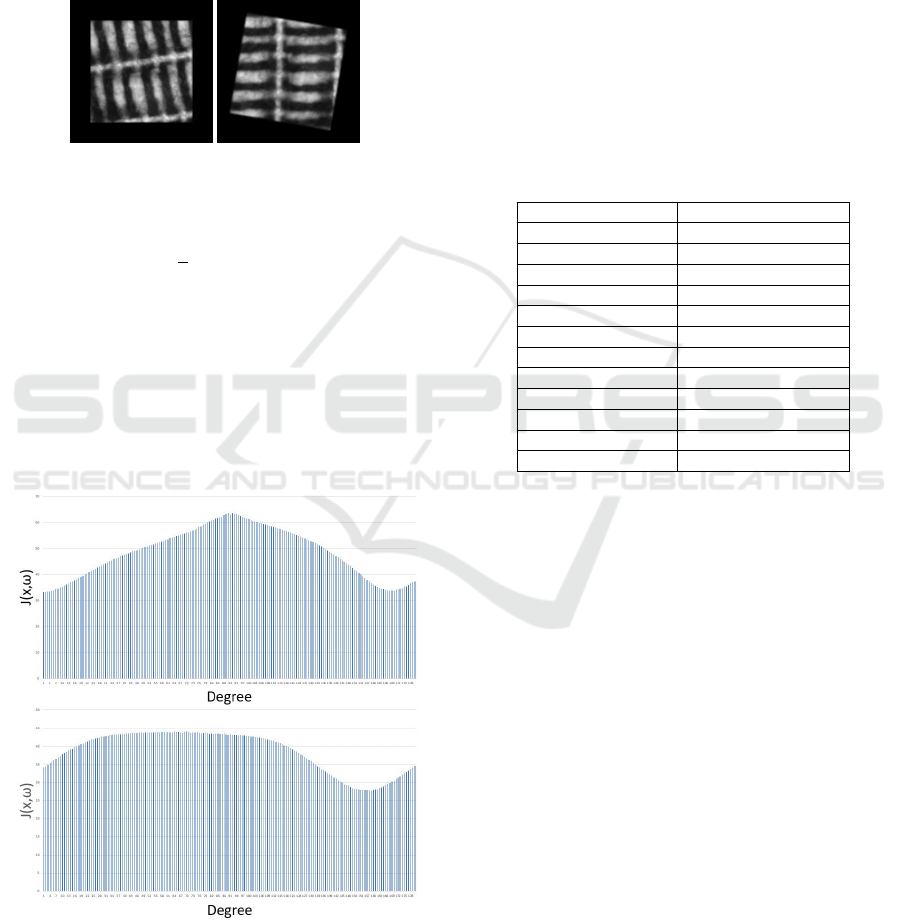
Figure 6: Input image from class Texture 1 with 0 padding

and its rotated version.

The loss function of the STN is deﬁned as:

J(x, ω) =

∑

|(M ◦

x) ~ G

(7)

where

x is the output of the STN network, and M is a

rotated mask for the central region of the 0 padded im-

age. The 0 padding is necessary to avoid losing infor-

mation when some parts of the rotated image lay out-

side the original frame. See illustration in Fig. 6. The

element-wise product with M is to get rid of possible

high gradient areas where the padding region meets

the central content.

Figure 7: Illustrations for the loss value for two images from

class Texture 1 at different rotation angles.

Fig. 7 illustrates the loss values for two images

from the Texture 1 class. In the top example we can

see that there are two minima of the function with ap-

proximately 10 degrees difference but both functions

are quite smooths. This means that we don’t expect

to ﬁnd always exactly the same orientation but the

smoothness of the function and the differentiability

of STNs (Jaderberg et al., 2015) can result almost the

same orientation.

6.1 The Localisation Network

There is no speciﬁc rule about the architecture of a

localisation network (except for its ﬁnal regression

layer), fundamentally, it can be either a convolutional

neural network or a fully connected network. The ar-

chitecture of our localisation network can be seen in

Table 2.

Table 2: Architecture of the localisation network.

Name of the layer Activation function

Convolution 1 Relu

MaxPool 1 None

Convolution 2 Relu

MaxPool 2 None

Convolution 3 Relu

MaxPool 3 None

Convolution 4 Relu

MaxPool 4 None

Flatten None

Fully-connected 1 Relu

Fully-connected 2 Relu

Fully-connected 3 None

Its task is to obtain the θ matrix which holds the

parameters of spatial transformation. As explained

above, in our implementation, we limited θ to rota-

tions, that is:

θ =



cos(α) −sin(α) 0

sin(α) cos(α) 0



(8)

As for the θ

−1

, we simply extend the transforma-

tion matrix with a row of [0,0,1] and calculate the in-

verse, followed by the cropping the unnecessary row.

For training the STN we feeded 10,000 images to the

network (80% for training, 20% for validation). The

image size was set to 128 × 128. The network was

trained for 50 epochs, using the ADAM optimizer,

where the learning rate was set to 2 × 10

−4

, while the

value of the weight decay was 10

−5

. At the end of the

training, we saved the weights of the network for later

utilization.

7 DATASETS

To evaluate to performance of the autoencoders we

used three datasets: the two texture image sets (Tex-

Improving the Efﬁciency of Autoencoders for Visual Defect Detection with Orientation Normalization

655

ture 1 and Texture 2) were provided by (Bergmann

et al., 2018), while the Screw class is from (Bergmann

et al., 2019). The original texture sets included 100-

100 defect-free images, and 50-50 defective images,

with various faults. Pixel-wise ground truth images

were also provided by the authors. All of the origi-

nal texture images are of the size of 512× 512 pixels.

The Screw class has 320 defect-free images of size

1024 × 1024; the defective class Thread-top, used in

our defect detection tests, has 23 images. First im-

ages were resized to 256 × 256 pixels, then patches

of size 128 × 128 were created. At this point, we ap-

plied various augmentation procedures such as rota-

tions and cropping. It is vital in order to enrich our

dataset. Then we added 0 padding with the minimally

necessary size to avoid clipping the content when ro-

tating them by the STN: this resulted in an image size

of 181 × 181 pixels. Finally, these images were re-

sized to 128 × 128. For the illustration of the three

classes see Fig. 6, Fig. 8, and Fig. 9, each class

contained ﬁnally 10,000 images used for training and

validation.

Figure 8: Test images from the Texture 2 dataset.These ex-

amples shows some defects to be detected.

Figure 9: Train and test images from the Screw dataset.

8 TESTS AND DISCUSSIONS

In this section we ﬁrst investigate the reconstruction

abilities of the differently trained variants of the struc-

ture given in Section 5 and illustrated by Fig. 2. It has

already been shown in (R

adli and Cz

uni, 2021) that

higher reconstruction accuracy does not strictly im-

ply better detection rates that is the reason we also

run tests for their application for defect detection.

8.1 Testing the Reconstruction

Accuracy

Four cases are under investigation:

1. For reference we trained the plain AE deﬁned in

Section 3.1.

2. Both STN and AE are initialized with random

weights.

3. STN is pre-trained to normalize the orientation of

input patterns. During the training of the AE the

localisation network is frozen.

4. The same as above but allowing the reﬁnement of

STN weights.

These four cases correspond to the four columns

in Table 3, 4, and 5, where SSIM and mean squared

error (MSE) values are computed as the mean of 2000

test images. (Lower MSE and higher SSIM mean bet-

ter quality). Hyper parameters were exactly the same

in all cases: Networks were trained on NVIDIA RTX

5000 GPU for 200 epochs with ADAM optimizer, ini-

tial learning rate was 2 × 10

−4

with 10

−5

weight de-

cay. The latent space was set to d = 100. All exper-

iments were repeated 5 times, data given are average

values. (Abbreviations in Table 3, 4, 5, 6, 7, 8 and 9

are the following: S: STN; rnd. in. S w.: randomly

initialized STN weights; pre-tr. frz. S w.: pre-trained

frozen STN weights; pre-tr. n. frz. S w.: pre-trained

not frozen STN weights.)

Table 3: Reconstruction quality of images of the class Tex-

ture 1. Abbreviations are given in the text.

Texture 1

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in.

S w.

S+AE

pre-tr. n.

frz. S w.

MSE 82.4781 77.1195 83.0611 74.8105

SSIM 0.8453 0.8790 0.8411 0.8883

Table 4: Reconstruction quality of images of the class Tex-

ture 2. Abbreviations are given in the text.

Texture 2

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in.

S w.

S+AE

pre-tr. n.

frz. S w.

MSE 88.3534 86.1341 89.9087 87.9534

SSIM 0.7915 0.8174 0.7675 0.7911

Table 5: Reconstruction quality of images of the class

Screw. Abbreviations are given in the text.

Screw

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in.

S w.

S+AE

pre-tr. n.

frz. S w.

MSE 36.2071 34.2324 37.7939 35.2554

SSIM 0.8729 0.9075 0.8707 0.8893

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

656

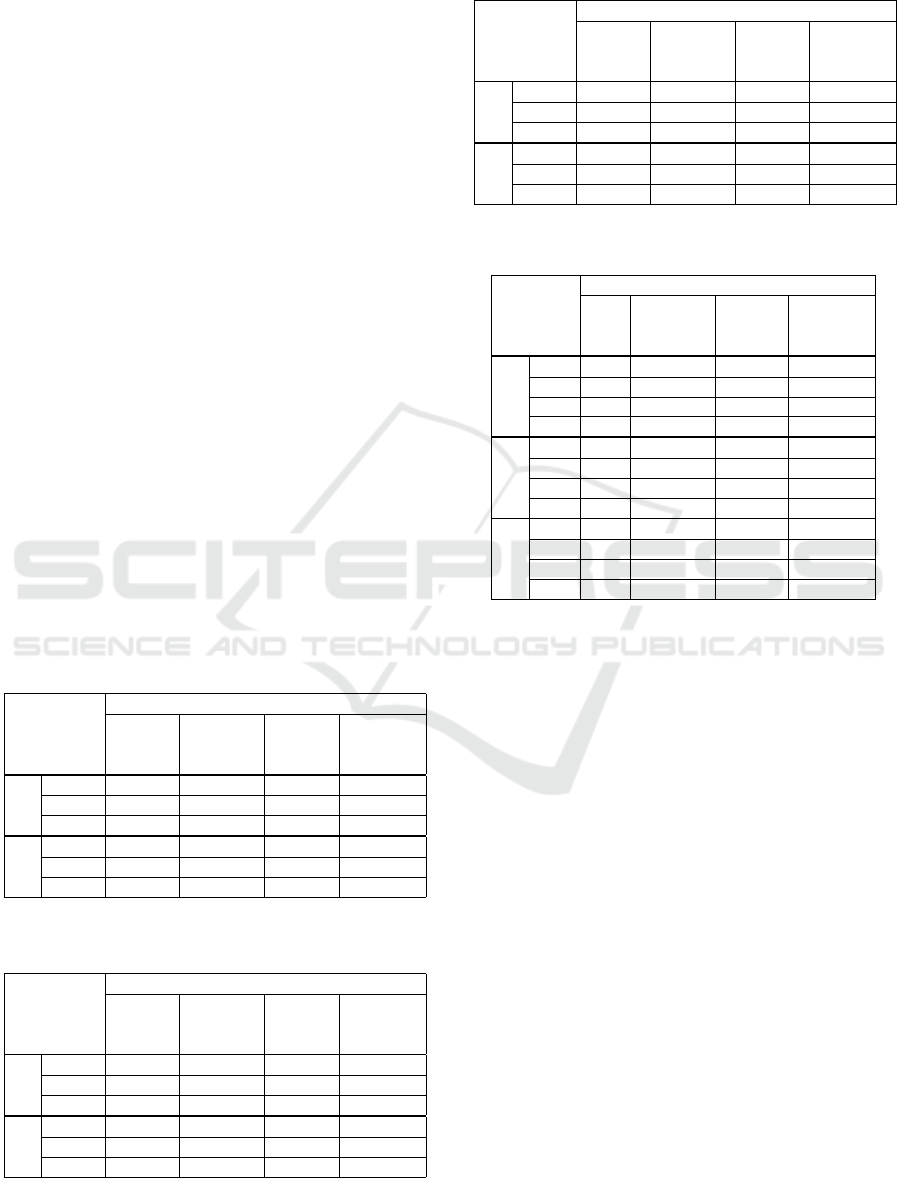
In accordance with the observation of (Bidart and

Wong, 2019), quoted in Section 5, we found that in

all three image classes the insertion and random ini-

tialization of the STN (and the insertion of the corre-

sponding inverse transformation) could not improve

reconstruction quality, in all cases we got worse re-

sults. Pre-training the STN with the method intro-

duced in Section 6 resulted in improved quality com-

pared to the plain AE. Moreover, allowing the ﬁne-

tuning of STN weights, simultaneously with the train-

ing of the AE resulted in lower quality in two cases of

the three.

8.2 Defect Detection

For the further evaluation of the proposed method

we tested defect detection using the ground truth

defect images of the sources named in Section 7.

Three well-known pixel-level metrics were used

for comparisons: receiver operating characteristic

(ROC) curves, precision-recall curves (PRC), and

intersection over union (IoU). In case of all curves

the area under curve (AuC) was calculated. Residual

maps (between the inputs and the decoded and

inverse transformed outputs) were created using both

SSIM and MSE with different thresholding, resulting

in the above mentioned curves. The differences were

computed only on the central regions of the padded

test images (excluding the 0 padding areas).

Table 6: Defect detection using SSIM and MSE metrics for

the Texture 1 class. Abbreviations are given in the text.

Texture 1

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in

S w.

S+AE

pre-tr. n.

frz S w.

SSIM

ROC 0,8622 0,8752 0,8591 0,8712

PRC 0,3996 0,3993 0,3882 0,4008

IoU 0,1228 0,1228 0,1228 0,1227

MSE

ROC 0,6514 0,6694 0,6635 0,6672

PRC 0,2007 0,2229 0,2093 0,2215

IoU 0,0744 0,0796 0,0768 0,0803

Table 7: Defect detection using SSIM and MSE metrics for

the Texture 2 class. Abbreviations are given in the text.

Texture 2

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in

S w.

S+AE

pre-tr. n.

frz S w.

SSIM

ROC 0,8379 0,8409 0,8216 0,8253

PRC 0,2785 0,3228 0,2648 0,2683

IoU 0,1148 0,1242 0,1113 0,1141

MSE

ROC 0,5826 0,6087 0,5833 0,5879

PRC 0,1795 0,1976 0,1710 0,1808

IoU 0,0661 0,0702 0,0647 0,0656

Table 8: Defect detection using SSIM and MSE metrics for

the Screw class. Abbreviations are given in the text.

Screw

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in

S w.

S+AE

pre-tr. n.

frz S w.

SSIM

ROC 0,7586 0,7911 0,7829 0,7902

PRC 0,4191 0,4234 0,4162 0,4219

IoU 0,0088 0,0093 0,0088 0,0092

MSE

ROC 0,5179 0,5541 0,4833 0,4751

PRC 0,3136 0,3228 0,2886 0,2823

IoU 0,0081 0,0093 0,0055 0,0048

Table 9: Rankings of different defect detection approaches.

Abbreviations are given in the text.

Ranking

S+AE

pre-tr.

frz. S w.

S+AE

rnd. in

S w.

S+AE

pre-tr. n.

frz S w.

Texture 1

1st 1 4 0 2

2nd 1 1 0 3

3rd 1 1 3 1

4th 3 0 3 0

Texture 2

1st 0 6 0 0

2nd 4 0 0 2

3rd 1 0 1 4

4th 1 0 5 0

Screw

1st 0 6 0 0

2nd 3 0 0 3

3rd 2 0 5 0

4th 1 0 1 3

Results, regarding the three test classes, can be

seen in Table 6, 7, and 8. Best values are highlighted

in bold. As can be seen, in all metrics the proposed

S+AE (pre-tr.frz. S w.) conﬁguration outperformed

the plain AE in the Texture 2 and Screw classes. On

the other hand, in the Texture 1 class, the plain AE

scored the highest IoU value, when the SSIM met-

ric was selected. However, since the SSIM detec-

tion mechanism showed signiﬁcantly better results, it

would be not reasonable to use MSE as the error de-

tection metrics. The overall ranking of the methods

can be seen in Table 9: for two test classes the pro-

posed technique was better in all measures, for the

Texture 1 class is was best in 4 cases, once second

and once third.

9 CONCLUSIONS AND FUTURE

WORK

In our paper we dealt with the application of STNs to

boost the performance of AEs for coding and defect

detection. STNs have shown good results in many ap-

plications such as classiﬁcation, change detection, im-

age registration, but it was not clear how the require-

Improving the Efﬁciency of Autoencoders for Visual Defect Detection with Orientation Normalization

657

ment of accurate image encoding/decoding could be

achieved and whether the simultaneous learning of

AE and STN weights is applicable. Our answer for

the later is negative, from either the reconstruction

or anomaly detection point of view, but a pre-trained

STN, to normalize the orientation of input patters, can

improve the reconstruction and defect detection, even

if the input patterns produce multiple minima in the

loss (J(x, ω)), when applying the orientation normal-

izing ﬁlter mechanism (Section 6). To underlie the

above statements we tested the models for three dif-

ferent datasets. We found that the often used Tensor-

Flow implementation of STNs (STN, 2016) has in-

accurate interpolation (Fig. 4). Our proposed nor-

malization approach, using an accurate transforma-

tion block, could outperform the base AE method in

almost all cases and metrics. In future we are to in-

vestigate the performance of other transformations.

ACKNOWLEDGEMENTS

We acknowledge the ﬁnancial support of the projects

2018-1.3.1-VKE-2018-00048 under the

UNKP-19-

3 New National Excellence Program, 2020-4.1.1-

TKP2020 under the Thematic Excellence Program,

and the Hungarian Research Fund grant OTKA K

135729.

REFERENCES

(2016). TensorFlow implementation of STN. https://github.

com/daviddao/spatial-transformer-tensorﬂow. Ac-

cessed: 2021-11-04.

Alaverdyan, Z., Jung, J., Bouet, R., and Lartizien, C.

(2020). Regularized siamese neural network for un-

supervised outlier detection on brain multiparametric

magnetic resonance imaging: application to epilepsy

lesion screening. Medical Image Analysis, 60:101618.

Beggel, L., Pfeiffer, M., and Bischl, B. (2019). Robust

anomaly detection in images using adversarial autoen-

coders. arXiv preprint arXiv:1901.06355.

Bergmann, P., Batzner, K., Fauser, M., Sattlegger, D., and

Steger, C. (2021). The MVTec anomaly detection

dataset: a comprehensive real-world dataset for un-

supervised anomaly detection. International Journal

of Computer Vision, 129(4):1038–1059.

Bergmann, P., Fauser, M., Sattlegger, D., and Steger, C.

(2019). MVTec AD–A comprehensive real-world

dataset for unsupervised anomaly detection. In Pro-

ceedings of the IEEE/CVF Conference on Computer

Vision and Pattern Recognition, pages 9592–9600.

Bergmann, P., L

owe, S., Fauser, M., Sattlegger, D., and Ste-

ger, C. (2018). Improving unsupervised defect seg-

mentation by applying structural similarity to autoen-

coders. arXiv preprint arXiv:1807.02011.

Bidart, R. and Wong, A. (2019). Afﬁne variational autoen-

coders: An efﬁcient approach for improving gener-

alization and robustness to distribution shift. arXiv

preprint arXiv:1905.05300.

Chianucci, D. and Savakis, A. (2016). Unsupervised change

detection using spatial transformer networks. In 2016

IEEE Western New York Image and Signal Processing

Workshop (WNYISPW), pages 1–5. IEEE.

Ding, P., Wan, S., Jin, P., and Zou, C. (2020). A rotation

invariance spatial transformation network for remote

sensing image retrieval. In Twelfth International Con-

ference on Digital Image Processing (ICDIP 2020),

volume 11519, page 115191P. International Society

for Optics and Photonics.

Dosovitskiy, A. and Brox, T. (2016). Generating images

with perceptual similarity metrics based on deep net-

works. Advances in neural information processing

systems, 29:658–666.

Jaderberg, M., Simonyan, K., Zisserman, A., et al. (2015).

Spatial transformer networks. Advances in Neural In-

formation Processing Systems, 28:2017–2025.

Lee, M. C., Oktay, O., Schuh, A., Schaap, M., and Glocker,

B. (2019). Image-and-spatial transformer networks

for structure-guided image registration. In Inter-

national Conference on Medical Image Computing

and Computer-Assisted Intervention, pages 337–345.

Springer.

Li, G., Xu, S., Liu, X., Li, L., and Wang, C. (2018). Jer-

sey number recognition with semi-supervised spatial

transformer network. In Proceedings of the IEEE

Conference on Computer Vision and Pattern Recog-

nition Workshops, pages 1783–1790.

Park, D. and Chun, S. Y. (2018). Classiﬁcation based grasp

detection using spatial transformer network. arXiv

preprint arXiv:1803.01356.

adli, R. and Cz

uni, L. (2021). About the application of

autoencoders for visual defect detection. In 2021 29.

International Conference in Central Europe on Com-

puter Graphics, Visualization and Computer Vision,

pages 181–188. WSCG.

Sakurada, M. and Yairi, T. (2014). Anomaly detection

using autoencoders with nonlinear dimensionality re-

duction. In Proceedings of the MLSDA 2014 2nd

Workshop on Machine Learning for Sensory Data

Analysis, pages 4–11.

Tuluptceva, N., Bakker, B., Fedulova, I., Schulz, H.,

and Dylov, D. V. (2020). Anomaly detection

with deep perceptual autoencoders. arXiv preprint

arXiv:2006.13265.

Wang, Z., Bovik, A. C., Sheikh, H. R., and Simoncelli, E. P.

(2004). Image quality assessment: from error visi-

bility to structural similarity. IEEE Transactions on

Image Processing, 13(4):600–612.

Zhai, J., Zhang, S., Chen, J., and He, Q. (2018). Autoen-

coder and its various variants. In 2018 IEEE Interna-

tional Conference on Systems, Man, and Cybernetics

(SMC), pages 415–419. IEEE.

VISAPP 2022 - 17th International Conference on Computer Vision Theory and Applications

658