Towards Lightweight Neural Animation: Exploration of Neural Network

Pruning in Mixture of Experts-based Animation Models

Antoine Maiorca

, Nathan Hubens

1,2

, Sohaib Laraba

and Thierry Dutoit

ISIA Lab, Faculty of Engineering, University of Mons, Mons, Belgium

Artemis, TelecomSud Paris, Paris, France

Keywords:

Neural Character Animation, Neural Network Pruning.

Abstract:

In the past few years, neural character animation has emerged and offered an automatic method for animating

virtual characters. Their motion is synthesized by a neural network. Controlling this movement in real time

with a user-deﬁned control signal is also an important task in video games for example. Solutions based

on fully-connected layers (MLPs) and Mixture-of-Experts (MoE) have given impressive results in generating

and controlling various movements with close-range interactions between the environment and the virtual

character. However, a major shortcoming of fully-connected layers is their computational and memory cost

which may lead to sub-optimized solution. In this work, we apply pruning algorithms to compress an MLP-

MoE neural network in the context of interactive character animation, which reduces its number of parameters

and accelerates its computation time with a trade-off between this acceleration and the synthesized motion

quality. This work demonstrates that, with the same number of experts and parameters, the pruned model

produces less motion artifacts than the dense model and the learned high-level motion features are similar for

both.

1 INTRODUCTION

Virtual characters animation is a trending topic for

video game and movie industry. It is important that

the motion generation algorithm can guarantee a plau-

sible and natural synthesis in order to increase the im-

mersive factor of the movie or the video game. Thus,

the computer vision research community has a special

interest in the task of motion synthesis. Moreover, the

real-time control of the character trajectory and ac-

tions may be an important constraint depending on

the use case.

(Holden et al., 2017) showed that, with the use of

a relatively simple neural network architecture based

on Multi-Layer Perceptrons (MLP), it is possible to

draw several modes of locomotion for a biped char-

acter. The motion data needs ﬁrst to be aligned on

a phase vector that represents the timing of the mo-

tion cycle. Then, a regression network whose param-

eters change dynamically according to the phase vec-

tor generates the pose-by-pose motion in an autore-

gressive manner. Finally, a regression network whose

weights vary dynamically according to the phase vec-

tor generates the pose-by-pose motion in an autore-

gressive way. (Zhang et al., 2018) keeps the same

regression network as (Holden et al., 2017) but pro-

poses upstream a Mixture-of-Experts (MoE) to gen-

eralize this architecture for the motion of quadruped

characters whose the different locomotion gaits are

difﬁcult to align on one phase signal.

However, fully-connected layers are computation-

ally expensive in terms of number of parameters and

ﬂoating point operations (FLOPs) compared to other

architectures like Convolutional Neural Network for

example. Once the network is trained, some weights

in the neural network may not learn information that

signiﬁcantly contributes to the quality of the gener-

ated signal. Thus, the network capacity may be not

fully exploited. Moreover, some of recent architec-

tures can be highly greedy in term of hardware re-

sources and may not be suitable for embedded deploy-

ment but reducing its number of parameters would be

too costly in terms of performance. Neural network

pruning is a research area that aims to compress a

neural network while keeping its performance intact.

It is widely used when there are non-negligible con-

straints on hardware resources, such as on embedded

devices. The idea behind this concept is to remove

unnecessary weights and to retrain the pruned neu-

ral network. Practically, these are not removed but

286

Maiorca, A., Hubens, N., Laraba, S. and Dutoit, T.

Towards Lightweight Neural Animation: Exploration of Neural Network Pruning in Mixture of Experts-based Animation Models.

DOI: 10.5220/0010908700003124

In Proceedings of the 17th International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications (VISIGRAPP 2022) - Volume 1: GRAPP, pages

286-293

ISBN: 978-989-758-555-5; ISSN: 2184-4321

nulliﬁed. This induces that the pruned weight matri-

ces become sparse. The proportion of zero parame-

ters compared to the original network size is termed

as sparsity. In this paper, we explore the impact of

pruning a MLP-and-MoE based neural network in the

context of neural character animation. The beneﬁts of

this method is to reduce the number of the network

parameters and thus theoretically accelerate the com-

putation time while minimizing the performance loss.

To the best of our knowledge, this work is the ﬁrst

that applied pruning methods in the context of neural

animation.

First, the state of the art on modern data-driven an-

imation techniques as well as on neural network prun-

ing is presented in section 2. Then, the experiments

performed are described in section 3 and the related

results in section 4.

2 RELATED WORK

2.1 Data-driven Animation

The task of interactive motion generation is a broad

ﬁeld of research focusing on synthesizing a natural

motion from control signals. The problematic of real-

time pose prediction from a user-deﬁned trajectory

belongs to this paradigm. This has been addressed

by data-driven methods using machine learning tech-

niques (Park et al., 2002; Tilmanne and Dutoit, 2010;

Clavet, 2016). More recent works lie in the ﬁeld

of autoregressive models where, along with the con-

trolled trajectory, the next character pose is predicted

with the previous ones. More recent models consider

deep learning algorithms with time series analysis ar-

chitectures such as RNNs (Lee et al., 2018; Pavllo

et al., 2018). This family of models combined with

probabilistic generative methods draw motions that

exhibit less artefact than deterministic models (Wang

et al., 2021; Henter et al., 2020; Chen et al., 2021).

(Holden et al., 2017) has shown that real-time con-

trolled locomotion of a bipedal character can be real-

ized thanks to a phase vector representing the timing

of the motion cycle and computed from foot contact

with the ground, like said in section 1, since MLPs

do not initially extract any correlation in sequential

data. This variable is used to cyclically generates the

weights of a MLP-based regression network that syn-

thesizes, from motion features such as joint positions,

velocities and rotations at the frame t, the pose as

the next frame. However, this system fails when the

motion is difﬁcult to align to a single phase vector,

such as quadruped locomotion. To tackle this issue,

(Zhang et al., 2018) proposes to use the technique of

MoE (Jacobs et al., 1991). This technique is based on

n experts models. Each of them is specialized in the

realization of a particular subtask of the given prob-

lem. The output y

of each expert is further weighted

by n coefﬁcients ω

computed by a so-called gating

network. It learns to quantify the importance of each

expert to resolve the given task. Thus, the ﬁnal result

y takes into account the effect of the n expert models.

y =

∑

(1)

In the work of (Zhang et al., 2018), the gating net-

work computes coefﬁcients from the skeleton leg fea-

tures and simulates the effect of the phase function

in (Holden et al., 2017) for quadruped character. In

this case, the experts are sets of parameters learned

during training that are then blent. Then, this recom-

bination is used as weights of the regression network.

This technique has shown encouraging results in the

ﬁeld of interactive motion generation and constitutes

the backbone of recent interactive locomotion gener-

ation algorithms. (Starke et al., 2019) employed this

method so that a character is able to interact adap-

tively with objects of variable shape deﬁned in the vir-

tual environment. For example, he can sit on a chair

or carry a box without having any prior knowledge

of their shape. More complex movements than loco-

motion can also be synthesized. (Starke et al., 2020)

propose a framework to generate basketball move-

ments with awareness of the ball and a direct oppo-

nent. The model must therefore learn to analyze con-

tacts other than feet on the ground, such as the hand-

ball contact. For this, they introduce the concept of

local phase where each phase is linked to a partic-

ular subset of the body. The movement is thus no

longer aligned on a single global phase but on sev-

eral phases and they showed that this helps the model

to learn multi-contact motion. More recently, (Starke

et al., 2021) have succeeded, still with MoE, in gener-

ating with simple user-deﬁned control signals a vari-

ety of martial arts movements while allowing a close-

character interaction. (Ling et al., 2020) implemented

the method of (Zhang et al., 2018) with a VAE archi-

tecture. This solution allows to deﬁne the character

controller through Reinforcment Learning. Thus, the

avatar can be controlled from joystick input, learn to

follow a predeﬁned trajectory or even freely explore

an environment like a maze.

2.2 Pruning

Pruning methods primarily differ according to three

factors: (1) the granularity at which pruning is oper-

ated, (2) the criteria uses for selecting parameters to

remove, and (3) the schedule followed for pruning.

Towards Lightweight Neural Animation: Exploration of Neural Network Pruning in Mixture of Experts-based Animation Models

287

Granularity. Pruning granularity is usually di-

vided into two groups: unstructured pruning, i.e. the

weights are removed individually, without any intent

to keep structure in the weights (LeCun et al., 1989;

Hassibi et al., 1993). This method leads to matri-

ces able to reach a high sparsity level, but difﬁcult to

speed-up due to the lack of regularity in the pruning

patterns. For those reasons, structured pruning, i.e.

removing groups of weights, have been introduced

(He et al., 2017). Those structures can include vec-

tor of weights, or even kernel or entire ﬁlters when

pruning convolutional architectures.

Criteria. Early methods proposed to use the second-

order approximation of the loss surface to ﬁnd the

least useful parameters (LeCun et al., 1989; Hassibi

et al., 1993). Later work also explored the use of vari-

ational dropout (Molchanov et al., 2017a) or even l

regularization for parameter removal (Louizos et al.,

2018). However, it has been shown recently that, even

though those heuristics may provide good results un-

der particular conditions, they are more complex and

less generalizable than computing the l

norm of the

weights, and using that value as a measure of the im-

portance of the weights, thus removing the ones with

the lowest norm (Gale et al., 2019). Moreover, when

comparing the importance of weights, one might do it

locally, i.e. only compare weights that belong to the

same layer, which will provide a pruned model that

possesses the same sparsity in each layer. One also

might compare the weights globally, i.e. the weights

from the whole model are compared when the pruning

is applied, resulting in a model with different sparsity

levels for each layer. Comparing the weights globally

usually provides better results but may be more ex-

pensive to compute when the model grows larger in

size.

Scheduling. There exist many ways to schedule

the network pruning. Early methods proposed to re-

move weights of a trained network in a single-step,

the so-called one-shot pruning (Li et al., 2017). Such

a strategy typically required further ﬁne-tuning of the

pruned model in order to recover from the lost per-

formance. However, performing the pruning in sev-

eral steps, i.e. the iterative pruning, is able to provide

better results and reach a higher sparsity level (Han

et al., 2015; Molchanov et al., 2017b). Nevertheless,

such methods were usually time-consuming because

of the alternation of many iterations of pruning and

ﬁne-tuning (Li et al., 2017). Recently, another family

of schedules has emerged, performing a pruning that

is more intertwined with the training process, allow-

ing to obtain a pruned network in a more reasonable

time (Zhu and Gupta, 2017; Hubens et al., 2021).

3 EXPERIMENTS

The experimental setup consists in applying unstruc-

tured global pruning to the model proposed by (Zhang

et al., 2018) with a hidden layer size h

size

= 512 and

8 experts. As explained in section 2.1, it is deﬁned by

two fully connected-based subnetworks : the gating

network extracting the coefﬁcients ω

and the motion

prediction network whose its weights are the result of

the MoE processus. The chosen pruning scheduling is

the one cycle pruning (Hubens et al., 2021) with the

weights l1 norm criterion (Gale et al., 2019). We use

the same training data as (Zhang et al., 2018) which

is composed of motion capture recording of dog loco-

motion with various gaits.

First of all, we increase the network sparsity step-

by-step from 10% to 90% of the total amount of pa-

rameters to extract the relationship between the net-

work sparsity and the motion quality. To quantita-

tively assess the performance of each model, we mea-

sure the foot skating artifact on the generated motion.

Foot skating is the fact that the character foot slides

when the related joint on the skeleton is considered on

contact with the ground which is practically deﬁned

if this joint foot height h is under a height threshold

H. That effect has a bad impact on the motion nat-

uralness and is induced by the mean regression dur-

ing the training process as explained by (Zhang et al.,

2018). We use the equation from (Zhang et al., 2018)

to quantify the foot skating s where v stands for the

foot horizontal velocity. We ﬁxed the threshold H at

2.5cm.

s = v(2 −2

h/H

) (2)

Then, we draw a comparison of the generated mo-

tion quality between the same size dense (unpruned)

and sparse models (pruned). Next, the qualitative con-

tribution of each expert in the generation of the move-

ment is established through an ablation study in order

to visualize possible differences between their roles in

the case where the initial model is pruned. Finally, the

dynamic behavior of the gating network output vector

ω is extracted and subjectively compared between the

dense and sparse network.

For these experiments, we use the Fasterai frame-

work (Hubens, 2020) built on top of Fastai (Howard

et al., 2018) to implement the pruning methods. We

train 150 epochs on a GTX-1080 Nvidia GPU with

a batch size of 32, a learning rate η = 1e − 4 and a

weight decay rate λ = 2.5e − 3 with a AdamWR al-

gorithm (Loshchilov and Hutter, 2018) warm restart

with the same parameters as (Zhang et al., 2018).

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

288

4 RESULTS

This section presents the experimental results of the

analysis setup described in section 3.

4.1 Performance/Sparsity Analysis

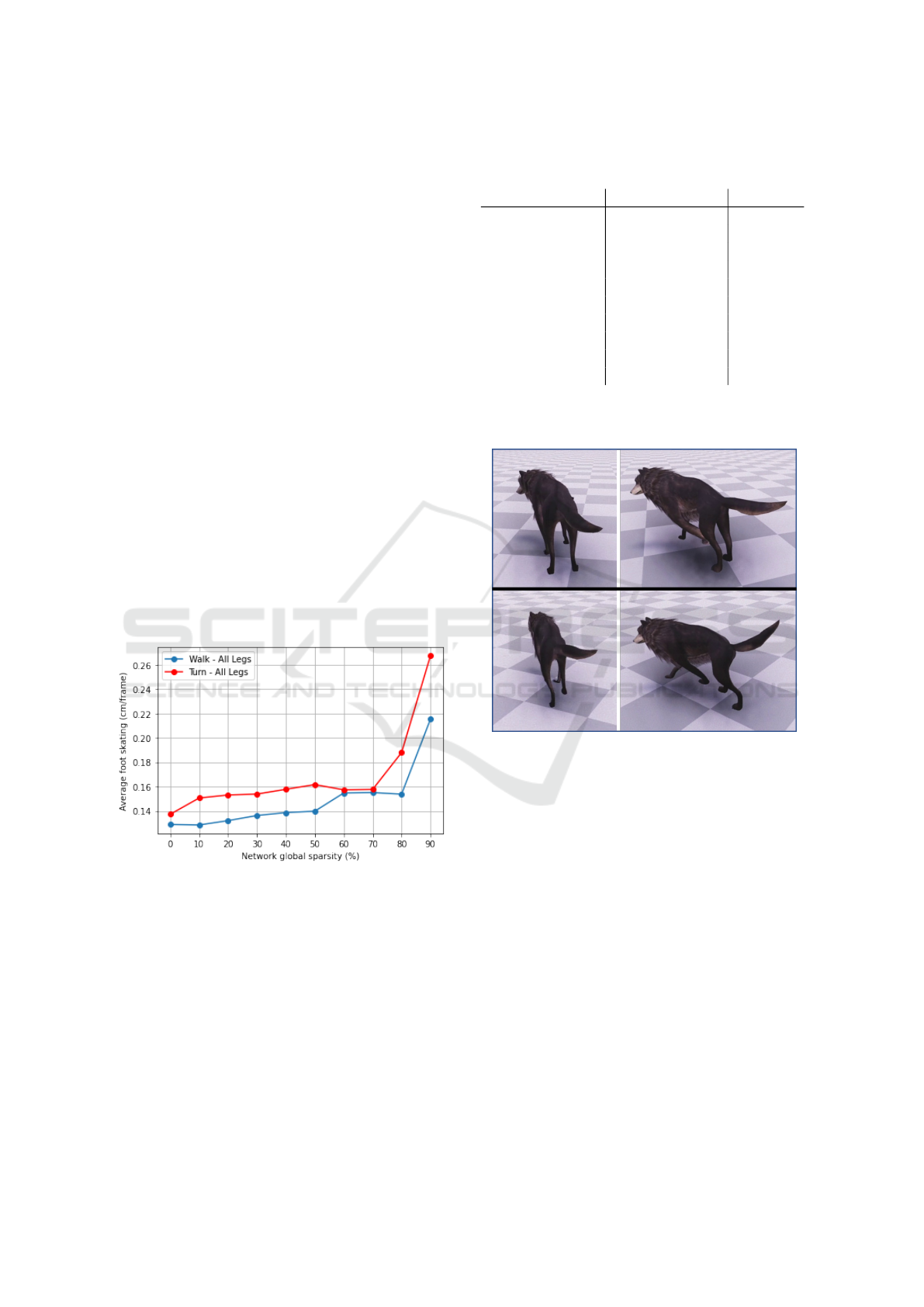
Figure 1 draws the average foot skating curves along

the network sparsity. The generated dog motion

is evaluated when he walks and when he performs

sudden turns. The trend is that skating increases

with the network sparsity. So, there is a trade-

off between the number of non-zero parameters and

the quality of the synthesized motion. This is due

to the fact that the network is less able to learn

complex relationships when it has fewer parame-

ters and the generated motion tends towards an av-

erage pose which is reﬂected in the motion by an

excess of foot skating. So, following Table 1 that

shows the relationship between the sparsity imposed

on the network, the number of non-zero parameters

and the ﬂoating point operations, the same trade-off

exists between the synthesized motion quality and

the model size and FLOPs. A video showing the

degradation of the motion quality when the num-

ber of non-zero parameters decreases is available at

https://www.youtube.com/watch?v=RHNLQ2Cbz3Y.

Figure 1: Average Foot Skating on all legs (cm/frame). The

generated motion has been evaluated on foot skating while

the dog was walking around and abruptly turning.

4.2 Comparison between Same Size

Models

This section presents a comparison of the quality of

the motion generated by two models with an equiv-

alent number of parameters: the size of the dense

model hidden layer h

size

is set to 256, 128 and then

64. Starting from the original network (8 experts and

size

= 512), we prune the network until we reach

Table 1: Relationship between network size and FLOPs.

Each individual parameter is stored as a 32 bits ﬂoat.

Network sparsity Model size (Mb) MFLOPs

0% 178 11.10

10% 160 10.06

20% 142 9.02

30% 124 7.98

40% 106 6.94

50% 88 5.89

60% 71 4.86

70% 53 3.82

80% 35 2.78

90% 17.8 1.74

an equivalent number of parameters for each dense

model.

Figure 2: Top: Animation generated by the dense model.

- Bottom: Animation generated by the sparse model. Both

models have the same number of non-zero parameters. In

this example, we keep 10% of parameters from the initial

model. The output motion of the sparse model exhibits less

motion artifact than the dense one such as back legs stiffness

while turning. The videos about these observations can be

found at https://youtu.be/AuJ0q019-nc.

The observations from the related videos show

that the quality of motion decreases with the hidden

layer size. Indeed, since the network training is a re-

gression problem, it suffers from mean regression and

the output poses may converge to a mean pose that

minimizes the mean squared error. When reducing

the number of parameters, the network has less ca-

pacity to learn complex features and it enhances the

mean pose regression issue. However, sparse models

eliminate globally rough artifacts such as the absence

of motion while turning or unnatural poses. This phe-

nomenon is illustrated by Figure 2 showing an ex-

ample of the virtual dog animation comparing pruned

Towards Lightweight Neural Animation: Exploration of Neural Network Pruning in Mixture of Experts-based Animation Models

289

model with 90% of sparsity and the equivalent dense

model. The dog motion from the dense model is very

static while turning.

Then, average foot skating is measured for each

of the three dense and sparse models while the dog is

walking. The abrupt turn motion is not evaluated by

skating because the motion artifacts produced by the

dense model when reducing h

size

are too harsh and

may not be correctly assessed by Equation 2. The

results of this evaluation are shown in Figure 3. It il-

lustrates the fact that sparse models synthesize motion

with less skating than the dense models with the same

number of parameters and experts. This points out the

beneﬁts of the application of this pruning method on

this neural network : while ﬁxing the training bud-

get at 150 epochs in our case, pruning a dense model

into a sparse one leads to more reasonable movements

than the dense network with the same number of non-

zero parameters.

Figure 3: Comparison on average foot Skating on all legs

(cm/frame) for dense and sparse models with the same num-

ber of parameters and experts. Sparse models exhibit less

skating than dense model.

4.3 Ablation Study

In order to visualize the contribution of each expert

to the generation of the movement, we make an abla-

tion study as it is done in (Zhang et al., 2018) : each

expert is deactivated one by one and we observe the

impact of this deactivation on the synthesized move-

ment. This study is realized for the initial model with

8 experts and the one pruned with to a sparsity of 90%

(90% of the total amount of parameters are removed

from the network) and is presented in Table 2. For

example, when removing the ﬁrst expert α

, the dog

cannot properly sit or lie on the ground and this be-

havior is observed on both models. Since each obser-

vation while removing the same experts in both mod-

els is similar, this ablation study shows that, even in a

case of extreme sparsity, each expert in both models

corresponds qualitatively to the same high-level fea-

tures perceived in the movement.

4.4 Expert Activation Behavior

Since section 4.3 shows that the high-level motion

features learned by the experts are not affected by

the employed pruning paradigm, the same behav-

ior of the ω

(values weighting each expert to com-

pute pose regression network parameters) is thus ex-

pected. So, the experts activations are compared be-

tween the initial and the sparse model for the same

movement. These activations are shown in Figure 4.

When the quadruped performs a speciﬁc action, the

same weighting proﬁle is applied to experts for both

models. However, the activations in the sparse model

are slightly more distributed among the different ex-

perts compared to the original model. We believe that

this is due to the fact that, as the number of non-zero

parameters in the pruned model experts is lower than

in the dense one, the sparse network exploits those

of other experts in order to synthesize similar move-

ments.

5 LIMITATIONS AND

PERSPECTIVES

In this work, we applied an unstructured parameter-

by-parameter pruning method, i.e. with a granularity

at the weight level. Using such a method leads, from a

dense matrix, to a sparse matrix where no constraint is

a priori imposed on the structure of the sparsity of the

matrix. This means that, in order to take advantage

of the optimization that pruning theoretically brings,

it is necessary to have an adequate hardware that can

handle sparse matrices. The most evident way to over-

come this limitation would be to perform a structured

pruning, which would remove blocks of weights, al-

lowing to change the initial architecture, instead of

keeping sparse matrices.

Then, The model we considered in our experi-

ments constitutes the backbone of recent models as

shown in section 2.1. One of the perspectives of this

work is to be able to prune these models in order to

visualize and measure the impact on more complex

movements.

Finally, other methods can be employed to opti-

mize a neural network such as knowledge distillation

(Hinton et al., 2015) in which a lightweight student

model learns the output of a large master model and

tries to reach its performance) or fully-connected lay-

ers decomposition by singular value decomposition

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

290

Figure 4: Expert activation ω

performing various motion. The left column shows the results for the dense model and the

right column for the 90% sparse model. The action performed from top to bottom: walk, run, sit, jump and turn. A similar

behavior is observed for both models: the same experts contribute to the same movements. However, the curves are slightly

ﬂatter for the sparse model, which implies that the most signiﬁcant expert in the dense model is a little less signiﬁcant in the

sparse model.

Towards Lightweight Neural Animation: Exploration of Neural Network Pruning in Mixture of Experts-based Animation Models

291

Table 2: Comparison between the ablation study of the dense and the sparse model. Both models exhibit the same experts

behavior.

MANN8 pruned MANN8

fail to sit and lie fail to sit and lie

turn badly and fail to lie turn badly and fail to lie

cannot turn while walking walk badly and cannot turn while walking

cannot jump or run cannot jump or run and turn badly

cannot run and badly walk,turn and jump can barely move

badly right turn badly right turn

can only jump can only jump

cannot jump and run cannot jump and run

technique (Golub and Reinsch, 1970) which replaces

them by an approximation of two smaller layers)

6 CONCLUSION

In this work, we explored the inﬂuence of pruning on

MLP-MoE based architectures, measured and visual-

ized the impact on the generated motion. These anal-

yses showed that:

• There is a trade-off between the naturalness of the

generated motion and the size of the network and

its computational cost.

• For an equivalent number of parameters, a pruned

network performs better at generating natural mo-

tion than a dense network.

• Even in the case of extreme sparsity (90% of the

network parameters have been removed), the high

level motion features that each expert learns are

very similar between the dense and sparse mod-

els, which is consistent with the similarity of the

activation proﬁles between these models.

As far as we know, this work is the ﬁrst to make

use of pruning techniques in the context of neural

network animation and we hope that this work will

open the way to further research in the context of

lightweight neural animation.

AKNOWLEDGMENTS

Unity materials and dog motion capture ﬁles we used

here is given by Sebastian Starke

. We would partic-

ularly like to thank him for his precious help.

https://github.com/sebastianstarke/AI4Animation

REFERENCES

Chen, X., Xu, J., Zhou, R., Chen, W., Fang, J., and Liu, C.

(2021). Trajvae: A variational autoencoder model for

trajectory generation. Neurocomputing, 428:332–339.

Clavet, S. (2016). Motion matching and the road to next-

gen animation. In GDC.

Gale, T., Elsen, E., and Hooker, S. (2019). The state of

sparsity in deep neural networks. The International

Conference on Machine Learning, ICML.

Golub, G. H. and Reinsch, C. (1970). Singular value

decomposition and least squares solutions. Numer.

Math., 14(5):403–420.

Han, S., Pool, J., Tran, J., and Dally, W. J. (2015). Learn-

ing both weights and connections for efﬁcient neural

networks. CoRR, abs/1506.02626.

Hassibi, B., Stork, D. G., Wolff, G., and Watanabe, T.

(1993). Optimal brain surgeon: Extensions and per-

formance comparisons. In Proceedings of the 6th In-

ternational Conference on Neural Information Pro-

cessing Systems, NeurIPS.

He, Y., Zhang, X., and Sun, J. (2017). Channel pruning for

accelerating very deep neural networks. In 2017 IEEE

International Conference on Computer Vision, ICCV.

Henter, G. E., Alexanderson, S., and Beskow, J. (2020).

Moglow: Probabilistic and controllable motion syn-

thesis using normalising ﬂows. ACM Trans. Graph.,

39(6).

Hinton, G., Vinyals, O., and Dean, J. (2015). Distilling

the knowledge in a neural network. In NIPS Deep

Learning and Representation Learning Workshop.

Holden, D., Komura, T., and Saito, J. (2017). Phase-

functioned neural networks for character control.

ACM Trans. Graph., 36(4).

Howard, J. et al. (2018). fastai. https://github.com/fastai/

fastai.

Hubens, N. (2020). Fasterai. https://github.com/

nathanhubens/fasterai.

Hubens, N., Mancas, M., Gosselin, B., Preda, M., and Za-

haria, T. (2021). One-cycle pruning: Pruning convnets

under a tight training budget.

Jacobs, R. A., Jordan, M. I., Nowlan, S. J., and Hinton, G. E.

(1991). Adaptive Mixtures of Local Experts. Neural

Computation, 3(1):79–87.

GRAPP 2022 - 17th International Conference on Computer Graphics Theory and Applications

292

LeCun, Y., Denker, J. S., and Solla, S. A. (1989). Opti-

mal brain damage. In Advances in Neural Information

Processing Systems, NeurIPS.

Lee, K., Lee, S., and Lee, J. (2018). Interactive character

animation by learning multi-objective control. ACM

Trans. Graph., 37(6).

Li, H., Kadav, A., Durdanovic, I., Samet, H., and Graf,

H. P. (2017). Pruning ﬁlters for efﬁcient convnets. In-

ternational Conference on Learning Representations,

ICLR.

Ling, H. Y., Zinno, F., Cheng, G., and Van De Panne, M.

(2020). Character controllers using motion vaes. ACM

Trans. Graph., 39(4).

Loshchilov, I. and Hutter, F. (2018). Fixing weight decay

regularization in adam.

Louizos, C., Welling, M., and Kingma, D. P. (2018). Learn-

ing sparse neural networks through l

regularization.

In International Conference on Learning Representa-

tions, ICLR.

Molchanov, D., Ashukha, A., and Vetrov, D. (2017a). Vari-

ational dropout sparsiﬁes deep neural networks. In

Proceedings of the 34th International Conference on

Machine Learning, ICML.

Molchanov, P., Tyree, S., Karras, T., Aila, T., and Kautz,

J. (2017b). Pruning convolutional neural networks for

resource efﬁcient inference. In International Confer-

ence on Learning Representations, ICLR.

Park, S. I., Shin, H. J., and Shin, S. Y. (2002). On-line loco-

motion generation based on motion blending. In Pro-

ceedings of the 2002 ACM SIGGRAPH/Eurographics

Symposium on Computer Animation, SCA ’02, page

105–111, New York, NY, USA. Association for Com-

puting Machinery.

Pavllo, D., Grangier, D., and Auli, M. (2018). Quaternet: A

quaternion-based recurrent model for human motion.

In British Machine Vision Conference (BMVC).

Starke, S., Zhang, H., Komura, T., and Saito, J. (2019).

Neural state machine for character-scene interactions.

ACM Transactions on Graphics (TOG), 38:1 – 14.

Starke, S., Zhao, Y., Komura, T., and Zaman, K. (2020). Lo-

cal motion phases for learning multi-contact character

movements. ACM Trans. Graph., 39(4).

Starke, S., Zhao, Y., Zinno, F., and Komura, T. (2021). Neu-

ral animation layering for synthesizing martial arts

movements. ACM Trans. Graph., 40(4).

Tilmanne, J. and Dutoit, T. (2010). Expressive gait synthe-

sis using pca and gaussian modeling. In Boulic, R.,

Chrysanthou, Y., and Komura, T., editors, Motion in

Games, pages 363–374, Berlin, Heidelberg. Springer

Berlin Heidelberg.

Wang, Z., Chai, J., and Xia, S. (2021). Combining recurrent

neural networks and adversarial training for human

motion synthesis and control. IEEE Transactions on

Visualization and Computer Graphics, 27(1):14–28.

Zhang, H., Starke, S., Komura, T., and Saito, J. (2018).

Mode-adaptive neural networks for quadruped motion

control. ACM Transactions on Graphics (TOG), 37:1

– 11.

Zhu, M. and Gupta, S. (2017). To prune, or not to prune:

exploring the efﬁcacy of pruning for model compres-

sion. CoRR, abs/1710.01878.

Towards Lightweight Neural Animation: Exploration of Neural Network Pruning in Mixture of Experts-based Animation Models

293