Development of a Piezoelectric Micromachined Ultrasound

Transducer using Microfabrication Technology for in Vitro

Neuromodulation

Ryo Furukawa

and Takashi Tateno

Bioengineering and Bioinformatics, Graduate School of Information Science and Technology, Hokkaido University,

Kita 14, Nishi 9, Kita-ku, Sapporo, Hokkaido 060-0814, Japan

Keywords: Numerical Calculations, Microfabrication, Neuromodulation, Piezoelectric Micromachined Ultrasound

Transducer, Ultrasound Brain Stimulation.

Abstract: Ultrasound neuromodulation, in which local and deep areas of the brain are stimulated, is promising for

clinical applications. However, the mechanisms of action underlying the stimulation are still unknown. To

elucidate the induction mechanisms, in vitro experiments are useful because they allow the extracellular

conditions to be easily controlled. In this study, we developed a piezoelectric micromachined ultrasound

transducer (PMUT) to modulate the activity of brain slices at the micrometer scale. To examine the

relationship between the transducer size and the resonant frequency of the voltage-driven oscillations, we

modeled the multi-layered structure and performed numerical calculations. A simple mathematical expression

to estimate the size of the PMUT was obtained. We also designed and fabricated a PMUT with identical

circular diaphragms with 580-μm radius. In addition, recording microelectrodes were fabricated into the

PMUTs to monitor the transducer-driven neural activity. To characterize the PMUT properties, including the

intensity and resonant frequency, we measured the pressure oscillations of the transducer driven by the applied

sinusoidal voltage. Finally, we discuss the possibility of using our PMUT to stimulate brain slices in future

applications.

1 INTRODUCTION

Neuromodulation techniques have been studied as

promising tools for the treatment of brain diseases

(Bewernick et al., 2010). Because the intensity of

electromagnetic waves attenuates with increasing

distance, noninvasively inducing transcranial neural

responses in deep brain regions is difficult using

conventional methods, such as transcranial direct

current and magnetic stimulation methods (Wagner et

al., 2007). Overcoming this limitation, transcranial

ultrasound stimulation has recently drawn attention

owing to its low- or non-invasiveness and higher

spatial resolution (Tufail et al., 2010).

Neural impulses have historically been considered

to be electrical signals; the suprathreshold

depolarization of neural membranes was also

influenced by mechanical mechanisms. Thus,

https://orcid.org/0000-0001-8920-1025

https://orcid.org/0000-0001-9429-9880

describing a neural impulse via a mechanical pathway

could support a physical basis for ultrasound-driven

neuromodulation. However, its underlying

mechanisms at the cellular level are still unknown. A

reason for this is the lack of an in vitro method for

stimulating local circuits in the brain with this

technology at high spatial resolution. In addition,

indirect neural activity through polysynaptic

pathways could affect the neuromodulation, which

further complicates the investigation of the

mechanism of action (Sato et al., 2018). conventional

ultrasound transducers are of limited use for brain

stimulation because they are too large (>10 mm) to

locally stimulate neurons on a spatial scale of tens to

hundreds of micrometers.

Microelectromechanical system (MEMS)

technology has recently been used to produce a

transducer for ultrasound brain stimulation. For

example, Kim et al. developed a capacitive

196

Furukawa, R. and Tateno, T.

Development of a Piezoelectric Micromachined Ultrasound Transducer using Microfabrication Technology for in Vitro Neuromodulation.

DOI: 10.5220/0010938500003123

In Proceedings of the 15th International Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 1: BIODEVICES, pages 196-203

ISBN: 978-989-758-552-4; ISSN: 2184-4305

micromachined ultrasound transducer (CMUT) and

conducted an in vivo experiment to stimulate the

brain of a freely moving mouse (Kim et al., 2019) ;

their CMUT stimulated the brain regions on a scale of

2.8 mm. In addition, Lee et al. developed a

piezoelectric micromachined ultrasound transducer

(PMUT) and demonstrated its effectiveness for

elucidating the cellular mechanisms of

neuromodulation in cultured neural networks in vitro

(Lee et al., 2019). However, in their experiments with

cultured brain cells, because neurons in the neural

tissue were isolated and rewired in cultured networks,

the original neural networks were rebuilt in networks

with a random connection.

For a given energy input, PMUTs are more

effective than CMUTs in driving micrometer-sized

ultrasound transducers (Manwar et al., 2020).

Therefore, we used PMUTs in this study. We

examined how the device structure influences the

resonant frequency and the intensity of the generated

ultrasound. In addition, we propose that an in vitro

experimental system is useful for examining the

cellular mechanisms of ultrasound neuromodulation

because it allows the extracellular conditions of the

targeted neurons to be easily controlled.

We first examined the relationships among the

multi-layered PMUT structure, the size of the

diaphragms in the transducer, and the resonant

frequency of the transducer. Each of the diaphragms

was designed to resonate at 500 kHz for neural

stimulation. A physical model of the PMUT was

constructed. The relationships among the PMUT

properties were analytically calculated using this

model and the physical parameters of the PMUT

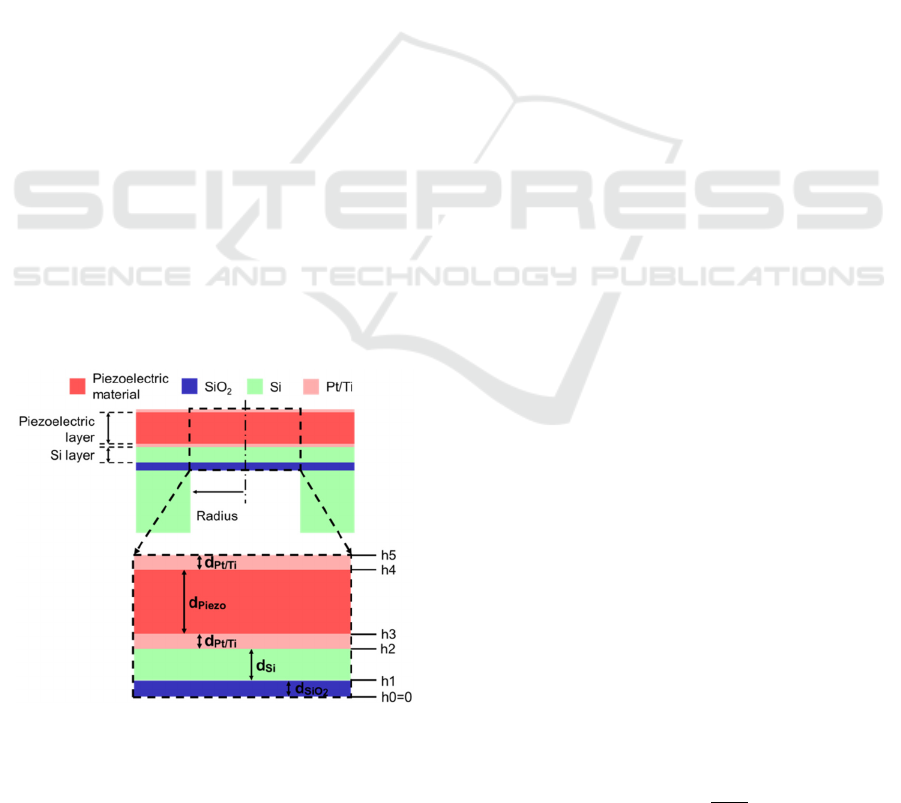
Figure 1: Cross-section of the PMUT, which consisted of

piezoelecctric material, Si, SiO

, and Pt/Ti layers. The

expanded view of the top pannel (dashed square) is shown

in the bottom panel. The layer thicknesses are indicated by

arrows, which are considered in Eqs (5) and (7).

materials. In addition, the result of the analytical

calculation was compared with that of numerical

simulations using multiphysics software. We then

designed a PMUT and circular diaphragms as

microelectrodes to simultaneously record the neural

activity in a brain slice under ultrasound stimulation.

Because the ultrasound-driven response is strongly

dependent on the background activity of neural

circuits, we consider that PMUT devices equipped

with recording electrodes are more appropriate than

conventional methods without recording functions

for neural stimulation. To characterize the PMUT

properties, including the intensity and resonant

frequency, we measured the pressure oscillations of

the transducer driven by the applied sinusoidal

voltage. Finally, we examine whether our PMUT has

the potential to effectively stimulate local networks in

brain slices in future studies.

2 METHODS

To locally stimulate brain slices, we aimed to develop

a PMUT that satisfies three numerical conditions: (i)

a resonant frequency of the diaphragm of 500 kHz,

(ii) an ultrasound intensity for stimulation greater

than 0.5 W/cm

, and (iii) a diaphragm radius smaller

than 0.6 mm (Lee et al., 2019).

2.1 The PMUT Model and Numerical

Calculations

Our PMUT consisted of the following five

components: a piezoelectric film, a silicon (Si) layer,

a SiO

membrane, top and bottom Pt/Ti electrodes,

and a Si supporting layer (Fig. 1). To convert electric

(voltage) signals into ultrasound pressures, a thin film

of a piezoelectric material was used as the transducer.

To achieve a thin diaphragm as a vibrating plate,

circular drains were designed from the back side of

the supporting Si substrate (Fig. 1, top); for the

experiments, the PMUT device was inverted.

The simple diaphragm model of the PMUT is

described below. A diaphragm was first modeled as a

single-layered circular plate with radius r

, before a

multi-layered case was considered. The position on

the plate was represented by a two-dimensional polar

coordinate (r, θ) with the plate center defined as r = 0.

If a uniform radial tension 𝑇 is applied to the plate,

the deflection 𝑤(𝑟,𝜃) of the plate from the resting

state can be expressed as (Wah, 1962):

𝐷∇



𝑤−𝑇∇



𝑤+𝜌

𝜕



𝑤

𝜕𝑡



=0 ,

(1)

Development of a Piezoelectric Micromachined Ultrasound Transducer using Microfabrication Technology for in Vitro Neuromodulation

197

where t is the time, ∇



and ∇



are the Laplace

operator and the biharmonic operator, respectively.

Here, 𝜌 is the density per unit area of the plate, and 𝐷

is the flexural rigidity of the plate, which can be

written as:

𝐷=

𝐸ℎ



12(1 − 𝜈



)

(2)

where 𝐸 is Young’s modulus, ℎ is the thickness, and

𝜈 is the Poisson ratio (Wah, 1962).

The actual circular diaphragm consists of multiple

layers, as shown in Fig. 1. Thus, using each thickness,

𝑑



, of the layers and the corresponding volume

density, 𝜌



, from the bottom to the top (i = 1, ⋯, 5),

the total mass per plate area, 𝜌



, for the multiple

layers can be described as:

𝜌



=𝜌



𝑑



(3)

Similarly, the height, ℎ



, of the n-th layer (n = 1, ⋯,

5) is defined as:

ℎ



= 𝑑







(4)

Furthermore, according to Ref. (Muralt et al., 2005),

the stress center 𝑧



is defined as:

𝑧





ℎ





−ℎ





𝑠𝑒(𝑛)



𝑑



𝑠𝑒(𝑛)

 ,

(5)

where 𝑠𝑒(𝑛) indicates the relevant compliance of the

n-th layer. 𝑠𝑒(𝑛) can be described as (Muralt et al.,

2005):

𝑠𝑒

(

𝑛

)

=𝑠



(



)

(

1−𝑣(𝑛)



)

(6)

where 𝑠



()

denotes the elastic compliance term of

each layer, and the subscript represents the usual

tensor compliance notation. For the multi-layered

plate, the flexural rigidity, 𝐷



, of the diaphragm can

be described as (Muralt et al., 2005):

𝐷





(ℎ



−𝑧



)



−(ℎ



−𝑧



)



𝑠



(



)

(1 − 𝑣(𝑛)



)



(7)

Two extreme types of boundary conditions for the

vibrating plate governed by Eq. (1) were considered:

(i) a clamped condition (CC) and (ii) a simply

supported condition (SSC). On the boundary of the

plate (r = r

), the CC is described as:

𝑤=0,

(8a)

𝜕𝑤

𝜕𝑟

=0.

(8b)

The SSC is described as:

𝑤=0, (9a)

𝜕



𝑤

𝜕𝑟



+𝜈

𝑟

𝜕𝑤

𝜕𝑟

𝑟



𝜕



𝑤

𝜕𝜃



=0 , (9

)

where θ represents an angular variable of the polar

coordinates. In this manuscript, both ideal boundary

conditions were applied in the numerical calculation.

By solving Eq. (1) analytically with the CC or SSC,

the relationship among the plate radius, r

, resonant

frequency f

, and other plate parameters can be

described as:

𝑟





𝛼𝛽

2𝜋

𝑓





𝐷



𝜌



(10)

where 𝛼 and 𝛽 are constants that depend on the

boundary conditions (Wah, 1962): (𝛼, 𝛽) = (2.84,

6.16) for the CC and (𝛼, 𝛽) = (2.31, 3.71) for the SSC.

We note that actual vibration of such plates

corresponds to a boundary condition between these

two extreme boundary conditions.

To characterize the relationships among the radius

and thickness of a diaphragm, and the resonant

frequency, we performed the numerical calculation of

the multi-layered circular plate. First, we calculated

the forced oscillation properties for the physical

model of the plate with five layers: top Pt/Ti

electrode, piezoelectric material, bottom Pt/Ti

electrode, Si, and SiO

layers (Fig. 1, bottom). The

thicknesses of these layers were assumed to be 0.10,

𝑑



, 0.10, 𝑑



, and 1.0 μm, respectively (Table 1).

For convenience, the two Ti/Pt-electrode layers were

simplified as single Pt layers. The thicknesses of the

Pt/Ti electrode and SiO

layers were fixed because

they were much thinner than the other two materials.

The goal of the numerical calculation was to

determine the appropriate radius of the diaphragm,

and thicknesses of the piezoelectric material and Si

layers when the diaphragm resonates in response to a

500-kHz sinusoidal input.

BIODEVICES 2022 - 15th International Conference on Biomedical Electronics and Devices

198

Table 1: Material parameters used in the numerical calculation.

Material Thickness in

m Youn

’s modulus in GPa Densit

in k

Poisson’s ratio

PZT d

piezo

63 7500 0.34

Si d

170 2329 0.28

SiO

1.0 70 2200 0.17

Pt 0.1 168 2145 0.38

To confirm the results from the numerical

calculation, we also performed a numerical

simulation, using general-purpose physics simulation

software (COMSOL Multiphysics, Ver. 5.5,

COMSOLAB, Sweden) on a supercomputer system

(PRIMERGY CX400/CX2550, FUJITSU, Japan) at

the Hokkaido University Computer Center. Using the

finite-element method (FEM) in this simulation

software, we calculated the resonant frequency and

determined the sizes of the PMUT. We modeled the

five-layered plate with 𝑑



and 𝑑



and compared

the results with those of the calculation. Before the

simulation, we determined the mesh size, which split

the modeling domain into a discrete number of

elements; the mesh size ranged from 12.6 to 70.0 μm.

In the simulation, the resonant frequencies were

calculated using frequency-domain analysis. We used

lead zirconate titanate (PZT) as the piezoelectric

material in the simulation because this was used in

our microfabrication process, which is described

below. The thicknesses of the PZT and Si layers

ranged from 25 to 250 μm and 7 to 35 μm,

respectively. All parameters of the four materials

used in the simulation are listed in Table 1.

To obtain simple mathematical relationships

among r

, 𝑑



, and 𝑑



under a 500-kHz resonant-

frequency condition with the first resonant mode (0,

1) (Hong et al., 2006), we collected 50 data points of

the triplet parameters (r

, 𝑑



, 𝑑



) from the FEM

simulation. Low-order polynomial functions of the

three parameters were fitted to the data points using a

Figure 2: Design of a printed circuit board (left) and the

PMUT (lower right) with an array of four diaphragms and

eight recording electrodes (upper right).

least-square approximation. For the five-layered

model, optimal functions were determined on the

basis of minimizing the square errors between the

fitted functions and the data points.

2.2 PMUT Design and

Microfabrication Processes

To stimulate a brain slice with high-spatial resolution,

the PMUT was designed with an array of four

diaphragms (Fig. 2). Microelectrodes (200  200

μ m

) were also designed on the substate to

simultaneously record the electrical activity of the

brain slice. The sizes of the diaphragms were

determined from the results of the numerical

simulation to optimally resonate the plates at 500

kHz.

Our microfabrication process was based on

MEMS technology and the initial substrate was a

silicon-on-insulator (SOI) wafer consisting of three

layers: a device layer (Si), an insulating membrane

(SiO

), and a handle layer (Si). Briefly, our

microfabrication process is described as follows:

(1) We used an SOI substrate with a Si handle

layer (500 µm), an insulating membrane (1

µm), and a Si device layer (10 µm). We

deposited 1-µm-thick SiO

on the bottom side

(Fig. 3A).

(2) As the electrode material, a layer comprising a

100-nm-thick Pt coating and 10-nm-thick Ti

coating was deposed on the substrate using a

sputtering system (RSC-3ERD, Riken-sha Co.,

Japan). Subsequently, the recording electrodes

and their wires were patterned on the bottom

side by photolithography (Fig. 3B).

(3) We formed the recording electrodes and their

wires on the substrate using an inductively

coupled plasma reactive ion etching (ICP-

RIE) system (RIE-101HU, SUMCO Co.,

Japan). Subsequently, the protective film for

the wires was formed on the bottom side (Fig.

3C).

(4) An epoxy resin (bond E205) was applied on

the bottom side by the sputtering system.

Thereafter, the PZT film was attached on the

top of the substrate (Fig. 3C).

Development of a Piezoelectric Micromachined Ultrasound Transducer using Microfabrication Technology for in Vitro Neuromodulation

199

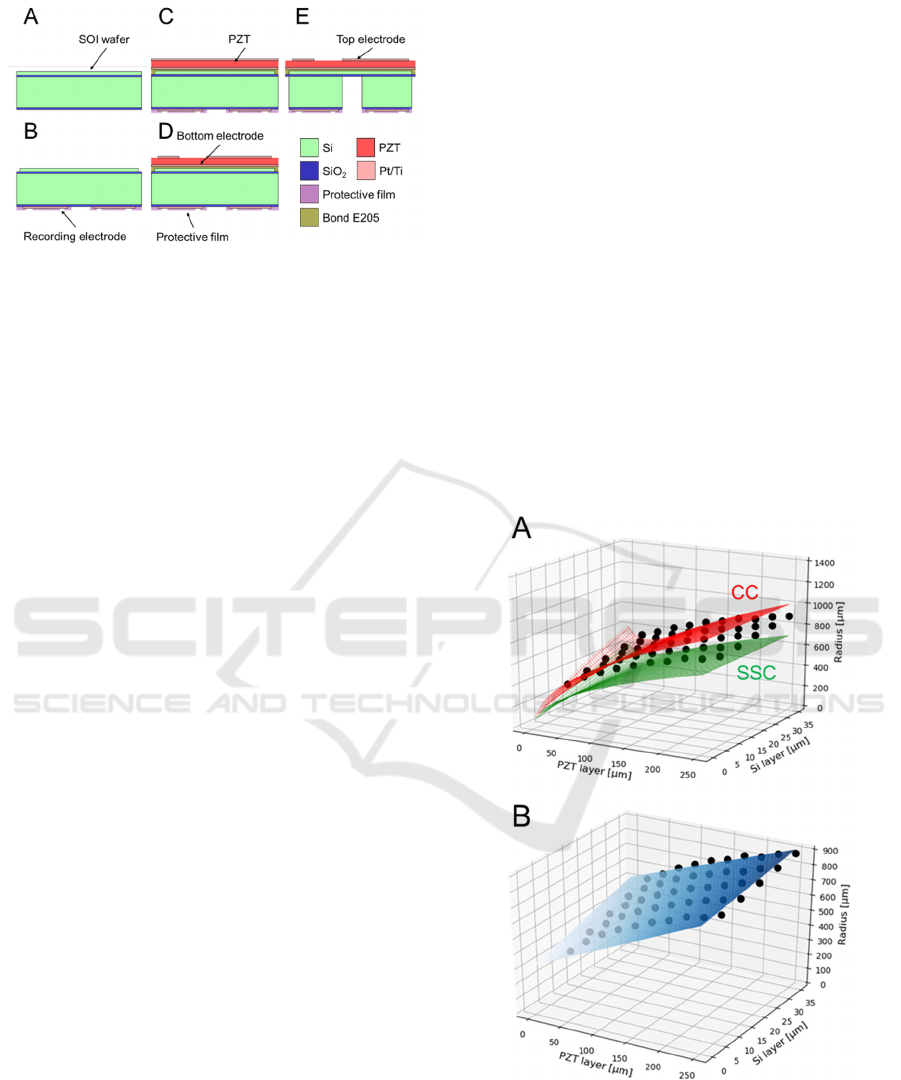
Figure 3: Microfabrication processes used to construct our

PMUT. The different colors represent the different

materials (Si, PZT, SiO

, Pt/Ti, protective film, and epoxy

resin E205). The thickness of each material in the figure

does not reflect its actual size.

(5) The top electrodes of the PZT and their wires

to drive the diaphragms were patterned and

formed using the ICP-RIE system (Fig. 3D).

(6) As the final step to create the diaphragm shape,

the Si handle layer was removed from the back

side using a Deep-RIE instrument (MUC-21

ASE-SRE, SPP Technologies Co., Japan). The

last remaining surface-resist layer was

removed using acetone and isopropyl alcohol

(Fig. 3E).

2.3 Measurement of PMUT Properties

To characterize the properties of the fabricated

PMUTs, we measured the resonant frequencies of the

diaphragms. In the present study, four PMUT devices

were used in the measurement. Initially, a cylindrical

acrylic chamber with an internal diameter of 30 mm

was attached to the substrate on a custom-made

printed circuit board (Fig. 2, left). Subsequently,

individual diaphragms in the PMUT were driven by a

sinusoidal signal with a voltage amplitude of 10 V,

which was generated by a multifunction generator

(WF1947, NF Electronic Instruments, Japan) through

a high-speed bipolar amplifier (HSA4014, NF

Electronic Instruments) with a 10-times voltage gain.

The frequencies ranged from 250 to 800 kHz. In the

measurement, the chamber, including the PMUT, was

filled with water. The generated acoustic pressure just

above the diaphragm in the chamber was measured

with a calibrated needle hydrophone (HY05N, Toray

Engineering Co., Japan); the distance between the

diaphragm and the hydrophone was approximately 1

mm. The data obtained from the hydrophone was

recorded by an oscilloscope (DSOX1102G, Keysight

Technologies, USA) with a digital data-acquisition

system. In the measurement, the measured resonant

frequency was obtained as the frequency at which the

maximum peak response was in the frequency range

(i.e., 250–800 Hz) of the applied voltage signals. The

error rate (%) was calculated as 100 × |fr − 500 | / 500

(fr in kHz). In addition, as an index of ultrasound

intensity, we used the time-integral intensity (spatial

peak pulse average, I

sppa

) (Fomenko et al., 2018),

which is defined as the time-averaged power of

acoustic pressure, normalized by the density of the

fluid medium (i.e., water) and the velocity inside the

medium, during a certain period.

3 RESULTS

3.1 Expression of the Three

Parameters

Figure 4 shows the relationships among the size

parameters (r

, 𝑑



, and 𝑑



) of the diaphragm under

a resonant frequency of 500 kHz. In both plots, the

Figure 4: Relationships among the three size parameters (r

PZT

, d

). In both plots, the black dots represent the data

points from the FEM simulations of the five-layered

physical model. (A) The red and green curves represent the

relationships obtained Eq. (10) under the CC and SSC,

respectively. (B) The blue curve represents the relationship

described by Eq. (11).

BIODEVICES 2022 - 15th International Conference on Biomedical Electronics and Devices

200

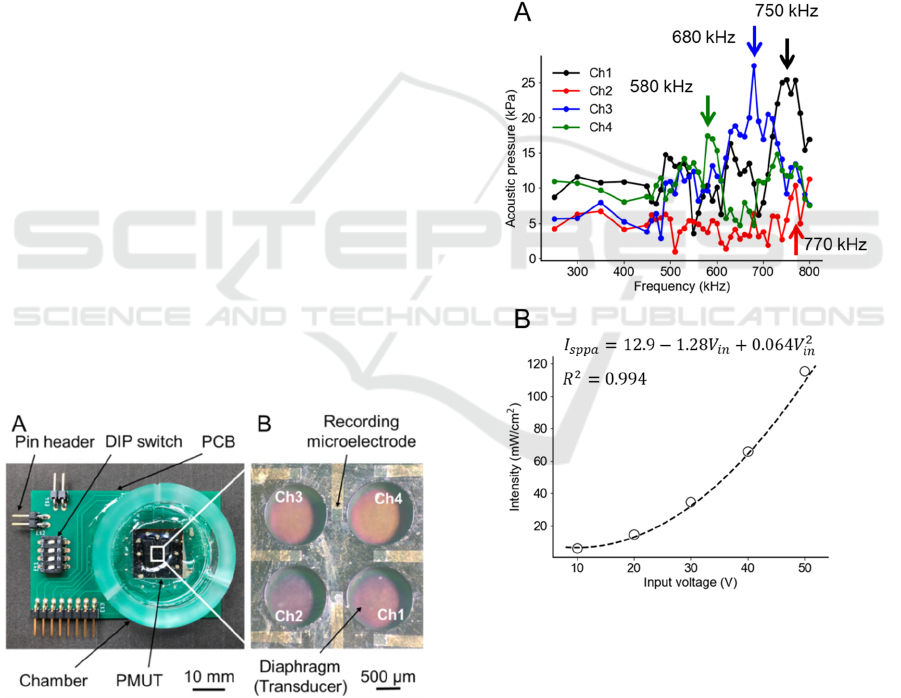
data points indicated by dots were obtained from the

FEM simulation of the five-layered plate model; these

data points are identical in the two plots. The

simulation result indicates that r

monotonically

increases as the thickness of the PZT layer or the Si

layer increases. Moreover, Eq. (11) was determined

by applying the least-squares method to the FEM data

(Fig. 4B):

𝑟



(

𝑑



,𝑑



)

=315+ 5.72𝑑



+ 1.98𝑑



−11.9  10



𝑑



𝑑



(11)

The relationship for the five-layered plate was

approximately described as four terms, including a

second-order polynomial of 𝑑



 𝑑



( 𝑅



0.975). The result (Fig. 4A) shows that the red curve

of the three size parameters for the model under the

CC overestimates the plate radius compared with the

FEM simulation (black dots). By contrast, the green

curve for the five-layered model under the SSC

underestimates the plate radius. These numerical

results suggest that the actual vibration of such plates

corresponds to a boundary condition between the CC

and SSC. In addition, we determined 𝑑



and 𝑑



be 100 and 10 μm, respectively, and r

to be 580 μm

based on the numerical calculations (Fig. 2).

3.2 Microfabrication of the Diaphragm

We successfully microfabricated the PMUT device

with four diaphragms and eight microelectrodes (Fig.

5). The packaged and enlarged PMUTs are illustrated

in Fig. 5A and 5B, respectively.

Figure 5: Images of the microfabricated PMUT. (A) The

packaged substrate with the PMUT device. (B) Front side

of the PMUT with four diaphragms (channels, Chs) and

eight electrodes (corresponding to the bottom side of the

schematic illustration in Fig. 3E).

3.3 Response Characteristics of the

Fabricated PMUT

To characterize the response of the fabricated PMUT,

we measured the acoustic pressure of individual

diaphragms when the PMUT was driven by

sinusoidal voltage signals (AC amplitude, 10–50 V).

A typical example of the frequency response for four

diaphragms (channels 1 to 4) is illustrated in Fig. 6A

for an AC amplitude of 10 V. In the pressure

measurement, the maximum of acoustic pressure was

27.4 kPa in channel 3 at 680 kHz. In channels 1, 3,

and 4, resonance phenomena were seen at specific

frequencies, while the resonant acoustic pressure was

smaller in channel 2 (10.4 kPa) than ones in other

channels. In addition, although each of the resonant

Figure 6: Measured acoustic characteristics of the

fabricated PMUT and an intnsity estimation from the data

points. (A) Measured acoustic pressure as a function of

frequency for a sinusoidal voltage input. These frequency

response characteristics were obtained by applying a 10-V

signal at different frequencies. The channel numbers

correspond to those shown in Fig. 5B. The resonant

frequencies are indicated by the arrows in each channles.

(B) Resonant acoustic intensities for different input

voltages. The dashed line represents the relationship

between input voltages and resultant intensities as a

quadratic function described by Eq. (12).

Development of a Piezoelectric Micromachined Ultrasound Transducer using Microfabrication Technology for in Vitro Neuromodulation

201

frequencies was different from the targeted frequency

(i.e., 500 kHz), the error rate of the four diaphragms

was 39 ± 15% for the PMUT device (Fig. 6A).

Overall, the error rate of the seven diaphragms out of

three examined PMUT devices was 42±12%.

Moreover, when the input voltage amplitude was

increased, the response intensity at the resonant

frequency monotonically was increased (Fig. 6B).

The relationship between the response intensity, 𝐼



(in mW/cm

), and input voltage amplitude, V

(in V),

was approximated by the following quadratic

function (𝑅



=0.994):

𝐼



(

𝑉



)

=12.9 − 1.28𝑉



+ 0.064𝑉





(12)

Here, a standard linear regression method was used to

minimize the mean square error between the data

points and the quadratic function of V

with three

parameters. From Eq. (12), we can estimate that

individual diaphragms of the PMUT could

approximately generate 0.5 W/cm

integral intensity

when a sinusoidal voltage signal of 100 V is applied,

which satisfies our initial target intensity in this study.

4 DISCUSSION

In this study, we developed a MEMS-based PMUT to

locally stimulate brain slices in vitro. We performed

numerical simulations to examine the relationships

between the diaphragm size and the resonant

frequency of the voltage-driven oscillations.

Modeling the multi-layered structure of the PMUT

diaphragms and FEM simulations provided a simple

mathematical expression to estimate the PMUT size.

For the five-layered diaphragm, the curve describing

the relationship among the three size parameters was

positioned between those based on the analytical

results (Eq. (12)) under the CC and SSC. Therefore,

the analytical expression of Eq. (12) gives a rough

estimate of the three size parameters and would be

useful for selecting the size parameters in preliminary

study stages. In addition, the data points obtained

from the FEM simulation were approximated as a

function of the low-order polynomials. The

expression of the low-order polynomials provides a

direct quantitative formula for a specific structural

condition under the resonant frequency of 500 kHz.

Thus, the result of the simple expression may be also

useful for the design of PMUT devices because a

frequency of 500 kHz is often selected for ultrasound

brain stimulation.

On the basis of the numerical results, we designed

and microfabricated a PMUT with four identical

circular diaphragms with 580-μm radius and eight

recording electrodes. To the best of our knowledge,

this is the first time that recording electrodes have

been fabricated in a PMUT, although we did not

evaluate their electrical properties. Furthermore, to

characterize the PMUT properties, including the

intensity and resonant frequency, we measured the

response of the transducer driven by a sinusoidal

voltage input. Some diaphragms (e.g., channel 4) had

a measured value (f

= 580 kHz)) close to the target

resonant frequency. We compared the difference

between numerically predicted and measured

resonant frequency with some previous reports. Then,

our mean error rate 39% was relatively large

compared with the previous studies (10-30%) (Cheng

et al., 2019; Dangi et al., 2020; Lee et al., 2019; Lucia

MS, 2017). In addition, among the four diaphragms,

the variance of the resonance frequency was large

(standard deviation = 74 kHz), and frequency-

response characteristics were not identical. Although

the reasons for the differences between the

numerically predicted and measured values are not

clear, we speculate that there was discrepancy

between the fabricated and designed layer thicknesses

of the diaphragms. To confirm this speculation in

future work, we will take scanning electron

microscope images of the PMUT cross-section to

measure the layer thicknesses.

In addition, the input–output characteristic

properties of the diaphragms imply that the intensities

generated by the fabricated PMUT were similar to

those predicted (> 0.5 W/cm

), which is sufficient for

the stimulation of brain slices in vitro. Our estimation

requires feeding more than 100-V input into the

device, how the electric artifacts affect the activity of

neural tissue will be one of our future challenges.

Several recent review papers (Cardenas-rojas et

al., 2021; Pasquinelli et al., 2019) summarized four

potential mechanisms by which ultrasound signals

could trigger action potentials: (i) the generation of

capacitive currents as a result of membrane

displacements, (ii) the activation of mechanosensitive

channels, (iii) sonoporation in the lipid bilayer, and

(iv) coupling with membrane waves along the axon.

Effective ultrasonic neurostimulation may be

possible by combining these mechanisms. Examining

the mechanisms will be included in our future work.

ACKNOWLEDGEMENTS

All authors appreciate Dr. Shuichi Murakami and Dr.

Kazuo Satoh (Osaka Research Institute of Industrial

Science and Technology) for their cooperation on

BIODEVICES 2022 - 15th International Conference on Biomedical Electronics and Devices

202

MEMS processes. This work was supported by a

Grant-in-Aid for Exploratory Research [grant number

18K19794] and a Grant-in-Aid for Scientific

Research (B) [grant number 19H04178] (Japan).

REFERENCES

Bewernick, B. H., Hurlemann, R., Matusch, A., Kayser, S.,

Grubert, C., Hadrysiewicz, B., Axmacher, N., Lemke,

M., Cooper-Mahkorn, D., Cohen, M. X., Brockmann,

H., Lenartz, D., Sturm, V., & Schlaepfer, T. E. (2010).

Nucleus Accumbens Deep Brain Stimulation Decreases

Ratings of Depression and Anxiety in Treatment-

Resistant Depression. Biological Psychiatry, 67(2),

110–116. https://doi.org/10.1016/j.biopsych.2009.09.0

Cardenas-rojas, A., Pacheco-barrios, K., Giannoni-luza, S.,

Fregni, F., Rehabilitation, S., Hospital, M. G., Loyola,

S. I. De, & Health, M. (2021). HHS Public Access.

20(4), 401–412. https://doi.org/10.1080/147371

75.2020.1738927.Non-invasive

Cheng, C. Y., Dangi, A., Ren, L., Tiwari, S., Benoit, R. R.,

Qiu, Y., Lay, H. S., Agrawal, S., Pratap, R., Kothapalli,

S. R., Mallouk, T. E., Cochran, S., & Trolier-Mckinstry,

S. (2019). Thin Film PZT-Based PMUT Arrays for

Deterministic Particle Manipulation. IEEE

Transactions on Ultrasonics, Ferroelectrics, and

Frequency Control, 66(10), 1605–1615. https://doi.org/

10.1109/TUFFC.2019.2926211

Dangi, A., Cheng, C. Y., Agrawal, S., Tiwari, S., Datta, G.

R., Benoit, R. R., Pratap, R., Trolier-Mckinstry, S., &

Kothapalli, S. R. (2020). A Photoacoustic Imaging

Device Using Piezoelectric Micromachined Ultrasound

Transducers (PMUTs). IEEE Transactions on

Ultrasonics, Ferroelectrics, and Frequency Control,

67(4), 801–809. https://doi.org/10.1109/TUFFC.20

19.2956463

Fomenko, A., Neudorfer, C., Dallapiazza, R. F., Kalia, S.

K., & Lozano, A. M. (2018). Low-intensity ultrasound

neuromodulation: An overview of mechanisms and

emerging human applications. Brain Stimulation,

11(6), 1209–1217. https://doi.org/10.1016/j.brs.20

18.08.013

Hong, E., Trolier-McKinstry, S., Smith, R., Krishnaswamy,

S. V., & Freidhoff, C. B. (2006). Vibration of

micromachined circular piezoelectric diaphragms.

IEEE Transactions on Ultrasonics, Ferroelectrics, and

Frequency Control, 53(4), 697–705. https://doi.org/

10.1109/TUFFC.2006.1611029

Kim, H., Kim, S., Sim, N. S., Pasquinelli, C., Thielscher,

A., Lee, J. H., & Lee, H. J. (2019). Miniature ultrasound

ring array transducers for transcranial ultrasound

neuromodulation of freely-moving small animals.

Brain Stimulation, 12(2), 251–255. https://doi.org/

10.1016/j.brs.2018.11.007

Lee, J., Ko, K., Shin, H., Oh, S. J., Lee, C. J., Chou, N.,

Choi, N., Tack Oh, M., Chul Lee, B., Chan Jun, S., &

Cho, I. J. (2019). A MEMS ultrasound stimulation

system for modulation of neural circuits with high

spatial resolution in vitro. Microsystems and

Nanoengineering, 5(1). https://doi.org/10.1038/s413

78-019-0070-5

Lucia MS, H. K. and T. J. D. C. (2017). HHS Public Access.

Physiology & Behavior, 176(10), 139–148.

https://doi.org/10.1109/ICSENS.2018.8589733.Evalua

tion

Manwar, R., Kratkiewicz, K., & Avanaki, K. (2020).

Overview of ultrasound detection technologies for

photoacoustic imaging. Micromachines, 11(7), 1–24.

https://doi.org/10.3390/mi11070692

Muralt, P., Ledermann, N., Paborowski, J., Barzegar, A.,

Gentil, S., Belgacem, B., Petitgrand, S., Bosseboeuf,

A., & Setter, N. (2005). Piezoelectric micromachined

ultrasonic transducers based on PZT thin films. IEEE

Transactions on Ultrasonics, Ferroelectrics, and

Frequency Control, 52(12), 2276–2288. https://doi.org/

10.1109/TUFFC.2005.1563270

Pasquinelli, C., Hanson, L. G., Siebner, H. R., Lee, H. J., &

Thielscher, A. (2019). Safety of transcranial focused

ultrasound stimulation: A systematic review of the state

of knowledge from both human and animal studies.

Brain Stimulation, 12(6), 1367–1380. https://doi.org/

10.1016/j.brs.2019.07.024

Sato, T., Shapiro, M. G., & Tsao, D. Y. (2018). Ultrasonic

Neuromodulation Causes Widespread Cortical

Activation via an Indirect Auditory Mechanism.

Neuron, 98(5), 1031-1041.e5. https://doi.org/10.1016/

j.neuron.2018.05.009

Tufail, Y., Matyushov, A., Baldwin, N., Tauchmann, M. L.,

Georges, J., Yoshihiro, A., Tillery, S. I. H., & Tyler, W.

J. (2010). Transcranial Pulsed Ultrasound Stimulates

Intact Brain Circuits. Neuron, 66(5), 681–694.

https://doi.org/10.1016/j.neuron.2010.05.008

Wagner, T., Valero-Cabre, A., & Pascual-Leone, A. (2007).

Noninvasive human brain stimulation. Annual Review

of Biomedical Engineering, 9, 527–565. https://doi.org/

10.1146/annurev.bioeng.9.061206.133100

Wah, T. (1962). Vibration of Circular Plates. The Journal

of the Acoustical Society of America, 34(3), 275–281.

https://doi.org/10.1121/1.1928110

Development of a Piezoelectric Micromachined Ultrasound Transducer using Microfabrication Technology for in Vitro Neuromodulation

203