Privacy-preserving Copy Number Variation Analysis with Homomorphic

Encryption

Hüseyin Demirci

and Gabriele Lenzini

Interdisciplinary Center for Security Reliability and Trust (SnT), University of Luxembourg,

6, avenue de la Fonte, L-4364 Esch-sur-Alzette, Luxembourg

Keywords:

Privacy-preserving Genomic Data Processing, Copy Number Variation, Homomorphic Encryption, Applied

Cryptography.

Abstract:

Innovative pharma-genomics and personalized medicine services are now possible thanks to the availability

for processing and analysis of a large amount of genomic data. Operating on such databases, is possible

to test for predisposition to diseases by searching for genomic variants on whole genomes as well as on

exomes, which are collections of protein coding regions called exons. Genomic data are therefore shared

amongst research institutes, public/private operators, and third parties, creating issues of privacy, ethics, and

data protection because genome data are strictly personal and identifying. To prevent damages that could

follow a data breach—a likely threat nowadays—and to be compliant with current data protection regulations,

genomic data ﬁles should be encrypted, and the data processing algorithms should be privacy-preserving.

Such a migration is not always feasible: not all operations can be implemented straightforwardly to be privacy-

preserving; a privacy-preserving version of an algorithm may not be as accurate for the purpose of biomedical

analysis as the original; or the privacy-preserving version may not scale up when applied to genomic data

processing because of inefﬁciency in computation time. In this work, we demonstrate that at least for a well-

known genomic data procedure for the analysis of copy number variants called copy number variations (CNV)

a privacy-preserving analysis is possible and feasible. Our algorithm relies on Homomorphic Encryption, a

cryptographic technique to perform calculations directly on the encrypted data. We test our implementation for

performance and reliability, giving evidence that it is practical to study copy number variations and preserve

genomic data privacy. Our proof-of-concept application successfully and efﬁciently searches for a patient’s

somatic copy number variation changes by comparing the patient gene coverage in the whole exome with a

healthy control exome coverage. Since all the genomics data are securely encrypted, the data remain protected

even if they are transmitted or shared via an insecure environment like a public cloud. Being this the ﬁrst study

for privacy-preserving copy number variation analysis, we demonstrate the potential of recent Homomorphic

Encryption tools in genomic applications.

1 INTRODUCTION

Thanks to the technological revolution brought up by

Next Generation Sequencing (NGS), which makes

possible to sequence a human genome in hours and

for a few hundred USD, national large-scale projects

(e.g., the 100,000 Genomes Project

) and private ini-

tiatives can now afford sequencing the genomes of

hundreds of thousand of individuals. Large digital

genomic databases of sequenced raw data and other

genomic data (i.e., .bam ﬁles) are being created for

https://orcid.org/0000-0002-0538-2074

https://orcid.org/0000-0001-8229-327

https://www.genomicsengland.co.uk/ (11/2021)

present and future data analysis and research.

The availability of genomic databases is already

paving the way for innovative genomic medicine,

for instance personalized immunotherapeutic meth-

ods for cancer treatment (Kakimi et al., 2017), with

unquestionable beneﬁts in terms of quality of future

treatments and healthcare. But, storing and process-

ing genomic data also raises serious concerns about

privacy rights: genomic data contains extremely sen-

sitive and personal information, for instance about the

owner’s, his/her relative’s, and future kin’s suscepti-

bility and predisposition to speciﬁc diseases such as

Alzheimer’s, schizophrenia, and cancer. This is not an

hypothetical threat: cases of misuse of genomic data

for individual discrimination have already reported

Demirci, H. and Lenzini, G.

Privacy-preserving Copy Number Variation Analysis with Homomorphic Encryption.

DOI: 10.5220/0011012400003123

In Proceedings of the 15th Inter national Joint Conference on Biomedical Engineering Systems and Technologies (BIOSTEC 2022) - Volume 5: HEALTHINF, pages 821-831

ISBN: 978-989-758-552-4; ISSN: 2184-4305

821

(Naveed et al., 2015), showing that an extensive avail-

ability of genomic databases can have serious ethical

and legal concerns.

Several methods have been proposed and stud-

ied for genomic data protection. The most com-

mon and simplistic is pseudonymization i.e., remov-

ing from a genome data ﬁle any reference that could

link it back to its owner. For genomic data protection,

pseudonymization has been proved to be ineffective

(Gymrek et al., 2013). Genomic data are rich in in-

formation, and retrieve to whom a piece of genomic

data belong is easily done by triangulating data.

Another way to protect genomic data is to obfus-

cate (i.e., ﬁlter out) private sensitive sequences of nu-

cleotids from the raw data (Decouchant et al., 2018).

The idea is worth, but ﬁltering information affects

the quality of processing, even if the ﬁltering is done

selectively and in small amount. Besides, changing

well-established NGS protocols and machines require

time and effort, for instance due to the deﬁnition of

new standards, which is delaying the availability of

this technology.

Yet another option is to encrypt the genomic data

before they are stored. This strategy should at least

protect the data in case data leakage and as such,

promises to be compliant with legal requirements in

directives such as the Europe’s General Data Pro-

tection Regulation (GDPR) and the California Con-

sumer Privacy Act (CCPA). However, data base en-

cryption is insufﬁcient to ensure a long-lasting pro-

tection if, for the purpose of processing, encrypted

data decrypted before use. Decrypted data are unpro-

tected. It is hard to control that they are not copied and

stored unencrypted, or re-transmitted in clear. The

risks of privacy violation remains high.

A better solution would be to run the analysis di-

rectly on the encrypted data without ever decrypt-

ing them. The practices is, at least in theory, possi-

ble thanks to secure data processing algorithms. Re-

searchers have explored this possibility and for spe-

ciﬁc procedures of genomic analysis, mostly about

small variants, namely Single-Nucleotide Polymor-

phisms and indels (i.e., small insertion - deletions).

The challenge is that producing a secure (i.e., privacy-

preserving) version of a speciﬁc data processing pro-

cedure requires redesigning the algorithm of analy-

sis by using only speciﬁc secure functionalities. A

privacy-preserving version of an algorithm with com-

parative and acceptable quality of analysis and per-

formance of the original version is not always possi-

ble. And even if it were possible a privacy-preserving

variant may remain inefﬁcient, unable to scale up to

process large size data as those required for medical

purposes.

We study how to realize secure data processing

for an important class of genomic data procedures,

those aiming at the analysis of copy number varia-

tions (see Section 2.1). We assess the performances of

this new privacy-preserving processing, and we give

evident that a professional implementation can be ef-

ﬁcient. To calculate copy number variation values on

encrypted genomic data, we use Homomorphic En-

cryption (HE) (see Section 2.4), a cryptographic tech-

nique that enables to operate directly and exclusively

on encrypted data and that produce results that are

still encrypted. By using HE, data processors never

get to know the genomic data they process, nor they

can make sense of the results of the processing unless

authorized to do so: both genomic data and the copy

number variation analysis can be safely outsourced to

third parties e.g., research laboratories specialized in

that type of analysis or a cloud service with sufﬁcient

power of computation for the data processing.

Contribution. We design a proof-of-concept algo-

rithm for the detection of copy number variations that

uses HE operations, thus providing the ﬁrst privacy-

preserving procedure for CNV analysis which relies

on this cryptographic technique. Our algorithm uses

basic homomorphic operations (addition, subtraction,

multiplication), for which an efﬁcient implementation

exists in standard cryptographic software libraries,

making it possible to implement a prototype of the

procedure.

We test the quality of our privacy-preserving ver-

sion by looking for somatic copy number variation

changes in an exome sample

in comparison to ref-

erence exome samples used as control group. These

samples come from an existing Melanoma whole ex-

ome study (Magi et al., 2013).

The results of our privacy-preserving procedure

(once decrypted) are proven compatible with those re-

ported in the study. We also show that we can extend

our privacy-preserving procedure to calculate copy

number variation values for the whole genome and

not only for exomes. Our work reveals the potential

of using HE in the analysis of copy number variation

over an exome and potentially on the whole genome,

and that it is practical if we assume a convenient sam-

pling strategy.

Our proof-of-concept software and the data sets

we have used are on git

Exomes are collections of protein coding regions of the

genome, regions that are singularly called exons.

github.com/huseyindemirci44/privateCNVanalysis

Scale-IT-up 2022 - Workshop on Scaling-Up Health-IT

822

2 BACKGROUND

Before describing the core of our privacy-preserving

procedure, we remind a few basic facts on copy

number variation, variant data sets and analysis, and

Homomorphic Encryption (HE). We mention rele-

vant works on private genomic data processing that

use cryptographic techniques, and we comment their

use in copy number variation.

2.1 Copy Number Variation (CNV)

The Human Genome Project, the international sci-

entiﬁc research project that had been running from

1990 to 2003 and whose goal was determining the

base pairs of the human genome

, has revealed ab-

sence and replications of genetic material inside the

genome. These structural variants in the number of

copies of speciﬁc regions are the result of genomic

mutations, called deletions and duplications. They

cover large regions of the genome and involve several

genes.

Copy number variations are structural variants in

a person’s genome involving more than one thousand

bases. They differ from small variants such as in-

dels and repetitions that involves only a few bases. A

non-mutated genome region is expected to occour in

2 copies, respectively coming from the chromosomes

of the mother and of the father, but because of dele-

tion or duplication, the number of copy of the region

may respectively fall down to 1 or 0, or raise up to

3, 4, or more copies. These copy number variations

also change the number of genes and gene expression

levels inside copy number variation regions. Recent

studies claim that around 4.8% − 9.7% of the human

genome is copy number variation (Zarrei et al., 2015).

Generally copy number variations do not have

a direct phenotypic effect, but elevated copy num-

ber variations of particular genes have been shown

be associated with speciﬁc cancer types (Shlien

and Malkin, 2009; Shao et al., 2019). Changes

in copy number variation are correlated with in-

creased risk of developing psychiatric disorders such

as schizophrenia (Joober and Boksa, 2009; Marshall

et al., 2017); with major disease classes including

autoimmune, cardio-metabolic, oncologic, and neu-

ropsychiatric diseases (Li et al., 2020); and with

Mendelian and complex diseases such as Alzheimer

and autism (Zhang et al., 2009).

Needless to say, the interest to ﬁnd copy number

variations and to understand how copy number varia-

tion affect to the phenotype is increasing.

An organism’s genome is its complete set of DNA.

2.2 CNV Analysis

It is a common practice to keep and maintain data

bases of genomic variants for research. For instance,

DECIPHER (Bragin et al., 2014) and “Database of

Genomic Variants” (MacDonald et al., 2014) stores

copy number variation data for both patient and

healthy individuals. Data were usually calculated us-

ing traditional methods such as ﬂuorescence in situ

hybridization (FISH) and array comparative genomic

hybridization (aCGH), but nowadays computational

methods working on digital genomic data are pre-

ferred.

The detection of copy number variation is done

using specif algorithms and procedures, and we refer

to (Zhang et al., 2019) and (Moreno-Cabrera et al.,

2020) for a comprehensive discussion on them. In

this work, we refer to one of such methods, the Ex-

cavator tool (Magi et al., 2013), whose output values

are reported Table 1. They tell about the presence of

variations in a genome. Copy number variants can be

calculated using read depth of coverage information

(Yoon et al., 2009). For instance, in the Excavator

tool, the mean read count (EMRC) for each exon e in

a genomic region is calculated by the following for-

mula:

EMRC =

where RC is the number of reads aligned in the region

and L is its size in base pairs. EMRC calculated from

the genome of an individual are then compared with

reference values calculated from control genomes, af-

ter a normalization step.

Comparing with control genomes is a common

method in structural variant analysis. It serves to ﬁlter

polymorphic variants and to increase statistical signif-

icance. Statistical methods, such as Hidden Markov

Models, are used to estimate the locations and prob-

ability of genomic events. Such a justiﬁed need to

analyze this class of genomics variants as well as

other variants would surely beneﬁt from methods of

processing that are privacy-preserving and capable to

protect the personal sensitive health related informa-

tion contained in the genome of patients without com-

promising the quality of the analysis.

2.3 Private Genomic Data Processing

There has been several studies about using crypto-

graphic technique in ensuring privacy in genomic

data processing. Differential Privacy, tailored to ge-

nomic databases, has been tested to enable privacy-

preserving Genome Wide Association Study (GWAS)

applications (Simmons et al., 2016). Another tech-

nique, Secure Multiparty Computation, has been

Privacy-preserving Copy Number Variation Analysis with Homomorphic Encryption

823

Table 1: Copy Number Variation.

Copy Number Explanation Notation

Double Gain ≥ 2 extra copies are duplicated 2

One copy gain Extra 1 copy is obtained 1

Normal case 2 copies exist 0

Heterozygous deletion One of the copies is lost -1

Homozygous deletion There is no DNA sequence -2

tested in “trio exome analysis” for small cohorts of

patients, and demonstrated to be executable in sec-

onds whereas the remaining variant set of any patient

remained privately protected (Jagadeesh et al., 2017;

Akgün et al., 2020). These methods are not directly

applicable to copy number variation analysis, because

the detection of variants is generally out of their work-

ing pipeline, which focus on Single-Nucleotide Poly-

morphisms and short indels. Instead,Homomorphic

Encryption (HE) has been applied to realize a se-

cure exact logistic regression model for rare disease

GWAS studies (Wang et al., 2016), but to our best

knowledge at the moment of writing

, there is no spe-

ciﬁc work that studies how to protect genomic privacy

in copy number variation detection, nor one that pro-

poses using HE for this task. Once copy number vari-

ation values are calculated in a private manner and

stored (even in encrypted form) in a .vcf ﬁle, all the

cryptographic methods previously mentioned can be

employed to ensure privacy protection in further data

analysis, tests, and processing.

2.4 Homomorphic Encryption

This cryptographic technique can be considered as a

bridge (i.e., an homomorphism) between operations

on a plaintext (unencrypted) domain and operations

on an encrypted domain. This means that HE makes

it possible to perform computations directly on the en-

crypted. The output of the computation, which is en-

crypted, once decrypted, is the same as the output that

would have been produced if the computation were

performed on the unencrypted data.

For example, an additive HE scheme would ensure

that Enc

(d + d

) = Enc

(d) ⊕ Enc

), where Enc

is the encryption function, k encryption key, ⊕ the

homomorphic addition, and d and d

pieces of data.

HE enables outsourcing the computation of per-

sonal data while ensuring privacy. A subject that has

encrypted some personal data by using its public key

can send it safely to an insecure party to get them pro-

cessed. The party processes the data without ever get-

ting access to the plain data and returns the encrypted

results back to the subject who is the only one who

June 2021

can decrypt them by using the private key. Even if the

data breach were breached on the party side, conﬁden-

tiality is ensured because the data cannot be decrypted

without the private key.

For reasons of space, we have to limit our account

of HE schemes. The reader can refer to (Acar et al.,

2018) for a comprehensive survey on their theory and

implementations, but for the scope of this work we

point out that there are different types of HE schemes.

The most common ones are the following:

• Partially Homomorphic Encryption. They pre-

serve the homomorphism only for computations

using one operation, for example only addition,

or only multiplication.

• Somewhat Homomorphic Encryption. They pre-

serve homomorphism for bounded computations,

for instance computation using a speciﬁc number

of additions and multiplications.

• Fully Homomorphic Encryption (FHE). They are

schemes that preserve the homomorphism for ar-

bitrary computations, for instance, computations

with an arbitrary number of additions and multi-

plications.

The latter is the most general, and a proof for its ex-

istence for arbitrary computation using addition and

multiplication has been presented in 2009 by Gentry

who used mathematical lattices for the purpose (Gen-

try, 2009). Most of the HE schemes of today also

rely on solutions for hard-to-solve computational al-

gebraic problems over lattices, known as Ring Learn-

ing with Errors (Regev, 2009). Recently, libraries

such as Microsoft’s SEAL

and IBM’s Fully Homo-

morphic Encryption Toolkit For Linux

have been

made available for developing HE applications.

3 REFERENCE SCENARIO

To contextualize the copy number variation (CNV)

analysis with HE, let us refer to the following situ-

ation. A patient, who had his genome sequenced and

https://github.com/microsoft/SEAL

https://github.com/IBM/fhe-toolkit-linux

Scale-IT-up 2022 - Workshop on Scaling-Up Health-IT

824

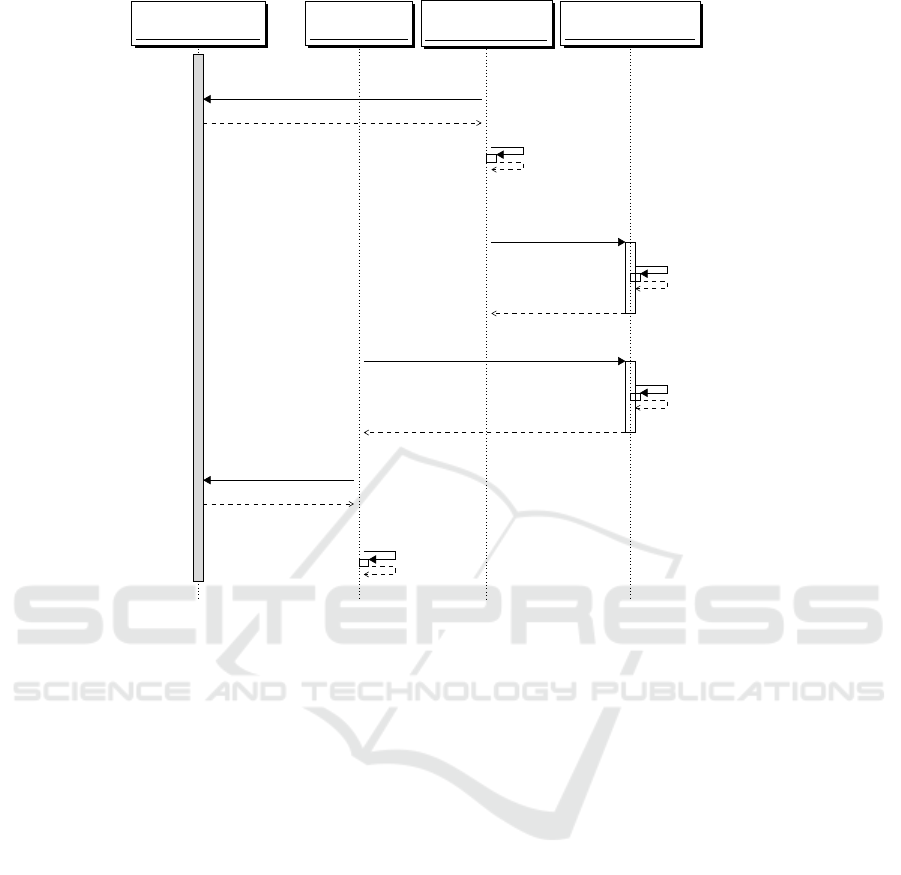
Trusted Party (TP)

(pk,sk)

Medical Unit

(MU)

Patient P

Cohort Patients

Storage Processing

Unit (SPU)

1. Req(PubKey)

Encrypt

,~g

Enc

), Enc

(~g)

2. Enc

), Enc

(~g)

Store

encrypted data

3. Req(CNV)

Calculate Secure CNV

on Enc

), Enc

(~g)

Enc

(CNV(g

,~g))

4. Enc

(CNV(g

,~g))

5. Req(PrivKey)

Decrypt Enc

(CNV(g

,~g))

using sk

CNV(g

,~g)

Figure 1: Message ﬂow for a secure processing in our scenario.

genomic data coverage ﬁles stored in a biobank, con-

sults a doctor. The doctor suggests a test which re-

quires identifying copy number variants because he

intends to investigate changes in the tumor suppressor

genes like TP53 for a possible drug resistance anal-

ysis. This could ideally be carried out by the same

biobank by comparing the patient’s tumor sequence

coverage data with those other patients used as a con-

trol set.

Since both the patient’s and other patients’ ge-

nomic data, in this example the sequence coverage

ﬁles, are personal data, such data are stored encrypted

by the biobank.

Figure 1 shows a possible secure processing pro-

tocol. The message exchange involves the follow-

ing agents: a Trusted Party (TP), usually an authority

such as the Public Health System Institute or a na-

tional Certiﬁed Institution, which is in charge of cre-

ating a pair of encryption-decryption keys (pk, sk), re-

spectively, public and private meant to be used in sup-

port to secure genomic processing; the Medical Unit

(MU), usually a doctor or a researcher in the need of

processing genomic data; the Storage and Processing

Unit (SPU), which is generally represented by a pub-

lic cloud service for instance run by a biobank; the

patients, which are the data subjects of the genomic

data, which herein we assume to be a particular pa-

tient’s genomic data (P

and g

), and the genomic data

ﬁles of a cohort of reference patients (

P and ~g).

Figure 1 protocol exchange is as follows: Before

storing their genomic data on the clouds, the patients

, as well as

P), request (message 1) and obtain the

public key pk from TP, using which they encrypt their

genomic data, respectively g

and ~g. The encrypted

data, resp. Enc

), Enc

(~g), are send to the SPU

(message 2), which stores them for future uses.

When a MU, having agreed with patient P

make a CNV analysis for which it needs the patient’s

genome g

and/or those of the cohort (~g), makes a re-

quest for the analysis to the SPU (message 3). The

SPU performs on behalf of MU the calculation by

running the secure homomorphic encryption version

of copy number variation algorithm (see later, Algo-

rithm 1) on the encrypted genomic data previously

stored. The SPU sends back to the MU the encrypted

outcome of the analysis, Enc

(CNV(g

,~g)), which

cannot yet be decrypted. MU requests for and ob-

tains the decryption key from the TP (message 6), af-

ter which MU gets to know the result of the analysis.

None of the agents but the data subjects even know

the patients’ personal genomic data in cleartext. It

is important to stress that the protocol in Figure 1

Privacy-preserving Copy Number Variation Analysis with Homomorphic Encryption

825

does not protect against active intruders, such as an

SPU that tries to fool TP into getting the private key.

Additional measures need to be in place for reach-

ing higher levels of security, which is a goal out of

the scope of this work. The protocol is meant to en-

sure data privacy against a passive but curious SPU,

for which the use of privacy-preserving copy number

variation is an adequate measure.

4 A PRIVACY-PRESERVING CNV

We now present our implementation of the secure

CNV detection that relies on HE. The pseudocode

is reported in Algorithm 1.

For simplicity of exposition, we assume that all

the computations are performed locally in one ma-

chine instead of being distributed as they should be

according to Figure 1. Consequence of this simpli-

ﬁcation is that we do distinguish between different

roles, not we show the interroles communication. The

feasibility and performance benchmarks that we ob-

tain from the experiment remain valid because we are

not interested in measuring the overhead due to the

communication but only the impact of the HE com-

putation for a CNV analysis on genomic data.

The procedure PPCNV is inspired by the pro-

cedure we described in Section 2. It takes in input

the coverage ﬁles

for patient and control cases, re-

spectively, CovPatient and CovControl, and the list of

genes Genelist to point out the regions to be analyzed.

It returns the list CNV of copy number predictions for

the genes in Genelist. The procedure refers to certain

threshold parameters (th

in the pseudocode), which

represent the boundary conditions to have 0, 1, 2, 3, 4

or more copies of DNA parts.

The rationale of procedure PPCNV is as follows

(we assume basic knowledge about coverage ﬁles, ex-

omes, and genes): the patient’s gene coverage ﬁle,

which contains the number of occurrences of each

gene on the different reads (i.e., overlapping frag-

ments) of the patient’s genome after sequencing, is

compared with a control coverage ﬁle of an healthy

individual. The number of copy variants for a gene

g is determined looking at the difference between the

coverage ﬁles. For instance if the difference is zero,

then there is no variants; if it is bigger than 2 there

are more than 2 copy variants. Intermediate values

are determined reasoning on the value of the differ-

ence: if it is bigger then 1.5, there are quite likely 2

copy variants, whereas if it is bigger then 0.5, there is

quite likely 1 copy variation. We use a window of ﬁve

Coverage ﬁles contain information regarding the

base/read coverage of each sequence in an assembly ﬁle.

overlapping consecutive gene regions, and we take the

value that occurs in the majority of the cases as the

ﬁnal copy variant value. The key point of PPCNV

is to implement this ideas using homomorphic opera-

tions, namely ⊗ and ⊕ (and therefore ). There is no

homomorphic operator that can be used to determine

whether e.g., (x−y) > 1.5. The idea is then to rewrite

the expression as x − (1.5 × y), which can be calcu-

lated homomorphically. That done, we can encrypt

the coverage ﬁles and calculate x  (1.5 ⊗ y) for all

genes, keeping the sensitive coverage ﬁles protected.

Algorithm 1: Privacy-preserving CNV Procedure.

PPCNV(CovPatient,CovControl, Genelist)

2 // SPU calculation

3 forall g ∈ Genelist

4 for i = 0 to 4 do

5 c

:= Enc

(th

⊗ CovControl

);

6 for i = 0 to 3 do

7 d

:= c

 c

i+1

8 return (d

)

10 // MU calculation

11 forall g ∈ Genelist

12 for i = 0 to 3 do

13 d

:= Dec

)

14 n

:= 0 ;

15 if d

> 0 then n

:= 2

16 else if d

> 0 then n

:= 1

17 else if d

< 0 then n

:= −1

18 else if d

< 0 then n

:= −2;

19 n

20 maxCount({n

g+1

g+2

g+3

g+4

})

21 CNV

:= n

22 return CNV

In Algorithm 1 Enc and Dec represent HE en-

cryption and decryption operations with the public

and private keys. Values th

,th

are the HE

threshold parameters where th

≈ 2., th

≈ 1.5, th

≈

0.5 and th

≈ 0. The threshold numbers represent the

boundary conditions to have 0, 1, 2, 3, 4 or more

copies of DNA parts. After obtaining the initial copy

number variant predictions, we select the prediction

value that occurs with maximal frequency (i.e., func-

tion maxCount ) over a non-overlapping window of

length 5 to ﬁlter out instant ﬂuctuations since the copy

number variation values do not change frequently.

The most frequent element in the window is estimated

as the copy number variation value for that window.

In Algorithm 1, we made another simpliﬁcation,

this time with consequences. The ﬁnal calculation of

copy number variation values is estimated after cer-

Scale-IT-up 2022 - Workshop on Scaling-Up Health-IT

826

tain intermediate values, d

s in the code, have been

decrypted (step 11–13). This means that the SPU has

to send the d

values back to the MU, and it will MU

that ﬁnalizes the calculation.

This simpliﬁcation is motivated because imple-

menting homorphically the test ‘> 0’ (lines 16–18)

is not straightforward and it would introduce a com-

putational burden that seems unnecessary. The ge-

nomic data to protect are the coverage ﬁles, while the

encrypted values d

, once sent back to the MU, who

decrypts them, do not disclose, to MU, more informa-

tion then the values CNV

, which MU gets to know

eventually.

The current implementation runs efﬁciently be-

cause we implemented HE encryption and decryption

using natif3 operations for vectors. The comparison

for the list of whole exome genes is calculated using

4 vector encryption-decryption pairs and the required

intersections conveniently as described in Algorithm

1. In this way, we could label all the gene coverages to

a CNV value using the threshold parameters. The ac-

tual values of the parameters can be adjusted accord-

ing to the coverage settings, tumor/normal sample ra-

tio, including the normalization step for the samples.

5 EXPERIMENTAL SETTING,

DATA SETS, AND LIBRARIES

To test the feasibility of this CNV query using HE we

have set up the following experiment setting. We con-

sidered a publicly available Melanoma tumor sample

data and compared it with a healthy control individ-

ual. We have calculated the mean read count (GMRC)

per gene as follows:

GMRC =

where RC is the number of reads aligned in the gene,

L is the size of the gene in base pairs. We use

GMRC values to make a comparison for case and

control cases. First, we compare GMRC values for

a single gene such as TP53 or PTEN. Later we have

used the same comparison query for a list consist-

ing of 100 genes, representing a gene panel. Then

we have carried out analysis over the chromosome

level. We have used the whole list of 1228 genes in

Chromosome 9. This chromosome is chosen since

it contains CDKN2A gene which is highly damaged

in Melanoma cancer (Pfarr et al., 2016). Finally,

we have conducted this experiment on the whole set

of Refseq curated list of genes, consisting of 23.882

genes out of 31.848 locations where both the samples

have coverage greater than 5 (Supplementary Files:

geneslist.txt, allgeneshealthy.csv, allgenespatient.csv,

genes_Ch9_healthy.csv genes_Ch9_patient.csv ). We

have measured the performance of the encryption and

decryption processes for these queries. We have com-

pared our CNV results for Chromosome 9 with the

original study (Magi et al., 2013) to analyze the accu-

racy of the secure CNV detection algorithm.

The data we have used in this paper has been

taken from the samples that has been used in the

Excavator CNV detection tool (Magi et al., 2013).

The data consists of a tumor whole exome sequence

from a Melanoma patient (Melanoma

) and a con-

trol healthy individual (Sample

). We have uploaded

the .bam ﬁles of the samples with accession num-

ber ERR174231 and ERR174237 which were aligned

according to Genome Reference Consortium Human

Build 37 (GRCh37, hg19) from the Sequence Read

Archive (SRA) database (Leinonen et al., 2010) to

the Galaxy web platform. We have used the pub-

lic server usegalaxy.org (Afgan et al., 2018) to calcu-

late the coverage values with .bed tools. Then using

these base read coverage values, we calculate the read

counts per gene (GMRC) as described above, which

provide the input of Algorithm 1.

The HE operations throughout this work are ex-

ecuted with the help of Pyfhel: PYthon For HE Li-

braries

which uses the SEAL (Chen et al., 2017) li-

brary as a backend. Pyfhel provides vector and frac-

tion encryption/decryption capabilities which were

especially helpful while performing operations on the

list of genes. We note that the available implemen-

tations of HE only allow simple operations such as

addition, subtraction, and multiplications.

6 RESULTS

Using Algorithm 1, we have compared the coverage

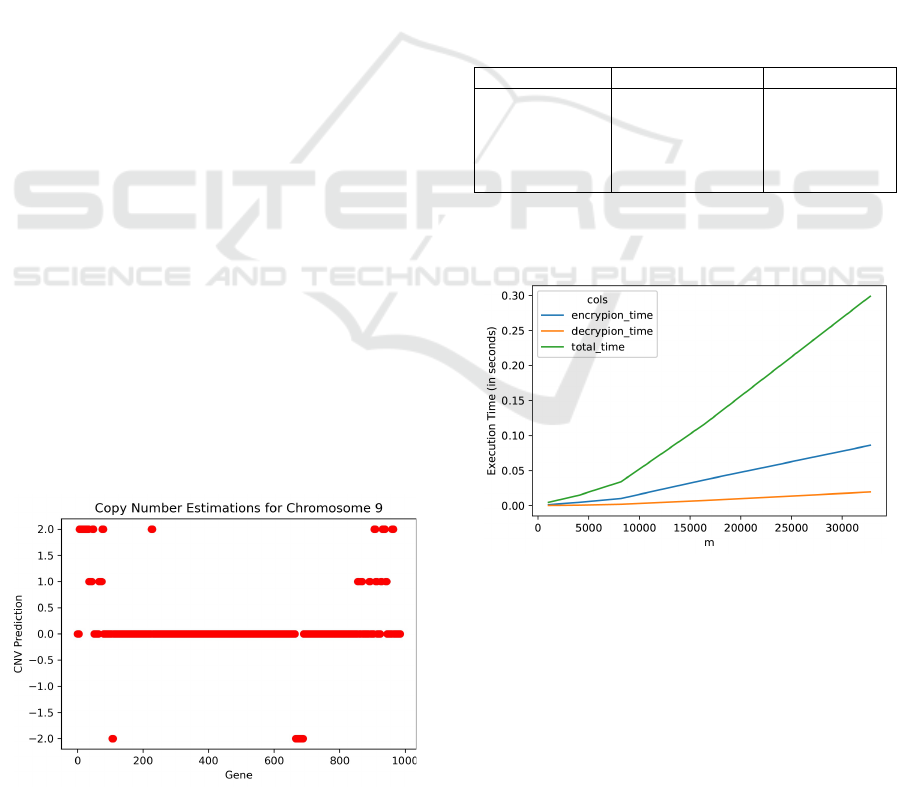
values gathered from two .bam ﬁles. Figure 2 depicts

the copy number variant estimations for Chromosome

9 obtained by comparing the Melanoma tumor ﬁle

with the healthy sample ﬁle which indicates double

copy gains at the beginning and end of Chromosome

9, and two double deletion regions. We also detect

one copy gains at certain points. We check these re-

sults against the CNV values reported in the original

study (Magi et al., 2013). Among these variants, 29 of

the 30 double deletion genes are the same with (Magi

et al., 2013). Our algorithm has predicted the CNV

region a little larger so that we have the MTAP gene

in the boundary. In particular we are able to detect the

double loss of CNV in the gene CDKN2A which is as-

https://github.com/ibarrond/Pyfhel

Privacy-preserving Copy Number Variation Analysis with Homomorphic Encryption

827

sociated with Melanoma cancer. For double copy gain

genes, 22 of the 65 do not appear in the Excavator list.

This comes from the fact that Excavator algorithm did

not report the variations at the end of Chromosome

9. Both works predicted no one copy losses wher-

ever our algorithm detected 50 one copy gains where

19 of them were reported as double gain in Excava-

tor list. Excavator did not identify any one copy gains

or losses. Table 2 presents the ratio of genes that are

consistent with the results of the (Magi et al., 2013)

tool.

The whole list of genes and their estimated CNVs

for Chromosome 9 are presented in the Supplemen-

tary File (Chromosome9_Estimated_CNV.csv). It is

an expected phenomena that two CNV detection al-

gorithms may slightly differ since they have different

sensitivity to parameters such as depth of the sequenc-

ing and they use different statistical models (Zhang

et al., 2019). Nevertheless, the comparison results

demonstrate the usability of a HE based CNV predic-

tion. We emphasize that our aim is not to improve the

performance of CNV detection but to demonstrate the

feasibility of a secure version of CNV analysis using

existing HE framework.

Computational Performances. The time perfor-

mance of the HE experiment is provided in Table 3.

These experiments are carried out with a laptop with

i-7 1.8- 2.3 GHz. CPU and 16 GB RAM with 64

bit Windows Enterprise operating system. We used

Python version 3.7.4 on the Spyder Environment. We

note that time performance depends on the HE pa-

rameters. For a single gene value the calculations can

be executed using Pyfhels’s homomorphic operations

for fraction. For larger gene lists, vector operations

can be used. To have a decryption without noise, the

vector parameter deﬁned by m must be larger than

our query list. Figure 3 represents the performance

of the encryption, decryption and total time processes

Figure 2: Copy Number Estimations for Chromosome 9.

which are collected while encrypting a list of 1000

genes with respect to the HE parameter m. The graph

demonstrates a linear increase for encryption and de-

cryption times according to the parameter m. For a

ﬁxed vector size m, the execution times do not change

with the length of the gene list since actually the al-

gorithm implements encryption and decryption oper-

ations along the vector size. In the worst case where

we choose the vector size m = 32.768 to ensure the

inclusion of the whole exome gene list in the encryp-

tion array, the results are still in the order of decisec-

onds. In Table 3 only the time performance of the

HE operations are demonstrated. The preprocess re-

quired to obtain the read count tables have not been

considered since, this is a standard step in any CNV

analysis without an encryption. Our aim is to measure

the workload of the computations executed in the en-

crypted domain.

Table 2: Comparison of CNVs for Chromosome 9 with

(Magi et al., 2013).

CNV Detected Number of genes Overlap ratio

∗

2 65 0.66

1 50 0.38

∗∗

0 841 0.90

-1 0 1

-2 30 0.96

∗

The ratio of genes that exist in (Magi et al., 2013)

∗∗

19 of the 50 Double Gain genes are found in the in One Copy

list of (Magi et al., 2013).

Figure 3: Time performance according to the encryption

parameter m.

7 DISCUSSION

What we have exposed so far shows that is feasible to

code a CNV analysis algorithm using HE, that repre-

sents a privacy-preserving version of CNV detection.

This task is greatly simpliﬁed thanks to software li-

braries that offer reliable and optimized implemen-

tations of HE operations such as vector encryption

Scale-IT-up 2022 - Workshop on Scaling-Up Health-IT

828

Table 3: Time performance of the HE experiments. The Execution Time includes the Encryption + Decryption Time

Analysis Region Number of

Locations

HE parameters Execution

Time (Sec.)

Single Gene 1 p = 65.537, m = 1.024 0.0005

Gene Panel 100 p = 65.537, m = 1.024 0.0035

Chromosome 9 1.289 p = 65.537, m = 2.048 0.0088

Whole Exome 23.882 p = 65.537, m = 32.768 0.3448

Whole Genome

∗∗

320.00 p = 65.537, m = 32.768 4.7972

∗∗

Estimated Time from whole exome study

and decryption, and that they already solve otherwise

time-consuming and tricky technical issues e.g., boot-

strapping strategies to control noise in the scheme.

Our experiments show that the execution is efﬁ-

cient, that is within seconds. We estimate that it re-

mains efﬁcient when extended to processing a whole

genome.

We also demonstrated that this privacy-preserving

version of the algorithm performs a meaningful anal-

ysis of copy number variants. This has been demon-

strated initially by comparing two coverage ﬁles for

certain genomic positions or a gene panel, and then

extending the approach to process the whole exome

level. We speculate that it can be further extended

to a whole genome analysis, if we apply a cover-

age comparison strategy. For instance, 10% of the

whole genome can be covered with a window size of

1000 bases, which will result around 320.000 cov-

erage regions to compare which is of order 10-15

times larger magnitude compared to the whole ex-

ome study. Since copy number variation values do

not change frequently through the genome, we may

identify the values with good precision by sampling

10% of the genome. If this speculation is correct, the

whole genome CNV analysis can still be conducted in

seconds.

In our use case, we have taken a healthy exome

sequence as control to simulate somatic CNV detec-

tion. For a standard CNV analysis, the number of

samples can be increased to improve statistical signif-

icance. In this case, the execution time will increase

linearly with the number of samples. Notably, this

step is completely parallelizable where we can use

the computational power of the public cloud environ-

ment. Since the encryption-decryption processes are

fast, the total time performance still remains feasible

for real time applications.

An alternative strategy to direct comparison of

genomes is calculating the mean of the copy num-

ber variation values over the control samples as a base

line and use this base line as a reference for CNV de-

tection. The required averaging computation can be

done in the encrypted domain and needs to be exe-

cuted only once in the ofﬂine mode. Then comparing

each genome coverage with this average control base-

line will have the similar performance with this work.

The results demonstrate that the existing libraries

of HE enable real time analysis for small ﬁles like

coverage or .vcf ﬁles. However, a complete genomic

analysis pipeline requires to perform operations on

raw ﬁle types such as .sam, .bam or .fastq. At

the moment performing tasks like genome alignment

on encrypted data is not feasible since there are yet

no efﬁcient algorithms for operations like compari-

son of two strings in the encrypted domain. More-

over, whenever there are conditional statements, the

HE implementation slows down substantially and the

data size expands as a result of re-linearization pro-

cess in encryption. Therefore, it is crucial to deﬁne an

algorithm with the most basic operations.

Security Assumptions and Parameters. In the

proposed protocol we have deployed a Trusted Party

for the generation of encryption and decryption keys.

TP as a certiﬁed and controlled institute, could access

genomic data but has not storage and processing ca-

pabilities. These tasks are executed at the storage and

processing unit, SPU. The SPU is not reliable. A pas-

sive malicious adversary who has somehow access to

the SPU (the admin of SPU, for instance), can not ob-

tain sensitive data since the security of the HE is guar-

anteed by the Public Key encryption system. The im-

plemented HE algorithm in Pyfhel library is the BGV

somewhat homomorphic encryption scheme without

any bootstrapping

. This method also depends on

the Learning with Errors over Rings (RLWE) prob-

lem and we refer the interested reader to the paper

(Brakerski et al., 2014) for mathematical details of the

algorithm. We have chosen a security level equivalent

to 128-bit symmetric (AES) encryption according to

the suggestions in (Albrecht et al., 2018). The pa-

rameter p is the integer modulus and m is the vector

size where the Ring operations are deﬁned. The pri-

vate and public keys of the Homomorphic Encryption

system are generated according to the speciﬁcations

of the scheme, where public key is a secret Ring el-

Personal communication with the developers.

Privacy-preserving Copy Number Variation Analysis with Homomorphic Encryption

829

ement and private key is a pair of two Ring elements

which satisfy certain criteria, respectively.

We note that the requirement of a Trusted Party is

inevitable for this kind of study, since for the deriva-

tion of the genome sequence at least, there needs to be

a certiﬁed trusted authority. We note that previous re-

lated work also followed this assumption (see (Wang

et al., 2016; Ayday et al., 2013)).

Limitations. We limited our HE to simple arith-

metic operations in our redesigned CNV algorithm,

leaving to the MU (i.e., the doctor) the task to run in-

equality tests on the plain data. We argued that this

choice does not affect security, but it would be inter-

esting to measure the performance of a full HE ver-

sion of CNV. We leave it for future work.

An obvious limitation of this work is the number

of cases analyzed. As we intended to prove that a

copy number variation analysis using HE is feasible,

we chose as example the analysis of a single exome.

We plan to extend this work to several exoms and

whole genome samples to have a better evaluation of

accuracy and ﬁne tuning of the threshold parameters

in future work.

Another issue is the normalization of sequenc-

ing data coming from various runs and technologies.

Comparison of data obtained from different sequenc-

ing technologies or parameters is a challenging pro-

cess. Tumor-normal sampling ratio is also of critical

importance while working with tumor data. A care-

ful normalization is required before data analysis for

accurate CNV results.

8 CONCLUSIONS

In this work we have presented a proof-of-concept

study for the estimation of copy number variation val-

ues by implementing a secure coverage comparison

using Homomorphic Encryption (HE).

We are able to calculate the copy number values

for a predeﬁned list of genes privately without reveal-

ing personal genomic information. We have worked

on a somatic diagnosis use case with a Melanoma

whole exome data and compared the copy number

variation results with the original study (Magi et al.,

2013). Our results demonstrate the practicality and

accuracy of a privacy-preserving copy number varia-

tion (CNV) analysis at the whole exome and whole

genome levels.

As CNV analysis takes a broader deployment in

genomic pipelines, making it possible to perform in

a privacy preserving manner in compliance with data

protection regulations is becoming important. This

study is the ﬁrst work focusing on this important class

of variants which have been neglected up to now.

As a future work, we plan to apply the proposed

CNV method to a set of whole genome sequences.

This will satisfy a better evaluation for the validity of

the sampling strategy and its precision on large whole

genome cohorts and more accurate determination of

the algorithm parameters.

Another upcoming line of research is the use of

HE for privacy-preserving .vcf queries to execute

applications such as private rare mutation discovery,

variant prioritization for causes of disease, and dis-

ease predisposition calculation. Although there exist

individual examples, there is still work to do for de-

veloping more efﬁcient and uniﬁed approaches. Re-

cent HE libraries enable various types of genomic ap-

plications which can now be executed in real time hin-

dering mathematical and implementation difﬁculties

and opening the door for the age of privacy-preserving

personalized medicine.

ACKNOWLEDGEMENTS

This work has been supported by the EU 956562,

MSCA-ITN-2020 - Innovative Training Networks,

“Legality Attentive Data Scientists” (LeADS). The

authors wish to thank Dr. Patrick May for valuable

discussions on the topic of copy number variation.

REFERENCES

Acar, A., Aksu, H., Uluagac, A. S., and Conti, M. (2018).

A survey on homomorphic encryption schemes: The-

ory and implementation. ACM Computing Surveys

(CSUR), 51(4):1–35.

Afgan, E., Baker, D., Batut, B., Van Den Beek, M., Bou-

vier, D.,

Cech, M., Chilton, J., Clements, D., Coraor,

N., Grüning, B. A., et al. (2018). The Galaxy platform

for accessible, reproducible and collaborative biomed-

ical analyses: 2018 update. Nucleic acids research,

46(W1):W537–W544.

Akgün, M., Ünal, A. B., Ergüner, B., Pfeifer, N., and

Kohlbacher, O. (2020). Identifying disease-causing

mutations with privacy protection. Bioinformatics.

Albrecht, M., Chase, M., Chen, H., Ding, J., Goldwasser,

S., Gorbunov, S., Halevi, S., Hoffstein, J., Laine,

K., Lauter, K., Lokam, S., Micciancio, D., Moody,

D., Morrison, T., Sahai, A., and Vaikuntanathan, V.

(2018). Homomorphic Encryption Security Stan-

dard. Technical report, HomomorphicEncryption.org,

Toronto, Canada.

Ayday, E., Raisaro, J. L., McLaren, P. J., Fellay, J., and

Hubaux, J.-P. (2013). Privacy-preserving computation

Scale-IT-up 2022 - Workshop on Scaling-Up Health-IT

830

of disease risk by using genomic, clinical, and envi-

ronmental data. In 2013 USENIX Workshop on Health

Information Technologies (HealthTech 13).

Bragin, E., Chatzimichali, E. A., Wright, C. F., Hurles,

M. E., Firth, H. V., Bevan, A. P., and Swaminathan,

G. J. (2014). DECIPHER: database for the interpre-

tation of phenotype-linked plausibly pathogenic se-

quence and copy-number variation. Nucleic acids re-

search, 42(D1):D993–D1000.

Brakerski, Z., Gentry, C., and Vaikuntanathan, V. (2014).

(leveled) fully homomorphic encryption without boot-

strapping. ACM Transactions on Computation Theory

(TOCT), 6(3):1–36.

Chen, H., Laine, K., and Player, R. (2017). Simple en-

crypted arithmetic library-SEAL v2. 1. In Inter-

national Conference on Financial Cryptography and

Data Security, pages 3–18. Springer.

Decouchant, J., Fernandes, M., Völp, M., Couto, F. M.,

and Esteves-Veríssimo, P. (2018). Accurate ﬁltering

of privacy-sensitive information in raw genomic data.

Journal of Biomedical Informatics, 82:1–12.

Gentry, C. (2009). Fully homomorphic encryption using

ideal lattices. In Proceedings of the forty-ﬁrst annual

ACM symposium on Theory of computing, pages 169–

178.

Gymrek, M., McGuire, A. L., Golan, D., Halperin, E., and

Erlich, Y. (2013). Identifying Personal Genomes by

Surname Inference. Science, 339(6117):321–324.

Jagadeesh, K. A., Wu, D. J., Birgmeier, J. A., Boneh, D.,

and Bejerano, G. (2017). Deriving genomic diag-

noses without revealing patient genomes. Science,

357(6352):692–695.

Joober, R. and Boksa, P. (2009). A new wave in the genet-

ics of psychiatric disorders: the copy number variant

tsunami. Journal of psychiatry & neuroscience: JPN,

34(1):55.

Kakimi, K., Karasaki, T., Matsushita, H., and Sugie, T.

(2017). Advances in personalized cancer immunother-

apy. Breast cancer (Tokyo, Japan), 24(1):16—24.

Leinonen, R., Sugawara, H., Shumway, M., and Collabora-

tion, I. N. S. D. (2010). The sequence read archive.

Nucleic acids research, 39(suppl_1):D19–D21.

Li, Y. R., Glessner, J. T., Coe, B. P., Li, J., Mohebnasab,

M., Chang, X., Connolly, J., Kao, C., Wei, Z., Brad-

ﬁeld, J., et al. (2020). Rare copy number variants in

over 100,000 European ancestry subjects reveal mul-

tiple disease associations. Nature communications,

11(1):1–9.

MacDonald, J. R., Ziman, R., Yuen, R. K., Feuk, L.,

and Scherer, S. W. (2014). The database of ge-

nomic variants: a curated collection of structural vari-

ation in the human genome. Nucleic acids research,

42(D1):D986–D992.

Magi, A., Tattini, L., Cifola, I., D’Aurizio, R., Benelli,

M., Mangano, E., Battaglia, C., Bonora, E., Kurg, A.,

Seri, M., et al. (2013). EXCAVATOR: detecting copy

number variants from whole-exome sequencing data.

Genome biology, 14(10):R120.

Marshall, C. R., Howrigan, D. P., Merico, D., Thiruvahin-

drapuram, B., Wu, W., Greer, D. S., Antaki, D.,

Shetty, A., Holmans, P. A., Pinto, D., et al. (2017).

Contribution of copy number variants to schizophre-

nia from a genome-wide study of 41,321 subjects. Na-

ture genetics, 49(1):27–35.

Moreno-Cabrera, J. M., Del Valle, J., Castellanos, E., Feli-

ubadaló, L., Pineda, M., Brunet, J., Serra, E., Capellà,

G., Lázaro, C., and Gel, B. (2020). Evaluation of CNV

detection tools for NGS panel data in genetic diagnos-

tics. European Journal of Human Genetics, pages 1–

11.

Naveed, M., Ayday, E., Clayton, E. W., Fellay, J., Gunter,

C. A., Hubaux, J.-P., Malin, B. A., and Wang, X.

(2015). Privacy in the Genomic Era. ACM Comput.

Surv., 48(1).

Pfarr, N., Penzel, R., Klauschen, F., Heim, D., Brandt,

R., Kazdal, D., Jesinghaus, M., Herpel, E., Schir-

macher, P., Warth, A., et al. (2016). Copy number

changes of clinically actionable genes in melanoma,

non-small cell lung cancer and colorectal cancer—A

survey across 822 routine diagnostic cases. Genes,

Chromosomes and Cancer, 55(11):821–833.

Regev, O. (2009). On lattices, learning with errors, random

linear codes, and cryptography. Journal of the ACM

(JACM), 56(6):1–40.

Shao, X., Lv, N., Liao, J., Long, J., Xue, R., Ai, N., Xu,

D., and Fan, X. (2019). Copy number variation is

highly correlated with differential gene expression: a

pan-cancer study. BMC medical genetics, 20(1):175.

Shlien, A. and Malkin, D. (2009). Copy number variations

and cancer. Genome medicine, 1(6):1–9.

Simmons, S., Sahinalp, C., and Berger, B. B. (2016). En-

abling Privacy-Preserving GWASs in Heterogeneous

Human Populations. Cell Systems, 3(1):54 – 61.

Wang, S., Zhang, Y., Dai, W., Lauter, K., Kim, M., Tang,

Y., Xiong, H., and Jiang, X. (2016). HEALER: homo-

morphic computation of ExAct Logistic rEgRession

for secure rare disease variants analysis in GWAS.

Bioinformatics, 32(2):211–218.

Yoon, S., Xuan, Z., Makarov, V., Ye, K., and Sebat, J.

(2009). Sensitive and accurate detection of copy num-

ber variants using read depth of coverage. Genome

research, 19(9):1586–1592.

Zarrei, M., MacDonald, J. R., Merico, D., and Scherer,

S. W. (2015). A copy number variation map of the

human genome. Nature reviews genetics, 16(3):172–

183.

Zhang, F., Gu, W., Hurles, M. E., and Lupski, J. R. (2009).

Copy number variation in human health, disease, and

evolution. Annual review of genomics and human ge-

netics, 10:451–481.

Zhang, L., Bai, W., Yuan, N., and Du, Z. (2019). Com-

prehensively benchmarking applications for detecting

copy number variation. PLoS computational biology,

15(5):e1007069.

Privacy-preserving Copy Number Variation Analysis with Homomorphic Encryption

831