Algorithms for Freight Train Scheduling

Lucas Morais

, Rodrigo Gonc¸alves

, Alexandre Tazoniero

and Fernando Gomide

1 a

School of Electrical and Computer Engineering, University of Campinas, Campinas, S

ao Paulo, Brazil

Nitryx Progress Rail, Research and Development, Campinas, S

ao Paulo, Brazil

Keywords:

Train Scheduling, Genetic Algorithms, Scheduling Generation Algorithms.

Abstract:

This paper develops train scheduling algorithms for freight railroads using scheduling generation and genetic

algorithms. First scheduling generation procedures developed in the realm of job shop manufacturing are

tailored for freight railroad applications. The scheduling generation procedures are used to create feasible

populations to start genetic algorithms. Next, it suggests a novel representation and encoding mechanism

based on random keys and job permutation encoding inspired in ﬂexible job shop scheduling. In freight

railroads a common goal is to minimize overall maximum transit time, analogous to minimize the makespan

in manufacturing systems. The genetic algorithms whose initial population are produced by the scheduling

generation algorithms are compared with the random key-job permutation algorithm developed herein. An

example rail line is used to evaluate the performance of the algorithms. The exact optimal solution for the

example rail line, found using the OR Tools solver, is used as a baseline. The results suggest that all approaches

may produce optimal solutions, but the random key-job permutation algorithm consistently performs best

amongst the remaining ones.

1 INTRODUCTION

Freight rail transportation systems are one of the pre-

ferred solutions to move raw materials, commodities

and goods between warehouses, production and dis-

tribution centers, port and airport terminals. To re-

main competitive in a market with increased pressure

for efﬁciency, sustainability and reliability, continu-

ous improvement is required to keep the railroads at-

tractive. Today railroads are looking for new tech-

nologies and restructuring their operation and man-

agement practice to better ﬁt market demand and for

better transportation services. Advanced train control

and planning systems and their associated technolo-

gies and algorithms have substantially improved the

railroad industry productivity during the last decades

(Harker, 1995). Undoubtedly, movement planning of

trains in a rail network is a challenge, and the sched-

ules a movement plan produces have a major impact

in the operational economics and performance of the

network.

Many railroad networks are made of single tracks

segments with sidings at intervals along the line. The

sidings allow trains running in opposing directions to

meet and pass, or trains running in the same direction

https://orcid.org/0000-0001-5716-4282

to overtake each other. Sidings are short stretches of

double track, usually long enough to hold one train.

The task of train scheduling is to develop a safe, con-

ﬂict free feasible meet-pass plan, a movement plan

in which trains cross or overtake each other at sidings

only. Traditionally, movement planning and train con-

trol are done by experienced dispatchers who, in addi-

tion to safety, must avoid line blocking situations, and

attempt to minimize train delays and operating costs.

Train scheduling is a very large, complex, com-

binatorial problem consisting of tens of thousands of

variables. One way to tackle the complexity of the

problem is to select an appropriate tool to help the

dispatchers in the decision-making process. Decision

support systems with automated techniques to gen-

erate and optimize train schedules is a tool that has

been shown to be effective in practice. Many differ-

ent approaches can be used to generate train sched-

ules: artiﬁcial intelligence, combinatorial optimiza-

tion, simulation, and their combinations, as it will be

discussed in the next section. The approach taken

in this paper is based on genetic algorithms because,

when endowed with an appropriate representation and

encoding mechanism, they can effectively explore the

search space and ﬁnd schedules with satisfactory per-

formance. As is well recognized in evolutionary com-

Morais, L., Gonçalves, R., Tazoniero, A. and Gomide, F.

Algorithms for Freight Train Scheduling.

DOI: 10.5220/0011379500003332

In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 74-81

ISBN: 978-989-758-611-8; ISSN: 2184-3236

putation area, representation and encoding is of ulti-

mate importance in evolutionary computation due to

the impact they have in producing feasible schedules

using genetic operations efﬁciently.

The aim of this paper is to address freight train

scheduling from the point of view of scheduling gen-

eration algorithms, combination of scheduling gener-

ation algorithms with genetic algorithms, and a novel

approach based on random keys and job permutation

encoding. Much of the conceptual inspiration of the

approaches addressed here comes from job shop and

ﬂexible job shop scheduling theory. It is known that,

if trains are viewed as jobs, and tracks as machines,

then train scheduling can be modeled as a job shop

problem (Liu and Kozan, 2009). However, to the

best of the authors knowledge, train scheduling has

not yet been approached from the point of view ad-

dressed in this paper. In particular, the representation

and encoding scheme suggested herein is novel and

beneﬁts from the effectiveness of random keys to en-

code sequences, and from the representation power

of permutation schedules. These are important is-

sues because the genetic operators will always pro-

duce feasible individuals during generations, which

precludes the need of repairing or similar feasibil-

ity checking techniques, what considerably increases

computational efﬁciency. The paper also solves a

simple example to show how the solutions produced

by the scheduling algorithms addressed in the paper

compare with the optimal value found by OR-Tools,

a state of the art, industry standard solver.

After this introduction, the paper proceeds as fol-

lows. Next section gives a brief overview of the main

approaches developed for train scheduling. Section 3

details the scheduling generation and the genetic al-

gorithms for train scheduling addressed in this work.

Section 4 reports the results for the example rail line,

and Section 5 concludes the paper summarizing its

contributions and work to be developed in the future.

2 TRAIN SCHEDULING REVIEW

The complexity of rail operations, the current traf-

ﬁc increase trend, and obstacles to expand railroad

infrastructure turn train scheduling and management

strategies into a key mechanism to improve railroad

operation and services. There is an extensive lit-

erature on train scheduling. This section focuses

mainly on optimization models, genetic algorithms,

and heuristic methods to develop optimized train

schedules. Further information can be found in e.g.

(Harrod, 2012) and the references therein.

The ﬁrst explicit mathematical programming ap-

proach to train scheduling was formulated as a lin-

ear integer optimization model (Szpigel, 1973). The

formulation and the solution algorithm was inspired

in the job-shop problem. In this formulation, branch-

ing is done dynamically by adding constraints accord-

ingly to the value of the branching decision variable.

This scheme speeds up the solution of the candidate

problems of each node in the search tree. This for-

mulation eliminates the direct manipulation of binary

variables, but at the cost of unrealistic assumptions

such as unlimited siding capacity.

In a similar vein, optimal pacing of trains in

freight railroads has been studied in (Kraay et al.,

1991) using a nonlinear mixed optimization model

that outputs meet-pass plans and the speed of trains in

each track segment to simultaneously minimize tran-

sit time and fuel consumption. A modiﬁed branch and

bound algorithm has been devised in (Higgins et al.,

1996), adopting a modeling scheme similar to (Kraay

et al., 1991). The goal is to minimize train delays

at the destination station, considering trains priorities,

and operating costs.

Using genetic algorithms, taboo search, and their

combinations, (Higgins et al., 1997) also solves the

single line train scheduling aiming at minimizing de-

lays. A more sophisticated genetic algorithm ap-

proach was developed in (Tornos et al., 2008) to

minimize the average delay of trains at their des-

tinations. The authors use a sequence of pairs

(train, single track) to represent the order in which

the trains travel through the tracks, track allocation to

trains always occurring at the earliest time allowed.

The authors also uses a regret-based biased random

sampling technique to generate a population of feasi-

ble initial schedules.

Heuristic techniques for single line train schedul-

ing was addressed in (Sahin, 1999) using a proce-

dure that attempts to reduce the difference between

the schedule produced and the one expected by a train

dispatcher. A fuzzy set-based approach was devised

in (Vieira et al., 1999) as well as in (Tazoniero et al.,

2007) where it is compared with a heuristic search al-

gorithm. A genetic algorithm is also adopted in (Gar-

risi and Cristina, 2020) with a heuristic procedure to

generate initial populations. The purpose is to min-

imize train delays with penalties for routes of lower

priority.

Multi-objective schemes include (Ghoseiri et al.,

2004) under the ε-constraint formulation to generate

non-inferior solutions considering fuel consumption

and the transit time of trains. Alternatively, (Sun et al.,

2014) produces optimal train schedules also using a

multi-objective genetic algorithm, but considering the

Algorithms for Freight Train Scheduling

average transit time of each train, the total transit time

of trains, and energy consumption as goals.

Recently, advances in decision support, manage-

ment and communication systems, as well as data

technologies opened a range of novel possibilities,

such as data-driven movement planning and opera-

tions management (Wen, 2019). Train operation data

from control and monitoring rooms are an invaluable

resource to examine and assess actual operations to

improve railroad network performance based on data-

driven decisions.

3 SCHEDULING ALGORITHMS

Roughly speaking, train schedules are timetables that

identify the arrival and departure time of each train at

each rail station or track segment in the train route.

This section introduces a class of algorithms for train

scheduling. It starts by deﬁning the train schedule

problem of interest. Next it details the scheduling

generation algorithm and its use in the genetic algo-

rithms addressed in the paper.

3.1 Train Scheduling

A typical train scheduling problem consists of ﬁnding

a set of arrival and departure times for each train at

each track segment of their routes in a rail line, taking

into account possible conﬂicts between trains over the

track segments. Routes are speciﬁed by a set of con-

tiguous track segments connecting trains’ origins to

their destinations. In addition to the arrival and de-

parture times for each train at each track segment, a

solution of a train scheduling problem must satisfy all

the temporal ordering constraints, and avoid track oc-

cupation conﬂicts. Solutions are evaluated according

to an objective function. This paper assumes that the

objective function is to minimize the maximum tran-

sit time of the schedule, which is called the makespan

in job shop literature.

The ﬁrst step to develop train schedules is to char-

acterize the feasible solutions, the ones that make

physical sense. In railroads, feasibility means con-

tinuity of movement of each train from one track to

the immediate next track in its route, which induce

temporal ordering constraints. Each track segment in

turn has a capacity, which is one train only for sin-

gle track segments, and a prescribed number of tracks

for sidings. Trains meet-pass, that is, crossing and

overtaking must occur at the sidings only. This pa-

per assumes that the sidings have enough capacity to

accommodate as many trains as needed.

A schedule in which trains move along the tracks

as soon as they are available, that is, in which there

are no unnecessary waits, is called semiactive. The

set of semiactive schedules is equivalent to the set of

all schedules with no superﬂuous idle time. This set

dominates the set of all schedules, which means that

it is sufﬁcient to consider only semiactive schedules

to optimize any time measure of performance. This

is important because the number of semiactive sched-

ules is ﬁnite, although it may well be quite large. The

exact number is usually difﬁcult to determine. For a

n trains scheduling problem, in which each train tra-

verses exactly once each of the m tracks, each track

must process n trains. The number of possible se-

quences is therefore n! for each track. If the sequences

on each track were entirely independent, there would

be (n!)

semiactive schedules (French, 1982). How-

ever, the precedence structure of the route of each

train, as well as the track occupancy constraints usu-

ally render some of the potential combinations infea-

sible which means that the number of feasible sched-

ules is bounded by (n!)

Moreover, the transit time of a train can usually be

reduced by changing the order of one of the trains in

a sequence that orders train movements in the tracks.

A schedule in which there are no unnecessary waits,

and it is not possible to reorder a movement of one of

the trains without increasing the total transit time is

called an active schedule. Similarly as in the job shop

problem, active schedules are the smallest dominant

set of the class of train scheduling problem treated in

this paper. It can be shown that an optimal solution

is an element of the set of active solutions (French,

1982).

3.2 Generation of Train Schedules

As pointed out earlier, train scheduling is conceptu-

ally similar to job-shop scheduling. This similarity

suggests the use of the schedule generation algorithm

introduced in (Gifﬂer and Thompson, 1960) as a start-

ing point to produce schedules which simultaneously

are feasible and active (Yamada and Nakano, 1997).

Schedule generation procedures treat trains in an or-

der that is consistent with the precedence relation in-

duced by the train route. In other words, no train is

assigned to a track segment until all its predecessors

have been scheduled. Generation of active schedules

procedures are important because they produce only

schedules that are candidates for an optimal solution.

An instance of a systematic approach to gener-

ate active train schedules, denoted as GT for short,

is summarized by the GT Algorithm below. The GT

algorithm sequentially assigns trains to each track,

considering the transit times (tt) of the trains in each

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

track segment they must pass through in its route to

destination, and solves track occupation conﬂicts us-

ing an appropriate resolution strategy, or randomly.

Random conﬂict resolution generates schedules eas-

ily and quickly.

Algorithm 1: GT Algorithm.

1: for all trains and line track segments do

2: identify the shortest transit time ts

3: if number of trains with (tt ≥ ts) > 1 then

4: select one randomly (or using a rule)

5: end if

6: identify next track the trains will move to

7: if trains compete for track occupation then

8: select one randomly (or using a rule)

9: end if

10: schedule the selected train

11: end for

It worth to note that the generation of feasible and

active solutions for train scheduling may require that

multiple trains occupy a siding simultaneously, a fact

that does not occur in the classic job-shop models.

Notice that steps 4 and 8 of Algorithm GT al-

lows conﬂict resolution randomly, but instead of

purely random decisions, the algorithm opens possi-

bilities for more efﬁcient conﬂict resolution mecha-

nisms aiming at minimizing the total transit time e.g.

using priority rules.

3.3 Genetic Algorithms

This section brieﬂy explains the idea of genetic al-

gorithm for application oriented readers, and charac-

terizes the class of genetic algorithm adopted in the

paper.

A genetic algorithm can be understood as a

population-based optimization procedure inspired in

the evolutionary process (Eiben and Smith, 2015).

Genetic algorithms are iterative procedures that move

a population of candidate solutions towards popula-

tions whose individuals have higher chance to achieve

better ﬁt, that is, toward solutions with better values

of the objective function. The canonical genetic al-

gorithm is summarized in Algorithm GA below. The

idea is to mimic the selective pressure, inspired by the

Darwinian natural selection mechanism, and to apply

operators to select (Selection), crossover (Recombi-

nation), and mutate (Mutation) individuals of the pop-

ulation, expecting to produce better solutions in future

generations than those of the current population.

Solutions are, in general, represented by encod-

ing the original variables of the problem, e.g. using

binary, real, alpha numeric strings, or combinations.

The ﬁtness (objective function) measures the suitabil-

ity of each individual of the population, as a candi-

date solution. Selection is an operation that chooses

the individuals which should be part of the popula-

tion of the next generation (iteration). Often, a ran-

dom choice criteria that favor higher ﬁtness individu-

als are used. Crossover is a recombination operation

that produces off-springs by splitting and merging the

selected individuals. Its purpose is to exchange parts

of the individuals that contribute most to improve the

objective function. Mutation operator produces varia-

tions in the off-springs to promote variability and di-

versity, enhancing the search process in ﬁnding opti-

mal solutions.

This paper uses the binary tournament selection

operator, which consists of random choices of two in-

dividuals, with replacement, from the population, but

selecting only the one with the highest ﬁtness. The

genetic algorithm adopted is elitist, namely, the best

solutions found are kept in the population of the fu-

ture generations.

Algorithm 2: GA Algorithm.

1: P ← GT train schedule . initial population

2: while stop criteria does not hold do

3: S ← Selection(P)

4: R ← Recombination(S)

5: P ← Mutation(R)

6: end while

7: return best individual . optimal solution

3.4 Random Keys to Set Priority Rules

in the GT Algorithm

Random keys is an effective encoding strategy for se-

quencing problems (Bean, 1994). Sequences are en-

coded indirectly as lists of random numbers. The

sequence implied by a list is the one that aligns the

ﬁrst element of the sequence with the lowest random

component, the second element with the next lowest,

and so on. Hence, the position in the sequence de-

pends on the position it occupies in the ordered list

of elements, not on the value of the variable. There-

fore, random keys guarantee feasible off-springs after

crossover and mutation operations. Clearly, a genetic

algorithm with random keys encoding can be used to

evolve conﬂict resolution rules needed in the steps 4

and 8 of the GT algorithm as an attempt to improve

the quality of the schedules generated.

One of the simplest approaches, denoted by GT1,

assigns a ﬁxed priority to each train to resolve track

occupancy conﬂicts: the train with highest priority is

the one assigned to the track. A second, more ﬂexible

approach denoted by GT2, is to set a priority per train

per single track line segment, which means that single

track assignments to trains will be done according to

the train-track priority list when resolving conﬂicts.

Algorithms for Freight Train Scheduling

3.5 Genetic Algorithm with Train

Activity List Encoding

Differently from the approach suggested in the next

section of this paper, the encoding scheme of (Tornos

et al., 2008) uses an activity list to represent a solu-

tion. In other words, a schedule is encoded as a feasi-

ble precedence list of pairs (train, single track

), that

is, if (train, single track

) and (train, single track

)

are the jth and kth gene of a chromosome of the same

individual and x < y, then j < k.

Specialized crossover and mutation operators are

required to keep the precedence constraints feasible

during evolution. Crossover is such that, for each

pair of parents, the two offspring inherit their ﬁrst l

genes from one of the parents, the remaining genes

sequentially inherited from the other parent, skipping

the genes that are the same as those of the ﬁrst parent.

The value of l is chosen randomly. Mutation is done

as follows: for each pair (train, single track

) in the

sequence, a new position is randomly chosen. This

new position must be higher than its predecessor and

lower than its successor.

The initial population in (Tornos et al., 2008) is

created using an iterative heuristics based on a ran-

dom sampling methods repeated as many times as

the population size. Unfortunately, no further details

were reported. However, the activity list encoding and

genetic operations can be used with an initial popula-

tion created as follows: 1) GT algorithm with random

conﬂict resolution, denoted by TRA, 2) GT algorithm

with priority rule by train, denoted by TGT1, and 3)

GT generation algorithm with priority rules by train

and per single track line segment, denoted by TGT2.

3.6 Genetic Algorithm with Random

Keys Encoding of the Train Order

A novel alternative, inspired by the ﬂexible job shop

literature approaches (Driss et al., 2015), uses an en-

coding with random keys in a step prior to the encod-

ing schemes used in ﬂexible job shop. In this new

encoding scheme, each individual consists of blocks

to represent the trains to be scheduled. A train block

is represented by a real-valued vector with as many

components as the number of single track segments

of the rail line. Each value does not specify a speciﬁc

single track for the train as this will be determined

when decoding the individual. This encoding step is

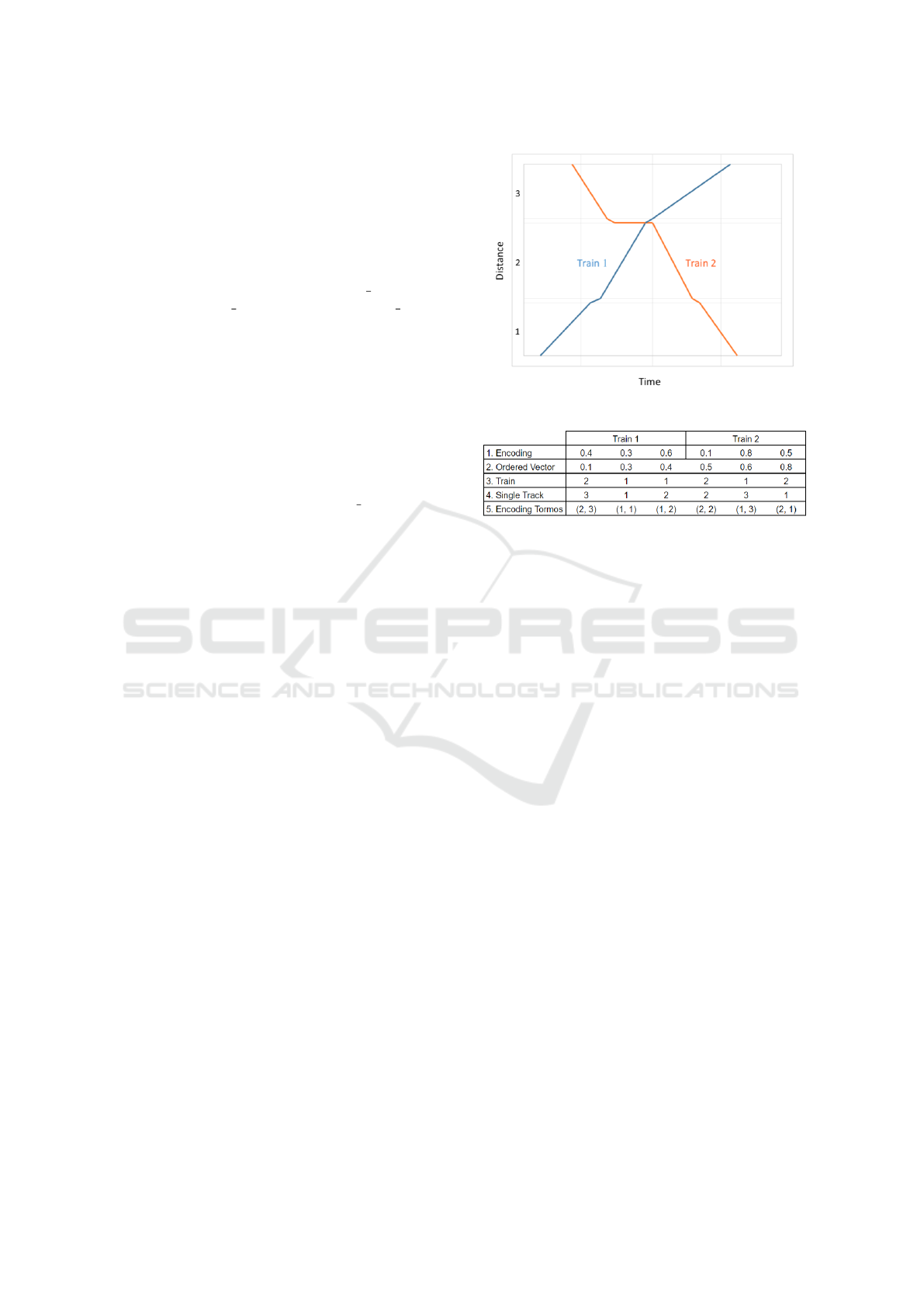
shown as step 1 in Fig. 2. The ﬁgure refers to the ex-

ample depicted in Fig. 1, which consists of two trains

running in opposing directions in a line with three sin-

gle tracks segments numbered 1, 2 and 3, a siding of

capacity 2 between segments 1 and 2 shown as a hor-

Figure 1: Example for the RDK encoding.

Figure 2: Interpretation of RKD encoding.

izontal line, and another siding with capacity 2, the

horizontal line between segments 2 and 3.

Random keys decoding requires the components

of the real vector representation of each individual

to be ordered, in ascending order in this paper, illus-

trated as step 2 in Fig. 2. After ordering, each variable

value corresponds a train, as shown in step 3 of Fig. 2.

Next, each train is assigned to the sequence of single

tracks in the route from its origin to its destination,

shown in step 4. Interestingly, as the step 5 shows,

this new encoding scheme subsumes the one devel-

oped in (Tornos et al., 2008).

Because this novel encoding scheme is based on

random keys, simple crossover and mutation opera-

tors, such as arithmetic crossover and Gaussian muta-

tion can be readily used, with no need of repairing or

any procedure to keep scheduling feasibility. The ge-

netic algorithm with this encoding scheme is denoted

by RKD.

4 RESULTS

The performance of the algorithms were evaluated us-

ing a six trains, seven tracks scheduling problem in-

stance. Brieﬂy, the case study used here considers

a rail line with four single track segments with three

sidings between them, each siding with capacity of

ﬁve tracks. Three trains depart from each end of the

line, with the departure time interval between trains

limited by track availability, like in typical tonnage-

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

based freight rail operation. Single track segments

can be occupied by one train only, which means that

there are no signaling blocks in the single tracks be-

tween sidings. It is worth to recall that the complex-

ity of a n trains and m tracks scheduling problem is

bounded by (n!)

. For n = 6 and m = 4 the cardinal-

ity of the search space is bounded by 10

. Table 1

summarizes the remaining data needed to develop the

schedules.

Evaluations were done running the genetic algo-

rithms 100 times each for 100 generations using a

population of 100 individuals. The TGT1 and TGT2

algorithms started using the GT1 and GT2 schedule

generation and run for a warm-up period of 50 gen-

erations before the remaining 100 generations run for

comparisons. This give them an extra advantage, but

was done purposely to hard check the performance of

RKD.

The parameters, namely the crossover and muta-

tion rates, employed by the algorithms were found ex-

perimentally. The values of the parameters that pro-

duced the best results are given in Table 2.

Evaluation and comparison of the results pro-

duced by the algorithms are done against the

solution of a mixed-integer optimization train

scheduling model formulated similarly as the

job shop problem reported in (Rardin, 2017).

That is, for benchmark purposes, the optimal

solution of the model found by the OR-Tools

solver (https://developers.google.com/optimization/

scheduling/job shop) is used as the baseline. Cur-

rently, the OR-Tools job-shop scheduling solver

is one of the standards adopted by academia and

industry. The objective function value of the optimal

solution found by the solver is 8.93 hours. This is the

minimum value of the maximum overall transit time

achieved.

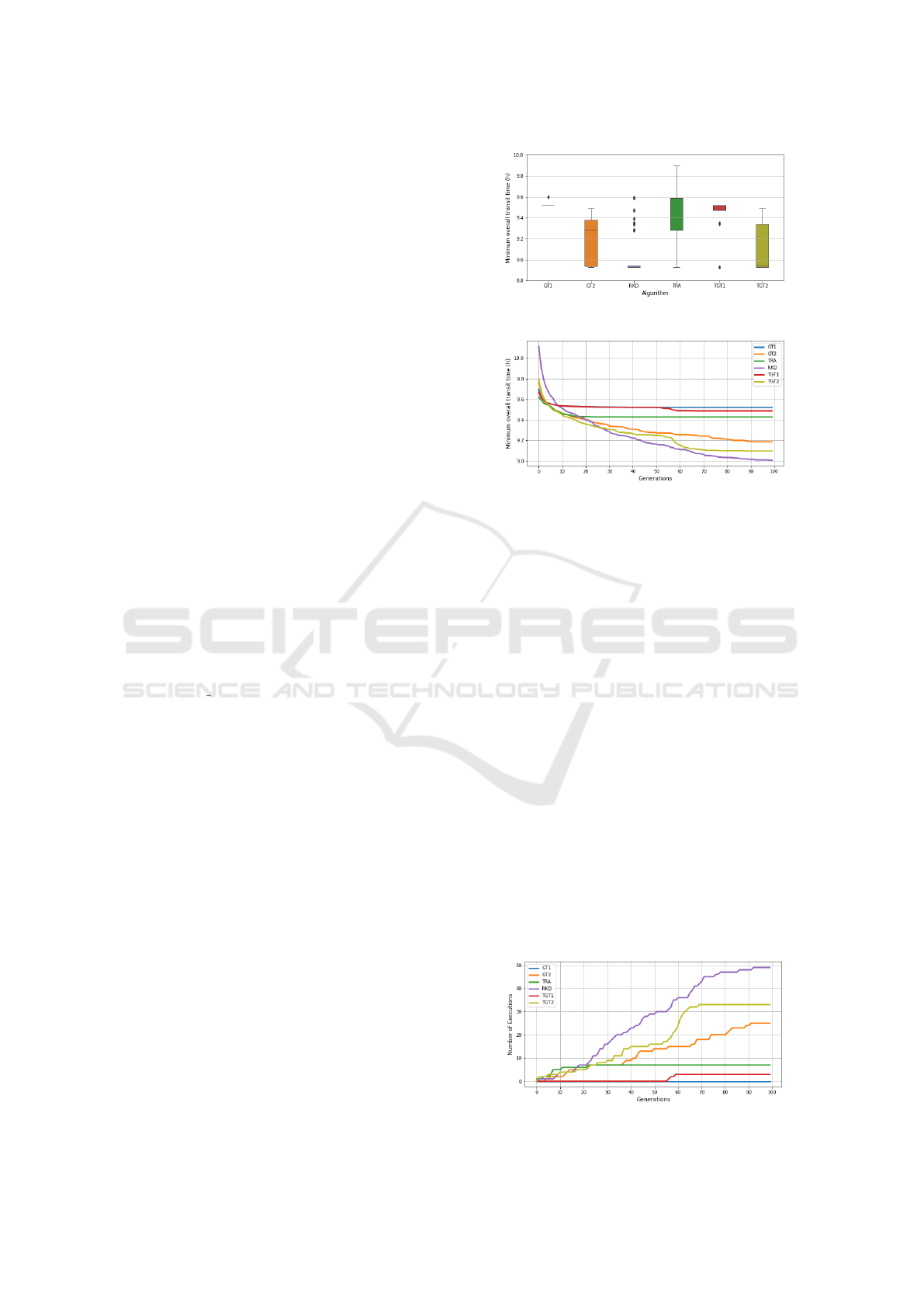
Fig. 3 shows that GT1 was the only approach that

did not produce the optimal solution in any run, while

the RKD and TGT2 consistently did it. Fig. 4 and

Fig. 5 show that, despite the initial unfavorable ini-

tialization, RDK produces superior solutions within

few generations. Fig. 4 also suggests that the solu-

tions produced by GT2 and RKD could be improved

if more generations were allowed, what is not the case

with the remaining algorithms. Fig. 5 further shows

that TGT1 and TGT2 improve the initial populations

of GT1 and GT2, respectively, but only TGT2 per-

forms better than TRA. Fig. 6 shows the train graph

of the optimal schedule.

Table 3 gives the average run time of each algo-

rithm. Notice that, because its efﬁcient encoding ap-

proach, the RKD is the fastest. Also notice that GT1,

GT2, TGT1 and TGT2 algorithms are considerably

Figure 3: Minimum transit time for 100 runs.

Figure 4: Average best solutions.

slower because of the iterative nature of the schedul-

ing generation algorithm GT. The run times ﬁgures

are for runs using the Google Colaboratory Intel(R)

Xeon(R) CPU @ 2.20GHz, with 12GB of RAM.

Summing up, the novel representation and encod-

ing mechanism based on random keys and job per-

mutation encoding developed herein has shown to be

very effective for the class of train scheduling ad-

dressed in this paper. It gives a simple and mean-

ingful way to represent sequences and precedence,

and allows the use of the efﬁcient genetic operators

to speed up the resulting genetic algorithm. The com-

putational experiments also suggest that random keys

and job permutation encoding increases the chance of

the genetic algorithm to produce optimal schedules,

and runs faster than alternative genetic algorithms de-

veloped for train scheduling. Currently, mathematical

programming-based decision support systems for ex-

act train scheduling remain a challenge for railroads

worldwide. There is, however, no doubt that even an

imperfect scheduling and movement planning tool is

preferable over no tool at all, or manual planning. It

is clear that mathematical programming software and

computing power have advanced dramatically during

Figure 5: Number of runs to produce the optimal solution.

Algorithms for Freight Train Scheduling

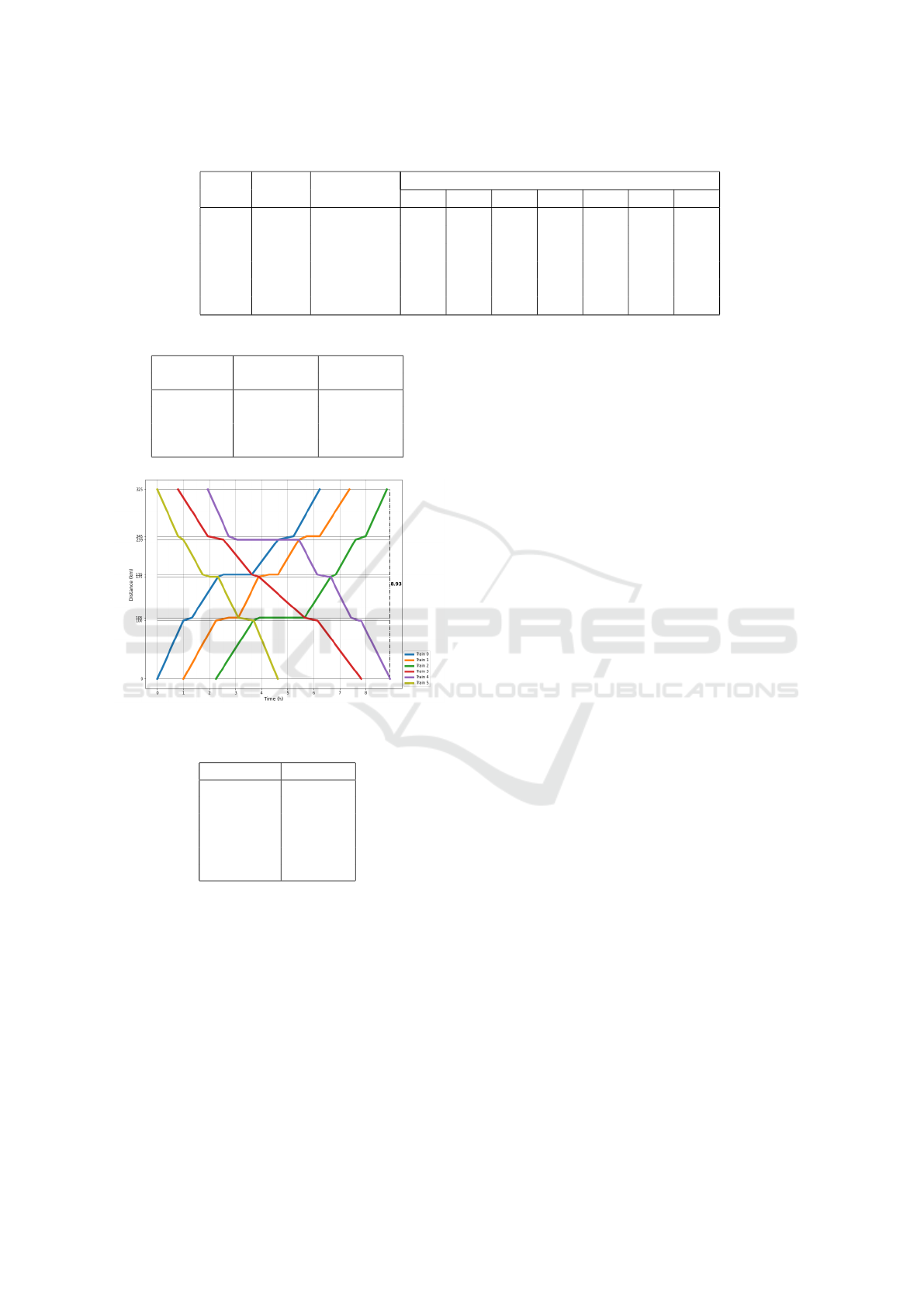
Table 1: Train scheduling example data.

Train Origin Destination Transit Time on Track (in hours)

Track Track 0 1 2 3 4 5 6

0 0 6 1 0.33 1 0.2 1 0.6 1

1 0 6 1.25 0.5 0.78 0.4 0.8 0.3 1.14

2 0 6 1.43 0.25 1 0.2 0.75 0.4 0.8

3 6 0 1.67 0.5 1.75 0.27 1.09 0.6 1.14

4 6 0 1.11 0.3 0.78 0.4 0.71 0.33 0.8

5 6 0 0.91 0.6 0.78 0.27 0.75 0.2 0.8

Table 2: Parameters of the genetic algorithms.

Algorithm Crossover Mutation

probability probability

GT1 1.0 0.40

GT2 0.8 0.40

TRA 0.8 0.05

RKD 1.0 0.30

Figure 6: Train graph of the optimal schedule.

Table 3: Average run times (sec/generation).

Algorithm Run time

GT1 0.5062

GT2 0.5006

TRA 0.0635

TGT1 0.2915

TGT2 0.3034

RKD 0.0460

last years, but train scheduling and movement plan-

ning are computationally demanding enough to war-

rant precise modeling and exact solutions.

5 CONCLUSION

This paper has introduced a class train scheduling al-

gorithms for freight railroads within the framework of

scheduling generation and genetic algorithms. First

it suggested an instance of scheduling generation al-

gorithm that constructs feasible active train sched-

ules. Next it developed genetic algorithms that starts

with the feasible populations created by the schedul-

ing generation algorithms and maintains feasibility of

all individuals during the generations. No repair tech-

nique is required to keep populations feasible.

A novel encoding scheme based on random keys

and job permutation was suggested in the paper. The

genetic algorithm that uses this novel scheme has

shown to particularly effective to ﬁnd the optimal so-

lution, that is, the schedule that minimizes the maxi-

mum transit time of the set of trains.

The algorithms were compared against the exact

solution found by solving a corresponding mixed-

integer optimization model using OR-Tools, currently

an academic and industry standard. The results sug-

gest that the genetic algorithm with random keys and

job permutation encoding performs best when com-

pared with the remaining ones, and appears to be a

promising avenue for further exploration. This is im-

portant because in practice many complex operational

constraints must be accounted for, which is easier to

be handled by genetic algorithms than classic opti-

mization algorithms.

However, more work is needed to measure how

the algorithms scale when the number of trains and

tracks increase, when sidings capacity are tightened,

when there is a need to trade-off transit time against

fuel consumption and environment impact, or when

uncertainties in transit times, maintenance of the way,

re-crew, and track outages are relevant for the opera-

tional agenda.

Parallel and multi-threading processing appear to

be a potential path to explore, especially when real-

time re-scheduling decisions should be undertaken.

These are issues to be pursued in the near future.

ACKNOWLEDGEMENTS

The authors acknowledge the anonymous reviewers

for their helpful and constructive comments. The last

author is grateful to the Brazilian National Council for

Scientiﬁc and Technological Development for grant

302467/2019-0

ECTA 2022 - 14th International Conference on Evolutionary Computation Theory and Applications

REFERENCES

Bean, J. (1994). Genetic algorithms and random keys for

sequencing and optimization. In ORSA Journal on

Computing. vol. 6, no. 2, pp. 154–160.

Driss, I., Mouss, K., and Laggoun, A. (2015). A new ge-

netic algorithm for ﬂexible job-shop scheduling prob-

lems. In Journal of Mechanical Science and Technol-

ogy. vol. 29, pp. 1273–1281.

Eiben, A. and Smith, J. (2015). Introduction to Evolution-

ary Computing. Springer, London, 2nd edition.

French, S. (1982). Sequencing and Scheduling: An Intro-

duction to the Mathematics of the Job-Shop. Wiley

Ellis Horwood Series in Mathematics and its Applica-

tions, London.

Garrisi, G. and Cristina, C. (2020). Train scheduling op-

timization model for railway networks with multiple

stations. In Sustainability. vol. 12, no. 1, pp. 257–282.

Ghoseiri, K., Szidarovszky, F., and Asgharpour, M. (2004).

A multi-objective train scheduling model and solu-

tion. In Transportation Research Part B: Methodolog-

ical. vol. 38, no. 10, pp. 927–952.

Gifﬂer, B. and Thompson, G. (1960). Algorithms for solv-

ing production scheduling problems. In Operations

Research. vol. 8, no. 4, pp. 487–503.

Harker, P. (1995). Services and technology: Reengineering

the railroads. In Interfaces. vol. 25, no. 3, pp. 72–80.

Harrod, S. (2012). A tutorial on fundamental model struc-

ture for railway timetable optimization. In Surveys in

Operations Research and Management Science. vol.

17, pp. 85–96.

Higgins, A., Kozan, E., and Ferreira, L. (1996). Optimal

scheduling of trains on a single line track. In Trans-

portation Research Part B: Methodological. vol. 30,

no. 2, pp. 147–161.

Higgins, A., Kozan, E., and Ferreira, L. (1997). Heuristic

techniques for single line train scheduling. In Journal

of Heuristics. vol. 3, no. 1, pp. 43–62.

Kraay, D., Parker, P., and Chen, B. (1991). Optimal pacing

of trains in freight railroads: Model formulation and

solution. In Operations Research. vol. 39, no. 1, pp.

82–99.

Liu, S. and Kozan, E. (2009). Scheduling trains as a block-

ing parallel-machine job shop scheduling problem. In

Computers and Operations Research. vol. 36, no. 10,

pp. 2840–2852.

Rardin, R. (2017). Optimization in Operations Research.

Pearson Higher Educations, Hoboken, 2nd edition.

Sahin, I. (1999). Railway trafﬁc control and train schedul-

ing based on inter-train conﬂict management. In

Transportation Research Part B: Methodological. vol.

33, no. 7, pp. 511–534.

Sun, Y., Cao, C., and Wu, C. (2014). Multi-objective opti-

mization of train routing problem combined with train

scheduling on a high-speed railway network. In Trans-

portation Research Part C: Emerging Technologies.

vol. 44, pp. 1–20.

Szpigel, B. (1973). Optimal train scheduling on a single

track railway. In Operational Research ’72, Proceed-

ings of the Sixth IFORS International Conference on

Operational Research. IFORS, North-Holland Pub-

lishing, London. pp. 343–352.

Tazoniero, A., Gonc¸alves, R., and Gomide, F. (2007). Deci-

sion making strategies for real-time train dispatch and

control. In Analysis and Design of Intelligent Systems

using Soft Computing Techniques. Springer, vol. 41,

pp. 195–204.

Tornos, A., Lova, A., Ingolotti, L., Abril, M., and Salido, M.

(2008). A genetic algotiyhm for railway scheduling

problems. In Studies in Computational Intelligence.

vol. 128, pp. 255–276.

Vieira, P., Bessa, E., and Gomide, F. (1999). Railway dis-

patch planning and control. In Proc. l8th International

Conference of the North American Fuzzy Information

Processing Society, NAFIPS. pp. 134–138.

Wen, C. (2019). Train dispatching management with data-

driven approaches: A comprehensive review and ap-

praisal. In IEEE Access. vol. 7, pp. 114547–114571.

Yamada, T. and Nakano, R. (1997). Job-shop scheduling. In

Genetic Algorithms in Engineering Systems. IEE Con-

trol Engineering Series 55, pp. 134–160.

Algorithms for Freight Train Scheduling