
Keep It Simple: Local Search-based Latent Space Editing
Andreas Meißner
1,2 a
, Andreas Fr
¨
ohlich
1 b
and Michaela Geierhos
2 c
1
Zentrale Stelle f
¨
ur Informationstechnik im Sicherheitsbereich, Zamdorfer Straße 88, 81677 Munich, Germany
2
Research Institute CODE, Bundeswehr University Munich, Carl-Wery-Straße 22, Munich, Germany
Keywords:
Latent Space Editing, Semantic Image Editing, Generative Adversarial Networks, StyleGAN, Local Search.
Abstract:
Semantic image editing allows users to selectively change entire image attributes in a controlled manner with
just a few clicks. Most approaches use a generative adversarial network (GAN) for this task to learn an
appropriate latent space representation and attribute-specific transformations. While earlier approaches often
suffer from entangled attribute manipulations, newer ones improve on this aspect by using separate specialized
networks for attribute extraction. Iterative optimization algorithms based on backpropagation constitute a
possible approach to find attribute vectors with little entanglement. However, this requires a large amount of
GPU memory, training instabilities can occur, and the used models have to be differentiable. To address these
issues, we propose a local search-based approach for latent space editing. We show that it performs at the
same level as previous algorithms and avoids these drawbacks.
1 INTRODUCTION
Semantic image editing is about modifying a mean-
ingful attribute within a target image, such as chang-
ing the age of a person in a portrait, the weather in
a landscape image, or the color of certain objects in
different scenes. Examples from the domain of facial
manipulation are shown in the appendix. The ability
to semantically edit images is useful for a wide range
of real-world tasks, such as photo enhancement, artis-
tic visualization, targeted data augmentation, and im-
age animation. For most applications, the goal is to
modify one or more target attributes while preserving
all other attributes and the overall image content.
Most state-of-the-art approaches for semantic im-
age editing are based on generative adversarial net-
works (GANs) (Goodfellow et al., 2014) and can be
roughly divided into two groups:
(i) Image-to-image translation methods employ
GANs to map one image domain to another.
These approaches suffer from limiting attribute
changes to predefined factors rather than allowing
arbitrary adjustments (Choi et al., 2018, 2020;
Isola et al., 2017b; Lee et al., 2020; Wu et al.,
2019; Zhu et al., 2017b,c).
a
https://orcid.org/0000-0002-6200-7553
b
https://orcid.org/0000-0002-0698-3621
c
https://orcid.org/0000-0002-8180-5606
(ii) Latent space editing methods use a GAN trained
to generate images and search for directions in its
latent space to enable continuous semantic image
editing. Early GAN models were not optimized
for a disentangled latent space, so changing one
attribute in an image usually resulted in changing
other unintended attributes as well (Karras et al.,
2019). Current style-based approaches (Karras
et al., 2019, 2020, 2021) have significantly im-
proved the disentanglement between attributes
and enable the targeting of specific features.
Latent space editing methods can be further di-
vided into supervised and unsupervised approaches.
Unsupervised approaches do not use a labeled dataset
or a regressor to specify the attribute to be manipu-
lated (Voynov and Babenko, 2020; H
¨
ark
¨
onen et al.,
2020). In contrast, supervised approaches require
a labeled dataset or a regressor, but have the ad-
vantage that a desired attribute can be defined for
manipulation rather than searching for a suitable la-
tent vector in all extracted latent vectors of an unsu-
pervised approach. While attribute vectors as com-
puted by Larsen et al. (2015) are often entangled with
other attributes, newer approaches attempt to solve
this problem. For example, StyleCLIP (Patashnik
et al., 2021) and Enjoy Your Editing (Zhuang et al.,
2021) improve the disentanglement of computed at-
tribute vectors by defining a loss function based on a
deep learning model and iteratively optimizing a la-
Meißner, A., Fröhlich, A. and Geierhos, M.
Keep It Simple: Local Search-based Latent Space Editing.
DOI: 10.5220/0011524700003332
In Proceedings of the 14th International Joint Conference on Computational Intelligence (IJCCI 2022), pages 273-283
ISBN: 978-989-758-611-8; ISSN: 2184-3236
Copyright © 2023 by SCITEPRESS – Science and Technology Publications, Lda. Under CC license (CC BY-NC-ND 4.0)
273

tent vector for the desired attributes using gradient
descent. On the downside, their approaches require
a significant amount of GPU memory for backpropa-
gation. Applying the approach proposed by Zhuang
et al. (2021) to the best model considering the image
quality from Karras et al. (2021) (called “stylegan3-r-
ffhqu-1024x1024.pkl”) requires 39 GB of GPU mem-
ory for a batch size of one, which is too much for even
a Tesla-V100. Additionally, only differentiable mod-
els can be used to compute the gradients, which in-
creases the implementation overhead for models im-
plemented in other frameworks and limits the use of
black-box models. We have furthermore observed
some instability issues when using smaller batch sizes
for Zhuang et al. (2021).
Contributions. We propose an iterative latent space
editing approach based on local search that achieves
comparable results to Zhuang et al. (2021) in terms of
identity preservation, attribute preservation, and run-
time, while requiring significantly less GPU memory
(12 GB for “stylegan3-r-ffhqu-1024x1024.pkl” com-
pared to the 39 GB required by our reimplementation
of Enjoy Your Editing), allowing the use of a much
wider range of GPUs. Moreover, our approach solves
the problem of numerical instabilities and does not
require a differentiable regressor. Our simplified loss
function has only one hyperparameter instead of the
usual three, which speeds up hyperparameter tuning.
We also discuss shortcomings of the evaluation met-
ric introduced in Zhuang et al. (2021) and suggest an
extension to the metric, which allows for better com-
parisons of different approaches.
2 RELATED WORK
Semantic image editing has a long history across the
domains of computer vision, computer graphics, and
machine learning. In the last years, GANs have re-
ceived particular attention as they facilitate efficient
image manipulations by image-to-image translation
or latent space editing.
2.1 Generative Adversarial Networks
GANs (Goodfellow et al., 2014) have achieved
impressive results in image generation in recent
years (Radford et al., 2016; Brock et al., 2019; Kar-
ras et al., 2017, 2019). However, image generation
is not the only application. Image inpainting (Yu
et al., 2018; Demir and
¨
Unal, 2018), super resolu-
tion (Ledig et al., 2017; Wang et al., 2018), data aug-
mentation (dos Santos Tanaka and Aranha, 2019) and
the creation of 3D objects (Gadelha et al., 2017) are
additional research areas.
A typical GAN consists of two modules: a gener-
ator and a discriminator. While the generator learns
to generate fake samples based on a random distribu-
tion as input, the discriminator learns to distinguish
between real and fake samples. A generator trained
in this way learns to reproduce the distribution of the
training samples, but does not provide control over the
category of generated samples or semantic attributes.
By providing the generator with labels for each train-
ing sample, a conditional GAN can learn to generate
samples based on the class – however, this requires a
labeled dataset (Mirza and Osindero, 2014).
In recent years, large-scale GAN models such as
BigGAN (Brock et al., 2019) and StyleGAN (Karras
et al., 2019) have paved the way for the generation of
photorealistic images. BigGAN (Brock et al., 2019)
is a comprehensive GAN model trained on ImageNet
(Deng et al., 2009) that supports image generation in
multiple categories due to its conditional architecture.
StyleGAN (Karras et al., 2019) is another popular
GAN model in which the generator maps the random
sampling distribution to an intermediate latent space,
using a fully connected network (often referred to as
mapping network). In this approach, the intermediate
latent space is not tied to the random distribution of
the input, resulting in an automatically learned, unsu-
pervised separation of high-level attributes.
2.2 Image-to-Image Translation
Image-to-image translation allows to transform one
image domain into another, such as creating a drawing
out of a selfie (Kim et al., 2017; Zhu et al., 2017a).
For example, Pix2pix (Isola et al., 2017a) learns this
task in a supervised manner using cGANs (Mirza and
Osindero, 2014). It combines an adversarial loss with
an L
1
loss to not only fool the discriminator, but also
be close to ground truth in the L
1
sense. The main
drawback is that paired data samples are required. To
circumvent the problem of obtaining paired data, un-
paired image-to-image translation frameworks have
been proposed (Kim et al., 2017; Liu et al., 2017; Zhu
et al., 2017b). CycleGAN (Zhu et al., 2017b) pre-
serves key attributes between the input and the trans-
lated image by using a cycle consistency loss.
However, all these methods are only capable of
learning the relationships between two different do-
mains simultaneously. As a result, these approaches
have limited scalability when processing multiple do-
mains and cannot interpolate between the two do-
mains.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
274

2.3 Latent Space Editing
Many works have investigated how the latent space of
a pre-trained generator can be used for image manip-
ulation (Collins et al., 2020; Tov et al., 2021; Zhang
et al., 2022). Some methods learn to perform end-to-
end image manipulations by training a network that
encodes a given image into a latent representation of
the manipulated image (Nitzan et al., 2020; Richard-
son et al., 2021; Alaluf et al., 2021).
Other methods aim at finding latent paths in such
a way that their traversal leads to the desired manip-
ulation. Such methods can be be divided into two
classes:
(i) Supervised methods use either image annotations
to find meaningful latent paths (Shen et al., 2020),
or a pre-trained model that classifies image at-
tributes (Zhuang et al., 2021; Patashnik et al.,
2021). The latter also allow for iterative optimiza-
tion.
(ii) Unsupervised methods find reasonable directions
without supervision, but require manual anno-
tation for each direction afterwards (H
¨
ark
¨
onen
et al., 2020; Shen and Zhou, 2020; Voynov and
Babenko, 2020).
In particular, the intermediate latent spaces in
StyleGAN architectures (Karras et al., 2019, 2020,
2021) have shown to facilitate many disentangled and
meaningful image manipulations.
Many approaches perform image manipulations in
the W -space (Voynov and Babenko, 2020; H
¨
ark
¨
onen
et al., 2020; Shen et al., 2020; Zhuang et al.,
2021), the more disentangled intermediate latent
space generated directly by StyleGAN’s mapping net-
work (Karras et al., 2019). The W+-space is an ex-
tension of the W -space, where a different latent vec-
tor w is fed to each generator layer. While W+
was originally used for mixing styles from differ-
ent sources (Karras et al., 2019), it is also used for
semantic image editing by Patashnik et al. (2021).
StyleSpace S, the space spanned by the channel-wise
style parameters, was proposed by Wu et al. (2021)
and is also used by Patashnik et al. (2021). It is shown
that S is even more disentangled than W and W+ (Wu
et al., 2021).
3 METHOD
We propose an iterative approach for controllable se-
mantic image editing via latent space navigation in
GANs. We start with a pre-trained GAN generator G.
The input of G is a latent vector from a latent space.
Given a target attribute, we try to find a vector in
the latent space that, by adding it to the original la-
tent vector, allows the target attribute to change while
leaving other attributes intact.
Our approach for discovering an attribute-specific
latent vector consists of two pre-trained networks G
and R, and a local search component. While G and
R are used to evaluate a given latent vector, the local
search component provides an iterative framework for
optimization by navigating through the latent space.
G is a GAN generator network. In practice, we
used StyleGAN2 for our experiments in Section 4
– however, our overall approach is generic and not
limited to this specific choice. As discussed in Sec-
tion 2, StyleGAN architectures have several latent
spaces that can be used to modify an attribute. In
addition to the original input space Z, three different
intermediate latent spaces W , W+, or S can be used:
The Z-space is normally distributed, but attributes are
more entangled. The W -space has less entanglement
and, therefore, allows better control over a target at-
tribute. It has been shown that the W+-space as well
as the StyleSpace S are even less entangled (Wu et al.,
2021). Since the W -space is still most commonly
used for exploring the latent space in StyleGAN, we
decided to also use the W -space for an initial proof-
of-concept implementation of our local search-based
approach to provide a fair comparison with existing
methods. Extending our approach to W+-space or S-
space will be an interesting direction for future work.
StyleGAN2’s generator network consists of two
consecutive parts: a mapping network G
map
and a
synthesis network G
synth
. The input to G
map
is a nor-
mally distributed latent vector z from the original la-
tent space Z, which is then mapped to a new latent
vector w in the intermediate latent space W . G
synth
then generates an image using w as input.
R is a regressor network pre-trained on the CelebA
dataset (Liu et al., 2015) and estimates 40 attributes
for the image. Similar to Zhuang et al. (2021), our ap-
proach is iterative and R is used to directly compute a
loss function in each iteration. To facilitate compari-
son, we use the same regressor model as Zhuang et al.
(2021). The vector to be optimized, d ∈ W , controls
the attribute change in the image. Adding or subtract-
ing d is to increase or decrease the attribute in a given
image – this is evaluated by the loss function. Fig. 1
illustrates a single iteration within this optimization
framework.
The main novelty of our approach lies in the use
a local search component to optimize d. In contrast,
Zhuang et al. (2021) use backpropagation for their op-
timization. While backpropagation is a powerful tool
for many applications in the deep learning context,
Keep It Simple: Local Search-based Latent Space Editing
275
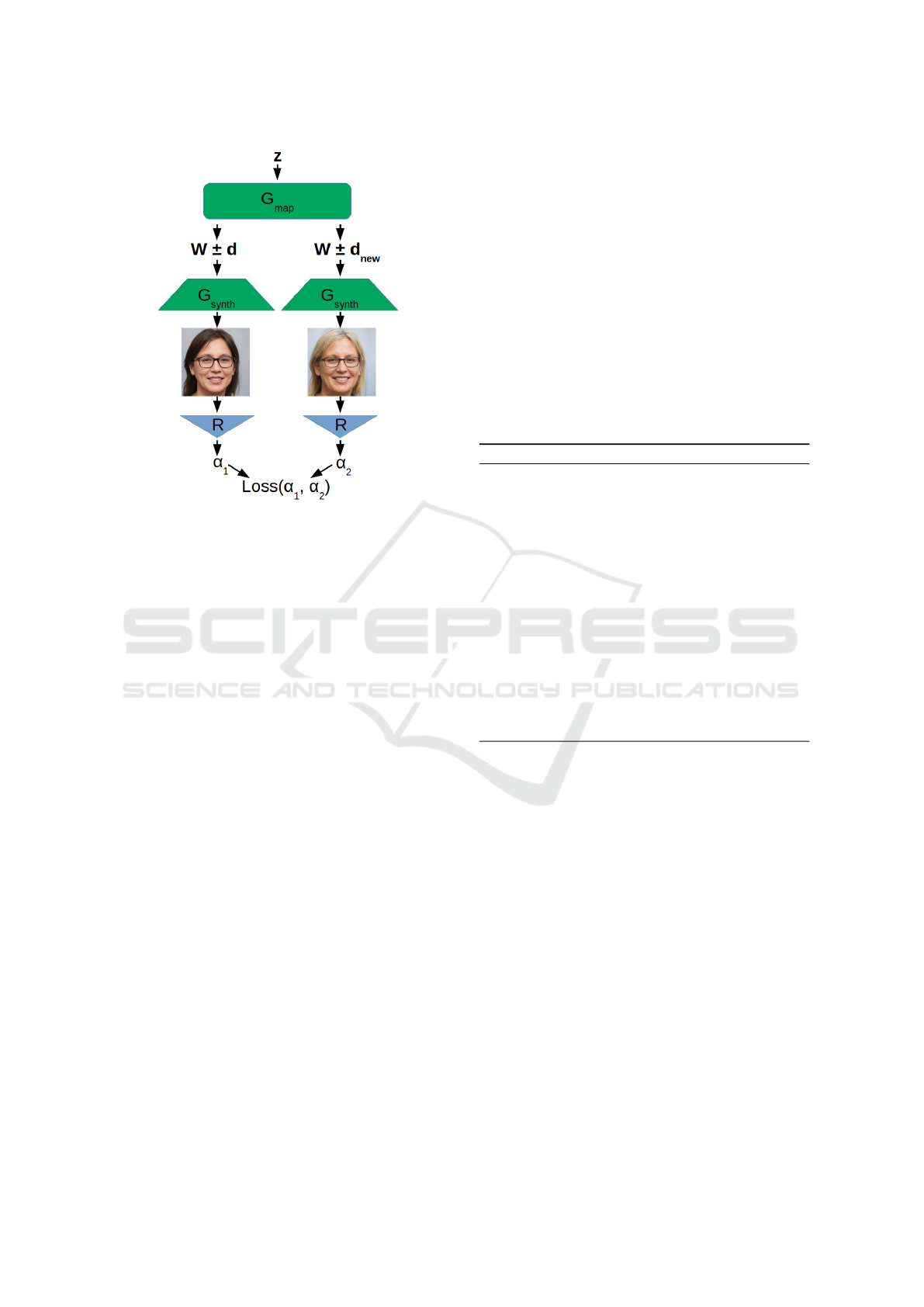
Figure 1: Illustration of the steps that are performed in a
single iteration of our local search-based optimization.
its performance comes at the price of high memory
consumption and computational cost. Compared to
other applications, such as training the weights of a
deep learning network, our task is less complex and
requires only the optimization of the attribute vec-
tor; the weights of G and R remain unchanged. Lo-
cal search provides a simple but efficient framework
for this kind of optimization task. Starting from an
initial point in a search space, local search algorithms
iteratively move to “better” points according to an ob-
jective function using heuristics. While local search
is mainly applied to computationally intensive opti-
mization problems in discrete search spaces, there are
also methods for real-valued search spaces. In partic-
ular, our local search component is based on the con-
cept of random optimization (Matyas et al., 1965).
As hyperparameters, our algorithm requires a
sample radius r and a maximum length L, both re-
stricting the choice of our attribute vector d. We ini-
tialize d to be a null vector before entering the main
loop. In each iteration, we first sample a new latent
vector, which is the origin for the current local search
step. To do this, we take a normally distributed sam-
ple z ∈ Z and then feed it to G
map
to compute the cor-
responding intermediate representation w ∈ W . We
also sample a sign (+ or −, each with probability 0.5)
to decide whether to evaluate the attribute vector in
terms of its ability to increase or decrease the target
attribute in the current iteration. A manipulated latent
vector is then obtained by adding or subtracting d ac-
cording to the chosen sign; G
synth
is used to generate
the respective manipulated image, and R provides a
value α to estimate the degree to which the target at-
tribute is present.
Next, the actual local search space is sampled by
adding a normally distributed vector to d, resulting
in a new candidate attribute vector d
0
. If the length
of d
0
exceeds the previously defined maximum length
of L, d
0
is reduced accordingly to avoid reaching too
sparsely sampled parts of the latent space. In the same
way as α was determined for d, a new value α
0
is now
calculated for d
0
using G
synth
and R.
d
0
is considered better than d if (i) α
0
> α and
the attribute vectors have been evaluated according to
their positive direction, or (ii) α
0
< α and the attribute
vectors have been evaluated according to their nega-
tive direction. If this is the case, d is updated to the
value of d
0
. The whole algorithm is outlined in Alg. 1.
Algorithm 1: Local search algorithm.
Input: sampleRadius r, maxLength L
1: d ←
~
0
2: for i = 0,...,max do
3: w ← G
map
(N (
~
0,I))
4: ± ← rand{+,−}
5: α ← R(G
synth
(w ± d))
6: d
0
← d + N (
~
0,r · I)
7: if ||d
0
|| > L then
8: d
0
= L · d
0
/||d
0
||
9: end if
10: α
0
← R(G
synth
(w ± d
new
))
11: if ±α < ±α
0
then
12: d ← d
0
13: end if
14: end for
We decided to keep our optimization criterion as
simple as possible. We only used α and α
0
to eval-
uate attribute vectors d and d
0
, respectively. There-
fore, our objective function can be solely calculated
by the use of a regressor loss. In contrast, Style-
CLIP uses a loss term based on the CLIP model (Rad-
ford et al., 2021), L
2
distance between latent vectors,
and an identity loss based on a pre-trained ArcFace
model. Similarly, Enjoy Your Editing uses a regres-
sor loss, a content loss based on a VGG model, and an
additional discriminator loss. The discriminator loss
is supposed to measure the quality of the generated
images. Since StyleCLIP has no visible artifacts and
contains no discriminator loss, we assume that the lat-
ter is not required to produce realistic images. We also
expect that content loss, identity loss, and L
2
distance
mainly limit the maximum length of the attribute vec-
tor during optimization. This leads to the hypothesis
that a vector of predefined length, which is then op-
timized to modify a target attribute as much as possi-
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
276

ble, automatically preserves the remaining attributes
and the identity of the person due to the disentangle-
ment properties of the W -space. The length of the at-
tribute vector can be interpreted as a hyperparameter.
Since StyleGAN2 produces high quality images near
the center of the input distribution, a sufficiently small
length limits the amount of artifacts. Both, Patashnik
et al. (2021) and Zhuang et al. (2021), use three hyper-
parameters in their respective loss functions, which
requires careful balancing.
4 EXPERIMENTS
Since Zhuang et al. (2021) proposed the method that
is most similar to our approach, we decided to use
their work as a baseline for comparison. Unfortu-
nately, we encountered a strange behavior when test-
ing their StyleGAN2 implementation
1
. We observed
some sporadic runtime errors due to a compatibility
issue between CUDNN and the NVIDIA driver ver-
sion, as well as significant variations in the output
results. When using the same input multiple times
with constant noise, the output images sometimes dif-
fered. While most output images were nearly identi-
cal, mean pixel differences up to 9.06 were occasion-
ally observed in a 0–255 image. This pixel difference
resulted in prediction differences up to 14.4% from
the regressor, which severely limited our ability to
consistently reproduce the results. For this reason we
use in this work NVIDIA’s official StyleGAN2-ADA-
PyTorch implementation
2
. While the StyleGAN2 im-
plementation of Enjoy Your Editing generates im-
ages with a size of 256x256 pixels, we use Style-
GAN’s FFHQ model, which provides a resolution of
1024x1024, since most applications use the best pos-
sible image quality.
For all experiments with our algorithm, we use the
settings r = 3 · 10
−4
and L = 0.8. As proposed in
Zhuang et al. (2021), we use the regressor loss coeffi-
cient λ
1
= 10, the content loss coefficient λ
2
= 0.05,
and the discriminator loss coefficient λ
3
= 0.05 for
their algorithm. For their optimization, an Adam op-
timizer with a learning rate of 10
−4
is used.
Both, the implementation of our local search-
based algorithm and the reimplementation of Enjoy
Your Editing, are available in our GitHub repository
3
.
We also provide the evaluation scripts used in our ex-
periments.
1
https://github.com/KelestZ/Latent2im
2
https://github.com/NVlabs/stylegan2-ada-pytorch
3
https://github.com/meissnerA/LocalSearchLSpaceE
4.1 Quantifying Instabilities of Enjoy
Your Editing
In Zhuang et al. (2021), StyleGAN2 images have a
resolution of 256x256 pixels, which allows the use
of larger batch sizes compared to 1024x1024 models.
Larger models, such as used by StyleGAN3, require
even more GPU memory, further limiting the viable
batch size. To investigate the impact of using smaller
batch sizes on training stability, we ran our reimple-
mentation of Enjoy your Editing for 20,000 iterations
with 10 different random seeds and checked how of-
ten numerical instabilities (i.e., NaN values in the at-
tribute vector) occurred.
• In the first experiment, we performed 10 runs
for StyleGAN3, using their biggest model
“stylegan3-r-ffhqu-1024x1024.pkl” with a batch
size of one and a learning rate of 10
−4
. All ten
runs ended up with numerical instabilities.
• In the second experiment, we investigated the
influence of batch size on the stability of En-
joy Your Editing. Since “stylegan3-r-ffhqu-
1024x1024.pkl” requires 39 GB of GPU memory
at a batch size of one, we decided to use Style-
GAN2’s 1024x1024-ffhq-model – which we used
in all following experiments – to test larger batch
sizes. For a batch size of one and a learning
rate of 10
−4
, 7/10 runs ended in numerical in-
stabilities. For batch sizes of 2, 4, and 8, 2/10
runs also ended in numerical instabilities. Hence,
while training stability got better with batch sizes
larger than one, numerical instabilities were still
observed for a batch size of 8. Since instabilities
occurred with both StyleGAN2 and StyleGAN3,
this suggests that the issue of instabilities is not a
model-specific effect, but is caused by the under-
lying approach.
• In the third experiment, we investigated the influ-
ence of the learning rate. While 7/10 runs ended in
numerical instabilities at a learning rate of 10
−4
,
only 4/10 runs did so at a learning rate of 10
−5
.
• We traced the cause of the numerical instabilities
to the regressor loss, which uses a binary cross
entropy (BCE) function:
L
reg
= E[−
ˆ
α
0
log α
0
− (1 −
ˆ
α
0
) log (1 − α
0
)] (1)
If α
0
is close to 0 and 1, the terms log(α
0
) and
log(1−α
0
) take on very large values, respectively.
Those terms often cannot be compensated by
ˆ
α
0
and (1 −
ˆ
α
0
). This high loss leads to large gradi-
ents that can be traced back to the output layer of
StyleGAN2, where the first NaN values appear.
Keep It Simple: Local Search-based Latent Space Editing
277

Table 1: Influence of the vector length on the evaluation metric for the target attribute “Smiling”. The rows show results for
(1) the vector calculated by our approach and (2) a scaled version thereof. Regarding the preservation metrics, the short vector
performs better than the original one. However, target attribute manipulation is reduced.
Smile
Attribute Preservation Identity Preservation Buckets
(0, .3] (.3, .6] (.6, .9] (0, .3] (.3, .6] (.6, .9] (0, .3] (.3, .6] (.6, .9]
d
0.0268
±0.0671
0.0669
±0.1336
0.0980
±0.1866
0.9990
±0.0022
0.9976
±0.0032
0.9964
±0.0039
5442 1370 2309
d/5
0.0114
±0.0333
0.0405
±0.0968
0.0599
±0.1396
0.9998
±0.0005
0.9995
±0.0008
0.9993
±0.0007
9563 410 27
We observed that switching from BCE to a mean
squared error (MSE) function appears to be a pos-
sible way to avoid those instabilities. When using
a MSE-based loss, no NaN values occurred in our
experiments and the visual quality of edited images
stayed the same. However, this was just a first impres-
sion and we did not perform a full experimental eval-
uation using MSE-based loss, since this was not the
scope of our work. When inspecting the GitHub im-
plementation of Enjoy Your Editing, we found some
differences to the pseudocode provided in their paper
(Zhuang et al., 2021). In particular, one difference is
related to sampling a random value ε, which is then
used to calculate α
0
for their BCE loss. While we de-
cided to base our reimplementation on their official
paper, it is possible that using the sampling distribu-
tion from their Github implementation would also re-
duce instabilities. Nevertheless, both possible fixes
emphasize the well-known fact that backpropagation
is sensitive to careful choice of many hyperparame-
ters, such as loss function and learning rate. More-
over, even without numerical instabilities, approaches
based on backpropagation still have the disadvantage
of requiring differentiable models and large amounts
of GPU-memory. Local search can provide a simple
framework to circumvent those difficulties in the con-
text of latent space editing.
4.2 Evaluation Metric
To evaluate attribute values, we use the evaluation
metric proposed by Zhuang et al. (2021). We generate
1,000 original images, produce 10,000 edited images
with different editing strengths, and calculate the dif-
ference in the target attribute between the original im-
ages and their respective edited images. Depending
on the degree of change in the target attribute, an im-
age pair is saved in one of the three buckets (0,0.3],
(0.3,0.6] or (0.6, 0.9]. For each bucket, two different
metrics are calculated:
(i) The identity preservation is calculated by us-
ing the popular image identity recognition model
VGGFace2 pre-trained on the VGGface2 dataset
(Cao et al., 2018). When VGGFace2 is applied to
a face image, it outputs a feature vector. The iden-
tity preservation is the cosine similarity between
the face feature vector of the original image and
the edited image.
(ii) The attribute preservation metric is calculated
with the same pre-trained regressor network that
was used for estimating the target attribute (Liu
et al., 2015). We calculate the 40 attribute predic-
tions for all original images and all edited images.
Ideally, editing only changes the target attribute
and all other attributes remain the same. There-
fore, the change in all attributes except the target
attribute is calculated. The attribute preservation
metric is the average attribute difference over all
image pairs.
Unfortunately, we encountered an issue with
the described metric: Short attribute vectors tend
to achieve considerably better results compared to
longer ones. This comes at no surprise, since the
length of the attribute vector directly influences the
distance between the latent vectors for the original im-
age and the manipulated image. For example, using
a null vector does not change the image at all. As a
result, a null vector achieves perfect scores in regard
to identity preservation and attribute preservation. A
similar effect can also be observed for any sufficiently
short non-zero vector. In Table 1, both preservation
metrics are calculated for an attribute vector that was
found by our approach and a down-scaled version
thereof. The down-scaled version appears to perform
better than the original attribute vector if no additional
criterion is used for evaluation. In practice, a good
attribute vector needs to preserve the image content
while changing the target attribute as much as pos-
sible, both at the same time. This trade off is heavily
affected by the length of a vector. In particular, down-
scaling improves the preservation metrics but also re-
duces target attribute manipulation. As a result, eval-
uating only the preservation component turns out to
be insufficient. To address this shortcoming, we also
provide the bucket distribution in all our evaluations.
The bucket distribution is an indication for the degree
of change in regard to the target attribute.
While emphasizing an important aspect, the
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
278

Table 2: Comparing attribute preservation (a lower score is better) and identity preservation (a higher score is better) for
Shen et al. (2020) (Shen), our reimplementation of Enjoy your Editing (Zhuang), and our local search-based approach (with
batch size=1 and batch size=8) after scaling the vectors to cause the same degree of target attribute change. While the bucket
distribution is similar after scaling, the resulting length of the attribute vectors can differ. The first four rows show metrics for
the attribute “Smiling”, the last four rows show the metrics for “Hair color”.
Smile
Attribute Preservation Identity Preservation Buckets
|d|
(0, .3] (.3, .6] (.6, .9] (0, .3] (.3, .6] (.6, .9] (0, .3] (.3, .6] (.6, .9]
Shen
0.0264
±0.0659
0.0657
±0.1319
0.0977
±0.1875
0.9988
±0.0027
0.9974
±0.0034
0.9956
±0.0047
5429 1330 2307 1.31
Zhuang
0.0300
±0.0739
0.0718
±0.1393
0.1020
±0.1887
0.9991
±0.0020
0.9979
±0.0026
0.9966
±0.0038
5416 1418 2320 1.32
Ours bs=1
0.0268
±0.0671
0.0669
±0.1336
0.0980
±0.1866
0.9990
±0.0022
0.9976
±0.0032
0.9964
±0.0039
5442 1370 2309 1.40
Ours bs=8
0.0252
±0.0628
0.0641
±0.1300
0.0958
±0.1855
0.9990
±0.0022
0.9976
±0.0034
0.9963
±0.0039
5426 1338 2315 1.30
Hair color
Attribute Preservation Identity Preservation Buckets
|d|
(0, .3] (.3, .6] (.6, .9] (0, .3] (.3, .6] (.6, .9] (0, .3] (.3, .6] (.6, .9]
Shen
0.0429
±0.1008
0.0789
±0.1372
0.0988
±0.1744
0.9851
±0.0229
0.9542
±0.0346
0.9370
±0.0430
5428 1122 1520 2.44
Zhuang
0.0399
±0.0967
0.0745
±0.1317
0.0936
±0.1700
0.9869
±0.0197
0.9543
±0.0347
0.9357
±0.0431
5395 1279 1689 2.01
Ours bs=1
0.0447
±0.1003
0.0880
±0.1461
0.1093
±0.1829
0.9814
±0.0283
0.9409
±0.0449
0.9201
±0.0531
5380 1134 1447 3.20
Ours bs=8
0.0452
±0.1047
0.0842
±0.1479
0.1030
±0.1800
0.9849
±0.0233
0.9538
±0.0358
0.9396
±0.0412
5345 1129 1536 2.79
bucket distribution still does not automatically allow
for a direct ranking of different algorithms. Due to the
strong negative correlation between target attribute
change and preservation metrics, approaches usually
tend to be better in one or the other. A naive attempt
to address this limitation could be to normalize the at-
tribute vectors before evaluation. Unfortunately, this
turns out insufficient. Even slight variations in an al-
gorithm, e.g., a different random seed or a different
batch size, lead to different latent vectors. In our eval-
uation, we observed that different attribute vectors re-
quire different lengths for the same degree of attribute
editing. This comes at no surprise, since w does not
follow a known distribution. To tackle this problem,
we propose to scale attribute vectors such that they
change the target attribute by the same degree.
However, the target attribute change is influenced
by various aspects and no straightforward measure-
ment exists. In consequence, we decided to approxi-
mate target attribute change by the number of samples
with an attribute change of at most 0.3, roughly cor-
responding to the samples in bucket (0,0.3]. When
implementing the scaling of the vector, we wondered
what range we should take as the measure of attribute
change. Values greater than 0.9 are not represented
in the buckets, but an attribute vector that changes
the target attribute by more than 0.9 should be con-
sidered for determining the scaling factor. Therefore,
we decided to scale the vectors so that the number
of samples with an attribute change of at most 0.3
is within ±1%. In turn, this means that number of
samples which change the attribute for more than 0.3
is also within ±1%. All together, we ran our reim-
plementation of Enjoy Your Editing with a batch size
of 1 for 20,000 iterations, yielding a bucket distribu-
tion of [5416, 1418,2320] for the attribute “Smiling”,
and scaled all latent vectors in our experiments for the
same attribute so that bucket (0,0.3] = 5416 ± 54. To
have comparable runtimes, we also used this run for
reference, which took 4,105 seconds on a NVIDIA
Quadro GV100, and stopped each run after this time.
In the original implementation of Enjoy Your Editing,
d is initialized with a random distribution. However,
this random initialization affects the performance of
the computed attribute vector. For reasons of repro-
ducibility, we initialize the attribute vector in Enjoy
Your Editing with a null vector. Since the loss net-
works use pre-trained weights, this does not nega-
tively affect performance.
4.3 Results
An important advantage of our approach are lower re-
quirements in regard to GPU memory, since we do
not have to calculate backpropagation for optimiza-
tion. This lower constraint on GPU memory allows
us to use bigger batch sizes than backpropagation-
based optimization strategies. A higher batch size
results in a higher runtime per iteration but gives us
a more reliable loss value. Comparison of the re-
sults for Shen et al. (2020), our reimplementation of
Zhuang et al. (2021), and our local search approach
Keep It Simple: Local Search-based Latent Space Editing
279

in Table 2 shows that there is no clear winner. Con-
sidering the evaluation metric as well as comparing
edited images in the appendix, all three approaches
seem to perform on a par with each other. In contrast,
the quantitative evaluation by Zhuang et al. (2021)
claimed a considerably worse performance for Shen
et al. (2020). In part, this gap can be attributed to dif-
ferent vector lengths. This further emphasizes the im-
portance of evaluating the bucket distribution or scal-
ing vectors for fair comparison. Since Zhuang et al.
(2021) used a different StyleGAN2 model and did not
provide details on their use of Shen et al. (2020), we
were not able to reproduce their results and lack of a
satisfactory explanation for the remaining gap in their
performance.
While showing comparable performance of our
approach, we were able to achieve those results with-
out using a large number of hyperparameters. In par-
ticular, we do not use any hyperparameter in our ob-
jective function. As discussed in Section 3, the max-
imum vector length L takes a role similar to those of
hyperparameters within the loss functions of Patash-
nik et al. (2021); Zhuang et al. (2021) – however, both
approaches require three hyperparameters instead of
just a single one. Although we define the sample ra-
dius r as another hyperparameter, it mainly affects the
way in which the search space is traversed. In conse-
quence, it is more closely related to other hyperpa-
rameters, such as the learning rate during backpropa-
gation. Both, Patashnik et al. (2021) and Zhuang et al.
(2021), use the Adam optimizer, which comes with
further hyperparameters on top of the already exist-
ing ones.
5 CONCLUSION
We proposed an effective local search-based approach
to semantically edit images in regard to a specified
target attribute. Our method enables continuous im-
age manipulations, comparable to state-of-the-art ap-
proaches. At the same time, it requires significantly
less GPU memory than existing iterative approaches
based on backpropagation. Since we do not rely on
backpropagation, our method is applicable to use non-
differentiable black-box models for both, the genera-
tor and the regressor, and does not suffer from insta-
bilities. Furthermore, our approach has fewer hyper-
parameters, which allows for more efficient tuning.
We also discussed the importance of comparing vec-
tors with similar degree of attribute change. As a re-
sult, we suggested an extension to allow for a better
evaluation.
A possible direction for future work could be the
use of more sophisticated local search algorithms,
e.g., by adopting heuristics that have shown to be suc-
cessful in other local search domains. Similarly, lift-
ing our approach to other latent spaces, such as W+
and S, seems promising. Finally, further refining ex-
isting evaluation metrics is certainly of great interest.
REFERENCES
Alaluf, Y., Patashnik, O., and Cohen-Or, D. (2021). Only a
matter of style: age transformation using a style-based
regression model. ACM Trans. Graph., 40(4):45:1–
45:12.
Brock, A., Donahue, J., and Simonyan, K. (2019). Large
scale GAN training for high fidelity natural image
synthesis. In 7th International Conference on Learn-
ing Representations, ICLR 2019, New Orleans, LA,
USA, May 6-9, 2019. OpenReview.net.
Cao, Q., Shen, L., Xie, W., Parkhi, O. M., and Zisserman,
A. (2018). Vggface2: A dataset for recognising faces
across pose and age. In 13th IEEE International Con-
ference on Automatic Face & Gesture Recognition,
FG 2018, Xi’an, China, May 15-19, 2018, pages 67–
74. IEEE Computer Society.
Choi, Y., Choi, M., Kim, M., Ha, J.-W., Kim, S., and Choo,
J. (2018). Stargan: Unified generative adversarial net-
works for multi-domain image-to-image translation.
In Proceedings of the IEEE Conference on Computer
Vision and Pattern Recognition (CVPR).
Choi, Y., Uh, Y., Yoo, J., and Ha, J.-W. (2020). Stargan v2:
Diverse image synthesis for multiple domains. In Pro-
ceedings of the IEEE/CVF Conference on Computer
Vision and Pattern Recognition (CVPR).
Collins, E., Bala, R., Price, B., and S
¨
usstrunk, S. (2020).
Editing in style: Uncovering the local semantics of
gans. In 2020 IEEE/CVF Conference on Computer
Vision and Pattern Recognition, CVPR 2020, Seattle,
WA, USA, June 13-19, 2020, pages 5770–5779. Com-
puter Vision Foundation / IEEE.
Demir, U. and
¨
Unal, G. B. (2018). Patch-based image in-
painting with generative adversarial networks. CoRR,
abs/1803.07422.
Deng, J., Dong, W., Socher, R., Li, L., Li, K., and Fei-Fei,
L. (2009). Imagenet: A large-scale hierarchical image
database. In 2009 IEEE Computer Society Conference
on Computer Vision and Pattern Recognition (CVPR
2009), 20-25 June 2009, Miami, Florida, USA, pages
248–255. IEEE Computer Society.
dos Santos Tanaka, F. H. K. and Aranha, C. (2019). Data
augmentation using gans. CoRR, abs/1904.09135.
Gadelha, M., Maji, S., and Wang, R. (2017). 3d shape in-
duction from 2d views of multiple objects. In 2017
International Conference on 3D Vision, 3DV 2017,
Qingdao, China, October 10-12, 2017, pages 402–
411. IEEE Computer Society.
Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B.,
Warde-Farley, D., Ozair, S., Courville, A., and Ben-
gio, Y. (2014). Generative adversarial nets. In Ghahra-
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
280

mani, Z., Welling, M., Cortes, C., Lawrence, N., and
Weinberger, K., editors, Advances in Neural Infor-
mation Processing Systems, volume 27. Curran Asso-
ciates, Inc.
H
¨
ark
¨
onen, E., Hertzmann, A., Lehtinen, J., and Paris, S.
(2020). Ganspace: Discovering interpretable gan con-
trols. In Larochelle, H., Ranzato, M., Hadsell, R.,
Balcan, M., and Lin, H., editors, Advances in Neu-
ral Information Processing Systems, volume 33, pages
9841–9850. Curran Associates, Inc.
Isola, P., Zhu, J., Zhou, T., and Efros, A. A. (2017a). Image-
to-image translation with conditional adversarial net-
works. In 2017 IEEE Conference on Computer Vision
and Pattern Recognition, CVPR 2017, Honolulu, HI,
USA, July 21-26, 2017, pages 5967–5976. IEEE Com-
puter Society.
Isola, P., Zhu, J.-Y., Zhou, T., and Efros, A. A. (2017b).
Image-to-image translation with conditional adversar-
ial networks. In 2017 IEEE Conference on Computer
Vision and Pattern Recognition (CVPR), pages 5967–
5976.
Karras, T., Aila, T., Laine, S., and Lehtinen, J. (2017). Pro-
gressive growing of gans for improved quality, stabil-
ity, and variation. CoRR, abs/1710.10196.
Karras, T., Aittala, M., Laine, S., H
¨
ark
¨
onen, E., Hellsten, J.,
Lehtinen, J., and Aila, T. (2021). Alias-free generative
adversarial networks. In Beygelzimer, A., Dauphin,
Y., Liang, P., and Vaughan, J. W., editors, Advances in
Neural Information Processing Systems.
Karras, T., Laine, S., and Aila, T. (2019). A style-based
generator architecture for generative adversarial net-
works. In Proceedings of the IEEE/CVF Conference
on Computer Vision and Pattern Recognition (CVPR).
Karras, T., Laine, S., Aittala, M., Hellsten, J., Lehtinen,
J., and Aila, T. (2020). Analyzing and improving
the image quality of stylegan. In 2020 IEEE/CVF
Conference on Computer Vision and Pattern Recog-
nition, CVPR 2020, Seattle, WA, USA, June 13-19,
2020, pages 8107–8116. Computer Vision Foundation
/ IEEE.
Kim, T., Cha, M., Kim, H., Lee, J. K., and Kim, J. (2017).
Learning to discover cross-domain relations with gen-
erative adversarial networks. In Precup, D. and Teh,
Y. W., editors, Proceedings of the 34th International
Conference on Machine Learning, ICML 2017, Syd-
ney, NSW, Australia, 6-11 August 2017, volume 70
of Proceedings of Machine Learning Research, pages
1857–1865. PMLR.
Larsen, A. B. L., Sønderby, S. K., and Winther, O. (2015).
Autoencoding beyond pixels using a learned similar-
ity metric. CoRR, abs/1512.09300.
Ledig, C., Theis, L., Huszar, F., Caballero, J., Cunning-
ham, A., Acosta, A., Aitken, A. P., Tejani, A., Totz,
J., Wang, Z., and Shi, W. (2017). Photo-realistic sin-
gle image super-resolution using a generative adver-
sarial network. In 2017 IEEE Conference on Com-
puter Vision and Pattern Recognition, CVPR 2017,
Honolulu, HI, USA, July 21-26, 2017, pages 105–114.
IEEE Computer Society.
Lee, H.-Y., Tseng, H.-Y., Mao, Q., Huang, J.-B., Lu, Y.-D.,
Singh, M. K., and Yang, M.-H. (2020). Drit++: Di-
verse image-to-image translation viadisentangled rep-
resentations. International Journal of Computer Vi-
sion, pages 1–16.
Liu, M., Breuel, T. M., and Kautz, J. (2017). Unsuper-
vised image-to-image translation networks. CoRR,
abs/1703.00848.
Liu, Z., Luo, P., Wang, X., and Tang, X. (2015). Deep learn-
ing face attributes in the wild. 2015 IEEE Interna-
tional Conference on Computer Vision (ICCV), pages
3730–3738.
Matyas, J. et al. (1965). Random optimization. Automation
and Remote control, 26(2):246–253.
Mirza, M. and Osindero, S. (2014). Conditional generative
adversarial nets. CoRR, abs/1411.1784.
Nitzan, Y., Bermano, A., Li, Y., and Cohen-Or, D. (2020).
Face identity disentanglement via latent space map-
ping. ACM Trans. Graph., 39(6):225:1–225:14.
Patashnik, O., Wu, Z., Shechtman, E., Cohen-Or, D., and
Lischinski, D. (2021). Styleclip: Text-driven manip-
ulation of stylegan imagery. In Proceedings of the
IEEE/CVF International Conference on Computer Vi-
sion (ICCV), pages 2085–2094.
Radford, A., Kim, J. W., Hallacy, C., Ramesh, A., Goh,
G., Agarwal, S., Sastry, G., Askell, A., Mishkin, P.,
Clark, J., Krueger, G., and Sutskever, I. (2021). Learn-
ing transferable visual models from natural language
supervision. In Meila, M. and Zhang, T., editors, Pro-
ceedings of the 38th International Conference on Ma-
chine Learning, ICML 2021, 18-24 July 2021, Virtual
Event, volume 139 of Proceedings of Machine Learn-
ing Research, pages 8748–8763. PMLR.
Radford, A., Metz, L., and Chintala, S. (2016). Unsu-
pervised representation learning with deep convolu-
tional generative adversarial networks. In Bengio, Y.
and LeCun, Y., editors, 4th International Conference
on Learning Representations, ICLR 2016, San Juan,
Puerto Rico, May 2-4, 2016, Conference Track Pro-
ceedings.
Richardson, E., Alaluf, Y., Patashnik, O., Nitzan, Y., Azar,
Y., Shapiro, S., and Cohen-Or, D. (2021). Encoding
in style: A stylegan encoder for image-to-image trans-
lation. In IEEE Conference on Computer Vision and
Pattern Recognition, CVPR 2021, virtual, June 19-25,
2021, pages 2287–2296. Computer Vision Foundation
/ IEEE.
Shen, Y., Gu, J., Tang, X., and Zhou, B. (2020). Interpreting
the latent space of gans for semantic face editing. In
CVPR.
Shen, Y. and Zhou, B. (2020). Closed-form factorization of
latent semantics in gans. CoRR, abs/2007.06600.
Tov, O., Alaluf, Y., Nitzan, Y., Patashnik, O., and Cohen-Or,
D. (2021). Designing an encoder for stylegan image
manipulation. CoRR, abs/2102.02766.
Voynov, A. and Babenko, A. (2020). Unsupervised discov-
ery of interpretable directions in the GAN latent space.
In III, H. D. and Singh, A., editors, Proceedings of the
37th International Conference on Machine Learning,
volume 119 of Proceedings of Machine Learning Re-
search, pages 9786–9796. PMLR.
Keep It Simple: Local Search-based Latent Space Editing
281

Wang, X., Yu, K., Wu, S., Gu, J., Liu, Y., Dong, C., Loy,
C. C., Qiao, Y., and Tang, X. (2018). ESRGAN:
enhanced super-resolution generative adversarial net-
works. CoRR, abs/1809.00219.
Wu, P.-W., Lin, Y.-J., Chang, C.-H., Chang, E. Y., and Liao,
S.-W. (2019). Relgan: Multi-domain image-to-image
translation via relative attributes. 2019 IEEE/CVF In-
ternational Conference on Computer Vision (ICCV),
pages 5913–5921.
Wu, Z., Lischinski, D., and Shechtman, E. (2021).
Stylespace analysis: Disentangled controls for style-
gan image generation. In IEEE Conference on Com-
puter Vision and Pattern Recognition, CVPR 2021,
virtual, June 19-25, 2021, pages 12863–12872. Com-
puter Vision Foundation / IEEE.
Yu, J., Lin, Z., Yang, J., Shen, X., Lu, X., and Huang, T. S.
(2018). Generative image inpainting with contextual
attention. CoRR, abs/1801.07892.
Zhang, Y., Wu, Z., Wu, Z., and Meng, D. (2022).
Resilient observer-based event-triggered control for
cyber-physical systems under asynchronous denial-
of-service attacks. Sci. China Inf. Sci., 65(4).
Zhu, J., Park, T., Isola, P., and Efros, A. A. (2017a).
Unpaired image-to-image translation using cycle-
consistent adversarial networks. In IEEE Interna-
tional Conference on Computer Vision, ICCV 2017,
Venice, Italy, October 22-29, 2017, pages 2242–2251.
IEEE Computer Society.
Zhu, J.-Y., Park, T., Isola, P., and Efros, A. A. (2017b).
Unpaired image-to-image translation using cycle-
consistent adversarial networks. In 2017 IEEE In-
ternational Conference on Computer Vision (ICCV),
pages 2242–2251.
Zhu, J.-Y., Zhang, R., Pathak, D., Darrell, T., Efros, A. A.,
Wang, O., and Shechtman, E. (2017c). Toward mul-
timodal image-to-image translation. In Guyon, I.,
Luxburg, U. V., Bengio, S., Wallach, H., Fergus,
R., Vishwanathan, S., and Garnett, R., editors, Ad-
vances in Neural Information Processing Systems,
volume 30. Curran Associates, Inc.
Zhuang, P., Koyejo, O. O., and Schwing, A. (2021). Enjoy
your editing: Controllable GANs for image editing via
latent space navigation. In International Conference
on Learning Representations.
APPENDIX
Figure 2: Comparison of Smiling: Shen et al. (first row),
Zhuang et al. (second row) and our approach (third row) for
image seed=0. Left column: less smiling, middle column:
original image, right column: more smiling.
Figure 3: Comparison of Smiling: Shen et al. (first row),
Zhuang et al. (second row) and our approach (third row) for
image seed=1. Left column: less smiling, middle column:
original image, right column: more smiling.
NCTA 2022 - 14th International Conference on Neural Computation Theory and Applications
282

Figure 4: Comparison of Smiling: Shen et al. (first row),
Zhuang et al. (second row) and our approach (third row) for
image seed=2. Left column: less smiling, middle column:
original image, right column: more smiling.
Figure 5: Comparison of hair color: Shen et al. (first row),
Zhuang et al. (second row) and our approach (third row) for
image seed=0. Left column: darker hair, middle column:
original image, right column: lighter hair.
Figure 6: Comparison of hair color: Shen et al. (first row),
Zhuang et al. (second row) and our approach (third row) for
image seed=1. Left column: darker hair, middle column:
original image, right column: lighter hair.
Figure 7: Comparison of hair color: Shen et al. (first row),
Zhuang et al. (second row) and our approach (third row) for
image seed=2. Left column: darker hair, middle column:
original image, right column: lighter hair.
Keep It Simple: Local Search-based Latent Space Editing
283
